Interaction energies between β-lactam antibiotics and E. coli penicillin-binding protein 5 by reversible thermal denaturation

Abstract

Penicillin-binding proteins (PBPs) catalyze the final stages of bacterial cell wall biosynthesis. PBPs form stable covalent complexes with β-lactam antibiotics, leading to PBP inactivation and ultimately cell death. To understand more clearly how PBPs recognize β-lactam antibiotics, it is important to know their energies of interaction. Because β-lactam antibiotics bind covalently to PBPs, these energies are difficult to measure through binding equilibria. However, the noncovalent interaction energies between β-lactam antibiotics and a PBP can be determined through reversible denaturation of enzyme–antibiotic complexes. Escherichia coli PBP 5, a d-alanine carboxypeptidase, was reversibly denatured by temperature in an apparently two-state manner with a temperature of melting (T_m) of 48.5°C and a van't Hoff enthalpy of unfolding (ΔH_VH) of 193 kcal/mole. The binding of the β-lactam antibiotics cefoxitin, cloxacillin, moxalactam, and imipenem all stabilized the enzyme significantly, with ΔT_m values as high as +4.6°C (a noncovalent interaction energy of +2.7 kcal/mole). Interestingly, the noncovalent interaction energies of these ligands did not correlate with their second-order acylation rate constants (k₂/K′). These rate constants indicate the potency of a covalent inhibitor, but they appear to have little to do with interactions within covalent complexes, which is the state of the enzyme often used for structure-based inhibitor design.

Penicillin-binding proteins (PBPs) are involved in the biosynthesis of bacterial cell wall peptidoglycan. All bacteria analyzed to date have multiple PBPs, which function to crosslink the cell wall peptides (transpeptidation) and to remove the C terminal d-alanine residue from cell wall peptides (carboxypeptidation). PBPs are the targets of β-lactam antibiotics, which react with these enzymes to form stable covalent complexes, leading to inactivation of the PBP and ultimately to cell death (Tipper and Strominger 1965; Wise and Park 1965; Ghuysen and Dive 1994). A broad range of β-lactam antibiotics, including penicillins, cephalosporins, monobactams, and carbapenems, are used clinically, and seemingly subtle structural differences have dramatic effects on their biological activity (Neuhaus and Georgopapadakou 1992).

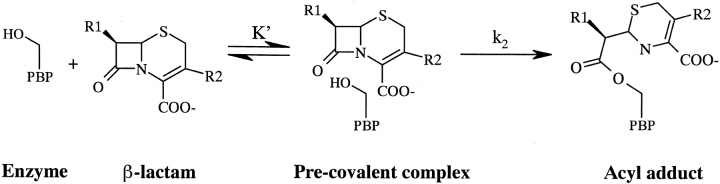
Despite much interest in understanding the molecular interactions of β-lactams with PBPs, their interaction energies have been difficult to determine. The noncovalent first encounter complex between the antibiotic and enzyme proceeds quickly to an acyl-enzyme adduct by attack of the catalytic serine hydroxyl on the carbonyl carbon of the β-lactam ring (Fig. 1 ▶). Because of this covalent bond formation and the resultant β-lactam ring opening, β-lactam antibiotics essentially bind irreversibly to PBPs, and there is no equilibrium between the free and covalently bound ligand. Hence, a thermodynamic interaction energy (ΔG_interaction) cannot be determined for the covalent complex.

Fig. 1.

A simplified mechanism for the binding of β-lactam antibiotics to PBPs.

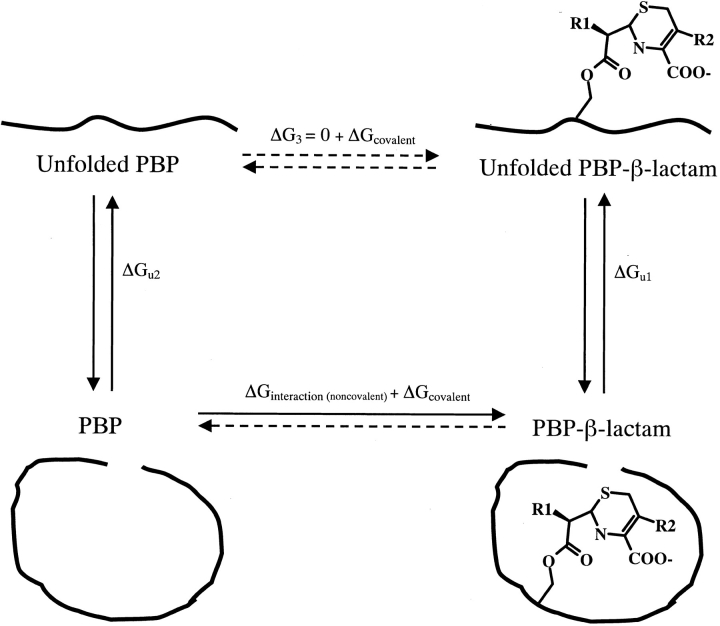
Previously, differential protein stability has been used to measure the thermodynamic complementarity of both β-lactam and non-β-lactam ligands for β-lactamase enzymes (Rahil and Pratt 1994; Beadle et al. 1999), which are structurally and functionally related to PBPs (Kelly et al. 1986; Massova and Mobashery 1998; Fonze et al. 1999; Davies et al. 2001). Rather than measuring the equilibrium constant between bound and free ligand, this technique measures the equilibrium constant between folded and unfolded protein (Schellman 1976), in the presence and absence of a ligand. The free enzyme and the enzyme in complex with a covalent ligand are reversibly denatured by temperature; each denaturation is described by a temperature of melting (T_m), a van't Hoff enthalpy of denaturation (ΔH_VH), and an entropy of denaturation (ΔS_u). Because thermal denaturation does not break covalent bonds, the difference between the unfolding energy of the free enzyme and that of the covalent complex reflects the noncovalent interaction energy between the ligand and the enzyme in the covalent complex (ΔG_interaction). Using a thermodynamic cycle (Fig. 2 ▶), this process can be described by the following equation: ΔG_interaction + ΔG_covalent + ΔG_u1 − ΔG₃ − ΔG_covalent − ΔG_u2 = 0. If we assume that the noncovalent interactions between the ligand and the denatured state are negligible (i.e., ΔG₃ = 0) and that the covalent energies between the enzyme and the ligand (ΔG_covalent) are the same in the folded and unfolded states, then: ΔG_interaction = ΔG_u2 − ΔG_u1 = ΔΔG_u. Thus, the noncovalent interaction energy is equal to the net differential stability between the apo- and ligand-bound enzyme. This method closely resembles that used to determine stabilization energies of mutant enzymes, and it is reliable provided that the denaturation of both the apo- and bound enzyme is reversible, can be modeled as two-state, and the noncovalent energy of the denatured state is not significantly affected by the covalently bound ligand.

Fig. 2.

A thermodynamic cycle for determining the noncovalent interaction energy (ΔG_interaction) between PBP 5 and a β-lactam. This process can be described by the following equation: ΔG_interaction + ΔG_covalent + ΔG_u1 − ΔG₃ − ΔG_covalent − ΔG_u2 = 0. If we assume that the noncovalent interactions between the ligand and the denatured state are negligible (i.e., ΔG₃ = 0), and that the covalent energies between the enzyme and the ligand (ΔG_covalent) are the same in the folded and unfolded states, then: ΔG_interaction = ΔG_u2 − ΔG_u1 = ΔΔG_u.

In this study, we investigated the complementarity of β-lactam antibiotics for E. coli PBP 5, a d-alanine carboxypeptidase, by reversible thermal denaturation of free PBP 5 and PBP 5 covalently bound to several β-lactam antibiotics. These studies provide the first quantitative measurement of the noncovalent interaction energies of a PBP with covalently bound β-lactam antibiotics. Intriguingly, these noncovalent interaction energies do not correlate with the second-order rate constants for formation of the acyl–enzyme complex (k₂/K′), which are considered the best indicators of the inhibitory potency of β-lactam antibiotics with PBPs (Frere et al. 1975; Frere et al. 1992; Jamin et al. 1993; Graves-Woodward and Pratt 1998; Lu et al. 1999).

Results

Denaturation of PBP 5

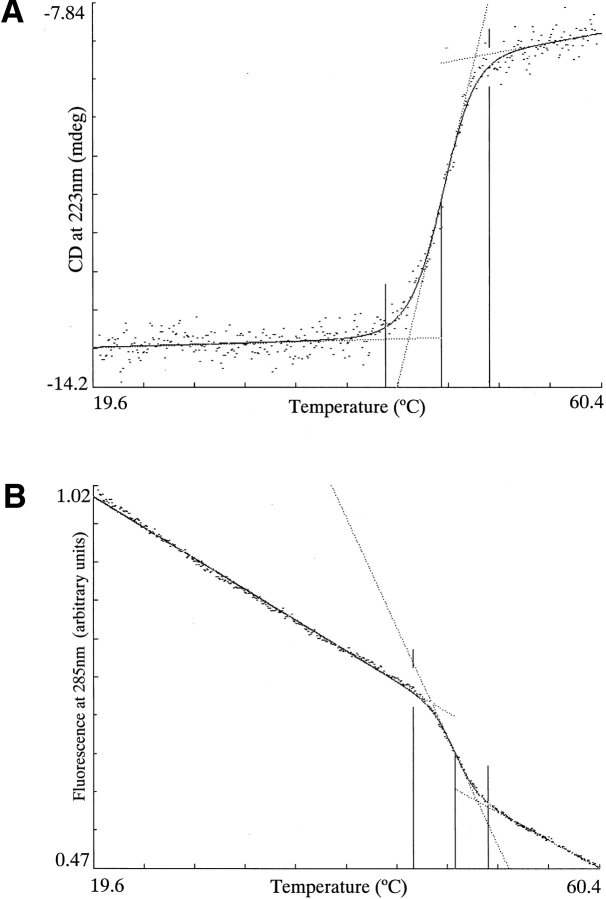
PBP 5 was reversibly denatured by temperature (Fig. 3 ▶). When monitored by far-UV CD, a measure of secondary structure, PBP 5, has an average T_m of 47.9°C and a ΔH_VH of 156 kcal/mole. Following denaturation, the sample was immediately cooled, and 100% of the folded CD signal returned. Moreover, cooling the denatured sample at a rate of 2°C/min, the same rate at which it had been denatured produced a renaturation curve that overlaid almost exactly the denaturation curve (data not shown). These data suggest that renaturation follows the same pathway as denaturation and that the folded and unfolded states are in thermodynamic equilibrium throughout the transition, a requirement for thermodynamic analysis.

Fig. 3.

Reversible, thermal denaturation of PBP 5 as monitored by two independent spectral techniques: (A) Far-UV CD. PBP 5 has an average T_m of 47.9°C and a ΔH_VH of 156 kcal/mole. (B) Fluorescence. PBP 5 has an average T_m of 48.5°C and a ΔH_VH of 193 kcal/mole.

To investigate whether PBP 5 exhibited two-state behavior, thermal denaturations and renaturations of PBP 5 were also monitored by fluorescence emission following excitation at 285 nm, a measure of tertiary structure. By fluorescence, PBP 5 has an average T_m of 48.5°C and a ΔH_VH of 193 kcal/mole (Fig. 3 ▶). The T_m and ΔH_VH values of PBP 5 when monitored by fluorescence were essentially the same as those when monitored by far-UV CD. These data suggest that the values are independent of spectral technique, consistent with PBP 5 melting in a two-state fashion.

Denaturation of PBP– β-lactam adducts

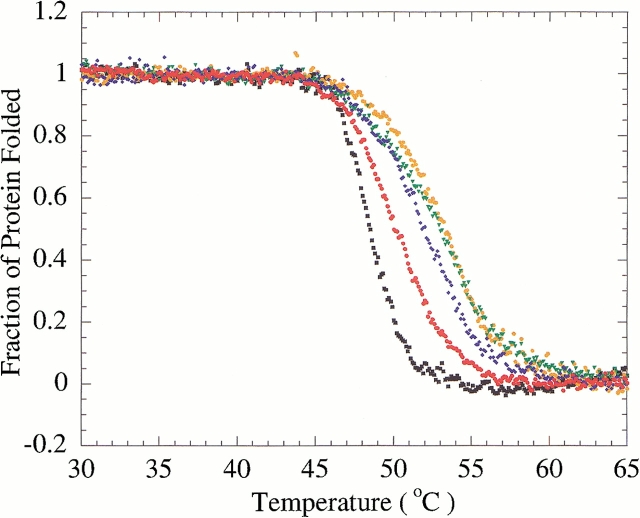
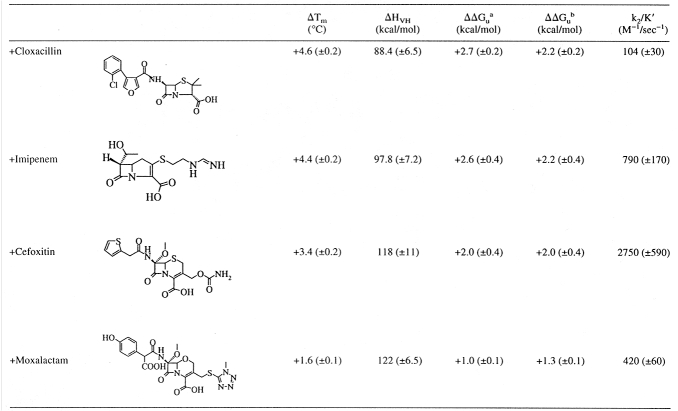
To assess the complementarity of β-lactams for PBP 5, covalent complexes were formed by incubation of PBP 5 with each of cefoxitin, cloxacillin, imipenem, or moxalactam. These complexes were then reversibly denatured by temperature, and the T_m and ΔH_VH values were determined. Binding of each of these antibiotics increased the stability of PBP 5 (Fig. 4 ▶; Table 1); cloxacillin and imipenem stabilized PBP 5 to a greater extent than either cefoxitin or moxalactam. We note that the van't Hoff enthalpies of denaturation are often reduced in the ligand complexes. We suspect that this reflects the difficulty in fitting to the fluorescent denaturation curves, which are innately temperature dependent. However, a direct comparison of the free energies was also made by comparing the equilibria of unfolding at a reference temperature using the Gibbs-Helmholtz equation. By picking a temperature within the range of melting temperatures, namely 51.3°C, extrapolation errors are minimized. For these analyses, we used the van't Hoff enthalpies of each curve to determine equilibria. The two methods gave similar values for ΔΔG_u (Table 1). The free energies of stabilization reported are valid near the temperature of melting, but some caution is warranted when extrapolating these values to room temperature.

Fig. 4.

Reversible, two-state thermal denaturation of PBP 5 alone and with various β-lactam antibiotics. Black squares, PBP 5 alone; red circles, PBP 5–moxalactam complex; blue diamonds, PBP 5–cefoxitin complex; green triangles, PBP 5–cloxacillin complex; orange circles, PBP 5–imipenem complex.

Table 1.

The interactions of β-lactams with PBP 5 as judged by ΔT_m, ΔΔG_u, and k₂/K′ values

^a Determined by the method of Schellman (Becktel and Schellman 1987): ΔΔG_u = ΔT_m • ΔS_apo-enzyme.

^b Determined by direct comparison of the equilibria within the unfolding region, namely at T = 51.3°C, using the Gibbs-Helmholtz equation.

Determination of second-order rate constants for formation of the acyl–enzyme complex

The second-order rate constant (k₂/K′) is considered the best indicator of inhibitory activity of a β-lactam antibiotic against a PBP (Frere et al. 1992). The k₂/K′ constant of [¹²⁵I]penicillin V ([¹²⁵I]IPV) for PBP 5 was determined from a time course of the formation of the acyl–enzyme complex as described in Materials and methods. The k₂/K′ values of cefoxitin, cloxacillin, imipenem, and moxalactam with PBP 5 were then determined by competition of [¹²⁵I]IPV binding. No clear relationship between the ΔΔG_u and k₂/K′ values was evident (Table 1).

Discussion

β-Lactam binding to PBP 5

The β-lactam antibiotics cloxacillin, cefoxitin, moxalactam, and imipenem all stabilized the enzyme when covalently complexed with PBP 5. Surprisingly, their noncovalent interaction energies do not correlate with the second-order rate constants (k₂/K′) for these compounds. Based on k₂/K′ values, the order of potency of the β-lactams for inhibiting PBP 5 is: cefoxitin > imipenem > moxalactam > cloxacillin. Based on ΔΔG_u values, the order of complementarity of the β-lactams for PBP 5 is: cloxacillin ≥ imipenem > cefoxitin > moxalactam. Strikingly, cloxacillin, the β-lactam that best complements PBP 5 in the acyl state, is the least potent inhibitor of PBP 5. Thus, β-lactam antibiotics with greater complementarity to PBP 5 in the acyl–enzyme complex, as shown by more favorable interaction energies, are not better inhibitors of PBP 5.

The discrepancy between the interaction energies and second-order rate constants becomes less troubling when one considers that these values are determined for different states of the enzyme and ligand. The second-order acylation rate constant (k₂/K′) measures the fit of the ligand to the active site in the precovalent complex multiplied by the rate of the chemical step. The noncovalent interaction energies measure the complementarity of a β-lactam to a PBP in the acylated, postcovalent complex. Because acylated, ring-opened β-lactam antibiotics bound to PBPs differ significantly from their precovalent, closed-ring forms (Kelly et al. 1989), and because there is no kinetic component to the noncovalent interaction energies measured by stability, the lack of correlation between the acylation rate constants and noncovalent interaction energies can be understood. An effective β-lactam must complement the active site of its target sufficiently to allow rapid acylation, be chemically predisposed to the acylation reaction itself, and then deacylate very slowly. The rate of deacylation can depend on many factors, including steric blockage of hydrolytic attack (Patera et al. 2000). Once acylated, complementarity within the acyl–enzyme complex may play only a secondary role in determining how effective an inhibitor is. In this light, efforts to improve inhibitors by improving complementarity within covalent complexes may be misguided.

Conclusions

The ability to determine the energetic complementarity of β-lactams for PBP 5 provides a method for understanding their interactions in the covalent complex, which is the state often used as a basis for structure-based drug design. The only requirements for such thermodynamic analyses are the reversible denaturation of the enzyme and enzyme–ligand complex and the ability to isolate a stable enzyme–ligand complex. This method may be used to study the binding of a broad variety of covalent ligands and their enzyme targets. However, it is clear that improving the noncovalent complementarity within a covalently bound complex will not necessarily improve the potency of an inhibitor.

Materials and methods

Enzyme preparation

A soluble form of PBP 5 constructed by deletion of the last 17 amino acids from the C terminus was expressed in the cytoplasm of E. coli. PBP 5 was precipitated from the soluble fraction of cell lysates with 50% ammonium sulfate, and the protein was redissolved in 50 mM Tris, 150 mM NaCl, pH 7.5 (Buffer A), and purified by covalent ampicillin affinity chromatography as previously described (Nicholas and Strominger 1988). The enzyme was dialyzed against Buffer A, concentrated to 6–8 mg/mL, and stored at −80°C.

Sample preparation

PBP 5 was diluted to a concentration of approximately 6 μg/mL in 3.5 mL of 50 mM potassium phosphate, 200 mM potassium chloride, 38% (v/v) ethylene glycol, pH 6.8. The buffer was prepared using ACS reagent grade potassium chloride from Sigma Chemical, potassium phosphate from Aldrich Chemical, spectroscopic grade ethylene glycol from Sigma, and doubly deionized water.

To form antibiotic–PBP 5 complexes, PBP 5 was incubated with a 50- to 100-fold molar excess of cloxacillin, moxalactam, cefoxitin (all from Sigma Chemical), or imipenem for periods of 5 min to 45 min. We note that some β-lactam antibiotics took a longer incubation time to reach a constant, maximal T_m; we report the largest reproducible ΔT_m observed. An aliquot of the incubation mixture was then added to 3.5 mL of buffer solution, and the denaturation experiments were performed (see below). ΔΔG_u values were determined by the method of Schellman for all complexes of enzyme with inhibitor (Becktel and Schellman 1987):

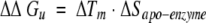1

where

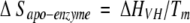2

Because of the variations observed in the ΔH_VH values of the thermal denaturations, we also compared the ΔΔG_u values within the transition region directly using the Gibbs-Helmholtz equation:

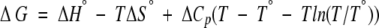3

For each denaturation, the ΔG value was calculated using its thermodynamic parameters (T_m, ΔH_VH, ΔS) as the reference values (T°, ΔH°, ΔS°) with T set to a temperature within the range of the observed T_m values, specifically at 51.3°C. ΔΔG_u values were calculated as the difference between the ΔG value of each complex and the enzyme alone. Positive ΔΔG_u values indicate increases in the T_m, hence stabilization; negative ΔΔG_u values indicate decreases in the T_m, hence destabilization.

Thermal denaturation as monitored by CD and fluorescence

CD and fluorescence experiments were performed in a Jasco J-715 spectropolarimeter with a fluorescence emission attachment, which allows both spectra to be measured simultaneously. Temperature was controlled with a Jasco PTC-348WI peltier-effect temperature controller, using an in-cell probe to measure temperature. All solutions were stirred with a magnetic stirbar. Quartz cells with a 1-cm path length from Hellma (Jamaica, NY) were used for all experiments. The program EXAM (Kirchhoff 1993) was used to calculate all T_m and ΔH_VH values. For these analyses, the change in heat capacity upon denaturation, (ΔC_p) was set to 6.0 kcal/mol•K, consistent with theoretical considerations (Myers et al. 1995); neither the T_m nor the ΔH_VH values varied appreciably with ΔC_p values.

Samples were monitored for helical content by CD in the far-UV region at 223 nm, and for the tertiary structure by fluorescence emission following excitation at 285 nm. Thermal melting was performed at ramp rates of 2°C/min. Reversibility was judged using two criteria: the return of the original CD signal upon quick cooling and retracing of the path of the denaturation curve on slow cooling (at a ramp rate equal to that of unfolding, 2°C/min).

Acylation rate constant determination

Second-order rate constants for acylation (k₂/K′) of PBP 5 by β-lactam antibiotics were determined from a time course of formation of the acyl–enzyme complex essentially as described (Frere et al. 1992), except k₂/K′ for [¹²⁵I]IPV was determined by a time course for acyl–enzyme formation at a single concentration of [¹²⁵I]IPV at 30°C (van der Linden et al. 1994). Briefly, PBP 5 (4.0 μg; 100 pmole) was diluted into 80 μL of 40 μM [¹²⁵I]IPV in 50 mM Tris•HCl, 500 mM NaCl, 10% glycerol. At 15-sec intervals up to 1 min (and 2-min intervals after that), 10-μL aliquots were removed and added to 5 μL 3× SDS-PAGE sample buffer. The samples were submitted to electrophoresis on a 10% polyacrylamide gel, and the levels of [¹²⁵I]IPV–PBP 5 complex were quantitated with ImageQuant software following phosphoimager analysis on a Storm 840 Phosphoimager (Molecular Dynamics, Sunnyvale, CA). The k₂/K′; value was calculated by dividing the apparent first-order rate constant derived from the time course by the concentration of [¹²⁵I]IPV.

The second-order rate constants (k₂/K′) for cefoxitin, imipenem, cloxacillin, and moxalactam were determined by the competition method. Variable concentrations of the unlabeled antibiotic were mixed with a fixed concentration of [¹²⁵I]IPV (40 μM), followed by addition of PBP 5 (0.25 μg; 6.3 pmole), and the mixture was incubated at 30°C for 10 min. The level of radioactivity bound to the proteins was quantitated as described above. k₂/K′ constants were calculated using the equation:

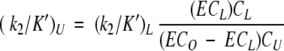4

where EC_o and EC_L represent the ([¹²⁵I]IPV–PBP 5) formed in the absence and presence of the unlabeled antibiotic, respectively, and C_U and C_L represent the concentrations of the unlabeled and labeled antibiotic, respectively (Frere et al. 1992).

Abbreviations

• [¹²⁵I]IPV, [¹²⁵I]penicillin V

• ΔC_p, change in heat capacity at constant pressure

• ΔG_interaction, noncovalent interaction energy

• ΔG_u, Gibbs free energy of unfolding

• ΔH_VH, van't Hoff enthalpy of unfolding

• ΔS_u, entropy of unfolding

• k₂/K′, second-order rate constant

• K_eq, equilibrium constant

• PBP, penicillin-binding protein

• T_m, temperature of melting