Peptide-plane flipping in proteins

Abstract

A peptide-plane flip is a large-scale rotation of the peptide plane that takes the φ,ψ angles at residues i and i + 1 to different structural regions in the Ramachandran plot with a comparatively small effect on the relative orientation of their side chains. This phenomenon, which is expected to play an important role during the early stages of protein folding, has been investigated using 76 proteins for which two high-resolution X-ray conformations are available. Peptide-plane flips are identified by looking for those cases where changes in |ψ_i| + |φ_{i + 1}| are large (>200°), but changes in |ψ_i + φ_{i + 1}| are comparatively small (<50°). Of a total of 23 cases, the most common peptide-plane flip was identified to be the type I to type II β-turn interconversion. Although individually rarer, there are many other types of flips that are collectively more common. Given the four main accessible regions α_R, α_L, β and ɛ, identified from the φ,ψ distribution corresponding to non-hydrogen-bonded peptide planes, 32 main types of peptide-plane flip are identified. Only 8 of these are "passive," in that they require only relatively minor adjustments in the orientation of adjacent peptide planes. Of these, only the type I to type II β-turn interconversion, denoted, β(i) + α_L(i + 1) ― α_R(i) + α_R(i + 1), and the rarer α_R(i) + α_L(i + 1) ― β(i) + α_R(i + 1), do not involve the ɛ region. "Active" peptide-plane flips affect the orientation of adjacent peptide planes. The flip, α_L(i) + α_L(i + 1) ― β(i) + β(i + 1), of which one example was found, shows how concerted peptide-plane flips can convert the α_L structure to the β structure without affecting the relative orientations of the side chains.

Some time ago Diamond (1965) pointed out that the path traced out by C^α atoms depends largely on ψ_i + φ_{i + 1}, whereas the orientations of the intervening peptide planes depend mainly on ψ_i − φ_{i + 1}. This can be appreciated by noting that for peptides in the trans conformation, the C^α—C bond vector, the ψ-dihedral axis of residue i, is almost parallel to the N—C^α bond vector of residue i + 1, the φ-dihedral axis of residue i + 1. This implies that, all other angles remaining unchanged, δψ_i + δφ_{i + 1} gives the approximate rotation of all groups on the C-terminal side of the peptide plane (the "tail"), including the side chain of residue i + 1, relative to all groups on the N-terminal side of the plane (the "head"), including the side chain of residue i. If the side chains of adjacent residues are unable to undergo a relative rotation then the intervening peptide plane may still undergo a large rotation, provided δψ_i + δφ_{i + 1} is small. In proteins, large isolated backbone dihedral angle rotations are expected to occur only at the termini. Elsewhere, compensating changes will occur. Peptide-plane rotations represent the most local form of compensation in dihedral angle changes whereby changes in ψ_i are accompanied by compensating changes in φ_{i + 1}. Although the two dihedral axes are almost parallel, they are not colinear and large counter-rotations do result in small relative translations of the side chains.

In this paper, a peptide-plane flip is defined to be a large-scale rotation of the peptide plane that takes the φ,ψ angles at residue i and i + 1 to different structural (stable) regions in the Ramachandran plot with a relatively small effect on the relative orientation of their side chains and consequently the head and tail groups. As we shall see below, peptide-plane flips so defined do feature in protein native state dynamics, but would be expected to play a much more important role during the early stages of protein folding, when the atoms of the peptide plane are not hydrogen-bonded to other parts of the polypeptide chain. In this state, a single flip can take two adjacent residues from one structural region to another. Although there is no direct evidence of peptide-plane flips occurring during the early stages of protein folding, if they can be found to occur in the loop regions of proteins in their native states, then they are likely to occur in the unfolded polypeptide. The idea that the study of loop regions can help us to understand the early stages of protein folding has support from Raman Optical Activity experiments (Wilson et al. 1996; Barron et al. 1997), and underpins the work on the intrinsic φ,ψ propensities of amino acids (Serrano 1995; Swindells et al. 1995).

Evidence of the occurrence of peptide-plane rotations in native state dynamics was found in the earliest simulation studies on proteins in vacuum (McCammon et al. 1977; Levitt 1983). More recently Kitao et al. (1998) showed in a 1-nsec simulation of human lysozyme in water, that backbone rotamer transitions occurred in pairs at ψ_i and φ_{i + 1} for values of i that located them in the loop regions of the protein. This study also revealed that rotamer transitions of all kinds occur within 100 fsec, showing that peptide-plane transitions are exceedingly fast.

Gunasekaran et al. (1998) have made a study of the interconversion of β-turns by examining a set of 250 nonhomologous protein crystal structures in comparison to sets of homologous structures. Their study showed how a single peptide-plane flip can lead to the interconversion of type I and type II β-turns, and type I` and type II` β-turns. Glycine residues were found to occur overwhelmingly at the k + 2 position (k = i − 1 is the index number of the first residue of the turn).

The dipole moment of a peptide plane is practically perpendicular to its axis of rotation, which together with a high rotational diffusion constant indicates that it will be very sensitive to local electric fields. However, the degree to which it is able to align to the local electric field will depend on the energy profile of its rotational degree of freedom. The energy profile of peptide-plane rotation, calculated by Gunasekaran et al. (1998) for the type I/type II β-turn interconversion using semiempirical molecular orbital methods, showed that for a peptide with a glycine in the i + 1 position there are two stable states that are separated by a low energy barrier in one direction and a high energy barrier in the other. Along the low energy path the angular separation between these stable states was calculated to be about 160°, indicating the transition between stable states is a process, whereby the peptide plane flips practically upside down. In reality, in the unfolded protein, peptide-plane atoms will form hydrogen bonds to water molecules and therefore not only will the energetics be influenced by the presence of water, but the kinetics of peptide-plane flipping will be intimately connected to the kinetics of water. Although we have no direct information on the rate constants for peptide-plane flips, the Raman Optical Activity work of Wilson et al. (1996) on proteins in non-native states indicates that individual residues flicker between α, β, and poly(L-proline) II regions at a rate of ∼10¹² sec⁻¹.

This paper presents the results of a study of peptide-plane flips using native state protein structures.

Results and Discussion

Relationship between δψ_i and δφ_{i + 1} and the change in angle between the side chains of residues i and i + 1

To measure the relationship between the changes in ψ_i and φ_{i + 1} and the relative rotation of the side chains of two adjacent residues, an alanine dipeptide with minimum-energy bond lengths and angles was constructed using MOLDEN (Schaftenaar and Noordik 2000). The values for these quantities were taken from the GROMOS force field set (van Gunsteren et al. 1996). The dihedral angles ψ₁ and φ₂ were varied from −180° to 180° in 20° intervals again using MOLDEN. The conformation at each interval was compared to the conformation at ψ₁ = 0° and φ₂ = 0°, and the difference in the angle between the side chains δθ_1,2 was calculated as detailed in the Materials and Methods section. As the C^α—C bond vector, the ψ-dihedral axis of residue i, is not perfectly parallel to the N—C^α bond vector, the φ-dihedral axis, it is to be expected that δθ_1,2 only approximates δψ₁ + δφ₂. This calculation shows that

(1)

is valid over a wide range of angles. The root-mean-square difference between the left and right sides of equation 1 is just 2.8°. The maximum error occurs when δψ₁ = 180° and δφ₂ = −180°or vice versa, where the error is 14.5°. This calculation shows that provided the dihedral angle changes are large in comparison to bond-angle variations, then the angle of rotation of the side chain of residue i + 1 relative to residue i, δθ_i,i+1, can be approximated as

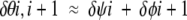(2)

Equation 2 will be used to define peptide-plane flipping. Obviously if |δψ_i| and |δφ_{i + 1}| are large but |δψ_i + δφ_{i + 1}| is small, then equation 2 tells us that the relative rotation of the side chains at residues i and i + 1 is small but the rotation of the intervening peptide plane is large. This simple idea is used to search for peptide-plane flips among the pairs of X-ray conformers as detailed below.

Analysis of X-ray conformer pairs for peptide-plane flips

The calculations of Gunasekaran et al. (1998) have shown that peptide-plane flipping will involve dihedral angle changes of ∼160°. A set of 76 X-ray conformer pairs were selected from the protein database as detailed in the Materials and Methods section. The main-chain dihedral angle changes at all residues in all 76 pairs were calculated. Those satisfying the following inequality:

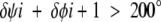(3)

are plotted in Figure 1 ▶ against a background of φ_{i + 1} and ψ_i values taken from the first conformation of each of the 76 pairs. Only 43 out of a possible 16,837 satisfied inequality 3. The lines in Figure 1 ▶ indicate the 43 transitions that satisfy inequality 3.

Fig. 1.

A φ_{i + 1},ψ_i plot showing transitions that satisfy inequality 3, indicated by the broken lines and continuous lines, and those that satisfy inequalities 3 and 4, indicated by continuous lines only. Those indicated by triangles joined by continuous lines are group 1 transitions; those by squares and continuous lines, group 2; all others are indicated by small circles joined by broken lines. Group 1 transitions have ψ_i in the extended region when φ_{i + 1} is positive, whereas group 2 transitions have ψ_i in the α-helix regions when φ_{i + 1} is positive. The background gray dots are the φ_{i + 1},ψ_i values taken from the first of each of the 76 pairs of conformations. The path taken by the transitions is almost certainly not the one indicated by the lines that cross the high energy region around φ = 0°, but follows the direction indicated by the arrow through φ = −180°,180°, applying the usual periodicity of torsion space.

To analyze peptide-plane flipping only those of the 43 transitions satisfying

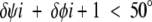(4)

were considered. As described in the previous section, the simultaneous agreement of inequalities 3 and 4 is consistent with the idea of a peptide-plane flipping between two largely unaffected side chains. In all, 23 cases satisfy both inequalities 3 and 4 simultaneously, although most of the 43 examples that satisfy inequality 3 show some degree of compensation (see Fig. 1 ▶). The 20 cases that do not satisfy inequality 4 are those for which the rotation of the peptide plane is accompanied by some relative rotation of the side chains. These will not be studied further in this paper. For ease of analysis these 23 flips are grouped in two according to their starting and ending points. These two groups can be readily identified in Figure 1 ▶. Those represented by triangles in Figure 1 ▶ belong to group 1 and those by squares, group 2. There are 12 flips in group 1 (from 9 different proteins) and 9 in group 2 (from 8 different proteins); the remaining 2 that satisfy inequalities 3 and 4 could not be assigned to either. Group 1 flips have ψ_i values that are in the extended region when φ_{i + 1} is positive, whereas group 2 transitions have ψ_i values that are in either α_R- or α_L-helix regions when φ_{i + 1} is positive. For group 1 ≤|δψ_i|> = 151.8°, ≤|δφ_{i + 1}|> = 158.4°, and ≤|δψ_i + δφ_{i + 1}|> = 15.2°; for group 2 ≤|δψ_i|> = 147.8°, ≤|δφ_{i + 1}|> = 139.2°, and ≤|δψ_i + δφ_{i + 1}|> = 21.5°. It is immediately clear that peptide-plane flipping associates transitions between regions with positive and negative φ values for residue i + 1 with transitions from the extended to α-helical regions or vice versa for residue i.

Group 1 flips

Flips belonging to group 1 are characterized by having ψ_i values that are in β or ɛ regions when φ_{i + 1} is positive. Figure 2a ▶ shows the group 1 transitions in a Ramachandran plot with the φ_i,ψ_i transition illustrated by continuous lines and the φ_{i + 1},ψ_{i + 1} transition illustrated by broken lines. Based on the earlier work by Efimov (1986) and Thornton et al. (1988), Wilmot and Thornton (1990) have assigned symbols to regions of the Ramachandran plot according to location. In Figure 2a ▶ the main transition for residue i is between β, representing, the poly(L-proline) II region, and the α_R-helix region. Here the two α_R-helix regions centered on φ = −60° and ψ = −30°, and, φ = −90° and ψ = 0° will be denoted as α_R¹-helix and α_R²-helix, respectively. For residue i + 1 the main transition is from the α_L-helix to the α_R²-helix region. The main transition can be written symbolically as: β(i) + α_L(i + 1) ― α_R¹(i) + α_R²(i + 1), or more conveniently as β + α_L ― α_R¹ + α_R². These peptide-plane flips are the interconversion of type I and type II β-turns studied by Gunasekaran et al. (1998). There are two directions that the peptide-plane rotation can take. Using semiempirical molecular orbital calculations, Gunasekaran et al. (1998) have showed that the low energy path (with a barrier of about 3 kcal/mole) takes residue i + 1 through φ = −180°,180°, with residue i passing through ψ = 0°. The high energy path (with a barrier of about 20 kcal/mole), has residue i + 1 crossing the largely forbidden region of the Ramachandran plot at φ = 0°, and residue i passing through ψ = −180°,180°. The transition energy along the high energy route found by Gunasekaran et al. comes primarily from the steric interactions that occur around φ = 0°. The lines in Figures 1 ▶ and 2a ▶ do not indicate the actual paths taken in the low energy flip.

Fig. 2.

(a) Ramachandran plots for the group 1 flips and (b) group 2 flips. (a) Residue i is in the β or ɛ region, when residue i + 1 has positive φ values. (b) Residue i is in the α regions when residue i + 1 has positive φ values. Symbols joined by continuous lines show changes in φ_i,ψ_i for each peptide-plane flip. Equivalent symbols joined by broken lines show changes in φ_{i + 1},ψ_{i + 1} for the same flip. The lines joining the symbols do not necessarily indicate the paths taken. The vertical and horizontal arrows indicate the general direction of the low energy paths taken at residues i and i + 1, respectively. The background gray dots are the φ_i,ψ_i values taken from the first structure of the 76 pairs.

Given that it is required that φ_{i + 1} take on positive values if peptide-plane flipping is to occur, it is perhaps to be expected that the residue at i + 1 is often glycine. In fact, 5 of the 12 group 1 flips have an Xxx-Gly m, where Xxx represents any amino acid residue at position i. If the residue at i + 1 were a glycine, then the proposed route through the φ = −180°,180° boundary would be a lower energy one than for any other amino acid residue at i + 1. Consequently it is expected that the rate constant is higher for the flipping of the peptide plane with a glycine in the i + 1 position.

Group 2 flips

Group 2 flips are characterized by having ψ_i values that are in α_R or α_L regions when φ_{i + 1} is positive. Figure 2b ▶ shows the changes in φ_i,ψ_i and φ_{i + 1},ψ_{i + 1} for group 2 flips. The type I` and type II` β-turn interconversions belong to this group. It is immediately clear that there is a greater variety in this group, but in almost all cases a transition of residue i + 1 from the ɛ or the α_L region to the β or α_R-helix regions is accompanied by a transition of residue i from the α_R or α_L region to the β or ɛ region. If we take as an example the transition α_R¹ + α_L ― β + α_R² (one example found), then in the forward direction, as residue i moves from the α_R¹-helix to the β region, residue i + 1 moves from the α_L region to the α_R² region. Again there are two possible directions for the rotation, the high energy path where residue i + 1 crosses φ = 0°, and the low energy path where it crosses φ = −180°,180°. Compensation along the low energy path requires that residue i moves in a negative direction, passing though ψ = −180°,180° . If the φ = −180°,180° boundary is crossed, then as for group 1 transitions a glycine residue at i + 1 should also increase the rate constant over non-glycine residues at this position. In addition a glycine at i would also increase the rate constant for this route by lowering the energy barrier across the ψ = −180°,180° boundary region. The lines in Figure 1 ▶ and 2b ▶ do not indicate the path taken in the low energy flip.

Again glycine residues appear to be relatively common at i + 1 with 3 out of the 9 cases having the Xxx-Gly m.

Analysis of peptide planes without hydrogen bonds

The analysis presented above gives an idea of the different types of peptide-plane flips that can occur in native state proteins, but owing to their scarcity a different approach is required if we are to learn more about peptide-plane flipping in general. The analysis presented above has shown that in the main, peptide-plane flipping associates transitions in the ψ-dihedral angle of residue i between the β or ɛ region and the α_R or α_L region with transitions in the φ-dihedral angle of residue i + 1 between the ɛ or α_L region and the α_R or β region. To study further the types of peptide-plane flips that could occur if a peptide plane were free to rotate, the φ,ψ distribution for peptide planes free of any hydrogen bonds was studied using the first of each of the 76 protein pairs listed in Materials and Methods. This kind of analysis is analogous to previous ones that have selected regions of proteins in the random-coil conformation to find intrinsic φ,ψ propensities (Serrano 1995; Swindells et al. 1995). Here the program DSSP (Kabsch and Sander 1983) is used to determine whether the C—O of residue i and the N—H of residue i + 1 are hydrogen-bonded to other residues. The program DSSP uses a cutoff value of −0.5 kcal/mole for the hydrogen-bond energy. Figure 3 ▶ shows the φ,ψ distribution plotted for residue i, and separately for residue i + 1, where the C—O of residue i and the N—H of residue i + 1 have interaction energies greater than −0.2 kcal/mole. These two distributions should give us the values for the ψ-dihedral at residue i and the φ-dihedral at residue i + 1 when the peptide plane is free of hydrogen bonds and perhaps free to rotate. It reveals the two α_R regions, α_R¹-helix and α_R²-helix, which represent the type I β-turn. These two regions are not clearly seen using a cutoff of −0.5 kcal/mole. There are four regions for residue i: β, α_R¹, ɛ, α_L; and four regions for residue i: β, α_R², ɛ, α_L. The central points of these distributions are shown in Table 1. The central points are close to those identified for the β-turns, apart from the β region, which is centered on −66°,149°, rather than −60°,120° given in Wilmot and Thornton (1990) (66°,−149° for the ɛ region), and is closer in value to the accepted central point for the poly(L-proline) II value of −78°,149° (Arnott and Dover 1968). If we assume that peptide-plane flips can occur between all four regions, then there are 32 different types of peptide-plane flips that can associate transitions between regions with positive and negative φ values at residue i + 1, with transitions between α and β or ɛ regions (or vice versa) at residue i. This can be understood as follows: There are 4 possible transitions at residue i from either β or ɛ to α_R¹ or α_L. These 4 transitions can be accompanied by transitions at residue i + 1 from α_L or ɛ to α_R² or β, making 16 group 1 transitions. There are 4 possible transitions at residue i from either α_R¹ or α_L, to β or ɛ. These 4 transitions can be accompanied by transitions at residue i + 1 from α_L or ɛ to α_R² or β, making 16 transitions belonging to group 2. Therefore there are 32 different kinds of peptide flips altogether. Table 2 shows all 32 peptide-plane flips, the first 16 in the list belonging to group 1, the second 16 belonging to group 2. Only 8 of these 32 do not involve the ɛ region. This means that the remaining 24 will require a glycine residue at either i or i + 1, or both. The values for δφ_i, δψ_i, δφ_{i + 1}, and δψ_{i + 1} in Table 2 are calculated from the values given in Table 1. The flips in Table 2 are idealized, in the sense that they assume central-point values for the four regions. Five of the 23 flips found above do not belong to any of the 32. For some of the flips, |δψ_i + δφ_i+1| can be quite large (∼100°) if we use the central-point values and would not therefore satisfy inequalities 3 and 4. However, φ,ψ values are obviously not restricted to these central points, especially in the case of glycines, and |δψ_i + δφ_i+1| need not be large if the transition starts and ends at appropriate points. For this same reason, some flips not listed in Table 2 could also be classified as peptide-plane flips (see footnote to Table 2). The 32 types of flip listed in Table 2 have been selected on the basis that |δψ_i + δφ_i+1| is small when using central-point values in Table 1. They are expected therefore to be the main ones, not the only ones.

Fig. 3.

Ramachandran plot, where black circles give φ_i,ψ_i values and gray circles φ_{i + 1},ψ_{i + 1} values for nonbonding peptide planes taken from the first structure of the 76 pairs. The peptide plane formed from residues i and i + 1 is defined to be nonbonding when the carbonyl group of residue i and the amide group of residue i + 1 both have electrostatic interactions greater than −0.2 kcal/mole according to the DSSP definition of hydrogen-bonding energy (Kabsch and Sander 1983).

Table 1.

Central-point values of structural regions determined from Figure 3

Structural type	φ, ψ values at central points of distributions
αRL	−63°,−23°
αR2	−90°,0°
β	−66°,149°
ɛ	66°,−149°
αL	72°,21°

Table 2.

Changes in angles caused by the 32 different types of peptide-plane flips and number of cases found, calculated from angles in Table 1

Peptide-plane flip	δφi+1	δψi	δψi + δφi+1	δφi	δψi+1	No of casesa
β + αL ― αR1 + αR2	198	−172	26	3	−21	8
β + αL ― αL + αR2	198	−128	70	−222	−21	—
ɛ + αL ― αR1 + αR2	198	−234	−36	231	−21	—
ɛ + αL ― αL + αR2	198	−190	8	6	−21	—
β + αL ― αR1 + β	222	−172	50	3	128	1
β + αL ― αL + β	222	−128	94	−222	128	—
ɛ + αL ― αR1 + β	222	−234	−12	231	128	—
ɛ + αL ― αL + β	222	−190	32	6	128	—
β + ɛ ― αR1 + αR2	204	−172	32	3	149	1
β + ɛ ― αL + αR2	204	−128	76	−222	149	—
ɛ + ɛ ― αR1 + αR2	204	−234	−30	231	149	—
ɛ + ɛ ― αL + αR2	204	−190	14	6	149	—
β + ɛ ― αR1 + β	228	−172	56	3	62	—
β + ɛ ― αL + β	228	−128	100	−222	62	—
ɛ + ɛ ― αR1 + β	228	−234	−6	231	62	—
ɛ + ɛ ― αL + β	228	−190	34	6	62	—
αR1 + αL ― β + αR2	198	−188	10	−3	−21	1
αR1 + αL ― ɛ + αR2	198	−126	72	−231	−21	—
αL + αL ― β + αR2	198	−232	−34	222	−21	—
αL + αL ― ɛ + αR2	198	−170	28	−6	−21	1
αR1 + αL ― β + β	222	−188	34	−3	128	2
αR1 + αL ― ɛ + β	222	−126	96	−231	128	—
αL + αL ― β + β	222	−232	−10	222	128	1
αL + αL ― ɛ + β	222	−170	52	−6	128	—
αR1 + ɛ ― β + αR2	204	−188	16	−3	149	1
αR1 + ɛ ― ɛ + αR2	204	−126	78	−231	149	—
αL + ɛ ― β + αR2	204	−232	−28	222	149	1
αL + ɛ ― ɛ + αR2	204	−170	34	−6	149	—
αR1 + ɛ ― β + β	228	−188	40	−3	62	1
αR1 + ɛ ― ɛ + β	228	−126	102	−231	62	—
αL + ɛ ― β + β	228	−232	−4	222	62	—
αL + ɛ ― ɛ + β	228	−170	58	−6	62	—

^a Region assigned is that with nearest central point, where distance is measured as |δφ| + |δψ|. Angle changes are calculated on the assumption that the path does not cross the region φ = 0°. Note, not all of these would satisfy inequalities 3 and 4 that were used to search for flips among the conformer pairs. Conversely, 5 cases that do satisfy inequalities 3 and 4 are not among these idealized flips. These occur because φ, ψ values are obviously not confined to the central-point values. They are β + ɛ ― ɛ + β, α_R + ɛ ― β + ɛ, α_L + α_R ― α_R + ɛ, β + β ― α_R + α_R, and α_L + α_R ― α_R + α_R.

Passive peptide-plane flips

Eight of the 32 peptide-plane flips are passive in the sense that they do not require large changes (<100°) in φ_i and ψ_{i + 1} (see Table 2), that is, the orientation of the adjacent peptide planes is largely unaffected. These flips involve α_R¹ ― β or α_L ― ɛ transitions at residue i, and α_R² ― α_L or β ― ɛ transitions at residue i + 1, that is, they do not involve diagonal movements across the Ramachandran plot. Passive flips have the least effect on neighboring groups, and are expected therefore to be the most common. Of these 8, only 2 do not involve the ɛ region. These are the group 1 flip β + α_L ― α_R¹ + α_R² for the type II to type I β-turn interconversion, and the group 2 flip α_R¹ + α_L ― β + α_R¹. These should be the main peptide-plane flips seen for non-glycine pairs. In light of the fact that there many types of peptide-plane flips, the classification into two groups above is somewhat aicial and arises from the missing information (the φ_i and ψ_{i + 1} values) in the φ_{i + 1},ψ_i plots. However, for non-glycine pairs there are indeed just two main types of passive peptide-plane flips, namely, β + α_L ― α_R¹ + α_R² and α_R¹ + α_L ― β + α_R². The former represents group 1 and will be called type 1; the latter represents group 2 and will be called type 2. For the type 1 flip, δψ_i = −172°, δφ_{i + 1} = 198°, and |δψ_i + δφ_i+1| = 26°; and for the type 2 flip, δψ_i = −188° δφ_{i + 1} = 198°, and |δψ_i + δφ_i+1| = 10°. The |δψ_i + δφ_i+1| values indicate that the type 2 flip has even less effect on the relative orientation of the side chains at i and i + 1 than the type 1 flip and the same effect on φ_i and ψ_{i + 1}.

The essential difference between these two transitions is the angle between the two side chains. In the type 1 transition the C_i^β—C_i^α—C_{i + 1}^α—C_{i + 1}^β dihedral is 50°–60°depending on the location of the peptide plane, and for the type 2 transition it is 120°–125°. In comparison to the type 1 flip, which represents the type I to type II β-turn interconversion, the type 2 flip is rare (only one example was found, compared to 8 for the type 1 flip). The reason for this is that the peptide plane between the k + 1 and k + 2 positions in a type I or type II β-turn is not usually hydrogen-bonded to any other protein residues, whereas the α_R¹ + α_L structure of the type 2 flip is associated with the α-helix-terminating Schellman m and the α_L m, both of which involve the peptide plane in hydrogen bonds to neighboring main-chain atoms. They are consequently unable to flip into the β + α_R² conformation, which is a half-turn (Arseniev 1988). Although this type 2 flip is rare in native state dynamics, it may not be during the early stages of protein folding.

One of the 8 passive flips is α_R¹ + ɛ ― β + β. This means a single passive peptide-plane flip can bring two non-β residues both into β conformations provided the i + 1 residue is a glycine. One example of this transition was found. In this sense it is analogous to the main type 1 transition, which in a single flip brings two non-α_R residues both into the α_R region.

Active peptide-plane flips

Of the 32 peptide-plane flips, 24 are not passive, in the sense that they are accompanied by a large change (>100°) in either φ_i or ψ_{i + 1}. They involve diagonal movements across the Ramachandran plot. These peptide-plane flips are likely to have an effect on the conformation of adjacent residues. For example, an α_L + α_L ― β + β flip has little effect on the relative orientation of the side chains but it does require δφ_i = 222° and δψ_{i + 1} = 128° (or −232°), the same values for δφ_{i + 1} and δψ_i. It is intriguing to realize that the relative orientations of the side chains in the α_L structure are the same as in the β structure (the C_i^β—C_i^α—C_{i + 1}^α—C_{i + 1}^β dihedral is ∼−90° for both) and that the conformational difference arises from the relative displacements of the side chains attributable to the noncolinearity of the dihedral axes. This means that a concerted set of peptide-plane flips could convert one structure into the other without changing the relative orientation of the side chains. One example of this flip is found between residues Arg214 and Gly215 in human guanine nucleotide exchange factor (PDB codes: 1a12_A and 1a12_B; Renault et al. 1998). The next peptide plane between residues Gly215 and Gly216 does not undergo an identical flip but the α_L + ɛ ― β + α_R flip. This example shows how peptide-plane flips can propagate along the polypeptide chain, or how concerted peptide-plane flips can transform the local structure. An analogous example is the ɛ + ɛ ― α_R¹ + α_R² flip, for which no example was found.

Conclusions

Peptide-plane flips are expected to play an important role during the early stages of protein folding, first because the peptide plane is less likely to be hydrogen-bonded to other regions of the polypeptide, and second because they can occur without requiring large changes even between the flanking side chains. An analysis of pairs of protein conformations has shown that there are many types of peptide-plane flips in native state dynamics beyond the already known β-turn interconversions. By ideying regions of the Ramachandran plot that are associated with peptide planes free of hydrogen bonds, 32 different types of peptide-plane flips have been identified as the main ones. Although only 10 of these were seen among the pairs of conformations, it is reasonable to assume that all 32 types do occur, particularly in the early stages of protein folding. The 32 flips presented in Table 2 represent an idealization of this flipping process based on the accepted idealization of associating structures with specific φ,ψ angles. Although no energy calculations were made, a high energy path and a low energy path like that found for the type I to type II β-turn interconversion are expected, where the high energy path involves crossing the φ = 0° region. The rates of peptide-plane flips are expected to be enhanced by glycines, particularly at the i + 1 position, as they will present lower energy barriers across the φ = −180°,180° boundary. Passive peptide plane flips require only minor adjustments in the orientation of adjacent peptide planes, whereas active flips require considerable adjustments. One such active flip can convert the α_L structure to a β structure without requiring any appreciable relative rotation of side chains.

Materials and methods

Data selection process

Protein structures with 100% sequence identity to another indicating the same protein in different conformations were identified by doing pairwise alignments using the program FASTA (Pearson and Lipman 1988) on a library of sequences from proteins of solved structure. Protein pairs with more than 30% sequence identity with another pair were not included in this list, and protein pairs for which either structure was solved to a resolution of worse than 1.75 Å were also eliminated (NMR and modeled structures were also excluded). From the resulting set of pairs, members that showed missing residues and the like were also eliminated, leaving 76 pairs in total. In the study of Gunasekaran et al. (1998) less stringent requirements were imposed in that the homologous proteins could have 40% identity and proteins solved to a resolution of less than 2.0 Å were permitted. The following are the PDB codes, and chain identifiers where applicable, of the 76 protein pairs used in this study: 1a12_A,1a12_B; 104m,1vxh; 121p,5p21; 135l,1tew; 153l,154l; 1a2z_A,1a2z_B; 1a7u_A,1a7u_B; 1aal_A,1aal_ B; 1adl, 1lid; 1agj_A,1agj_B; 1aho,1ptx; 1ajr_A,1ajr_B; 1amf,1wod; 1amm,4gcr; 1aoe_A,1aoe_B; 1aop,2aop; 1ar5_A,1ar5_B; 1arm,1yme; 1aru,1arv;1avs_A,1avs_B; 1awq_A,1awr_A; 1axw_A,1axw_B; 1b32_ A,1jev_A; 1bbz_A,1bbz_C; 1bd0_A,1bd0_B; 1bg4,1b31_A; 1bp2, 1mkt; 1bu7_A,1bu7_B; 1cpc_A,1cpc_K; 1csc,2csc; 1dif_A,1dif_B; 1dim,2sil; 1dos_A,1dos_B; 1eca,1eco; 1enx_A,1enx_B; 1ftr_A,1ftr_B; 1fvk_A,1fvk_B; 1gdj,2gdm; 1hbg,2hbg; 1hbi_A,1hbi_B; 1icm,1ifc; 1igd,2igd; 1isu_A,1isu_B; 1jbc,1scs; 1kpt_A,1kpt_B; 1lam,1lcp_A; 1lt5_D,1lt5_E; 1mol_A,1mol_B; 1mrj,1mrk; 1mro_A,1mro_D; 1mty_ D,1mty_E; 1myr,2myr; 1nwp_A,1nwp_B; 1pcf_A,1pcf_B; 1pha,1phb; 1pip_A,9pap; 1rst_B,1rsu_B; 1tad_A,1tad_B; 1utg,2utg_B; 1xik_A, 1xik_B; 256b_A,256b_B; 2aac_A,2aac_B; 2bbk_H,2bbk_J; 2ccy_A, 2ccy_B; 2cth_A,2cth_B; 351c,451c; 3bto_A,3bto_B; 3pvi_A,3pvi_B; 3vub,4vub; 4pga_A,4pga_B; 6gsv_A,6gsv_B; 8ruc_A,8ruc_C; 1a3h, 3a3h; 1svf_A,1svf_C; 1dpt_A,1dpt_B; 1ugi_A,1ugi_B.

Calculation of the change in angle between side chains with variations in ψ_i and φ_{i + 1}

To measure the difference in the angle of relative orientation of the side chains in two different conformations, the tetrahedron formed from the N, C^α, C^β, and C atoms of residue i were superimposed using a least-squares best-fit routine. The angle between the corresponding tetrahedron of residue i + 1 in its two orientations was then determined by calculating the rotation vector by the method of Hayward et al. (1997).