Skip to main content
NCBI home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2001 Nov;10(11):2325–2335. doi: 10.1110/ps.17001

Salt-dependent monomer–dimer equilibrium of bovine β-lactoglobulin at pH 3

Kazumasa Sakurai 1, Motohisa Oobatake 2, Yuji Goto 1
PMCID: PMC2374064  PMID: 11604538

Abstract

Although bovine β-lactoglobulin assumes a monomeric native structure at pH 3 in the absence of salt, the addition of salts stabilizes the dimer. Thermodynamics of the monomer–dimer equilibrium dependent on the salt concentration were studied by sedimentation equilibrium. The addition of NaCl, KCl, or guanidine hydrochloride below 1 M stabilized the dimer in a similar manner. On the other hand, NaClO4 was more effective than other salts by about 20-fold, suggesting that anion binding is responsible for the salt-induced dimer formation, as observed for acid-unfolded proteins. The addition of guanidine hydrochloride at 5 M dissociated the dimer into monomers because of the denaturation of protein structure. In the presence of either NaCl or NaClO4, the dimerization constant decreased with an increase in temperature, indicating that the enthalpy change (ΔHD) of dimer formation is negative. The heat effect of the dimer formation was directly measured with an isothermal titration calorimeter by titrating the monomeric β-lactoglobulin at pH 3.0 with NaClO4. The net heat effects after subtraction of the heat of salt dilution, corresponding to ΔHD, were negative, and were consistent with those obtained by the sedimentation equilibrium. From the dependence of dimerization constant on temperature measured by sedimentation equilibrium, we estimated the ΔHD value at 20°C and the heat capacity change (ΔCp) of dimer formation. In both NaCl and NaClO4, the obtained ΔCp value was negative, indicating the dominant role of burial of the hydrophobic surfaces upon dimer formation. The observed ΔCp values were consistent with the calculated value from the X-ray dimeric structure using a method of accessible surface area. These results indicated that monomer–dimer equilibrium of β-lactoglobulin at pH 3 is determined by a subtle balance of hydrophobic and electrostatic effects, which are modulated by the addition of salts or by changes in temperature.

Keywords: β-Lactoglobulin; monomer, dimer equilibrium; ultracentrifuge; heat capacity change

Bovine β-lactoglobulin (β-LG) is the major whey protein abundant in cow's milk, but not present in human mother's milk (Godovac-Zimmermann 1988; Hambling et al. 1992; Sawyer and Kontopidis 2000). β-LG consists of 162 amino acid residues (18 kD), and contains two disulfide bonds (Cys66–Cys160 and Cys106–Cys119) and a free thiol (Cys121). It is a predominantly β-sheet protein consisting of nine β-strands (A–I) and one major α-helix at the C-terminal end of the molecule (Fig. 1 ▶) (Brownlow et al. 1997; Qin et al. 1998a, 1998b; Kuwata et al. 1998, 1999; Uhrínová et al. 2000). A–H β strands form an up-and-down β-barrel with a hydrophobic cavity inside, where hydrophobic compounds such as retinol bind. Bovine β-LG forms a dimer at neutral pH, while the monomeric native state is stable at pH values below 3. The dimer is stabilized by hydrogen bonds distributed between the surface AB loop and the antiparallel β-sheet between βI strands (Fig. 1 ▶), and by tight packing of the residues in the interface.

Fig. 1.

Fig. 1.

Open in a new tab

Dimer interface of β-LG from the X-ray coordinates, 1BEB. Side view (a) and top view (b) with respect to βI strands. Close-up views of AB loops (a) and βI strands (b) are also shown, where intersubunit hydrogen bonds between side chains and main chains can be seen.

We have been studying the folding mechanism of bovine β-LG (Hamada et al. 1995, 1996; Shiraki et al. 1995; Kuroda et al. 1996; Hamada and Goto 1997; Kuwata et al. 1998, 1999, 2001; Forge et al. 2000). Although it is a predominantly β-sheet protein, it has a markedly high helical propensity (Nishikawa and Noguchi 1991; Shiraki et al. 1995; Kuroda et al. 1996). During its refolding reaction, an intermediate with non-native α-helical structure accumulates because of the inconsistency of local and nonlocal interactions (Hamada et al. 1996). Thus, β-LG is an intriguing model for studying the interplay between local and nonlocal interactions during protein folding. It may provide clues for clarifying the α-to-β-transition (Dalal et al. 1997; Mihara and Takahashi 1997) suggested for several biologically important processes, such as the conformational transitions of prion protein (Prusiner 1997; Cohen 1999; Jackson et al. 1999) or Alzheimer Aβ peptide (Benzinger et al. 2000). A recent study (Kuwata et al. 2001) clarified that, in the intermediate accumulated over the time range of milliseconds, non-native α-helix is formed at the βA region and that the non-native α-helix is transformed slowly to the native β-strand through a process by which the core β-sheet extends to the native β-barrel.

In addition, one of the intriguing topics of β-LG is the monomer–dimer equilibrium. The dimer is the predominant species of β-LG at neutral pH regions and at protein concentration above 1 mg mL−1. However, because the dimerization constant (KD) is not large (∼5 × 104 M−1), the population of monomers increases at low protein concentrations. It has been known that the chemical modification of a free thiol at Cys121 on the βH strand, which is completely buried under the C-terminal α-helix, results in a decrease in KD (Zimmerman et al. 1970; Cupo and Pace 1983; Burova et al. 1998; Yamasaki et al. 1999). In our previous study (Sakai et al. 2000), we characterized the monomer–dimer equilibrium dependent on the modification of Cys121 by 5,5`-dithiobis(2-nitrobenzoic acid) (DTNB), and indicated that the dissociation into monomer is coupled with the substantial disorganization of the β-LG structure by modification of the buried thiol group.

On the other hand, while the native monomer is the major species under low salt conditions at pH 3, it has been shown that an increase in the salt concentration stabilizes the dimer (Townend et al. 1960; Joss and Ralston 1996). However, the thermodynamic mechanism by which salt stabilizes the dimer is unknown. In the present study, we characterized the salt-induced dimer formation of β-LG at pH 3 by sedimentation equilibrium and isothermal titration calorimetry (ITC). Our results indicated that the monomer–dimer equilibrium of β-LG at pH 3 is determined by a subtle balance between the hydrophobic interactions between the dimer interface, which favor dimer formation, and electrostatic repulsion between the positively charged monomers, which favors the monomer. The addition of salt decreases the electrostatic repulsion by anion binding, resulting in stabilization of the dimer. Intriguingly, Gdn-HCl, a neutral salt known as a strong denaturant, stabilized the dimer before it worked as a denaturant. From the temperature dependence of the monomer–dimer equilibrium, we determined the enthalpy change (ΔHD) and the change in heat capacity (ΔCp) on dimer formation. The observed ΔCp values were consistent with the value calculated by the method of accessible surface area (Oobakate and Ooi 1993) based on the X-ray structure of the dimer.

Results

Salt effects

We measured the sedimentation equilibrium of β-LG in the presence of various concentrations of salts at pH 3.0 and 20°C. Salts used were NaCl, KCl, sodium perchlorate (NaClO4), and Gdn-HCl. The plots of concentration versus radius data clearly indicated that the profile was dependent on the salt concentration (Fig. 2 ▶). The results were explained satisfactorily on the basis of a monomer (M)–dimer (D) equilibrium.

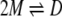graphic file with name M1.gif (1)

Fig. 2.

Fig. 2.

Open in a new tab

Sedimentation equilibrium analysis of β-LG in the presence of various concentrations of Gdn-HCl (a) and at various temperatures (b). The panels show the concentration versus radius plot. The solid lines are theoretical curves based on Equation 2. The data with a larger inclination in the outer region have a higher association constant.

Although it is difficult to interpret the concentration versus radius profile intuitively, data with a larger inclination in the outer region have a higher association constant. We obtained the KD values by fitting the theoretical curve (Eq. 2) to the plots (Figs. 2, 3 ▶ ▶; Table 1). Under the present experimental conditions, a reliable protein concentration range to be determined after sedimentation equilibrium was from 0.1 to 2.0 mg mL−1. This corresponded to a range of KD from 102 to 108 M−1, or a range of dimer fraction (w/w) from 1% to 99%. The optimal KD range to be determined was about 103–106 M−1, corresponding to a range of dimer fraction from 10 to 90%.

Fig. 3.

Fig. 3.

Open in a new tab

Dependence of KD on salt concentration at 20°C. The salts examined were NaClO4 (down open triangles), NaCl (open circles), KCl (open diamonds), and Gdn-HCl (open squares). The right axis shows dimer fraction (w/w) at a β-LG concentration of 1.0 mg mL−1. The slope of the broken lines (dlogKD/dlog[salt]) is Δn, and the values for the perchlorate- and chloride-induced transitions were 2.6 and 1.5, respectively.

Table 1.

Sedimentation equilibrium analysis of β-lactoglobulin A at pH 3.0 in various salts at 20°C

NaCl (mM) KD (M−1) NaClO4 (mM) KD (M−1)
10 1.84 × 102 1.25 9.34 (±7.02) × 102
20 3.26 (±1.24) × 102 2.5 3.01 (±0.72) × 103
50 4.93 (±1.18) × 103 5 1.84 (±0.40) × 104
100 1.60 (±0.17) × 104 10 2.91 (±0.30) × 104
200 5.71 (±0.10) × 104 15 2.27 (±0.67) × 105
1000 1.79 (±0.36) × 105 20 4.04 (±1.18) × 105
25 2.10 (±0.73) × 106
KCl (mM) KD (M−1) Gdn-HCl (mM) KD (M−1)
10 3.91 (±2.18) × 103 10 1.23 (±0.67) × 103
20 1.81 (±0.29) × 103 20 1.64 (±0.31) × 103
50 6.58 (±1.30) × 103 50 5.44 (±1.12) × 103
100 1.64 (±0.19) × 104 100 1.66 (±0.13) × 104
200 2.94 (±0.26) × 104
1000 6.01 (±5.59) × 105
5000 2.20 (±0.97) × 103
Open in a new tab

Under the minimal salt conditions (i.e., 20 mM glycine-HCl at pH 3.0 and 20 mM NaCl), the KD value was 103 M−1. For all the salts examined, the addition of salt increased KD, and thus the fraction of dimer. However, the dependence on salt concentration varied, depending on the salt species (Fig. 3 ▶). The effects of NaCl and KCl were essentially the same and, at a β-LG concentration of 1.0 mg mL−1, more than 80% (w/w) of β-LG formed a dimer in the presence of 1 M NaCl. The salt-induced transition was cooperative, and the midpoint, where the dimer fraction was 50%, was at 0.1 M NaCl or KCl. In contrast, NaClO4 was much more effective than NaCl or KCl. All β-LG molecules formed dimers in the presence of 25 mM NaClO4 and the midpoint salt concentration was as low as 6 mM. Thus, NaClO4 was 20-fold more effective than NaCl or KCl.

Gdn-HCl is the most commonly used denaturant of proteins. However, at low concentrations Gdn-HCl behaved similarly to NaCl or KCl, stabilizing the dimer. The dimer fraction in 1 M Gdn-HCl at a β-LG concentration of 1 mg mL−1 was 80% (w/w). Then, 5 M Gdn-HCl decreased the fraction of dimer to 20%. Although the decrease in the dimer fraction at 5 M Gdn-HCl was due to the Gdn-HCl-induced denaturation of β-LG, the increase in the dimer fraction below 1 M Gdn-HCl was due to the salt effects of Gdn-HCl.

Goto and coworkers (Goto and Fink 1990Goto and Fink 1994; Goto et al. 1990a, 1990b; Hagihara et al. 1993, 1994) studied the salt effects on several acid-denatured proteins (e.g., cytochrome c, apomyoglobin, β-lactamase) at pH 2, where, in the absence of salt, the proteins are unfolded maximally because of the charge repulsion between the positive charges. The effects of various salts on the acid-unfolded proteins were explained by the binding of anions to the positively charged groups on proteins. The binding of counter ions shields the charge repulsion, and consequently the hydrophobic interactions come to play a significant effect, stabilizing the compact molten globule state. Alternatively, the anion-induced folding transition can be explained by the preferential binding of anions to the compactly folded state with the higher positive charge density. One of the most important characteristics of the anion binding-dependent mechanism is that the effectiveness of various anions follows the electroselectivity series: among the monovalent anions, chaotropic anions such as perchlorate, ClO4−, are more effective than chloride, Cl−. Another interesting consequence of the salt effects is the differential effects of Gdn-HCl on the conformational stability of proteins (Hagihara et al. 1993, 1994; Mayr and Schmid 1993). Although Gdn-HCl below 1 M works as a neutral salt because of the chloride effects, it works as a denaturant above 1 M. This results in the consecutive refolding and unfolding transitions of acid-unfolded proteins by the addition of Gdn-HCl.

The effects of four different salts on the monomer–dimer equilibrium of β-LG were very similar to the effects of these salts on the acid-unfolded proteins (Goto and Fink 1990Goto and Fink 1994; Goto et al. 1990a, 1990b; Hagihara et al. 1993, 1994; Mayr and Schmid 1993), although the conformations stabilized by salts were different in the two cases. This similarity suggested that the salts stabilize the dimer of β-LG by the same mechanism as they stabilize the molten globule states (Goto et al. 1990b). Anion binding decreased the charge repulsion between the positively charged monomers, and consequently, intrinsic hydrophobic effects stabilized the β-LG dimer.

The preferential anion binding can be characterized by Δn, the number of anions preferentially and thermodynamically bound to the dimer, which can be obtained by plotting logKD against log[salt] (Fig. 3 ▶; Record et al. 1976, 1991; Goto et al. 1990b). Δn for the perchlorate-induced dimer formation (2.6) was slightly larger than that (1.5) for the chloride-induced transition, representing a slightly higher cooperativity of the perchlorate-induced transition.

Temperature dependence

Sedimentation equilibrium was measured at various temperatures between 5 and 40°C in the presence of different concentrations of NaCl and NaClO4. For all salt conditions, the fraction of dimer decreased with increasing temperature (Fig. 2 ▶), i.e., the decrease in KD with increase in temperature (Fig. 4 ▶). In the presence of 5 mM NaClO4 at a β-LG concentration of 1 mg mL−1, the dimer fraction was 70% at 5°C, and it decreased to 10% at 40°C (Table 2, Fig. 4b ▶). In the presence of 50 mM NaCl, the dimer fraction was 50% at 5°C and 7% at 40°C (Table 2, Fig. 4a ▶). van't Hoff plots (i.e., lnKD versus 1/T) give the enthalpy change (ΔHD) of dimer formation (Fig. 4 ▶). It was evident that for both NaCl or NaClO4 the plots were not linear, indicating that ΔCp values were not zero. For each salt, we estimated the ΔHD and ΔCp values by global curve fitting on the basis of Equation 6 (Table 3). Then, with Equations 3–6, temperature dependencies of ΔGD, ΔHD, and TΔSD were plotted (Fig. 5 ▶).

Fig. 4.

Fig. 4.

Open in a new tab

Dependence of KD on temperature represented as a form of van't Hoff plot (lnKD versus K−1). The KD values were obtained in (a) 50 mM NaCl (open circles), 500 mM NaCl (up open triangles), (b) 5 mM NaClO4 (open squares), and 20 mM NaClO4 (down open triangles). The right axis shows dimer fraction (w/w) at a β-LG concentration of 1.0 mg mL−1. The solid lines show the theoretical curves with Equation 6 with ΔCp as the adjustable parameter and the broken lines show the curves with a fixed ΔCp of −0.72 kJ mol−1 K−1, calculated by the method of Oobatake and Ooi (1993). In case of NaClO4 (b), the line solid completely overlaps the broken line.

Table 2.

Dimerization constants of β-lactoglobulin A at pH 3.0 obtained by sedimentation equilibrium analysis

KD (M−1)
Temperature (°C) 50 mM NaCl 500 mM NaCl 5 mM NaClO4 20 mM NaClO4
5 1.68 (±0.37) × 104 2.89 (±1.36) × 105 8.20 (±3.40) × 104 NDa
10 1.45 (±0.26) × 104 2.79 (±0.69) × 105 2.99 (±0.97) × 104 NDa
15 9.65 (±1.44) × 103 2.19 (±0.07) × 105 2.16 (±0.73) × 104 1.75 (±0.62) × 106
20 6.37 (±0.83) × 103 1.78 (±0.16) × 105 1.08 (±0.18) × 104 5.52 (±2.72) × 105
25 5.67 (±1.69) × 103 1.12 (±0.22) × 105 7.07 (±2.44) × 103 2.23 (±0.75) × 105
30 1.87 (±0.15) × 103 8.30 (±0.20) × 104 3.42 (±0.81) × 103 1.27 (±0.35) × 105
35 1.50 (±0.35) × 103 5.53 (±0.76) × 104 1.90 (±0.57) × 103 6.53 (±1.94) × 104
40 7.22 (±3.89) × 102 4.56 (±0.61) × 104 1.18 (±0.94) × 103 3.46 (±0.99) × 104
Open in a new tab

a It was not possible to determine the value because of the limits of sedimentation equilibrium analysis.

Table 3.

Thermodynamic parameters obtained from sedimentation equilibrium at pH 3.0

Conditions ΔH20 (kJ mol−1) ΔCp (kJ K−1 mol−1) ΔS20 (J K−1 mol−1) K20 (M−1) ΔG20 (kJ mol−1)
    50 mM NaCl −50.4 −1.93 −99.2 6.92 × 103 −21.3
500 mM NaCl −71.3 1.62 × 105 −29.5
5 mM NaClO4 −90.9 −0.75 −232 1.17 × 104 −22.9
20 mM NaClO4 −201 5.91 × 105 −32.1
Open in a new tab

Fig. 5.

Fig. 5.

Open in a new tab

Dependence of ΔGD, ΔHD, and TΔSD on temperature in NaCl (a) and NaClO4 (b). In (a), the values of β-LG isomer B at pH 2.6 and I = 0.16 taken from Joss and Ralston (1996) are shown: (open squares) ΔGD, (open circles) ΔHD, (down open triangles) TΔSD. In (b), ΔHD obtained by ITC measurements (circles) are shown.

Under all salt conditions examined, ΔGD was negative and increased slightly (i.e., decrease in magnitude) with increasing temperature. These slight changes in ΔGD were due to the large changes in ΔHD and TΔSD, as observed for the corresponding parameters of protein unfolding (Oobakate and Ooi 1993; Makhatadze and Privalov 1995 ).Figure 5a ▶ also shows the data reported by Joss and Ralston (1996), in which the values for β-LG isomer B at pH 2.6 and I = 0.16, controlled by NaCl, were determined by sedimentation equilibrium. β-LG isomer B is different from isomer A used in the present study at two positions: whereas isomer A has Asp and Val at positions 64 and 118, respectively, isomer B has Gly and Ala at the corresponding positions. In addition, the buffer conditions used by Joss and Ralston (1996) were not the same as those used in the present study. Nevertheless, the agreement of two results in the presence of NaCl was remarkable, indicating the reliability of the present measurements. This agreement is explained by the fact that the thermodynamic values of the dimer formation are not affected by Asp and Val at positions 64 and 118, respectively, due to no change of ASA values of those residues (see Table 4). Thus, although the number of data points was not sufficient to determine ΔCp precisely, the negative ΔCp values will be valid (Table 3).

Table 4.

Estimation of thermodynamic parameters using X-ray coordinates, 1 BEB

ΔASAn (Å2) ΔASAp (Å2) ΔASAt (Å2) ΔCp,h (nonpolar) (J K−1 mol−1) ΔCp,h (polar) (J K−1 mol−1) ΔCp,h (total) (J K−1 mol−1)
Asp28A 0.0 −8.3 −8.3 0 8 8
Ile29A −89.0 0.0 −89.0 −138 0 −138
Asp33A −1.6 −70.2 −71.7 −3 34 31
Ala34A −46.2 −2.2 −48.3 −71 0 −71
Gln35A −18.8 −1.1 −19.9 −29 0 −29
Arg40A 0.0 −47.1 −47.1 0 2 2
Met145A 0.0 −13.6 −13.6 0 13 13
His146A −73.8 −33.1 −106.8 −99 25 −74
Ile147A −24.8 0.0 −24.8 −38 0 −38
Arg148A −73.6 −52.6 −126.2 −109 28 −81
Leu149A −60.4 0.0 −60.4 −94 0 −94
Ser150A −2.4 −54.8 −57.2 −4 18 14
Phe151A −9.3 −13.5 −22.8 −13 13 0
Asn152A −10.6 −0.4 −11.0 −16 0 −16
Gln155A 0.0 −17.8 −17.8 0 14 14
Asp28B 0.0 −1.8 −1.8 0 2 2
Ile29B −72.5 0.0 −72.5 −112 0 −112
Asp33B −1.6 −50.1 −51.7 −3 24 21
Ala34B −31.4 −2.4 −33.8 −49 0 −49
Gln35B −3.0 −0.7 −3.7 −5 0 −5
Arg40B 0.0 −20.4 −20.4 0 1 1
Met145B 0.0 −5.1 −5.1 0 5 5
His146B −36.8 −22.2 −59.0 −48 15 −33
Ile147B −24.6 0.0 −24.6 −38 0 −38
Arg148B −19.6 −36.5 −56.1 −30 18 −12
Leu149B −41.9 0.0 −41.9 −65 0 −65
Ser150B −2.8 −43.6 −46.4 −4 17 12
Phe151B −7.8 −2.9 −10.7 −10 3 −7
Asn152B 0.0 −26.5 −26.5 0 8 8
Gln155B 0.0 −20.6 −20.6 0 16 16
Total −652.4 −547.3 −1199.7 −977 262 −715
Open in a new tab

A and B after residue number mean the chain names of dimer, respectively. ΔASAn, ΔASAp, and ΔASAt represent ASA changes of nonpolar, polar, and total heavy atoms, respectively, upon dimer formation. ΔASA = ASA (dimer) − ASA (monomer) and ΔCp,h = Cp,h (dimer) − Cp,h (monomer).

Isothermal titration calorimetry

Heat of the dimer formation upon addition of salts at pH 3.0 was directly measured by ITC at 30 and 40°C (Fig. 6 ▶). This measurement was possible only with NaClO4, because its concentration required for dimer formation was low enough to perform the ITC experiment (Hamada et al. 1994). The dilution of NaClO4 was endothermic, absorbing heat. The titration of β-LG with NaClO4 was first exothermic, and then became endothermic, indicating that the interaction between β-LG and NaClO4 upon dimer formation is exothermic (Fig. 6a ▶). After subtracting the dilution heat of NaClO4 and integrating the net heat effect of each step, we obtained the plot of total heat effect against NaClO4 concentration (Fig. 6b ▶). The plot showed a saturating curve with a slightly sloped baseline. Assuming that the dimer fraction is 100% on the baseline, dimer fraction at 30°C was 48% at 5 mM NaClO4 and 87% at 20 mM NaClO4. Considering the β-LG concentration of 5.0 mg mL−1 in ITC measurements, these percentages were in good agreement with those calculated from KD values obtained from the sedimentation equilibrium analysis (i.e., 49% for 5 mM NaClO4 and 89% for 20 mM NaClO4, Fig. 4 ▶). We consider that the extrapolated total heat effect from the saturated regions above 40 mM corresponds to the total heat of dimer formation, i.e., ΔHD. In fact, the ΔHD values obtained from ITC measurements at 30 and 40°C were close to those obtained by sedimentation equilibrium analysis (Fig. 5b ▶). Although the ΔCp value suggested from these ΔHD values is positive, inconsistent with the negative value obtained from sedimentation equilibrium measurements, we do not consider that the ΔHD values obtained from ITC measurements have a high enough quality to determine ΔCp (see below).

Fig. 6.

Fig. 6.

Open in a new tab

Heat effects of dimer formation measured by ITC. (a) Solid line shows typical calorimetric titration of the monomeric β-LG with NaClO4 at 30 °C at pH 3.0. 1 μL of 0.45 M NaClO4 was added five times, and then 2 μL of the same stock salt solution was added for each injection. The broken line indicates the control titration without protein. (b) Net heat effect obtained after subtracting the control heat effect data and integrating each peak by time. We assumed that the net heat effect obtained by extrapolation to zero salt concentration (solid line) corresponded to ΔHD. Temperatures were 30 (up open triangles) and 40 (down open triangles) °C. Solid data show the control experiments at 40 (down filled triangles) °C under the same conditions except including 8 M urea, in which β-LG is unfolded and monomeric.

As control experiments, we carried out titration experiments in the presence of 8 M urea at pH 3.0, where β-LG was unfolded and monomeric measured by sedimentation equilibrium (data not shown). No significant heat effect was observed (Fig. 6b ▶), confirming that the heat effects in the absence of denaturant were due to the monomer–dimer transition. We performed the ITC measurements at various temperatures. However, because the results below 30°C were likely to include the contribution of aggregation of proteins at high salt concentrations, we did not report these data in the present paper.

Calculation of thermodynamic parameters

With the PDB coordinates 1BEB, a dimeric β-LG obtained at pH 6.5, we calculated the change in ASA (ΔASA) on dimer formation, assuming that the monomeric structures were the same as those in the dimer (Table 4). In the total decrease in ASA (1200 Å2 dimer−1) upon dimer formation, nonpolar and polar surfaces were 652 and 547 Å2 dimer−1, respectively. The two monomers in the dimer were not exactly the same, although they were very similar. For both monomer units, the residues with ΔASA larger than 50 Å2 dimer−1 were Ile29, Asp33, His146, Arg148, Leu149, and Ser150. For many of these residues, the contribution of the nonpolar surface to the total ΔASA was slightly larger than that of the polar surface. We estimated the ΔCp,h value upon dimer formation on the basis of the method of Oobatake and Ooi (1993). The estimated ΔCp,h value was −0.72 kJ K−1 (mole of dimer)−1 (Table 4). Because ΔASAn and ΔASAp contribute to ΔCp,h negatively and positively, respectively, the negative value of calculated ΔCp,h means the major contribution of nonpolar surfaces to ΔCp,h. Considering errors in the experimental determination of the small ΔCp value, the estimated value was consistent with the values obtained by sedimentation equilibrium analysis (−1.93 and −0.75 kJ K−1 (mole of dimer)−1 for NaCl and forNaClO4, respectively; Table 3), arguing that the observed ΔCp of dimer formation is mostly ΔCp,h.

Discussion

Although β-LG assumes a predominantly monomeric native structure at around pH 3 in the absence of salt, the addition of salt stabilizes the dimeric structure. In fact, the salt-dependent monomer–dimer equilibrium has been proposed to be a good standard to calibrate monomer–dimer analysis with sedimentation equilibrium (Joss and Ralston 1996). X-ray crystallographic studies (Brownlow et al. 1997; Qin et al. 1998a, 1998b) have characterized dimeric structures of bovine β-LG, in which βI strands join two monomers forming an antiparallel β-sheet (Fig. 1 ▶). The monomers are associated by 12 hydrogen bonds distributed between AB loops (eight side chain bonds) and βI strands (four main chain bonds). The dimer interface buries about 1200 Å2 of the accessible surface area per dimer, corresponding to about 6% of the total surface area of the isolated native structures. This value lies at the lower end of the range for strongly associated dimers (Brownlow et al. 1997), suggesting that this dimeric interaction is not very tight. Consistent with this, the dimerization constant was only 5 × 104 M−1 at pH 6.5, and a significant fraction of the molecules existed as monomers at low protein concentrations (Sakai et al. 2000). Therefore, it is not surprising that a decrease of pH easily destabilizes the dimer, forming a monomer at pH values below 3 under conditions of low salt. On the other hand, because of this weak interaction, the detailed mechanism by which the salts stabilize the dimer at around pH 3 has not been clarified. To obtain further insight into the mechanism, we studied the salt-dependent monomer–dimer equilibrium of β-LG with analytical ultracentrifugation and ITC. The sedimentation equilibrium was used to characterize the change in the monomer–dimer equilibrium dependent on salt conditions and temperature. ITC directly measured ΔHD of dimer formation. The results clarified several characteristics of the thermodynamic mechanism of monomer–dimer equilibrium of β-LG.

Salt effects

We first showed that the salt-induced stabilization of the β-LG dimer is similar in mechanism to the salt-induced stabilization of the molten globule state of acid-unfolded proteins as studied by Goto and coworkers (Goto and Fink 1990,Goto and Fink 1994,Goto et al. 1990a, 1990b). In the case of acid-denaturation, pH conditions as low as pH 2 caused an increase in the net charge of protein molecules. Under low salt conditions, this produces the unfavorable charge repulsion, resulting in global unfolding of the protein molecule. The anions produced by salts or even strong acids shield this charge repulsion by the direct interaction with positive charges. The importance of the direct interaction was demonstrated by the observation that the order of the effectiveness of various anions follows the electroselectivity series of anions toward anion-exchange resins. In the electroselectivity series, multivalent anions are more effective than monovalent anions. Among monovalent anions, chaotropic anions are more effective than kosmotropic anions: SCN− > ClO4− > I− > Br− > Cl− > F−. Anions are preferentially bound to the compact molten globule state because the electrostatic interaction becomes stronger when the protein assumes a compact state with a high charge density.

In the salt-induced stabilization of the dimer of β-LG, NaClO4 is about 20-fold more effective than NaCl or KCl, consistent with the anion binding-induced dimerization mechanism. Otherwise, such a large difference in the effects of NaClO4 and NaCl or KCl would not be explained. The Debye-Hückel screening effect of salts is independent of anion species. The difference in the number of thermodynamically bound anions, Δn, was obtained from the plot of logK versus log[salt] (Fig. 3 ▶) and the estimated Δn value of NaClO4 is slightly larger than that of NaCl or KCl, indicating that the NaClO4-induced transition is a little more cooperative than the NaCl or KCl transitions. In addition, Δn value per β-LG dimer of both salts was about 2, consistent with the idea that the monomer–dimer equilibrium depends critically on the subtle balance of the stabilizing and destabilizing forces. Candidates of the anion-binding residues responsible for the dimer formation are R40, H146, and R148, as shown in Figure 1 ▶. The most reasonable one is R148 because the distance between ɛ-nitrogens of R148 on each monomer is shorter than any other pairs of the positive charges. It is likely that anion binding suppresses the repulsion caused by these positive charges.

β-LG is resistant against acid-denaturation, and it assumes a native conformation even at pH 2.0 as has been characterized by NMR analysis (Kuwata et al. 1998, 1999). In fact, its stability against denaturant at pH 2 is higher than at pH 7.0 (Sakai et al. 2000). The pI value of β-LG is 4.6 and the net charges at pH 7.5 and pH 2.0 were calculated to be −9 and +20, respectively, on the basis of the amino acid composition. Therefore, the net charge repulsion, which is stronger at pH 2.0 than at pH 7.5, cannot explain the increased stability at pH 2, and the precise reason of these phenomena is still unclear. We considered that the binding of counter ions shields the charge repulsion at pH 2.0 and, consequently, the dimer is stabilized by the interactions similar to those that stabilize the native dimer at neutral pH. As the salt bridges involved in the dimer interface would be difficult to form at the acidic pH where carboxyl groups are protonated (Fig. 1 ▶), the hydrophobic effects are the most important factors for stabilizing the dimer at pH 3.

In this context, it is intriguing that many nonruminant β-LG are monomeric at neutral pH (Hambling et al. 1992). Consideration of sequence variation suggested that Ala34 or Arg40 in the AB loop is important for stabilizing the dimer of bovine β-LG (Hambling et al. 1992). Recently, the conformation and folding of horse β-LG have been characterized (Ikeguchi et al. 1997; Fujiwara et al. 1999). Intriguingly, horse β-LG is unstable against acid, and forms an intermediate conformation with an increased α-helical content at pH 2.

Hydrophobic effects

The major contribution of hydrophobic effects in protein folding or protein–protein interactions produces a positive value of the heat capacity change upon disappearance of the interactions, for example, exposure of hydrophobic surfaces upon protein unfolding (Makhatadze and Privalov 1990a,1990b, 1995; Murphy and Gill 1991; Oobakate and Ooi 1993). To examine the role of hydrophobic effects, we measured the temperature dependence of the monomer–dimer equilibrium (Fig. 4 ▶). For both NaCl and NaClO4, KD decreased with increases in temperature, resulting in dissociation into monomers. The thermodynamic parameters showed that both ΔHD and TΔSD are negative and change largely with temperature and the entropy–enthalpy compensation results in a slight increase in ΔGD with increasing temperature, as observed for the corresponding parameters of protein unfolding (Makhatadze and Privalov 1990a; Oobakate and Ooi 1993). Temperature dependencies of the changes of ΔHD in NaCl and NaClO4 were similar, and could be explained by a common negative value of ΔCp (Table 3).

The only thermodynamic parameter that can be estimated on the basis of X-ray structures at the moment is ΔCp (Makhatadze and Privalov 1990a,1990b,1995;Oobakate and Ooi 1993). ΔHD and ΔSD have been difficult to predict correctly because several formidable factors, especially electrostatic energy and freedom, are involved. The ΔCp of protein unfolding is largely determined by the hydration of hydrophobic groups, which contribute positively, and the hydration of hydrophilic groups including polar side chains and peptide groups, which contribute negatively. The same argument will be valid for the process of dimer formation, although the signs of these factors are opposite (Oobakate and Ooi 1993). As expected, the ΔCp value (−0.72 kJ K−1 (mole of dimer)−1) of dimer formation calculated from the X-ray coordinates of the dimeric structure is negative (Table 4), consistent with the ΔCp value obtained in the presence of NaClO4, and, considering the possible errors, with the ΔCp value in the presence of NaCl (Table 3).

Conclusions

Monomer–dimer equilibrium of β-lactoglobulin at pH 3 is determined by a subtle balance between stabilizing and destabilizing forces because only a small ASA is buried on dimer formation. Although the net hydrophobic effects stabilize the dimer, the electrostatic charge repulsion between positive charges dissociates the dimer. This equilibrium is modulated by the addition of salts or by changes in temperature. The addition of salt at pH 3 shifts the equilibrium to the dimer because counterion binding to the positive charges of the monomer suppresses the charge repulsion; consequently, the intrinsic forces stabilizing the native dimer manifesting themselves. The anion-dependent dimer formation is similar in mechanism to the anion-dependent stabilization of the molten globule state as observed for several acid-unfolded proteins. On the other hand, increases in temperature destabilize the dimer because of the negative ΔHD of dimer formation. The analysis of the temperature dependence of the monomer–dimer equilibrium indicated the negative ΔCp of dimer formation, confirming the dominant role of the hydrophobic effects. Finally, one of the most important points in this study is that we succeeded in directly measuring ΔHD of the dimer formation by ITC with NaClO4 as a titrant.

Materials and methods

Materials

Bovine β-LG isomer A was purchased from Sigma and used without further purification. Other reagents were from Nacalai Tesque. The buffer used was 20 mM glycine-HCl (pH 3.0). The stock buffer solution of 1 M was prepared and the salts were added when the stock buffer solution was diluted 50-fold.

Analytical ultracentrifugation

Prior to the ultracentrifugation experiments, proteins were dialyzed against the desired buffer or passed through a PD10 column equilibrated with the buffer. Sedimentation equilibrium experiments were performed with a Beckman Optima XL-A analytical ultracentrifuge at 20,000 rpm. The measurements in the presence of various concentrations of different salts were performed at 20°C. The data were obtained after 20 h of centrifugation by monitoring the absorbance at 278 nm. β-LG with a molecular weight of 18,400 was assumed to have a partial specific volume (|gn) of 0.751 mL g−1 at 25°C (Joss and Ralston 1996), independent of the buffer conditions. A value of 0.961 mL mg−1 cm−1 at 280 nm (Townend et al. 1960) was used as the absorbance coefficient of β-LG. The density (ρ) of glycine-HCl buffer (pH 3.0) at 20°C was assumed to be 0.9990 g mL−1.

Concentration versus radius data acquisition was as an average of 20 absorbance measurements over 0.001-cm intervals. All experiments used double-sector 12 mm-thick charcoal–epon centerpieces and matched quartz windows. Protein concentration (CT) was plotted against radius (r) from the arbitrary radius point (r0). The CT versus r plots were analyzed to determine KD according to the theoretical equation for monomer–dimer equilibrium:

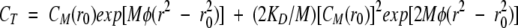graphic file with name M2.gif (2)

where CM(r0) is the monomer concentration at r0, M is the molecular weight of monomer, φ = ω2(1−|gnρ)/(2RT), and R, T, and ω are the gas constant, absolute temperature, and rotor speed, respectively (Teller et al. 1969). The measurements at three different protein concentrations under the same buffer conditions were carried out using a rotor with three cells, and the results at different concentrations were analyzed individually with Equation 2, and the average of the three values was presented. Least-squares curve fitting was performed using the Igor software program (WaveMetrics).

Sedimentation equilibrium measurements were also performed at various temperatures between 5 and 40°C at an interval of 5°C. The results were analyzed as described above. The densities of glycine-HCl buffer (pH 3.0) at various temperatures were estimated assuming that the density ratio of the buffer and water was the same as that at 20°C, where the density of water at various temperatures is available from the literature (Svedberg and Pedersen 1940).

The temperature dependence of the dimerization constant, KD, was analyzed assuming the following standard equations:

graphic file with name M3.gif (3)
graphic file with name M4.gif (4)
graphic file with name M5.gif (5)

and

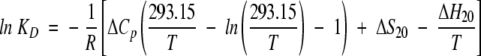graphic file with name M6.gif (6)

where ΔGD, ΔHD, and ΔSD are Gibbs free energy, enthalpy, and entropy changes, respectively, of dimer formation, and ΔS20 and ΔH20 are entropy and enthalpy changes of dimer formation at 20°C, respectively.

ITC measurements

The β-LG solution in the cell was titrated with a solution of NaClO4 in a similar way as used for titration of the acid-unfolded cytochrome c with NaClO4 (Hamada et al. 1994). The lyophilized β-LG was dissolved into 20 mM glycine-HCl (pH 3.0) buffer and dialyzed against the same buffer. Then, the concentration of the β-LG solution was adjusted to 5.0 mg mL−1. The stock NaClO4 solution at 0.45 M was prepared with the buffer solution after dialysis. An MCS ITC unit calorimeter (MicroCal Inc.) was used. Measurements were carried out at 30 and 40°C. After setting the solutions, temperature was equilibrated for at least 3 h before measurement. The salt concentration was increased from 0 to 80 mM by stepwise addition of the stock NaClO4 solution. As a control titration measurement, the buffer solution after dialysis was titrated with the same NaClO4 solution.

Estimation of thermodynamic parameters

The hydration heat capacity change ΔCP,h value and other thermodynamic parameters of dimer formation were calculated using the X-ray dimeric structure (1BEB) by the method of Oobatake and Ooi (1993). The ΔCP,h value on protein unfolding contributes to most of the total ΔCP value (Makhatadze and Privalov 1990a,1990b, 1995; Oobakate and Ooi 1993). The values of ΔASA and ΔCP,h are divided into the contributions of nonpolar atoms (C) and polar atoms (N, O, and S).

Acknowledgments

We thank Thomas Kiefhaber (University of Basel, Switzerland) for valuable discussion, Saburo Aimoto (Institute for Protein Research) for help with the ITC equipment, and Miyo Sakai (Institute for Protein Research) for assistance with the ultracentrifuge experiment. This work was supported in part by Grants-in-Aid for Scieic Research from the Japanese Ministry of Education, Science, Culture and Sports.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.

Abbreviations

  • ASA, accessible surface area

  • β-LG, β-lactoglobulin

  • CD, circular dichroism

  • ΔCp, heat capacity change of dimer formation

  • ΔCp,h, hydration heat capacity change of dimer formation

  • ΔGD, Gibbs free energy change of dimer formation

  • ΔHD, enthalpy change of dimer formation

  • ΔSD, entropy change of dimer formation

  • Gdn-HCl, guanidine hydrochloride

  • HSQC, heteronuclear single quantum coherence

  • ITC, isothermal titration calorimeter

  • KD, dimerization constant

  • NMR, nuclear magnetic resonance

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1101/ps.17001.

References

  1. Benzinger, T.L.S., Gregory, D.M., Burkoth, T.S., Miller-Auer, H., Lynn, D.G., Botto, R.E., and Meredith, S.C. 2000. Two-dimensional structure of β-amyloid(10–35) fibrils. Biochemistry 39 3491–3499. [DOI] [PubMed] [Google Scholar]
  2. Brownlow, S., Cabral, J.H.M., Cooper, R., Flower, D.R., Yewdall, S.J., Polikarpov, I., North, A.C.T., and Sawyer, L. 1997. Bovine β-lactoglobulin at 1.8 Å resolution—Still an enigmatic lipocalin. Structure 5 481–495. [DOI] [PubMed] [Google Scholar]
  3. Burova, T.V., Choiset, Y., Tran, V., and Haertlé, T. 1998. Role of free Cys121 in stabilization of bovine β-lactoglobulin B. Protein Eng. 11 1065–1073. [DOI] [PubMed] [Google Scholar]
  4. Cohen, F.E. 1999. Protein misfolding and prion diseases. J. Mol. Biol. 293 313–320. [DOI] [PubMed] [Google Scholar]
  5. Cupo, J.F. and Pace, C.N. 1983. Conformational stability of mixed disulfide derivatives of β-lactoglobulin B. Biochemistry 22 2654–2658. [DOI] [PubMed] [Google Scholar]
  6. Dalal, S., Balasubramanian, S., and Regan, L. 1997. Transmuting α-helices and β-sheets. Fold. Des. 2 R71–R79. [DOI] [PubMed] [Google Scholar]
  7. Forge, V., Hoshino, M., Kuwata, K., Arai, M., Kuwajima, K., Batt, C.A., and Goto, Y. 2000. Is folding of β-lactoglobulin non-hierarchic? Intermediate with native-like β-sheet and non-native α-helix. J. Mol. Biol. 296 1039–1051. [DOI] [PubMed] [Google Scholar]
  8. Fujiwara, K., Arai, M., Shimizu, A., Ikeguchi, M., Kuwajima, K., and Sugai, S. 1999. Folding-unfolding equilibrium and kinetics of equine β-lactoglobulin: Equivalence between the equilibrium molten globule state and a burst-phase folding intermediate. Biochemistry 38 4455–4463. [DOI] [PubMed] [Google Scholar]
  9. Godovac-Zimmermann, J. 1988. The structural m of β-lactoglobulin and retinol-binding protein. Trends Biochem. Sci. 13 64–66. [DOI] [PubMed] [Google Scholar]
  10. Goto, Y. and Fink, A.L. 1990. Phase diagram for acidic conformational states of apomyoglobin. J. Mol. Biol. 214 803–805. [DOI] [PubMed] [Google Scholar]
  11. –––. 1994. Acid-induced folding of heme proteins. Methods Enzymol. 22 3–15. [DOI] [PubMed] [Google Scholar]
  12. Goto, Y., Calciano, L.J., and Fink, A.L. 1990a. Acid-induced folding of proteins. Proc. Natl. Acad. Sci. 87 573–577. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Goto, Y., Takahashi, N., and Fink, A.L. 1990b. Mechanism of acid-induced folding of proteins. Biochemistry 29 3480–3488. [DOI] [PubMed] [Google Scholar]
  14. Hagihara, Y., Aimoto, S., Fink, A.L, and Goto, Y. 1993. Guanidine hydrochloride-induced folding of proteins. J. Mol. Biol. 231 180–184. [DOI] [PubMed] [Google Scholar]
  15. Hagihara, Y., Tan, Y., and Goto, Y. 1994. Comparison of the conformational stability of the molten globule and native states of horse cytochrome c. J. Mol. Biol. 237 336–348. [DOI] [PubMed] [Google Scholar]
  16. Hamada, D. and Goto, Y. 1997. The equilibrium intermediate of β-lactoglobulin with non-native α-helical structure. J. Mol. Biol. 269 479–487. [DOI] [PubMed] [Google Scholar]
  17. Hamada, D., Kidokoro, S., Fukada, H., Takahashi, K., and Goto, Y. 1994. Salt-induced formation of the molten globule state of cytochrome c studied by isothermal titration calorimetry. Proc. Natl. Acad. Sci. 91 10325–10329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hamada, D., Kuroda, Y., Tanaka, T., and Goto, Y. 1995. High helical propensity of the peptide fragments derived from β-lactoglobulin, a predominantly β-sheet protein. J. Mol. Biol. 254 737–746. [DOI] [PubMed] [Google Scholar]
  19. Hamada, D., Segawa, S., and Goto, Y. 1996. Non-native α-helical intermediate in the refolding of β-lactoglobulin, a predominantly β-sheet protein. Nat. Struct. Biol. 3 868–874. [DOI] [PubMed] [Google Scholar]
  20. Hambling, S.G., MacAlpine, A.S., and Sawyer, L. 1992. β-lactoglobulin. In Advanced dairychemistry (ed. P.F. Fox), pp. 141–190. Elsevier, Amsterdam.
  21. Ikeguchi, M., Kato, S., Shimizu, A., and Sugai, S. 1997. Molten globule state of equine β-lactoglobulin. Proteins Struct. Funct. Genet. 27 567–575. [DOI] [PubMed] [Google Scholar]
  22. Jackson, G.S., Hosszu, L.L.P., Power, A., Hill, A.F., Kenney, J., Sibil, H., Craven, C.J., Waltho, J.P., Clarke, A.R., and Collinge, J. 1999. Reversible conversion of monomeric human prion protein between native and fibrilogenic conformations. Science 283 1935–1937. [DOI] [PubMed] [Google Scholar]
  23. Joss, L.A. and Ralston, G.B. 1996. β-Lactoglobulin B: A proposed standard for the study of reversible self-association reactions in the analytical ultracentrifuge? Anal. Biochem. 236 20–26. [DOI] [PubMed] [Google Scholar]
  24. Kuroda, Y., Hamada, D., Tanaka, T., and Goto, Y. 1996. High helicity of peptide fragments corresponding to β-strand regions of β-lactoglobulin observed by 2D-NMR spectroscopy. Fold. Des. 1 255–263. [DOI] [PubMed] [Google Scholar]
  25. Kuwata, K., Hoshino, M., Era, S., Batt, C.A., and Goto, Y. 1998. α → β Transition of β-lactoglobulin as evidenced by heteronuclear NMR. J. Mol. Biol. 283 731–739. [DOI] [PubMed] [Google Scholar]
  26. Kuwata, K., Hoshino, M., Forge, V., Era, S., Batt, C.A., and Goto, Y. 1999. Solution structure and dynamics of bovine β-lactoglobulin A. Protein Sci. 8 2541–2545. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kuwata, K., Shastry, R., Cheng, H., Hoshino, M., Batt, C.A., Goto, Y., and Roder, H. 2001. Structural and kinetic characterization of early folding events in β-lactoglobulin. Nat. Struct. Biol. 8 151–155. [DOI] [PubMed] [Google Scholar]
  28. Makhatadze, G.I. and Privalov, P.L. 1990a. Heat capacity of proteins. I. Partial molar heat capacity of individual amino acid residues in aqueous solution: Hydration effect. J. Mol. Biol. 213 375–384. [DOI] [PubMed] [Google Scholar]
  29. ———. 1990b. Heat capacity of proteins. II. Partial molar heat capacity of the unfolded polypeptide chain of proteins: Protein unfolding effects. J. Mol. Biol. 213 385–391. [DOI] [PubMed] [Google Scholar]
  30. –––. 1995. Energetics of protein structure. Adv. Protein Chem. 47 307–425. [DOI] [PubMed] [Google Scholar]
  31. Mayr, L.M. and Schmid, F.X. 1993. Stabilization of a protein by guanidinium chloride. Biochemistry 32 7994–7998. [DOI] [PubMed] [Google Scholar]
  32. Mihara, H. and Takahashi, Y. 1997. Engineering peptides and proteins that undergo α-β transitions. Curr. Opin. Struct. Biol. 7 501–508. [DOI] [PubMed] [Google Scholar]
  33. Murphy, K.P. and Gill, S.J. 1991 Solid model compounds and the thermodynamics of protein unfolding. J. Mol. Biol. 222699–709. [DOI] [PubMed]
  34. Nishikawa, K. and Noguchi, T. 1991. Predicting protein secondary structure based on amino acid sequence. Methods Enzymol. 202 31–44. [DOI] [PubMed] [Google Scholar]
  35. Oobakate, M. and Ooi, T. 1993. Hydration and heat stability effects on protein unfolding. Prog. Biophys. Mol. Biol. 59 237–284. [DOI] [PubMed] [Google Scholar]
  36. Prusiner, S.B. 1997. Prion diseases and the BSE crisis. Science 278 245–251. [DOI] [PubMed] [Google Scholar]
  37. Qin, B.Y., Bewley, M.C., Creamer, L.K., Baker, H.M., Baker, E.N., and Jameson, G.B. 1998a. Structural basis of the Tanford transition of bovine β-lactoglobulin. Biochemistry 37 14014–14023. [DOI] [PubMed] [Google Scholar]
  38. Qin, B.Y., Qreamer, L.K., Baker, E.N., and Jameson, G.B. 1998b. 12-Bromododecanoic acid bind inside the calyx of bovine β-lactoglobulin. FEBS Lett. 438 272–278. [DOI] [PubMed] [Google Scholar]
  39. Record, Jr., M.T., Lahman, T.M., and de Haseth, P. 1976. Ion effects on ligand-nucleic acid interactions. J. Mol. Biol. 107 145–158. [DOI] [PubMed] [Google Scholar]
  40. Record, Jr., M.T., Ha, J.-H., and Fisher, M.A. 1991. Analysis of equilibrium and kinetic measurements to determine thermodynamic origins of stability and specificity and mechanism of formation of site-specific complexes between proteins and helical DNA. Methods Enzymol. 208 291–343. [DOI] [PubMed] [Google Scholar]
  41. Sakai, K., Sakurai, K., Sakai, M., Hoshino, M., and Goto, Y. 2000. Conformation and stability of thiol-modified bovine β-lactoglobulin. Protein Sci. 9 1719–1729. [PMC free article] [PubMed] [Google Scholar]
  42. Sawyer, L. and Kontopidis, G. 2000. The core lipocalin, bovine β-lactoglobulin. Biochim. Biophys. Acta 1482 136–148. [DOI] [PubMed] [Google Scholar]
  43. Shiraki, K., Nishikawa, K., and Goto, Y. 1995. Trifluoroethanol-induced stabilization of the α-helical structure of β-lactoglobulin: Implication for non-hierarchical protein folding. J. Mol. Biol. 245 180–194. [DOI] [PubMed] [Google Scholar]
  44. Svedberg, T. and Pedersen, K.O. 1940. The ultracentrifuge. Oxford University Press, New York.
  45. Teller, D.C., Horbett, T.A., Richards, E.G., and Schachman, H.K. 1969. Ultracentrifuge studies with Rayleigh interference optics. III. Computational methods applied to high-speed sedimentation equilibrium experiments. Ann. NY Acad. Sci. 164 66–101. [Google Scholar]
  46. Townend, R., Winterbottom, R.J., and Timasheff, S.N. 1960. Molecular interactions in β-lactoglobulin. II. Ultracentrifugal and electrophoretic studies of the association of β-lactoglobulin below its isoelectric point. J. Am. Chem. Soc. 82 3161–3168. [Google Scholar]
  47. Uhrínová, S., Smith, M.H., Jameson, G.B., Uhrín, D., Sawyer, L., and Barlow, P.N. 2000. Structural changes accompanying pH-induced dissociation of the β-lactoglobulin dimer. Biochemistry 39 3565–3574. [DOI] [PubMed] [Google Scholar]
  48. Yamasaki, R., Hoshino, M., Wazawa, T., Ishii, Y., Yanagida, T., Kawata, Y., Higurashi, T., Sakai, K., Nagai, J., and Goto, Y. 1999. Single molecular observation of the interaction of GroEL with substrate proteins. J. Mol. Biol. 292 965–972. [DOI] [PubMed] [Google Scholar]
  49. Zimmerman, J., Barlow, G.H., and Klotz, I.M. 1970. Dissociation of β-lactoglobulin near neutral pH. Arch. Biochem. Biophys. 138 101–109. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES