Structure of the transmembrane region of the M2 protein H⁺ channel

Abstract

The transmembrane domain of the M2 protein from influenza A virus forms a nearly uniform and ideal helix in a liquid crystalline bilayer environment. The exposure of the hydrophilic backbone structure is minimized through uniform hydrogen bond geometry imposed by the low dielectric lipid environment. A high-resolution structure of the monomer backbone and a detailed description of its orientation with respect to the bilayer were achieved using orientational restraints from solid-state NMR. With this unique information, the tetrameric structure of this H⁺ channel is constrained substantially. Features of numerous published models are discussed in light of the experimental structure of the monomer and derived features of the tetrameric bundle.

High-resolution three-dimensional structure is a fundamentally important goal in the structural biology of membrane proteins, but very difficult to achieve because of the heterogeneous nature of the lipid bilayer environment and the altered balance of interactions that stabilize membrane proteins versus water soluble proteins. To help circumvent the first problem, model membrane environments have been used both in making crystals for X-ray crystallography and in making micellar solutions for solution-state NMR spectroscopy; even so, high-resolution has been difficult to achieve. However, it is possible to obtain high-resolution structure from a protein in a planar bilayer environment and, importantly, even in the liquid crystalline native phase using a different technology.

On endocytosis of the Influenza A virus, the low pH environment of the endosome activates the M2 protein H⁺ channel, presumably through protonation of the histidine side chain in the transmembrane section of the protein. The acidification of the viral interior disrupts the ribonucleoprotein core, leading to fusion of the viral envelope with the endosomal wall and continuation of the infectious life cycle (Lamb et al. 1994). Blockage of the H⁺ channel with the alu drug, amantadine, results in a disruption of this life cycle (Duff et al. 1992; Wang et al. 1993). The M2 protein has 97 amino acids, with a putative single 19-residue transmembrane helix, a 24-residue extraviral segment, and 54 intraviral residues. As a tetramer, the protein forms the H⁺ channel (Holsinger and Lamb 1991; Sakaguchi et al. 1997). Here, the polypetide that is characterized structurally (M2-TMP; residues 22–46) is a 25-residue peptide spanning the putative transmembrane segment with a few hydrophilic residues on either end. M2-TMP and the transmembrane portion of the M2 protein adopts primarily an α-helical structure as determined by circular dichroism (Duff et al. 1992; Kovacs and Cross 1997). Furthermore, evidence has been presented that M2-TMP is oligomeric in bilayers (Kovacs et al. 2000) and tetrameric in micelles (Salom et al. 1999). Duff and Ashley (1992) reported that M2-TMP showed channel activity similar to M2 protein; however, in studying truncated M2 proteins, this result has been questioned (Tobler et al. 1999). With this caveat, M2-TMP has been, and is continuing to be, viewed as a significant stepping stone for structural characterization of this very important drug target (Duff et al. 1994).

The interstices of the lipid bilayer generate a unique environment for membrane proteins (Arumugam et al. 1996; Zhou et al. 2000). The balance of molecular interactions that stabilizes water soluble proteins is altered dramatically in this environment in which electrostatic interactions dominate and hydrophobic interactions are absent. This altered balance has substantial implications for protein folding (Engelman 1996; Hunt et al. 1997), for the role of "rare" water molecules that act potentially as catalysts for hydrogen bond exchange (Xu and Cross 1999), for influencing the potential energy surface of ion conducting channels (Koeppe and Andersen 1996; Cotten et al. 1999; Phillips et al. 1999), and so forth.

High-resolution structural restraints can be obtained from solid-state NMR spectra of uniformly aligned samples (Ketchem et al. 1997). In the absence of rapid isotropic molecular motions, the anisotropic nuclear spin interactions, such as dipolar and chemical shift interactions, provide detailed information on how individual atomic sites are oriented with respect to both the magnetic field and bilayer normal axes. Here, the analysis of ¹⁵N-¹H dipolar and ¹⁵N chemical-shift-correlated spectra are enhanced dramatically by resonance patterns that demonstrate uniquely an α-helical structure throughout the transmembrane segment (Wang et al. 2000; Marassi and Opella 2000). Moreover, these orientational restraints can be used to refine the α-helical structure to a high-resolution backbone structure.

Cysteine mutagenesis data (Pinto et al. 1997), although indicating only a small tilt angle, defined a rotational orientation that placed the hydrophilic residues toward the tetrameric axis in a left-handed helical bundle. Preliminary solid-state NMR data was consistent with a helical structure and indicated a tilt of the helical axis with respect to the bilayer of 33°–38° (Kovacs and Cross 1997; Song et al. 2000; Wang et al. 2000). Experiments using homogeneous preparations of either DMPC or DOPC have shown tilt angles in this range indicating that the tilt is an intrinsic property of this polypeptide (Kovacs et al. 2000). Furthermore, the rotational orientation for this helix and the left-handed symmetry of the tetrameric bundle were confirmed. Recently, Kukol et al. (1999) used infrared linear dichroism of specific site ¹³C labeled M2-TMP in DMPC bilayers to indicate a similar helical tilt and rotational angle. Here, a nearly complete data set for the hydrophobic region of M2-TMP is presented, leading to a high-resolution backbone structure of the monomer and implications for a tetrameric model.

Results and Discussion

Solid-state NMR spectra

Recently, the Polarization Inversion Spin Exchange at Magic Angle (PISEMA) experiment (Wu et al. 1994) has become a powerful tool for studying membrane protien structure by solid-state NMR. The M2-TMP PISEMA data displayed in Figure 1▶ was obtained from hydrated lipid bilayers uniformly aligned with respect to the magnetic field axis. All samples were aligned such that the bilayer normal was parallel to the magnetic field axis; the spectra were recorded above the gel to liquid-crystalline phase transition temperature. These spectra correlate the anisotropic ¹⁵N-¹H dipolar interaction with the anisotropic ¹⁵N chemical shift. Although the dipolar interaction leads to a pair of transitions, only one of the resonances is displayed, because the symmetry-related resonances (about the 0 kHz axis) are redundant. These spectra represent a superposition of spectra from single- and multiple-site-labeled peptides and therefore the resonance assignments are known absolutely.

Fig. 1.

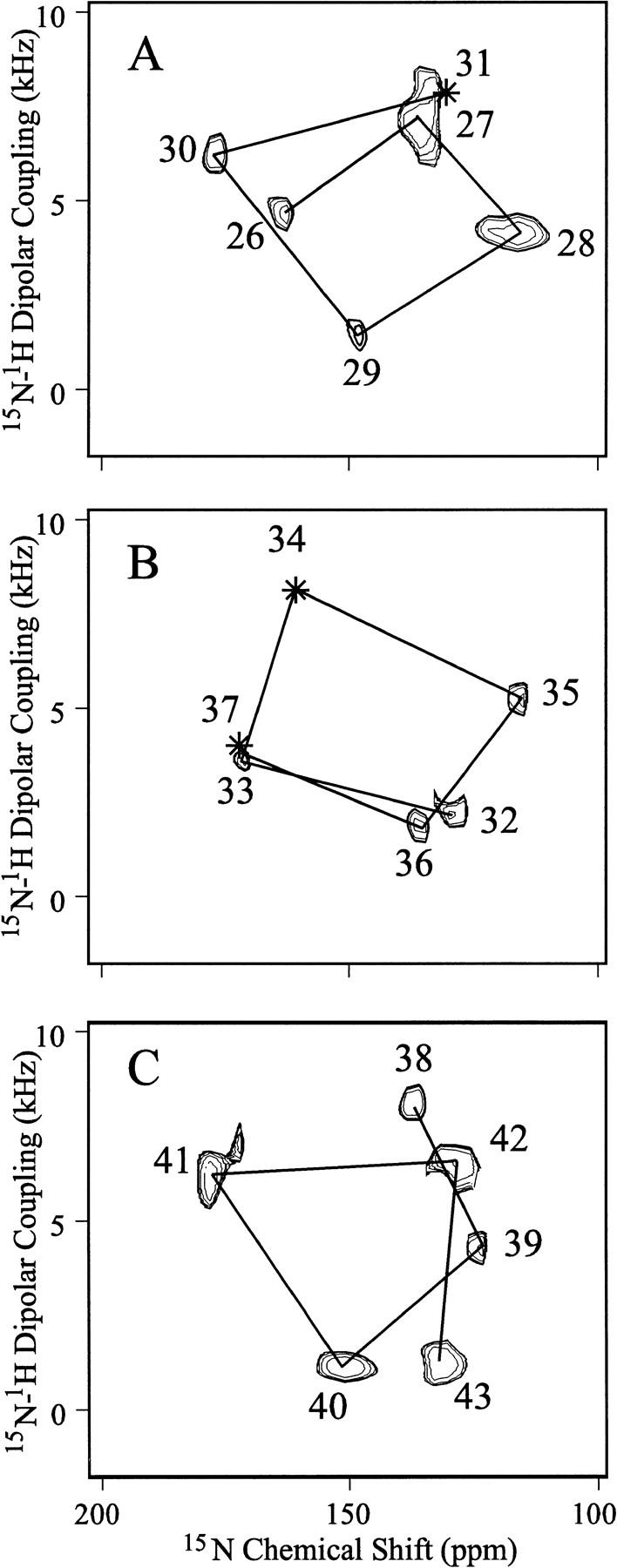
PISEMA spectra of single- and multiple-site-labeled samples that have been superimposed in three sequential groups: (A) sites 26–31, (B) sites 32–37, and (C) sites 38–43. Three sites in the hydrophobic transmembrane domain from residues 26–43 have not been observed: residues 31, 34, and 37. The samples are uniformly aligned DMPC bilayers containing M2-TMP in a 1:16 molar ratio oriented such that the bilayer normal is parallel to B_o. Hydration is ∼50%, pH is ∼7, and samples were observed at room temperature, above the gel to liquid-crystalline phase transition. The phase-alternated Lee-Goldberg homonuclear decoupling scales the dipolar interaction by 0.81 and, consequently, the dipolar scale has been adjusted appropriately. Only one of a symmetric pair of dipolar resonances is shown. Seven different M2-TMP preparations with the following labeled sites were used: 26–30; 26, 36, 38; 27, 28; 32, 33, 35, 39, 42; 40; 41; and 43. All spectral assignments have been confirmed by specific site labeling. Lines have been drawn between resonances from sequentially adjacent amino acids showing the presence of PISA wheels in the spectra directly reflecting helical wheels.

The resonances are relatively sharp, having a linewidth in the chemical shift dimension of ∼10 ppm and <1 kHz in the dipolar dimension. Consequently, the samples are well-aligned. Indeed, the difference in orientation of the σ₃₃ tensor element for an observed chemical shift of 150 versus 140 ppm is just 3.9° and the difference between 5 versus 6 kHz (Δν_obs of 10 versus 12 kHz) is just 3.6° in the orientation of the N–H bond with respect to the magnetic field axis. Because evidence has been presented previously that this peptide forms a functional state (Duff and Ashley 1992) and that the functional state of the protein is tetrameric (Sakaguchi et al. 1997), the observation here of a single resonance for each site makes it clear that this tetramer is symmetric or pseudo-symmetric with respect to the bilayer normal. Therefore, each monomer has the same precise orientation with respect to this axis.

Initial structure development and refinement

Lines have been drawn in the spectra connecting resonances from adjacent residues in the amino acid sequence. These lines illustrate clearly that helical wheels (Schiffer and Edmunson 1967) are being imaged directly in the PISEMA spectra. The spectra were divided into three subsets, or sequential fragments, only to avoid substantial resonance overlap, not because there is any break in the helical wheel pattern between these segments. Whereas it is known that the peptide is largely α-helical, it was not known for certain that the helical region extended without a break through the hydrophobic sequence. Directly, by observation of this resonance pattern, it is now clear that residues 26–43 are entirely helical.

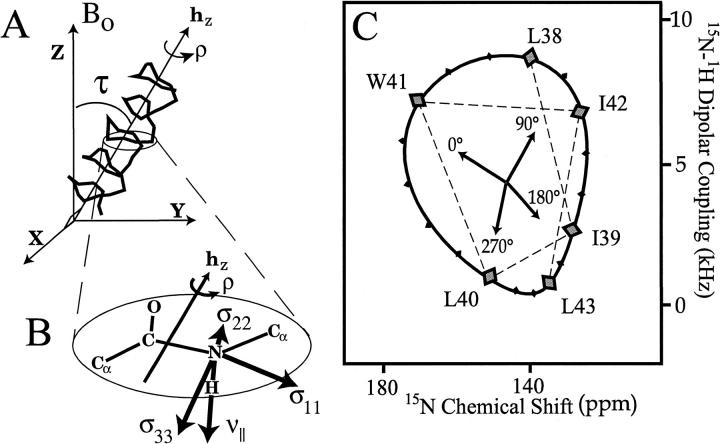
The origin of this resonance pattern stems from the anisotropic nature of the spin interactions. In Figure 2▶ a helix is tilted by 38° with respect to B_o and the bilayer normal. As shown for an ¹⁵N site (Fig. 2B▶), the dipolar (ν_obs) and chemical shift (σ_obs) interactions can be calculated based on the orientation of the principal axis frames, which are fixed in the molecular frame. Such calculations for each amide in the backbone of this helix result in the displayed pattern of resonances reflecting a helical wheel. We refer to this pattern as a PISA wheel, after the PISEMA spectrum and for Polar Index Slant Angle (Marassi and Opella 2000; Wang et al. 2000). Indeed, the position of this pattern of resonances within the spectrum defines the tilt (or slant angle, τ) of the helix with respect to B_o. However, the position of the resonances around the ring is dependent on another angle, the rotational orientation of the helix about its axis, ρ_o. This PISA wheel is calculated for a tilt angle of 38° and a rotational angle of −50°; ρ_o = 0° is defined when the peptide plane containing the Leu-26 nitrogen is perpendicular to the B_oh_Z plane in the "upper" surface of the helix (Fig. 2▶).

Fig. 2.

The PISA wheels can be simulated for a given ideal helical tilt (A) by calculating the ¹⁵N-¹H dipolar coupling and anisotropic ¹⁵N chemical shift as a function of rotational orientation, ρ (B). When a peptide plane is perpendicular to the plane B_oh_z, ρ is defined as either 0 or 180°. 0° or the "upper" surface is distinguished by a smaller N-H bond orientation with respect to B_o and the bilayer normal. It is shown that for a given position in the PISEMA spectrum it is possible to define the orientation of the laboratory frame of reference (C).

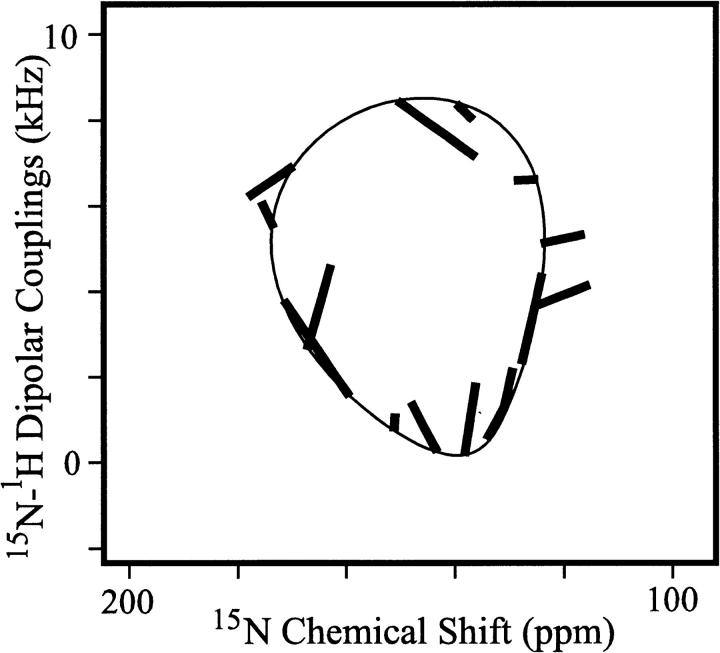
The data in Figure 1▶ fits this specific PISA wheel remarkably well. Shown in Figure 3▶ are line segments for each amide resonance connecting the theoretical (based on an ideal helix) and experimental values. The RMSD for the anisotropic chemical shift using average chemical shift tensors is just 7.3 ppm and for the dipolar interaction using an average dipole coupling constant is 1.2 kHz. Such values translate into only a few degrees of error, despite the fact that this fit is based on averaged tensors and an ideal helix with absolutely uniform torsion angles and covalent geometry. Although ambiguities exist in the interpretation of isolated anisotropic dipolar and chemical shift values (Quine et al. 1997; Quine and Cross 2000), here the ambiguities can be resolved completely as it is known that the protein segment is an α-helix from the observed PISA wheel. As a result, an initial structure can be defined from the NMR data and, importantly, the structural orientation is defined with respect to its environment. Based on the correlation between pairs of chemical shift and dipolar data, a general approach for developing an initial structure can be achieved (Wang, Quine, Denny, and Cross, unpubl.).

Fig. 3.

Line segments are shown illustrating differences between theoretical positions on a PISA wheel based on an ideal helix, average chemical shift tensor values, and the observed PISEMA resonances. The RMSD for the heteronuclear dipolar coupling is 1.2 kHz and for the anisotropic chemical shift is 7.3 ppm. These small deviations mean that the M2-TMP helix in the lipid bilayer environment forms a nearly ideal helix. The shape of this PISA wheel pattern indicates relatively uniform chemical shift tensor element magnitudes and uniform relative orientation of the dipolar and chemical shift tensor elements (Wang et al. 2000). On refinement of the M2-TMP helix a virtually perfect fit of predicted and observed values is achieved.

Using an initial structure with varied tilt and rotational orientation, refinement against the CHARMM energy, standard α-helical hydrogen bonding distances with an error bar of ±0.3 Å, and the set of experimental orientational restraints was performed. However, because of the precision of the experimental restraints and the fact that these restraints orient the protein in the laboratory frame of reference, only small changes in the structure can be tolerated in any single step in this simulated annealing approach. Indeed, a single torsional change may affect the orientation of a large portion of the structure with respect to the magnetic field significantly, thereby inducing numerous experimental restraint penalties. Consequently, compensating torsional moves of ξ_i and φ_i+1 of equal magnitude (≤3°) and opposite sign were used. In this way, considerable conformational space was traversed in a typical annealing run of more than 30,000 successful steps, as has been demonstrated previously (Ketchem et al. 1997; Kim, Quine, and Cross, unpubl.).

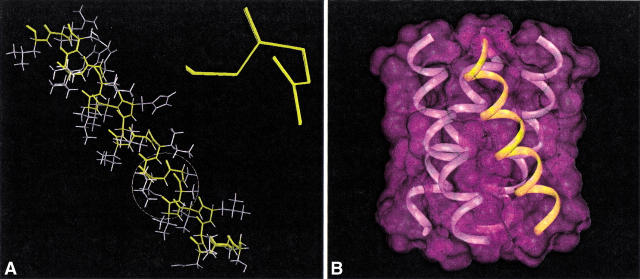
Thirty refinements resulted in a set of backbone structures that superimposed with an RMSD of 0.05 Å. In Figure 4A▶, the α-helical values of the torsion angles are shown in a Ramachandran diagram. Although the helix is nearly ideal, the refinement defines torsion angles consistently that are significantly different from neighboring sites, as shown in Figures 4B and 4C▶. The outlying φ angle for Leu-26 results from the neighboring residue being Pro-25. The narrow range of torsion angles given for each site as a standard deviation about the average value among the set of thirty structures shows that the experimental restraints have resulted in a very high-resolution structure for this monomer, as shown in Figure 5A▶. It is important to recognize that this structure represents a time-averaged characterization and that such high-resolution should not be confused with a rigid structure.

Fig. 4.

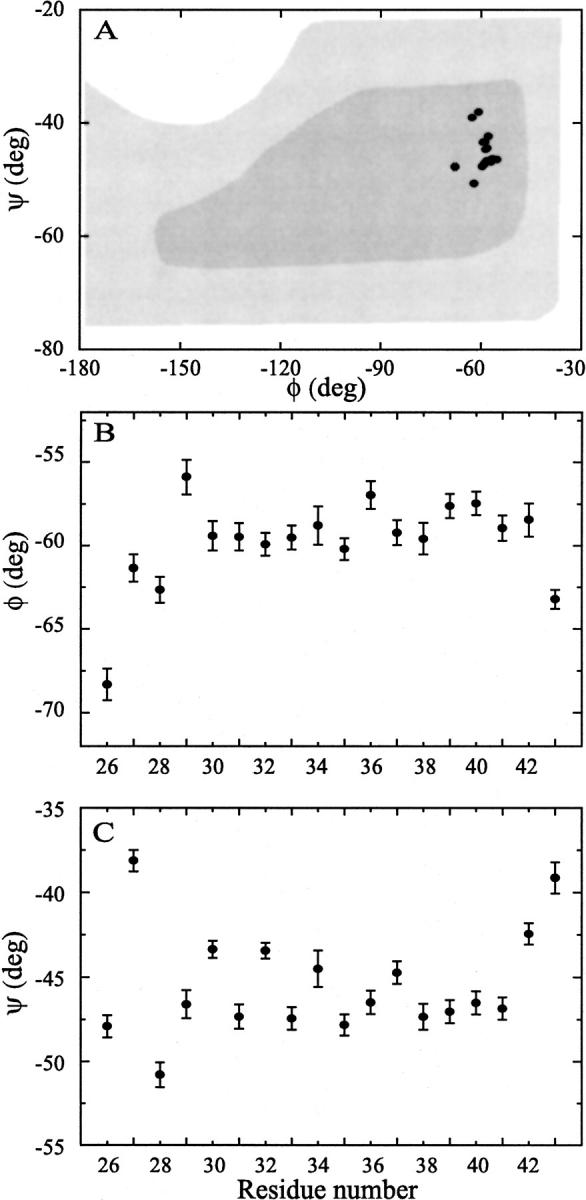
(A) On refinement of the M2-TMP helix a small but significant dispersion in both φ and ξ angles is observed within the α-helical region of the Rhamachandran diagram (here adapted from Voet and Voet (1990)). (B) φ distribution for each of the resonances in the sequence 26–43 contained within M2-TMP. Note that residue 25 is a proline. The distribution for each residue is obtained from a set of 30 refinements. (C) ξ distribution as for the φ in B. Note that the individual residue distributions are small compared to the distribution of angles for the various residues.

Fig. 5.

(A) A set of 30 refined backbone structures of M2-TMP. Residues 29–31 are expanded to show the quality of the refinements. (B) A model of the tetrameric structure is illustrated, showing symmetry between the four helices as observed experimentally and consistent with the refined monomer structure. Note that the crossing point between adjacent helices may not be at the very center of the bilayer. Such a change in the tetramer structure can be achieved without changing the monomer backbone structure or its orientation with respect to the bilayer normal.

A tetrameric model and comparison to other models

With a well-defined monomeric structure it is possible to constrain a model of the tetramer. In addition, it is known that the tetramer is symmetric or pseudosymmetric and that a left-handed bundle is formed. A unique m of the tetramer requires characterization of two additional independent variables, the radii for the bundle at the N-terminal membrane surface and at the C-terminal membrane surface. These variables have a considerable range over which the tilt and rotational orientation of the monomer remain absolutely fixed. If the precise sidechain orientations were known, docking of the four helices might lead to a most-probable structure. Alternatively, distance restraints between helices could lead to structural characterization of the bundle. Despite not having such information, it is possible to evaluate features of the tetrameric models, and their monomers, that have been put forth in the literature. For comparison purposes a tetrameric model with equal N- and C-terminal bundle radii is shown in Figure 5B▶.

To compare various models, simulated PISEMA data have been generated for Figure 6▶ and analyzed as if they were experimental results. There are five models, in addition to the experimental results displayed in Figure 6A▶, that are compared by presenting information from the N-terminal (27–31 residues) and C-terminal (40–43 residues) regions of the transmembrane domain of this polypeptide. The experimental PISEMA data (Figure 6A1▶) fit a theoretical PISA wheel based on an ideal helix with only a small RMSD in ppm and kHz, as noted previously. Consequently, there is no significant change in the helical tilt from one end of the helix to the other. The rotational orientation of a helix is characterized (Figure 6A2) by correlating experimental ρ values obtained from analysis of the PISEMA spectra as in Figure 2C▶ with predicted values from a helical wheel in which Leu-26 is assigned arbitrarily to 0° and 3.6 residues per turn is assumed. If the native helix has 3.6 residues per turn, the correlation in Figure 6A2▶ should conform to a line with a slope of 1.0. The experimental data in Figure 6A2▶ shows that there is little, if any, change in ρ_o from one end of the observed M2-TMP structure to the other. Again, the uniformity of the helical structure permits the linear extrapolation to ρ_o with only a small error bar (±10°).

Fig. 6.

Comparison of M2-TMP models using experimental and simulated PISEMA results. (A) From the experimental data and structural refinement presented in this publication; (B) from Kukol et al. (1999), this structure is based on limited infrared linear dichroism orientational constraints and a constant separation of helical axes resulting in a coiled coil structure; (C) from Pinto et al. (1997) using cysteine mutagenesis data and model building; (D) from Zhong et al. (1998) this molecular dynamics structure was developed in an octane/water environment; (E) from Forrest et al. (1999), this molecular dynamics structure was developed in a water/POPC bilayer environment; (F) from Schweighofer and Pohorille (2000), this molecular dynamics structure was also developed in a bilayer environment using water/DMPC. Column 1 (A) represents the experimental (A1) and simulated (B1–F1) PISEMA spectra for the molecular models. Column 2 represents an analysis of the data in column 1 in which ρ values determined from the PISEMA spectra are plotted against predicted ρ values from the M2-TMP helical in which Leu-26 is assigned a value of 0°. The lines in column 2 have a slope of 1.0 (thereby assuming 3.6 residues/turn) and reflecting ρ_o values for an ideal helical segment superimposed on the model with minimal C_α carbon RMSD. In columns 1 and 2, data for N-terminal regions are labeled by * and C-terminal regions by Δ. Column 3 represents the backbone structure for different models, in which the analyzed helices are labeled in yellow or cyan.

However, this ρ analysis is dependent on the tilt angle. Small tilt angles result in a poor characterization of experimental ρ values, because the experimental errors do not scale with the size of the PISA wheel. Furthermore, several of the models display considerable local distortion resulting in greater variability in chemical shift and dipolar interactions than in the time-averaged observed data. Consequently, the lines of slope (= 1.0) in the second column of Figure 6▶ are calculated by fitting the C_α carbons of an ideal helix to the model peptide segments to achieve a linear extrapolation to ρ_o (Table 1▶). Therefore, the simulated `data points' from the models in the second column of Figure 6▶ do not always match the calculated lines. This is particularly evident in the molecular dynamics `snapshot' models in which there is considerable local distortion.

Table 1.

τ and ρ0 values from models of M2 protein

		Monomer 1		Monomer 2
		N	C	N	C
Experimental	τ	38°	38°
	ρ0	−43°	−62°
Kukol et al. 1999	τ	31°	31°
	ρ0	−52°	20°
Pinto et al. 1997	τ	12°	12°
	ρ0	−28°	−33°
Zhong et al. 1998	τ	25°	35°	23°	9°
	ρ0	−61°	−40°	11°	−80°
Forrest et al. 1999	τ	19°	19°	9°	9°
	ρ0	−9°	−54°	−56°	−82°
Schweighofer and Pohorille 2000	τ	23°	23°	43°	7°
	ρ0	−57°	−70°	−44°	−90°

The model of M2-TMP developed by Arkin, Brunger and coworkers in Figure 6B▶ (Kukol et al. 1999) utilized novel orientational restraints from infrared linear dichroism of ¹³C₁-labeled M2-TMP. Like the NMR-derived orientational restraints, these data restrain both the tilt and rotational orientation of the helix. Using this very limited data set and assumed helical tilt, a search of rotational orientations with the OPLS force field was conducted, resulting in the structure presented in Figure 6B3▶. The model presents helices tilted by 31° to the bilayer normal, a value quite similar to the value of 38° shown in Figure 6A▶. However, in the model building for this tetramer, harmonic restraints were employed to maintain helical geometry and assumed distance restraints were employed to maintain the helical centers within 10.5 Å of one another. Tetrameric symmetry was also assumed, as is consistent with our experimental results. Because of these assumptions, a coiled coil structure was formed. Such a helical deformation caused the ρ_o value to change by 72° from the N- to C-terminal regions of the transmembrane peptide as shown in Figure 6B2▶ and Table 1▶. This substantial change in ρ_o is inconsistent with the experimental results in Figure 6A2▶. Therefore, the assumption of a constant interhelical separation is not supported by our experimental data. Note, however, that the N-terminal segment of this model, from which the infrared linear dichroism data was acquired (site Ala-29 and Ala-30), has approximately the same ρ_o value as in the experimental data of Figure 6A2▶.

DeGrado and coworkers (Pinto et al. 1997) obtained extensive cysteine mutagenesis data from intact M2 protein in Xenopus laevis oocytes followed by modeling of the transmembrane fragment in a tetrameric bundle. A number of tetrameric structures were developed consistent with the mutagenesis data and energy-minimized in vacuo using molecular mechanics with Discover (Biosym Technologies, San Diego). The resultant models converged to a set of structures that differed by 1.1 Å RMSD. This model in Figure 6C▶ is one of the seven models closest to the centroid of minimized models (Pinto et al. 1997) and displays a helix tilt of only 11°. Consequently, it is seen that the cysteine cross-linking data is relatively insensitive to helix tilt. However, the symmetry of the bundle is consistent with our data, as are the ρ values for the N- and C-terminal segments. It should also be noted that differences in the sample preparation may be responsible for the observed differences in helix orientation.

The remaining three models represent molecular dynamics efforts and the structures shown are `snapshots'. Klein and coworkers (Zhong et al. 1998) have developed a tetrameric model based on an original model by Duff and Ashley (1992). This structure was placed in the octane phase of a water/octane membrane-mimetic environment with a TIP3P water model. A 4 ns trajectory using the CHARMM force field results in Figure 6D3▶ in which it is clear that the tetramer is not symmetric; indeed, each of the helices is different. In analyzing just two of the helices, the terminal segments span tilt angles of 7° to 45° and ρ angles from −80° to +11° (Table 1▶). This high degree of variability is due, in part, to the short time constant associated with the `snapshot' images of the tetramer, but the extent of local and monomer deformations is greater for this model than others and particularly large compared to the ideality of the monomer structure determined from the time-averaged NMR data.

Sansom and coworkers (Forrest et al. 1999) have used water/POPC bilayers as the environment for molecular dynamics calculations with the GROMOS 87 force field and SPC modeled water molecules. Polypeptides of 18 and 22 residues were modeled in a tetrameric bundle. The molecular dynamics led to a structure that appears to approximate a dimer of dimers (Figure 6E3▶). This break in symmetry is not supported by the experimental results. Although this structure shows considerable variability in local structure, it is the most regular of the molecular dynamics structures. The ρ values are quite similar to the observed results, but the helical tilt is still much less than what we observe. Schweighofer and Pohorille (2000) have also used a water/lipid bilayer environment. In this case, the water is a TIP3P model and the lipid is DMPC. The force field used is AMBER 4.1. The `snapshot' image in Figure 6F3▶ has uniform ρ values, but the tilt angles vary dramatically both between helices and within helices.

Implications from a high resolution structure in a bilayer environment

The experimental data presented in this manuscript defines to high-resolution the structure of the M2-TMP monomer, most probably in a tetrameric state. This structure shows a remarkably uniform helix of 3.56 ± 0.04 residues per turn, modest if any coiling of the helices in the tetrameric bundle, and a helical tilt from one end to the other that is 38 ± 3°. This structure has been determined in a hydrated lipid bilayer environment above the gel to liquid-crystalline phase transition temperature. We suggest that the low dielectric environment of the bilayer interstices force the hydrogen bonds to have uniform geometry, minimizing the exposure of the amide partial charges to the hydrocarbon environment. This explains the lack of local distortions, as well as the lack of changes in tilt and rotational orientation from one end of the helix to the other. The low dielectric of the environment also explains the lack of coiling, which forces non-uniform geometry on the hydrogen bonds on the exterior of the bundle versus the interior. The result of this environment is nearly an ideal helix as shown by the refined φ, ξ torsion angles.

Various tetrameric models have been compared to the known monomeric structure and the known orientation of this structure with respect to the bilayer normal. Present tetrameric models rely heavily on computational methods and energy calculations that do not yet have the necessary subtlety to characterize uniquely the α-helical interface or to reproduce the high-resolution experimental backbone structure. The complexity of the task associated with a heterogeneous environment and weak interactions between monomers that forms this four-helix bundle is considerable. The models developed by others and made available to us graciously have stimulated much of our thinking about the lipid bilayers as a unique environment for proteins. With the present data, time-averaged symmetry or pseudosymmetry is an essential feature for this tetrameric bundle, as is the avoidance of kinked or bent helical structures. Even local distortions are unlikely in such a low dielectric environment where electrostatic interactions are far more important than hydrophobic interactions.

The experimental data and analysis for the transmembrane segment of the M2 protein provides a major advance for the modeling of this critically important protein in the control of influenza A viral infections. Membrane protein structures that have an extensive lipid-exposed surface, such as M2, will be influenced substantially by the heterogeneous membrane environment. How this environment is modeled for either experimental or computational studies continues to be a very important issue for nearly 30% of the proteins from known genomes.

Materials and methods

Peptide synthesis and sample preparation

Isotopically labeled amino acids were purchased from Cambridge Isotope Laboratories (Cambridge, MA) and used to prepare the Fmoc derivatives as described previously (Fields et al. 1988, 1989). All of the peptides were made using solid phase peptide synthesis on an Applied Biosystems 433 A peptide synthesizer (Foster City, CA) and cleaved from the resin as described previously (Kovacs and Cross 1997). Oriented samples of the peptide in hydrated lipid bilayers were prepared by first co-dissolving M2-TMP and dimyristoylphosphatidylcholine (DMPC) in trifluoroethanol (TFE). The solution was then spread onto approximately 60 glass plates (70 μm thickness). After vacuum drying to remove TFE, 2 μl of sterile-filtered water was added to each plate; then the plates were stacked into a glass tube and placed in a chamber containing a saturated solution of K₂SO₄ for hydration. Oriented bilayers formed after equilibrating the sample in this chamber at 42°C overnight. This sample container was then sealed with a microscope cover glass and epoxy to maintain sample hydration during the experiments.

Solid-state NMR spectroscopy

Solid-state NMR measurements were performed on a home-built 400 MHz spectrometer using a Chemagnetics data acquisition system and a wide-bore Oxford Instrument 400/89 magnet. A home-built probe with a rectangular coil was double-tuned to the resonance frequencies of ¹H at 400.4 MHz and ¹⁵N at 40.6 MHz. Conditions for the PISEMA experiments were used as described previously (Song et al. 2000). All ¹⁵N chemical shifts are relative to the resonance for a saturated solution of ¹⁵NH₄NO₃ at 0 ppm.

Structural analysis

The PISEMA spectra of different structural models were simulated from their coordinates. The magnetic field axis, B_o, was set parallel to the tetrameric axis and the bilayer normal. Average values from experimental data for the chemical shift tensors (σ₁₁ = 31.3 ppm, σ₂₂ = 55.2 ppm, σ₃₃ = 201.8 ppm) were used, as well as a value for the dipolar magnitude of 10.735 kHz. A typical relative orientation for the σ₃₃ CSA tensor element and ν_|| of the dipolar tensor of 17° was used and confirmed (Wang et al. 2000).

For a given tilt angle, PISA (Polar Index Slant Angles) wheels were calculated by rotating the helix about its axis by an angle, ρ, while calculating the anisotropic dipolar and chemical shift observables (Wang et al. 2000). To determine the tilt angle of a α-helix relative to B_o, a series of simulated PISA wheels were overlaid with experimental or modeled data in a PISEMA spectrum which was obtained either from experiments or model simulations. The rotational orientation of the helix can also be assessed from the PISA wheel by correlating an angle calculated using the theoretical PISA wheel and a value from an ideal helical wheel. The assessed ρ values of each resonance were plotted against the predicted ρ values assuming an ideal helix of 3.60 residues per turn. The extrapolation and intersection of the best fit line (with a slope of 1.0) generates a referenced ρ value for Leu-26, known as ρ₀.

Structural refinement

The refined M2-TMP monomer structure was obtained by a geometrical search using a search algorithm to obtain a minimum of the global penalty function that incorporates all the orientational restraints and the CHARMM empirical function (Brooks et al. 1983).

The penalty function used to control the structural refinement is the sum of the structural penalties and the energy, in which each structural penalty refers to a particular data type (e.g. ¹⁵N chemical shift or ¹⁵N-¹H dipolar couplings) and

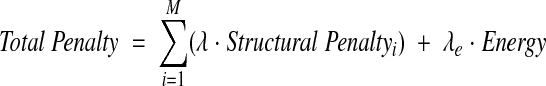in which M is the number of structural penalties and λ is a scaling factor. The individual structural penalties are calculated as,

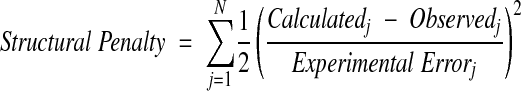in which N is the number of measurements of a specific data type.

The simulated annealing is used to perform the minimization of this penalty function in this high-dimensional configuration space (Metropolis et al. 1953; Kirkpatrick et al. 1983). Modifications to the structure are made by allowing the complete geometry of the polypeptide to vary through modifications of the atomic coordinates and changes in peptide plane orientation (Ketchem et al. 1997). To search the necessary conformational and local structural space, both atom and torsional modifications were used. Random atom moves with a small diffusion parameter of 5 × 10⁻⁴ Å in each of three Cartesian axes relaxed the atomic geometry and helped minimize the global penalty. Torsional moves were generated as compensating ξ_i and φ_i+1 moves of equal magnitude and opposite sign (Peticolas and Kurtz 1980) by a random amount up to + 3° per step. Because the structural restraints are absolute restraints (i.e., they orient the molecular structure with respect to B_o), it is necessary that global orientation be refined, as well as local structure. Torsional movements help to adjust the global orientation whereas atomic movements allow the local conformational space to be searched. The ratio of attempted atom and torsional moves and other annealing parameters were optimized through numerous refinement attempts (Kim, Quine, and Cross, unpubl.).

The orientational restraints imposed on the structure during refinement are 15 ¹⁵N chemical shifts and 15 ¹⁵N-¹H dipolar couplings from PISEMA experiments. The observed chemical shifts are compared to calculated values from the molecular coordinates and the known tensor element magnitudes and assumed tensor orientations (Teng et al. 1992; Kovacs and Cross 1997; Wang et al. 2000). A change in the orientation of the atomic coordinates leads to a change in the calculated chemical shifts and a resultant change in the penalty. The observed dipolar couplings are also compared to calculated values derived from the atomic coordinates and knowledge of the interaction tensors in the molecular frame of reference. The refinement was carried out in vacuo with the initial coordinates of an ideal α-helix structure (3.6 residues per turn) having a range of tilt and rotational orientations with respect to the bilayer spanning the values obtained from the PISA wheels. During the calculation, to constrain the structure of the α-helix, typical α-helical hydrogen bond distance constraints of N to O of 2.99 Å and O to H of 2.06 Å (Jeffrey and Saenger 1994) were used with an error bar of ±0.3 Å. The initial structures were aligned in different orientations to search the global orientation values that we have obtained from PISA wheels (Kim, Wang, and Cross, unpubl.).

The simulated annealing refinement procedure was performed according to the following temperature and annealing schedule. The initial value of the temperature was set at 350 K and an equilibration period of 5000 attempted modifications with constant temperature was used to initiate the refinement. Then the system configuration underwent 2000 attempted modifications or 200 accepted modifications, whichever was first, before the temperature was lowered by 1%. The refinement was terminated when either no successful structural modifications were found at a particular temperature after the 2000 attempted modifications or after 500 temperature steps. After equilibration, the temperature dropped relatively fast as many of the initial moves were accepted. As the refinement continued, the temperature dropped less often as fewer accepted moves were found. All calculations were performed by the program TORC (Total Refinement of Constraints) developed for incorporating orientational restraints and CHARMM energy (Ketchem et al. 1996).

After refining the monomer structure of M2-TMP, the symmetric tetramer was generated by duplicating the helix and rotating it by 90°, 180°, and 270°. An inter-helix distance of 10 Å, which is the mean interhelical distance for many known tetrameric bundled structures (Harris et al. 1994), was chosen for the separation of C_α carbons of the Gly-34 residues. The symmetric tetramer was then energy minimized to avoid steric conflicts between the monomers.