Electrostatic contributions to protein–protein interactions: Fast energetic filters for docking and their physical basis

Abstract

The methods of continuum electrostatics are used to calculate the binding free energies of a set of protein–protein complexes including experimentally determined structures as well as other orientations generated by a fast docking algorithm. In the native structures, charged groups that are deeply buried were often found to favor complex formation (relative to isosteric nonpolar groups), whereas in nonnative complexes generated by a geometric docking algorithm, they were equally likely to be stabilizing as destabilizing. These observations were used to design a new filter for screening docked conformations that was applied, in conjunction with a number of geometric filters that assess shape complementarity, to 15 antibody–antigen complexes and 14 enzyme-inhibitor complexes. For the bound docking problem, which is the major focus of this paper, native and near-native solutions were ranked first or second in all but two enzyme-inhibitor complexes. Less success was encountered for antibody–antigen complexes, but in all cases studied, the more complete free energy evaluation was able to idey native and near-native structures. A filter based on the enrichment of tyrosines and tryptophans in antibody binding sites was applied to the antibody–antigen complexes and resulted in a native and near-native solution being ranked first and second in all cases. A clear improvement over previously reported results was obtained for the unbound antibody–antigen examples as well. The algorithm and various filters used in this work are quite efficient and are able to reduce the number of plausible docking orientations to a size small enough so that a final more complete free energy evaluation on the reduced set becomes computationally feasible.

The ability of many proteins to form specific stable complexes with other molecules is fundamental to all biological processes. Understanding the structural and physical chemical factors that determine affinity and specificity in complex formation is thus a problem of considerable general importance. The ability to predict the structure of complexes from a knowledge of the structures of the individual subunits alone, the docking problem, provides a test of our level of understanding but also has many practical applications. Protein/small molecule docking is a central component in most structure-based drug design strategies, and, for example, a solution of the protein–protein docking problem would allow the prediction of the structure of multidomain proteins from the structures of the individual components.

Docking is generally divided into the bound and unbound problems. The bound problem attempts to reproduce the structure of a complex, assuming that the conformation of the individual subunits in their monomeric states is identical to their conformation in the complex. This assumption is removed in the unbound problem, which begins with the observed conformations of the free monomers and thus requires that conformational changes that accompany binding be accounted for. For cases in which these changes are significant, the assumptions of the bound problem are clearly not applicable. In addition to treating problems involving minimal conformational change, the value in studying the bound problem lies in providing a framework for generating geometrically correct conformations and evaluating them in energetic terms. A true solution to the bound problem would imply that the energetic determinants of binding are properly understood, thus providing an important step toward the solution of the unbound problem.

In this paper, the receptor is defined as the member of a complex that is kept fixed, whereas the ligand, which will in general be another protein, is the molecule that is docked against the receptor. For rigid body docking, possible binding modes of the ligand can be described in terms of a simple linear transformation of the ligand coordinates. Because such a transformation depends on a very small number of parameters, exhaustive sampling of the rotational and translational degrees of freedom using a finite step size is a viable technique to generate possible relative orientations of the two molecules. Several docking methods have been described that use such an approach (Katchalski-Katzir et al. 1992; Gabb et al. 1997; Bliznyuk and Gready 1999; Ritchie and Kemp 2000). Although exhaustive sampling results in a high probability of generating a binding mode that is close to native, the computational cost of evaluating each solution often requires that methods be developed that limit the number of binding orientations that must be considered, which can be on the order of hundreds of millions (Ritchie and Kemp 2000) or even billions (Roberts and Pique 1999). In this paper, we use a method that defines both the rotational and translational components of the ligand transformation as those that map pairs of surface points of the ligand and their associated normals onto pairs of surface points and normals of the protein (Norel et al. 1995Norel et al 1999a^,Norel et al. b). The entire surface of both interacting molecules is searched. That is, there is no restriction that the search be limited to a known binding region of the receptor.

A variety of approaches have been used to rank the large number of possible docking orientations that are generated by different algorithms. Shape complementarity is an essential criterion and has been represented with several functional forms (Katchalski-Katzir et al. 1992; Helmer-Citterich and Tramontano 1994; Norel et al. 1995; Palma et al. 2000); however, there are many cases where nonnative binding modes display better shape complementarity than native or near-native conformations. Estimates of binding affinities based on simplified potential functions have also been used in ranking (Totrov and Abagyan 1994; Gabb et al. 1997; Moont et al. 1999); however, a detailed calculation of binding free energies is too computationally demanding to be used in large-scale screens. In general, considerable success has been encountered in problems involving protein–ligand and enzyme–inhibitor complexes, but antibody–antigen systems have been more challenging (Jiang and Kim 1991; Helmer-Citterich and Tramontano 1994; Norel et al. 1995; Meyer et al. 1996). More detailed energetic evaluation has led to improved results (Totrov and Abagyan 1994; Jackson et al. 1998; Shoichet et al. 1999; Camacho et al. 2000) indicating that, given adequate computer time, an accurate ranking procedure might be developed.

A goal of this work is to develop a simplified scoring function that is fast enough to rank a large number of conformations and accurate enough so that a native or near-native conformation is highly ranked. Our focus is on the bound problem because this allows us to deal directly with the energetic determinants of binding without the need to describe the conformational changes that accompany binding. However, we show in the following sections that the scoring function developed for bound docking leads to a significant improvement for the unbound problem as well. We first show that a free energy evaluation based on the Poisson-Boltzmann equation (Froloff et al. 1997) is extremely successful in distinguishing correct from incorrect docked conformations. On this basis, a simplified energy-based scoring function is developed that contains some of the elements of the more complete free energy evaluation. Its inclusion as one in a series of fast filters allows us to reliably idey the native and near-native conformations for a significant number of antibody–antigen and enzyme–inhibitor complexes.

Results

Calculations of binding affinities

We selected a set of experimentally determined protein–protein complexes from the Protein Data Bank (PDB) (see Materials and Methods for a complete list of these complexes) and used a previously described docking algorithm (Norel et al. 1994Norel et al. 1995) to generate many nonnative binding modes for these complexes. This algorithm is described in detail following. Briefly, after generating a set of possible binding modes, it uses a set of filters to eliminate those modes that would be expected to be incorrect based on geometric and simple energetic criteria. To evaluate the ability of a complete binding free energy evaluation (within the assumptions of continuum electrostatics) to idey correct complex geometries, calculations were performed on a subset of proteins. The subset included structures generated for three antibody–antigen complexes: D1.3 and HyHEL5 antibodies with lysozyme (PDB codes 1fdl [Fischmann et al. 1991] and 3hfl [Cohen et al. 1996]) and the complex of neuraminidase N9 with the antibody NC41 (PDB code 1nca [Tulip et al. 1992]). For each complex, the native structure, along with 10 nonnative orientations, were chosen—a total of 33 complexes. These all corresponded to conformations that passed geometric filters. Among the top orientations as defined by their geometric score, we removed orientations with a low number of interfacial hydrogen bonds and low interfacial hydrophobic and total surface areas as compared with those of native conformations. This eliminated orientations that were clearly nonnative-like.

Table 1 shows the binding free energies (referred to as ΔG'_total and calculated using equation 4), as well as several structural features of the native binding mode and of the 10 nonnative binding modes for each of the three antibody–antigen complexes in our test subset. Despite the requirement that nonnative solutions have a comparable buried interfacial area and shape complementarity as measured by the geometric score, the native and/or near-native (the best solution in terms of root mean square deviation [RMSD] that was generated by the docking algorithm) binding modes consistently have the lowest free energy of binding. Many more examples will be given following of the ability of a full free energy evaluation to idey the native conformation. It is also notable that in all examples listed in Table 1, the electrostatic component free energy of binding, which we term ΔG_elec and calculate using equation 5, has its lowest value for the native conformation.

Table 1.

Energetic and structural properties of various binding modes

Structurea	RMSD	GS	ΔGelec	TΔSac	ΔAc	ΔG`total	κ
1fdl-native	0.0	328.0	19.4	−16.5	1018.5	−15.0	0.0
Model 1	43.9	431.3	150.0	−34.7	2662.3	51.6	−6.5
2	72.4	372.0	82.6	−27.1	1499.8	34.7	−5.0
3	55.4	353.0	56.2	−22.3	1405.0	8.3	−1.5
4	53.2	345.9	109.4	−34.8	1684.7	59.9	−8.0
5	18.9	344.0	89.5	−19.6	1422.9	37.9	−1.5
6	61.9	337.0	74.3	−24.4	1541.5	21.6	−3.0
7	43.6	333.0	154.2	−37.2	2401.7	71.3	−7.5
8	35.1	330.0	79.5	−24.5	1240.4	42.0	−5.5
9	46.5	326.0	78.9	−25.8	1714.5	19.0	−5.5
10	60.3	297.0	88.1	−24.2	1331.9	45.7	−4.0
1nca-native	0.0	535.0	33.4	−21.5	1582.0	−24.2	−0.5
Model 1	85.8	489.9	111.2	−25.7	2356.1	19.2	−6.5
2	2.1	440.0	50.3	−21.6	1588.0	−7.5	−1.0
3	42.7	440.0	160.9	−27.3	2162.0	80.0	−10.5
4	99.3	435.0	156.4	−22.4	1860.1	85.9	−7.5
5	2.2	423.0	53.4	−20.0	1554.0	−4.3	−2.0
6	99.0	420.0	168.6	−25.4	1925.1	97.7	−8.5
7	57.5	418.0	74.4	−16.1	1688.4	6.1	−3.0
8	77.7	413.0	65.8	−18.7	1660.7	1.5	−2.0
9	55.4	409.0	45.4	−19.9	1644.6	−17.0	−1.5
10	2.3	298.6	50.2	−26.2	1962.2	−21.7	−0.5
3hfl-native	0.0	500.0	18.7	−18.8	1629.1	−43.9	1.0
Model 1	59.1	469.0	92.9	−19.4	1633.7	30.7	−3.0
2	22.5	413.0	72.1	−18.9	1562.6	12.8	−4.0
3	44.2	401.0	111.7	−21.3	1645.4	50.7	−2.0
4	59.3	399.0	98.3	−22.4	1622.9	39.5	−5.5
5	87.8	388.0	97.5	−24.3	1646.2	39.4	−4.5
6	42.6	374.0	31.4	−22.7	1131.4	−2.5	−1.0
7	73.7	365.0	77.6	−21.3	1528.4	22.5	−0.5
8	52.7	352.0	95.3	−22.2	1520.9	41.5	−3.5
9	3.1	172.0	43.9	−20.8	1703.4	−20.5	1.0
10	2.0	151.0	26.2	−20.5	1953.3	−51.1	−1.0

All energies are expressed in kcal/mole and areas in Ų.

^a Model structures are ordered according to their geometric score.(RMSD) Root mean square deviation between the model and the native binding mode: (GS) the geometric score calculated with Equation 2; (ΔG_elec) electrostatic contribution to the binding affinity as defined in Equation 5; (TΔS_ac) entropy loss binding; (ΔA_c) curvature corrected surface lost on formation of the complex; (ΔG`_total) ΔG_elect + TΔS_sc + γΔA_c; (κ) burch score calculated using Equation 1.

Correlation of binding free energies with structural features

In Figure 1 ▶ ΔG_elec is plotted against a number of descriptors of the interface to see if there is any simple correlation between the calculated affinity and structural parameters. The descriptors include (a) number of intermolecular hydrogen bonds in a complex; (b) coulomb interaction between monomers in a complex (calculated with an effective dielectric constant of 80); (c) total accessible polar area (N and O atoms only are considered polar here) buried on formation of the complex; (d) surface area of interfacial N and O atoms that do not form intermolecular H bonds. Here and throughout this paper, an atom or residue is defined to be interfacial if it loses at least 1 Ų of accessible surface area on formation of the complex. It is clear that no meaningful correlation is detectable. In accord with this observation, Norel et al. (1999a) recently reported, for a much larger set of nonnative binding modes, that the amount of buried polar surface area or the number of intermolecular hydrogen bonds formed in a trial complex do not appear to be accurate structural descriptors for the ideication of a near-native complex among the alternatives generated by a docking algorithm.

Fig. 1.

Correlation of ΔG_elec with (a) N_HB: number of intermolecular hydrogen bonds; (b) E_coulombic: coulombic interaction between monomers (calculated with the dielectric constant ɛ = 80); (c) ΔA_polar: total polar accessible area buried on formation of the complex (Ų); and (d) ΔA_{polar–unsatisfied}: unsatisfied polar accessible area buried on formation of the complex (Ų).

To better understand the structural origins of the relatively more favorable electrostatic free energy of the native geometry (see Table 1), we calculated the contribution of individual interfacial residues to binding, referred to as ΔG_elec(r), using equation 7 (see Materials and Methods). Figure 2 ▶ describes the contributions of individual charged residues to the binding affinities of their respective complexes as a function of the degree of burial of the residue's charged group within the complex. The charged groups are defined to be CD, NE, CZ, NH1, and NH2 atoms for arginine; the CE and NZ atoms for lysine; the CG, OD1, and OD2 atoms for aspartate; and the CD, OE1, and OE2 atoms for glutamate. The burial of a charged group here was assessed relative to the sum of the accessible areas of the atoms in the group in an extended conformation in Gly–X–Gly tripeptides. Accessible surface areas were calculated using the surfcv program (Sridharan et al. 1992) with radii taken from the CHARMM param22 parameter set (MacKerell Jr. et al. 1998). It is evident from the figure that deeply buried charges (those buried by more than 90%) contribute most significantly (either stabilizing or destabilizing) to the binding affinity. Moreover, for the native complexes, the buried charged groups tend to favor binding or are only moderately destabilizing. For the nonnative complexes, deeply buried charged groups are as likely to stabilize a complex as to destabilize it.

Fig. 2.

Relationship between the percent of burial of the charged group of an interfacial residue r within a complex and ΔG_elec(r). Nonnative binding modes are shown with a plus sign and native binding modes are shown with filled circles.

Figure 3 ▶ plots the total electrostatic contribution to binding of all charges buried by more than 90%, as a function of ΔG_elec, the electrostatic contribution of all protein charges to the binding affinity. It can be seen that there is quite a strong correlation between these two contributions indicating, perhaps not surprisingly, that buried charges make the most important electrostatic contribution to binding. This is also evident from the fact that the slope of a line fit to the data points is close to 1.0. As is seen from Figure 3 ▶, the total electrostatic contribution to binding, ΔG_elec, is about 50 kcal/mole more positive than the contribution of buried charges. This results primarily from the burial of polar groups (e.g., polar atoms in the backbone) in the interface that are not included in the sum over electrostatic contributions of charged residues.

Fig. 3.

The contribution of buried charged groups to ΔG_elec plotted as a function of ΔG_elec.

Burch score—A simple filter based on buried charges

The fact that buried ionizable groups play an important role in binding indicates that a fast scoring filter that focuses exclusively on these residues might be effective. Based on the fact that buried charges will be destabilizing unless the loss of solvent interactions is compensated by ionic or hydrogen bond interactions with other charges and polar groups, we have defined a function κ, the burch (buried charge) score, given by

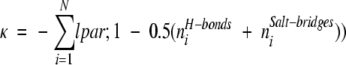(1)

The summation in this equation is carried over all interfacial ionizable residues that have charged functional groups buried by more than 90% (i.e., the sum of the accessible areas of the atoms in the group is <10% of the area of the same atoms when in extended Gly–X–Gly tripeptides).

The rationale for the definition of κ is straightforward. A charged group that becomes buried on formation of a complex that participates in no hydrogen bonds or salt bridges is unfavorable and is assigned a score of −1. When two stabilizing interactions are present, the score is zero, whereas greater than two interactions leads to a positive value of κ. The filter is designed so that positive values are favored. For the bound examples, possible binding modes with a burch score <2.5 were discarded.

Hydrogen bonds were ideied using the geometric criteria described by Stickle et al. (1992) with the exception that the distance between donor and acceptor heavy atoms was extended to 3.8 Å to allow for inaccuracies in the proposed docking conformations. Salt bridges are present when NZ atoms of lysine, either NH1, NH2, NE atoms of arginine, and either OD1, OD2 atoms of aspartate or either OE1, OE2 atoms of glutamate are within 4.0 Å of each other. If an interaction involving these atoms satisfied both the distance criteria for a salt bridge and the geometric criteria of a hydrogen bond, only the hydrogen bond was counted.

In one studied case, the burch filter discards the correct solution. Although a near-native solution was generated for the complex of carboxypeptidase A with potato carboxypeptidase A inhibitor (PDB code 4cpa [Rees and Lipscomb 1982]), the burch score of both this structure and the crystal structure (−4.5) are calculated to be below the threshold of −2.5 and they were consequently discarded. This appears to be due to the fact that for 4cpa, two of the residues that contribute to the unfavorable burch score are already significantly buried in the monomer, so that penalizing these residues for being buried in the complex overestimates the effect of desolvation. The estimate of the binding affinity for this complex is further complicated by the presence of a zinc atom. Another source of favorable interactions that is not accounted in burch is the C terminus of the inhibitor, which is in close proximity (<4.5 Å) to two arginines of the enzyme, but, based on our definition, does not form salt bridges.

As is evident from Figure 4 ▶, there is a strong correlation between κ and ΔG_elec. Moreover, the results shown in Table 1 indicate that most nonnative complexes have negative burch scores, indicating that this score can be used as a filter for nonnative complexes. The calculation of κ is extremely fast (about 1 sec per configuration), and thus can be readily used to evaluate a large number of trial complexes generated by a docking algorithm.

Fig. 4.

Relationship between the burch score (κ) and ΔG_elec.

Combining simplified filters with detailed free energy calculations

Table 2 lists the rank order of the native and best near-native complex for both enzyme–inhibitor and antibody–antigen complexes. As has been found in previous work, the geometric score alone is generally capable of detecting the native structure for enzyme–inhibitor complexes, and the near-native structure is highly ranked as well. The burch score offers little improvement for these cases. In contrast, the results with or without the burch filter are less satisfactory for antibody–antigen complexes, a result that is consistent with previous studies. Nevertheless, the burch score offers significant improvement for both native and near-native structures.

Table 2.

Effect of various scoring filters

		Rank
		without Pra				with Pra
		without κb		with κb		without κb		with κb
	RMSDb	near-native	native	near-native	native	near-native	native	near-native	native
Antibody/antigen complexes
1fdl	1.2	337	270	94	74	4	3	1	1
1jrh	1.4	8	2	5	1	1	1	1	1
1kb5	2.7	53	1	3	1	1	1	1	1
1mlc	1.2	83	9	13	3	4	1	1	1
1mlc2	1.0	216	25	52	6	4	1	1	1
1nca	1.4	2	1	1	1	1	1	1	1
2je	1.1	707	32	107	4	3	1	1	1
3hfl	1.0	2	1	1	1	1	1	1	1
3hfm	1.0	27	2	5	1	1	1	1	1
Casp2	4.7	2333	36	475	4	2	1	1	1
1fbi	0.7	2	2	2	2	1	1	1	1
1kip	2.6	205	114	67	32	1	2	1	2
1kiq	1.7	131	79	21	10	2	1	1	1
1vfb	1.6	251	25	104	7	3	1	1	1
1iai	1.9	9	12	1	2	1	2	1	2
Enzyme/inhibitor complexes
1acb	1.8	6	1	6	1
1cse	1.5	1	1	1	1
1tec	0.7	1	1	1	1
1tgs	1.5	1	1	1	1
1tpa	1.3	1	1	1	1
2kai	1.0	1	1	1	1
2ptc	0.8	1	1	1	1
2sec	0.5	1	1	1	1
2sic	0.9	1	1	1	1
2sni	0.9	1	1	1	1
2tgp	0.9	1	1	1	1
4cpa	3.3	7	1	n.a.	n.a.
4sgb	1.9	8	1	7	1
4tpi	1.7	1	1	1	1

All ranks reported here are based on the geometric score alone and calculated for all predicted binding modes that are not discarded by the filters described in the text.

^a Pr measures Tyr and Trp enrichment; see text for detail.

^b Symbols and abbreviations are as defined for Table 1.

Table 3 reports detailed free energy calculations for cases where the native or near-native structures were not ranked as the top hit. For the cases where the native orientation is among the top 10 hits, all of the orientations with a higher rank than native were selected for full energy calculation. For the remaining two cases (1fdl and 1kip), a clustering scheme (see Materials and Methods) was used to reduce the number of calculations of ΔG_elec that were performed. Forty-nine conformations were considered for 1fdl and 16 for 1kip (only the 10 conformations with the lowest values of ΔG'_total are listed in Table 3). The native structure is ranked first in all cases and the near-native structure is ranked no worse than third (not counting the native structure). It is also evident from Table 3 that ΔG_elec is an excellent discriminator of the native structure. Some of the elements of ΔG_elec are included in the burch score, but clearly there are other factors that determine the electrostatic free energy that have not yet been captured. We will attempt to do so in future work.

Table 3.

Energetic and structural features of nonnative binding modes that are ranked higher than the native structure on the basis of geometric score

	RMSD	GS	ΔGelec	TΔSsc	ΔAc	ΔG`total		RMSD	GS	ΔGelec	TΔSsc	ΔAc	ΔG`total
1fdl	55.9	388	67.5	−24.9	1517	16.6	casp2	83.8	516	86.8	−34.5	1871	27.8
	74.6	378	61.9	−28.8	1475	17.1		75.6	453	68	−37.3	1861	12.3
	82.3	363	61.4	−21.9	1392	13.8		73.6	449	81.3	−22.9	1904	9.1
	70.6	359	43.6	−21.8	1373	−3.2		0.0	445	22.7	−17.7	1269	−22.9
	82.7	342	49.3	−28.2	1285	13.3		4.4	315	37.5	−14.1	1218	−9.3
	79.9	340	59.9	−20.1	1359	12.2
	55.8	338	53.2	−27.3	1431	9	1fbi	48.4	538	122	−41.6	2246	50.9
	69.1	328	47.6	−24.4	1418	1		0.0	507	12.1	−21.2	1605	−46.9
	0.0	328	19.4	−16.5	1019	−15		0.6	479	20.3	−21.2	1642	−40.6
	1.6	323	16.6	−17.7	1047	−17.9
							1kip	41.2	380	75.8	−29.5	1757	17.5
1jrh	0.0	456	19.7	−17.6	1476	−36.4		50.0	369	79.2	−21.2	1435	28.5
	59.9	442	119	−31.7	2152	43.3		65.9	342	78	−19	1455	24.3
	44.8	441	89.4	−34.9	1610	43.9		60.8	341	60.9	−25.2	1579	7.2
	61.1	440	102	−27.5	2033	27.8		56.7	341	70.7	−24.6	1342	28.1
	60.6	440	107	−28.2	2107	29.5		52.4	338	47.5	−16.9	1439	−7.5
	2.2	432	34.3	−15.8	1467	−23.1		59.3	335	87.2	−26.1	1677	29.5
								28.9	335	63.9	−23.1	1206	26.7
1kb5	0.0	502	44	−25.2	2088	−35.2		0.0	324	7.8	−16.5	1032	−27.3
	74.4	442	100	−35.3	1695	50.7		2.6	310	57.9	−24.2	1444	9.9
	74.4	425	85	−23.9	1565	30.8
	2.9	413	46.7	−26.9	1969	−24.7	1kiq	59.1	391	106	−27.5	1579	54.5
								56.8	368	77.9	−27.2	1453	32.4
1mlc	55.4	443	52.7	−27.9	1947	−16.7		50.2	365	96.5	−31.7	1572	49.6
	60.1	424	71.3	−38.1	1511	33.8		47.6	365	99.8	−31.2	1679	47.2
	0.0	418	4.2	−16.1	1237	−41.6		49.2	362	82.8	−26.2	1466	35.7
	1.8	365	4.9	−16.1	1161	−36.9		56.7	346	103	−25.6	1573	49.6
								31.2	346	66	−23.2	1431	17.7
1mlc2	57.5	477	101	−36.4	2151	29.6		61.4	341	95.7	−23	1625	37.5
	54.7	474	120	−43.9	2303	49.1		0.0	340	10.9	−17.2	1127	−28.1
	57.8	466	98.4	−38.4	1905	41.5		2.7	326	21.7	−18.2	1186	−19.4
	55.5	415	88.5	−24.7	1888	18.8
	58.1	408	84.4	−34.5	1792	29.3	1vfb	0.0	363	28.8	−17.2	1207	−14.2
	0.0	407	6.7	−14.4	1252	−41.4		70.1	390	50.2	−17.5	1363	−0.4
	1.7	344	10.6	−16.1	1280	−37.2		63.3	378	60.6	−26	1560	8.6
								52.6	372	70.1	−20.4	1328	24.1
2jel	57.9	439	122	−22.1	1403	73.8		62.7	367	52.4	−23.1	1609	−4.9
	51.3	435	116	−31.2	2069	43.4		52.4	364	74.9	−21.9	1335	30.1
	48.3	431	124	−24.1	1313	82.6		52.5	364	74.5	−20.4	1368	26.4
	0.0	430	20.7	−19.2	1360	−28.1		2.3	309	28.3	−18.8	1325	−19
	1.9	313	23.9	−19.2	1257	−19.7
3hfm	0.0	476	42.6	−19.9	1318	−3.4
	51.5	439	84.5	−30.2	1904	19.4
	76.0	438	59.6	−25.7	1668	1.9
	51.6	413	98.3	−25.6	1929	27.5
	64.3	400	59.6	−25.7	1553	7.7
	1.2	398	45.7	−19.9	1217	4.8

All symbols are as defined for Table 1.

Enrichment of Tyr and Trp residues in antibody–antigen interfaces

The docking results reported in Table 2 are based on a complete search of the surfaces of both interacting proteins. It is often the case that additional information is available, such as the identity of active site residues (Bacon and Moult 1992; Walls and Sternberg 1992; Helmer-Citterich and Tramontano 1994; Gabb et al. 1997; Hendrix et al. 1999; Moont et al. 1999; Ritchie and Kemp 2000) or evolutionary conservation patterns (Pazos et al. 1997). In practical applications, there is no reason not to include this information in a docking procedure. As an example of how this might be done, we have introduced an additional filter in our docking procedure that is specifically tailored to the antibody–antigen problem.

It is well known that there is an overabundance of tyrosine and tryptophan residues in the complementarity determining regions of antibodies (Kabat et al. 1977; Padlan 1990; Mian et al. 1991). We have exploited this observation by developing a filter that requires that there be a large number of contacts between the ligand and receptor involving tyrosines and tryptophans in antibody–antigen interfaces. To measure this, we define a propensity function, Pr = f^c_r/f_r. In this formula, f_r is the fraction of a given type of residue on the surface of the antibody, that is, the number residues of that type on the surface of the antibody divided by the total number of antibody surface residues, and f^c_r is the fraction of interfacial residues of that type in the antibody that contact the antigen. A contact is defined to occur when an atom on the side chain of that residue of the antibody is within 5 Å of an atom of the antigen. A residue is defined to be on the surface if it has a nonzero molecular surface area. Pr values greater than unity imply a greater than expected number of contacts of residues of that type with the antigen.

As can be seen in Table 4, there is a large enrichment of contacts involving tyrosine and tryptophan in antibody–antigen complexes. The categories in the table and the proteins they contain were compiled by Lo Conte et al. (1999), except for the antibody–antigen category that contains more antibody–antigen complexes than those in the original category. Tryptophans in particular are often enriched in other interfaces as well, and other residues are enriched in other types of interfaces, but the Pr values for tyrosines and tryptophans in the antibody–antigen complex are the largest for any of the categories considered.

Table 4.

Propensities of amino acids to be in the interface for several classes of protein-protein interfaces^a

^a Cyan denotes Pr scores of residues with propensities to be in the interface of at least twice the expected value. Red denotes Pr scores of residues with propensities to be in the interface at least five times the expected value. (rec) receptor; (lig) ligand.

We incorporated the enrichment of tyrosine and tryptophan residues into the docking algorithm as a filter by requiring that binding modes with Pr values for tyrosines and tryptophans less than max{3.5, 0.3*max{Pr}}, where max{Pr} is the maximum Pr value over all the binding modes, be discarded. This threshold was determined in the same manner as the thresholds for the other filters used and is described in Materials and Methods. The functional form of this threshold arises from the fact that the Pr values vary greatly for different complexes. No native binding mode in the five cases used to optimize this threshold had a Pr value <3.5 (already a significant enrichment of tyrosines and tryptophans). However, some native binding modes had a much more significant enrichment and many more incorrect solutions could be removed if the threshold used were defined to be a fraction of the maximum Pr over all predicted binding modes.

It is evident from Table 2 that the combination of the Tyr/Trp filter and burch filter leads to excellent results. After application of these filters, native and near-native structures (<3.5 Å RMSD ) are ranked first or second in all cases. Except for two cases, the algorithm performs equally well for the enzyme–inhibitor examples. The RMSDs between the predicted solutions and the native structure are all quite low, as shown in Table 2, except for the CASP2 example. However, as shown in Figure 5 ▶, the top-ranked predicted binding mode is clearly quite similar to the native for that example.

Fig. 5.

The native binding mode of hemagglutinin (green) and the best (i.e., lowest root mean square deviation) docked conformation (red) generated by the docking algorithm. The antibody is shown in blue. The figure was produced with the program Troll (D. Petrey and B. Honig, in prep.).

As expected, the results shown in Table 5 for the unbound examples are not as good as for the bound examples. Slightly different parameters were used for the new filters in an attempt to account for the effect of conformational changes. A threshold of −4.5 was used for the burch score. Also, more steric clashes are allowed in these cases (see Materials and Methods for a description of how steric clashes are ideied). A threshold of max{3.5, 0.5*max{Pr}} was used for the Pr filter to account for this increase in allowable steric clashes. For this set of structures, deviations in terms of RMSD between the predicted solutions and the native structure are calculated with respect to the unbound ligand superimposed on the structure of the ligand solved in the presence of the receptor. For all tested unbound cases, a good solution is found among the first 10 clusters. ΔG`_total was calculated for the representative of the top 10 ranking clusters. No optimization of the structures was performed. The last column in Table 5 shows that a ranking based on the evaluation of the relative binding affinities improves the rank of the near-native structure in four of the five cases.

Table 5.

RMSD and rank of near-native binding mode for the unbound examples

		Rank of near-native solutions/# of remaining solutions
		without	with		using
Complex	RMSD	without κ	with κ	clustered	using ΔG`total
1vfa+1lza	2.6	23/43	5/15	4/13	2
1mlb+1lza	4.1	11/46	11/42	5/27	1
3hfla+1lza	2.8	17/40	13/32	8/19	1
3hfma+1lza	2.6	2/42	1/35	1/29	10
T0018	2.0	25/39	15/27	10/19	4

All symbols and abbreviations are as defined in Table 1. RMSDs for this table were calculated by superimposing the structure of the ligand in its unbound form onto the structure of the ligand in its bound form. RMSDs of the near-native binding modes were then calculated with respect to this superimposed structure (same method as in Norel et al. [1999a]). The bound forms of the ligand were taken from experimentally determined structures with PDB accession codes 1fdl, 1mlc, 3hfl, 3hfm. T0018 is an example from the CASP2 exercise.^a The bound antigen is docked to the unbound lysozyme.

Discussion

We have exploited a fast docking algorithm (Norel et al. 1994Norel et al. 1995) to generate a large number of trial geometries for protein–protein complexes. An important finding in our paper is that, for the bound problem, a binding free energy calculation based on continuum electrostatics (the FDPB method) and a surface area-based method of evaluating the nonpolar contribution to binding (Froloff et al. 1997), reliably ideies the native conformation as well as near-native conformations generated by the docking algorithm. Related approaches have been used to discriminate native protein structures from misfolded decoys (Janardhan and Vajda 1998; Vorobjev et al. 1998; Lazaridis and Karplus 1999; Petrey and Honig 2000).

These results, together with other studies of protein–protein docking (Jiang and Kim 1991; Katchalski-Katzir et al. 1992; Meyer et al. 1996; Gabb et al. 1997), indicate that the physical chemical forces that control protein folding and protein–protein interactions are reasonably well understood. This of course does not ensure that reliable prediction methods will follow. With reference to docking, the free energy evaluation is too slow to be used to screen large numbers of possible docked conformations and, moreover, treating the conformational changes associated with unbound docking is largely an unsolved problem. Nevertheless, the fact that it is possible, with sufficient computational effort, to idey the native structure provides an encouraging framework for future developments.

An analysis of the factors that determine the binding free energy indicates that the electrostatic contribution to binding, ΔG_elec, is strongly correlated with the total binding free energy and indicates that simple screens based on electrostatics may provide a useful means of limiting complex geometries to native-like conformations. We have previously developed a simple electrostatic function for protein structure prediction (Petrey and Honig 2000) and we have attempted, in this work, to construct a simple electrostatic scoring function for protein–protein interactions. The burch score penalizes buried charged groups that do not form stabilizing hydrogen bonds and ionic interactions. It is quite successful in limiting the number of complex geometries, but it clearly does not completely capture all of the factors that determine the electrostatic contribution to binding. We are currently trying to develop an improved scoring function that will almost certainly have to account in part for coulomb interactions between interfacial residues.

In all cases considered in this work, ΔG_elec is positive, indicating that electrostatic interactions oppose binding. This is due to the fact that favorable pairwise interactions rarely succeed in overcoming the cost of removing charged and polar groups from water (Honig and Hubbell 1984; Hendsch and Tidor 1994^; Yang and Honig 1995a,^1995b). That individual charged groups favor binding is only true in the sense that replacing such a charge with a nonpolar isosteric group would destabilize the complex. For example, one member of a buried ion pair or hydrogen bond can appear to be stabilizing because its removal will result in a loss of stability due to the fact that the other member is still buried, while stabilizing coulombic interactions have been lost (see, for example, Hendsch and Tidor [1999]; Sheinerman et al. [2000]). However, this does not imply that the ion pair itself is stabilizing relative to the uncomplexed state.

Our results confirm previous studies that show that the docking problem is more difficult for antibody–antigen complexes than for enzyme-inhibitor complexes. It is of interest to consider why this might be the case, but it is clearly related to the geometric properties of antibody–antigen interfaces (see, for example, Table 2). Shape complementarity has long been recognized as an important feature of stable complexes (Katchalski-Katzir et al. 1992; Helmer-Citterich and Tramontano 1994; Norel et al. 1995; Palma et al. 2000), although it is clear from this and other studies (Jiang and Kim 1991; Helmer-Citterich and Tramontano 1994; Norel et al. 1995; Meyer et al. 1996;) that nonnative binding modes can display better shape complementarity than the native. Lawrence and Colman (1993) introduced a shape correlation function, S_c, that assumes values between zero and one. A surface correlation of one implies perfect shape complementarity, whereas lower values reflect less effective packing. The six antibody–antigen interfaces that they studied had S_c values that were consistently lower, ranging from 0.64 to 0.67, than the four enzyme–inhibitor and five oligomeric systems they considered, which had S_c values ranging from 0.70 to 0.76. Jones and Thornton (1996) calculated the volume between interfacial surfaces and found on this basis that antibody–antigen systems were less well packed than enzyme–inhibitor complexes, although there was considerable overlap between the two categories. In contrast, Lo Conte et al. (1999) concluded that there is little difference between the interfacial packing of antibody–antigen systems and oligomeric proteins or protease–inhibitor systems. Older studies have reached similar conclusions (Davis et al. 1988; Walls and Sternberg 1992). Using the software of Lawrence and Colman (1993), we calculated S_c values for the 15 antibody–antigen systems used in this study. We find that many antibody–antigen complexes have Sc values in the range of those found for protease–inhibitor systems, indicating that imperfect shape complementarity is not responsible for the relatively poor performance of docking algorithms for the former set of complexes.

Another possibility is based on the observation of Jones and Thornton (1996) that antibody–antigen interfaces are more planar than interfaces in other classes of complexes that they studied. In this sense antibody–antigen interfaces may be characteristic of other interfaces not involving enzymes. As shown in this work, including known characteristics of an interface, in this case the enrichment of tyrosines and tryptophans can be an effective means of improving the discriminatory ability of docking algorithms. An important characteristic of the Tyr/Trp filter is that it does not require a priori knowledge of the location of the antibody binding loops. Different strategies will certainly have to be used for other protein families, but the results reported here indicate that sequence information can be effectively incorporated into docking algorithms. Such an approach may prove extremely effective in assembling multiprotein complexes from their individual components.

The docking algorithm and filters used in this work are quite fast and are extremely effective in ranking the native and near-native binding geometries. The computational efficiency of the matching stage of the algorithm, which applies minimal criteria to restrict both the translational and rotational components of the transformations that describe the possible binding modes, has been noted previously (Norel et al. 1995, 1999a^,Norel et al. b). Both the speed of our approach and its success in ranking compare quite favorably with recent studies of both bound and unbound docking (Gabb et al. 1997; Bliznyuk and Gready 1999; Hendrix et al. 1999; Moont et al. 1999; Norel et al. 1999a; Palma et al. 2000; Ritchie and Kemp 2000). The time required to dock two complexes ranges from a minute for small complexes to about an hour for large complexes, and for the bound problem a near native structure is always top ranked. For unbound docking, near-native solutions are also highly ranked and could in principle be detected in a binding free energy evaluation of the top-ranked geometries that emerge from the filtering procedure.

Materials and methods

Docking

Rotations and translations of the ligand that specify a possible binding mode are defined as those that map pairs of critical points of the ligand and their associated normals onto complementary pairs of critical points and normals of the protein. Critical points are defined to be a small subset of the dots generated by the molecular surface (MS) representation program (Connolly 1983a,1983a). An MS dot is selected as a critical point if the value of a shape function at that dot is a local extremum among the 12 nearest surface dots. The shape function measures the local curvature of the surface and is calculated as follows. A three-dimensional grid, 0.25 Å grid size, is placed over the molecule and each grid box (voxel) is marked as interior if it is within a van der Waals radius of an accessible atom or a van der Waals radius plus 1.5 Å of a buried atom. Next, a probe sphere of defined radius is placed at each MS dot and the volume of the intersection between the molecule and the probe sphere is calculated by counting the number of interior grid voxels that are within the probe. The volume of this intersection defines the shape function. We use a probe with a 5 Å radius, instead of the 6 Å radius used previously (Norel et al. 1994Norel et al. 1995). Even if a surface dot is a local extremum of this shape function, it is only retained as a critical point if the value of the shape function at that dot is less than 1/3 V or greater than 2/3 V, where V is the volume of the 5 Å radius sphere. This increases the probability that local extrema of the shape function will actually correspond to protrusions ("knobs") or deep clefts ("holes") in the surface (Connolly, 1986), since spheres placed at such points will have very small or very large volumes of intersection with the molecule. The volume of the intersection on a roughly planar region of the surface would be approximately V/2.

A signature is computed for each pair of critical points on both the receptor and ligand. The signature contains the label of the dots (knob or hole), the distance between the two dots, the two angles between the line joining the two critical points and their respective normals, and the torsion angle between the two normals. For each pair of critical points on the ligand, all pairs of critical points on the receptor with complementary signatures are found. A hashing algorithm is used to make the search for complementary pairs of critical points computationally efficient. The best rigid body transformation that superimposes the critical points and normals of the ligand onto the complementary pairs of critical points on the receptor is calculated. These transformations define a possible binding mode of the ligand. The signatures of two pairs of critical points are complementary if the following conditions are true: (1) a knob from one molecule matches a hole from the other molecule; (2) the difference between the distance between both critical points in each signature is <2 Å; (3) the differences between the corresponding x and y angles are <0.6 radians; (4) the differences between the torsion angle are <0.75 radians; and (5) the sum of the differences of the three angles is <1.2 radians. These thresholds were determined previously (Norel et al. 1995).

Typically an antibody is represented by 600 critical points, a small protein such as lysozyme by 200 critical points, and larger antigens such as neuraminidase or hemagglutinin are represented by 600 critical points, generating on average 2 × 10⁶ conformations. Enzymes are represented typically with 300–400 critical points and their inhibitors with 100 critical points, generating, on average, 2 × 10⁵ conformations.

Ranking and filters

Geometric filters

As described previously (Norel et al. 1994Norel et al. 1995), a three-dimensional grid is placed over the receptor with a grid resolution of 2 grids/Å. Each grid box (voxel) is then labeled as core (c), exterior (e), or surface (s). Core voxels are those that are within a van der Waals radius of atoms that do not produce any MS dots. Exterior voxels are those that are within a van der Waals radius of atoms that produce MS dots. Surface voxels are those that are within 1 Å of an MS dot (see Fig. 6 ▶). For bound cases, any orientation with the property that an atomic nucleus of the ligand falls within a core or exterior voxel is discarded. To allow for possible conformational changes, this restriction is removed for unbound docking.

Fig. 6.

Example of mapping of a molecule onto a grid. A two-dimensional slice of the grid is shown. Buried grid points are shown in red, exposed grid points are shown in black, and the molecular surface dots, mapped as spheres of radius 1 Å, are shown in green.

A geometric score (GS) is computed using the MS dots of the ligand. The GS of a particular binding mode of the ligand is a function of three variables, S, E, and C corresponding to the number of MS dots of the ligand falling within surface, exterior, or core voxels of the protein, respectively. It is computed using a method slightly different from that described previously (Norel et al. 1995):

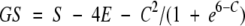(2)

The first term in this function rewards the presence of surface dots of the ligand near the surface of the protein. The second term slightly penalizes small penetrations of the ligand surface into the protein. The third term significantly penalizes more than approximately five deep penetrations of the ligand surface into the interior of the protein. This small tolerance for core contacts and the definition of the surface voxels—as opposed to just interior and exterior voxels—are designed to allow for small inaccuracies in the predicted binding modes. The relative weighting of the individual terms was determined empirically by optimizing results for the test group of proteins 1fdl, 1jrh, 1kb5, 3hfl, and 3hfm for the bound examples and complexes of 1lza, 1vfa, 3hfl, and 3hfm for the unbound examples. Binding modes with negative GS are discarded.

To distinguish between solutions that have a low GS because their contact areas are small and solutions that might have a large contact area and a low GS because of a large number of "slight" overlaps of the ligand into the core of the receptor (solutions that should be discarded), a normalized geometric score, NS, is defined (NS = GS/S). NS is equal to one when the score is generated entirely by allowed surface contacts (i.e., S ≠ 0 and E = C = 0) and decreases with increasing steric overlap (C, E > 0). Solutions having a normalized score below a threshold are discarded. Different thresholds are used for bound (NS = 0.85) and unbound docking (NS = 0.6), to allow for inaccuracies due to possible conformational changes in the unbound case. The thresholds were determined from the same test group of proteins as described earlier. The average reduction factor for a particular filter is defined to be the ratio of the number of solutions subjected to the filter over the number of solutions remaining after the application of the filter. The reduction factor is 40 for the three surface complementarity filters for the bound examples and 12 for the unbound examples.

Electrostatic "clashes"

Each charged amino acid is represented as a pseudo-C_β atom, 3 Å from the C_α atom along the C_α–C_β vector. This representation is similar to the one presented in Bryant and Lawrence (1993), where the mean projection of all side-chain centroids was computed for 161 proteins. The charged pseudo-residues are classified as positive (Arg, Lys) or negative (Asp, Glu). A binding mode is considered to contain an electrostatic clash if a pseudo-C_β of a charged residue in the receptor and a pseudo-C_β of a similarly charged residue in the ligand are within a certain distance (T_e) of each other. A T_e value of 3 Å was used in this work and was determined by examining the distribution of distances between pseudo-C_β atoms of charged residues in native structures. The native structures examined are 1fdl, 1jrh, 1kb5, 3hfl, and 3hfm. Any possible binding mode with such a clash is discarded.

Interface geometry

All solutions that pass the various filters are ranked by the GS and the top 100 are retained. We make the assumption that the surface patch of the ligand that interacts with the receptor will be contiguous, that is, will not consist of two or more nonintersecting patches. This is based on visual inspection of the same test group of structures listed earlier and several false positive solutions (high GS and high RMSD) generated for those examples. The 100 solutions with the highest GS values are tested to ensure that they correspond to a single patch. This test is performed as follows. Each dot that is in contact with the protein is labeled `C', and those that are not in contact are labeled `N'. A surface dot is defined to be in contact with the protein if it falls in any core, exterior, or surface voxel. For each C dot, a list of neighbors is computed where a neighboring dot is defined to be any other surface dot within 1.8 Å. Starting from any C dot, each neighbor is visited, going from one neighbor to another, until no more visits are possible. Each dot can be visited only once. When no more visits are possible, the dots that were visited starting from a given dot define a connected component or a patch. If any C dot was not visited, the procedure starts again at this dot. The procedure is repeated until all C dots have been visited. The size of a given patch is simply the number of dots that belong to that patch. Ideally, all binding modes that consist of more than one patch should be discarded, but, again, to allow for possible conformational changes, we discard only binding modes for which the second largest patch contains >87 dots, or approximately three atoms (using a sampling density of 1 dot/Ų and a probe size of 1.5 Å).

Even if the interface consists of a single surface patch as defined earlier, it may contain "holes" (see Fig. 7 ▶). To test for the existence of holes in the interface, we applied the same procedure to the dots that do not belong to the interface (`N'). If the N dots form more than one contiguous patch, then the interface has a hole (see Fig. 7 ▶). "Small" holes may contain up to approximately two atoms for the bound case or three atoms for the unbound case to bridge the interface. Those atoms might correspond to water molecules. The orientations that were examined to determine the thresholds were the same orientations used to define contiguous patches; in addition, a few false-positive orientations from the unbound cases 1vfa/1lza and 3hfl/1laza were examined.

Fig. 7.

Two-dimensional projection of the surface of a ligand, illustrating different surface topologies of predicted binding modes. The shaded regions represent the surface of the ligand that is in contact with the receptor, which can consist of a single surface patch (A), a single surface patch with holes (B), or multiple surface patches (C).

Clustering

Inspection of the set of orientations generated by the docking procedure shows that many are very similar and represent essentially the same solution. To eliminate similar solutions, we used a clustering scheme that was described previously (Norel et al. 1997, 1999a). The solutions are first sorted by geometric score and then clustered. The solution with highest score is then selected as a representative of the cluster. Two solutions are defined as being in the same cluster if their relative angular distance is <60° and if the relative translation of the center of mass of the ligand–receptor interfaces is <5 Å. Each rotation matrix can be represented as a single rotation around an equivalent axis. The angular distance definition coincides with this angle. If the rotations are Ra and Rb for conformations A and B, then B is rotated against A by R=RbRa-1. When the rotation matrix R is known between two conformers, the rotational angle, in radians, between them is

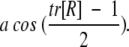Free energy of association

The free energy of association of two interacting proteins can be written in the form (Froloff et al. 1997):

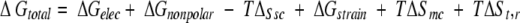(3)

ΔG_elec and ΔG_nonpolar are the electrostatic and the nonpolar contributions to the binding affinity. TΔS_sc describes the reduction of entropy due to the loss of torsional freedom of interfacial side chains on association. ΔG_strain and TΔS_mc account for changes in the internal free energy of the monomer conformation and in the conformational entropy of the main chain of interfacial residues that result from binding. ΔG_strain might correspond, for example, to less favorable intramolecular van der Waals interactions or to a loss of vibrational entropy due to the constraints of binding. TΔS_mc reflects the change in the conformational space accessible to the backbone of interfacial residues in the complex compared with the one in a monomer. TΔS_t,r corresponds to the loss of six translational and rotational degrees of freedom in bimolecular association. We assume that the last three terms are similar for different modes of binding and therefore include only the first three terms in the evaluation of relative binding affinities. The sum of these terms is denoted here by ΔG`_total.

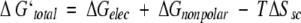(4)

The electrostatic contribution to binding, ΔG_elec, is calculated as in Froloff et al. (Froloff et al. 1997; Gilson et al. 1987):

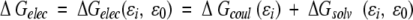(5)

ΔG_elec(ɛ_i, ɛ_o) is the total electrostatic contribution to the binding of two molecules that have an interior dielectric of ɛ_i, and are embedded in a solvent with dielectric constant ɛ_o, ΔG_coul (ɛ_i) is the free energy due to coulomb interactions between associating molecules that are hypothetically placed in a medium of dielectric constant ɛ_i, and ΔG_solv (ɛ_i, ɛ_o) is the difference in the reaction field (solvation) free energy between the isolated proteins and the complex.

The nonpolar contribution to binding, ΔG_nonpolar, is calculated as a surface area proportional term (Nicholls et al. 1991; Tanford 1979):

(6)

where, γ is the coefficient relating ΔG_nonpolar to the buried surface area, set to 50 cal/mole/Ų here (De Young and Dill 1990; Nicholls et al. 1991; Yang and Honig 1995a) and ΔA_c is the curvature corrected surface area lost on association. Because water is more restricted in the vicinity of concave patches on a protein surface, such regions are expected to be more hydrophobic than convex or planar regions. The curvature correction of the accessible surface area is an attempt to account for this effect (Nicholls et al. 1991).

TΔS_sc was calculated with the method of Pickett and Sternberg (1993). In this method, a side chain, whose solvent accessible surface area is <60% of that in a fully extended state, is assumed to be fixed in a single conformation, whereas a more solvent-exposed side chain is assumed to rotate freely. An entropy scale is obtained from the observed distribution of side-chain rotamers in 50 nonhomologous protein structures (Pickett and Sternberg 1993).

ΔG_elec was obtained from the finite difference Poisson Boltzmann (FDPB) method as implemented in the DelPhi program (Nicholls and Honig 1991). Atomic charges and radii from the param22 parameter set (MacKerell Jr. et al. 1998) of the CHARMM package (Brooks et al. 1983) were used. The ionic strength was set to 0.1 M and the ion exclusion radius to 2.0 Å. The dielectric constants ɛ_i = 2 and ɛ_o = 80 were assigned to the proteins' interior and solvent, respectively. Boundary conditions were approximated by the Debye-Huckel potential of the charge distribution. Delphi calculations were run on a cubic grid with a resolution of 1.5 grids per Å. The size of a grid was chosen so that the grid fill did not exceed 90% in any of the calculations (this corresponded to the grid size of 190–250 grids on a side for different complexes). To reduce numerical errors, we placed proteins in the same position in the grid both in the complexed and isolated state for both bound and unbound docking (this procedure would not work if conformational changes were taken into account in the unbound problem). Calculations were run until the total energy converged to within 10⁻⁴ k_BT, where k_B is a Boltzmann constant and T is the absolute temperature.

Before performing binding energy calculations, the structures of all trial complexes were processed as follows. Hydrogen atoms were built for each trial complex with the CHARMM program (Brooks et al. 1983). This was followed by a short energy minimization with the steepest descent method (20 steps), followed by conjugate gradient energy minimization until a gradient of 0.05 kcal/mole/Å is reached. All energy minimizations are performed in vacuo (ɛ = 1). Harmonic constraints with a force of 50 kcal/mole/Ų were applied on the proteins' heavy atoms to keep them in the vicinity of their original positions during minimization. All aspartic and glutamic acids were modeled as negatively charged, and all arginines and lysines as positively charged. In all proteins, N termini and C termini were modeled with a charge of +1 and −1, respectively. Histidine residues were modeled as neutral.

The calculation of curvature-corrected surface area, A_c is done with the surfcv program (Sridharan et al. 1992). The solvent-accessible surface areas of interfacial side chains before and after association, as well as in a fully extended state (within Gly–X–Gly peptide, where X is a residue being examined), were also computed without the curvature correction and used to assess the reduction of the conformational entropy of side chains on association (Pickett and Sternberg 1993). All surface area calculations are performed using atomic radii of the CHARMM param22 parameter set (MacKerell Jr. et al. 1998).

Electrostatic contributions to binding of individual charged residues on the interface

The electrostatic contribution of an individual residue r to binding, ΔG_elec(r), is calculated as:

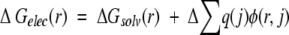(7)

ΔG_solv(r) is the loss of favorable solvation interactions of a residue r on complex formation. Δ [Σq(j)φ(r,j)] is the change, on complex formation, of pairwise electrostatic interactions of residue r with all atoms, j, that do not belong to residue r. q(j) is the charge on atom j, and φ(r,j) is the electrostatic potential generated by charges on a residue r at the position of a charge j. Because it is assumed that in the free state the interacting molecules are infinitely far apart, only intramolecular interactions are calculated for this state. ΔG_elec(r) was only calculated for interfacial residues defined as those that bury at least 1 Ų of solvent-accessible surface area on binding. The total electrostatic contribution of all interfacial residues is not a simple sum of individual contributions, given by equation 7, because in such a sum pairwise interactions between interfacial residues would be double counted. To calculate the total electrostatic contribution of a subset of interfacial residues to binding, we recalculated the individual contributions, with pairwise interactions between the selected residues multiplied by 0.5. The total contribution is obtained by summing the corrected individual contributions of the selected residues.

Electrostatic free energies and potentials were calculated as described earlier, although to improve precision for individual residues, a cubic lattice of a resolution of 2.5 grids per Å centered at the C_β atom of that residue was used. To reduce the time required for the computations, we used a lattice with 130 grids on a side. Thus, electrostatic interactions with groups located farther than ∼26 Å from the residue examined are ignored. Trial calculations indicated that the inclusion of interactions with the groups located farther than 26 Å does not change ΔG_elec(r) significantly (Δ (ΔG_elec(r)) <0.5 kcal/mole). In all other respects (preparation of structures, protein parameters, dielectric constants, etc.) the computations were performed as described earlier for calculation of the total electrostatic contribution to binding.