Correlated conformational fluctuations during enzymatic catalysis: Implications for catalytic rate enhancement

Abstract

Correlated enzymatic conformational fluctuations are shown to contribute to the rate of enhancement achieved during catalysis. Cytidine deaminase serves as a model system. Crystallographic temperature factor data for this enzyme complexed with substrate analog, transition-state analog, and product are available, thereby establishing a measure of atomic scale conformational fluctuations along the (approximate) reaction coordinate. First, a neural network-based algorithm is used to visualize the decreased conformational fluctuations at the transition state. Second, a dynamic diffusion equation along the reaction coordinate is solved and shows that the flux velocity through the associated enzymatic conformation space is greatest at the transition state. These results suggest (1) that there are both dynamic and energetic restrictions to conformational fluctuations at the transition state, (2) that enzymatic catalysis occurs on a fluctuating potential energy surface, and (3) a form for the potential energy. The Michaelis-Menten equations are modified to describe catalysis on this fluctuating potential energy profile, leading to enhanced catalytic rates when fluctuations along the reaction coordinate are appropriately correlated. This represents a dynamic tuning of the enzyme for maximally effective transformation of the ES complex into EP.

It is well appreciated that large-scale domain motions are crucial to an enzyme molecule's ability to capture and sequester substrate within the active site (Wierenga et al. 1992; Greenwald et al. 1999; Ilyin et al. 2000). However, the role of atomic scale conformational fluctuations during the actual chemical event itself is not fully understood and is the focus of recent studies (Kohen et al. 1999; Ringe and Petsko 1999; Balabin and Onuchic 2000). Several years ago, the importance of dynamic processes for catalysis was stressed (Cannon et al. 1996), and in this light even the idea of transition state stabilization has been brought into question (Bruice and Benkovic 2000). Results of an interesting molecular dynamics simulation have shown that energetically allowed thermal fluctuations in the enzyme–substrate complex modify the structure of the bound substrate to resemble that of the transition state (Young and Post 1996). In this paper, we propose that correlated thermal fluctuations in the enzyme body couple with the chemical reaction coordinate and contribute to the catalytic rate enhancement. Therefore, our focus is strictly on mechanisms for more efficient chemical reaction barrier crossings. Conformational adjustments for substrate binding or product release are only tangentially addressed in this work. The presentation is built in three parts.

First, results highlighting significant changes in thermal fluctuation magnitudes along the reaction coordinate of cytidine deaminase are presented. The chemical coordinate is approximated by crystal structures of enzyme with bound substrate analog, transition state analog, and product (Xiang et al. 1995, 1996, 1997). We have developed a Kohonen-type artificial neural network (Gasteiger et al. 1994; Zupan and Gasteiger 1999) that projects the entire three-dimensional structure of the enzyme molecule, coarse-grained to the amino acid residue level, onto two dimensions in a topologically consistent fashion. We visually identify each projected amino acid residue by coloring it according to the magnitude of its crystallographic temperature factor, thereby marking that residue's degree of thermal disorder. The three- to two-dimensional projections allow for visualization of the spatial relations, relative to each other and to the bound reaction coordinate species, between those amino acids that change in fluctuation magnitude as the enzymatic reaction proceeds. Our results point to a significant decrease in conformational fluctuations at the transition state of the reaction.

Second, we derive a dynamic free energy profile for the catalytic pathway. The traditional Michaelis-Menten scheme for enzymatic catalysis E + S ↔ ES ↔ EP → E + P is modified such that the conversion of the enzyme–substrate (ES) complex into enzyme–product (EP) complex is described through a Fokker-Planck or diffusion equation (Agmon and Hopfield 1983a,b; Agmon 1985; Astumian 1997; Schienbein and Gruler 1997). Description of protein conformational changes through diffusion equations in general has a long history (for example, see Agmon and Hopfield 1983a,b; Agmon 1985; Cartling 1985; Scheinbein and Gruler 1997). In our work, the position of the enzyme–ligand complex along the now continuous reaction coordinate ES ↔ EP is captured by the variable ξ, representing the conformation of the complex at that reaction coordinate position. The formalism leads to a dynamic free energy, which in turn is used to calculate the effective flux velocity through each conformation ξ along the reaction coordinate. Results from this and the fluctuation magnitude work are interpreted to mean that enzymatic catalysis proceeds along a fluctuating potential energy surface.

The third and most important thrust of our work will show that—if suitable correlations are introduced into this fluctuating potential surface—the transformation rate of the ES complex into EP increases significantly above that for the nonfluctuating potential energy profile. Therefore, we propose that correlated enzymatic conformational fluctuations are key to a dynamic optimization of the catalytic process.

To attack the problem of catalysis on a fluctuating potential surface, we solve the Michaelis-Menten rate equations with fluctuating rate coefficients. The correlated fluctuations in the energetic profile arise solely from intrinsic thermally induced spatial motions in a way that will be discussed below. Particularly, we suggest a means by which atomic coordinate fluctuations in the enzyme molecule lead to correlated fluctuations in the energetic profile for the active site chemistry. Note that the effects of externally supplied oscillating fields on enzymatic catalysis have been investigated (Astumian et al. 1989; Robertson and Astumian 1990a,b), as has been the role of barrier fluctuations and stochastic resonance in membrane transport (Fulinski 1997, 1998). Although the kinetics of escape over an energy-driven fluctuating barrier are well studied, theoretical work on reaction dynamics on intrinsically thermally fluctuating potentials is relatively recent (Berezhkovskii et al. 1999 and references within).

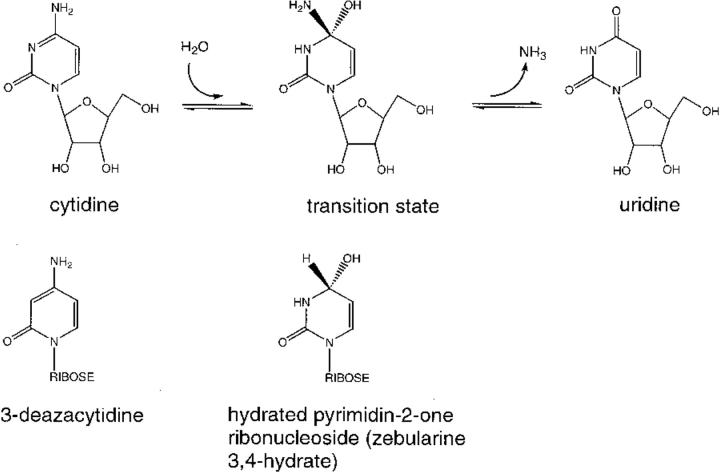
Cytidine deaminase catalyzes the hydrolytic deamination of cytidine into uridine (Betts et al. 1994; Carter 1995; Xiang et al. 1995, 1996, 1997; Schramm and Bagdassarian 1999; Snider et al. 2000). The enzyme is homodimeric and each of the two identical active sites is built from amino acid residues from both monomers. Crystal structures have been established for enzyme complexed with (1) substrate analog 3-deazacytidine; (2) the transition state analog zebularine 3,4-hydrate (hydrated pyrimidin-2-one ribonucleoside); and (3) uridine, the product (see Fig. 1 ▶ for the reaction coordinate and analog structures). These structures provide approximate atomic-level information about cytidine deaminase when nestled around the true substrate, transition state, and product.

Fig. 1.

Reaction coordinate for cytidine deaminase. 3-Deazacytidine and zebularine 3,4-hydrate are substrate and transition-state analogs, respectively.

Because the enzyme binds transition state analog much more tightly than it does substrate analog and product (Radzicka and Wolfenden 1995), we might expect that atomic scale enzymatic thermal fluctuations are diminished as transition state is accessed from substrate along the reaction coordinate. These intuitive ideas are borne out by study of the crystallographic temperature factors for the three enzyme complexes. Isotropic temperature factors, or B-values, are related to the mean-square spatial fluctuations at each average, crystallographically determined, atomic coordinate and therefore, measure the total disorder, including that from thermal agitation (McCammon and Harvey 1987; Karplus and Petsko 1990). Changing fluctuation magnitudes along the reaction coordinate of cytidine deaminase are quantified by comparing temperature factors for the three enzyme–ligand complexes.

The full and necessary statistical justification for exploring fluctuation magnitudes along the chemical coordinate through temperature factors is presented elsewhere (R.C. Noonan, C.W. Carter, and C.K. Bagdassarian, unpubl.). For the present work, suffice it to say that all enzyme–inhibitor complexes were crystallized and analyzed under identical or near-identical conditions (Xiang et al. 1995, 1996, 1997) and are globally nearly identical in structure except for small differences in the active sites. Most important, analysis of a second transition state analog complex, that of flourinated zebularine 3,4-hydrate (Betts et al. 1994), provides an estimate of error in temperature factor determination and establishes that fluctuation magnitude differences between transition state and ground state complexes are statistically significant (R.C. Noonan, C.W. Carter, and C.K. Bagdassarian, unpubl.).

Results and Discussion

Kohonen network projections

We present a projection of the entire three-dimensional structure of cytidine deaminase onto a plane, giving a means of visualizing the changing fluctuation magnitudes from substrate to transition state to product. The projection from three to two dimensions, accomplished at the amino acid level, is topologically sound. If two amino acid residues have similar spatial coordinates in the three-dimensional enzyme, they remain together after projection. Our work was motivated by the molecular electrostatic potential surface projections of Gasteiger et al. (Gasteiger et al. 1994; Zupan and Gasteiger 1999).

Because the crystallographic coordinates of the three cytidine deaminase complexes—enzyme with substrate analog, transition state analog, and with product—are very similar (Carter 1995; Xiang et al. 1995, 1996, 1997), projection of the substrate complex establishes the two-dimensional profile of amino acids for all three complexes. The inhibitor molecule itself is projected as well and serves to define the center of the active site. Each projected residue, occupying a single unique locus on a checkerboard-like square lattice, is colored coded according to the magnitude of its average temperature factor (calculated by averaging over atomic temperature factors) in the enzyme–inhibitor complex of interest. Thus, a given lattice site is occupied by the same amino acid residue for each of the three complexes, but its color depends on its temperature factor in the complex under consideration. In this way, for each complex, temperature factor distributions across all amino acids can be captured in a single easily comprehensible snapshot.

Comparisons of such temperature factor distributions for the three complexes highlight fluctuation magnitude changes along the reaction coordinate from substrate to transition state to product. Most important, because the projected residues enjoy the same topologic relationships as they did in the original three-dimensional enzyme, the projections capture these spatial relationships.

At the heart of the projection scheme lies a self-organizing Kohonen neural network (Gasteiger et al. 1994; Zupan and Gasteiger 1999). A detailed analysis of our algorithm will be presented elsewhere, and a brief description is provided in the Materials and Methods section here.

Figure 2a ▶ shows the projection for the cytidine deaminase complex. The enzyme complex contains a total of 588 amino acids and two ligand molecules (two active sites are present in the dimeric enzyme). These 590 residues are projected, as described in Materials and Methods, onto a 25 by 25 square lattice with periodic boundary conditions: squares on the left edge of the lattice are continuous with squares on the right, whereas squares on the upper edge are juxtaposed to those on the lower. Because the various enzyme–ligand complexes are structurally very similar, the amino acid projection pattern resulting from the substrate–analog complex (that of 3-deazacytidine) serves as the template for the transition state analog and product complexes as well. Each square, with the exception of the 35 white, or "empty," ones, is uniquely associated with either a projected amino acid or a ligand molecule. Amino acids from one monomer of the dimeric cytidine deaminase are colored yellow, whereas those from the other are colored light blue. Recalling that periodic boundary conditions are implied in the image, note the clustering of amino acids from the same monomer and the well-defined interfacial boundary. The two magenta squares represent positions of the two ligand molecules in their respective active sites. Because the actual three-dimensional active site includes residues from both monomers, each projected ligand lies at the interface between the two monomers.

Fig. 2.

Kohonen topologic projections for cytidine deaminase. Periodic boundary conditions apply. The 590 enzymatic residues (588 amino acids and 2 ligand molecules) are projected onto 625 lattice squares, leaving 35 unoccupied "white" squares. Each occupied square is associated with a unique amino acid residue or ligand molecule. Yellow and light blue squares differentiate amino acids belonging to the two subunits of cytidine deaminase. The positions of the two ligand molecules are highlighted by the two magenta squares. (a) Comparison of average amino acid temperature factors for enzyme–substrate and enzyme–transition state complexes. Dark blue squares represent those amino acids whose temperature factors are decreased by >15%in the transition state as compared to substrate. Red squares represent those amino acids whose temperature factors are increased in the transition state by >15%. (b) Comparison of average amino acid temperature factors for enzyme–product and enzyme–transition state complexes. Color scheme as in a.

Figure 2a ▶ compares the average temperature factors for residues in the enzyme–substrate complex and the transition state complex. The dark blue squares highlight those amino acids with temperature factors that are significantly decreased (by >15%) in the transition state complex as compared to substrate. The red squares represent those few residues with temperature factors significantly greater (by ≥15%) in the transition state.

The figure highlights the loss of conformational freedom at the transition state as compared to substrate. In this sense, the enzyme–substrate complex goes through a fluctuation bottleneck as the reaction proceeds. The lost conformational freedom is pinpointed to amino acids largely at or near the dimeric interface—the number density of interfacial amino acids showing reduced temperature factors is greater than the density of "frozen" residues within each monomer proper. Furthermore, of these conformationally restricted residues a proportionally large number are in close proximity to the bound ligand molecules—these residues are near the bound ligands in three dimensions as well.

This restriction of conformational freedom within the active site is an important point. Snider et al. (2000), using thermodynamic measurements, report that entropic changes in cytidine deaminase upon going from the substrate complex to the transition state are very small. Their measurements of k_cat as a function of temperature address the response of the entire water-solvated enzyme–substrate complex, thereby masking any local losses in conformational entropy for amino acids close to the active site. We propose that the entropy stays relatively constant along the reaction coordinate from substrate to transition state for the global enzyme–water system while active site amino acid residues do "freeze up" at the transition state.

In Figure 2b ▶, transition state complex fluctuations are compared to those of product, with the same color scheme as the comparison to substrate. For comparison with the substrate transition state results in Figure 2a ▶, note the now increased number of conformationally restricted amino acids at the transition state of the reaction. Note also that, in contrast to Figure 2a ▶, a number of noninterfacial residues are freed in going from the transition state to the product, pointing to a more homogeneous global "loosing" of the enzyme matrix for product release. This result is in agreement with the proposed ground-state destabilization for the product complex due to bond distortion in the bound uridine (Xiang et al. 1997).

Comparison of substrate complex and product complex fluctuations shows similar fluctuation magnitudes in both (most amino acids are within the 15% cutoff).

We will argue that these conformational restrictions at the transition state are intimately linked to the rate of reaction barrier crossing from the ES complex to EP. First, we need to couple these results to a dynamic picture of catalysis.

Dynamical free energy and local flux velocity

The Michaelis-Menten scheme for enzyme catalysis will be modified such that the dynamical nature of catalysis can be explored. The expression

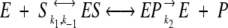will be developed as follows. The binding and unbinding of enzyme and substrate E + S ↔ ES will be described through the usual rate equations with k₁ and k₋₁ representing the forward and reverse rate constants, respectively. Similarly, product release from the enzyme–product complex EP → E + P is described though a rate equation with forward rate constant k₂. The reverse reaction is not included here because it is assumed that the product concentration is fixed at zero. Similarly, the substrate concentration is fixed as well, and therefore, the reaction is constrained to proceed in a constant concentration substrate and product bath.

The reversible transformation of the enzyme–substrate complex into enzyme–product complex ES ↔ EP is handled through a diffusive scheme by the Fokker-Planck (or, more correctly, Smoluchowski) equation (Serra et al. 1986). Here we use the Fokker-Planck formalism to arrive at a dynamic free energy for the catalytic process.

Note that ES ↔ EP is exactly that part of the catalytic scheme for which we have crystallographic, and therefore, equilibrium averaged, information about the magnitude of conformational fluctuations. In the diffusive description, this chemical reaction coordinate is described through a continuous variable ξ, capturing in an abstract fashion changes in enzyme–ligand atomic scale conformations during the chemical transformation.

Let P(ξ,t) be the probability density that the enzyme– ligand conformation is between ξ and ξ + dξ at time t. ξ = 0 will correspond to the enzyme–substrate conformation just at the beginning of the ES ↔ EP transformation. That is, ξ = 0 represents the ES complex. Likewise, ξ = 2 represents the EP complex at the completion of the chemical leg ES ↔ EP. Therefore, 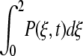is the total probability at time t that the enzyme is engaged in the chemistry at hand and, therefore, not in its unbound state E. In this same spirit, let P(E,t) be the probability density for enzyme in its free form. This modified treatment of the Michaelis-Menten scheme leads to the following coupled equations for the time–evolution of the probability densities:

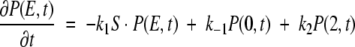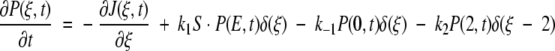1

where 0 ≤ ξ ≤ 2. The delta functions ensure that substrate binding and unbinding events occur only at ξ = 0, whereas product release occurs only at ξ = 2. That is, because δ(ξ) is peaked at ξ = 0 on the continuous chemical reaction coordinate, changes to the probability density P(ξ,t) with time due to substrate binding or unbinding can only occur at ξ = 0, where the probability density is P(0,t). The function δ(ξ − 2), peaked at ξ = 2, allows for changes in P(ξ,t) due to product release to occur only at ξ = 2, where the probability density is P(2,t). Changes to P(ξ,t) along the chemical reaction coordinate itself are driven by the gradient in the flux J(ξ,t), where:

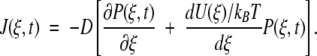2

The flux contains a diffusive element given by the gradient of the probability distribution and a deterministic force −d(U/k_BT)/dξ term where U/k_BT is the dimensionless potential energy along the chemical reaction coordinate (k_B is Boltzmann's constant and T is temperature). The form of the potential energy will be described shortly. D is the diffusion constant, effectively scaling the intrinsic rate at which enzymatic conformations can change along the reaction coordinate. The flux is related to the ensemble averaged rate of enzymatic conformational change during catalysis.

As in Michaelis-Menten kinetics, we seek steady-state solutions to the above system of differential equations which when set to zero become

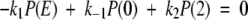3

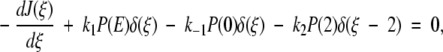4

where the probability densities and flux J(ξ) are now time independent. Note that in equations (3) and (4) the constant substrate concentration S has been absorbed into the rate constant k₁.

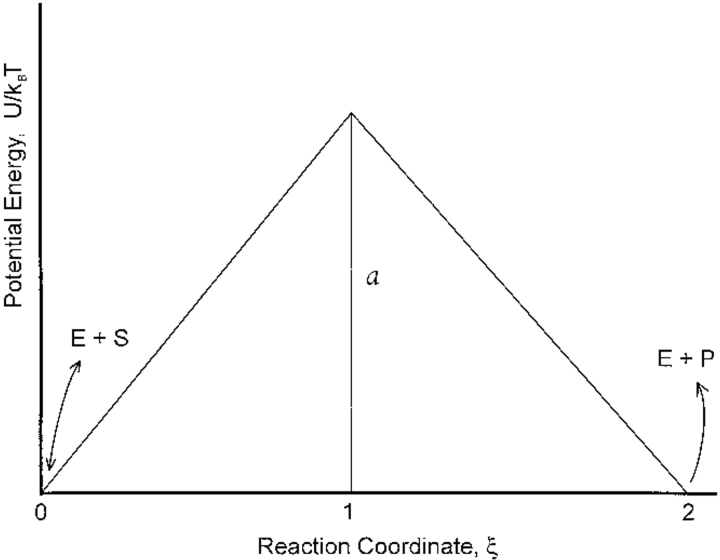
To facilitate our presentation, the dimensionless potential energy along the enzymatic reaction coordinate is chosen as the piecewise continuous form shown in Figure 3 ▶, which shows also the binding and unbinding steps. The dimensionless barrier height at ξ = 1, corresponding to the transition state of the chemical reaction, is a. Choosing a piecewise potential energy with U(0)/k_BT = U(2)/k_BT does not affect any of our conclusions. The solution of equations (3) and (4) is discussed in the Appendix.

Fig. 3.

Piecewise potential energy used to solve steady-state diffusion equation (Eq. 4 in text).

In addition to explicit forms for the probability densities P₁(ξ) and P₂(ξ) along the first and second legs, respectively, of the potential energy (see Appendix), we learn that the ensemble-averaged flux along the reaction coordinate ES ↔ EP is constant (in accord with steady-state) and is given by

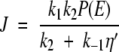5

where η = 1 + 2k₂/aD(e^a − 1).

The flux refers to the overall forward velocity along the Michaelis-Menten scheme, and its magnitude decreases with increasing barrier height a. We want to specialize to a flux velocity at conformation ξ.

Motivated by Doi and Edwards (1988), we write a local free energy for the enzyme–ligand complex at conformation ξ, which captures the thermodynamics along the reaction coordinate. The total free energy, averaged over the probability distribution along the entire reaction coordinate, is expressed as

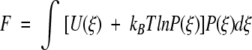6

so that Ω(ξ) = U(ξ) + k_BT ln P(ξ) defines a local free energy. For our piecewise potential energy U(ξ), therefore, the local free energies (to within an additive constant) for the first and second legs become

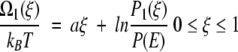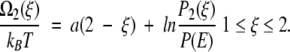7

Equations (A4)–(A8) in the Appendix establish the values of P₁(ξ)/P(E) and P₂(ξ)/P(E).

Consider now an obvious expression for the overall constant flux written as an ensemble average over the entire reaction coordinate 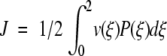where v(ξ) = J/P(ξ). In the same way that we established a local free energy, we identify v(ξ) as the local flux velocity at reaction coordinate ξ. It is also clear that

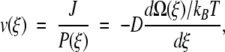8

showing that v(ξ) satisfies a force-flux equation of irreversible thermodynamics (Haase 1990). Therefore, the driving force for the local flux velocity is the gradient of the local free energy. The value for v(ξ) is calculated from our expressions for the probability density P(ξ) and flux J (equations A4–A9).

As the reaction proceeds, the substrate's molecular architecture is modified, and adjustments in the enzyme molecule's conformation (at least locally within the active site) must accommodate the chemical modifications. Consequently, this local flux or velocity v(ξ) along the reaction coordinate is intimately related to the rate of enzymatic conformational change at ξ. Fluctuations in those enzymatic atoms directly responsible for the reaction necessarily proceed at the same rate as the chemistry—we maintain that accommodating conformational rearrangements in amino acids not involved directly in the chemistry also proceed at the same rate.

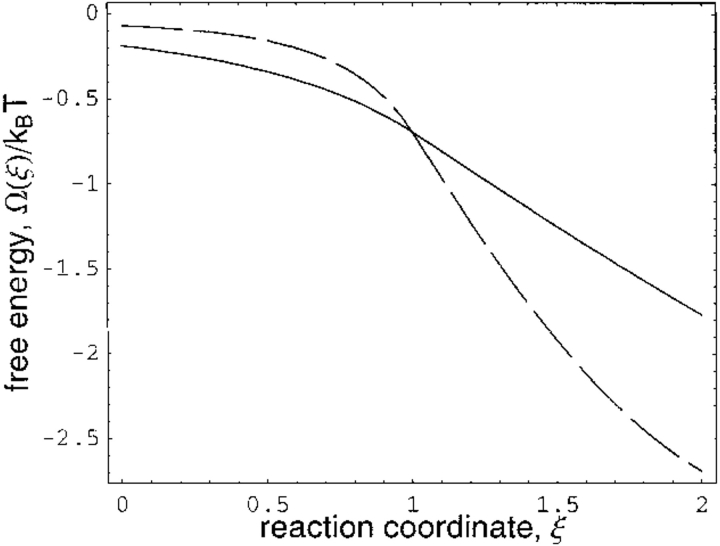
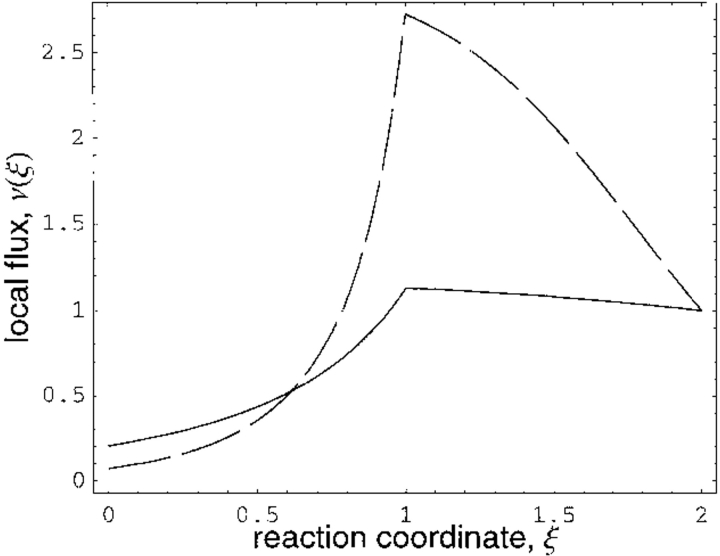
Figure 4 ▶ shows the decrease in local free energy along the reaction coordinate for two values of the barrier height a. For these two barrier heights, Figure 5 ▶ shows that the local flux velocity increases as the transition state is approached. This result is readily explained. Because the observed ensemble-averaged flux is constant along the reaction coordinate, the local flux must be maximum at the transition state where the probability density is minimum. In analogy, if water is to flow through a pipe with constant flux, its local velocity increases as the pipe diameter decreases. Although the overall flux (Eq. 5) decreases with increasing barrier height, note that the local flux v(ξ), as seen in Figure 5 ▶, increases at the transition state with increasing barrier height. This is a consistent result. The global and local fluxes are related through the expression J ∝ ∫v(ξ)P(ξ)dξ and the increased local flux (with increasing barrier height) at the transition state is more than compensated for by the decreased probability density. Also, the discontinuity in the local flux at the transition state is a mathematical artifact stemming from the piecewise potential energy and does not affect the results.

Fig. 4.

Decrease in local free energy along reaction coordinate ξ. Solid curve is for barrier height a = 1.2; for dashed curve a = 3. All rate coefficients and diffusion constant D are scaled to unity in appropriate equations in text and in the Appendix.

Fig. 5.

Flux velocity at enzymatic conformation ξ along reaction coordinate (as determined by Eq. 8 in text). Solid curve is for barrier height a = 1.2; for dashed curve a = 3. All rate coefficients and diffusion constant D are scaled to unity.

An important conclusion follows. Because the residency time at conformation ξ decreases as the transition state is accessed, enzymatic conformational adjustments commensurate with modifications to the substrate's structure are established with increasing rapidity as the transition state is approached. Consequently, the enzyme–ligand complex must undergo catalytically efficient and productive fluctuations at the transition state to "keep up" with the rapid local chemical flux there: "stray" fluctuations—those not seminal to the chemistry—are minimal. Furthermore, as inferred from the temperature factor study, additional restrictions to local conformational fluctuations come into play as substrate– enzyme interaction strengths increase on the way to the transition state. Crystallographic temperature factors represent time-averaged, and therefore equilibrium, measures of spatial fluctuations. Although such a full-time averaging during the actual dynamic chemical process is improbable (especially for the short-lived transition state), the tight-binding transition state will nonetheless impose greater bounds on the fraction of conformation space explored than will the less tightly held (and longer lived) ground state. Therefore, restriction of conformational fluctuations because of the tight-binding nature of the transition state, its short-lived nature, and the increased dynamical flux through it go hand-in-hand to ensure that only catalytically productive fluctuations remain at the transition state, driving the reaction over the activation barrier with maximum efficacy.

A possible connection exists between our work and the near attack conformers postulated by Bruice and Benkovic (2000). These ground-state conformers closely resemble the transition state. Relative conformational freedom in the ground-state complex can allow access of various near-attack conformers. Once accessed, the conformational fluctuation space available to a near attack conformer is necessarily finely honed for effective targeting of the transition state.

Correlated fluctuations and catalysis

Return to the Michaelis-Menten scheme:

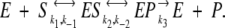In what follows, the entire process will be treated through rate equations. Focus on conformational fluctuations in the ES and EP complexes where, as stated above, the fluctuation magnitudes are comparable. Spatial fluctuations at the transition state, for both dynamical and static reasons, are diminished.

Conformational fluctuations in the ES complex lead to fluctuations in the rate coefficient k₂ for the ES ↔ EP transformation. Indeed, beautiful recent work on the photosynthetic reaction center has shown that electron transfer processes exploit such opportunistic thermal fluctuations in the protein structure. Tunneling events take place in protein conformations where destructive interference between various tunneling pathways is minimized (Balabin and Onuchic 2000). Essentially, our ES complex "awaits" an opportunistic conformational atomic scale rearrangement where the catalytic rate is maximized by a relatively small barrier to reaction. Therefore, a "window of conformational opportunity" provides for a reduced barrier to reaction. Similarly, the EP complex is transformed back to ES with a fluctuating rate coefficient k₋₂. Our focus is on the interplay between the fluctuating rate coefficients describing the reversible ES ↔ EP transformation.

Energetic fluctuations in the active site, as well as conformational ones, are diminished at the transition state of the reaction. It has been shown that thermal conformational fluctuations in charged and polar amino acid residues lead naturally to fluctuating electrostatic interactions with the substrate molecule (Sitnitsky 1994, 1995). Because conformational fluctuations are greatest at the substrate and product of the enzymatic reaction, fluctuations in the electrostatic coupling between amino acid groups and the reactive species—therefore in the potential energy of their interaction—are also greatest at the ground state complexes.

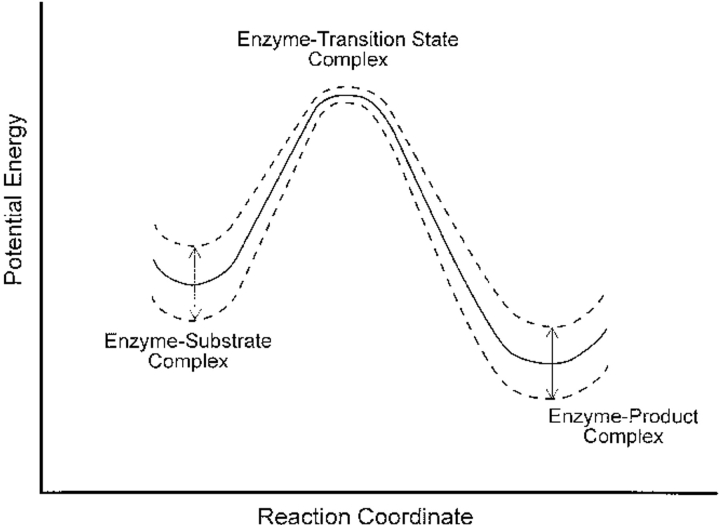
Consequently, the enzymatic reaction proceeds along a fluctuating potential energy surface as shown in Figure 6 ▶ (at least with respect to electrostatic contributions, although a similar argument holds for van der Waals interactions). Energetic fluctuations—arising from the fluctuating interactions between reactant and the amino acid residues—are shown to be minimal at the transition state. It must be emphasized that this fluctuating potential energy does not represent the profile for the entire enzyme; the entire enzyme–ligand complex is an equilibrated thermodynamic system and its equilibrium energy fluctuations will be the same along the entire reaction coordinate. We are sketching energetic fluctuations localized to the active site chemistry that arise through electrostatic interactions between active site amino acids and the chemically reactive ligand.

Fig. 6.

Fluctuating potential energy profile for enzymatic catalysis. See text for explanation.

Correlated enzymatic fluctuations have a long history, with speculations on their importance initiated some 27 years ago (Careri 1974). Furthermore, even early molecular dynamics simulations have uncovered coordinated motions in proteins (Karplus and McCammon 1986). We propose that energy fluctuations in the ES and EP complexes are correlated in the following fashion. Probabilistically, the ES complex will surmount the reaction barrier when energetic fluctuations have minimized the activation energy. It would seem advantageous for the energy of the resulting enzyme–product complex to be the minimum value allowed by its conformational fluctuations, thereby trapping the product by inhibiting the reverse reaction. However, the EP energy will subsequently increase because of its intrinsic energetic fluctuations, decreasing the barrier to the reverse reaction and complicating the scenario. We have found that the frequency of fluctuations in substrate and product complexes and the phase relation between these fluctuating complexes are important for tuning the rate at which the reaction barrier is traversed.

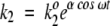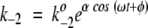For mathematical simplicity, the fluctuating rate coefficients k₂ and k₋₂ are chosen to be oscillatory: and . Therefore, fluctuations in the activation energies for the reactions ES → EP and EP → ES are at the heart of the fluctuating rate coefficients (see Robertson and Astumian 1990a,b, for a similar mathematical treatment). ω is the oscillation frequency, and k₂^o and k₋₂^o are the rate constants that would appear in the rate equations for the usual, nonfluctuating Michaelis-Menten scheme. The dimensionless parameter α indicates the magnitude of energetic fluctuations around the mean activation energy. For example, barrier oscillations have been calculated to be approximately 2.5 RT in an Ecto-ATPase model system (Markin et al. 1992). As noted previously, fluctuation magnitudes are similar at the substrate and product complexes. In this work, we report results using α = 2 for both substrate complex and product complex oscillations. The phase factor φ describes phenomenologically the fluctuation correlations going from ES → EP and back again to the substrate complex. Fluctuations in the forward and reverse rate coefficients are, therefore, of the same magnitude but out of phase with respect to each other by a factor φ.

The goal is to find the oscillation frequency ω and phase factor φ leading to the greatest increase over the nonoscillatory reaction velocity. Although our oscillating potential energy surface arises through internal thermal fluctuations, there are similarities to the ideas of stochastic resonance where a resonant matching of an externally applied oscillating field and intrinsic thermal noise lead to enhanced signal-to-noise ratios (McNamara and Wiesenfeld 1989; Gammaitoni et al. 1998).

The Michaelis-Menten equation with oscillatory rate coefficients k₂ and k₋₂ leads to the following system of equations:

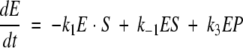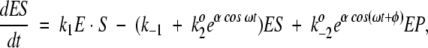with an additional condition describing the conservation of the total amount of enzyme E₀ in the usual way. Solution of these equations under steady-state conditions (dE/dt = dES/dt = 0)—in the absence of oscillations with α = 0—establishes the baseline catalytic velocity. For the oscillatory scenario, the time-dependent system of equations is solved numerically in (ω,φ) space. The reaction velocities are calculated after transient time dependencies in the values of ES, EP, and E have stabilized. A good indication of stability in the solutions is equivalence of the velocities calculated from the three legs of the Michaelis-Menten equation:

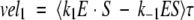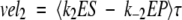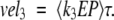9

The calculated velocities are averaged over an oscillation period τ, and we expect that vel₁ = vel₂ = vel₃ ≡ vel after the differential equations have been propagated to sufficiently long times. Recall that the amount of substrate and product are held constant (S, P = 0).

When ω → ∞, the time-scale for catalysis is much longer than the oscillatory period for the potential energy profile. In this limit of high frequency oscillations, the system achieves steady-state behavior described by the rate coefficients k₂ and k₋₂ when averaged over an oscillatory period; that is,

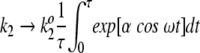and

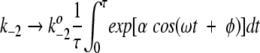10

where τ = 2π/ω. Note that these averages depend on α, but not on the values of the phase factor and frequency.

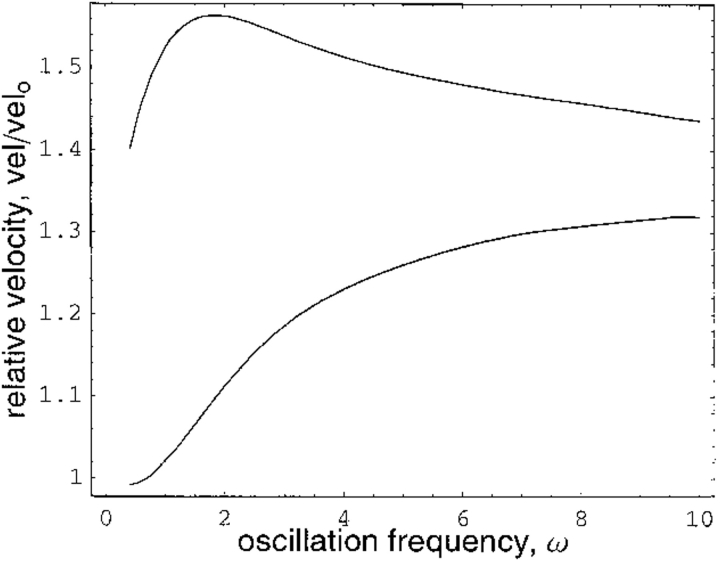
Because we are interested in the catalytic rate along the fluctuating potential energy surface relative to that for the nonoscillatory profile, the average velocity values reported are relative to those of the steady-state scenario where α = 0. For dimensionless parameters k₁ = k₋₁ = k₃ = 0.4, k₂⁰ = k₋₂⁰ = 0.2, E₀ = S = 1, and α = 2, for example, Figure 7 ▶ shows the normalized average velocity—that is, vel/vel₀ where vel₀ is the steady-state velocity for the parameter set—plotted against (dimensionless) oscillation frequency ω. In the lower curve, the phase factor φ is chosen to give the smallest value of the normalized velocity at each given oscillation frequency. The upper curve shows the maximum velocity at each ω achieved by an appropriate value for the phase factor. For the range of ω plotted, the values of φ producing the maximum and minimum velocity curves are essentially constant; φ = 0.5π gives the maximum velocity at every frequency, whereas φ = 1.6π corresponds to the minimum velocity at each frequency.

Fig. 7.

Relative reaction velocity plotted as a function of potential energy oscillation frequency. For upper curve, the phase factor φ is tuned for maximum velocity at each frequency. For lower curve, phase factor is tuned for minimum velocity at each frequency. See text for details.

The maximum rate enhancement over the nonoscillatory kinetics occurs at well-defined values of the oscillation frequency and phase factor—this represents the dynamical tuning of the enzyme for maximally efficient reaction–barrier crossing.

In the high frequency regime, the velocity of reaction is increased over the nonoscillatory situation because, as explained above, a new effective steady-state solution is reached with the now larger, time-averaged rate coefficients of equation (10). However, we are particularly interested in oscillations having time scales commensurate with that of the chemistry, as this is where the maximum velocity enhancements are achieved. For the parameter set above, the maximum velocity is achieved when ω ≈ 2, corresponding to an oscillatory time period of ∼π,which is close in value to the reciprocal of the averaged rate constants k₁^o and k₂^o. Similar conclusions can be drawn from other parameter sets.

In conclusion, both the frequency of conformational fluctuations and their phase relation between the substrate and product state are important for catalytic tuning. Our simple model leads to a maximum rate enhancement over the nonoscillatory case of vel/vel₀ = 1.56. As opposed to the simple one-dimensional reaction coordinate in Figure 6 ▶, realistic enzymatic conformational fluctuations take place on a multidimensional landscape. It is tempting to speculate that in this complex, multidimensional conformational space even greater rate enhancements can be achieved.

Materials and methods

Kohonen network projections

Our presentation is motivated by the work of Gasteiger et al. (Gasteiger et al. 1994; Zupan and Gasteiger 1999).

Conceptually, the Kohonen projection algorithm works as follows. Each amino acid in the three-dimensional enzyme is labeled by its average x, y, and z coordinates (resulting from averaging over all atomic coordinates for that particular residue). Therefore, the ith amino acid is characterized by the coordinate set (x_i, y_i, z_i). Each monomer of cytidine deaminase contains 294 amino acids and a bound ligand molecule. Therefore, the entire input for the Kohonen network contains the set of 2 × 295 (x_i, y_i, z_i) triplets. These 590 residues (588 amino acids and 2 ligand molecules) are projected onto a 25 by 25 square lattice with periodic boundary conditions: squares on the left edge of the lattice are continuous with squares on the right, whereas squares on the upper edge are juxtaposed to those on the lower edge. Strictly speaking, the projection surface is toroidal. Note that 590 residues are projected onto 625 squares where each residue occupies its own square. Consequently, 35 "empty" squares will result but without any negative implications for the projection algorithm.

Initially, each square is assigned a randomly chosen triplet of numbers. For the jth square, then, we assign the random numbers 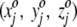, where the superscript o stresses that these numbers are associated with the square in the projection plane and are not the three-dimensional average coordinates of the amino acid residue. All random numbers are scaled such that the range between their minimum and maximum values is comparable to that of the amino acid three-dimensional spatial coordinates. Next, a first residue (either an amino acid or ligand molecule) is chosen at random from the protein and its coordinates (x₁, y₁, z₁) are compared with the triplets 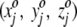assigned to each square. This first residue is projected to the single square, call it square c, whose triplet of random numbers is most similar to the residue's actual three spatial coordinates. That is, we seek, by comparing the residue to every square in the plane, to minimize the quantity 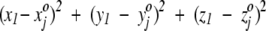. The index j runs from 1 to 625 with the final result that the j = c square minimizes the distance measure. After this first residue is projected, the randomly assigned triplet of numbers 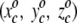is algorithmically modified to further minimize the distance measure to the projected amino acid's actual coordinates. Furthermore, triplets associated with the nearest and next-nearest neighbors of the c square are also systematically modified to resemble more closely the coordinates of the first projected residue. Indeed, the quality of the projections ultimately depends on the algorithm for updating the initial randomly assigned triplets, and a full description of the scheme is reserved for elsewhere.

After the random numbers associated with the c square and its neighbors are adjusted as described, a second randomly chosen residue is projected onto the square whose defining triplet of numbers matches most closely that residue's three-dimensional coordinates. And, in the same fashion as above, the triplets of numbers associated with this square and its neighbors are modified to match more closely the coordinates of this second residue. The scheme continues for all 590 protein residues, representing a first cycle of projection. A second cycle begins by choosing again at random a first residue to project onto the plane, but recall that the entire set of triplets defining the squares has already been updated through the previous projection cycle. These projection cycles—each involving modification of the entire set of triplets—continue until a satisfactory criterion for convergence is met.

This is a self-organizing neural network. No global "energy" function drives the organization of the projection. Instead, local update rules modify the 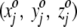triplets of the projection squares, leading to an emergent global pattern of projected amino acid residues. Say an amino acid residue is projected onto square c. As stated, that square's 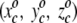value, as well as those for neighboring squares, is modified to match more closely the amino acid's spatial coordinates in the crystal structure. A second enzymatic residue, therefore, if spatially close to the first amino acid, will with increased probability be projected onto a square in the immediate neighborhood of the first residue. Repetition through a number of projection cycles results in a global pattern where spatially juxtaposed amino acids in three dimensions end up close together in the two-dimensional representation. Finally, 590 of the 625 squares are occupied by amino acids, and each square can be either labeled by its amino acid number for identification purposes or colored according to the temperature factor of that particular residue occupying the square. The computer algorithm is run on a Silicon Graphics Origin 200. The resulting projections are visualized with the Mathematica 4.0 program.

Dynamic free energy and local flux velocity and correlated fluctuations and catalysis

The Results and Discussion sections and the Appendix provide a self-contained presentation of the formalisms used. The resulting differential equations for the oscillatory Michaelis-Menten scheme are numerically integrated and graphed with the Mathematica 4.0 program.

Appendix

Here we solve the system of equations (3) and (4) from the text. The goal is to derive expressions for both the ensemble-averaged flux (Eq. 2 in text) and the probability distribution along the continuous reaction coordinate ξ. The equations to be solved are

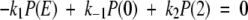A1

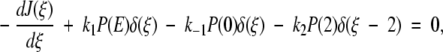A2

where the probability densities and flux J(ξ) are now time independent for steady state. The time-independent flux is given as

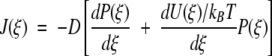A3

The piecewise potential energy in Figure 3 ▶ is used for U/k_BT and 0 ≤ ξ ≤ 2. A first integration of equation (A2) starts from ξ = 0 and ends at some arbitrary ξ ≤ 1. This integration, contained within the first leg of the piecewise potential and effectively spanning the delta function δ(ξ), yields the expression − J₁(ξ) + J₁(0) + k₁P(E) − k₋₁P(0) = 0. Here the subscript 1 on the fluxes stresses that this result refers to the first leg of the potential. A second and independent integration of equation (A2), this time from an arbitrary ξ ≥ 1 to ξ = 2 gives − J₂(2) + J₂(ξ) − k₂P(2) = 0 for the second leg of the potential (as denoted by the subscript 2). Formally only one half of each δ function at either end of the reaction coordinate is spanned so a factor of 1/2, which we absorb into the rate constants, effectively appears in the integration of each δ- function.

It is clear from these two integrations that the ensemble-averaged flux J(ξ) must be constant along each leg and at each value of ξ (indeed, this is the steady-state condition). Furthermore, setting J₁(ξ) = J₂(ξ) and using equation (A1) tells us that J₁(0) = J₂(2). It is also clear that these two constants of integration are equal to zero. Explicitly, as k₁P(E) − k₋₁P(0) is the net substrate binding rate, or velocity of the forward reaction, in the expression J₁ = J₁(0) + k₁P(E) − k₋₁P(0), we must set J₁(0) to zero so that the flux along the reaction coordinate is equal to the net forward velocity of the reaction E + S ↔ ES, thereby ensuring steady state.

We are left with the expressions J₁ = k₁P(E) − k₋₁P(0) and J₂ = k₂P(2). Furthermore, we know that J₁ = J₂ and we let the constant flux be defined as J₁ = J₂ ≡ −A. For the first leg of the potential energy d(U/k_BT)/dξ = a, whereas d(U/k_BT)/dξ = −a for the second leg. From the definition of the differential equation for the flux (Eq. A3), we determine the probability densities P₁(ξ) and P₂(ξ) along the first and second legs of the piecewise potential energy (Fig. 3 ▶). With the demand that P₁(1) = P₂(1) the results are

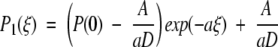A4

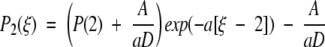A5

where

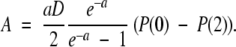A6

Here, P(0) and P(2) refer to the probability densities at the end points of the first and second legs of the potential, respectively. Using equation (A6), the fact that the flux along the reaction coordinate is equal to −A, and that J₁ = k₁P(E) − k₋₁P(0) and J₂ = k₂P(2) (where J₁ = J₂), we solve for P(0) and P(2) as

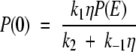A7

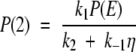A8

where η = 1 + 2k₂/aD (e^a − 1). With these results the flux along the reaction coordinate is compactly expressed as

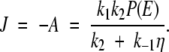A9

Now, the conservation of total enzyme can be used to evaluate P(E); however, for our purposes it suffices to work with the quantities P₁(ξ)/P(E) and P₂(ξ)/P(E).