A critical investigation of the Tanford-Kirkwood shceme by means of Monte Carlo simulations

Abstract

Monte Carlo simulations are used to assess the adequacy of the Tanford-Kirkwood prescription for electrostatic interactions in macromolecules. Within a continuum dielectric framework, the approach accurately describes salt screening of electrostatic interactions for moderately charged systems consistent with common proteins at physiological conditions. The limitations of the Debye-Hückel theory, which forms the statistical mechanical basis for the Tanford-Kirkwood result, become apparent for highly charged systems. It is shown, both by an analysis of the Debye-Hückel theory and by numerical simulations, that the difference in dielectric permittivity between macromolecule and surrounding solvent does not play a significant role for salt effects if the macromolecule is highly charged. By comparison to experimental data, the continuum dielectric model (combined with either an approximate effective Hamiltonian as in the Tanford-Kirkwood treatment or with exact Monte Carlo simulations) satisfactorily predicts the effects of charge mutation on metal ion binding constants, but only if the macromolecule and solvent are assigned the same or similar permittivities.

It seems reasonable to believe that the binding of a charged ligand to a protein or some other macromolecule will depend, at least in part, on purely electrostatic interactions. All chemically interesting interactions for molecular systems ultimately stem from an electrostatic origin, of course, as only Coulombic potential terms enter the Schrödinger equation. Very often, however, to render a many-body problem tractable, an effective Hamiltonian is introduced where large classes of microscopic interactions are replaced by a suitable average and not accounted for explicitly. Partitioning an effective interaction into an electrostatic (ionic) term, which dominates at long range, and other terms of covalent character with much shorter range is, then, a useful heuristic and computational device. Consider, for example, the titration of a residue side chain in a protein. The free energy change for proton transfer will be broadly similar to that of the corresponding process in the isolated amino acid, but further augmented by an electrostatic term that depends on the overall charge and charge distribution of the protein. In such cases, the binding constant shift arising solely from electrostatic interactions can amount to several pK units.

The role of electrostatic interactions in protein structure and function has long attracted interest. In one of the first theoretical attempts to deal with the problem, Tanford and Kirkwood assumed that the long-range part could be described within a dielectric continuum model (Tanford and Kirkwood 1957). This effective Hamiltonian model has been invoked extensively to study the interaction between charged ligands and proteins, membranes, and other macromolecules (Hill 1955, 1956; Warwicker and Watson 1982; Warshel et al. 1984; Harvey 1986; Bashford et al. 1988) (the reference list given is by no means exhaustive). The original Tanford-Kirkwood (TK) scheme considers the macromolecule as a sphere of low dielectric permittivity different from the surrounding (aqueous) solution of high permittivity. With respect to the rigid macromolecular reference frame supporting fixed charged groups, the salt ions and other charged ligands are supposed to be in relative motion throughout the solvent medium. Tanford and Kirkwood avoided the formidable statistical thermodynamics problem this motion implies by again appealing to the effective interaction construct, eliminating explicit reference to the mobile particles and introducing the Debye-Hückel potential.

Despite the evident success of the TK result, it suffers from two significant limitations: (1) closed form analytical solutions are only available in simple geometric configurations (usually spherical); and (2) nonlinear effects and explicit ion–ion correlations are ignored.

At the cost of computational simplicity, the first constraint has been removed in a number of calculations by several groups (Warwicker and Watson 1982; Bashford et al. 1988; Bashford and Karplus 1990; Beroza et al. 1991; Juffer et al. 1999). The second limitation has only been partially tested by replacing the DH equation with the nonlinear Poisson-Boltzmann equation (Fushiki et al. 1991), though the description remains at the mean-field level ignoring ion–ion correlations. Monte Carlo (MC) simulations have addressed the full statistical mechanical problem but then only for a model with a uniform dielectric permittivity (Fushiki et al. 1991; Kesvatera et al. 1994; Penfold et al. 1998). An additional simplification of the TK prescription, which may prove unrealistic at low ionic strength, lies in the assumption of infinitesimally small macromolecule concentration (Linse et al. 1995). In NMR studies of proteins the typical protein concentration is around 1 mM, whereas the concentration of accompanying counterions can be an order of magnitude larger or more.

The original application of the TK scheme dealt with titrating groups in proteins and how the pK_a for an ionizable amino acid is affected by the rest of the protein. The quantity calculated is the shift in pK_a between the "free" amino acid and the same residue in the protein. It became clear at an early stage that the scheme invoking a low dielectric interior for the protein did not properly reflect the difference in solvation energy between the free amino acid and when it is part of a protein (Tanford and Roxby 1972; Shire et al. 1974; Warshel et al. 1984; Papazyan and Warshel 1997). It seems, however, as there is no consensus of how to best tackle the problem (King et al. 1991; Warshel and Åqvist 1991; Antonsiewicz et al. 1994a, b; Simonson and Perahia 1995; Simonson and Brooks 1996; Löffler et al. 1997; Sham et al. 1997; Baptista and Soares, unpubl.) without invoking additional empirical parameters describing solvation and water penetration (Dwyer et al. 2000). A simple alternative is to assume a uniform dielectric response throughout the solution, including the macromolecule, equal to that of pure water. For titrating groups at or close to the protein surface this latter ansatz seems to give better agreement with experiment (Spassov and Bashford 1998; Kesvatera et al. 1999, 2001).

Another application of the TK scheme is to the binding of a charged ligand to a protein at different conditions, that is, mutation of charged amino acids and/or addition of inert salt. The ΔpK for such a process does not invoke the problematic solvation term mentioned above, and we will use the binding of divalent cations to a negatively charged protein as a model throughout this work. By using MC simulation to resolve the statistical mechanical problem, we will present a critical investigation of the dielectric continuum model originally studied by Tanford and Kirkwood. The simulations will be performed for a model including the dielectric discontinuity and the mobile species in the solution will comprise of salt particles as well as additional counterions in order to maintain electroneutrality.

Model systems

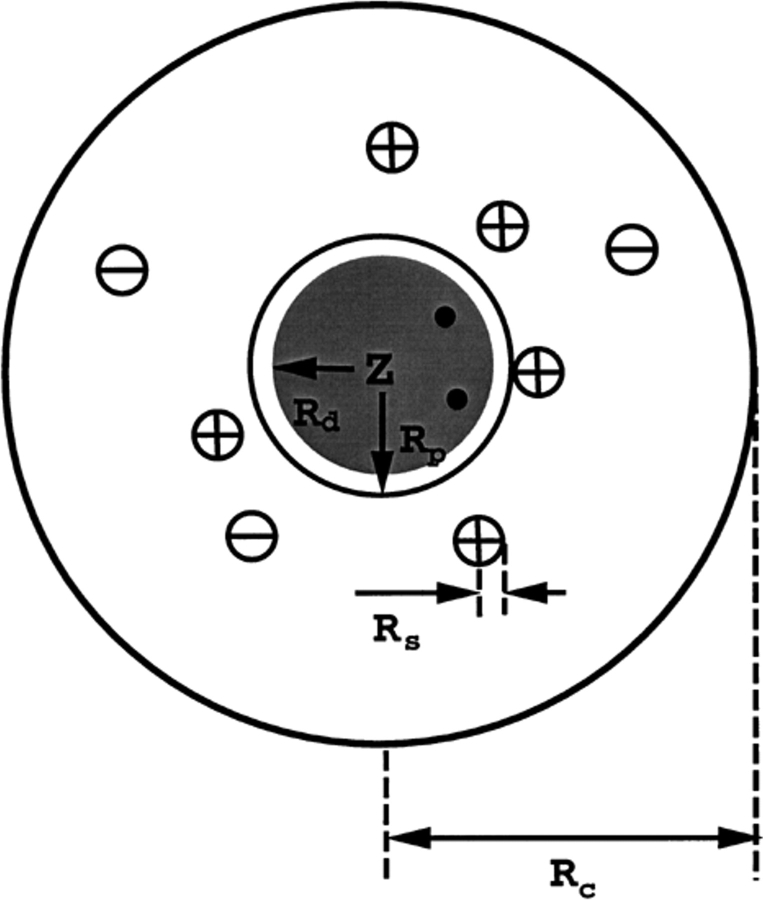
We investigate a model system mimicking a globular protein with a net charge, which is supposed to bind divalent ions. It could, for example, be a caricature of calbindin D_9k (Linse et al. 1988), and consists of a rigid sphere with radius R_p and a centrally located charge of valency Z. A surrounding electrolyte solution, including neutralizing counterions, is described by the so-called restricted primitive model (Levesque et al. 1986). Each uniformly charged mobile ion k with valency z_k is treated as a hard sphere of radius R_k; the solvent degrees of freedom are characterized only by an average dielectric permittivity ɛ_s that is also assigned to the ionic interior. Internal structural details of the biopolymer are neglected so that the protein interior is represented by a concentric spherical cavity of radius R_d (referred to as the dielectric radius) with a continuum dielectric permittivity ɛ_p < ɛ_s). Typically, R_d < R_p though this is not a constraint of the model. In any case, max{R_d,R_p} defines an exclusion boundary impenetrable by mobile salt particles and counterions. The entire system is placed in a spherical cell of radius R_c determined by the protein concentration (see Fig. 1 ▶).

Fig. 1.

Schematic representation of the model systems (see also Table 1). A spherical protein in a spherical cell with radii R_p and R_C, respectively. The protein interior with a low dielectric permittivity is shown as a shaded region of radius R_d < R_p. A central charge of valency Z and two binding sites marked as black dots.

Although the approach is quite general, the model parameters are chosen here to roughly suggest the calcium binding protein calbindin. Calbindin D_9k is a small globular protein with 722 atoms (46 charged for the wild-type apo form giving a net charge of −8) that binds two calcium ions Ca⁺² with high affinity (Linse et al. 1988) at sites located about 10.34Å and 11.08Å from the protein center of mass with cartesian coordinates (7.340, 7.114, −1.607) and (10.503, −3.509, −0.364), respectively, in Å units. The binding properties of calbindin have been studied in detail both experimentally and theoretically (Linse et al. 1988, 1991; Svensson et al. 1991). Effects arising from mutations of charged residues as well as varying salt and protein concentrations have been investigated (Linse et al. 1995). The agreement between experiments and MC simulations for this protein is excellent provided that the protein is treated as a medium of high dielectric permittivity (Svensson et al. 1990, 1991). Poisson-Boltzmann and DH calculations using a low dielectric response for the protein predict binding constant shifts that are qualitatively different from those observed by experiment (Penfold et al. 1998; Spassov and Bashford 1998; Kesvatera et al. 2001).

Classical techniques suggest a straightforward development of the electrostatic potential at any point (because of a fixed charge distribution and a dielectric discontinuity) in an orthogonal polynomial basis (Böttcher 1973), that is, the multipole expansion. This power series is not ideally suited for computer simulations, though, as the number of terms required for satisfactory convergence increases sharply when sources lie very close to the dielectric interface. Nevertheless, if the charges are more than ≈0.5Å from this boundary, it is feasible to achieve a precision of about 10⁻¹⁰, with an acceptable number of terms, that is, <1000. Given the elementary charge e and the vacuum permittivity ɛ₀, two ionised sites of valency z_i, z_j (either fixed or mobile) located at radial positions r_i, r_j and subtending an angle θ_ij, contribute an electrostatic potential energy given by,

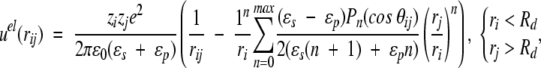1

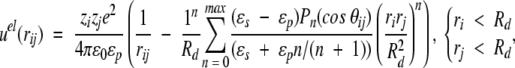2

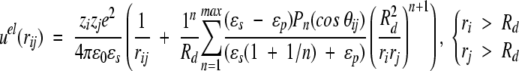3

where r²_ij = r_i² + r_j² − 2r_ir_j cos θ_ij if the spatial separation, P_n is the Legendre polynomial of order n, and n_max is the maximum number of terms included in the sum. The first term in Equations 1–3 is the direct Coulomb interaction, whereas the second describes the reaction field accounting for induced polarization charge at the dielectric discontinuity. In the absence of a dielectric inhomogeneity (ɛ_p = ɛ_s), it is easy to verify that Equations 1–3 reduce to the ordinary Coulomb potential,

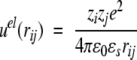4

with the characteristic divergence at small separation (r_ij → 0). On the other hand, for a nonuniform dielectric response, the reaction field term converges in this limit to yield a nonvanishing contribution, that is, the so-called self-image energy. Together with electrostatic interactions, the simulation Hamiltonian also includes a short-ranged hard-core overlap restriction among the mobile ions (thereby preventing Coulomb collapse in the configurational Markov chain),

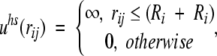5

as well as a one-body external field that accounts for the protein excluded volume and imposes the cell boundary constraint acting as a hard wall,

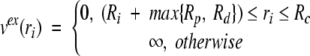6

The full configurational energy of the system then becomes,

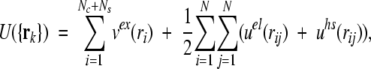7

where N = N_c + N_s + N_p is the total number of charges comprising N_c mobile counterions, N_s mobile added salt ions, and N_p fixed protein charges.

The calbindin-like model, introduced above, with a central net charge and two binding sites located at the usual positions, will be denoted SC8 (Spherical model with a Central charge of −8). Three other variations of this model, listed in Table 1, have been considered. A mutation that neutralizes a charged amino acid of the wild type will, in this model, simply lead to a change of the protein net charge, that is, we will refer to this "mutant" as SC7. Slightly more realistic is the Spherical model with a central charge of −7 and a Peripheral charge of −1 close to the protein surface, referred to as SP8 (see Table 1 for further details). One purpose of this work is to investigate the limitations of the DH approximation in a biophysical context. We have, therefore, also included a model protein that is otherwise identical to SC8 but with a variable central charge (ranging from −4 to −24). The most highly charged model system with Z = −24, SC24, has been studied in greater detail.

Table 1.

Summary of the main model systems

Model	Z1	position	Z2	position	Nc
SC8	−8	(0,0,0)	−	−	8
SC24	−24	(0,0,0)	−	−	24
SC7	−7	(0,0,0)	−	−	7
SP8	−7	(0,0,0)	−1	(13.5,0,0)	8

The coordinates (in Å units) of the fixed charges Z_k are listed along with the number N_c of positive counterions added to the system to maintain global electroneutrality. All four models have two divalent cation binding sites located at coordinates (7.340, 7.114, −1.607) and (10.503, −3.509, −0.364), respectively.

Results and Discussion

Gauging the validity range of the linear DH approximation is the primary objective of this work. In addition, the extent to which the ion binding characteristics of a protein is affected by the presence of a low dielectric interior region is also of interest. Not only does this notion underlie the original TK description, but it has also become a staple modeling supposition widely implemented in a number of generalized program packages used to study biomolecular phenomena (Warwicker and Watson 1982; Bashford and Gerwert 1992; Honig and Nicholls 1995).

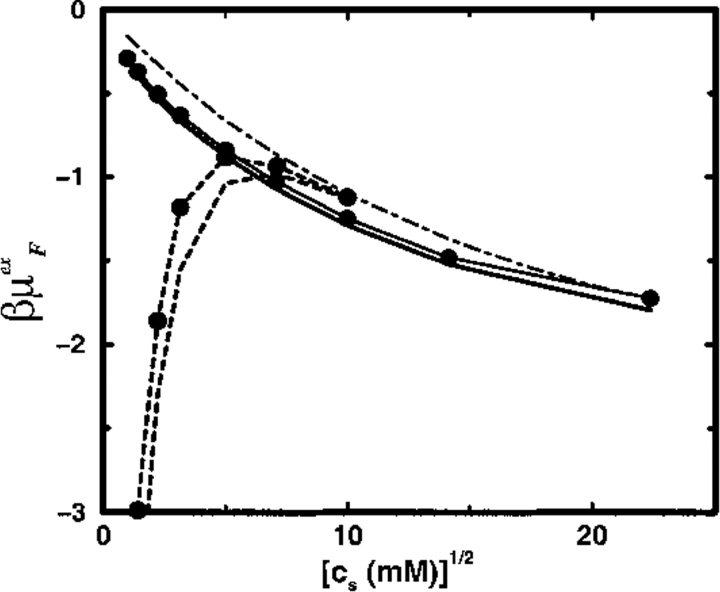
The binding constant shift ΔpK is related to the free energy cost for the protein to incorporate a mobile ion from the solution, see Equations 9 and 10. To calculate ΔpK, therefore, estimates of μ^ex for both free and bound ions are required. The free ion contribution μ_F^ex is usually minor, but can become significant in some circumstances. Figure 2 ▶ illustrates the dependence of μ_F^ex on salt concentration c_s for a protein solution at experimental conditions (c_p = 0.02 mM) typically encountered. A moderately charged protein (model SC8) has only a small effect on the free ion chemical potential at low c_s, whereas it is efficiently screened at higher salt concentrations where μ_F^ex closely follows the ionic excess chemical potential of a bulk electrolyte solution. Moreover, without a very substantial net protein charge, μ_F^ex is entirely insensitive to the dielectric properties of the protein interior, as Figure 2 ▶ demonstrates, where any shifts on exchanging a solvent filled cavity for a vacuum are below the statistical noise level, regardless of salt content. On the other hand, a highly charged protein (model SC24) dramatically lowers μ_F^ex by several kT in dilute electrolyte. Added salt will screen the strong electrostatic field from the protein, however, effecting an increase in the excess chemical potential with increasing c_s, contrary to the behaviour in a bulk electrolyte solution at least up to physiological concentrations. A dielectric discontinuity now contributes a small but noticeable effect, amounting to a few tenths of kT, as displayed in Figure 2 ▶.

Fig. 2.

The reduced excess chemical potential for a free divalent cation in a 20 μM protein solution is indicated as a function of monovalent salt concentration. The (superimposed) solid lines refer to the SC8 model and the broken lines to the SC24 model. Lines marked by solid circles are calculated with a dielectric boundary radius R_d = 14Å; lines without symbols refer to R_d = 0Å. The thin broken line shows the excess chemical potential of a divalent ion in a bulk salt solution.

To complement the picture, Figure 3 ▶ demonstrates how μ_F^ex varies as a function of protein concentration c_p at a constant level of salt. At low salt content, a non-negligible effect of increasing c_p is observed for model SC8, but it is entirely screened out at c_s ≈ 100 mM. This effect is, of course, more pronounced for a highly charged protein, where the curve for c_s = 1 mM even exhibits non-monotonic behaviour.

Fig. 3.

The reduced excess chemical potential for a divalent cation as a function of protein concentration with a homogeneous dielectric response (dielectric radius R_d = 0). The solid lines refer to the SC8 model and the broken lines to the SC24 model. Lines marked by circles denote a monovalent simple electrolyte concentration of c_s = 100 mM; lines without symbols are for c_s = 1 mM. The arrows indicate the value of βμ_F^ex in the corresponding bulk salt solutions. The upper arrow indicates the system at c_s = 1 mM (βμ_F^ex = −0.156).

For a protein/salt solution, Figures 2 and 3 ▶ ▶ clearly demonstrate that all charged species present will contribute to the Coulomb shielding. Should the protein be only weakly charged, then the screening effects can be described, at least qualitatively, by the inverse length κ within the DH approximation. A highly charged protein, however, requires a more sophisticated theoretical treatment that can account for both nonlinear and ion–ion correlation terms. On the other hand, the chemical potential of a bound ion is only marginally affected by changes in protein concentration.

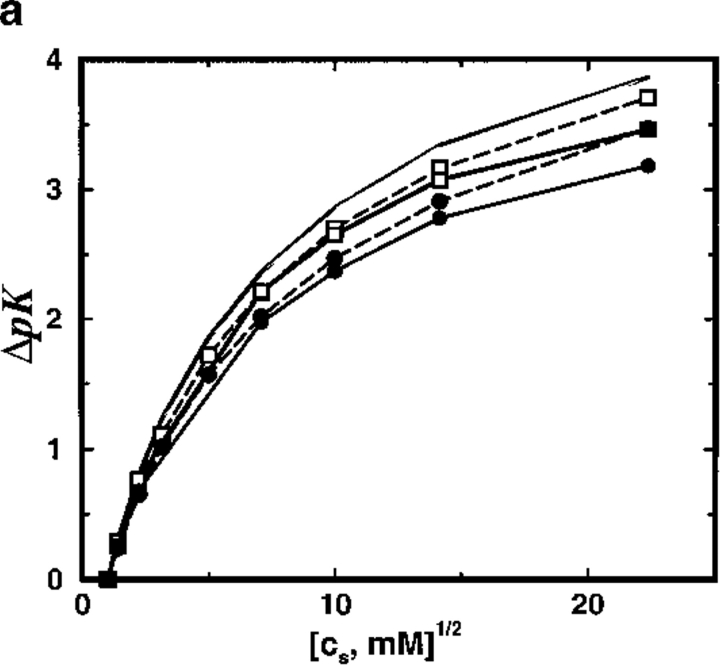
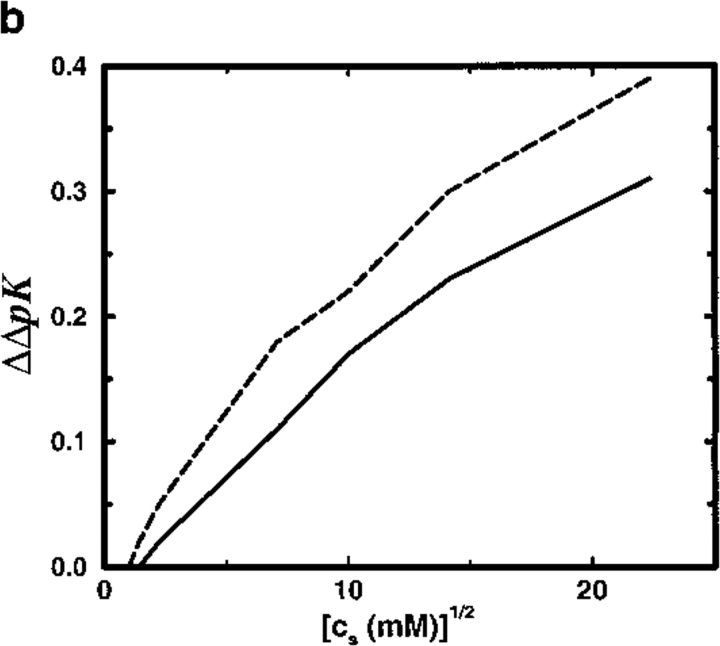
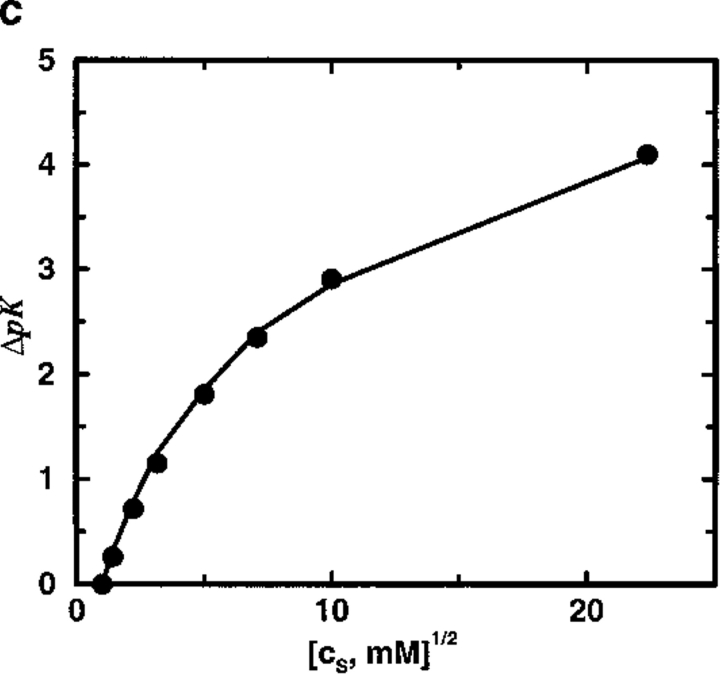
To mimic the calcium binding property of calbindin D_9k, the protein model SC8 binds two divalent ions. The stoichiometric ion binding constant κ varies with the amount of salt present and provides a suitable test of theoretical predictions for the shift ΔpK with respect to c_s. Figure 4a ▶ shows a very significant shift of 3–4 pK units on increasing c_s from 1 mM (reference state) to 500 mM. The simple TK calculation performs very satisfactorily in predicting ΔpK, disagreeing with MC simulation results by less than a few tenths of a pK unit. More significantly, it appears that the presence of a low dielectric protein interior has practically no influence on ΔpK. With a dielectric radius R_d = 12Å, ΔpK is ∼ 3.5, whereas a shift of 3.8 is obtained within a uniform dielectric model (see Fig. 4b ▶). Increasing R_d further to 18Å reduces the shift down to 3.2 but because the protein radius is 14Å this corresponds to suggesting that the contact water layer, about 4Å thick, is both impenetrable to salt ions and unpolarizable with a relative dielectric permittivity of unity. Experimental studies have measured ΔpK ≈ 4.6 for aqueous solutions of calbindin D_9k on raising the salt concentration from 1 mM to 500 mM (Kesvatera et al. 1994). Although model SC8, with the net charge contracted to a single point and no higher electric moments, is surely too crude a description for any real protein, the salt dependence of cation binding constant shifts for a model with eight randomly placed negative charges is almost indistinguishable from the results obtained with model SC8, as illustrated in Figure 4c ▶.

Fig. 4.

(a) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for the SC8 model. A reference state at c_s = 1 mM is chosen and the protein is allowed to bind two divalent cations. Results from MC simulations and TK calculations are compared as solid and broken lines, respectively. Lines marked by solid circles correspond to a dielectric boundary radius R_d = 18Å and those marked by open squares denote R_d = 12Å; unmarked lines refer to a homogeneous dielectric response (R_d = 0Å). (b) The shift of ΔpK arising from the presence of an interior vacuum ΔΔpK = ΔpK (R_d = 0Å) − ΔpK (R_d = 14Å) is demonstrated as a function of salt concentration c_s. In the solvent region, the relative dielectric permittivity is ɛ_s = 78.7. Solid line shows MC data and broken line indicates TK results. (c) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for a spherical protein model with eight randomly placed negative charges. Results from MC simulations and TK calculations are compared as solid line and solid circles, respectively. The protein dielectric boundary radius was R_d = 12Å in all calculations.

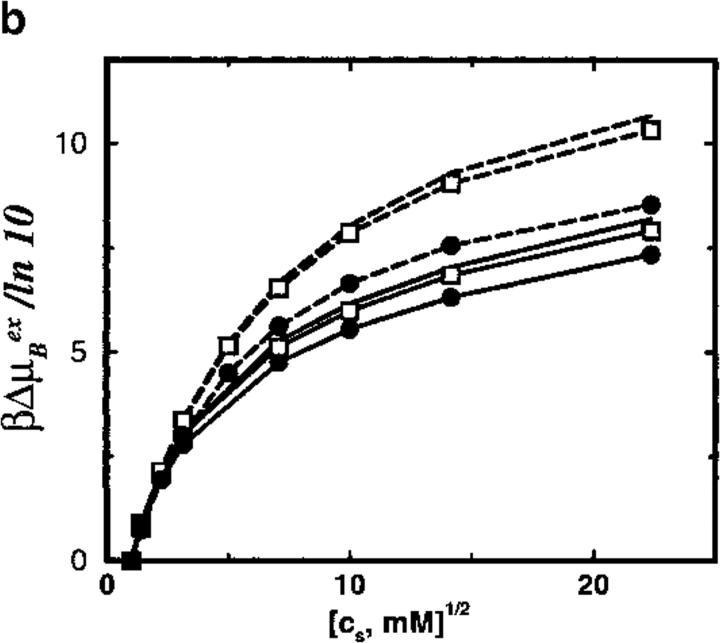
For the highly charged model SC24, the corresponding results are shown in Figure 5a ▶. In this case, the TK scheme breaks down regardless of the dielectric permittivity assigned to the protein interior. The discrepancy between calculated and simulated shifts can reach 5 pK units, implying an error five orders of magnitude in the binding constant! Obviously, the linear approximation is not capable of sensibly accounting for strong coupling and ion–ion correlations. In defence of the TK analysis, however, a protein as highly charged as SC24 is rare in biological systems. Because the binding constant shift depends on the difference between μ_B^ex and μ_F^ex, it is possible that the failure of the TK approximation is related to only one of these terms. Both are incorrectly predicted by the linear theory, it turns out, as demonstrated in Figure 5b ▶ and might have been guessed on the basis of Figure 2 ▶. The error arises from the neglect of both nonlinear effects and ion–ion correlations.

Fig. 5.

(a) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for the SC24 model. Other details are as for Fig. 4A ▶. (b) The difference of excess chemical potentials βΔμ_B^ex = βμ_B^ex(c_s) − βμ_B^ex(c_s = 1 mM) for a divalent cation in a bulk monovalent electrolyte solution is plotted as a function of salt concentration c_s.

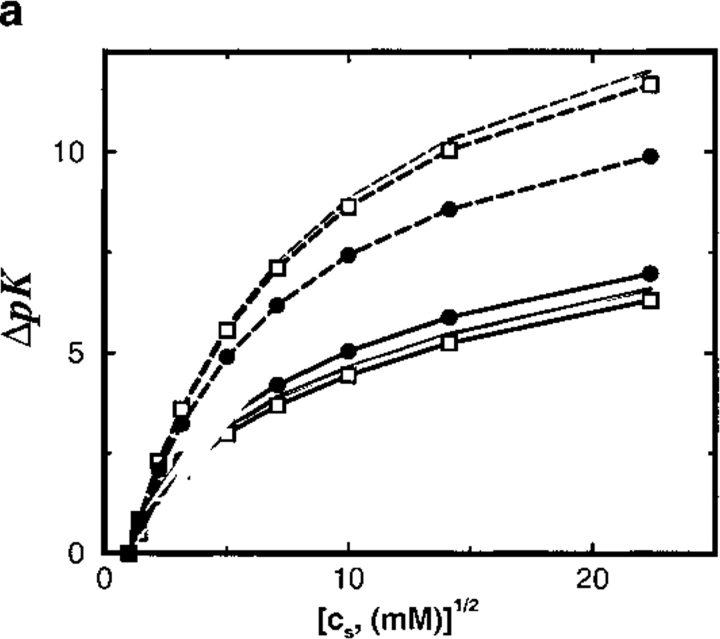
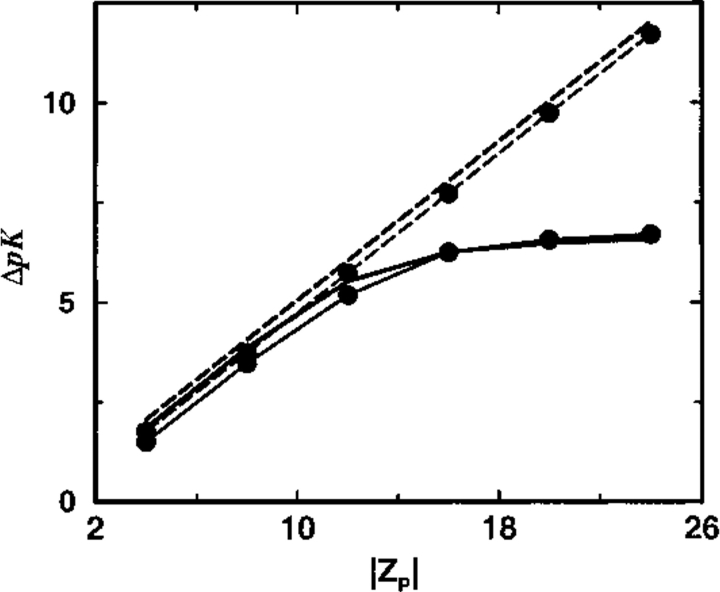
The effect of different protein charges is explored in more detail in Figure 6 ▶. For moderately charged proteins (Z < 12), the analytical theory correctly predicts the salt pK shifts. On further increasing the protein charge, however, nonlinear effects and ion–ion correlations progressively appear that result in a gradual breakdown of the TK scheme. This occurs at approximately the same protein charge irrespective of whether a uniform or inhomogeneous dielectric continuum model is used. Thus, Figure 6 ▶ serves a practical purpose by indicating the validity range of the TK prescription.

Fig. 6.

Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of the protein net charge (Z). A reference state at salt concentration c_s = 1 mM is chosen and the final salt concentration is 500 mM. Results from MC simulations and TK calculations are compared as solid and broken lines, respectively. Lines marked by solid circles correspond to a dielectric boundary radius R_d = 12Å; unmarked lines refer to a homogeneous dielectric response (R_d = 0Å).

In case the mean field is not small everywhere compared with the average thermal energy, the nonlinear part of the error can be recovered by using the Poisson-Boltzmann equation instead of the DH equation. At equilibrium, the motion of mobile salt and counterion charges is such that the average distribution of particles will follow the exponential Boltzmann law with the potential of mean force (pmf). Ordinarily, with a uniform dielectric response, say, where the protein surface charge density is small and salt concentrations/valencies are low, the pmf is well approximated by the mean electro-"static" potential. On the other hand, with a dielectric discontinuity the mobile ions will see strong correlations, at least with their own "images," just as the fixed charges do. This suggests that the pmf could be very different from the electrostatic potential, even if all the mean field conditions appropriate to a primitive dielectric model are satisfied. That is, when setting up the equations describing an inhomogeneous dielectric model, it is not generally sufficient to write the mobile ion distributions in terms of the electrostatic potentials, even though these do contain effects from the surface polarization induced by the fixed charges. There is the possibility of a sizeable correlation term (i.e. the self image correlation) that should be included, or its neglect needs to be justified. The effect of this correlation, a desolvation penalty, would be to remove mobile ions from the neighborhood of the dielectric boundary.

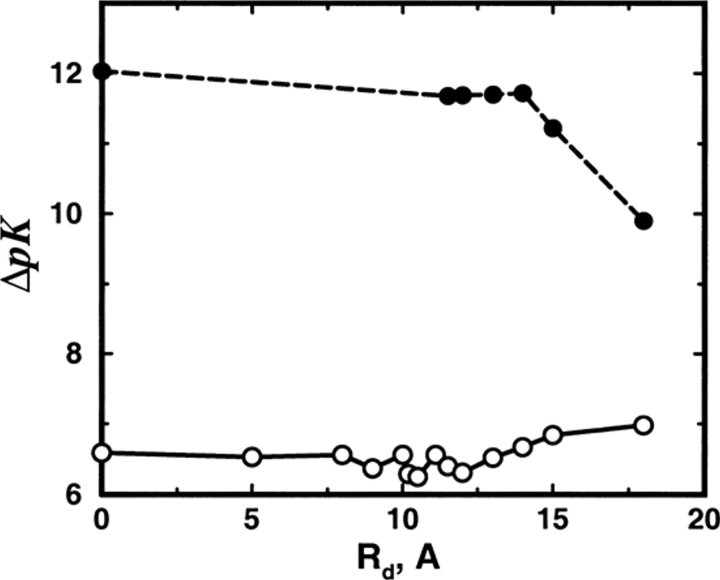
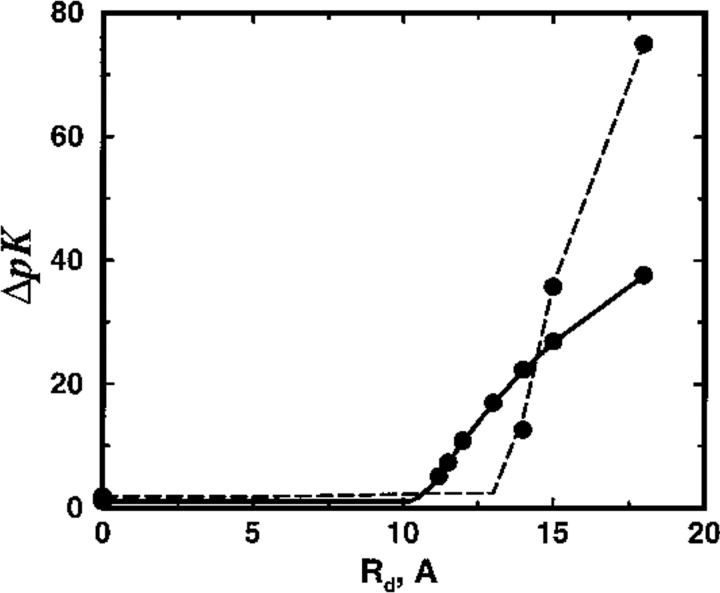
Turning now to the consequences of a dielectric boundary, even for weakly charged proteins, enlarging the interior region of low permittivity has only a marginal effect on the salt shift of the binding constant as depicted in Figure 7 ▶ for the SC8 model. Although both binding sites remain in the highly polarizable region, a small reduction in ΔpK is observed on expanding the dielectric radius R_d from zero to about 10Å. Further increasing R_d to incorporate the binding sites within the dielectric boundary has no effect at all on the calculated shift. When R_d extends beyond the protein radius (R_p = 14Å) a decrease of ΔpK is again seen. The latter is a trivial effect caused primarily by salt exclusion, as mobile ions are very strongly repelled from the low dielectric region. For the highly charged model SC24, see Figure 8 ▶, MC data is almost constant in this scale and TK completely overpredicts the shifts, although it behaves in a qualitatively similar manner to TK results for model SC8.

Fig. 7.

Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of the dielectric radius R_d for the SC8 model. A reference state at salt concentration c_s = 1 mM is chosen and the protein (of radius R_p = 14Å) is allowed to bind two divalent cations. Results from MC simulations and TK calculations are compared as solid and broken lines, respectively.

Fig 8.

Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of the dielectric radius R_d for the SC24 model. A reference state at salt concentration c_s = 1 mM is chosen and the protein (of radius Rp = 14Å) is allowed to bind two divalent cations. The final salt concentration is 500 mM. Results from MC simulations and TK calculations are compared as open and solid symbols, respectively, joined by straight line segments to guide the eye.

In view of these results, it can be concluded that (1) the shifts in binding equilibrium attributable to changes in aqueous salt content are well described by DH theory, provided the protein is not too highly charged; and (2) the existence of a weakly polarizable region within the protein has no significant effect on the salt concentration dependence of ion binding, even if the binding sites are located within the low dielectric boundary.

To assess the impact on ligand binding equilibria of perturbations in protein charge and charge distribution (realized experimentally by site directed mutagenesis of ionizable residues), a closely related model is also considered. By suggesting the replacement of, say, a carboxylic acid group by the corresponding amine, model SC7 represents a "mutant" protein obtained in either of two ways. First, the SC7 variant of model SC8 is formed by simply increasing the valency of the central charge from −8 to −7. Second, the peripheral charge of model SP8 is neutralized again decreasing the overall charge to −7 units. Figure 9 ▶ shows the change in pK of divalent cation binding attributable to both these mutations as a function of dielectric radius. In both cases, the shift ΔpK is very nearly independent of R_d as long as the binding sites are in the high dielectric region. Moreover, the calculated value of ΔpK is also in reasonable agreement with experimental observations (Kesvatera et al. 1994) of calbindin, where a single charge mutation typically alters the calcium binding constant with 0.5–1.5 pK units at low salt and protein concentration (Svensson et al. 1990). Once the low dielectric cavity incorporates the binding sites and the point of mutation, however, ΔpK climbs steeply and more so for the SP8 variant. When R_d matches the protein radius (R_d = 14Å), clearly unphysical binding constant shift around 25 pK units is apparent. Because the simulation results are faithfully tracked by the TK predictions over the full range of R_d, this failure must rest with inadequacies of the model rather than theoretical approximations.

Fig. 9.

Total shift in ion binding constant ΔpK, owing to a single charge mutation, is plotted as a function of the dielectric radius R_d for the SC8 and SP8 models. The salt concentration is c_s = 1 mM and the protein concentration is c_p = 0.02 mM. MC results are shown with solid (SC8) and broken (SP8) lines; TK data are denoted by solid circles.

The large ΔpK increase arises from the loss of "solvation" free energy as the charged ligand passes from a polarizable medium to vacuum. Not only is configurational entropy lost on binding, but the ligand is exposed to the bare protein charge without dielectric shielding and therefore incurs a significant electrostatic energy. Although this desolvation cost also appears in the pK shift because of variation in salt content, the energy term exactly cancels when computing the excess chemical potential difference, compare with Equation 9, as there is no change in overall protein charge.

Conclusion

The TK prescription based on the DH theory is an excellent approximation for studies of the binding of charged ligands to macromolecules. For sufficiently charged systems the linearization in the DH equation is unjustified and one must invoke a more accurate theory. Whether or not the nonlinear Poisson-Boltzmann theory is sufficient will depend on the system. For example, the description of highly charged aggregates, such as DNA in the presence of multivalent ions, where ion–ion correlations become important requires a correlated theory or numerical simulations (Guldbrand et al. 1986; Mel'nikov et al. 1999). The TK theory also becomes less reliable at high protein and low salt concentration, mainly because it approximates the excess chemical potential of the ligand with its value in the corresponding bulk salt solution. Typically this will happen when N_cc_p ≥ c_s.

The relative permittivity of the macromolecule is usually assumed to be much smaller than the surrounding aqueous solvent. For a highly charged macromolecule this is immaterial, when studying effects caused by salt concentration, as the leading term in the free energy difference is proportional to the net charge and the dielectric effect only enters in higher order terms. This can be demonstrated from the TK theory but is also found in MC simulations.

In a more general sense, any type of protein/solvent model that proposes an effective interaction potential by partitioning space into a finite number of dielectric continuna with different permittivities can be traced back to the intuitive design of Tanford and Kirkwood. Of course, the original TK analysis also simplifies the geometry of the ensuing electrostatic problem, but the essential idea of dielectrically distinct "background" regions remains common to more sophisticated models. The major weakness of applying such a scheme is the lack of an a priori prescription for locating the intervening dielectric boundaries and a method for estimating the dielectric response of the macromolecule. Charged ligand binding equilibria are highly sensitive to this aspect of electrostatic interactions, hence it may not always be possible to generate biologically relevant predictions without an independent method to sensibly determine these parameters. This is most clearly seen when studying the effect of charge mutations on the ligand binding, where models invoking a low dielectric response for the protein in many cases fail completely.

Materials and methods

Numerical simulations

Although the protein remains fixed at the center of the cell, the surrounding counterions and monovalent salt ions sample equilibrium configurations from the canonical (NVT) ensemble generated by the standard Metropolis MC algorithm (Metropolis et al. 1953). At high bulk protein concentrations, the cell radius is determined straightforwardly to obtain the appropriate volume per macromolecule, whereas for low protein and high salt concentrations the number of mobile particles required in the simulation rapidly becomes prohibitive. Tests have indicated, though, that the configuration-dependent part of the ligand chemical potential at the binding sites is rather insensitive to the cell size and that 50–100 salt pairs are typically sufficient to ensure convergence on the size-consistent limit. The excess chemical potential of the free calcium ion μ_F^ex is, however, greatly influenced by the macromolecular electrostatic field so that a naive reduction of the cell radius R_c would yield an erroneous result. Nevertheless, in low concentration, the protein will have only a marginal influence on μ_F^ex, particularly at high salt concentration where the electrostatic interactions are efficiently screened. Under these conditions it becomes more appropriate to calculate μ_F^ex from a bulk salt solution at the corresponding concentration. The number of counterions, N_c, was set to comply with overall electroneutrality, the temperature was fixed at T = 298.15K and the solvent dielectric constant was taken to be ɛ_s = 78.7.

The protein radius was chosen to be equal to R_p = 14Å whereas each mobile ion was assigned a common radius of R_k = R_s = 2Å for all k. The low dielectric response of the protein was explored in the extreme limit by introducing a spherical (radius R_d) vacuum cavity (ɛ_p = 1) centered on the cell origin. Commonly, the dielectric permittivity of a protein is taken to be comparable with that of a pure hydrocarbon phase, though there is no clear consensus on this issue (Warshel and Aqvist 1991; Antonsiewicz et al. 1994b; Simonson and Perahia 1995; Simonoson and Brooks 1996; Löffler et al. 1997^; Papazyan and Washel 1997^; Warshel and Papazyan 1998^; Sham et al. 1998^; Warwicker 1999; Baptista and Soares, unpubl.). To focus on qualitative physical mechanisms rather than quantitative prediction, we adopt the vacuum value here to exaggerate any effects arising from the dielectric discontinuity, although the consequences of high protein permittivity are examined in the following section. Note that the penetration of a real ion into a region of weak dielectric response is associated with a high energy, thereby implying a vanishingly low probability for the process. This is accounted for in the simulations by treating the dielectric discontinuity as an impenetrable boundary to the mobile ions. Normally we will set R_p > R_d so that the protein excluded volume overrides the dielectric depletion mechanism, though we admit the general condition R_s + max{R_p, R_d} defining the mobile ion exclusion sphere, see Equation 5. Values of R_d in the range of 0–18Å were studied, with the salt concentration c_s between 1 mM and 500 mM. For both equilibration and production runs, 10⁵ trial configurations per particle were generated.

Direct evaluation of the explicit TK equations (Tanford and Kirkwood 1957) was also carried out for the same model systems, with the limitation that all the protein charges and binding sites must lie inside the dielectric cavity. Moreover, these calculations were confirmed by numerical finite differece solutions obtained using the MEAD package (Bashford and Gerwert 1992).

Free energy calculations

When an ion binds to a protein, the changes in the free energy can be separated into two parts,

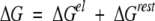8

where the first term represents the electrostatic interactions and the second accounts for all the remaining contributions (structural changes, etc.). If ΔG^rest is assumed to be independent of the salt concentration or charge mutations, then the logarithmic change in the stoichiometric binding constant is given by

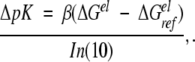9

where, for all the cases and models examined here, ΔG^el_ref identifies a reference electrostatic free energy for the system at c_s = 1 mM with respect to a standard state and β = 1/kT (k is the Boltzmann constant). In terms of the excess chemical potentials of protein (P), protein + ligand (P + L) and free ions (F), the electrostatic free energy can be expressed as

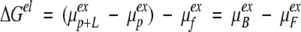10

where μ_B^ex is the excess chemical potential of the bound ion(ligand). If several ligands are involved in the binding process, than μ_F^ex should, besides the excess chemical potential of each bound ligand, also include the interaction between the ligands. Similarly, μ_F^ex should contain the excess chemical potential of the free ligands.

Widom's (1963) test particle insertion method is an effective way to evaluate chemical potentials in continuum simulations. When applying the Widom technique to Coulomb fluids, where the explicit particle density is not too high, it should be realized that insertion of a single ion means that the total system becomes nonelectroneutral, possibly introducing spurious systematic errors. Most of this error can be corrected for by rescaling some or all of the charges in the system in such a way that the total system including the ghost particle becomes electroneutral. Such a scheme, referred to as the modified Widom technique, has been implemented and described in detail elsewhere (Svensson and Woodward 1988). The chemical potential of a free calcium ion is obtained by random particle insertions over the entire system, whereas μ_B^ex is calculated from an insertion directly into the binding site. This is done at every fifth particle move throughout the simulation to obtain a typical statistical error on the excess chemical potential around 0.01 − 0.03 kT.

TK analysis

Instead of directly computing the excess chemical potential at a binding site as an ensemble average, it is conveniently expressed in terms of the total electrostatic free energy change on detaching a ligand from the protein,

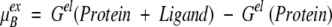11

Consistent with the linear response analysis of Tanford and Kirkwood, the chemical potential for a free charged hard sphere ion with valency z and radius R_s is approximated using the DH theory of strong electrolytes,

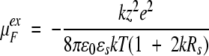12

where κ is the inverse DH screening length, which is proportional to the square root of the salt concentration. Following Tanford and Kirkwood, the electrostatic free energy of the neutral macromolecule is set to zero, and G^el for a protein containing N_p fixed charges becomes

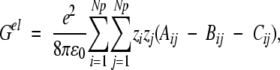13

with,

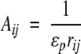14

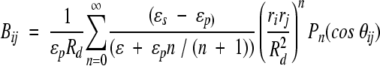15

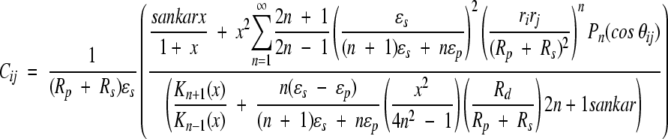16

The solution ionic strength enters only through the variable x = κ(R_p + R_s) and the auxiliary functions,

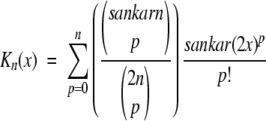17

described in an early paper by Kirkwood (1934). Notwithstanding the thorough discussion of results 13–16 in the original work by Tanford and Kirkwood (1957), it is instructive here to consider the three terms of Equation 13 in some detail. The direct Coulombic interaction between the charges of the protein is accounted for by the A_ijs and is independent of salt concentration, whereas the B_ijs are just the reaction field components (see Equation 2) contributing the effects from induced polarization charge at the dielectric boundary between protein and solvent. In the case of uniform dielectric permittivity, that is, ɛ_s = ɛ_p, all the B_ijs will vanish. The C_ij terms describe the effect of mobile counterions and added salt. Now suppose a ligand of valency z_l binds to the protein at radial position r_l subtending angles θ_kl with all other charges k, and consider the shift in its excess chemical potential on altering the salt concentration from x₁ to x₂, so that,

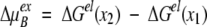18

It is easy to see that only the C_ij terms contribute to Δμ^ex_B. Writing the net charge of the apo protein Z = Σ^Np_i=1 z_i and retaining only the leading terms of the multipole expansion (16) yield,

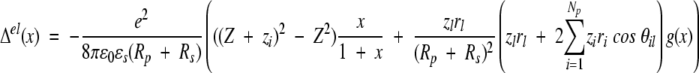19

With the additional geometric simplification R_p + R_s = R_d             , then g(x) takes the form,

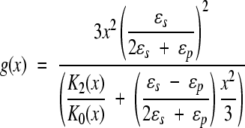20

Further, noting that K₀ = 1 and K₂(x) = 1 + x + x²/3, the limiting cases of interest are obtained,

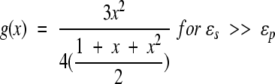21

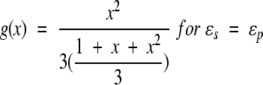22

so that the excess chemical potential of the bound ion Δμ_B^ex finally becomes,

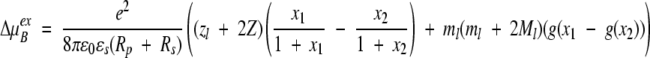23

For a weakly charged protein and a simple ligand (both Z and z_l small), the monopole term may well be dominated by "dipolar" contributions describing the first moment of the charge distribution with m_i = z_ir_i/(R_p + R_s) and M_l = Σ^Np_i=1 m_i cos θ_il. The ionic strength dependent factor of the dipole term is also sensitive to the location of the dielectric boundary as well as the ratio of permittivities and will be approximately doubled on changing from a high to a low dielectric interior.