Differential modulation of short-term synaptic dynamics by long-term potentiation at mouse hippocampal mossy fibre synapses

Abstract

Synapses continuously experience short- and long-lasting activity-dependent changes in synaptic strength. Long-term plasticity refers to persistent alterations in synaptic efficacy, whereas short-term plasticity (STP) reflects the instantaneous and reversible modulation of synaptic strength in response to varying presynaptic stimuli. The hippocampal mossy fibre synapse onto CA3 pyramidal cells is known to exhibit both a presynaptic, NMDA receptor-independent form of long-term potentiation (LTP) and a pronounced form of STP. A detailed description of their exact interdependence is, however, lacking. Here, using electrophysiological and computational techniques, we have developed a descriptive model of transmission dynamics to quantify plasticity at the mossy fibre synapse. STP at this synapse is best described by two facilitatory processes acting on time-scales of a few hundred milliseconds and about 10 s. We find that these distinct types of facilitation are differentially influenced by LTP such that the impact of the fast process is weakened as compared to that of the slow process. This attenuation is reflected by a selective decrease of not only the amplitude but also the time constant of the fast facilitation. We henceforth argue that LTP, involving a modulation of parameters determining both amplitude and time course of STP, serves as a mechanism to adapt the mossy fibre synapse to its temporal input.

Long-lasting changes in the strength of connections between neurons are assumed to underlie the storage of memory traces in the central nervous system (Bliss & Collingridge, 1993; Malenka & Nicoll, 1999; Martin et al. 2000). At most synapses throughout the central nervous system, synaptic plasticity such as long-term potentiation (LTP) and long-term depression (LTD) relies on the activation of postsynaptic NMDA receptors (Bear & Malenka, 1994; Nicoll & Malenka, 1995; Malenka & Bear, 2004), which endows these forms of plasticity with an associative component (Bliss & Collingridge, 1993; Malenka & Nicoll, 1999). Importantly though, also NMDA receptor-independent LTP has been found at various types of glutamatergic synapses (Harris & Cotman, 1986; Zalutsky & Nicoll, 1990; Salin et al. 1996a; Castro-Alamancos & Calcagnotto, 1999; Nicoll & Schmitz, 2005), but the functional role of this form of synaptic plasticity is not known (Henze et al. 2000).

A model synapse for an NMDA-receptor independent form of LTP is the hippocampal mossy fibre synapse (Nicoll & Malenka, 1995; Henze et al. 2000; Nicoll & Schmitz, 2005) at the interface between the dentate gyrus and CA3 region of the hippocampus. Although there is not unanimous agreement whether mossy fibre LTP is pre- and/or postsynaptically induced, it is generally accepted that it is independent of an association between pre- and postsynaptic spikes (Henze et al. 2000). Regardless of its induction mechanism, mossy fibre LTP is presynaptically expressed in that the release probability is increased, new release sites are recruited, and formerly silent synapses are activated (Tong et al. 1996; Reid et al. 2004; Nicoll & Schmitz, 2005). In addition to LTP, the mossy fibre synapse also shows unique short-term plasticity (STP). Here, a low basal release probability allows for remarkably strong facilitation (Salin et al. 1996b; Lawrence & McBain, 2003). Moreover, the decay time constant of mossy fibre facilitation is in the range of 10 s (Salin et al. 1996b; Nicoll & Schmitz, 2005), thus longer than at many other synapses.

The interdependence of LTP and STP has been studied before at synapses exhibiting NMDA receptor-dependent LTP. At neocortical synapses, LTP is accompanied by a redistribution of response amplitudes, where some responses are enhanced and others are attenuated (Markram & Tsodyks, 1996; Tsodyks & Markram, 1997). At hippocampal Schaffer collaterals and associational-commissural synapses, LTP has been found to uniformly enhance synaptic strengths (Selig et al. 1999). For NMDA receptor-independent forms of LTP, on the other hand, the interplay between LTP and STP has not been evaluated yet in detail.

Here we tackle the interplay of LTP and STP at the hippocampal mossy fibre synapse through in vitro electrophysiology as well as computational modelling. We find that LTP not only alters the amount of STP in terms of response amplitudes (Tsodyks & Markram, 1997; Toth et al. 2000) but also differentially modulates the kinetics of two distinct facilitatory processes that underlie the pronounced short-term plasticity on different time scales. LTP at the mossy fibre synapse therefore evokes changes of both synaptic response amplitudes and time constants of the dynamics of STP.

Methods

Slice preparation and general electrophysiology

Hippocampal slices were prepared from 3- to 6-week-old B6/C57 mice as described before (Schmitz et al. 2003). All experiments were performed according to the animal welfare guidelines of the Charité, Universitätsmedizin Berlin. In brief, the animals were anaesthetized with diethylether, then decapitated and the brains removed. Tissue blocks containing the subicular area and hippocampus were mounted on a microslicer in a chamber filled with cold artificial cerebrospinal fluid (ACSF) containing (mm): 87 NaCl, 75 sucrose, 10 glucose, 26 NaHCO₃, 2.5 KCl, 1 NaH₂PO₄, 0.5 CaCl₂, 7 MgSO₄ (pH 7.4). Parasagittal slices were cut at 300–400 μm thickness and heated to 35°C for 30 min. Slices were then cooled to room temperature and transferred to the storage and recording ACSF containing (mm): 119 NaCl, 26 NaHCO₃, 10 glucose, 2.5 KCl, 2.5 CaCl₂, 1.3 MgSO₄ and 1 NaH₂PO₄ (Ca²⁺/Mg²⁺ ratio: 2.5/1.3). In one set of experiments, the Ca²⁺/Mg²⁺ ratio of the recording ACSF was changed to 3.0/0.8, the solution then containing (mm): 119 NaCl, 26 NaHCO₃, 10 glucose, 2.5 KCl, 3.0 CaCl₂, 0.8 MgSO₄ and 1 NaH₂PO₄. All ACSF was equilibrated with 95% O₂ and 5% CO₂. The slices were stored in a submerged chamber where they were held for 1–7 h before being transferred to the recording chamber where they were perfused at a rate of 2–3 ml min⁻¹. Whole-cell recording electrodes were filled with intracellular solution containing (mm): 120 caesium gluconate, 5 CsCl, 10 TEA-Cl, 8 NaCl, 10 Hepes, 5 EGTA, 4 MgATP, 0.3 Na₃GTP and 5 QX-314; pH adjusted to 7.3 with CsOH. In whole-cell recordings, inhibitory responses were blocked with gabazine (1 μm). Field potential recordings were performed with low-resistance patch pipettes filled with external solution placed in stratum lucidum. Most of the recordings were done at room temperature. However, the most critical experiments were repeated at physiological temperature (see Results). Field EPSP and EPSC amplitudes were stored and analysed online and offline using Igor Pro (WaveMetrics Inc., Lake Oswego, OR, USA) and analysed offline using Matlab (The MathWorks Inc., Natick, MA, USA).

Mossy fibre stimulation

To stimulate mossy fibres, low-resistance patch pipettes were placed in the granule cell layer or the hilar region. We used several criteria to verify that the recorded synaptic responses were generated by mossy fibre synapses. Experiments were only accepted if responses showed more than 400% synaptic facilitation when stimulus frequency was changed from 0.05 Hz to 1 Hz (‘frequency facilitation’). In addition, we required the group II metabotropic glutamate receptor agonist (2S,2′R,3′R)-2-(2′,3′-dicarboxycyclopropyl)glycine (DCGIV; 0.5–1 μm) to lead to a complete blockage of the synaptic responses in field potential recordings (see online supplemental material, Supplemental Fig. 1A). In whole-cell recordings, application of DCGIV led to mainly the occurrence of failures with only a few medium-sized responses left and a mean inhibition of the EPSC amplitudes by 94% (Supplemental Fig. 1B and C). Synaptic failures of transmission were defined by a threshold criterion as responses upon stimulation with amplitudes < 8 pA.

Irregular stimulus trains

We used irregular stimulus trains resembling the natural spike statistics from dentate gyrus granule cells (Mizumori et al. 1989; Jung & McNaughton, 1993) to physiologically modulate transmission at the mossy fibre synapse (see also Discussion). Stimulus trains followed a 1/ISI distribution, where the probability of an interstimulus interval (ISI) was proportional to 1/ISI with minimal and maximal ISIs of 50 ms and 50 s, respectively, and a resulting median ISI of about 1.5 s. We applied the same stimulus trains in whole-cell and field potential recordings and used five different stimulus trains in total (i.e. different drawings from the same distribution) consisting of 90–100 pulses in about 10 min each.

Experimental paradigm LTP

Field potential experiments involving the induction of LTP were conducted as follows (Supplemental Fig. 2, which sketches the organization of experiments involving LTP induction and application of irregular stimulus trains). After establishing mossy fibre synaptic stimulation, irregular stimulus trains were applied at least twice. LTP was then induced by three repetitions of tetanic stimulation at 25 Hz for 5 s with 30 s pauses inbetween trains. After a stabilizing period of about 15 min following the induction protocol, the irregular stimulus trains were applied again.

Quantification of variability in fEPSPs

Within one field potential experiment, fEPSP amplitudes in response to a given stimulus train were highly reproducible for repetitive use of the same stimulus train (see Fig. 1G; correlation coefficient r > 0.99). The variability σ of the fEPSP amplitudes is estimated under the assumption of additive noise. We therefore applied the same random stimulus train at least twice before as well as after the induction of LTP to obtain two sets of fEPSP amplitudes A_n⁽¹⁾ and A_n⁽²⁾, with n = 1, …, N, where N is the number of stimulation pulses. To detect non-stationarities in the data, we calculated the slope α of the regression line of A_n⁽²⁾ as a function of A_n⁽¹⁾. The variability of the fEPSP amplitudes is then estimated as

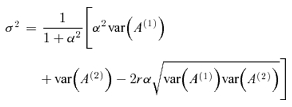(1)

The slope correction α accounts for weak non-stationarities. We checked that α and α⁻¹ never exceeded a value of 1.2. In this case and for a high value of r, σ² is about half of the so-called square error σ²_{2|1} of a linear regression of A_n⁽²⁾ on A_n⁽¹⁾.

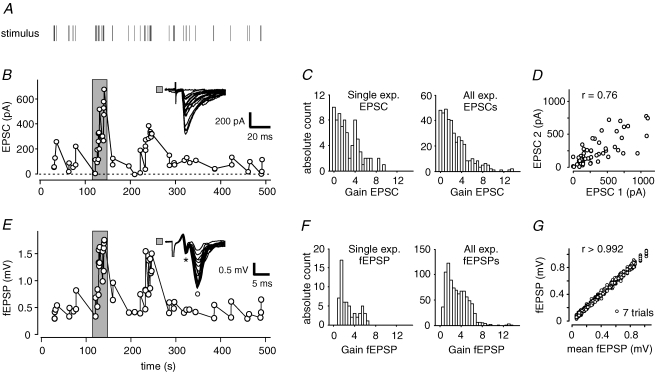
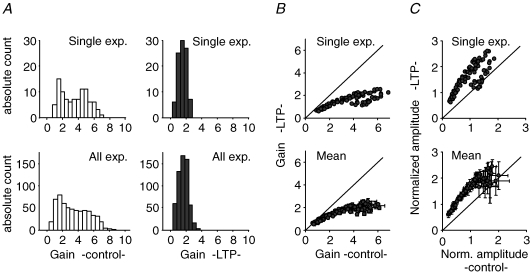
Figure 1. Modulation of synaptic efficacy by irregular stimulus trains.

A, presynaptic mossy fibres were extracellularly stimulated with an irregular stimulus train. B, in a whole-cell recording of a CA3 pyramidal cell, highly dynamic postsynaptic response amplitudes were elicited by the stimulus train. EPSCs exhibited failures of transmission pointing at minimal stimulation strength. Inset depicts example traces from time windows marked by grey area. C, gains of synaptic responses during stimulus trains (i.e. instantaneous amplitude/mean basal response to 0.05 Hz) ranged from 0 to ∼13. Left panel shows gains of the single experiment from B; right panel histogram is derived from data of n = 6 cells. D, two consecutive repetitions of the same stimulus train in a single whole-cell recording reveal large variability. Variability in EPSC amplitudes is mainly due to variance in synaptic transmission. E, in a field potential recording, postsynaptic mossy fibre responses are similarly modulated by the same irregular stimulus train. The fibre volley (*) is clearly separated from the postsynaptic component (°). F, gains of fEPSP responses of the experiment in E (left panel) and n = 13 fEPSP recordings (right panel). G, field EPSP responses to a given stimulus train were highly reproducible as seen in n = 7 consecutive presentations of identical stimulus train in one slice.

Modelling

To quantify STP at the hippocampal mossy fibre synapse, we developed a phenomenological model that can fit physiologically obtained response amplitudes. Our model is motivated by previous approaches (Sen et al. 1996; Varela et al. 1997; Hanson & Jaeger, 2002) that describe dynamical synaptic transmission at other synapses. Parameters of our model are the baseline amplitude A₀, the amplitude a_slow and time constant τ_slow of the slow facilitation, the amplitude a_fast and time constant τ_fast of the fast facilitation, and the factor g that describes the saturation of the slow facilitation. We omitted a saturation of the fast facilitation, as it did not improve the goodness of fit.

The variable x_slow(t) describes the strength of the slow facilitation at time t. It is increased by 1 at each time t of synaptic activation,

(2)

and decays exponentially to zero with time constant τ_slow afterwards. Similarly, we have

(3)

and a decay with τ_fast. In addition, the strength of the slow facilitation was limited by an upper bound, implemented by a Michaelis–Menten saturation function:

(4)

We calculated the response amplitude A from the baseline amplitude A₀ and a combination of two facilitation terms, for example an additive combination:

(5)

with fixed exponents k and m. The model was chosen such that a_slow and a_fast denote the relative amplitudes of the slow and fast process, respectively. This is convenient since experimental data generally provide normalized synaptic response amplitudes. For example, in our model the paired-pulse ratio amounts to:

(6)

in the limit of ISIs being much smaller than τ_fast. The relative frequency facilitation for stimulation frequencies f≪ 1/τ_fast can be computed as:

(7)

with:

(8)

as an abbreviation for the equilibrium value of the slow dynamical variable at stimulus frequency f. We tested various models with different exponents (k = 1, 2, 3, 4, 5 and m = 0, 1, 2) as well as a multiplicative combination of the two facilitation terms. For a specific model, the parameters A₀, a_slow,τ_slow, g, a_fast and τ_fast were determined by multidimensional minimization of the mean squared error between observed amplitudes and model predictions. We therefor used a line search algorithm (COBYLA: implementation of Powell's method from http://www.jeannot.org/~js/code/index.en.html). The procedure was implemented using the C programming language. For a set of N experimentally obtained fEPSP amplitudes A_n^(exp), n = 1, …, N, and the noise variance σ² from eqn (1), the quality of a model prediction A_n is quantified by the goodness of fit

(9)

where M is the number of parameters.

Estimation of the number of synapses contributing to field potential recordings

In whole-cell recordings of CA3 pyramidal cells, mossy fibre synaptic response amplitudes are highly variable due to stochastic release of transmitter (compare Supplemental Fig. 3, which illustrates the variability of mossy fibre synaptic response amplitudes at constant frequency stimulation). Under the assumption that this release is stochastically independent within a population of recorded synapses, one can derive an estimate of the number S of synapses contributing to a field potential recording through comparing the relative variabilities CV² of whole-cell (wc) and field potential recordings (field) as CV²_wc=S× CV²_field with:

(10)

Analysing exemplary 30–40 data points under constant frequency stimulation at 0.1 Hz, respectively, we determined mean values of CV²_wc= 0.3479 ± 0.0335 (n = 5 cells) and CV²_field= 0.0052 ± 0.0013 (n = 6 fEPSP recordings) and thus obtained S = 67 synapses. In other words, in order to acquire whole-cell data with the same low variability as observed in field potential recordings, one would need about 67 repetitions of whole-cell measurements. Even in a highly conservative calculation with 10 applications of a stimulus train before and after induction of LTP, respectively, and 12 min per stimulus train, plus induction and stabilization of LTP, one experiment would thus amount to almost 5 h, which is impossible to any satisfactory standards.

Results

First, we aimed at assessing the short-term transmission dynamics of the hippocampal mossy fibre synapse. Therefore, we recorded stimulus-evoked excitatory postsynaptic currents (EPSCs) from CA3 pyramidal neurons in whole-cell voltage-clamp mode. Low-intensity extracellular stimulation of presynaptic mossy fibres at constant frequency resulted in postsynaptic responses of variable amplitude (compare Supplemental Fig. 3) and an occurrence of failures of transmission of 14.2 ± 6.1% (n = 5 cells). This value is similar to results in Mori-Kawakami et al. (2003), where minimal stimulation techniques had been used. In order to elucidate short-term plasticity in a more physiological setting, we then stimulated presynaptic mossy fibres using irregular stimulus trains, covering a large range of instantaneous input frequencies.

Modulation of synaptic efficacy by irregular stimulus trains

Application of irregular stimulus trains that were motivated by in vivo spike train statistics of dentate gyrus granule cells (Mizumori et al. 1989; Jung & McNaughton, 1993; see also Methods) led to a strong modulation of postsynaptic response amplitudes in CA3 pyramidal cells: EPSCs following shorter interstimulus intervals (ISIs) were typically larger than responses following long ISIs (Fig. 1A and B). This pronounced modulation of synaptic response amplitudes reflects the short-term plasticity of mossy fibre synapses.

To be able to compare STP across experiments and conditions, we determined the synaptic ‘gain’ of response amplitudes (Klyachko & Stevens, 2006a; Klyachko & Stevens, 2006b). The gain is hereby defined as the ratio of each individual response amplitude during the stimulus train to the mean ‘basal response amplitude’ obtained by constant stimulation at 0.05 Hz (Fig. 1C, left panel). Gains of the cell shown in Fig. 1B ranged from 0 (indicating failures) to 8.9, with a mean value of 2.1 ± 1.9 (mean ± s.d.). The summary of n = 5 measured cells clearly illustrates the large dynamic range of EPSC amplitudes at the mossy fibre synapse with gains from 0 to 13.5 and a mean value of 2.7 ± 2.5 (Fig. 1C, right panel). These values are strikingly larger than at Schaffer collateral (SC) synapses with gains between 0.8 and 3 (Klyachko & Stevens, 2006a). Similarly, the coefficient of variation (CV) of response amplitudes was relatively high with a mean value of 0.88 ± 0.04 compared to 0.18 ± 0.07 at SC synapses (Dobrunz & Stevens, 1999).

In order to differentiate between two different sources of variability, namely (1) the modulation of response amplitudes due to short-term plasticity and (2) the stochastic transmitter release of mossy fibre synapses, we repetitively applied the same stimulus train in one single-cell recording. The correlation between EPSC amplitudes to the first and second presentation of the stimulus demonstrate comparable dynamics of responses within one experiment, but also a considerable amount of jitter (Fig. 1D, same cell as in Fig. 1A). Thus, the large variability in response amplitudes reflects both the short-term transmission dynamics in response to a varying presynaptic stimulus frequency and the intrinsic synapse-specific stochastic transmitter release.

In field excitatory postsynaptic potential (fEPSP) recordings, short-term dynamics was comparable to whole-cell recordings, given mossy fibre stimulation with the same irregular stimulus train (Fig. 1E). Synaptic gains for all fEPSP recordings (n = 13, using 5 distinct stimulus trains) ranged between 0.2 and 13.4 with a mean value of 2.9 ± 2.0, very similar to results in the whole-cell experiments (Fig. 1F). Additionally, the response amplitudes and gains of EPSCs and fEPSPs were significantly correlated given the same stimulus train. Thus, mossy fibre synaptic STP is equally reflected in field potential responses. Importantly, repetitive application of the same stimulus train evoked almost identical fEPSP amplitudes (Fig. 1G). Thus, using fEPSPs we were able to obtain the necessary data for assessing the dynamics of mossy fibre synaptic STP by means of a model fit.

Computational model of mossy fibre short-term plasticity

In order to quantitatively describe transmission dynamics, mathematical models have been established for several other synaptic systems (Tsodyks & Markram, 1997; Varela et al. 1997; Hanson & Jaeger, 2002). Here, we have developed a computational model of mossy fibre short-term plasticity based on the experimental data gained from fEPSP measurements using irregular stimulus trains.

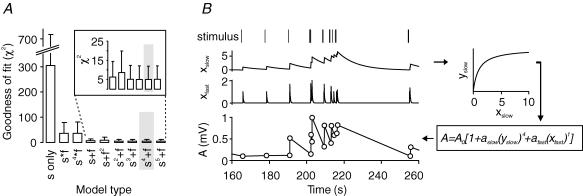
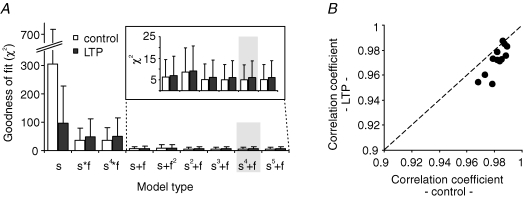
For determining the most suitable and yet minimal description of STP, we fitted the experimental data to a number of different model types. All of these were based on processes that after presynaptic stimulation facilitate transmission and exponentially decay to zero with a certain amplitude and time constant. Fitting experimental data to models with only one facilitatory process or two facilitatory processes (a slower one ‘s’ and a faster one ‘f’) interacting with different additive or multiplicative cooperativities resulted in significantly different values for the goodness of fit, as determined by the χ² test (Fig. 2A). A process with only one facilitatory component led to high χ² values. For two facilitatory processes, we obtained a much better goodness of fit, where additive models exhibited smaller χ² values with a weak dependence on the exponents of the two processes. In particular, a model of the form ‘s⁴+f’ yielded the lowest χ² value of on average 5.1 ± 6.9 (n = 12 experiments) and was therefore chosen for further analysis.

Figure 2. Model of mossy fibre STP.

A, to identify the most reliable model of mossy fibre STP, we tested several different additive and multiplicative interactions of slow and fast facilitatory processes for goodness of fit. The combination ‘s⁴+f’ yielded the lowest χ² values and was therefore chosen for all further analysis (highlighted in grey; n = 12 experiments). B, in our chosen model, a random stimulus train (top) is translated into two dynamical variables, x_slow and x_fast, via first-order kinetics. To account for saturation of facilitatory amplitudes, x_slow is inserted into a nonlinearity x_slow→y_slow=G(x_slow). Powers of y_slow and x_fast are then scaled by amplitudes a_slow and a_fast, respectively. Finally, the two components are added. Incorporating the baseline amplitude A₀, we obtained predictions for the fEPSP amplitudes A.

Our computational model describes mossy fibre short-term plasticity by two facilitatory processes, x_slow and x_fast, with a total of six parameters (Fig. 2B): A₀ reflecting the basal response amplitude, a_slow and a_fast for the specific amplitudes of facilitation, τ_slow and τ_fast as the time constants of facilitation, and g for a saturation of the slow process. Using this model we were able to reliably reconstruct response amplitudes within the stimulus trains.

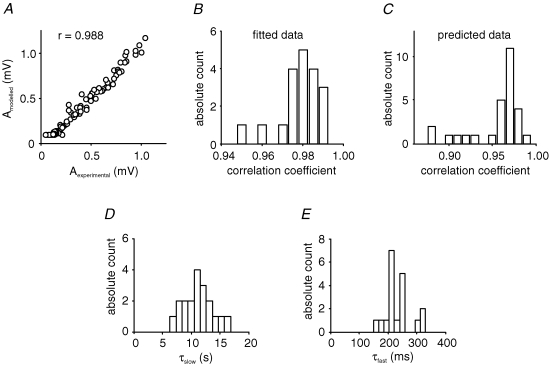
In general, correlations between experimentally measured fEPSP and fitted amplitudes were larger than 0.95 with a median value of 0.98 (n = 19), demonstrating the good characterization of mossy fibre short-term dynamics (Fig. 3A and B). Additionally, given the parameters obtained through fitting of one stimulus train, we were able to reliably predict amplitudes obtained with a different stimulus train in the same slice (Fig. 3C). Here, correlation coefficients between experimentally measured and predicted model amplitudes were larger than 0.88 with a median value of 0.97 (n = 28 predictions), highlighting the generalization capability of the model.

Figure 3. Characteristics and parameters of the ‘s⁴+f’ model.

A, fitted model amplitudes were highly correlated to measured fEPSP amplitudes, as shown for one example with corresponding experimental and model data. B, correlations between experimental and model amplitudes were generally high as seen in the histogram for correlation coefficients of n = 19 fits under control condition. C, predictions for response amplitudes, with parameters obtained from a fit of the model to a different data set, show similarly good correlations (n = 28 predictions). D and E, the time constant τ_slow of the slow facilitatory process ranged between 5 and 17 s, while the time constant τ_fast of the fast process was between 150 and 330 ms (n = 19).

Using the ‘s⁴+f’ model, we determined two relevant time scales of mossy fibre short-term plasticity as described by the two facilitatory processes. The slower process, x_slow, exponentially decays with a time constant of τ_slow= 11.2 ± 0.6 s, and the faster process, x_fast, decays with τ_fast= 232 ± 11 ms (Fig. 3D and E). These results are in line with the experimentally well-described STP phenomena of frequency facilitation and paired-pulse facilitation at the mossy fibre synapse (Salin et al. 1996b). Using the model parameters, we can also predict response amplitudes to regular stimulus trains, for example isolated pairs of pulses and stimulation at constant frequencies. Equations (6)–(8) in Methods describe how the so-called paired-pulse ratio and the relative frequency facilitation of mossy fibre synaptic responses can be calculated. The model also shows that the amplitudes of the slow process need to saturate as quantified by the saturation parameter g, whereas an additional saturation of the fast process did not improve the model fits, and so we discarded this parameter for simplicity. In general, synaptic depression was not observed to be a critical degree of freedom given our stimulus trains. Summarizing, our computational model allows us to qualitatively and quantitatively capture and predict essential features of short-term plasticity at the mossy fibre synapse with a high correlation to experimental data. Importantly, the qualitative results presented in all of the following did not depend on a specific additive model.

Interactions of short- and long-term plasticity

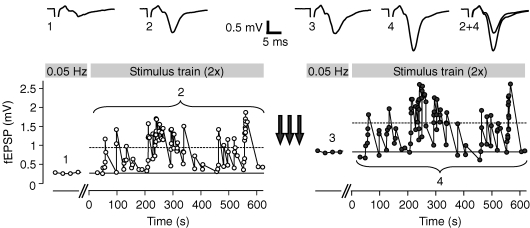
The hippocampal mossy fibre synapse not only exhibits pronounced short-term dynamics but is also a model synapse for the NMDA receptor-independent (Harris & Cotman, 1986; Zalutsky & Nicoll, 1990), presynaptic form of LTP (Weisskopf & Nicoll, 1995; Nicoll & Schmitz, 2005). To unravel the impact of long-term synaptic changes on short-term plasticity, we repetitively applied identical irregular stimulus trains before and after the induction of LTP by tetanic stimulation (see Supplemental Fig. 2). Following LTP, the mean fEPSP amplitudes, both averaged over all responses in a stimulus train and the basal response to constant frequency stimulation, were clearly enhanced (Fig. 4). Still, synaptic response amplitudes showed remarkable short-term plasticity, the amount of which, however, was changed after LTP.

Figure 4. STP before and after induction of LTP.

After initial constant stimulation at 0.05 Hz for establishing a basal response amplitude (solid lines), an irregular stimulus train was applied at least twice. Induction of LTP (arrows) led to increased responses in both basal response amplitude and mean response during complete stimulus train (dashed lines). Insets show averages of 10 sweeps each for 0.05 Hz stimulation before (1) and after LTP induction (3) and averages of all responses during the stimulus train (2 and 4).

After the induction of LTP, the dynamic range of synaptic responses was strongly reduced. The distributions of the measured synaptic gains for the experiment in Fig. 4 significantly differed between the control and LTP condition, with a lower mean gain and a more narrow distribution (Fig. 5A, upper panels). This tendency was a general phenomenon and independent of the specific realization of the used stimulus train for a given distribution of ISIs, in that LTP decreased the mean gain from 2.65 ± 1.68 in control condition to 1.50 ± 0.66 following LTP (Fig. 5A, lower panels; n = 8 experiments using 3 distinct stimulus trains). The alteration in the distributions of synaptic gains gives information only about the mean changes in short-term plasticity, but leaves the question of how each individual response amplitude is modulated after the induction of LTP unanswered.

Figure 5. Interaction of LTP and STP.

A, distributions of amplitude gains in a single experiment (upper panels) and pooled data (lower panels; n = 8 experiments with 3 different stimulus trains) differ remarkably before (left) and after the induction of LTP (right). B, gains of response amplitudes during the stimulus train are decreased after induction of LTP. The dynamic range of responses is significantly reduced, both in a single experiment and the summary of several analogue experiments (corresponding data to A). C, the amount of short-term potentiation after LTP induction is related to the corresponding response amplitude before LTP. Initially small responses are increased, whereas initially large ones are less potentiated or even slightly depressed as seen in single experiment (upper panel) and the summary of n = 7 analogue experiments (lower panel; mean ± s.d.). Amplitudes are normalized to the mean response amplitude during stimulus train in control condition.

As depicted in Fig. 5B, we found that the amount of change of a specific synaptic gain depended on its value before the induction of LTP: initially small synaptic gains were only slightly reduced, whereas initially large synaptic gains showed a drastic reduction (n = 7 experiments using the same stimulus train). This specificity can also be seen when directly comparing response amplitudes before and after the induction of LTP (Fig. 5C): initially small fEPSP amplitudes were uniformly enhanced after LTP, whereas initially large amplitudes were less potentiated or even slightly depressed. In summary, analysis of the experimental data indicates that the induction of mossy fibre LTP leads to amplitude-dependent changes in the size of fEPSPs, but does not reveal which dynamical properties of the synapse are modified. In the following, we will therefore utilize our computational model of transmission dynamics to disentangle the impact of LTP on different components of STP.

Long-term potentiation differentially modulates mossy fibre short-term dynamics

For the correct interpretation of the experimental results, it was crucial that our model of mossy fibre transmission dynamics fitted data well before and after the induction of LTP. The goodness of fit of our chosen ‘s⁴+f’ model as indicated by the mean χ² value was 6.0 ± 7.8 following LTP, and still the best model tested under LTP conditions (Fig. 6A). The correlation coefficients between measured and modelled response amplitudes for this model were > 0.95, with a median of 0.9 (Fig. 6B). Hence, our model of short-term dynamics allowed us to quantify the impact of LTP on STP. Induction of LTP modulated the synaptic parameters of the model as follows (Fig. 7).

Figure 6. Goodness of model fit before and after induction of LTP.

A, after the induction of LTP, the model ‘s⁴+f’ still yielded the lowest χ² value (n = 12). For comparison, control data from Fig. 2A are replotted. B, correlations between experimental and model amplitudes were high before and after the induction of LTP using the ‘s⁴+f’ model.

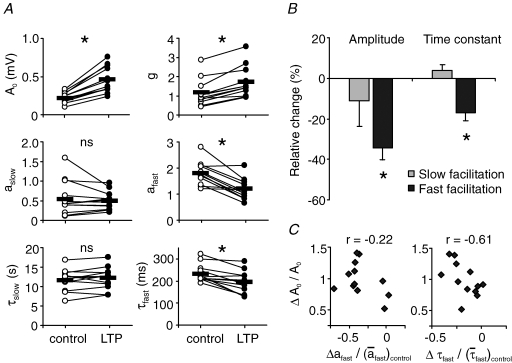
Figure 7. Differential impact of LTP on STP.

A, change in model parameters of mossy fibre STP after the induction of LTP. Asterisks point to significant changes in mean parameter values (paired Student's t test; *P < 0.001, ns: P > 0.14). B, both amplitude and time constant of the fast facilitation were significantly decreased in contrast to no significant changes in the corresponding parameters of the slow process. Changes are normalized to mean parameter values before LTP. Bars show mean ± s.e.m.; n = 12 experiments. Relative changes of parameters, for example 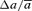, were calculated as Δa = a_LTP − a_control and 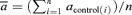. C, the decrease of the fast time constant τ_fast after LTP is significantly correlated to the relative change in A₀, while the amplitude of the fast process a_fast is not.

The basal response amplitude A₀ was increased by 100 ± 8% (mean ± s.e.m., n = 12 for all of Fig. 7), but the relative amount of overall facilitation was reduced. This finding is in agreement with an earlier description of LTP-induced modulation of STP at the mossy fibre synapse (Salin et al. 1996b). Extending this result, however, we find the two facilitatory processes to be attenuated differentially (Fig. 7A and B). The facilitation amplitude a_slow of the slow process was not changed significantly, and therefore suppression in amplitude of the slow facilitation is only due to an increase in the saturation parameter g by 59 ± 9% (P < 0.001, paired t test). In contrast, the fast facilitatory process is suppressed by a direct decrease of its amplitude a_fast by 34 ± 6% (P < 0.001). Hereby, the change in a_fast was not significantly correlated to the change in A₀ (Fig. 7C, left panel).

In addition to the quantification of facilitation amplitudes, our model also enabled us to unravel alterations of time constants of short-term dynamics. Again, we find that LTP differentially modulated the two facilitatory processes. While there was no significant change in the time constant τ_slow of the slow facilitation, the time constant τ_fast of the fast process was reduced by 17 ± 4% (P < 0.001). This tendency was also true in all additive models tested following the form of ‘s^k+f’ with k = 1, …, 5 (P < 0.008). Finally, the change in τ_fast was negatively correlated to the relative change in A₀ (Fig. 7C, right panel).

We also assessed the paired-pulse ratio (PPR) of fEPSP responses at various interstimulus intervals between 50 and 500 ms (Supplemental Fig. 4, which depicts the influence of LTP on paired-pulse facilitation). After the induction of LTP, the PPR was significantly reduced at short interstimulus intervals up to 200 ms, while remaining almost constant for ISIs of 400–500 ms.

Furthermore, experiments performed under nearly physiological recording temperatures (∼34°C) confirmed the reduction of both amplitude and time constant of the fast facilitation with concurrent stable parameters of the slow facilitation. Here, the induction of LTP decreased a_fast by 37 ± 14% and τ_fast by 11 ± 3% (n = 5 experiments, P < 0.05).

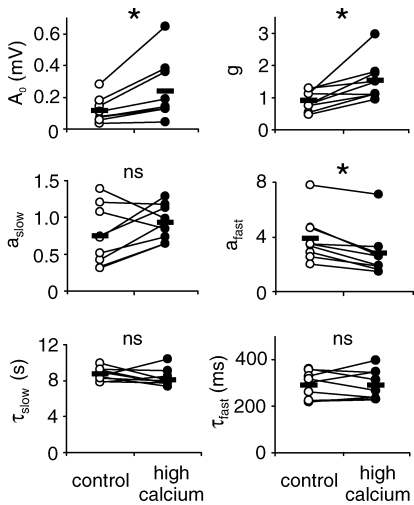
The expression of mossy fibre long-term potentiation is thought to be due to a presynaptic increase in neurotransmitter release (Weisskopf & Nicoll, 1995; Nicoll & Schmitz, 2005). To test whether the multiple effects of LTP on short-term plasticity described above are due to an enhancement of the transmitter release probability, we have quantified mossy fibre short-term dynamics under a change of the extracellular Ca²⁺/Mg²⁺ ratio using our computational model. An increase in the Ca²⁺/Mg²⁺ ratio from 2.5/1.8 to 3.0/0.8 resulted in significant increases of the basal response amplitude A₀ by 128 ± 33% as well as the saturation parameter g (P < 0.01, respectively), and a significant decrease of the amplitude a_fast of the fast facilitatory component by 31 ± 5% (P < 0.001) (Fig. 8, n = 9). This finding can explain the observed reduction in overall facilitation. In contrast to the changes of model parameters after the induction of LTP, however, the time constant τ_fast of the fast facilitatory process was not significantly changed under a higher Ca²⁺/Mg²⁺ ratio (P > 0.9). Finally, the slow facilitatory process was again not significantly affected by an increase in the Ca²⁺/Mg²⁺ ratio. Thus, the changes in mossy fibre short-term dynamics after the induction of LTP cannot completely be explained by a sole increase in transmitter release probability.

Figure 8. Effect of change in Ca²⁺/Mg²⁺ ratio on model parameters.

Model parameters of mossy fibre STP are modulated through increasing the Ca²⁺/Mg²⁺ ratio. Mean parameter values of basal response amplitude A₀, saturation g and facilitatory amplitude a_fast were significantly changed (paired Student's t test; *P < 0.05, ns: P > 0.13; n = 9).

Summarizing, mossy fibre long-term potentiation results in a relative decrease of the influence of the fast facilitatory process of short-term plasticity in that its amplitude and time constant are reduced. The change of the time constant τ_fast consequently narrows the range of presynaptic interstimulus intervals of the input distribution that are able to elicit the fast synaptic facilitation. This selective weakening of the fast process will thus result in altered postsynaptic response distributions.

Discussion

The results presented in this study offer new insights into the consequences of the presynaptic, NMDA receptor-independent form of long-term plasticity at the hippocampal mossy fibre synapse. We could demonstrate that LTP changes the kinetics of mossy fibre short-term dynamics, which is characterized by two facilitatory processes: a faster one with a time constant of a few hundred milliseconds and a slower one with a time constant of about 10 s. Moreover, we found that mossy fibre LTP selectively weakens the relative impact of the faster facilitatory processes by decreasing its amplitude and time constant. The differential modulation of synaptic dynamics is incompatible with other models of LTP (Markram & Tsodyks, 1996; Tsodyks & Markram, 1997; Selig et al. 1999), but well in line with previous experimental findings at the mossy fibre synapse (Salin et al. 1996b).

In vivo activity of neurons is irregular, whereas studies on synaptic plasticity typically use constant-frequency stimulation to activate synapses. Such regular stimulus trains cannot fully unravel the dynamic interplay between short- and long-term plasticity and effects on synaptic parameters other than response amplitudes. In order to quantify STP at the hippocampal mossy fibre synapse in a biologically reasonable setting, we have employed irregular stimulus trains. These should ideally resemble spike trains of dentate gyrus granule cells in vivo. However, little is known about the spiking statistics of hippocampal granule cells due to challenges in spike sorting within this area (Buzsaki & Czeh, 1992). The available spike data (Mizumori et al. 1989; Jung & McNaughton, 1993) suggests that the firing statistics do not follow a Poisson distribution, but rather a power law. Applying 1/ISI input statistics in vitro we found that synaptic responses of CA3 pyramidal cells are strongly modulated, varying 10-fold or more. This feature is in striking contrast to the neighbouring associational-commissural (A/C) synapses as well as to Schaffer-collateral synapses in area CA1, in which only little modulation occurs (Salin et al. 1996b; Dobrunz & Stevens, 1999). Even though the variability of response amplitudes within a train is very high (as seen in the large range of gains and a CV = 0.88), the modulation of synaptic strength in response to varying ISIs is precise and deterministic, as repetitive application of the same stimulus train revealed highly reliable responses in the field potential recordings of the synaptic responses.

On the level of a single synapse, however, mossy fibre EPSCs show a considerable variability in amplitude, including failures of transmission, even when stimulated with a constant input frequency (see Supplemental Fig. 3). This is due to stochastic transmitter release at the morphologically complex mossy fibre boutons, with up to 40 release sites (Jonas et al. 1993; Acsady et al. 1998; Henze et al. 2000; Hallermann et al. 2003; Mori-Kawakami et al. 2003). In order to establish a predictive computational model for quantifying STP, however, one needs reliable responses reflecting the preceding ISIs. There are two possibilities to acquire such reliable mean response amplitudes. (1) One could average postsynaptic responses over a large number of repetitions of stimulus trains with constant recording from the same cell and stable single fibre stimulation. One such experiment would amount to several hours of recordings (see Methods), which is impossible to any satisfactory standards, in particular with single fibre stimulation. Therefore, we used (2), field potential recordings, which simultaneously average over a large number of synaptic inputs and postsynaptic cells. As demonstrated in Fig. 1, these data exhibit a significant correlation with the single synaptic response distributions, and are highly reproducible over time. Thus, to characterize LTP-induced changes in the dynamics of STP, we believe that field potential recordings of mossy fibre responses are a well-suited approach.

The high reproducibility of field potential recordings allowed us to construct a quantitative model of synaptic dynamics at the hippocampal mossy fibre synapse. Using this model, we were able to characterize synaptic facilitation on all relevant time scales much faster, more accurately and more conveniently than with conventional constant-frequency stimulation paradigms. Data were best described by two facilitation processes acting on clearly distinct time scales. The faster process, which exponentially decays with a time constant of a few hundred milliseconds, might be due to the accumulation of residual Ca²⁺ in the presynaptic element and its effect on subsequent events. The slower process operates on a time scale larger than 10 s. This slow time course implies a downstream intermediate biochemical pathway that might rely on presynaptic calcium/calmodulin-dependent protein kinase II (CaMKII) (Salin et al. 1996b). Our model, which additively combines two facilitatory processes on different time scales, is different from quantitative studies of synaptic short-term dynamics at the neuromuscular junction (Sen et al. 1996), the visual cortex (Varela et al. 1997; Abbott et al. 1997) and the globus pallidus (Hanson & Jaeger, 2002). There STP was found to multiplicatively combine facilitatory and depressing terms that operate on similar time scales.

Our STP model fitted postsynaptic response amplitudes of mossy fibre synapses well before and after LTP, which allowed us to investigate the interplay of both forms of synaptic plasticity. Following LTP expression we found synaptic short-term dynamics to be changed such that the fast facilitatory process is selectively weakened in both its amplitude and time constant. Here, it is important to note that solely enhancing the transmitter release probability by changing the Ca²⁺/Mg²⁺ ratio does not mimic all the alterations of short-term plasticity following mossy fibre LTP. The observed selective reduction of relative facilitation is, however, consistent with previous experimental findings at the mossy fibre synapse by Salin et al. (1996b), who reported an overall reduction of frequency facilitation. From our model we can now conclude that this reduction is due to a nonlinear saturation effect rather than a direct decrease of the relative facilitatory amplitude of the slow process. Functionally, the observed decrease of the fast time constant reduces the range of ISIs that can trigger fast facilitation, which further supports that one of the roles of mossy fibre LTP is to adapt the synapse to its specific input features rather than being a mechanism for associative memory.

Presynaptic, NMDAR-independent forms of LTP not only expressed at hippocampal mossy fibre synapses (Harris & Cotman, 1986; Zalutsky & Nicoll, 1990; Nicoll & Schmitz, 2005), but were also found at cerebellar parallel fibre (Salin et al. 1996a) and corticothalamic terminals (Castro-Alamancos & Calcagnotto, 1999). It shall therefore be of further interest to investigate whether similar effects of LTP on short-term synaptic dynamics are expressed in these systems as well. In addition to long-lasting increases in synaptic strength, hippocampal mossy fibre synapses also express long-term depression (Kobayashi et al. 1996). Here, LTD is again NMDAR-independent and relies on presynaptic metabotropic glutamate receptors (Yokoi et al. 1996; Tzounopoulos et al. 1998). In this context, future studies will have to define whether the observed changes in short-term dynamics are bidirectional.

Supplemental material

Online supplemental material for this paper can be accessed at: http://jp.physoc.org/cgi/content/full/jphysiol.2007.143925/DC1 and http://www.blackwell-synergy.com/doi/suppl/10.1113/jphysiol.2007.143925