Skip to main content
PMC home page
Journal of Anatomy logoLink to Journal of Anatomy
. 2007 Jun;210(6):723–730. doi: 10.1111/j.1469-7580.2007.00730.x

The effects of muscular dystrophy on the craniofacial shape of Mus musculus

Donna Carlson Jones 1, Miriam L Zelditch 2, Paula Lightfoot Peake 3, Rebecca Z German 1
PMCID: PMC2375755  PMID: 17459142

Abstract

Skeletal anomalies are common in patients with muscular dystrophy, despite an absence of mutations to genes that specifically direct skeletogenesis. In order to understand these anomalies further, we examined two strains of muscular dystrophy (laminin- and merosin-deficient) relative to controls, to determine how the weakened muscle forces affected skull shape in a mouse model. Shape was characterized with geometric morphometric techniques, improving upon the limited analytical power of the standard linear measurements. Through these techniques, we document the specific types of cranial skeletal deformation produced by the two strains, each with individual shape abnormalities. The mice with merosin deficiency (with an earlier age of onset) developed skulls with more deformation, probably related to the earlier ontogenetic timing of disease onset. Future examinations of these mouse models may provide insight regarding the impact of muscular forces and the production and maintenance of craniofacial integration and modularity.

Keywords: craniofacial shape, geometric morphometrics, muscle force, muscle–bone interaction, muscular dystrophy, skeletal deformation

Introduction

A variety of developmental influences affect skeletal shape, including the physical forces generated by muscle and other soft tissues. Mechanical stimulus from muscle does significantly influence normal craniofacial development, altering both skeletal shape and size (Turner, 1998; Hallgrímsson et al. 2002) and is responsible for some cases of non-syndromic dysmorphology (e.g. Yu et al. 2004). In this vein, we expect muscular dystrophy (MD) to affect cranial shape due to the weakened muscles of mastication (Byron et al. 2006), which have a large impact on craniofacial shape (Kiliaridis, 1995).

In humans, MD is correlated with cranial skeletal abnormalities (Matsuyuki et al. 2006) and interferes with orthodontic treatment (Suda et al. 2004). In mouse models, the progressive loss of muscle strength due to MD has a significant impact on craniofacial skeletal growth (Lightfoot & German, 1998). Lightfoot & German (1998) documented differences in growth dynamics of craniofacial measurements, finding generally smaller skulls, with significant differences in later-developing skeletal elements, particularly within areas normally stimulated by masticatory muscles. Because the craniofacial skeleton is a composite of individual skeletal elements, it is likely that a disease with differential impact on these elements, such as MD, will produce an altered overall shape.

Most research examining the impact of muscle weakness on the skull has not measured shape in a quantitative way, for either the complete skull or discrete bones (e.g. Lightfoot & German, 1998; Yu et al. 2004; Matsuyuki et al. 2006). Although these analyses provided much information on the impact of MD on growth dynamics, our major objective herein is to elucidate any shape changes in the craniofacial skeleton of the Lightfoot & German (1998) mice with MD; our second objective is to determine whether the moderate and severe dystrophies they studied (laminin- and merosin-deficient MD, respectively) have similar or very disparate shapes. Although the strains are characterized by different protein mutations, similar shapes may result because the affected muscles, and their patterning of forces, are the same. However, as the ontogenetic progression of the two strains is not the same, the resultant skulls may have disparate characters.

Methods

Animal model and husbandry

We used the original radiographs analysed by Lightfoot & German (1998), who give full details regarding animal strains, breeding and husbandry. All animal procedures were approved and monitored by the University's Animal Care and Use Committee at the University of Cincinnati (IACUC #91-05-27-01). Two dystrophic, autosomal recessive strains of Mus musculus (C57BL/6J-dy/dy and C57BL/6J-dy2J/dy2J, designated as dy and 2J, respectively) were reared with controls (C57BL/6J–+/?). Breeding pairs (purchased from Jackson Laboratories, Bar Harbor, ME, USA) generated experimental animals for six groups (three treatments and two sexes, sample sizes listed in Table 1). After weaning (21–28 days), animals were housed, separated by sex, and given ad libitum access to food and water.

Table 1.

Numbers of male and female Mus musculus, for each of three treatments. 2J and dy designate mice with laminin- and merosin-deficient muscular dystrophies, respectively

Control 2J Dy
Male 9 4 5
Female 8 7 7
Open in a new tab

The genetic mutations present in these mice disrupt either the normal formation of laminin (2J mice) or merosin (dy mice), and lead to forms of MD equivalent to congenital muscular dystrophy in humans (Connolly et al. 2001; Shibuya et al. 2003; Head et al. 2004). Of the two strains, 2J mice are less severely affected: dy mice first manifest symptoms at 14 days, while the more moderate 2J mice begin to drag their hind legs at about 20–24 days postnatally. Generally, the disease manifests as progressive muscle weakening, caudal to cranial, and eventually leads to cardio-respiratory failure due to insufficient muscle strength (Hayes & Williams, 1998). As needed, affected animals were provided with curved sipper tubes and pulverized food in cage bottoms.

Data collection

For the dynamic growth study, animals were radiographed repeatedly during growth, and thus we have multiple images for each individual (for specifics on radiography and anaesthesia see Lightfoot & German, 1998). Previous work has demonstrated no adverse effects generated by this level of radiography (Fiorello & German, 1997). Animals were radiographed in both the dorsoventral (DV) and lateral (LT) planes and radiographs with noticeably misaligned images were retaken on the same day. In some cases, it was not discovered until digitizing that occasional landmarks were obscured and these images were not included in the present analysis. For the purposes of this study, we restricted analyses to adult animals (> 49 days of age, past the age of sexual maturity).

The original growth study continued radiography for each animal well past 49 days of age, but with uneven sampling times and variable mouse longevities. As a result, there were different numbers of radiographs per individual that spanned various age ranges. Therefore, we calculated each animal's average adult shape, using all available radiographs. This reduced measurement error normally associated with selecting a single representative radiograph, did not require us to define an arbitrary age to end examination, and provided a more accurate representation of each individual's craniofacial shape. Average shape was calculated in CoordGen6h (an IMP program; Sheets, 2000) and was defined as the simple arithmetic mean of the x and y components of each landmark, when set in a common reference frame.

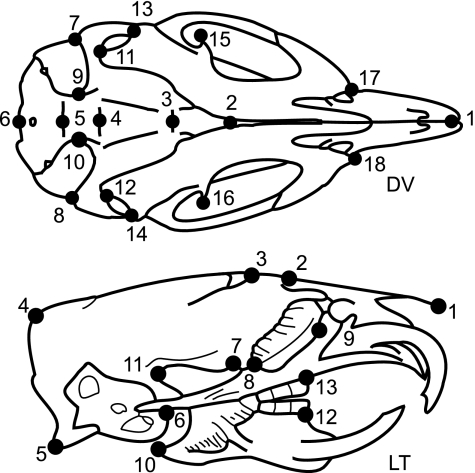
Landmarks were selected for homology, repeatability and even coverage of the skull (Fig. 1) and digitized on the radiographs. All digitizing was done by one person (P.L.P.) to exclude interobserver error. In the case of the bilaterally symmetric DV plane, the symmetric landmarks were reflected over the midline and averaged, both to remove random deviations from bilateral symmetry and to avoid the inflated degrees of freedom that results from treating the two sides as independent observations. Reflection and averaging was done using Sage (Marquez, 2004).

Fig. 1.

Fig. 1

Open in a new tab

Dorsoventral (DV) and lateral (LT) schematics, drawn from radiographic images. These collapse a three-dimensional structure (i.e. one can see both ventral and dorsal landmarks in DV). DV landmarks are: midpoint between the anterior tips of the incisors (1); anterior (2) and posterior (3) edge of hard palate; midpoint between posterior tips of pterygoid plates (4); suture between basisphenoid and occipital bones (5); posterior edge of skull (6); left (7) and right (8) anterolateral and left (9) and right (10) anteromedial tips of tympanic bulla; left (11) and right (12) mandibular condyle; left (13) and right (14) angle and left (15) and right (16) coronoid process of mandible; left (17) and right (18) anterior tip of zygomatic arch. LT landmarks are: anterior tip of nasal spine (1); suture between nasal and frontal (2) and frontal and parietal (3) bones; external occipital protuberance (4); occipital condyle (5); anterior edge of tympanic bulla (6); posterior edge of hard palate at palatine suture (7); posterior (8) and anterior (9) edge of eye orbit; angle (10) and condyle (11) of the mandible; anterior edge of mandibular (12) and maxillary (13) tooth rows.

Landmark coordinates were superimposed using a generalized least-squares (GLS) Procrustes superimposition. This superimposition, performed using CoordGen6h (Sheets, 2000), removes variation due to position, scale and orientation by translating, rescaling and rotating the configurations of landmarks to minimize the overall variation in the data as measured by the Procrustes distance (D). D equals the square root of the summed squared differences between coordinates of homologous landmarks, summed over all landmarks.

Before subjecting these data to statistical analyses based on linear models, we ensured that shape variation did not exceed the limits of the linear approximations, avoiding a potential pitfall in some geometric morphometric studies (Bookstein, 1991; Richtsmeier et al. 2002; Rohlf, 2003). This test was done by projecting the landmark configurations into tangent space and then comparing D among shapes in shape space to the corresponding distances in the linearized tangent space, a test implemented by tpsSmall 1.20 (Rohlf, 2003). For both views, the correlation between these distances was 1.0 and the slope of the regression through the origin exceeded 0.99, indicating that linear models could be safely applied to these data.

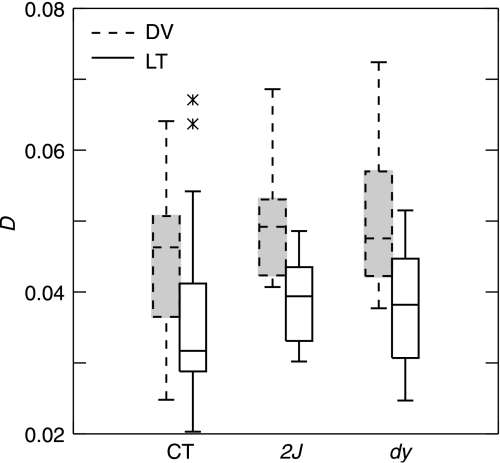
It is possible that the degenerative nature of muscular dystrophy continued to alter craniofacial shape even after adult size had been achieved. Therefore, we calculated D between the shapes recorded on each individual's first and last radiograph and compared the distribution of these distances among treatments (Fig. 2). Average D was 0.043 (0.012 standard deviation), with no statistically significant differences per individual among treatments (anova, P > 0.9999). In addition, there was no relationship between an individual's age range and D, as tested through least squares linear regression (tests performed in systat 11). This eliminates the possibility that potential shape differences among treatments could be generated by differential age ranges, numbers of radiographs or variable longevities of mice.

Fig. 2.

Fig. 2

Open in a new tab

Box plot of Procrustes distances (D) between the first and last radiograph of all individuals, by treatment. CT, 2J, and dy refer to control, laminin- and merosin-deficient mice, respectively. DV (dashed line with shading) designates shapes recorded on radiographs acquired in the dorsoventral plane, LT (solid line) are those from the lateral plane.

To determine whether the dystrophic condition affected shape, we used multivariate analysis of variance (manova). Litter effects were removed prior to conducting the analysis, but sexual dimorphism was retained because of the possibility of an interaction between sex and dystrophic condition. We used Goodall's F-test (Goodall, 1991) as generalized by Rohlf (1998). The mean square for each factor (and the interaction term) is the sum of squares, summed over all coordinates explained by that factor. The mean square is found by dividing the sum of squares by the degrees of freedom for each effect, which is a function of the number of landmarks and individuals.

Because MD mice are smaller (Lightfoot & German, 1998), and shape is dependent on size (e.g. Zelditch et al. 2004), significant shape differences between treatments could be a consequence of their different sizes. Therefore, we tested the following null hypotheses that (1) the mean centroid size of treatments was equal (standard anova using systat 11), and (2) any shape differences were due solely to size through a multivariate analysis of covariance (mancova). A significant interaction between group and size would indicate that shape differences between the treatment groups could not be explained by size differences alone. mancova was conducted using tpsRegress, version 1.31 (Rohlf, 2005). As usual, the F-ratio is found by dividing the mean square for the factor of interest by the error mean square and P < 0.05 was considered significant.

We generated thin plate spline deformation grids to interpolate differences between landmarks (Bookstein, 1989). To determine the degree of shape difference, we compared the mean partial Procrustes distance (defined above) among treatments and sexes. A relative measure (scaled to the sums of squares distances from the GLS consensus shape), larger distance values indicate more disparate shapes. Statistical significance (P < 0.05) between distances was determined by Goodall's F-test (Goodall, 1991). Distance and spline comparisons were completed with TwoGroup6h (an IMP program; Sheets, 2000).

We used the thin plate spline to illustrate the direction of change (in tangent shape space) needed to alter one shape into another. It is possible to have statistically different shapes (i.e. differing solely in degree) that lie along the same shape trajectory (i.e. direction; Zelditch et al. 2004). For instance, it may be the case that dy mice are shaped differently than the two other treatments, but this may be due to an extrapolation of the shape difference seen between the controls and 2Js.

To test this, average shape vectors were produced between each treatment couplet: control vs. 2J, control vs. dy and 2J vs. dy. These vectors were generated by regressing the full set of Procrustes coordinates against the variable of interest, in our case treatment. We then estimated the angle between and within these vectors using a bootstrap analysis (1600 bootstrap sets) and calculated upper 95% confidence limits for each comparison. The within-vector angle provides a measure of variation within each treatment couplet (e.g. the comparison between control and dy individuals). The between-vector angle describes how different two average vectors are from each other (e.g. control to dy compared with control to 2J). A value of 0° indicates that the vectors have the same direction in tangent shape space and 180° indicates that two target shapes are different from the comparison shape in exactly opposite ways. To test our null hypothesis (that the observed angles are no different than those obtained by resampling from the same population), we compare the within- and between-vector angles. If the angle between vectors exceeds the 95th percentile for within-group angles, then the comparison shapes are not on the same trajectory in tangent shape space and differ in direction. All analyses were completed using VecCompare6b (an IMP program; Sheets, 2000).

Results

manova revealed statistically significant differences among shapes across the three treatments and two sexes (Table 2). The level of variance in shape attributable to treatment was very high (37.6% DV, 42.3% LT) and sex explained a lesser but still significant amount (5.6% DV, 4.7% LT). Further analysis also showed significant differences in mean centroid size across treatments (anova; P < 0.0001). For both sets of radiographs, the dy mice are smaller than the control and 2J mice, a result that agrees with other size measurements for these mice (Lightfoot & German, 1998). Given that shape has an allometric component (Zelditch et al. 2004), it may be that the shape differences seen among treatments are the result of their different sizes. However, mancova revealed a highly significant interaction between treatment and size (P < 0.0001), indicating that the smaller MD individuals are not merely scaled-down versions of the controls.

Table 2.

manova results for average landmark coordinates of each treatment from dorsoventral (DV) and lateral (LT) anatomical planes. SS refers to sums of squares, d.f. is the degrees of freedom (a function of the number of landmarks and number of variables considered with each factor), MS designates the mean squares

SS d.f. MS F P
DV plane
 Treatment 0.0115 40 0.000288 11.71 < 0.0001
 Sex 0.0017 20 0.000085 3.46 < 0.0001
 Interaction term 0.0007 40 1.75E-05 0.71 0.91
 Error 0.0167 680 2.46E-05
 Total 0.0306 780
LT plane
 Treatment 0.0125 44 0.00028 14.26 < 0.0001
 Sex 0.0014 22 6.4E-05 3.19 < 0.0001
 Interaction term 0.0008 44 1.8E-05 0.91 0.63
 Error 0.0149 748 2E-05
 Total 0.0296 858
Open in a new tab

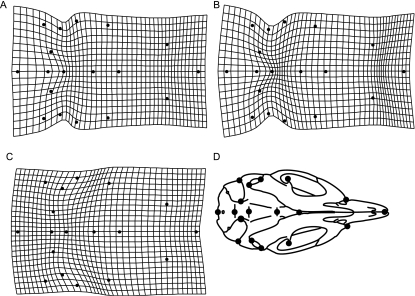
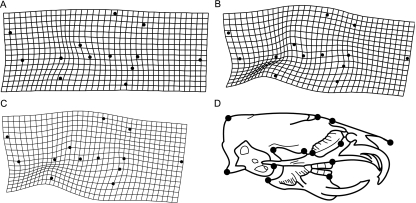
Figures 3 and 4 present thin plate spline deformation grids that graphically display the shape differences between treatments. Table 3 presents the mean partial Procrustes distance between groups. Compared with controls, in the DV radiographs, the skulls of both MD strains were wider relative to skull length, a difference more pronounced in the dy mice (i.e. the grid is more deformed; Fig. 3A–C). The posterior portion of the skull is slightly expanded in both MD strains, while the dy skulls had a visible narrowing in the medial portion of the skeleton. In shape space, controls and 2J mice are more similar to each other than either are to dy mice, as measured by mean partial Procrustes distance (Table 3). Indeed, the degree of shape difference between the controls and laminin-deficient mice is similar to that between males and females. In the lateral radiographs (Fig. 4) there is little evident difference between the 2J mice and the controls other than a subtle alteration of mandibular shape. In contrast, the dy strain exhibits a major difference in the shape of the skull: compared with the control, the skulls of the dy strain have generally wider braincases, a slight flexion in the middle, and rotated mandibles. Again, mean partial Procrustes distances indicate that the merosin deficiency (dy) results in a larger departure from the control shape (Table 3).

Fig. 3.

Fig. 3

Open in a new tab

Thin plate spline deformation grids of DV landmarks of the M. musculus craniofacial skeleton, following a Procrustes superimposition. Each grid shows the deformation needed to alter one shape into another: (A) control to 2J, (B) control to dy, and (C) 2J to dy. Deformation grids are exaggerated by a factor of 5 and off-midline landmarks were back reflected to allow for easier visualization and radiographic schematic (D) is provided for ease of visualization. See Fig. 1 for definitions of landmarks and text for discussion of shape differences.

Fig. 4.

Fig. 4

Open in a new tab

Thin plate spline deformation grids of LT landmarks of the M. musculus craniofacial skeleton, following a Procrustes superimposition. Each grid shows the deformation needed to alter one shape into another: (A) control to 2J, (B) control to dy, and (C) 2J to dy. Deformation grids are exaggerated by a factor of 3 and radiographic schematic (D) is provided for ease of visualization. See Fig. 1 for definitions of landmarks and text for discussion of shape differences.

Table 3.

Partial Procrustes distance* (and standard error*) between treatment and sex means for dorsoventral (DV) and lateral (LT) radiographs. 2J, dy and CT designate laminin- or merosin-deficient and control mice, respectively. All comparisons were statistically significant, based upon bootstrap analysis (100 iterations) at the 95% level

Couplet DV LT
CT:2J 1.83 (0.31) 1.51 (0.24)
CT:dy 3.39 (0.28) 3.94 (0.28)
2J:dy 2.96 (0.43) 3.27 (0.41)
Male : female 1.69 (0.28) 1.21 (0.41)
Open in a new tab
*

× 10−2.

The angle between average shape vectors for control–treatment couplets is provided in Table 4. This clearly shows that the two vectors (control:2J and control:dy) cannot lie along the same trajectory in tangent shape space. The skull shapes of dy mice are not merely a progressive alteration of the 2J mice.

Table 4.

Estimated angles between (BV) and within average shape vectors comparing control and treatment shapes for dorsoventral (DV) and lateral (LT) radiographs. Estimates were based upon 1600 bootstraps and show angles at the upper 95% confidence limit. 2J, dy and CT designate laminin- or merosin-deficient and control mice, respectively

CT:2J BV CT:dy
DV 47.2 60.5* 31.5
LT 52.4 53.6* 19.7
Open in a new tab
*

Those comparisons where the between-vector angle exceeds the upper 95% confidence limit of both of the within-vector angles.

Discussion

As predicted by our initial hypotheses, craniofacial skeletal shapes differ among treatments (Figs 3 and 4). Interestingly, despite being described as an ‘intermediate disease state’ (Connolly et al. 2001), 2J mice do not have an intermediate shape. They more closely resemble the controls than dys, but the two mutant strains differ from the control in more than degree – the mutations affect different aspects of shape (Tables 3 and 4). This is consistent with the hypothesis that these mutations affect bone tissue through the alteration of muscle force (Quinlivan et al. 2005). Because 2J and dy mice have slightly different time courses, the resultant adult shapes may reflect the timing of muscle degeneration. In general, 2J mice manifest symptoms at 22 days, while dy mice do so a full week earlier (Connolly et al. 2001). This is of importance given allometric differences in skull maturation: not all bones in the craniofacial skeleton mature at the same time (e.g. Smith, 1996) and growing tissues are more susceptible to shape deformation (e.g. Zelditch et al. 2004). Although it is widely known that muscular dystrophy alters bone growth (e.g. Suda et al. 2004; Matsuyuki et al. 2006), here we have shown that different strains can produce different effects. Although the muscles weakened by laminin deficiency (2J), with its later onset, produced a craniofacial shape more similar to the controls (as measured by Procrustes distance; Table 3), the shape was inherently different than either the controls or dy mice. These differences are probably related to the timing of pathological muscle condition, and further research examining the effect of other types of muscle-wasting disease on bone growth should take into account this aspect of developmental progression.

Although Lightfoot & German (1998) documented changes in growth parameters and skeletal measurements, not specific shape change, our results generally match theirs. They reported that MD lowered the projected final size of a skeletal measurement and decreased the age at which final size was achieved. Measurements in the face and mandible responded to the disease more strongly, and the 2J mice were more similar to controls. Their analyses indicated a significant sexual size dimorphism for some craniofacial measurements, but not others. They suggested that the differences between the male and female skulls were probably a result of the lower muscle mass in female mice generating less force during mastication. Males and females have significantly different skull shapes. However, the disparities between sexes do not mimic those seen in either strain of MD mouse (e.g. in lateral radiographs, a portion of the parietal bone is slightly compressed in females, relative to the length of the skull; data not shown). It is possible that the sexually dimorphic differences in skull shape have little to do with muscle mass and these differences were not impacted by the disease state (no significant interaction term for sex and treatment; Table 2).

Unlike the analysis performed by Lightfoot and German, ours here is fully multivariate and, given the integrated nature of the craniofacial skeleton (Cheverud, 1982; Cheverud et al. 1991; Leamy, 1993; Smith, 1996; Magwene, 2001; Hallgrímsson et al. 2006), a multivariate analysis is better suited to these data. The prior results, although suggestive, were difficult to interpret because each element had to be compared with all others simultaneously in order to comprehend the nature of the dysmorphology. Lightfoot & German (1998) even report that modelled final size differences among the genotypes were not always correlated with differences in other growth parameters and that, ‘it is possible that small differences in various parameters, while not significant in and of themselves, produce a significant cumulative effect on final size’ (p. 12). Using shape analysis, as we have here, allows for the cumulative effect to be directly studied, something not previously done for the effects of MD, in either humans or animal models.

Mice with MD are generally smaller (Lightfoot & German, 1998; Connolly et al. 2001) and its ultimate impact on adult shape reflects the differential affects of degenerating muscle on some regions of the skull. We hypothesize that the changes in shape associated with MD will be associated with lower levels of integration, as is the case when muscle forces are reduced experimentally (e.g. Corruccini & Beecher, 1984; He & Kiliaridis, 2003). A future study will examine this question. As issues of integration are currently being investigated (e.g. Hallgrímsson et al. 2006), future examinations of these mouse models may provide insight to the impact of muscular forces on the production and maintenance of craniofacial integration and modularity.

Conclusions

The progressive impact of MD, and the loss of muscle function, produced significant differences in the craniofacial shape of diseased mice. Portions of the skull altered by these treatments are correlated with the muscles of mastication and those mice with more diseased muscle developed craniofacial shapes less like the controls. However, there were marked shape differences between the two strains, indicating that the timing of pathological condition is an important contributor to the amount and type of dysmorphology.

Acknowledgments

We wish to thank Dr David Sheets for assistance with IMP software. Two anonymous reviewers helped to clarify the text. This work was partially supported by NIH DE9967 to R.Z.G. and University of Cincinnati Wendell funds to P.L.P.

References

  1. Bookstein FL. Principal warps: thin-plate splines and the decomposition of deformation. IEEE Trans Pattern Anal Machine Intelligence. 1989;11:567–585. [Google Scholar]
  2. Bookstein FL. Morphometric Tools for Landmark Data. Cambridge: Cambridge University Press; 1991. [Google Scholar]
  3. Byron CD, Hamrick MW, Wingard CJ. Alterations of temporalis muscle contractile force and histological content from the myostatin and mdx deficient mouse. Arch Oral Biol. 2006;51:396–405. doi: 10.1016/j.archoralbio.2005.09.006. [DOI] [PubMed] [Google Scholar]
  4. Cheverud JM. Phenotypic, genetic, and environmental morphological integration in the cranium. Evolution. 1982;36:499–516. doi: 10.1111/j.1558-5646.1982.tb05070.x. [DOI] [PubMed] [Google Scholar]
  5. Cheverud JM, Hartman SE, Richtsmeier JT, Atchley WR. A quantitative genetic-analysis of localized morphology in mandibles of inbred mice using finite-element scaling analysis. J Craniofacial Genet Dev Biol. 1991;11:122–137. [PubMed] [Google Scholar]
  6. Connolly AM, Keeling RM, Mehta S, et al. Three mouse models of muscular dystrophy: The natural history of strength and fatigue in dystrophin-, dystrophin/utrophin, and laminin alpha 2-deficient mice. Neuromuscular Disorders. 2001;11:703–712. doi: 10.1016/s0960-8966(01)00232-2. [DOI] [PubMed] [Google Scholar]
  7. Corruccini RS, Beecher RM. Occlusofacial morphological integration lowered in baboons raised on soft diet. J Craniofacial Genet Dev Biol. 1984;4:135–142. [PubMed] [Google Scholar]
  8. Fiorello CV, German RZ. Heterochrony within species: craniofacial growth in giant, standard, and dwarf rabbits. Evolution. 1997;51:250–261. doi: 10.1111/j.1558-5646.1997.tb02406.x. [DOI] [PubMed] [Google Scholar]
  9. Goodall C. Procrustes methods in the statistical analysis of shape. J Royal Statist Soc Series B. 1991;53:285–339. [Google Scholar]
  10. Hallgrímsson B, Willmore K, Hall BK. Canalization, developmental stability, and morphological integration in primate limbs. Yearb Phys Anthropol. 2002;45:131–158. doi: 10.1002/ajpa.10182. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hallgrímsson B, Brown JJY, Ford-Hutchinson AF, et al. The brachymorph mouse and the developmental-genetic basis for canalization and morphological integration. Evol Dev. 2006;8:61–73. doi: 10.1111/j.1525-142X.2006.05075.x. [DOI] [PubMed] [Google Scholar]
  12. Hayes A, Williams DA. Examining potential drug therapies for muscular dystrophy utilising the dy/dy mouse. J Neurol Sci. 1998;157:122–128. doi: 10.1016/s0022-510x(98)00084-7. [DOI] [PubMed] [Google Scholar]
  13. He TL, Kiliaridis S. Effects of masticatory muscle function on craniofacial morphology in growing ferrets (Mustela putorius furo) Eur J Oral Sci. 2003;111:510–517. doi: 10.1111/j.0909-8836.2003.00080.x. [DOI] [PubMed] [Google Scholar]
  14. Head SI, Bakker AJ, Liangas G. EDL and soleus muscles of the C57BL6J/dy2J laminin-α2-deficient dystrophic mouse are not vulnerable to eccentric contractions. Exp Physiol. 2004;89:531–539. doi: 10.1113/expphysiol.2004.027383. [DOI] [PubMed] [Google Scholar]
  15. Kiliaridis S. Masticatory muscle influence on craniofacial growth. Acta Odontol Scand. 1995;53:196–202. doi: 10.3109/00016359509005972. [DOI] [PubMed] [Google Scholar]
  16. Leamy L. Morphological integration of fluctuating asymmetry in the mouse mandible. Genetica. 1993;89:139–153. [Google Scholar]
  17. Lightfoot PS, German RZ. The effects of muscular dystrophy on craniofacial growth in mice: a study of heterochrony and ontogenetic allometry. J Morph. 1998;235:1–16. doi: 10.1002/(SICI)1097-4687(199801)235:1<1::AID-JMOR1>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
  18. Magwene PM. New tools for studying integration and modularity. Evolution. 2001;55:1734–1745. doi: 10.1111/j.0014-3820.2001.tb00823.x. [DOI] [PubMed] [Google Scholar]
  19. Marquez EJ. Sage. Ann Arbor, NY: University of Michigan; 2004. Version 1.2. [Google Scholar]
  20. Matsuyuki T, Kitahara T, Nakashima A. Developmental changes in craniofacial morphology in subjects with Duchenne muscular dystrophy. Eur J Orthodontics. 2006;28:42–50. doi: 10.1093/ejo/cji074. [DOI] [PubMed] [Google Scholar]
  21. Quinlivan R, Roper H, Davie M, et al. Osteoporosis in duchenne muscular dystrophy; its prevalence, treatment and prevention. Neuromuscular Disorders. 2005;15:72–79. doi: 10.1016/j.nmd.2004.09.009. [DOI] [PubMed] [Google Scholar]
  22. Richtsmeier JT, DeLeon VB, Lele SR. The promise of geometric morphometrics. Am J Phys Anthropol. 2002;35:63–91. doi: 10.1002/ajpa.10174. [DOI] [PubMed] [Google Scholar]
  23. Rohlf FJ. On applications of geometric morphometrics to studies of ontogeny and phylogeny. Syst Biol. 1998;47:147–158. doi: 10.1080/106351598261094. [DOI] [PubMed] [Google Scholar]
  24. Rohlf FJ. tpsSmall. Stony Brook, NY: State University of New York; 2003. Version 1.20. [Google Scholar]
  25. Rohlf FJ. tpsRegr. Stony Brook, NY: State University of New York; 2005. Version 1.31. [Google Scholar]
  26. Sheets HD. Buffalo, NY: Department of Physics, Canisius College; 2000. Integrated morphometrics package (IMP) software, freely available at http://www2.canisius.edu/~sheets/moremorph.html. [Google Scholar]
  27. Shibuya S, Wakayama Y, Inoue M, et al. Merosin (laminin-2) localization in basal lamina of normal skeletal muscle fibers and changes in plasma membrane of merosin-deficient skeletal muscle fibers. Med Electron Microsc. 2003;36:213–220. doi: 10.1007/s00795-003-0227-y. [DOI] [PubMed] [Google Scholar]
  28. Smith KK. Integration of craniofacial structures during development in mammals. Am Zool. 1996;36:70–79. [Google Scholar]
  29. Suda N, Matsuda A, Yoda S, et al. Orthodontic treatment of a case of Becker muscular dystrophy. Orthodontics Craniofacial Res. 2004;7:55–62. doi: 10.1046/j.1601-6335.2003.00271.x. [DOI] [PubMed] [Google Scholar]
  30. Turner CH. Three rules for bone adaptation to mechanical stimuli. Bone. 1998;23:399–407. doi: 10.1016/s8756-3282(98)00118-5. [DOI] [PubMed] [Google Scholar]
  31. Yu CC, Wong FH, Lo LJ, Chen YR. Craniofacial deformity in patients with uncorrected congenital muscular torticollis: an assessment from three-dimensional computed tomography imaging. Plastic Reconstructive Surg. 2004;113:24–33. doi: 10.1097/01.PRS.0000096703.91122.69. [DOI] [PubMed] [Google Scholar]
  32. Zelditch ML, Swiderski DL, Sheets D, Fink WL. Geometric Morphometrics for Biologists: a Primer. San Diego, CA: Elsevier; 2004. [Google Scholar]

Articles from Journal of Anatomy are provided here courtesy of Anatomical Society of Great Britain and Ireland

RESOURCES