Skip to main content
PMC home page
Journal of Anatomy logoLink to Journal of Anatomy
. 2007 Nov;211(5):673–680. doi: 10.1111/j.1469-7580.2007.00804.x

Fractal dimension as a quantitator of the microvasculature of normal and adenomatous pituitary tissue

Antonio Di Ieva 1, Fabio Grizzi 2, Giorgia Ceva-Grimaldi 2, Carlo Russo 2, Paolo Gaetani 1, Enrico Aimar 1, Daniel Levi 1, Patrizia Pisano 1, Flavio Tancioni 1, Giancarlo Nicola 1, Manfred Tschabitscher 3, Nicola Dioguardi 2, Riccardo Rodriguez y Baena 1
PMCID: PMC2375776  PMID: 17784937

Abstract

It is well known that angiogenesis is a complex process that accompanies neoplastic growth, but pituitary tumours are less vascularized than normal pituitary glands. Several analytical methods aimed at quantifying the vascular system in two-dimensional histological sections have been proposed, with very discordant results. In this study we investigated the non-Euclidean geometrical complexity of the two-dimensional microvasculature of normal pituitary glands and pituitary adenomas by quantifying the surface fractal dimension that measures its space-filling property. We found a statistical significant difference between the mean vascular surface fractal dimension estimated in normal versus adenomatous tissues (P = 0.01), normal versus secreting adenomatous tissues (P = 0.0003), and normal versus non-secreting adenomatous tissues (P = 0.047), whereas the difference between the secreting and non-secreting adenomatous tissues was not statistically significant. This study provides the first demonstration that fractal dimension is an objective and valid quantitator of the two-dimensional geometrical complexity of the pituitary gland microvascular network in physiological and pathological states. Further studies are needed to compare the vascular surface fractal dimension estimates in different subtypes of pituitary tumours and correlate them with clinical parameters in order to evaluate whether the distribution pattern of vascular growth is related to a particular state of the pituitary gland.

Keywords: fractal geometry, microvasculature, pituitary adenoma, pituitary gland, surface fractal dimension

Introduction

Human pituitary adenomas account for 10–15% of all primary brain tumours, although the percentage increases in autoptic samples (McComb et al. 1983; Kovacs & Horvath, 1986). They are usually benign, grow slowly and very rarely metastasise, and are most frequently found in (mainly pre-menopausal) females, with the highest incidence occurring between the third and sixth decades of life (Horvath & Kovacs, 1991). They are broadly categorised as functioning (i.e. secreting) or non-functioning on the basis of the characteristic endocrine syndromes associated with the abnormal secretion of adenopituitary hormones, or as micro- or macro-adenomas depending on whether they are more or less than 10 mm in diameter (Hardy, 1969).

The microvascular network of normal and tumoral pituitary glands has been widely investigated. Although the concept of ‘tumour angiogenesis’ associates the growth of a neoplastic tissue with increased microvascularity (Folkman, 1972; Folkman, 1990), some studies showed that pituitary tumours are less vascularized than normal pituitary tissues (Tiboldi et al. 1967; Schecter, 1972). Several analytical methods aimed at quantifying pituitary microvasculature under physiological and pathological conditions have been proposed. However, the use of qualitative or semi-quantitative methods has led to highly discordant results (Erroi et al. 1986; Jugenburg et al. 1995; Pawlikowski et al. 1997; Stefaneanu et al. 2000; Turner et al. 2000a,b,c; Vidal et al. 2000, 2001, 2003; Viacava et al. 2003; Niveiro et al. 2005; Pan et al. 2005).

One of the most widely used estimators of tumour microvascularity in two-dimensional histological sections is microvessel density (MVD) (Sharma et al. 2005). Although it has been shown to have a number of substantial limitations mainly due to the complex biology of tumour microvasculature (Hlatky et al. 2002) and the irregular geometry that the microvascular system assumes in real space (Grizzi et al. 2001b), MVD is currently used to estimate microvascularity in many tumours. MVD is expressed as the number of microvessels per square millimetre in the subjectively-selected most vascularized area of tumoral tissue (hot spots) (Weidner et al. 1991). However, this estimate does not meet the two-dimensional geometrical complexity of the microvascular system, which mainly depends on: (1) the number of vessels; (2) the variability in vessel shapes and magnitudes; and (3) the pattern of vessel distribution (Fig. 1) (Grizzi et al. 2001a,Grizzi et al. 2001b).

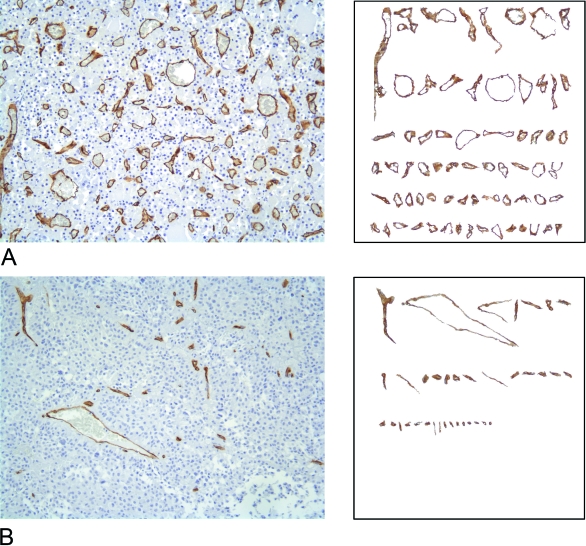
Fig. 1.

Fig. 1

Open in a new tab

Examples of the histomorphological complexity of pituitary vascularity. Two-dimensional sections of normal (A) and adenomatous pituitary gland tissue (B) stained with antibodies raised against CD34 that specifically react with vessels by a standardised immunohistochemical procedure. A vessel catalogue is subsequently created for each digitised section: the immunopositive vessels are selected on the basis of the similarity of their colour on the RGB scale using a computer-aided image analysis system, and ordered on the basis of their magnitude. The highly variable nature of the vessel shapes and surfaces can be clearly seen.

It is now well known that Euclidean geometry can only interpret regular and smooth objects that are almost impossible to find in nature (Goldberger & West, 1987; Cross, 1988; Nonnemacher et al. 1994; Losa & Nonnenmacher, 1996, 1998, 2002, 2005; Coffey, 1998; Baish & Jain, 2000; Grizzi et al. 2001a,Grizzi et al. 2001b; Gaudio et al. 2005; Gorski & Skrzat, 2006; Toumi et al. 2006), so it cannot be used to quantify the microvascular network accurately. Modern fractal geometry can overcome these limitations insofar as anatomical systems can be geometrically classified as natural fractals because of their irregular shape, statistically self-similar structure (in limited ranges of scale), non-integer or fractal dimension, and the fact that their measured properties depend on the scale at which they are measured.

In this study we investigated the non-Euclidean geometry of the two-dimensional microvasculature observed in normal and adenomatous pituitary tissues by quantifying its surface fractal dimension, which indexes the space-filling property of this irregularly shaped anatomical entity.

Materials and methods

Tissue samples

The study was conducted in accordance with the guidelines of the Ethics Committee of Istituto Clinico Humanitas IRCCS, Rozzano (Milan, Italy); all patients were informed of the possible discomforts and risks of the surgical procedure, and that their pathological specimens might be further used for research purposes.

The study involved 52 pituitary macroadenoma specimens (18 functioning and 34 non-functioning) taken from the files of the Department of Pathology, and six normal pituitary glands obtained from the Department of Anatomy, University of Vienna Medical School, Vienna, Austria, which had been taken from men who had died of reasons other than endocrine disease. The specimens were formalin-fixed and paraffin-embedded within 24 h from the sampling.

Histochemistry

Sections (2 µm thick) were stained with a freshly made hematoxylin & eosin solution, and analyzed under a light microscope (Leica DMLA, Milan, Italy) by the same pathologist in order to establish the absence of pituitary tissue abnormalities (due to technical manipulations or post-mortem alterations) or confirm the adenomatous state.

Immunohistochemistry

Sections (2 µm thick) were cut and processed for immunohistochemistry. After deparaffining and rehydration, the sections were immersed in an antigen retrieval bath (Dako, Milan, Italy) for 30 min at 98 °C in a freshly made EDTA 1 mM solution, incubated with 3% H2O2 for 15 min to quench endogenous peroxidase activity, and then incubated for 1 h at room temperature with primary antibodies raised against CD34 (Novocastra Laboratories Ltd, Newcastle, UK), or with 1 mg mL−1 mouse IgG1 (Dako) as a negative control. This was followed by 30 min incubation with the Envision system (Dako). 3,3′-diaminobenzidine tetrahydrochloride was used as a chromogen to yield brown reaction products. The nuclei were lightly counterstained with hematoxylin solution (Medite, Bergamo, Italy).

Image acquisition and preprocessing

All the available normal (mean surface 47.32 ± 28.79 mm2) and adenomatous tissue (mean surface 6.53 ± 2.67 mm2) was automatically digitized using a computer-aided image analysis system consisting of a Leica DMLA microscope (Leica) equipped with an x-y translator table, digital camera (Leica DC200), and an Intel dual Pentium IV 660 MHz computer with incorporated ad hoc constructed image analysis software (Bio-image Analyser, Laboratories of Quantitative Medicine, Istituto Clinico Humanitas IRCCS, Rozzano, Milan, Italy; patent pending) that automatically selects immunopositive vessels on the basis of RGB colour segmentation (Fig. 2). All of the measurements were made at 20 × objective magnification. The images have been acquired at a fixed resolution of 1.667 pixels micron−1. The same image intensity level was used throughout the study.

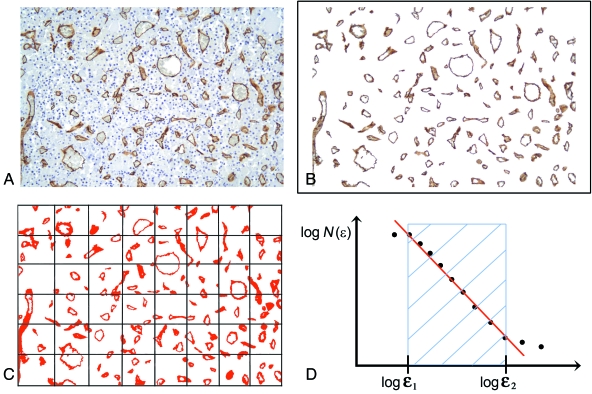
Fig. 2.

Fig. 2

Open in a new tab

Computer-aided estimate of the surface area fractal dimension (D) of a vascular network in two-dimensional biopsy sections. (A) Pituitary tissue section stained with antibodies raised against CD34 that specifically react with vessels. (B) Image segmentation: the immunopositive vessels are selected on the basis of the similarity of the colour of adjacent pixels. (C) Determination of D using the box-counting algorithm which, briefly, counts the number of boxes of length ɛ required to cover the object being measured, and indicated as N(ɛ). (D) Prototypical curve obtainable using the box-counting method that highlights the so-called fractal windows ranged by box size ɛ1 and ɛ2, and represents the appropriate region in which to estimate the dimension. Box sizes of more than ɛ2 approach the size of the image until one box covers it completely. Box sizes smaller than ɛ1 approach a single pixel or the resolution of the image.

Estimate of the global fractal dimension of vascular surface area

This was automatically estimated using the box-counting algorithm that applies the equation:

graphic file with name joa0211-0673-mu1.jpg (1)

where D is the box-counting fractal dimension of the immunoreactive vascular surface area, ɛ the side length of the box, and N(ɛ) the smallest number of contiguous and non-overlapping boxes of side ɛ required to cover the immunoreactive vascular surface completely (Fig. 2). As the zero limit cannot be applied to biological images, D was estimated by means of the equation:

graphic file with name joa0211-0673-mu2.jpg (2)

where d is the slope of the graph of log[N(ɛ)] against log(1/ɛ). As natural objects are ‘scale invariant’, they retain their fractal dimension in a fixed range of side lengths (ɛmin – ɛmax) by the constant fitting parameter D (Fig. 2) (ɛMAX was 1000 pixels ≅ 600 µm; ɛMIN was 10 pixels ≅ 6 µm). We applied the box-counting method because makes it possible to estimate the global complexity of a set of irregularly-shaped objects, like two-dimensional vascularity (Abu-Eid & Landini, 2003). In addition, this algorithm has been widely stated as a helpful method for quantifying the space-filling property of a biological structure (Paumgartner et al. 1981; Cross et al. 1993, Cross et al. 1994, 1995; Cross 1994; Losa & Castelli, 2005). The present study was aimed at quantifying only the global, and not the local complexity of the two-dimensional vascularity immunohistochemically recognized in normal and adenomatous pituitary tissues. It is know that other algorithms, like the mass radius relation at various local scales, have been developed for quantifying the local complexity derived by the irregular distribution pattern (anisotropic irregularity) (Landini & Rippin, 1993, 1996; Abu-Eid & Landini, 2006).

Statistical analysis

All of the data are expressed as mean values ± SD, and were analysed using Statistica software (StatSoft Inc., Tulsa, OK, USA). The parametric and categorical variables underwent univariate analysis using the Student t or chi-squared test as required. A P value of < 0.05 was considered statistically significant. The coefficient of variation (CV) given by the formula CV = (SD/mean) * 100 was used to evaluate the variability of the estimated two-dimensional geometrical complexity of the series of normal and adenomatous pituitary tissues.

Results

Baseline patient and tissue characteristics

We investigated surgical tissue taken from 52 patients (M:F = 22:30; mean age: 52.5 ± 16.1 years; range: 21–77 years) with pituitary adenomas: 34 (65%) classified on the basis of the characteristic clinical syndromes accompanying the production of the tumour hormone as clinically non-functioning, and 18 (35%) with functioning pituitary adenomas, including six growth hormone (GH) cell adenomas; three thyroid-stimulating hormone (TSH) cell adenoma; five adreno-cortico-trophic hormone (ACTH) cell adenomas; two prolactin (PRL) cell adenomas; and two adenomas with mixed secretin (one GH/PRL and one GH/ACTH).

Estimates of the fractal dimension of vascular surface area

The vascular surface area fractal dimension (indicated by the symbol D) was automatically evaluated in two-dimensional histological sections of normal pituitary glands and adenomatous tissues.

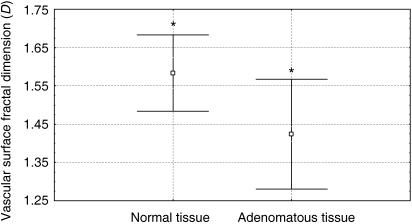
The minimum and maximum values of D obtained by measuring normal pituitary vascularity were 1.47 and 1.72, with a mean value of 1.58 ± 0.10; the corresponding values obtained by measuring adenomatous tissue vascularity were 1.12 and 1.8, with a mean value of 1.42 ± 0.14 (Fig. 3). The CV values of D were respectively 6.3% and 10.1%.

Fig. 3.

Fig. 3

Open in a new tab

Comparison of the mean estimated vascular surface area fractal dimension of normal and adenomatous pituitary tissues (*P = 0.01).

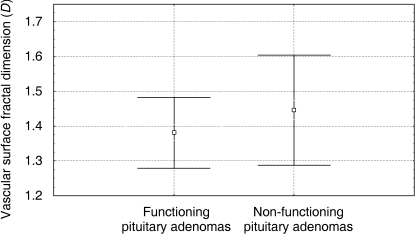
When the pituitary adenomas were divided into secreting (n = 18) and non-secreting forms (n = 34) on the basis of the characteristic clinical syndromes accompanying the production of the hormone, the mean D values were respectively 1.38 ± 0.1 (range: 1.21–1.60) and 1.45 ± 0.16 (range: 1.12–1.80)(Fig. 4). The CV values were respectively 7% and 11%.

Fig. 4.

Fig. 4

Open in a new tab

Comparison of the mean estimated vascular surface area fractal dimension of functioning and non-functioning pituitary adenomas.

There was a statistical significant difference between the mean D estimated in normal versus adenomatous tissues (P = 0.01), normal versus secreting adenomatous tissues (P = 0.0003), and normal versus non-secreting adenomatous tissues (P = 0.047), whereas the difference between the secreting and non-secreting adenomatous tissues was not statistically significant.

Fractal dimension of vascular surface area: clinical information

To examine whether D provides additional clinical information, we compared the values estimated in adenomatous tissues (secreting and non-secreting) with the patient's clinical and epidemiological characteristics (including age, sex, tumour invasiveness) but found no significant statistical correlations.

Discussion

Angiogenesis refers to the non-linear dynamic process of generating new vessels as a result of the sprouting and branching of capillaries from pre-existing arteries and veins (Holash et al. 1999; Hogan & Kolodziej, 2002; Jain, 2003; Lubarsky & Krasnow, 2003; Carmeliet, 2003; Grizzi et al. 2005). In adult human beings, it normally occurs in female reproductive organs and during wound healing, but may also occur as a result of a pathological condition such as cancer (Jain, 2003).

Geometrically, human vascularity is a complex three-dimensional system whose sizes, shapes and connecting patterns represent highly variable parameters in two-dimensional histological sections, and this geometrical complexity is the main cause of discordant results when assessing microvascularity in biopsy or surgical tissue specimens. One primary difficulty is that, like any other anatomical entity, the vascular system is irregularly shaped. This not only makes it difficult for even expert morphologists to provide an objective estimate, but also limits the identification of numerals capable of providing direct measures: i.e. capable of representing the close-to-reality variables that describe the vascular architecture observed through a light microscope.

One often-quantified index of tumoral vasculature is MVD because the results of studies carried out over the last ten years suggest that it has prognostic value in a wide variety of cancers, and it has also recently been assumed that it can reveal the degree of angiogenic activity taking place in a tumour. A number of authors agree that normal pituitary specimens have a higher MVD (i.e. are more vascularized) than neoplastic tissues, but the values obtained for different adenoma subtypes are highly discordant (Erroi et al. 1986; Jugenburg et al. 1995; Pawlikowski et al. 1997; Turner et al. 2000a,Turner et al. 2000b,Turner et al. 2000c; Vidal et al. 2000, Vidal et al. 2001, Vidal et al. 2003; Stefaneanu et al. 2000; Viacava et al. 2003; Niveiro et al. 2005; Pan et al. 2005).

MVD has a number of substantial limitations, which are mainly due to the complex biology of tumour vasculature and the highly irregular geometry of the vascular system in real space, which cannot be measured by means of classical Euclidean geometry because this can only interpret regular and smooth shapes that are almost impossible to find in Nature (Hlatky et al. 2002; Grizzi et al. 2005). However, the human vascular system can be geometrically interpreted as a natural fractal network of irregularly branching vessels whose lengths and diameters become systematically smaller (Goldberger & West, 1987; Cross, 1988; Zamir, 1999; Baish & Jain, 2000; Zamir, 2001; Grizzi et al. 2005).

The principles of fractal geometry were first described by Benoit Mandelbrot, built on previous studies by Jules Henri Poincaré, George Cantor and others (Mandelbrot, 1982).

There is no doubt that the human vascular system fulfils four of the main properties of natural fractal objects: (a) it is irregular, rough or fragmented in shape; (b) it has a non-integer or fractal dimension (i.e. the space-filling property of an irregularly shaped object); (c) it demonstrates statistical self-similarity (self-affinity), which means that its parts statistically resemble the whole; (d) it is subject to scaling, which means that its measured properties depend on the scale (i.e. objective magnification) at which they are measured.

One fundamental concept for evaluating geometric spaces is that of ‘dimension’, which has mainly been defined in two ways: as the ‘topological’ dimension introduced by Karl Menger, which assigns an integer number to every point in Euclidean space (indicated by the symbol E3), attributing zero to a point, 1 to a straight line, 2 to a plane surface, and 3 to a three-dimensional figure; and as defined by the mathematicians Felix Hausdorff and Abram S. Besicovitch, who attributed a real number to every natural object in E3 lying between the topological dimension and 3. Mandelbrot used the symbol Dγ to identify Menger's dimension and D to identify that of Hausdorff and Besicovitch: Dγ and D coincide (Dγ = D) in the case of all Euclidean figures, but remain unequal in the case of all natural fractals such as biological objects, in which D > Dγ because no biological entity corresponds to a regular Euclidean figure (Carmeliet, 2003).

The dimension of a two-dimensional section of the vascular system falls between zero (corresponding to the Euclidean dimension of a point) and 2 (the dimension of a plane). The more D tends towards 2, the more the analysed vascular configuration tends to fill a space and the greater its geometrical complexity. The vascular network irregularly fills the surrounding environment, and can thus be attributed a non-integer or fractal dimension whose number falls between 2 and 3, the Euclidean dimension of a three-dimensional (3D) space.

It has been clear since the introduction of fractal geometry that its principles could be applied to the apparently chaotic patterns of blood vessels. In 2003, Vidal et al. suggested using microvascular structural entropy (MSE) as a new index for the simultaneous measurement of the size of vessels and their arrangements in two-dimensional sections of pituitary tumours (Vidal et al. 2003). They found that MSE was significantly higher in pituitary adenomas than in PRL-producing carcinomas, and showed that microvessels are less chaotically distributed in the environment surrounding malignant tumours than in pituitary adenomas.

Different algorithms have been developed to estimate the fractal complexity of an irregularly shaped object. The box-counting method is one of the most used in biological sciences. However, it could be said that it is able to quantify only the global, but not the local complexity of an object. It is also true that methods quantifying the global complexity of a set of objects are ‘limited histopathological indexes’, mainly because the global complexity represents an average of the various local complexity values of the examined structure (Abu-Eid & Landini, 2003).

Mathematical fractals are known to be scale-invariant objects, but natural, including biological, entities are heterogeneous structures which maintain the fractal properties only in a limited ranges of scales (or magnifications). For this reason the study of the global complexity of a biological structure can underestimate the existence of different values of fractal dimension at different spatial scales, which means that it is possible to lose the local complexity (the monofractality) of the set (Zamir, 2001). Therefore the application of the box-counting method might appear as an oversimplification of the quantification of the microvascular architecture. We here first estimate the global complexity of the two-dimensional microvasculature of normal pituitary glands and pituitary adenomas based on quantifying its box counting fractal dimension.

We found that the microvasculature of the normal pituitary specimens was significantly more geometrically complex than that of pituitary adenomas which, on the basis of the principles of fractal geometry, indicates that normal pituitary tissue is more vascularized than pituitary adenomas, and that the microvasculature of normal pituitary glands is more complex than that of pituitary adenomas. It should be said that D is a quantitator that intrinsically expresses information relating to (a) the number of vessels, (b) their variability in shape and magnitude, and (c) their distribution pattern (Fig. 1) (Grizzi et al. 2001a,Grizzi et al. 2001b). We also found that non-secreting adenomas have a higher D than functioning tumours.

Analysis of variability showed that neoplastic vascularity had a higher CV than non-tumoral vascularity. It is now widely recognised that pathological anatomical systems have greater structural variability than their normal counterparts, that tumours are highly heterogeneous in terms of space and time, and that each neoplastic cell has different angiogenic potential. Moreover, the vascular D of the secreting adenomas had a lower CV than that of the non-secreting adenomas. These results all extend previous findings determining that pituitary PRL-producing carcinomas have a less chaotic distribution of vessels than benign adenomas (Vidal et al. 2003).

The present study makes it possible to draw the following conclusions. (1) D is an objective and valid quantitator of the two-dimensional geometrical complexity of both physiological and pathological pituitary gland vascular systems. (2) Unlike the currently used vascular estimators, D is a quantitative computer-aided measure that can be compared between laboratories. (3) The D of normal pituitary glands tends more toward 2 than that of pituitary adenomas, which means that the vascular configuration of normal pituitary glands tends to fill a two-dimensional space, and that its geometrical complexity is greater than that of pituitary adenomas. Density of microvessels is only one functional aspect of a tumour microvascular bed; other aspects, such as morphology (tortuosity, branching pattern, microvessel diameter), maturation, and endothelial wall permeability represent equally important attributes. (4) From these results we could speculate that pituitary adenomas may progress via a non-angiogenic pathway, a finding that extends those of previous studies showing that a subclass of primary non-small lung cancers and glioblastomas progress without neo-vascularisation and are clinically more aggressive than angiogenic tumours (Wesseling et al. 1994; Pezzella et al. 1997; Passalidou et al. 2002; Ribatti et al. 2003). In biological terms, these findings indicate that, in certain situations, tumours can obtain a sufficient blood supply from the pre-existing vascular bed because of the lower oxygen consumption of tumoral cells, which can also tolerate oxygen deprivation (Holash et al. 1999). However these speculations need more studies to be confirmed.

In conclusion, evaluating the global fractal dimension (D) when investigating the microvascularity of normal and adenomatous pituitary glands is a helpful means of assessing its complex structural organisation in two dimensions, and promises to improve the morphological assessment of the vascularization of normal and neoplastic pituitary specimens. The mono- or multi-fractal nature of the vascular network of the pituitary gland, in physiological as well as pathological conditions remains an open question to be investigated. In addition, further studies are needed to compare the estimates of the vascular surface fractal dimension in different subtypes of pituitary tumours and correlate them with clinical parameters in order to evaluate whether vascular growth and its distribution pattern may be related to a particular state of the pituitary gland.

References

  1. Abu-Eid E, Landini G. Quantification of the global and local complexity of the epithelial-connective tissue interface of normal, dysplastic, and neoplastic oral mucosae using digital imaging. Pathol Res Pract. 2003;199:475–482. doi: 10.1078/0344-0338-00448. [DOI] [PubMed] [Google Scholar]
  2. Abu-Eid R, Landini G. Morphometrical differences between pseudo-epitheliomatous hyperplasia in granular cell tumours and squamous cell carcinomas. Histopathology. 2006;48:407–416. doi: 10.1111/j.1365-2559.2006.02350.x. [DOI] [PubMed] [Google Scholar]
  3. Baish JW, Jain RK. Fractals and cancer. Cancer Res. 2000;60:3683–3688. [PubMed] [Google Scholar]
  4. Carmeliet P. Angiogenesis in health and disease. Nat Med. 2003;9:653–660. doi: 10.1038/nm0603-653. [DOI] [PubMed] [Google Scholar]
  5. Coffey DS. Self-organization, complexity and chaos: the new biology for medicine. Nat Med. 1998;4:882–885. doi: 10.1038/nm0898-882. [DOI] [PubMed] [Google Scholar]
  6. Cross SS. Fractals in pathology. J Pathol. 1988;182:1–8. doi: 10.1002/(SICI)1096-9896(199705)182:1<1::AID-PATH808>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
  7. Cross SS. The application of fractal geometric analysis to microscopic images. Micron. 1994;25:101–113. doi: 10.1016/0968-4328(94)90057-4. [DOI] [PubMed] [Google Scholar]
  8. Cross SS, Bury JP, Silcocks PB, Stephenson TJ, Cotton DW. Fractal geometric analysis of colorectal polyps. J Pathol. 1994;172:317–323. doi: 10.1002/path.1711720406. [DOI] [PubMed] [Google Scholar]
  9. Cross SS, Start RD, Silcocks PB, Bull AD, Cotton DW, Underwood JC. Quantitation of the renal arterial tree by fractal analysis. J Pathol. 1993;170:479–484. doi: 10.1002/path.1711700412. [DOI] [PubMed] [Google Scholar]
  10. Cross SS, Start RD, Stephenson TJ, Cotton DW, Variend S, Underwood JC. Fractal geometric analysis of the renal arterial tree in infants and fetuses. Pediatr Pathol Lab Med. 1995;15:259–268. doi: 10.3109/15513819509026961. [DOI] [PubMed] [Google Scholar]
  11. Erroi A, Bassetti M, Spada A, Giannattasio G. Microvasculature of human micro- and macroprolactinomas. A morphological study. Neuroendocrinology. 1986;43:159–165. doi: 10.1159/000124523. [DOI] [PubMed] [Google Scholar]
  12. Folkman J. Anti-angiogenesis: new concept for therapy of solid tumours. Ann Surg. 1972;175:409–416. doi: 10.1097/00000658-197203000-00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Folkman J. What is the evidence that tumours are angiogenesis dependent? J Natl Cancet Inst. 1990;82:4–6. doi: 10.1093/jnci/82.1.4. [DOI] [PubMed] [Google Scholar]
  14. Gaudio E, Chaberek S, Montella A, et al. Fractal and Fourier analysis of the hepatic sinusoidal network in normal and cirrhotic rat liver. J Anat. 2005;207:107–15. doi: 10.1111/j.1469-7580.2005.00436.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Goldberger AL, West BJ. Fractals in physiology and medicine. Yale J Biol Med. 1987;60:421–435. [PMC free article] [PubMed] [Google Scholar]
  16. Gorski AZ, Skrzat J. Error estimation of the fractal dimension measurements of cranial sutures. J Anat. 2006;208:353–9. doi: 10.1111/j.1469-7580.2006.00529.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Grizzi F, Ceva-Grimaldi G, Dioguardi N. Fractal geometry: a useful tool for quantifying irregular lesions in human liver biopsy specimens. Ital J Anat Embryol. 2001;106:337–346. [PubMed] [Google Scholar]
  18. Grizzi F, Colombo P, Barbieri B, et al. Correspondence re: E. Sabo et al., microscopic analysis and significance of vascular architectural complexity in renal cell carcinoma. Clin Cancer Res. 2001b;7:3305–3307. [PubMed] [Google Scholar]
  19. Grizzi F, Russo C, Colombo P, et al. Quantitative evaluation and modeling of two-dimensional neovascular network complexity: the surface fractal dimension. BMC Cancer. 2005;8:5–14. doi: 10.1186/1471-2407-5-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hardy J. Transsphenoidal surgery of the normal and pathological pituitary. Clin Neurosurg. 1969;16:185–217. doi: 10.1093/neurosurgery/16.cn_suppl_1.185. [DOI] [PubMed] [Google Scholar]
  21. Hlatky L, Hahnfeldt P, Folkman J. Clinical application of antiangiogenic therapy: microvessel density, what it does and doesn't tell us. J Nat Cancer Inst. 2002;94:883–893. doi: 10.1093/jnci/94.12.883. [DOI] [PubMed] [Google Scholar]
  22. Hogan BL, Kolodziej PA. Organogenesis: molecular mechanisms of tubulogenesis. Nat Rev Gen. 2002;3:513–523. doi: 10.1038/nrg840. [DOI] [PubMed] [Google Scholar]
  23. Holash J, Maisonpierre PC, Compton D, et al. Vessel cooption, regression, and growth in tumors mediated by angiopoietins and VEGF. Science. 1999;284:1994–1998. doi: 10.1126/science.284.5422.1994. [DOI] [PubMed] [Google Scholar]
  24. Horvath E, Kovacs K. The adenohypophysis. In: Kovacs K, Asa SL, editors. Functional Endocrine Pathology. Boston: Blackwell Science; 1991. pp. 245–281. [Google Scholar]
  25. Jain RK. Molecular regulation of vessel maturation. Nat Med. 2003;9:685–693. doi: 10.1038/nm0603-685. [DOI] [PubMed] [Google Scholar]
  26. Jugenburg M, Kovacs K, Stefaneanu L, Scheithauer BW. Vasculature in nontumorous hypophyses, pituitary adenomas and carcinomas: a quantitative morphologic study. Endocr Pathol. 1995;67:115–124. doi: 10.1007/BF02739874. [DOI] [PubMed] [Google Scholar]
  27. Kovacs K, Horvath E. Atlas of Tumor Pathology. Washington, D.C: Armed Forces Institute of Pathology; 1986. Tumors of the pituitary gland; pp. 1–269. fascicle 21, 2nd series. [Google Scholar]
  28. Landini G, Rippin J. Fractal dimension of the epithelial connective tissue interfaces in premalignant and malignant epithelial lesions of the floor of the mouth. Anal Quant Cytol Histol. 1993;15:144–149. [PubMed] [Google Scholar]
  29. Landini G, Rippin J. How important is tumour shape? Quantification of the epithelial–connective tissue interface in oral lesions using local connected fractal dimension analysis. J Pathol. 1996;179:210–217. doi: 10.1002/(SICI)1096-9896(199606)179:2<210::AID-PATH560>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
  30. Losa G, Merlini D, Nonnemacher TF, Weibel ER. Fractals in Biology and Medicine. Basel, Boston, Berlin: Birhkäuser Press; 2002. [Vol. III] [Google Scholar]
  31. Losa G, Merlini D, Nonnemacher TF, Weibel ER. Fractals in Biology and Medicne. Basel, Boston, Berlin: Birhkäuser Press; 2005. [Vol. IV] [Google Scholar]
  32. Losa GA, Castelli C. Nuclear patterns of human breast cancer cells during apoptosis: characterisation by fractal dimension and co-occurence matrix statistics. Cell Tissue Res. 2005;322:257–267. doi: 10.1007/s00441-005-0030-2. [DOI] [PubMed] [Google Scholar]
  33. Losa G, Merlini D, Nonnemacher TF, Weibel ER. Fractals in Biology and Medicine. Basel, Boston, Berlin: Birhkäuser Press; 1998. [Vol. II] [Google Scholar]
  34. Losa GA, Nonnenmacher TF. Self-similarity and fractal irregularity in pathologic tissues. Mod Pathol. 1996;9:174–182. [PubMed] [Google Scholar]
  35. Lubarsky B, Krasnow MA. Tube morphogenesis: making and shaping biological tubes. Cell. 2003;112:19–28. doi: 10.1016/s0092-8674(02)01283-7. [DOI] [PubMed] [Google Scholar]
  36. Mandelbrot BB. The Fractal Geometry of Nature. New York: Freeman; 1982. [Google Scholar]
  37. McComb D, Ryan N, Horvath E, Kovacs K. Subclinical adenomas of the human pituitary: New light on old problems. Arch Pathol Lab Med. 1983;107:488–491. [PubMed] [Google Scholar]
  38. Niveiro M, Aranda I, Peiro G, Alenda C, Pico A. Immunohistochemical analysis of tumor angiogenic factors in human pituitary adenoma. Hum Pathol. 2005;36:1090–1095. doi: 10.1016/j.humpath.2005.07.015. [DOI] [PubMed] [Google Scholar]
  39. Nonnemacher TF, Losa G, Merlini D, Weibel ER. Fractals in Biology and Medicine. Basel, Boston, Berlin: Birhkäuser Press; 1994. [Vol. I] [Google Scholar]
  40. Pan LX, Chen ZP, Liu SL, Zhao JH. Magnetic resonance imaging and biological markers in pituitary adenomas with invasion of the cavernous sinus space. J Neurooncol. 2005;74:71–76. doi: 10.1007/s11060-004-6150-9. [DOI] [PubMed] [Google Scholar]
  41. Passalidou E, Trivella M, Singh N, et al. Vascular phenotype in angiogenic and non-angiogenic lung non-small cell carcinomas. Br J Cancer. 2002;86:244–249. doi: 10.1038/sj.bjc.6600015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Paumgartner D, Losa G, Weibel ER. Resolution effect on the stereological estimation of surface and volume and its interpretation in terms of fractal dimensions. J Microsc. 1981;121:51–63. doi: 10.1111/j.1365-2818.1981.tb01198.x. [DOI] [PubMed] [Google Scholar]
  43. Pawlikowski M, Pisarek H, Jaranowska M. Immunocytochemical investigations on the vascularization of pituitary adenomas. Endocr Pathol. 1997;8:189–193. doi: 10.1007/BF02738785. [DOI] [PubMed] [Google Scholar]
  44. Pezzella F, Pastorino U, Tagliabue E, et al. Non-small-cell lung carcinoma tumor growth without morphological evidence of neo-angiogenesis. Am J Pathol. 1997;151:1417–1423. [PMC free article] [PubMed] [Google Scholar]
  45. Ribatti D, Vacca A, Dammacco F. New non-angiogenesis dependent pathways for tumour growth. Eur J Cancer. 2003;39:1835–1841. doi: 10.1016/s0959-8049(03)00267-3. [DOI] [PubMed] [Google Scholar]
  46. Schecter J. Ultrastructural changes in the capillary bed of human pituitary tumours. Am J Pathol. 1972;67:109–126. [PMC free article] [PubMed] [Google Scholar]
  47. Sharma S, Sharma MC, Sarkar C. Morphology of angiogenesis in human cancer: a conceptual overview, histoprognostic perspective and significance of neoangiogenesis. Histopathology. 2005;46:481–489. doi: 10.1111/j.1365-2559.2005.02142.x. [DOI] [PubMed] [Google Scholar]
  48. Stefaneanu L, Kovacs K, Scheithauer BW, et al. Effect of Dopamine Agonists on Lactotroph Adenomas of the Human Pituitary. Endocr Pathol. 2000;11:341–352. doi: 10.1385/ep:11:4:341. [DOI] [PubMed] [Google Scholar]
  49. Tiboldi T, Nemessanyi Z, Csernay I, Kovacs K. Effect of estrogen on pituitary blood flow in rats. Endocrinol Exp. 1967;1:73–77. [Google Scholar]
  50. Toumi H, Higashiyama I, Suzuki D, et al. Regional variations in human patellar trabecular architecture and the structure of the proximal patellar tendon enthesis. J Anat. 2006;208:47–57. doi: 10.1111/j.1469-7580.2006.00501.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Turner HE, Nagy Z, Gatter KC, Esiri MM, Harris AL, Wass JA. Angiogenesis in pituitary adenomas – relationship to endocrine function, treatment and outcome. J Endocrinol. 2000a;165:475–481. doi: 10.1677/joe.0.1650475. [DOI] [PubMed] [Google Scholar]
  52. Turner HE, Nagy Z, Gatter KC, Esiri MM, Wass JA, Harris AL. Proliferation, bcl-2 expression and angiogenesis in pituitary adenomas: relationship to tumour behaviour. Br J Cancer. 2000b;82:1441–1445. doi: 10.1054/bjoc.1999.1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Turner HE, Nagy Z, Gatter KC, Margaret ME, Harris AL, Wass JAH. Angiogenesis in Pituitary Adenomas and the Normal Pituitary Gland. J Clin Endocrinol Metab. 2000c;85:1159–1162. doi: 10.1210/jcem.85.3.6485. [DOI] [PubMed] [Google Scholar]
  54. Viacava P, Gasperi M, Acerbi G, et al. Microvascular density and vascular endothelial growth factor expression in normal pituitary tissue adenomas. J Endocrinol Invest. 2003;26:23–28. doi: 10.1007/BF03345118. [DOI] [PubMed] [Google Scholar]
  55. Vidal S, Horvath E, Kovacs K, Lloyd RV, Scheithauer BW. Microvascular structural entropy: a novel approach to assess angiogenesis in pituitary tumors. Endocr Pathol. 2003;14:239–247. doi: 10.1007/s12022-003-0016-0. [DOI] [PubMed] [Google Scholar]
  56. Vidal S, Kovacs K, Horvath E, Scheithauer BW, Kuroki T, Lloyd RV. Microvessel density in pituitary adenomas and carcinomas. Virchows Arch. 2001;438:595–602. doi: 10.1007/s004280000373. [DOI] [PubMed] [Google Scholar]
  57. Vidal S, Scheithauer BW, Kovacs K. Vascularity in nontumorous human pituitaries and incidental microadenomas: a morphometric study. Endocr Pathol. 2000;11:215–227. doi: 10.1385/ep:11:3:215. [DOI] [PubMed] [Google Scholar]
  58. Weidner N, Semple JP, Welch WR, Folkman J. Tumor angiogenesis and metastasis: correlation in invasive breast carcinoma. N Engl J Med. 1991;324:1–8. doi: 10.1056/NEJM199101033240101. [DOI] [PubMed] [Google Scholar]
  59. Wesseling P, van der Laak JA, de Leeuw H, Ruiter DJ, Burger PC. Quantitative immunohistological analysis of the microvasculature in untreated human glioblastoma multiforme. Computer-assisted image analysis of whole-tumor sections. J Neurosurg. 1994;81:902–909. doi: 10.3171/jns.1994.81.6.0902. [DOI] [PubMed] [Google Scholar]
  60. Zamir M. On fractal properties of arterial trees. J Theor Biol. 1999;97:517–526. doi: 10.1006/jtbi.1998.0892. [DOI] [PubMed] [Google Scholar]
  61. Zamir M. Fractal dimensions and multifractality in vascular branching. J Theor Biol. 2001;212:183–190. doi: 10.1006/jtbi.2001.2367. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Anatomy are provided here courtesy of Anatomical Society of Great Britain and Ireland

RESOURCES