Assessment of bronchial wall thickness and lumen diameter in human adults using multi-detector computed tomography: comparison with theoretical models

Abstract

A thickened bronchial wall is the morphological substratum of most diseases of the airway. Theoretical and clinical models of bronchial morphometry have so far focused on bronchial lumen diameter, and bronchial length and angles, mainly assessed from bronchial casts. However, these models do not provide information on bronchial wall thickness. This paper reports in vivo values of cross-sectional wall area, lumen area, wall thickness and lumen diameter in ten healthy subjects as assessed by multi-detector computed tomography. A validated dedicated software package was used to measure these morphometric parameters up to the 14th bronchial generation, with respect to Weibel's model of bronchial morphometry, and up to the 12th according to Boyden's classification. Measured lumen diameters and homothety ratios were compared with theoretical values obtained from previously published studies, and no difference was found when considering dichotomic division of the bronchial tree. Mean wall area, lumen area, wall thickness and lumen diameter were then provided according to bronchial generation order, and mean homothety ratios were computed for wall area, lumen area and wall thickness as well as equations giving the mean value of each parameter for a given bronchial generation with respect to its value in generation 0 (trachea). Multi-detector computed tomography measurements of bronchial morphometric parameters may help to improve our knowledge of bronchial anatomy in vivo, our understanding of the pathophysiology of bronchial diseases and the evaluation of pharmacological effects on the bronchial wall.

Introduction

Our current knowledge of lung physiology in human is mainly based on pulmonary function and relies on pulmonary functional tests (PFTs). However, many physiological parameters (resistance of the conducting airway tree, dynamics of flow through bronchi and responsiveness to various physiological or therapeutic events) depend on the geometric properties of bronchi (Bates, 1993). In vivo conducting airway morphometry has seldom been reported so far, due to the difficulty of imaging complex three-dimensional (3D) structures. Morphometric studies of the bronchial tree have previously been performed in a small number of cadavers of different species (Weibel & Gomez, 1962; Weibel, 1963; Horsfield & Cumming, 1968; Horsfield et al. 1976; Hooper, 1977; Phillips & Kaye, 1995). Some of these models describe airway length and diameter as a decreasing function of the order of generation, predicting the mean bronchial length and diameter of each generation as a function of trachea length and diameter (Weibel & Gomez, 1962; Weibel, 1997; Mauroy et al. 2004). Nevertheless, due to the method used, no information could be obtained on bronchial wall thickness. In addition, few studies have assessed bronchial morphometric parameters in vivo. Sauret et al. (2002) and Tawhai et al. (2004) recently focused on bronchial length, diameter or angulations assessed on human bronchial casts and in vivo on ovine and human bronchial trees using multi-detector computed tomography (MDCT) 3D imaging. These parameters are fundamental to simulate flow and inhaled particle transport (van Ertbruggen et al. 2005). Bronchial wall thickness (WT), however, has still not been fully evaluated, and WT changes may be a substantial indicator of the efficiency of inhaled treatments and in various pathological processes (Boser et al. 2005; Montaudon et al. 2007a). The evaluation of bronchial WT could benefit from recent MDCT developments that help to obtain isotropic images of bronchi in any reconstructed plane. For this purpose, 3D software packages enabling in vivo measurements of cross-sectional wall area (WA) and cross-sectional lumen area (LA) of any visible bronchus on MDCT have been developed (Palagyi et al. 2005; Brillet et al. 2007) and validated (Montaudon et al. 2007b).

The aims of our study were (1) to measure bronchial lumen diameter (LD) obtained by 3D quantitative thin-section CT in a population of adult healthy subjects, (2) to compare these measurements with values predicted by various theoretical models and (3) to provide a range of normal values for bronchial WA, LA, WT and LD for a given generation.

Materials and methods

Subjects

All subjects gave their written informed consent to participate in the study, which was approved by the ethical committee of the Centre Hospitalier Universitaire de Bordeaux. MDCT scans of ten subjects (nine males and one female) were prospectively used to carry out this study. Scans were obtained from healthy subjects referred to exclude parenchymal blebs before scuba diving. None of them presented a clinical history of thoracic disease, abnormal MDCT findings (including bronchial dilatation) or abnormal PFT results. Mean subject age was 39.2 (range 21–58) years.

Lung data acquisition

Volumetric acquisitions of the whole thorax performed using a 16-slice MDCT scanner (Somatom Sensation 16, Siemens Medical Solutions, Forchheim, Germany) were obtained at full inspiration with the following parameters: 120-kV tube voltage, 53-mA.s tube current, 0.75-mm collimation. Data were reconstructed with a high spatial frequency algorithm, 1-mm reconstruction section thickness, 1-mm reconstruction interval, 284–380-mm² field of view and 512 × 512 matrix, and displayed onscreen with parenchymal window width and level [W = 1800 Hounsfield Units (HU), L = – 600 HU]. Images were then transferred on a workstation and analysed using dedicated software.

Description of the software

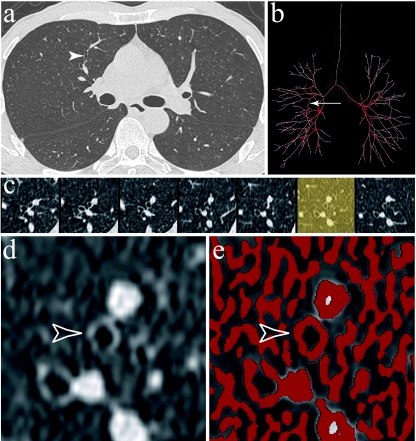
A dedicated software tool (SAB-3D: software for analysing bronchi in three dimensions) had been conceived to skeletonize the bronchial tree and to reconstruct 2D thin-section CT images orthogonal to the main bronchial axis of bronchi visible on MDCT scans in order to perform wall area and lumen area measurements. This software enabled analysis of the bronchial tree according to the bronchial generation and has been previously validated (Montaudon et al. 2007b). Briefly, it was based on two successive post-processing steps (Fig. 1). The first step provided 2D reformatted images strictly perpendicular to the central axis of any bronchus assessable on axial MDCT scans. They were obtained as follows: a first segmentation extracted from the MDCT data the airway tree using a seeded region growing algorithm (de Dietrich & Braquelaire, 2004; Montaudon et al. 2007b). Then, a seed-voxel was placed in the trachea on the first slice of the acquired volume. All voxels which density was included between two thresholded values and contigious to the seed were iteratively added to the seed-voxel, leading to the construction of a binary volume of the bronchial tree. A geodesic distance transform, propagating on the binary volume surface from the selected seed voxel, allowed us to extract isocontours separated one from another by a constant distance (10 voxels). An automated computation of the local centre of each isocontour was then performed, and local centres were connected in order to obtain the skeleton of the bronchial tree. The computed skeleton could be superimposed on the binary volume, supplying information about bronchial 3D orientation and division order (Fig. 1b). Errors in the computation of the skeleton at the point of large bronchi divisions (mainly the trachea, as shown in Fig. 1b) may occur, but are circumvented by using a greater distance for isocontour definition. Thin-section CT scans orthogonal to the skeleton were reconstructed between two contiguous local centres, giving cross-sectional images of any desired bronchus (Fig. 1c,d). The second post-processing step was an automated segmentation using a Laplacian of Gaussian algorithm to detect airway contours and perform semi-automated measurements of LA and WA, as previously described and validated (Fig. 1e) (Berger et al. 2005; Montaudon et al. 2007b).

Fig. 1.

SAB-3D software applied to a chest MDCT acquisition. Volumetric data of a thorax examination were used to reconstruct 1-mm thin-section CT images (a), from which a propagation algorithm allows us to obtain a binary volume and subsequently a skeleton of the airway tree (b, frontal view). An error occurred in the skeletonization of the tracheal division, but this was not detrimental to measurements of main bronchi morphometric parameters. Seven contiguous cross-sectional reconstructions of a bronchus perpendicular to its central axis are shown (c). The selected bronchus belonged to the fifth generation and the anterior segment of the right upper lobe; this is shown on the native CT section (a, arrowhead), and the binary volume and skeleton (b, arrow). The thin section on which measurements were performed was chosen with the minimum of contiguity with surrounding vessels (d, open arrowhead shows the selected bronchus). Detection of airway contours by a Laplacian of Gaussian algorithm was then performed (e, empty arrowhead) to provide automated measurements of LA and WA.

Using this software, we were able to assign each segmented bronchus to a generation according to Weibel's (1963) model, i.e. downwards from trachea to distal generations. We also indicated the bronchial generation according to a slightly modified Boyden (1955) classification: a bronchus was named according to its ventilated pulmonary segments. For example, the right superior lobar bronchus was named B1-3 and the left one B1-5. For each measured bronchus, the generation was assessed according to Weibel's model and the modified Boyden classification, and the software provided WA and LA. Assuming the hypothesis that bronchi are round on cross-sectional reformatted slices, LD was calculated using the formula 2√(LA/π). Mean WT was calculated as the difference between the total bronchus radius and the lumen radius, (√[(WA + LA)/π] – √(LA/π)]. Lastly, we calculated for each parameter (WA, LA, WT and LD) the ratio between two contiguous generations. Bronchial LD and ratios were then compared with the theoretical results as assessed in previously published studies (Murray, 1926; Weibel, 1963, 1997; Mauroy et al. 2004).

Theoretical bronchial measurements

Assuming the hypothesis that the geometry of the bronchial tree is fractal (West et al. 1986; Nelson & Manchester, 1988; Horsfield, 1990), these studies proposed two methods of LD computation. On the one hand, the mean LD in a particular generation could be calculated from the previous generation using a constant homothety ratio (HR) defined by Murray (1926), i.e. the ratio of the diameter between two successive generations in a biological tree with fractal geometry. So, the mean LD of bronchi in generation z can be calculated as

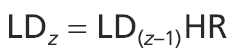(1)

. In human bronchi, an ideal HR value of 0.5^1/3 (= 0.79) was proposed by Murray (1926) and confirmed experimentally a few decades later on bronchial casts (Weibel, 1963). More recently, Weibel (1997) and Mauroy et al. (2004) reviewed precisely the casts used by Weibel (1963) and found an HR-value of 0.85, slightly greater than the theoretical 0.5^1/3. On the other hand, the mean LD in a given generation could also be calculated from the tracheal diameter. Using Weibel's (1963) equation, the mean LD of bronchi in generation z can be calculated as 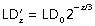, where 0 is the generation of trachea. It can also be calculated as a function of HR using the following formula 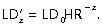. In a regular dichotomic tree, Eqs (1) and (2) would both yield to the same value of LD whatever the generation considered. But if a regular dichotomic division of bronchi is not considered the rule (trifurcations instead of bifurcations, asymmetry of the daughter branches), both equations may lead to slightly different results. A better concordance can be expected when evaluating theoretical LD for each generation from the previous one using the simple Eq. (1) than that obtained using Eq. (2). Conversely, differences may appear when comparing measured values with theoretical values computed for each generation from trachea LD, particularly in the most distal generations.

Bronchial measurements and comparison with theoretical values

In our study, we measured the HR per generation [HR_m = LD_z/LD_(z–1)] for each subject and over subjects and have compared these values with theoretical values (HR_t). We have also compared mean measured LD (LD_m) per generation for each subject and over subjects versus theoretical LD, given by the formula , using the two published values of HR_t: HR_(0.79) = 0.79 (Weibel, 1963) and HR_(0.85) = 0.85 (Mauroy et al. 2004). This equation applies to an ideal dichotomic bronchial tree, i.e. one in which each bronchus gives two daughter bronchi. But for generations more proximal than the segmental level, trifurcations frequently occur (Ghaye et al. 2001). So, we also performed comparisons using Boyden's classification downwards from segmental bronchi that was considered as the third generation.

Mean bronchial WA, LA and WT were then assessed for each generation and, because the bronchial tree geometry is fractal, a homothety ratio and a relationship with trachea WA, LA and WT per generation were calculated. Lastly, the LD/WT ratio was calculated for each bronchus and averaged per generation in each subject in order to compare LD/WT per generation over subjects.

Statistical analysis

All analyses were performed with NCSS software (Kaysville, UT, USA). Results were considered significant at P < 0.05.

We compared the measured LD (LD_m) and HR (HR_m) versus the expected LD (LD_t) and theoretical HR (HR_t) by using the paired t-test for normal data or its non-parametric equivalent test, i.e. the Wilcoxon rank-sum test, for data that were not found normal even after log-transformation. For this comparison we omitted the trachea diameters (when using Weibel's model) or segmental bronchi diameters (when using the modified Boyden classification). We also plotted LD_m and LD_t against bronchial generations on a semi-logarithmic scale. A graphical representation of the comparison between HR_m and HR_t was performed. The Kruskal–Wallis test was used to compare LD/WT averaged per generation amongst subjects.

Results

Qualitative analysis

Using Boyden's modified classification, the division of the bronchial tree was found as follows: trachea gave two daughter branches, B1-10 (main bronchus) in ten subjects.

In the right lung, B1-10 bifurcated in B1-3 and B4-10 in ten subjects. B1-3 trifurcated in B1, B2 and B3 in eight subjects, bifurcated in B1-2 and B3 in one subject, and bifurcated in B1a + 3 and B1b + 2 in one subject, so this patient did not have a segmental bronchus for the apical segment of the right upper lobe. B4-10 bifurcated in B4-5 and B6-10 in eight subjects, and trifurcated in B4-5, B6 and B7-10 in two subjects. B4-5 always bifurcated in B4 and B5. B6-10 bifurcated in B6 and B7-10 in all subjects (n = 8). B6 bifurcated in nine cases and trifurcated in one case. In ten subjects, B7-10 gave B7 and B8-10 and the latter bifurcated in B8 and B9-10 that divided in B9 and B10. Four subjects had a right B6*, i.e. a bronchus that arises from B7-10 or one of its branches and ventilates the apical segment of the lower lobe.

In the left lung, B1-10 bifurcated in all subjects; in nine it gave B1-5 and B6-10, and in one case it bifurcated in B1-3 and B4-10. B1-5 bifurcated in B1-3 and B4-5 in seven of nine subjects and trifurcated in B1-2, B3 and B4-5 in two subjects. B1-3 bifurcated in B1-2 and B3 in eight cases, bifurcated in B1-3 and B2 in one patient and trifurcated in one subject. B4-5 bifurcated in all cases in B4 and B5. B6-10 bifurcated in B6 and B7-10 in all subjects. B6 bifurcated in six subjects and trifurcated in four. B7-10 bifurcated in B7-8, giving B7 and B8, and B9-10, dividing in B9 and B10 in eight subjects.

In one case B7-10 gave B7 and B8-10, the latter dividing in B8 and B9-10. In another case B7-10 gave B7 and B8-10, the latter dividing in B8-9 and B10. Three subjects presented a B6*.

Quantitative analysis of bronchial lumen diameter

Using our software, bronchi generations could be assessed up to the 14th generation according to Weibel's model, and up to the 12th according to Boyden's classification. A mean of 256.8 bronchi per patient were measured: 34.2% belonged to upper lobes (Boyden's segments 1–3), 11.8% to the middle lobe (segments 4 and 5), and 54% to basal lobes (segments 6–10).

For each subject, comparisons between LD measured in the present study and theoretical LD, as well as comparisons between measured HR and theoretical HR are given Table 1. Using Weibel's classification of generations, measured LD was different from theoretical LD in all subjects when using Mauroy's equation and in six out of ten subjects when using Weibel's equation. Using Boyden's classification, differences were found only in four of ten subjects with Mauroy's model. Measured HR was not significantly different from theoretical HR whatever the bronchial classification used, except for one subject when using Weibel's model and Boyden's classification.

Table 1.

Comparison of lumen diameters and homothety ratios assessed by MDCT in each subject against the theoretical results based on Weibel's and Boyden's models

Subject	No. of bronchi	Generation no. (W)	LDm vs. LDt (W)	LDm vs. LDt (M)	HRm vs. HRt (0.79)	HRm vs. HRt (0.85)
1	156	10	0.016	< 0.001	NS	NS
2	246	12	0.029	< 0.001	NS	NS
3	288	12	0.02	< 0.001	NS	NS
4	339	13	NS (Wr)	< 0.001 (Wr)	NS	NS
5	257	12	0.04	< 0.001	NS	NS
6	185	13	NS	< 0.001	NS	NS
7	289	10	< 0.001	< 0.001	NS	NS
8	271	14	NS	< 0.001	NS	NS
9	199	10	0.02	< 0.001	NS	NS
10	338	13	NS (Wr)	0.001 (Wr)	NS	NS
Subject	No. of bronchi	Generation no. (B)	LDm vs. LDt (W)	LDm vs. LDt (M)	HRm vs. HRt (0.79)	HRm vs. HRt (0.85)
1	156	7	NS (Wr)	NS (Wr)	NS (Wr)	NS (Wr)
2	246	8	NS (Wr)	0.043 (Wr)	NS (Wr)	NS (Wr)
3	288	10	NS (Wr)	NS (Wr)	NS (Wr)	NS (Wr)
4	339	9	NS (Wr)	0.028 (Wr)	NS (Wr)	NS (Wr)
5	257	10	NS (Wr)	NS (Wr)	NS (Wr)	NS (Wr)
6	185	9	NS (Wr)	NS (Wr)	NS (Wr)	NS (Wr)
7	289	9	NS (Wr)	0.028 (Wr)	NS (Wr)	NS (Wr)
8	271	12	NS	NS	0.038	NS
9	199	8	NS (Wr)	0.043 (Wr)	NS	NS
10	338	9	NS (Wr)	NS (Wr)	NS	NS

For each subject, values are P-values from comparisons between mean measured values and theoretical values per generation.

No. of bronchi: number of assessable bronchi; Generation no. (W): number of generations assessed using Weibel's model; Generation no. (B): number of generations assessed using Boyden's classification; LD_m: measured lumen diameter; LD_t: theoretical lumen diameter; HR_m: measured homothety ratio; HR_t: theoretical homothety ratio according to Weibel's study (0.79) and to Mauroy's study (0.85). Comparisons were achieved using paired t-test or Wilcoxon rank-sum test (Wr).

Table 2 provides comparisons per generation between measured LD and HR and theoretical LD and HR values averaged over subjects. Using Weibel's generation classification, a significant difference was found between measured and expected LD when using Mauroy's equation but not when using Weibel's one. By contrast, using Boyden's classification downwards from segmental bronchi, no difference was found. No difference was also found when comparing measured HR and theoretical HR whatever the ordering of generations used, except for the 0.79 value of HR and Boyden's classification.

Table 1.

Comparison of mean lumen diameters and mean homothety ratios assessed by MDCT versus those calculated using Weibels and Boyden's models

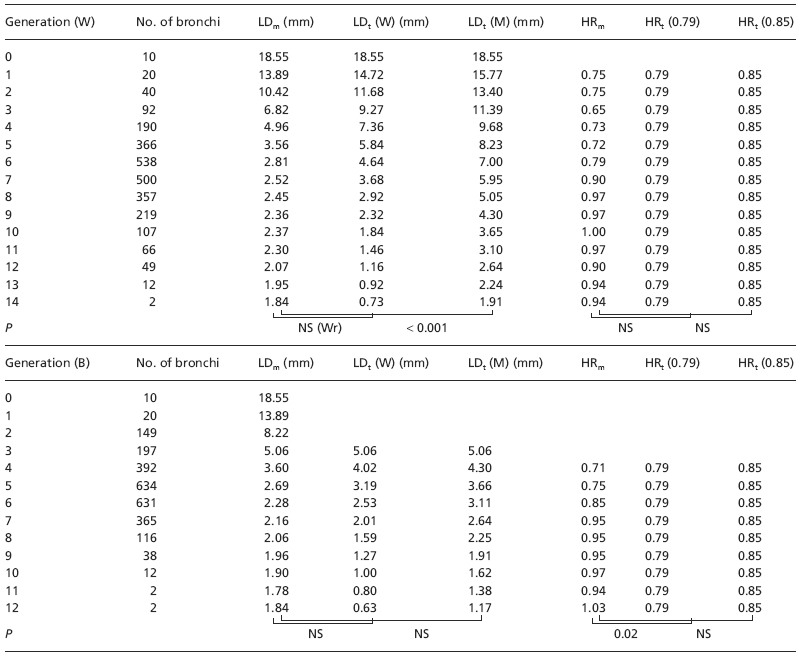For each generation, values are number of assessable bronchi (No. of bronchi), mean lumen diameter measured on MDCT scans per subject and averaged over subjects (LD_m), mean theoretical lumen diameter calculated from trachea diameter using Weibel's equation [LD_t (W)] and Mauroy's homothety ratio [LD_t (M)], homothety ratio measured on MDCT scans (HRm) and theoretical homothety ratio calculated using Weibel's study [HR_t (0.79)] or Mauroy's study [HR_t (0.85)]. Values are given for each bronchial generation using either the Weibel's model [upper part, generation (W)] or the more dichotomic Boyden's classification [lower part, generation (B)]. P, P-value of paired t-test when comparing measured parameters with theoretical parameters.

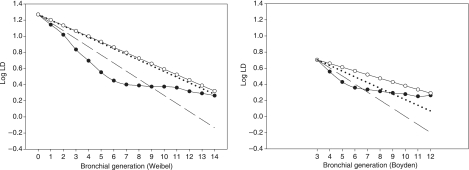
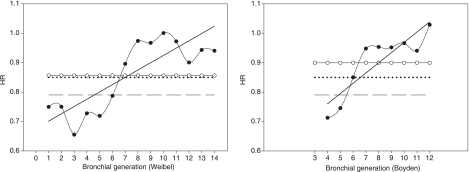
Plots show that LD was underestimated up to generation 8 of Weibel's classification, and up to generation 6 of Boyden's classification (Fig. 2). LD of downwards generations 8 and 6 were overestimated. As a consequence, HR was lower than expected up to generation 6 and greater than expected for generation 7 and later (Fig. 3). Nevertheless, the mean measured HR was 0.86 ± 0.12 when using Weibel's classification, and 0.90 ± 0.11 when using Boyden's classification.

Fig. 2.

Plots of mean lumen diameter over all subjects on a logarithmic scale (log LD) against bronchial generations according to Weibel's model (left graph) and Boyden's classification (right graph). Black circles: log of measured LD; open circles: log of theoretical LD calculated with the mean measured HR; dashed line: log of theoretical LD calculated using an HR value of 0.79 (Weibel); dotted line: log of theoretical LD calculated using an HR value of 0.85 (Mauroy).

Fig. 3.

Plots of mean homothety ratio over subjects (HR) against bronchial generations according to Weibel's model (left graph) and Boyden's classification (right graph). Black circles: measured HR, solid line: linear regression of the latter curve; open circles: mean measured HR; dashed line: HR value of 0.79 (Weibel); dotted line: HR value of 0.85 (Mauroy).

Quantitative analysis of bronchial WA, LA, WT and LD

Mean values of WA, LA, WT and LD according to bronchial generation are given in Table 3. For each parameter, HR is provided for each generation (Table 4), as well as the mean HR averaged over subjects and generations, and its derived equation. Figure 4 shows plots of mean WT on a logarithmic scale against bronchial generations. Mean values of LD/WT per generation are given for each subject in Table 5, as well as averaged values of LD/WT over subjects and per generation. No differences amongst subjects were found using the Kruskall–Wallis test (P = 0.07).

Table 3.

Values of bronchial parameters measured based on MDCT images according to bronchial generation

Generation	No. (Nt)	%	No. of subjects	WA (mm2)	LA (mm2)	WT (mm)	LD (mm)
0	10 (10)	100.00	10	85.9 ± 10.6	271.9 ± 45.1	1.4 ± 0.1	18.5 ± 1.6
1	20 (20)	100.00	10	65.3 ± 7.8	156.1 ± 30.4	1.3 ± 0.1	13.9 ± 1.4
2	40 (40)	100.00	10	49.1 ± 4.3	86.7 ± 14.9	1.3 ± 0.0	10.4 ± 0.9
3	92 (80)	115.00	10	33.7 ± 5.1	38.8 ± 8.8	1.3 ± 0.1	6.8 ± 0.8
4	190 (160)	118.75	10	23.2 ± 3.1	21.4 ± 4.9	1.2 ± 0.1	5.0 ± 0.6
5	366 (320)	114.38	10	15.6 ± 2.6	11.2 ± 3.0	1.0 ± 0.1	3.6 ± 0.5
6	536 (640)	84.06	10	11.7 ± 2.2	7.2 ± 2.1	1.0 ± 0.1	2.8 ± 0.4
7	500 (1280)	39.06	10	10.1 ± 1.9	5.8 ± 1.8	0.9 ± 0.1	2.5 ± 0.4
8	357 (2560)	13.95	10	9.8 ± 2.2	5.4 ± 2.0	0.9 ± 0.1	2.4 ± 0.5
9	219 (5120)	4.28	10	9.2 ± 1.8	4.9 ± 1.6	0.9 ± 0.1	2.4 ± 0.4
10	107 (10240)	1.04	10	9.2 ± 1.5	4.9 ± 1.6	0.9 ± 0.1	2.4 ± 0.4
11	66 (20480)	0.32	7	8.6 ± 0.4	4.4 ± 1.0	0.9 ± 0.1	2.3 ± 0.2
12	49 (40960)	0.12	7	7.2 ± 1.6	3.6 ± 1.3	0.8 ± 0.1	2.1 ± 0.4
13	12 (81920)	0.01	4	5.8 ± 1.8	3.1 ± 1	0.7 ± 0.1	2 ± 0.3
14	2 (163840)	0.00	1	6.5	2.7	0.8	1.8

Data are mean ± standard deviation of bronchial parameters per generation averaged over subjects: wall area (WA), lumen area (LA), wall thickness (WT) and lumen diameter (LD). Generations are numbered according to Weibel's model. No.: observed number of bronchi; N_t: theoretical number of bronchi; %: percentage of observed bronchi according to theoretical number of bronchi; No. of subjects: number of subjects in whom bronchi are assessable down to generation n.

Table 4.

Homothety ratios and relationship to trachea

Generation	WA	LA	WT	LD
1	0.76	0.57	0.98	0.75
2	0.75	0.56	0.99	0.75
3	0.69	0.45	0.98	0.65
4	0.69	0.55	0.91	0.73
5	0.67	0.53	0.89	0.72
6	0.75	0.64	0.91	0.79
7	0.86	0.80	0.95	0.90
8	0.97	0.94	0.99	0.97
9	0.94	0.92	0.98	0.97
10	1.00	0.99	1.00	1.00
11	0.94	0.91	0.98	0.97
12	0.83	0.82	0.91	0.90
13	0.81	0.86	0.87	0.94
14	1.12	0.86	1.15	0.94
	WA	LA	WT	LD
Mean HR	0.84	0.74	0.96	0.86
Relationship to trachea	WAZ = WA01.68−z/3 = WA00.84z	LAZ = LA02.45−z/3 = LA00.74z	WTZ = WT01.12−z/3 = WT00.96z	LDZ = LD01.60−z/3 = LD00.86z

Data are homothety ratios averaged over subjects per generation, mean homothety ratios averaged over subjects and generations (mean HR) and formulation of the relationship to trachea. Wall area (WA), lumen area (LA), wall thickness (WT), lumen diameter (LD) and bronchial generation order (z) considering trachea as generation 0.

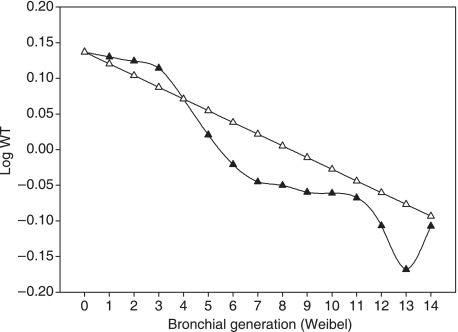
Fig. 4.

Plot of mean wall thickness on a logarithmic scale (log WT) against bronchial generations according to Weibel's classification. Black triangles: log of measured WT; open triangles: log of theoretical WT calculated with the mean measured HR.

Table 5.

Values of LD/WT ratio per generation

Subject	1	2	3	4	5	6	7	8	9	10	Mean
Generation
0	14.27	11.77	11.64	12.29	13.12	12.59	14.98	15.08	13.21	15.94	13.49
1	11.76	9.70	9.36	9.30	11.28	10.86	9.43	9.42	10.67	10.91	10.27
2	8.07	7.32	7.51	6.52	8.01	9.16	8.67	7.40	8.08	7.84	7.86
3	5.46	5.09	5.17	4.77	5.43	4.99	6.38	4.72	5.33	5.83	5.32
4	4.10	3.71	3.93	4.06	4.60	4.25	4.81	3.69	3.80	4.84	4.18
5	3.29	2.93	3.15	3.49	3.79	3.34	3.59	2.86	3.15	3.92	3.35
6	3.05	2.50	2.56	2.84	3.20	3.26	2.93	2.37	2.88	3.34	2.89
7	3.05	2.37	2.50	2.65	3.07	3.10	2.50	2.31	2.69	3.22	2.75
8	3.09	2.36	2.36	2.53	3.03	3.26	2.30	2.34	2.74	3.07	2.71
9	2.79	2.33	2.54	2.69	2.86	3.18	2.28	2.19	2.98	3.14	2.70
10	2.76	2.24	2.62	2.60	2.96	3.14	2.41	2.24	2.72	3.43	2.71
11		2.29	2.58	2.63	2.75	3.24		2.23		3.48	2.74
12		2.35	2.53	2.48	2.78	2.77		2.12		3.66	2.67
13				2.74		4.03		2.25		3.02	3.01
14								2.35			2.35

For each subject, values are the LD/WT ratio values of each bronchus averaged over each generation (Weibel's model). Mean is the averaged value over subjects in each generation. No difference was found between subjects (Kruskall–Wallis test).

Discussion

In this study we used a post-processing software package, previously validated for accuracy in vitro and in vivo (Montaudon et al. 2007b), for measuring bronchial morphometric parameters on 1-mm MDCT scans. We have compared our measurements with those calculated from theoretical models of bronchial anatomy and provided bronchial WA, LA, WT and LD values according to bronchial generation in healthy adults.

Amongst the bronchial parameters that we were able to measure, LD values only have previously been reported on a large number of bronchi per subject (Weibel, 1963, 1997; Horsfield et al. 1976; Horsfield, 1990; Mauroy et al. 2004). Although Weibel's model of airways is the best known, it is not the only one. Notably, Horsfield & Cumming (1968) developed another model of interest when considering airways as asymmetrical dichotomic structures. However, the latter model uses an upward numbering of bronchial generation, from distal generation to trachea. Because the most distal generations are not assessable using MDCT due to the limited spatial resolution of the technique and because the software we used works downwards from trachea, we have chosen for this study to apply Weibel's model and its derived HR. To take into account the impact of asymmetrical dichotomy and bronchial trifurcations occurring in segmental bronchi and upwards, we also used Boyden's classification of bronchi.

When comparing mean HR per generation versus theoretical values for each subject, no statistical difference was found (Table 1). However, when comparing mean measured LD with expected LD, differences were found in all cases when using a 0.85 value for HR and in six of ten with a 0.79 value for HR (Table 1). These differences are likely to be the consequence of a non-strictly dichotomic division of bronchi up to segmental bronchi. This hypothesis is strengthened by the fact that the number of subjects with differences diminishes when considering a more dichotomic classification of bronchial divisions (Boyden's classification).

When comparing measured values of HR averaged over generations and subjects against theoretical values, no difference was found using Weibel's classification of generations. By contrast, differences were found between measured and expected LD values using Mauroy's equation applied to Weibel's classification, but no difference when using Boyden's classification (Table 2). We believe this difference may be related to the equation used to predict theoretical values: the trachea LD directly influences LD of all other generations so its measurement must be made with great care. Trachea LD diminishes regularly from its origin to its bifurcation. Thus, the location where LD was measured very likely influenced all other bronchi LD values. On the other hand, when performing measurements downwards from the segmental bronchi, measurements fit the equation predicting LD of distal generations from segmental bronchi. Furthermore, measurements were performed from CT sections acquired at full inspiration whereas in other studies they were performed at 75% total lung capacity (TLC). If diameter changes for each generation are not proportional to LD, slight differences can be expected with theoretical models when attempting to predict distal bronchi LD from trachea LD.

Lastly, the mean theoretical LD was averaged over all bronchi belonging to a given generation. However, using MDCT allowed us to assess the largest bronchi only for the more distal generations because of a relatively limited spatial resolution. Therefore, lack of recognition of bronchi downwards from the eighth generation may induce a difference between mean measured LD and theoretical LD because only the largest bronchi are identified on CT. Conversely, evaluating mean theoretical LD of a generation from the mean measured LD of the previous generation may generate less error because the number of bronchi assessable per generation regularly decreases. De facto, the mean measured HR in this study was much closer to the theoretical value assessed by Mauroy et al. (2004) (0.85). Therefore we consider that, when studying bronchial morphometry using MDCT, the use of HR is more reliable than computing bronchial LD from trachea LD.

We have also presented here normal values of the different parameters studied (Table 3). Regardless of the parameter considered, when its average values are semi-logarithmically plotted against generation, it appeared to lie approximately on a straight line, as shown Fig. 4 for WT. Thus, based on the model of Weibel's equation for calculating mean bronchial LD of any generation and considering that all bronchial parameters are fractal, we proposed different equations that can be used to determine expected WA, LA, WT and LD of any assessable generation of bronchi explored at MDCT (Table 4). These equations expressed the considered parameter as a function of the related parameter of either trachea or of the previous generation. Lastly, we assessed the relationship between bronchial WT and LD per generation on MDCT scans (Table 5). Differences were found amongst subjects for LD/WT ratios per generation but not between subjects. This may be due to the low number of subjects studied. Nevertheless, when comparing values for each subject against mean values averaged over subjects, no difference was found.

The main limitation of our study is the number of subjects we investigated. The equations we propose to derive bronchial morphometric parameters from trachea morphometry need to be checked on a larger number of subjects of both sexes, with a wide age range, even given that Weibel used only five cadavers to construct his formulas. However, the use of MDCT is limited in healthy subjects, particularly children, by the radiation dose involved, despite the fact that the dose used here was similar to that received friom background radiation over 1 year. A limitation of the technique we used is that only the most proximal bronchial generations could be investigated due to the relative lack of resolution of MDCT, which is, nonetheless, the most suitable method for in vivo exploration of bronchi. Therefore, the equations we propose are only valuable for bronchial generations down to the 14th.

Conclusion

We have compared bronchial morphometry in healthy adults performed using a validated software package and 1-mm MDCT section images against those obtained from theoretical models. Despite being valid when studying a population, Weibel's equation applied to individuals may induce an error when determining LD of bronchi from the tracheal diameter. This error is probably due to anatomical variations in bronchial division upward from the segmental level. Finally, we proposed a range of normal values in adults and new equations for predicting WA, LA, WT and LD based on measurements of previous generations assessable on MDCT.