Muscle moment arms of pelvic limb muscles of the ostrich (Struthio camelus)

Abstract

Muscle moment arms were measured for major muscles of the pelvic limb of the ostrich (Struthio camelus) in order to assess specific functional behaviour and to apply this to locomotor performance. Pelvic limbs of six juvenile ostriches were used for this study. The tendon travel technique was used to measure moment arms of 21 muscles at the hip, knee, ankle and metatarsophalangeal joints throughout the ranges of motion observed during level running. Six of the 21 muscles measured were found to have moment arms that did not change with joint angle, whilst the remainder all demonstrated angle-dependent changes for at least one of the joints crossed. Moment arm lengths tended to be longest for the large proximal muscles, whilst the largest relative changes were found for the moment arms of the distal muscles. For muscles where moment arm varied with joint angle: all hip muscles were found to have increasing moment arms with extension of the joint, knee flexors were found to have moment arms that increased with extension, knee extensor moment arms were found to increase with flexion and ankle extensor moment arms increased with extension. The greatest relative changes were observed in the flexors of the metatarsophalangeal joint, for which a three-fold increase in moment arm was observed from flexion to full extension. Changes in muscle moment arm through the range of motion studied appear to optimize muscle function during stance phase, increasing the effective mechanical advantage of these muscles.

Introduction

The ostrich (Struthio camelus) is well adapted for high-speed overground locomotion, making it the fastest running biped, and enabling it to maintain high speeds during sustained periods of running. The muscular functional anatomy of the pelvic limb of the ostrich has been discussed in our previous paper (Smith et al. 2006) in terms of functional performance. Long lightweight limbs, significant proximal to distal reduction of muscle mass and long elastic tendons all contribute to enabling the ostrich to reach fast running speeds in an efficient manner, and large power- and force-generating hip extensors and high force ankle extensors are key muscular facilitators for this ability.

However, muscle tendon unit (MTU) architecture, such as volume, fibre length and pennation, can only be used to evaluate specific isolated MTU capacity. In order to understand how this applies to movement of the limb it is necessary to consider where an MTU is located relative to the limb segments that it acts on, and hence how it acts to move relative segments at a joint. Muscle contractions develop forces which are applied at the attachment sites of the muscle and tendon. The forces developed in turn are applied to the body segments creating torque, which defines a rotational force, about a joint. The amount of turning force, or moment, applied is determined by the perpendicular distance from the centre of rotation, or moment arm, such that the turning moment is derived from the force multiplied by the moment arm length. Hence, force acting at a greater distance from the joint centre has an increased turning effect at that joint and the moment arm determines exactly how much joint rotation a given muscle force will produce. Therefore, in order to evaluate the functional action of MTUs in the pelvic limb it is necessary to also measure muscle moment arms at the joints that they cross, giving a complete picture of the musculoskeletal interactions which can then be used in assessment of biomechanics.

Muscle moment arms are defined as the shortest perpendicular distance from the line of action of a muscle to the joint centre of rotation. Therefore, moment arm length will be dependent on muscle position, tendon path and joint structure. The shapes of articulating surfaces and bony prominences at a joint, plus relative movement between muscle position and segments, mean that both joint centres of rotation and tendon paths can vary with joint angle. Hence, the effectiveness of a muscle to move a segment may vary depending on the joint angle. It is thus helpful to ascertain if and how moment arm varies with angle in order to consider appropriately the muscle moment generated at a specific phase in the gait cycle.

Muscle moment arms have been measured for a wide range of muscles and joints in humans (Spoor et al. 1990; Visser et al. 1990; Herzog & Read, 1993; Pigeon et al. 1996; Hughes et al. 1997; Juul-Kristensen et al. 2000; Graichen et al. 2001) and in numerous other species, e.g. cat (Boyd & Ronsky, 1997), horse (Meershoek et al. 2001; Brown et al. 2003), frog (Lieber & Boakes, 1988), chimpanzee (Thorpe et al. 1999) and apes (Payne et al. 2006), by using various techniques. The simplest of these is physical measurement of the distance from the joint centre to the line of action (e.g. see Nemeth & Ohlsen, 1985; Graichen et al. 2001; Meershoek et al. 2001). However, exact location of the joint centre can be difficult to ascertain and may vary depending on the joint angle. Imaging techniques such as ultrasound, computed tomography (CT) and magnetic resonance imaging (MRI) allow direct measurement of moment arms in this way (Graichen et al. 2001; Hughes et al. 1997; Juul-Kristensen et al. 2000) but again rely on estimates of joint centre of rotation. Many of these techniques use single instantaneous values for muscle moment arms but because it has been shown that muscle moment arm can often vary with joint angle (An et al. 1984; Spoor et al. 1990; Visser et al. 1990) assuming fixed moment arms may lead to inaccuracies in estimates of muscle forces. Although measurements can be made at varying joint angles using imaging techniques this is time-consuming and expensive. A quicker and more effective technique is the tendon travel technique (Landsmeer, 1961; An et al. 1981), which also has the advantage of not relying on an estimated joint centre, as tendon motion is measured through a range of angles relative to the instantaneous joint centre, which does not need to be defined.

This study therefore used the tendon travel technique to determine muscle moment arms for major muscles of the pelvic limb of the ostrich and variations in these that occur through the range of motion observed during level running. These data can then be applied to muscle data previously reported (Smith et al. 2006) in order to gain a more complete understanding of functional implications of the musculoskeletal design of the ostrich pelvic limb.

Methods

Six pelvic limbs from six juvenile African black ostriches (Struthio camelusvar. domesticus), five male and one female, were used for this study (Table 1). Ostriches ranged in age from 24 to 28 weeks (range in mass: 53–75 kg) and were estimated to be between 40 and 60% of adult mass. All had all been raised from chicks with identical feeding and had been kept in a group in a large paddock to allow natural behaviour and free exercise, in addition to controlled exercise as a result of experimental protocols. In all birds one limb had been previously removed and dissected, the resulting data of which are presented in Smith et al. (2006). The designated moment arm limb was then retained with the full pelvis intact and frozen at –20 °C until required.

Table 1.

Subjects

Ostrich no.	Sex (M/F)	Age (weeks)	Mass (kg)	Height (m)	Scale factor	Leg (L/R)
372	M	24	53	1.07	1.11	R
373	M	24	55	1.08	1.15	L
371	M	25	73	1.22	1.01	L
365	M	26	69	1.17	1.00	L
357	M	27	55	1.10	1.02	L
378	F	28	75	1.23	1.02	L

Moment arms of major muscles acting to flex or extend at the hip, knee, tarsal and metatarsophalangeal joints were measured using the tendon travel method (Landsmeer, 1961; An et al. 1981; Spoor & van Leeuwen, 1992). The tendon travel method applies the fact that when a radius of a circle moves through an angle, any point on the radius will have moved through an arc equal in length to the distance between that point and the centre of the circle times the angle in radians. If the centre of the circle is considered to be the joint centre and the curve defined by the radius the tendon path, this relationship can be applied to enable calculation of the moment arm, such that the distance travelled by the tendon when the joint moves through an angle of one radian equals the perpendicular distance between the tendon and the joint centre, or the effective moment arm of the MTU. Therefore, the derivative of tendon displacement with respect to joint angle (in radians) expresses the moment arm of the line of action. Therefore, if L_m is distance moved by the tendon in metres and θ is the joint angle, the moment arm, r, of the MTU can be expressed as:

Moment arms of 21 muscles were measured, at multiple joints where appropriate, with the pelvic limb placed on a dissection bench. The superficial digital flexor muscles (flexor perforatus digiti III, flexor perforatus digiti IV and flexor perforans et perforatus digiti III) were measured together due to the interaction of the tendons of these muscles at both the tarsal and the metatarsophalangeal level. The order in which muscles were measured was chosen in order to avoid disturbing the line of action of muscles, as the measurement technique involves removal of the muscle belly. The origin of iliotibialis lateralis was removed first and marked with map pins for later measurement. Removal of this muscle and preparation of femorotibial knee muscles for measurement enabled exposure of the lateral surface of the femur, to which a measurement tape was glued in order to define the long axis of the bone and to act as a calibration scale for digital image calibration. Tendon travel for superficial muscles was measured first in the middle of the limb for the knee and ankle joints and preparation of these enabled exposure of the lateral surface of the tibiotarsus to which another measurement scale was glued prior to measurements as previously described. Measurement scales were also attached to the lateral surfaces of the tarsometatarsus and the proximal phalanx, ensuring tendons of muscles of interest were not disturbed. Superficial hip muscles were able to be measured next, then exposing deeper hip and knee muscles for measurement. Finally, distal muscles crossing the metatarsophalangeal joint were measured.

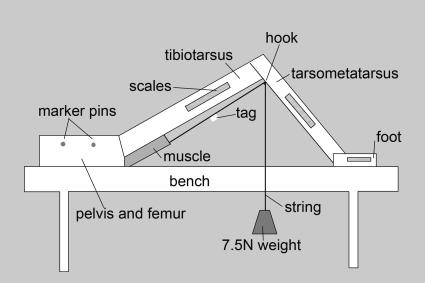
The measurement technique consisted of releasing muscle insertions, suturing a length of stiff fishing nylon (30 lb, 0.5 mm diameter, clear nylon Drennan Sea-Thru, tested to ensure it would not stretch under the loads used) around the muscle–tendon junction and passing the nylon through a hook drilled into the bone at a point estimated as the middle of the origin, ensuring that the wire followed the line of action of the muscle. A 0.75-kg mass was then hung from the end of the nylon to ensure it was kept taught throughout the measurement. A marker was placed on the wire, adjacent to the nearest calibration scale, so that the distance the wire moved with joint angle could be measured from the distance of the marker from the hook. A schematic diagram of this is shown in Fig. 1. The joint was then flexed from full extension to full flexion in the sagittal plane (of normal range of motion from kinematic data) in steps of approximately 5–10°, and at each angle a digital photograph (Nikon D70, Nikon Corp., Japan) was taken from above in a parallel plane to that of the limb motion. The process was then repeated from full flexion back to full extension. The measured angles were those used functionally, defined at the cranial aspects of the hip and ankle and the caudal aspects of the knee and metatarsophalangeal joint. Angles were defined increasing from flexion to extension at all joints, such that an angle of zero would describe a joint closed in full flexion. Ranges of motion were 60–85° for hip movement, 80–125° for knee movement, 50–150° for ankle movement and 110–240° for movement at the metatarsophalangeal joint. Where muscles crossed more than one joint the joints that were not being measured were maintained in a fixed position. For fan-shaped proximal muscles (iliotibialis lateralis, iliofemoralis externus, iliotrochantericus cranialis and iliotrochantericus caudalis) the midpoint of muscle origin and insertion was defined with coloured plastic map pins. The joint was then flexed and extended, as previously described, and the distance between the originating and inserting pins was measured as an equivalent to tendon displacement.

Fig. 1.

Schematic diagram of the experimental set-up for the tendon travel technique for measurement of muscle moment arms.

Direct measurements were made from the digital images using image analysis software (ImageJ freeware, NIH, MD, USA). For each image a calibration distance was measured on the scale, the marker position relative to the hook was measured and the angle between the axes of the long bones was measured. This was repeated for each image at each joint angle. Data were exported to a spreadsheet (Excel, Microsoft Office 2003) and actual relative position of the marker was then determined from the calibration measurement. Marker distance was plotted against joint angle (in radians) for each muscle. The muscle moment arm was defined as the derivative of the change in distance with respect to the change in angle and was therefore the gradient of the best-fit line. Linear and polynomial regression lines (least-squares best fit) were fit to these data and the R² value was used to define which of these fits best described the moment arm, such that some muscles showed a constant moment arm (linear regression) and some showed a change of moment arm with joint angle (second-order polynomial regression). Where linear and polynomial regressions showed a similar goodness of fit, with close R² values, the linear fit was used as long as the moment arm calculated from the regression at maximum and minimum joint angles did not vary by more than 10 mm. A similar procedure was followed for muscles defined by pin location.

Although the limbs used were similar in size, in order to allow comparison of data between subjects, measurements were scaled based on tibiotarsus length (Table 1), such that scaled moment arm values calculated were representative mean values for a 70-kg ostrich with a femur length of 280 mm and a tibiotarsus length of 500 mm. Mean moment arm values were calculated for minimum joint angle (r_min) and maximum joint angle (r_max) from data from all birds. A mean of multiple values calculated for 5° intervals for the active range of motion for all birds was also calculated (r_mean). Maximum muscle moment arm length was used to calculate maximum joint torque for each muscle, using values for maximum isometric force derived in our previous paper (Smith et al. 2006). Maximum force values were scaled to the mean bird mass and joint torque was determined from the product of the maximum force and the mean maximum moment arm.

Moment arms for mid-stance joint angles [hip 67°, knee 110°, ankle 135°, metetarsophalangeal (MTP) 235°] were determined from the derived regression equations. Joint angles shown in this paper were as measured from the long axes of the bone segments in the digital images. Kinematic range of motion and mid-stance joint angles were calculated from motion data using markers situated on palpable bony landmarks to estimate joint centres (Smith et al. 2006). Differences between the angles measured from the long axes of the bones and those derived from the marker placements were established from the locations of the landmarks in the images (maximum difference approximately 5°) and angle values were corrected accordingly.

Results

Moment arms were measured for 21 muscles in the pelvic limb of the ostrich. Three of these muscles were measured together due to the direct interactions of their tendons (flexor perforatus digiti III, flexor perforatus digiti IV and flexor perforans et perforatus digiti III), and are collectively referred to as the superficial digital flexors, one muscle was measured for multiple heads (gastrocnemius at the knee) and six muscles were measured at multiple joints (ambiens, iliofibularis, gastrocnemius, flexor digitorum longus, extensor digitorum longus and the superficial digital flexors). The remainder of the muscles of the pelvic limb were either too small or not situated in suitable locations for this measurement technique to be used (i.e. they were abductors or adductors). Regression equations describing mean tendon travel with joint angle are given in Table 2. Moment arms at maximum and minimum joint angles were calculated from derivatives of the regression lines along with the mean and mid-stance moment arm values and scaled means of these data are shown in Table 3. Positive and negative values for moment arms denote the muscle functions at the specific joint, such that negative values represent extension moment arms at the hip, knee and ankle and flexion at the MTP joint. The absolute value in all cases defines the moment arm length. Table 4 presents the estimated maximum joint torques of each muscle per kilogram of body mass.

Table 2.

Regression equations for tendon travel (m) with joint angle (radians) for pelvic limb muscles

Muscle	Joint	Regression equation	R2
Ambiens	Hip	0.0301x2 + 0.0002x – 0.0386	0.97
Caudofemoralis	Hip	–0.0636x2 + 0.1083x – 0.0418	0.91
Flexor cruris lateralis	Hip	–0.1022x2 + 0.1578x – 0.0439	0.89
Flexor cruris medialis	Hip	–0.0557x + 0.0567	0.69
Iliofemoralis externus	Hip	0.0106x2 + 0.0072x – 0.0200	0.85
Iliofibularis	Hip	–0.0697x2 + 0.0625x + 0.0217	0.91
Iliotibialis cranialis	Hip	0.1233x – 0.1357	0.95
Iliotibialis lateralis	Hip	–0.0586x2 + 0.1103x – 0.0505	0.78
Iliotrochantericus caudalis	Hip	0.0167x2 + 0.0007x – 0.0201	0.94
Iliotrochantericus cranialis	Hip	0.0346x2 – 0.0429x + 0.0069	0.92
Pubo-ischio-femoralis	Hip	–0.0747x2 + 0.1079x – 0.0345	0.97
Ambiens	Knee	–0.0254x + 0.0372	0.75
Femorotibialis externus	Knee	–0.0144x + 0.0216	0.56
Femorotibialis medius	Knee	0.0148x2 – 0.1075x + 0.1339	0.79
Gastrocnemius (caudalis)	Knee	0.0281x2 – 0.0812x + 0.0591	0.91
Gastrocnemius (lateralis)	Knee	0.0081x – 0.0111	0.58
Gastrocnemius (medialis)	Knee	0.0081x2 – 0.0171x + 0.0060	0.64
Iliofibularis	Knee	0.0212x2 + 0.0191x – 0.0597	0.92
Extensor digitorum longus	Ankle	0.0175x – 0.0198	0.96
Flexor digitorum longus	Ankle	–0.0223x + 0.0014	0.80
Fibularis longus	Ankle	–0.0243x + 0.0194	0.96
Flexors (FPDIII, FPDIV, FPetPDIII)	Ankle	–0.0053x2 – 0.0067x + 0.0027	0.86
Gastrocnemius	Ankle	–0.0126x2 – 0.0071x + 0.0102	0.85
Tibialis cranialis	Ankle	0.0260x – 0.0291	0.99
Extensor digitorum longus	MTP	0.0025x2 – 0.0016x – 0.0295	0.99
Flexor digitorum longus	MTP	0.0054x2 – 0.0620x + 0.1662	0.97
Flexors (FPDIII, FPDIV, FPetPDIII)	MTP	0.0076x2 – 0.0809x + 0.2066	0.99

Table 3.

Moment arm lengths

Muscle	Joint	Linear estimate*r (SD) (m)	r at max angle (m)	r at min angle (m)	r mean (SD) (m)	r mid-stance (m)	Fascicle length/r(m)
Ambiens*	Hip	(0.086 (0.016))	0.095	0.069	0.076 (0.015)	0.076	0.62
Caudofemoralis	Hip	(–0.067 (0.015))	–0.086	–0.026	–0.053 (0.025)	–0.042	2.39
Flexor cruris lateralis	Hip	(–0.123 (0.042))	–0.156	–0.061	–0.101 (0.031)	–0.087	2.20
Flexor cruris medialis*	Hip	–0.058 (0.013)	–0.058	–0.058	–0.058 (0.013)	–0.058	0.59
Iliofemoralis externus*	Hip	(0.037 (0.017))	0.046	0.031	0.038 (0.019)	0.034	1.47
Iliofibularis	Hip	(–0.136 (0.037))	–0.144	–0.083	–0.090 (0.051)	–0.071	2.86
Iliotibialis cranialis†	Hip	0.133 (0.013)	0.133	0.133	0.133 (0.013)	0.133	2.05
Iliotibialis lateralis*	Hip	(–0.045 (0.018))	–0.069	–0.014	–0.038 (0.026)	–0.022	3.21
Iliotrochantericus caudalis*	Hip	(0.047 (0.014))	0.059	0.038	0.043 (0.012)	0.043	1.05
Iliotrochantericus cranialis*	Hip	(0.050 (0.012))	0.074	0.031	0.045 (0.007)	0.040	1.40
Pubo-ischio-femoralis*	Hip	(–0.111 (0.012))	–0.139	–0.051	–0.081 (0.031)	–0.071	0.90
Ambiens	Knee	–0.027 (0.010)	–0.027	–0.027	–0.027 (0.010)	–0.027	1.74
Femorotibialis externus	Knee	–0.015 (0.009)	–0.015	–0.015	–0.015 (0.009)	–0.015	3.30
Femorotibialis medius	Knee	(–0.057 (0.013))	–0.045	–0.070	–0.055 (0.013)	–0.054	1.78
Gastrocnemius (caudalis)	Knee	(0.029 (0.018))	0.044	–0.003	0.019 (0.015)	0.028	5.26
Gastrocnemius (lateralis)	Knee	0.009 (0.010)	0.009	0.009	0.009 (0.010)	0.009	n/a
Gastrocnemius (medialis)*	Knee	(0.007 (0.006))	0.019	0.006	0.009 (0.008)	0.012	n/a
Iliofibularis	Knee	(0.107 (0.016))	0.119	0.083	0.095 (0.017)	0.106	2.71
Extensor digitorum longus	Ankle	0.018 (0.004)	0.018	0.018	0.018 (0.004)	0.018	3.96
Flexor digitorum longus*	Ankle	–0.024 (0.003)	–0.024	–0.024	–0.024 (0.005)	–0.024	1.72
Fibularis longus	Ankle	0.026 (0.002)	0.026	0.026	0.026 (0.002)	0.026	2.40
Flexors (FPDIII, FPDIV, FPetPDIII)	Ankle	(–0.025 (0.006))	–0.037	–0.017	–0.025 (0.007)	–0.034	0.80
Gastrocnemius*	Ankle	(–0.040 (0.006))	–0.052	–0.031	–0.038 (0.008)	–0.049	2.42
Tibialis cranialis	Ankle	0.028 (0.003)	0.028	0.028	0.028 (0.003)	0.028	0.46
Extensor digitorum longus†	MTP	(0.014 (0.004))	0.009	0.022	0.014 (0.002)	0.010	4.65
Flexor digitorum longus	MTP	(–0.029 (0.006))	–0.042	–0.015	–0.027 (0.006)	–0.040	1.56
Flexors (FPDIII, FPDIV, FPetPDIII)	MTP	(–0.034 (0.007))	–0.053	–0.015	–0.032 (0.009)	–0.050	0.63

N = 6 for all muscles except where indicated.

^*n = 5

^†n = 4.

Linear estimates are shown for all muscles as a comparison with the actual variation in moment arm observed through the range of motion, and for muscles where the moment arm was found to change with joint angle these data are shown in parentheses.

Maximum and minimum angles are those defined by the range of motion of each joint during level running.

Table 4.

Maximum torques of measured muscles at joints of the pelvic limb

Muscle	Joint	Mean maximum isometric muscle force (N)	Maximum joint torque (Nm kg−1)
Ambiens	Hip	1610	2.19
Caudofemoralis	Hip	1090	1.34
Flexor cruris lateralis	Hip	650	1.45
Flexor cruris medialis	Hip	1250	1.04
Iliofemoralis externus	Hip	2150	1.41
Iliofibularis	Hip	1520	3.13
Iliotibialis cranialis	Hip	600	1.14
Iliotibialis lateralis	Hip	3160	3.11
Iliotrochantericus caudalis	Hip	230	0.19
Iliotrochantericus cranialis	Hip	270	0.29
Pubo-ischio-femoralis	Hip	720	1.43
Ambiens	Knee	1610	0.62
Femorotibialis externus	Knee	890	0.19
Femorotibialis medius	Knee	1870	1.87
Gastrocnemius (caudalis)	Knee	890	0.56
Gastrocnemius (lateralis)	Knee	2250	0.29
Gastrocnemius (medialis)	Knee	2830	0.77
Iliofibularis	Knee	1520	2.58
Extensor digitorum longus	Ankle	620	0.16
Flexor digitorum longus	Ankle	1310	0.45
Fibularis longus	Ankle	2800	1.04
Flexors (FPDIII, FPDIV, FPetPDIII)	Ankle	6690	3.54
Gastrocnemius	Ankle	5970	4.43
Tibialis cranialis	Ankle	5110	2.04
Extensor digitorum longus	MTP	620	0.19
Flexor digitorum longus	MTP	1310	0.79
Flexors (FPDIII, FPDIV, FPetPDIII)	MTP	6690	5.07

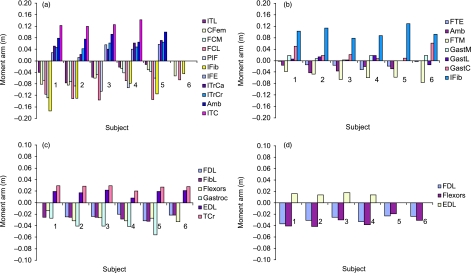
Tendon travel during joint motion varied between subjects. However, for most muscles the shape of the curve was similar in all birds. For those muscles where this was not the case the majority showed similar relationships, with one or two being slightly different and this may have been a result of both individual variation and/or limitations of the technique. Despite some differences in absolute values of moment arms as a result of this variability, the point in the range of motion at which maximum and minimum values of moment arm length occurred was consistent across subjects. For occasional measurements data were erratic, due to experimental error such as movement of the marker on the wire, and these data were not included, as due to the technique used measurements could not be checked or repeated (muscles needed to be discarded immediately after data collection so that others could be uncovered). The greatest variation between subjects was seen for the hip muscles, in particular those fan-shaped muscles that were measured using the pin technique described previously. Mean moment arms for the muscles measured at each joint for each bird are shown in Fig. 2. The number of subjects included for measurement of moment arms of each muscle in the table was six, unless otherwise stated, and values discussed in the text are the mean values of all of the subjects.

Fig. 2.

(a) Mean muscle moment arm lengths for muscles acting across the hip joint for each ostrich (muscles in order left to right: ITL, iliotibialis lateralis; Cfem, caudofemoralis; FCM, flexor cruris medialis; FCL, flexor cruris lateralis; PIF, pubo-iscio-femoralis; IFib, iliofibularis; IFE, iliofemoralis externus; ITrCa, iliotrochantericus caudalis; ITrCr, iliotrochantericus cranialis; Amb, ambiens; ITC, iliotibialis cranialis. Positive values indicate flexor moment arms and negative values indicate extensor moment arms. (b) Mean muscle moment arm lengths for muscles acting across the knee joint for each ostrich (muscles in order left to right: FTE, femorotibialis externus; Amb, ambiens; FTM, femorotibialis medius; Gast_M, medial head of gastrocnemius; Gast_L, lateral head of gastrocnemius; Gast_C, caudal head of gastrocnemius; IFib, iliofibularis). Positive values indicate flexor moment arms and negative values indicate extensor moment arms. (c) Mean muscle moment arm lengths for muscles acting across the ankle joint for each ostrich (muscles in order left to right: FDL, flexor digitorum longus; FibL, fibularis longus; Flexors, superficial digital flexors; Gastroc, gastrocnemius; EDL, extensor digitorum longus; TibCr, tibialis cranialis). Positive values indicate flexor moment arms and negative values indicate extensor moment arms. (d) Mean muscle moment arm lengths for muscles acting across the metatarsophalangeal (MTP) joint for each ostrich (muscles in order left to right: FDL, flexor digitorum longus; Flexors, superficial digital flexors; EDL, extensor digitorum longus). Negative values indicate flexor moment arms and positive values indicate extensor moment arms.

Moment arms of muscles of the hip joint

The largest moment arm values for muscles of the pelvic limb were observed for muscles crossing the hip joint. The extensor muscles showed a greater variation in moment arm length with joint angle than the flexor muscles (Fig. 3a). The trend for both hip flexors and extensors was to increase with extension of the hip, with the exception of iliotibialis cranialis and flexor cruris medialis, which both showed no significant variation in moment arm with increasing joint angle. Iliotibialis cranialis had the largest moment arm of all the hip flexors, with a value of 133 mm (mean). The moment arm of ambiens was also relatively large, increasing with hip extension from 69 to 95 mm. The small proximal hip flexors, iliotibialis cranialis, iliotibialis caudalis and iliofemoralis externus all showed a small increase in moment arm with extension of the hip but there was considerable variation between birds for moment arms of these muscles through the range of motion. The mean moment arms for these muscles were, however, relatively consistent.

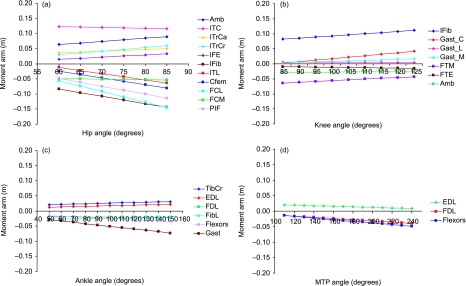
Fig. 3.

(a) Muscle moment arm lengths for muscles acting across the hip joint (muscles in order top to bottom: Amb, ambiens; ITC, iliotibialis cranialis; ITrCa, iliotrochantericus caudalis; ITrCr -iliotrochantericus cranialis; IFE, iliofemoralis externus; IFib, iliofibularis; ITL, iliotibialis lateralis; CFem, caudofemoralis; FCL, flexor cruris lateralis; FCM, flexor cruris medialis; PIF, pubo-iscio-femoralis). Positive values indicate flexor moment arms and negative values indicate extensor moment arms. Data are mean values scaled to a 70 kg ostrich from bone lengths. (b) Muscle moment arm lengths for muscles acting across the knee joint (muscles in order top to bottom: IFib, iliofibularis; Gast_C, caudal head of gastrocnemius; Gast_L, lateral head of gastrocnemius; Gast_M, medial head of gastrocnemius; FTM, femorotibialis medius; FTE, femorotibialis externus; Amb, ambiens). Positive values indicate flexor moment arms and negative values indicate extensor moment arms. Data are mean values scaled to a 70-kg ostrich from bone lengths. (c) Muscle moment arm lengths for muscles acting across the ankle joint. (muscles in order top to bottom: TibCr, tibialis cranialis; EDL, extensor digitorum longus; FDL, flexor digitorum longus; FibL, fibularis longus; Flexors, superficial digital flexors; Gast, gastrocnemius). Positive values indicate flexor moment arms and negative values indicate extensor moment arms. Data are mean values scaled to a 70-kg ostrich from bone lengths. (d) Muscle moment arm lengths for muscles acting across the metatarsophalangeal (MTP) joint (muscles in order top to bottom: EDL, extensor digitorum longus; FDL, flexor digitorum longus; Flexors, superficial digital flexors). Negative values indicate flexor moment arms and positive values indicate extensor moment arms. Data are mean values scaled to a 70-kg ostrich from bone lengths.

Of the hip extensors, the large-volume iliofibularis muscle, which crosses the knee, inserting on the fibula generated the largest moment arm at the hip, increasing from 83 to 144 mm as the hip extended and resulting in the largest estimated torque about the hip of 3.13 Nm kg⁻¹. Flexor cruris lateralis was also found to have a large moment arm at maximum extension, increasing from 61 to 156 mm through the range of motion, suggesting potential for moderate hip torque (1.45 Nm kg⁻¹), despite a relatively low capacity for generating force. Iliotibialis lateralis had the smallest moment arm at maximum flexion, due to the close alignment with the femur in the flexed posture, but this increased to a moderate 65 mm when the hip was at maximum extension. Both caudofemoralis and pubo-ischio-femoralis were found to have moderate moment arms at maximum flexion (26 and 51 mm, respectively) which, as for other extensors, increased with joint extension to 86 and 139 mm, respectively.

Moment arms of muscles of the knee joint

Iliofibularis, crossing both the hip and the knee from its origin on the lateral aspect of the ilium, was found to have the greatest moment arm at the knee joint (Fig. 3b) and also the greatest estimated joint moment (2.58 Nm kg⁻¹). The moment arm of iliofibularis showed a small increase during extension of the knee, from a minimum 83 mm at maximum knee flexion to 119 mm at maximum extension, as measured with the hip angle maintained in a fixed position. The other knee flexor measured using this technique was gastrocnemius, for which the caudal, lateral and medial heads were measured individually due to their differing origins. The lateral head of gastrocnemius was found to have only a negligible flexion–extension moment arm at the knee which showed no change throughout the range of motion. Both the caudal and the medial heads of gastrocnemius had negligible moment arms (of a few millimetres) at maximum knee flexion; however, in both of these moment arm increased with increasing joint angle to mean maximum values of 44 and 19 mm at maximum knee extension, respectively. As such, the caudal head of gastrocnemius showed the greatest change in moment arm through the range of motion of all the knee muscles measured.

Of the knee extensors, femorotibialis medius had the largest moment arm, with a maximum value of 70 mm at full flexion, decreasing with knee extension to 45 mm at maximum knee angle. The large capacity of femortibialis medius for generating force in addition to the large moment arm length resulted in this muscle showing the greatest knee extensor moment (1.87 Nm kg⁻¹).

Moment arms of muscles of the ankle joint

Moment arm lengths of muscles acting at the ankle were generally smaller than those of muscles acting at the hip or knee. The largest muscle in the pelvic limb of the ostrich is the ankle extensor gastrocnemius (averaging 18% of total pelvic limb muscle mass; Smith et al. 2006) and this was found to have the largest moment arm length at the ankle and the greatest change in moment arm length through the range of motion. The moment arm of gastrocnemius increased in a linear fashion with increasing joint angle (Fig. 3c), from 31 mm at full flexion (50°) to 52 mm at full extension (150°). The maximum torque of gastrocnemius at the ankle (4.43 Nm kg⁻¹) was almost three times the potential torque of this muscle at the knee. The moment arm of the superficial digital flexors also increased with ankle extension from 17 to 37 mm through the range of motion. Fibularis longus and flexor digitorum longus were both found to have constant moment arms of 26 and 24 mm, respectively. The main ankle flexor, tibialis cranialis, was found to have a moderate moment arm length, which increased marginally through the range of motion from 22 to 33 mm, while extensor digitorum longus was found to have a smaller constant moment arm of 18 mm.

Moment arms of muscles of the metatarsophalangeal joint

MTP joint angle was described from the caudal aspect of the limb, such that the maximum joint angle was observed at maximum joint extension (as occurs when the foot is on the ground) and minimum joint angle was observed at maximum joint flexion. All muscles acting across the MTP joint were found to have moment arms which varied linearly with joint angle (Fig. 3d). The superficial digital flexor group (FPDIII, FPDIV, FPetPDIII) and flexor digitorum longus moment arms all increased with joint extension. The digital flexors had the largest moment arm, increasing from 15 to 53 mm at maximum joint extension (240°). This maximum moment arm length along with the high capacity for force generation of the short-fibred flexor muscles resulted in the digital flexors having a large estimated moment about the MTP joint of 5.07 Nm kg⁻¹. The moment arm of the deep flexor digitorum longus increased to a lesser degree with joint extension to a maximum of 42 mm. In direct contrast, extensor digitorum longus was found to have a very small moment arm of 9 mm at full extension, which more than doubled with decreasing joint angle to a maximum of 22 mm when the joint was fully flexed.

Discussion

The action of a muscle on a body segment is defined by a number of factors including fibre length change, contraction velocity and the force generated. The moment arm of a muscle relates these parameters to joint parameters such that it defines the change in joint angle for a given fibre length change, the joint angular velocity for a given muscle contraction velocity and the joint torque for a given muscle force. As such, an increase in moment arm could allow a reduction in required force production to achieve the same joint torque. However, a greater moment arm also reduces the angle through which the segments can be moved relative to one another for a given muscle length change (Lieber & Friden, 2001) and the angular velocity of the joint for a given muscle contraction velocity, creating a trade-off between rotational force and rotational speed. Therefore, while long muscle fascicles enable larger angular movements than short fascicles, the moment arm length also influences this ability such that an important consideration is the ratio of fascicle length to moment arm (Alexander et al. 1981), where a large ratio indicates potential to move the joint through a large angle. These ratios were calculated for muscles with discernible flexion/extension moment arms, using mean moment arm lengths and our previously published muscle data (Smith et al. 2006), and are shown in Table 3.

In this study muscle moment arms were measured for 21 muscles in the pelvic limb of the ostrich, resulting in 27 measurements of moment arms due to moment arm lengths being measured for two separate joints for six of the muscles. The tendon travel technique was used, which enabled variation in moment arm with joint angle to be calculated. The specific limitations of this technique will be discussed later in this discussion.

Moment arms of muscles of the hip joint

Iliotibialis cranialis had the largest moment arm of all the hip flexors, with a mean value of 133 mm, equating to almost half the length of the femur, which did not vary with joint angle. This muscle occupies the most cranial aspect of the pelvic limb and is the largest hip flexor muscle with long parallel fascicles, making it the strongest hip flexor, and able to generate a high torque. Despite the large moment arm of this muscle the long fascicle length means it maintains a fairly high ratio of fascicle length to moment arm length (a ratio of 2.05), enabling it to move the joint through a large range of motion. This large moment arm would enable iliotibialis cranialis to create a moderate joint torque to flex the hip (1.14 Nm kg⁻¹) when swinging the limb forward and this is the primary muscle available for this function. Ambiens, a highly pennate high-force muscle, also had a relatively large moment arm at the hip, which increased with hip extension, suggesting a maximum muscle moment at full extension. The small ratio of fascicle length to moment arm length of ambiens means that this muscle is not suited to moving the hip through a large angle but may provide a high torque when initiating flexion from maximum hip extension.

Generally the moment arms of the hip extensors increased with hip extension, given that as the femur becomes more vertically orientated, muscle insertions, and hence the perpendicular distance of the line of action of the muscles (the MTU paths), are moved further away from the hip joint. There is a large muscle volume dedicated to hip extension in the pelvic limb of the ostrich and hip extension only occurs during the second half of the stance phase. This trend in moment arms suggests that the greatest muscle moment of these extensors would therefore be at the end of the stance phase. The largest volume muscle, iliotibialis lateralis, had only a small moment arm at maximum hip flexion which increased significantly with joint extension to a moderate value of 65 mm. This high force muscle has potential for significant joint torque (3.11 Nm kg⁻¹) and has a high ratio of fascicle length to moment, enabling it to move the joint through a large range of motion and would also appear to be important in stabilization and abduction of the limb, which role unfortunately cannot be evaluated from these measurements. The largest extensor moment arm and largest extensor torque were that of iliofibularis, which also has a large moment arm flexing the knee.

Moment arms of muscles of the ankle joint

Largely due to the smaller diameter of the distal part of the limb, muscle moment arm lengths at the distal joints were generally smaller than those at the proximal joints. This enables these muscles to move the distal segments at higher angular velocities, suitable for the large range of motion through which these joints must move during locomotion (Rubenson et al. 2005; Smith et al. in preparation). The longest moment arm at the ankle was that of gastrocnemius, which is the largest muscle in the pelvic limb and has a capacity to generate high forces. The moment arm of gastrocnemius increased slightly with joint angle, such that it was greatest at maximum extension. This is functionally important as gastrocnemius has potential to be the most significant muscle in extension of the ankle at the end of the stance phase. Comparatively this is important as the ankle extension of gastrocnemius is important for propulsion in the ostrich (Smith et al. 2006) and other bipeds, whilst quadrupeds do not use gastrocnemius directly for propulsion (in the horse it contains a substantial internal tendon hence linking hock and stifle extension) and propulsion must be primarily achieved by the stifle and hip extensor muscles (Payne et al. 2005; Usherwood & Wilson, 2005). Fibularis longus, a large muscle capable of producing high force and power which occupies the cranial aspect of the tibiotarsus, was found to have a relatively small and constant moment arm throughout the range of motion, enabling it to be effective for rapid extension of the ankle. Both of these muscles were found to have a relatively high ratio of fascicle length to moment arm length, with this being largest for gastrocnemius when the ankle is flexed, enabling them to operate through the large range of motion that occurs from full flexion to full extension of the ankle during running locomotion, and the greater range of motion required during the sit to stand transition. The other ankle extensors measured were those that crossed the ankle and flexed the digit, the dual action of which is required to resist ankle flexion and MTP extension during the stance phase. Ankle flexion moment arms were small and independent of angle. The main ankle flexor, tibialis cranialis, is short fibred and highly pennate with the capacity to generate high force and also has a substantial internal tendon, such that a smaller moment arm enables this muscle to flex the ankle with a high angular velocity, which is more useful than increasing the muscle moment.

Moment arms of muscles of the knee joint

Generally muscles of the knee joint had relatively high ratios of fascicle length to moment arm (all greater than 1.7), enabling these muscles to move the knee joint through a large range of motion. This could be important not only during locomotion, when change in joint angle is moderate, but particularly in the sit to stand transition when the required range of motion is much larger. The large moment arm of iliofibularis at the knee was found to be greatest at maximum extension, enabling maximum joint torque (2.58 Nm kg⁻¹) when the knee is extended at the beginning of the stance phase. The three heads of gastrocnemius had differing moment arms at the knee, suggesting specific and individual functions. The lateral head had a negligible flexion extension moment arm, which might be expected from its lateral position on the knee joint. Similarly, the medial head had only a small flexion–extension moment arm at full extension. The caudal head of gastrocnemius, while having a negligible moment arm at full flexion, had a large increase of moment arm with joint angle, such that despite its smaller size compared with the other heads it can potentially generate the greatest muscle flexion moment. The moderately long fascicle length of the caudal head of gastrocnemius, giving a high fascicle length/moment arm length ratio, also suggests suitability for moving the knee through a large range of motion. Of the knee extensors, femorotibialis medius was found to have the largest moment arm, increasing to its maximum at full flexion. This muscle is large and pennate, with potential to generate high forces, such that combined with femorotibialis accessorius (which, by virtue of its similar insertion, would be expected to have a similar moment arm) it would account for the majority of extension at the knee.

Moment arms of muscles of the MTP joint

All muscles measured at the MTP joint were found to have moment arms that varied with joint angle, with the flexors’ moment arms increasing with joint extension and the extensor moment arm increasing with joint flexion. The digital flexors are all relatively small, high-force muscles (Smith et al. 2006) with very long tendons, the main requirements of which are resisting MTP extension during stance and flexing the foot during the first part of the swing phase. The structure of the MTP joint enables much of this increase in moment arm of the digital flexor muscles by means of cartilaginous leverage during joint extension, altering the tendon path. The external moment of the ground reaction force (GRF) is greatest during mid-stance where maximal loading of the limb occurs. It is therefore beneficial that the moment arm of the flexors increases from foot on to mid-stance (as the limb joints flex) increasing the effective mechanical advantage (EMA), which is the ratio of the moment arm of the opposing muscle group (r) to the moment arm of the GRF (R). An increase in the muscle moment arm means that the muscles can resist a greater opposing external moment and the superficial flexor muscles’ moment arm is more than three times greater at mid-stance angle than at maximum joint flexion. This not only allows the relatively small flexor muscles to increase the effective muscle moment but, because length change of the short-fibred muscles is limited, also further stretches the long tendons of these muscles, allowing increased potential for elastic energy storage. The low ratio of fascicle length to moment arm, suggesting limited range of motion, further demonstrates the reliance of these muscles on the elastic properties of the tendons. The moment arm of extensor digitorum longus was found to be maximum at maximum flexion when this muscle is required to overcome the digit flexion caused by elastic recoil of the tendons of the high-force flexor muscles.

Individual variation and limitations of the technique

Variations in muscle moment arms were observed between individuals for all muscles (Fig. 2). However, trends in tendon travel with joint angle were mostly similar between birds, such that linear or polynomial regressions as appropriate applied to all, with only occasional deviations. As the ostriches used for this study were of slightly different sizes, moment arm lengths were scaled according to segment length. Segment length during ontogeny was found to scale on average proportional to Mass^0.4 (Smith et al. in preparation), and therefore moment arm lengths were scaled in a similar way. This scaling relationship has also been found for moment arm length between species in a study into allometry of leg muscles of mammals (Alexander et al. 1981). The greatest differences in absolute scaled values of moment arm were observed at the extremes of the range of motion measured, with mean values throughout the range of motion showing closer agreement between birds. This is indicative of the difficulty in defining the line of best fit, such that a small deviation in the tendon travel position or the measured joint angle can change the best-fit regression equation, the largest effect of which is observed at the extremes of the raw tendon travel data. Moment arms at maximum and minimum joint angles for each joint (for the range of motion observed during level running) were therefore analysed and averaged for all individuals, which gave the best indication of the trends observed through the range of motion and the extent to which the moment arm may increase or decrease during flexion or extension. Proximal muscle (hip and knee) moment arms were more variable than distal muscle (ankle and MTP) moment arms, in particular for those muscles in which tendon travel was, by necessity, represented by the distance between pins stuck into the mid-point of the origin and insertion (see Methods). Despite variation in absolute values, measured moment arms tended to be maximum or minimum at similar joint angles. Muscles with very small moment arms, such as the lateral head of gastrocnemius at the knee, also showed a high amount of variability between individuals, such that it would be difficult to ascertain from these results whether this is a true representation of a flexion–extension moment arm, or simply reflective of error in the technique, particularly when applied to muscles where flexion/extension action may be negligible. Therefore, it should be considered that this measurement technique is not suitable for measurement of moment arms of muscles without clear roles in flexion or extension.

The technique used only enabled calculation of the moment arms in the sagittal plane, which is not representative of the true movement of the limb segments. However, the vast majority of movement at all joints during locomotion occurs in this plane (Rubenson et al. 2005). During measurements, care was taken to move the segments purely in flexion and extension whilst avoiding adduction, abduction or rotation, which may affect the moment arms of some muscles. Therefore, it must be taken into account that the moment arms presented here may vary when accompanied by any other out of plane motion at the joints. Measurements relied on the pictures being taken in a parallel plane to that of the limb segments, which was achieved as far as practically feasible, but may account for some of the unexpected variations in the results. Both of these factors are particularly difficult to maintain for the proximal joints due to the large muscle mass present and this may account for some of the larger variations observed for proximal muscles. This technique also requires estimation of the muscle path as a single line and of the origin as a discrete point, which it is recognized is not the case, particularly in the larger proximal muscles. However, by maintaining the positions of adjacent musculature and selecting a mid-point origin any errors associated with this would be minimized and consistent throughout the range of motion. Small errors may also exist from any out-of-plane movement of the marker tape relative to the calibration scale, as the photos could only be analysed in two dimensions. Hence, while some variation between individuals can be expected to occur naturally, in some cases this may be exacerbated by limitations of the technique.

Variation of moment arm with joint angle

Moment arms were found to be constant for only nine of the 27 measurements made, defined by linear tendon travel regression or by a change of less than 10 mm for polynomial regression through the range of motion. Of these muscles three showed joint angle-dependent changes of moment arm at another joint. For all other muscles moment arms varied through the range of motion by more than 10 mm. For most muscles where change in moment arm with joint angle was found, with the exception of femorotibialis medius and extensor digitorum longus, moment arm was greatest at the maximum joint angle and hence at full extension of the joint. This is consistent with the fact that during locomotion the ostrich limb is more extended during the stance phase than swing phase (being most extended at foot on and foot off) and a greater moment arm increases the muscle EMA. Because the EMA is defined by the ratio of muscle moment arm (r) to GRF moment arm (R) this can be achieved by having a more extended limb posture during the stance phase (Biewener, 1989), aligning the GRF more closely with the limb and reducing the moment arm of the GRF (R), and/or by increasing the muscle moment arms (r) at the joints. This increase in EMA reduces the muscle forces required to produce the necessary muscle moment to balance the external moment of the GRF.

Estimated moment arms were calculated for a best-fit linear regression for all muscles (Table 3) as a comparison between assumed constant moment arms and actual variation during joint motion. For many muscles the linear fit of tendon travel with joint angle, giving a constant moment arm by differentiation, is close to the average moment arm calculated from the second-order polynomial regression, which gives a linear change in moment arm. However, these values cannot take account of the variation of moment arm with joint angle which has been shown to account for as much as a three-fold change in moment arm. Calculated moment arms for the mid-stance posture are also displayed in Table 3 and show that in most cases, and particularly for the distal muscles, mid-stance moment arm varies from the mean value and the linear estimate. This demonstrates that an assumption of constant moment arm is not appropriate for many of the muscles of the pelvic limb of the ostrich. In addition, where constant moment arm values are assumed, they are usually measured at a single joint position so may not even approximate to the average through the range of motion. The variations in moment arm lengths observed here demonstrate that limb posture and related moment arms of the muscles must be taken into account when considering the mechanics of the musculoskeletal system, and particularly when trying to construct accurate mechanical models. This technique could be further improved by measuring the continuous tendon travel, rather than the stepwise measurements demonstrated here. The continuous tendon travel method would be recommended for future studies of moment arm lengths in order to limit sources of error associated with individual step measurements and enable more detailed regression analysis, and hence description, of specific relationships between joint angle and moment arm.

Conclusions

Twenty-seven muscle moment arms of 21 pelvic limb muscles of the ostrich were measured using the tendon travel technique. Nine of the measurements made demonstrated constant moment arms or very little variation of moment arm through range of motion for muscles at specific joints. All other muscles showed changing effective moment arm with joint angle. The largest moment arms were observed in the proximal limb, with the hip flexor iliotibialis cranialis found to have the largest constant moment arm, and many of the hip extensors having moment arms which increased with joint extension to large values at maximum joint angle. Moment arms in the distal limb were generally smaller, perhaps enabling the greater angular velocity required in these segments. Gastrocnemius, the largest muscle of the pelvic limb, was found to have the largest moment arm at the ankle, with a slight increase during joint extension, such that the mechanical advantage is increased in the stance phase. The largest relative changes in moment arm were found to be those of the digital flexors, with the moment arm through joint extension increasing on average by a factor of three. Variation in moment arms was greater for the proximal muscles than distal muscles and was observed between all birds.