Tyrannosaur ageing

Abstract

Rate of ageing in tyrannosaurs was calculated from parameters of Weibull functions fitted to survival curves based on the estimated ages at death of fossilized remains. Although tyrannosaurs are more closely related to birds than to mammals, they apparently aged at rates similar to mammals of comparable size. Rate of growth in body mass of tyrannosaurs was similar to that of large mammals, and their rates of ageing were consistent with the estimated extrinsic mortality, which is strongly correlated with the rate of ageing across birds and mammals. Thus, tyrannosaurs appear to have had life histories resembling present-day large terrestrial mammals. Rate of ageing in warm-blooded vertebrates appears to be adjusted in response to extrinsic mortality and potential lifespan, independently of both physiological and developmental rates. However, individuals in species with the slowest rates of ageing suffer the highest proportion of ageing-related mortality, hence potentially strong selection to further postpone senescence. Thus, the longest observed lifespans in birds, tyrannosaurs and mammals might be close to the maximum possible.

1. Introduction

The life tables for four species of tyrannosaur produced by Erickson et al. (2006) invite comparison of their rates of ageing with wild populations of modern birds and mammals. Tyrannosaurs were more closely related to birds than to mammals, but their life histories resembled mammals more closely in their large body size and terrestrial locomotion. When compared with mammals of similar adult body mass, birds, especially species with altricial (dependent) young, grow more rapidly than mammals (Case 1978), have lower extrinsic mortality rates, plausibly related to their capacity for flight, and exhibit postponed senescence (Ricklefs 1998). Large tyrannosaurs probably maintained elevated body temperatures (Seebacher 2003; Gillooly et al. 2006; but see Farlow et al. 1995) and grew as rapidly (Erickson et al. 2001, 2004; Padian et al. 2001; Horner & Padian 2004) as mammals of similar size. In a comparison of birds and mammals, Ricklefs (1998) suggested that the rate of ageing is more closely related to extrinsic mortality—hence average potential lifespan—than to body size and related physiological measures. Thus, tyrannosaurs provide a further test of the relative influence of body mass, extrinsic mortality rates and growth rate on the rate of ageing.

Erickson et al. (2006) suggested that tyrannosaurs suffered relatively low juvenile mortality, but accelerated ageing in a pattern similar to that of humans and large mammals. Rate constants (γ) of the Gompertz function (m_x=m₀ exp(γx)) fitted to composite survival curves over age x for four species of tyrannosaurs varied between 0.187 and 0.221 yr⁻¹, which compares favourably with a typical value for humans of 0.125 yr⁻¹ (Finch 1990, table 3.1). However, γ varies inversely with the initial mortality rate (m₀; Strehler & Mildvan 1960; Gavrilov & Gavrilova 1991), which often cannot be estimated accurately and has declined dramatically in human populations. Therefore, γ is difficult to compare across species (Ricklefs & Scheuerlein 2002). Here, I fit dinosaur life-table data with Weibull ageing functions, which quantify ageing-related mortality independently of the initial mortality rate. These results are then placed in a comparative context to determine whether tyrannosaur rates of ageing resemble those of mammals of comparable size, or the lower rates of ageing exhibited by birds, extrapolated to tyrannosaur body size.

2. Material and methods

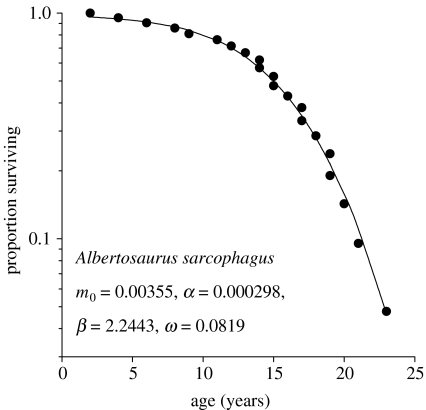
Data for tyrannosaurs presented by Erickson et al. (2006) were accepted at face value. Ages at death of fossils, estimated from age-calibrated rates of growth for each species, were assembled into composite survival curves describing the proportions of individuals alive as a function of age (e.g. figure 1). I fitted Weibull functions (Ricklefs & Scheuerlein 2002) to the decrease in proportion of individuals surviving (l_x) with age (x, yr),

$$\text{ln}{l}_x=-m_{0}x-\frac{\alpha }{\beta +1}{x}^{\beta +1},$$

where m₀ (yr⁻¹) is the minimum mortality rate of post-juvenile individuals; β (dimensionless) determines the acceleration of mortality with age; and α (yr^−(β+1)) scales the absolute rate of age-related mortality (Ricklefs 1998). The Weibull parameters can be combined into a rate of demographic ageing, ω=α^1/(β+1), which has units of 1/time (yr⁻¹). The parameters also can be used to estimate the proportion of mortality caused by ageing-related factors (Ricklefs 1998),

$$P_{\text{S}}={\int }_{x=0}^{\infty }\alpha x^{\beta }{l}_x\text{d}x.$$

Figure 1.

The logarithm of the proportion of individuals surviving as a function of age based on ages at death of 22 fossilized specimens of Albertosaurus sarcophagus (data from Erickson et al. 2006). The fitted Weibull curve is indicated by the solid line.

3. Results

As expected of big fierce animals, minimum post-juvenile mortality rates of tyrannosaurs (m₀=0.004–0.025 yr⁻¹) match the lowest values estimated for large mammals and pelagic seabirds (table 1). If these rates persisted throughout life, the average lifespans of tyrannosaurs would be 1/m₀=40–250 yr. Like most animals, however, tyrannosaurs exhibit a marked increase in mortality rate with age. Although the Weibull shape parameter (β) for Albertosaurus (2.24) was similar to that for long-lived birds (1.3–3.0), high values (5.4–5.9) for the other species suggest a more abrupt increase in age-related mortality, similar to large mammals (e.g. elephant, 4.0; hippopotamus, 5.4; Ricklefs 1998), including humans. The overall ageing parameters for tyrannosaurs (ω=0.057–0.082 yr⁻¹) were close to the lowest reported values for contemporary mammals (elephant Loxodonta africana, 0.036; hippopotamus Hippopotamus amphibius, 0.048) and birds (wandering albatross Diomedia exulans, 0.041). Tyrannosaurs appear to have had surprisingly short lifespans (less than 30 years), in view of their extremely low extrinsic post-juvenile mortality and consequently long potential lifespan, largely owing to rapid increase in the ageing-related mortality (accounting for an estimated 64–94% of adult deaths; table 1).

Table 1.

Demographic ageing parameters for four species of tyrannosaur, wandering albatross, hippopotamus and African elephant. (Data for the albatross and mammals are from Ricklefs 1998).

species	mass (kg)	m0	α	β	ω	PS
Daspletosaurus torosus	1728	0.0054	1.00×10−08	5.42	0.0566	0.880
Gorgosaurus libratus	1234	0.0250	1.00×10−08	5.89	0.0691	0.641
Tyrannosaurus rex	5551	0.0066	9.93×10−09	5.64	0.0622	0.877
Albertosaurus sarcophagus	1218	0.0036	2.98×10−04	2.24	0.0819	0.943
Diomedia exulans	7.65	0.013	6.64×10−05	2.01	0.041	0.672
Hippopotamus amphibius	1200	0.030	5.28×10−06	3.00a	0.048	0.460
Loxodonta africana	6607	0.040	1.70×10−06	3.00a	0.036	0.262

^aβ fixed.

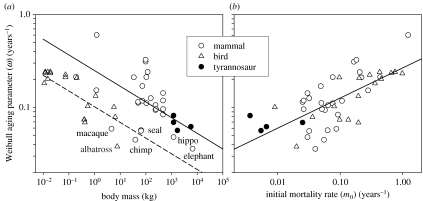
Rate of ageing among terrestrial vertebrates is not determined by body size and metabolic rate, as shown by the displacement of birds relative to mammals and tyrannosaurs (figure 2a), but conforms more closely to the minimum post-juvenile mortality (figure 2b), as predicted by evolutionary theories of ageing (Hamilton 1966). The relationship of the logarithm of ω to that of adult mass, with taxon (tyrannosaur, mammal and bird) as a main effect, was determined in an analysis of covariance (ANCOVA). The interaction term was not significant (F_2,43=0.6, p=0.56) and the common slope of the relationship was −0.166 (±0.034 s.e., t=−4.93, p<0.0001). Intercepts did not differ between tyrannosaurs and mammals (t=0.19, p=0.85), but rates of ageing in birds were significantly lower (a factor of 0.41) than those of tyrannosaurs and mammals combined (t=−3.54, p=0.0009; model F_2,46=16.2, p<0.0001, R²=0.412). In an ANCOVA relating the logarithm of ω to initial (extrinsic) mortality rate (m₀), with taxon as a main effect, neither the interaction term (F_2,43=1.56, p=0.22) nor the main effect (F_2,45=1.25, p=0.30) was significant. The logarithmic relationship of ω to m₀ had a slope of 0.324 (±0.048 s.e.; model F_1,47=45.3, p<0.0001, R² =0.491). When the logarithms of both mass and m₀ were included in the ANCOVA, rate of ageing was significantly related only to the initial mortality rate, with no effect of taxon.

Figure 2.

Rate of ageing as a function of (a) body mass and (b) initial mortality rate. Bird and mammal data from appendix tables A1 and A2 in Ricklefs (1998).

4. Discussion

Rates of ageing in tyrannosaurs not only approximate those of same-sized mammals, but also resemble those of birds three orders of magnitude smaller. The discrepancy of the ageing–size relationship between birds and mammals/tyrannosaurs appears to be associated with the level of extrinsic mortality suffered by young adults. This is in accordance with the evolutionary theory of ageing, which states that selection against early senescence increases as the expected lifespan permitted by extrinsic mortality causes increases, i.e. as early adult mortality rate decreases (Hamilton 1966; Rose 1991). Rate of ageing can vary independently of physiology. Same-sized birds and mammals have similar body temperatures and metabolic rates, but birds live 2.5 times longer, on average. This is apparently related to the safety afforded by flight (low m₀). Moreover, within a taxon, rate of ageing also can vary considerably. Among mammals, for example, aquatic species (seal) and primates (chimp, macaque), particularly humans (data not shown), appear to age relatively slowly (figure 2). Rate of ageing in tyrannosaurs corresponds to that of large mammals with respect to size, and to long-lived birds and large mammals with respect to minimum post-juvenile mortality. Thus, tyrannosaurs support the finding that variation in the rate of ageing is more closely related to selection by the demographic environment than to variation in the intrinsic physiological make-up of the organism.

Tyrannosaur growth rates are similar to those of present-day large mammals (table 2), suggesting a similar physiology, probably including a high body temperature. The wandering albatross (D. exulans) is typical of large birds with longevities that exceed those even of tyrannosaurs, and it is one of the slowest growing birds for its body size (Starck & Ricklefs 1998). Nonetheless, wandering albatrosses approach adult mass 10 times as fast as tyrannosaurs and large mammals, reaching adult body size within a year. Thus, growth rate and early development also can be adjusted independently of the rate of ageing, in spite of evidence for connections between early and late phases of the life history (Ricklefs 2006). It should be noted, however, that albatrosses do not become sexually mature until 10–12 years of age, similar to large mammals and tyrannosaurs and, hence, a long period of learning and accumulation of experience might be a common feature of long lifespan.

Table 2.

Growth rates (growth constants of logistic equations) fitted to growth curves of tyrannosaurs (Erickson et al. 2004), wandering albatross (Starck & Ricklefs 1998) and several large mammals (Zullinger et al. 1984).

species	mass (kg)	K (yrs−1)	mammal Kpred.a
Daspletosaurus torosus	1728	0.44	0.63
Gorgosaurus libratus	1234	0.38	0.73
Tyrannosaurus rex	5551	0.57	0.38
Albertosaurus sarcophagus	1218	0.43	0.74
Diomedia exulans (albatross)	7.65	10.95	7.00
Syncerus caffer (Cape buffalo)	517	1.40	1.08
Diceros bicornis (rhinoceros)	1080	1.77	0.78
Loxodonta africana (elephant)	2770	0.16	0.51

^aLogistic growth rate predicted by the regression equation for the Gompertz growth rate for a large sample of mammals: logK_G (days⁻¹)=−0.901 to 0.302 log asymptote (kg) (Zullinger et al. 1984).

Although variation in the rate of ageing suggests that the course of senescence is evolutionarily flexible, the estimated proportions of adult mortality due to senescent factors (P_S=64–94% among tyrannosaurs; table 1) indicate that selection to delay the demographic effects of ageing in long-lived vertebrates is potentially strong. Thus, if suitable genetic variation existed and if individuals were capable of reproducing to old age (Ricklefs et al. 2003), one would expect P_S to be reduced to a lower level. If albatrosses and large mammals/tyrannosaurs were close to the limit of longevity in warm-blooded vertebrates, this limit would appear to be independent of body size and rate of metabolism. Rates of senescence in dinosaurs underscore how poorly we understand the evolution of lifespan and its limits.