Quorum decision-making facilitates information transfer in fish shoals

Abstract

Despite the growing interest in collective phenomena such as “swarm intelligence” and “wisdom of the crowds,” little is known about the mechanisms underlying decision-making in vertebrate animal groups. How do animals use the behavior of others to make more accurate decisions, especially when it is not possible to identify which individuals possess pertinent information? One plausible answer is that individuals respond only when they see a threshold number of individuals perform a particular behavior. Here, we investigate the role of such “quorum responses” in the movement decisions of fish (three-spine stickleback, Gasterosteus aculeatus). We show that a quorum response to conspecifics can explain how sticklebacks make collective movement decisions, both in the absence and presence of a potential predation risk. Importantly our experimental work shows that a quorum response can reduce the likelihood of amplification of nonadaptive following behavior. Whereas the traveling direction of solitary fish was strongly influenced by a single replica conspecific, the replica was largely ignored by larger groups of four or eight sticklebacks under risk, and the addition of a second replica was required to exert influence on the movement decisions of such groups. Model simulations further predict that quorum responses by fish improve the accuracy and speed of their decision-making over that of independent decision-makers or those using a weak linear response. This study shows that effective and accurate information transfer in groups may be gained only through nonlinear responses of group members to each other, thus highlighting the importance of quorum decision-making.

Animal groups, including humans, often exhibit complex dynamic patterns that emerge from local interactions among group members (1–4). This collective behavior is of particular interest when individuals with limited personal information use cues and signals provided by others to decide on a course of action (5, 6).

It has been suggested that the accuracy of decision-making increases with group size (7). However, our understanding of exactly how behavioral interactions scale to collective properties, and the consequences of this process to individual survival, are limited because of the difficulty inherent in addressing the complicated feedbacks that arise from repeated social interactions (1, 4, 8): individuals both create and are influenced by their social context (9, 10). In many social interactions, it may not be possible to identify which individuals, if any, possess pertinent information. Simply copying the behavior of others indiscriminately may lead to cascades of information transfer where the nonadaptive behavior of single animals or small numbers of individuals is reproduced by many other individuals at no benefit to the copiers (11–13).

Recent advances in understanding collective decision-making have mostly come from studies of eusocial and gregarious insects (6, 14–19). These studies have emphasized the importance of quorum responses, where animals' probability of exhibiting a particular behavior is an increasing function of the number of conspecifics already performing this behavior (4). For example, cockroaches rest longer under shelters containing other resting cockroaches. As a result, they make a “consensus decision” to shelter together under one of two identical shelters (15). In Temnothorax ants, the probability that an ant will carry other ants to a new nest increases with the population of ants at that new nest (6). This quorum response can amplify the differences in the populations at two alternative nests, usually leading to preferential choice of the better of the two (17, 20).

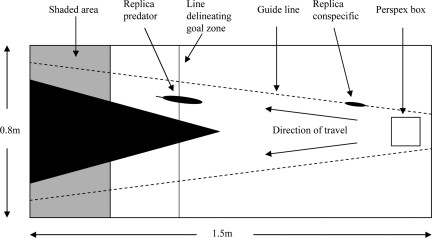
Although it is known that vertebrates do use social cues provided by conspecifics in making decisions about foraging (21–23), cooperation (24, 25), the timing of activities (9) and during navigation (26), less is known about how individual decisions contribute to, and are influenced by, collective patterns of behavior and how these decisions in turn facilitate individual-level adaptive responses to an uncertain environment (4). Fish provide a promising test-bed for new theories about collective behavior (27); aggregations of fish may display complex collective patterns yet, because of their small size and easy maintenance, are amenable to experimental studies. In this study, we presented three-spine sticklebacks with a choice of moving to one of two refugia in a simple Y-maze (see Fig. 1). Resin-cast, replica sticklebacks, which were attached to a motor and were towed through the maze to one of the refugia, were used in order that we could examine their effect on the movement decisions of the experimental fish. In the second phase of the study, we added a potential predation threat (a resin-cast replica of a sympatric predator) to one arm of the maze to manipulate the costs of following. By testing experimental fish in different group sizes (one, two, four, and eight fish) and with or without one or more replica conspecifics, we investigated the role of quorum responses in the movement decisions of fish.

Fig. 1.

Experimental set-up.

We used a simulation model to explore whether quorum responses allow for more accurate decisions than those made by individuals acting independently of conspecifics and how decision-making accuracy and speed change with group size. Our model is based on the hypothesis that the propensity to go either left or right in the maze increases as a function of the number of individuals that have recently gone left and right. In the absence of other individuals having taken a particular direction, uncommitted individuals choose the left right direction with a ratio l:r, i.e., they have a constant probability l/(l + r) of choosing the left option and r/(l + r) of choosing the right option.

In the presence of conspecifics, an individual's probability of going left increases as a function of the number of individuals that have gone left in the last T time steps and decreases with the number that have gone either right or remain uncommitted. In addition to T, two parameters determine the shape of this response: a, which is the spontaneous accept rate, and k, which is the steepness of response. Specifically, the probability of an individual going left on time step t + 1 is

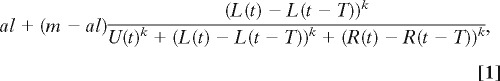where m is the maximum probability of committing to a decision; U(t) is the number of uncommitted individuals at time t; and L(t) and R(t) are, respectively, the total number of individuals that have gone left and right by time t. A similar commitment probability is set for going right, i.e., the probability of going right on time step t + 1 is

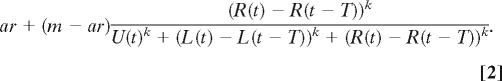We show examples of Eq. 2 for different parameter values in supporting information (SI) Fig. S1. When k = 1, the probability of going left is proportional to the number that have previously gone left. This weak linear response can be contrasted with that for larger values of k, where once a threshold number of individuals have gone left there is a dramatic increase in the probability of going left. We call the case where k > 1 a quorum response, because the probability of making a particular movement decision increases once a quorum is met. In the case of Eq. 1, the quorum size is determined by the size of the group of uncommitted individuals and the number taking the alternative direction. The parameter a determines the speed of decision when very few individuals have made a decision and U(t) together with R(t) determine the quorum threshold size.

Fitting the model to the data allows us to determine the form of the response of fish to conspecifics. In particular, we can distinguish between three alternative hypotheses: no response to conspecifics (indicated by m ≈ ar ≈ al); weakly linear response (m > ar and k ≈ 1); and quorum response (m > ar and k > 1). Details of model fitting are presented in Materials and Methods.

Results

Response of Test Fish to Replica Conspecific(s).

Across all treatments and group sizes, fish consistently took the direction initiated by the majority of the replica conspecifics within the Y-maze (Fig. 2), although the tendency to follow a single replica declined as group size increased (Fig. 2c). Solitary fish and focal fish in groups of two showed a significant tendency to follow a single replica (solitary: P < 0.001; n = 20; group of two: P = 0.003; n = 20), whereas focal fish in groups of four and eight did not (group of four: P > 0.05; n = 20; group of eight: P > 0.05; n = 20). The addition of a second replica produced a significant tendency to follow in the larger group sizes (group of four: P < 0.0001; n = 20; group of eight: P = 0.003; n = 20).

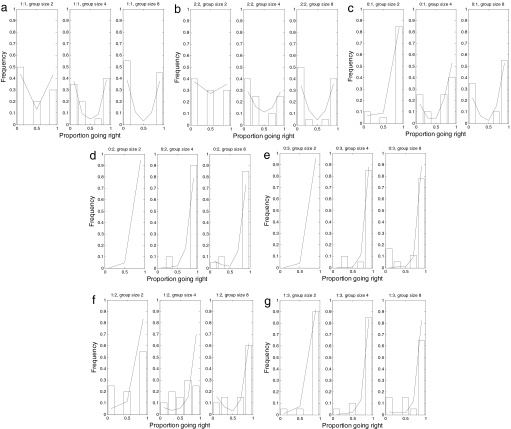
Fig. 2.

Comparison of the best fit of the model with experimental data when no predator was present. The conspecific replicas going left:right are, respectively, 1:1 (a), 2:2 (b), 0:1 (c), 0:2 (d), 0:3 (e), 1:2 (f), and 1:3 (g). Data are shown as histograms, and model outcomes are represented by a solid line.

The greater the relative difference between the numbers of replicas going in each direction, the more biased the test fish were toward the majority direction. In cases where an equal number of leaders traveled in each direction (Fig. 2 a and b), there was a U-shaped distribution of how many fish went left or right. The U-shaped distribution, contrasted with a binomial distribution with a single peak, indicates that the fish responded not only to the replicas but also to each other in making a decision of which direction to take. In cases where different numbers of replicas went in each direction, the distribution was J-shaped. There was thus a strong tendency for consensus among the fish, even when they did not take the direction of the majority of replicas. Aside from this bias toward the majority of replicas, there was no intrinsic bias to the left or right refuge either in the trials with a single fish and no replica leader (P > 0.8, n = 20) or in the trials with multiple fish and equal numbers of leaders in each direction (Fig. 2 a and b).

Fitting the model to the data indicates a quorum-like response to conspecifics and replica fish (Fig. 2). The parameters l = r = 1 were set in accordance to the lack of directional bias in single fish experiments. The best fit of model to the data for the other parameters was T = 40, a = 0.0078, and k = 3.2 (Fig. 3). The model fitted well provided a < 0.0078, 2 ≤ k ≤ 4 and T > 40 (Fig. S2a). The model did not fit well for a linear response (i.e., k = 1) or if the fish were assumed to make decisions independently of others. The best fit value of T = 40 was larger than the average time taken for all fish to make a decision in simulations. For simulations with a = 0.0078 and k = 3.2, the number of time steps, averaged over all treatments, before all fish made a decision was 12.7 ± 6.4 steps.

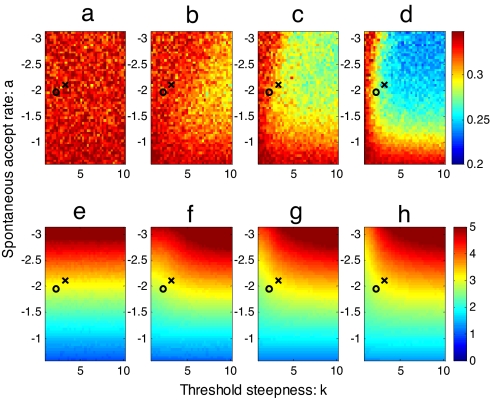
Fig. 3.

Accuracy and speed of individual decision-making of model simulations for different group sizes (a and e) n = 2; (b and f) n = 4; (c and g) n = 8; and (d and h) n = 16. Simulations were run 5,000 times for different combinations of spontaneous accept rates, a, and the threshold steepness, k. (a–d) The average proportion of fish making “errors”: the darkest blue indicates that on average 0.2 fish have made an error; darkest red indicates that on average 0.35 have made an error. (e and f) Log₁₀ (mean number of time steps over all individuals) until an individual moves left or right. Dark red indicates slow decisions, and blue indicates fast decisions. The black × on each panel represents the best fit parameter values for the fish in the absence of the predator, and the circle represents those values in the presence of the predator.

Response of Test Fish to Replica Conspecific(s) in Presence of Replica Predator.

In the previous trials, following the replica conspecific(s) comes at little or no cost. Therefore, we designed a second set of trials that involved the placement of a replica predator in one of the arms of the Y-maze to explore whether this potential cost changed the decision-making dynamics. In treatments with no replica conspecifics, fish in all group sizes strongly avoided the predator and moved to the alternative goal zone (Fig. 4a); in trials with single fish and no replicas, only one of 20 fish swam past the predator, which could be interpreted as an “error rate” of 0.05. In experiments where a single replica conspecific moved past the predator, solitary fish were significantly likely to follow (P < 0.001; n = 20), whereas focal fish in groups of two showed no clear trend and fish in larger groups largely disregarded the replica and moved to the alternative goal zone (group of 4: P < 0.001, n = 20; group of 8: P < 0.001, n = 20). Where two or three replica conspecifics moved past the predator, both solitary fish (P < 0.001, n = 20) and focal fish in a group of two (P = 0.04, n = 20) were significantly likely to follow past the predator, whereas focal fish in larger groups no longer showed any clear trend.

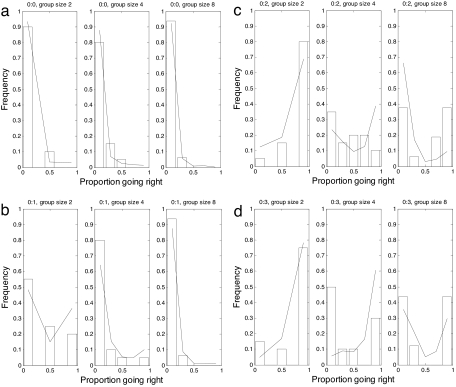
Fig. 4.

Comparison of best fit of the model with experimental data when a replica predator was present. We assume that the predator is on the right and the number of conspecific replicas going left:right are, respectively, 0:0 (a), 0:1 (b), 0:2 (c), and 0:3 (d). Data are shown in the histograms, and model outcome is represented by the solid line.

The model was fitted to experiments in the same way as the trial with no predator. To reflect predator avoidance we set r = 1/19 and l = 1. We set L(0) = 0 and R(0) to be the number of replica conspecifics going right, varied between 0 and 3. We then ran the mathematical model 1,000 times to generate a distribution of outcomes given the treatment stimulus. Robustness of the model was tested as above and the model fitted best when a < 0.0078, 2 ≤ k ≤ 4, and 5 < T < 10 (Fig. S2b). Fig. 4 shows the best fit of the model for the different combinations of R(0) and L(0) to the data.

The Role of Quorums and Group Size on Accuracy.

Are decisions based on quorum responses more accurate than those made by individuals acting independently of conspecifics? Do the fitted parameters compare with those tuned for accurate decision-making? To answer these questions, we ran simulations where we assumed that going left constituted the “correct” way to go and that going right was an error. Specifically, we set r = 1/2 and l = 1 so that the spontaneous probability of going left is twice that of going right. This assumption models the case of having a cryptic predator on the right that a solitary individual will detect only two times out of three, i.e., a solitary individual will go left with probability 2/3. We chose these parameters because an error one time in three is a high error rate, modeling a case where making an accurate decision is difficult. Model results with different error rates are qualitatively similar to those we present here (D.J.T.S., unpublished results). We simulated this model to test how the proportion of individuals making an error changed as a function of k, a, and the group size, n.

For small groups, n = 2 and n = 4, there was little improvement in the accuracy of decision-making with errors remaining close to 1/3 for all parameter values (Fig. 3). Improvements at such small group sizes are limited because the first individual to go left or right always has probability 1/3 of making an error. The second individual then gains no information by the direction of the first individual. It is only when the spontaneous decisions of a number of individuals have accumulated that they can begin to gain an advantage from following the decisions of others. Thus, larger groups, n = 8 and n = 16, do benefit from responding to the decisions of others (Fig. 3). This improvement strongly relies on having a disproportional response to conspecifics; that is a nonlinear quorum response. When k = 1 there is no improvement in the proportion of errors made, but as k increases so too does decision accuracy. Likewise, as the spontaneous accept rate decreases, decision accuracy increases.

k and a have the opposite effect on decision-making speed and accuracy. Speed trades off with accuracy for any set of parameter values. Above groups of size eight or so, group size has very little effect on speed. Large groups can make equally fast decisions as smaller ones without paying a cost of decreased accuracy. In nature, we would expect to find the same trend but for it to be reduced as groups become very large because some of the individuals may not be able to sense the direction others have taken because of restricted perception caused by crowding.

Discussion

In making decisions between two alternative routes, we found that fish exhibit relative choice: the probability of an individual taking a particular direction depends on the number of conspecifics going in each direction. Furthermore, we found that the size of the undecided group also plays a role in the movement decision. Larger, undecided groups decrease the probability that an individual moves at all in either direction. We have used these observations to propose a quorum response model where the probability of performing an action increases as a function of the number of individuals having recently taken that action and decreases as a function of the number taking the other action or remaining undecided. Despite its simplicity, this model accurately fits the data for different numbers of replica fish both in the absence and presence of a potential predator threat. Although this model is sufficient to account for the data, other models that do not include all aspects of relative choice are not. In particular, a model that does not include the effect of the undecided individuals does not match the data as accurately as the one we present here (D.J.T.S., unpublished data).

The best fit for two of the model's three parameters, the threshold steepness k and the spontaneous accept probability a, were similar both in the presence and in the absence of a predator. The third parameter T, the time frame over which the actions of others are taken into account, differs in the absence or presence of a predation threat. In the absence of a predator, this time frame is long and it is the total number of individuals who have gone left or right that determines an individual's propensity to copy this behavior. In the presence of a predator, the time frame is considerably shorter and it is only the very recent actions of conspecifics that determine directional propensity. The shorter time frame in the presence of a predator may be explained by the fact that only the most recent information is relevant; fish have to cope with a circumstance that may change rapidly.

The interactions among the fish are highly nonlinear: the best fit of the model was achieved when the threshold steepness was k = 3.25 in the absence of a predator, and k = 2.25 in the presence of a predator. Instead of reacting proportionally to the actions of others, fish react strongly in favor of the option chosen by the majority. It is this disproportional reaction to conspecifics that generates the U-shaped distribution of outcomes seen when stimuli are equal (as in Fig. 2 a and b). These distributions are characteristic of nonlinear positive feedback in decision-making (4, 14, 28).

Nonlinear positive feedback is often associated with the possibility of errors in decision-making at the collective level (11–13). Amplification of incorrect decisions is predicted by the model and seen in the experiments with the predator. In the absence of other fish, a focal individual passed a predator in only one of twenty trials, a 5% error. When two or more replicas go past the predator, the error increases dramatically: a group of two individuals have an error rate of 80% whereas groups of four or eight fish are misled 30–40% of the time. Interestingly, however, a single replica does not lead groups of four or eight fish effectively, especially in a risky situation. Interpreting these results in terms of our model, we see that uncommitted individuals in larger groups only follow above a threshold number of leaders. This threshold dramatically reduces the probability of errors being amplified throughout a group because, if the probability one individual makes an error is small, say a, then the probability that two fish independently make errors at the same time becomes very small, i.e., a².

The simulation model predicts that, although we can experimentally manipulate the fish to make “errors,” quorum responses generally improve the accuracy of decision-making. By biasing decisions according to the decisions of others the proportion of errors made is reduced, with larger groups making more accurate decisions. In the model, it is assumed that individuals cannot tell whether any particular individual has made a “correct” or “incorrect” decision, but by integrating the decisions of others individuals can improve their own accuracy. Only simulations for k > 2 showed strong improvements in decision-making accuracy. If the response was proportional, i.e., k = 1, then copying the actions of others offers no improvement over independent decision-making. The disproportionate threshold response of the real fish is therefore likely to be essential in improving decision accuracy in such situations. These results help explain the ubiquity of nonlinear response thresholds across different grouping species (4, 6, 14, 19). Individual fish use the decisions of others to improve their own decision-making.

Positive feedback and threshold responses have been identified as key proximate mechanisms in the decision-making of animal groups (4, 29). The possible importance of information transfer in animal groups in providing functional explanations of their evolution has been highlighted many times (10, 11, 22, 28), but has not been directly linked to proximate explanations. Making this link is crucial to understanding the evolution of grouping. It is not sufficient to say that group-living animals simply gain from information transfer, because it is specifically the nonlinear response to conspecifics that explains both the improvements in decision-making accuracy by individuals in groups. The nonlinear response also explains apparently maladaptive blind copying when the group is misled by replica fish. We now refine the information transfer hypothesis as follows: by joining a group and responding to the actions of others according to a steep quorum response, an individual can gain an information processing advantage over solitary individuals. Measuring the form of these responses across species will help determine the importance of information transfer in the evolution of group-living in these species.

Materials and Methods

Experiments were performed by using three-spined sticklebacks collected from the River Welland, Leicestershire (52° 30′ 35″ N; 0° 53′ 18″ W) during late 2003. To test the tendency of individuals to follow conspecifics in different contexts, we constructed an experimental arena that offered a choice of two identical refugia, both equidistant from a starting point (Fig. 1). Fish were added to this starting point and were then guided used remote-controlled replica fish. Sticklebacks are known to respond well to replica conspecifics (24). The stickleback replicas were constructed from resin plaster. The mould was made of a single 40-mm stickleback by using Gedeo molding alginate. This method preserved considerable detail in the finished models. Twelve replicas were then cast by using liquid resin plaster. Once set, these replicas were painted to resemble sticklebacks, and a hole was drilled lengthways along the dorsal surface to allow the replica to be threaded onto the guide line.

The replica was attached to one of two guide lines extending from one end of the arena, positioned near to a clear square Perspex box containing test fish, to each refuge. To investigate conflict of information, we manipulated the number of replica fish on each line. For example, we could attach an equal number of replicas to each line, or create a bias with more replicas moving to one refuge than the other. When multiple replicas (maximum of three per line) were placed on the same guide line, they were positioned one body length apart and facing (subsequently moving toward) the refuge.

In each trial, we acclimatized test fish for 5 min within the Perspex box before lifting it and freeing them. Simultaneously a motor started to tow the replica(s) at a speed of one body length per second to the far end of the arena. The experiments continued until all fish had entered the shaded goal zones or refuges (Fig. 1). These refuges are preferred by the fish even in the absence of a moving replica. The side at which the replica individual(s) were presented was randomized. In the vast majority of experiments, the fish quickly entered the goal area, but in a few cases a single “errant” fish stayed frozen to a spot for >100 s; these results were discarded. All trials were filmed from above.

We investigated the behavior of sticklebacks in response to the replica conspecifics both in the absence and presence of a potential threat in the form of a replica predator.

Response of Test Fish to Replica Conspecific(s).

Test fish were given an absolute choice [replica(s) on one side of arena only] or a relative choice [replica(s) on both sides]. Absolute choice was provided by 1 replica versus 0 replicas, 2 vs. 0 or 3 vs. 0. Relative choice could be divided into symmetrical stimuli: 1 vs. 1 and 2 vs. 2; and asymmetrical stimuli: 2 vs. 1 and 3 vs. 1. Again, we randomized the side at which the replicas were presented. We used four different group sizes of test fish: one, two, four, and eight, with 20 replicates for each. For group sizes four and eight, all treatments were performed, whereas for group sizes of one and two, we performed all treatments except for absolute choice 2 vs. 0 and 3 vs. 0. The omission of these absolute choice treatments for smaller group sizes reflected observations that the decisions in small groups were already strongly biased by the presence of one leader. We also performed experiments with single test fish and no replicas to examine the bias of fish for left or right.

Response of Test Fish to Replica Conspecific(s) in Presence of Replica Predator.

We examined the tendency of test fish to follow replicas that traveled into close proximity to a replica of a common sympatric predator, a perch (Perca fluviatilis) of 200-mm length. We randomized the side on which the replica predator was placed. Control experiments showed that sticklebacks (alone or in groups) strongly avoided this path when not under the influence of a replica stickleback. We tested four different treatments with 0, one, two, or three replica conspecifics each for groups of one, two, four, and eight fish. Twenty replicates were performed for each.

Data Analysis.

For each group size, an individual fish was selected at random before the beginning of the trial from the video playback. The goal zone that this fish entered was recorded and analyzed by using a binomial test with a null expectation of no preference for either goal zone.

Model Fitting.

The parameters l and r were first fit by using experimental trials with a single fish and no replica conspecifics. The parameter m was fixed to be 0.45, so that if all of the fish had made a particular movement decision then the probability of following this decision was large, but the total probability per time step was never >1. To test the fit of specific values of a, k, and T, we ran the mathematical model 1,000 times to generate a distribution of outcomes for each treatment and fish group size. We set R(0) and L(0) to be the number of replica fish going left or right at the start in each experimental treatment. We further assumed L(t) = R(t) = 0 for all t < 0, because no individuals go left or right before the start of the experiment. For convenience, we assume that the majority of replica fish traveled is always right, although the side on which the predictor replica was presented was randomized in the experiments. By systematically changing the parameters a, k, and T and running each combination 1,000 times, we were able to test which parameter combinations best fit the data (Fig. S1). Model fit was tested by comparing the distribution of individuals going right generated by the model with that of the data over each of the seven treatments and each group size of two, four, and eight fish. Specifically, for each treatment and group size we calculated the sum of squares (expected_i − observed_i)² where i denotes the histogram boxes for the proportion of fish going right 0–20, 20–40, …, 80–100. The sum of squares was then summed across all treatments and group sizes to give the overall fit of the model for a particular parameter combination.