The evolution of modularity in bacterial metabolic networks

Abstract

Deciphering the modular organization of metabolic networks and understanding how modularity evolves have attracted tremendous interest in recent years. Here, we present a comprehensive large scale characterization of modularity across the bacterial tree of life, systematically quantifying the modularity of the metabolic networks of >300 bacterial species. Three main determinants of metabolic network modularity are identified. First, network size is an important topological determinant of network modularity. Second, several environmental factors influence network modularity, with endosymbionts and mammal-specific pathogens having lower modularity scores than bacterial species that occupy a wider range of niches. Moreover, even among the pathogens, those that alternate between two distinct niches, such as insect and mammal, tend to have relatively high metabolic network modularity. Third, horizontal gene transfer is an important force that contributes significantly to metabolic modularity. We additionally reconstruct the metabolic network of ancestral bacterial species and examine the evolution of modularity across the tree of life. This reveals a trend of modularity decrease from ancestors to descendants that is likely the outcome of niche specialization and the incorporation of peripheral metabolic reactions.

Modularity is considered to be one of the main organizing principles of biological networks (1, 2). A biological network module consists of a set of elements (e.g., proteins/reactions) that form a coherent structural subsystem and have a distinct function. Several studies have explored the role of modularity and network organization in various protein-interaction and regulatory cellular networks (3–10). Focusing specifically on modularity in metabolic networks (which is also the subject of this article), the metabolic networks of 43 distinct organisms were shown to be organized in many small, highly connected topologic modules that hierarchically combine into larger units (11). The functional and evolutionary modularity of the human metabolic network was also investigated from a topological perspective by using network decomposition (12). The network was shown to be organized in a highly modular way into basic core metabolism modules and peripheral modules that have specialized functions and evolve at a faster rate.

Considering the evolution of modularity, two major hypotheses have been proposed: the “evolution of evolvability” and the congruence principle (13). The first posits that there is positive selection favoring modularity because it enhances evolvability by enabling evolutionary changes to take place in confined modules while preserving global cellular functions (14, 15). The second maintains that, although modularity is not directly selected for, there is nevertheless an evolutionary congruence between modularity and other directly selectable properties. Such properties may include acceleration of gene clustering due to horizontal gene transfer (HGT) (in accordance with the selfish-operon theory) (16), the minimization of pleiotropic effects (17), and adaptation to new environments (18, 19). Indeed, a recent study of 117 bacterial metabolic networks (20) has found that the level of variability of the environment in which a bacterial species resides is positively correlated with its modularity, supporting the hypothesis that environmental variability promotes modularity. Furthermore, modules formed in metabolic networks of organisms living in a variable environment were found to be more functionally coherent than modules formed in organisms living in constant environments (20).

As briefly reviewed above, several studies have focused on exploring various aspects of the modular organization of metabolic networks and understanding its evolution. Here, we perform a comprehensive study of metabolic modularity from numerous angles, tracing its evolution on a large scale. To this end, we revisit the relation between metabolic modularity and different habitats, considerably extending the number of analyzed bacterial species and the number of environmental properties examined. We go beyond environmental determinants and study the role of several topological network characteristics in modularity and the role of HGT as a putative central determinant of modularity. We further directly investigate the evolution of modularity across the tree of life. This is done by employing a phylogenetic reconstruction algorithm to infer ancestral metabolic networks in a pertaining bacterial phylogenetic tree and tracing the evolution of modularity across an evolutionary time scale. Overall, our analysis is applied to a large set of 325 reconstructed bacterial metabolic networks (of which 138 appear on the phylogenetic tree), offering insights concerning the forces that have shaped the modularity of metabolic networks since the dawn of bacterial life.

Results

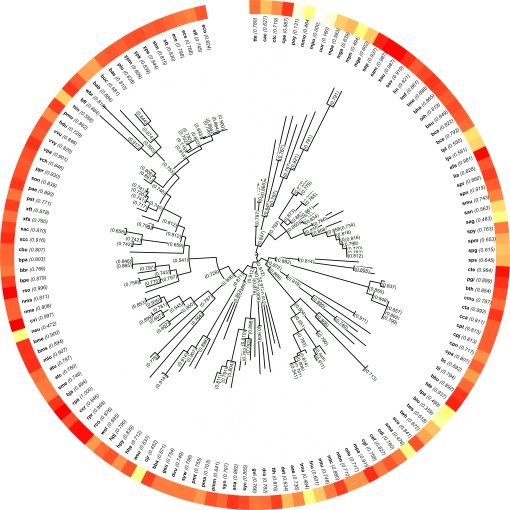
We reconstructed the metabolic networks of 325 bacteria from their genome sequences [supporting information (SI) Dataset S1], of which 138 could be placed on a well established tree of life (21) (Fig. 1). We then quantified the modularity of the network of each species by using Newman's algorithm (Methods). Subsequently, we used a phylogenetic reconstruction algorithm to infer the ancestral metabolic networks across the tree of life and quantify their modularity in a similar manner (Methods). The results of this analysis, assigning modularity scores to 138 contemporary metabolic networks and to 137 ancestral ones, are displayed in Fig. 1.

Fig. 1.

Modularity scores of bacterial metabolic networks across the tree of life of Ciccarelli et al. (21). The color scale indicates the range of modularity scores. Modularity scores are presented for both the 138 current species and 137 ancestral networks.

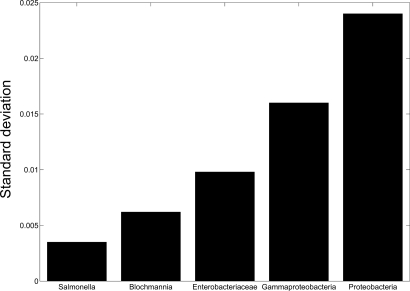
Because genetic relatedness between organisms implies a certain degree of metabolic similarity, we tested to what extent phylogenetically related organisms have similar modularity scores. The correlation between the difference in modularity scores of species and their distance across the phylogenetic tree (Methods) is 0.148 (P < 10⁻³⁰⁰, Spearman rank correlation) [comparable with the correlation of 0.1 but markedly less significant (P < 10⁻⁴), reported in ref. 20]. Given the moderate level of this overall correlation, it is instructive to examine a few specific cases, where different phylogenetic-modularity similarity patterns emerge. The class of Gammaproteobacteria demonstrates an example where modularity closely follows phylogenetic distance; different strains of Yersinia pestis have similar modularity values [perhaps reflecting their relatively recent emergence as a species <20, 000 years ago (22)]. The variation in modularity increases gradually, first within the family Enterobacteriaceae (including some highly reduced networks of obligatory endosymbionts) and then through the class of Gammaproteobacteria to the phylum Proteobacteria (Fig. 2 and Fig. S1). Obviously, habitat variability may also increase as larger classes are examined, so phylogenetic proximity probably involves both genetic and environmental similarities.

Fig. 2.

Standard deviations for modularity scores of the Proteobacteria at varying taxonomic levels: (i) Salmonella (strains of the same species); (ii) Blochmannia (species); (iii) Enterobacteriaceae (family); (iv) Gammaproteobacteria (class); (v) Proteobacteria (phylum). The variation in modularity increases gradually when extending the distance from strains of the same species to the phylum level.

Other cases, however, may involve substantial variation among strains of the same species. An interesting example involves two different strains of Bacteroides fragilis: although having metabolic networks of highly similar size and content (Dataset S1), these strains have markedly different modularity scores—strain YCH46 having a considerably larger modularity score (0.872782) than strain NCTC9343 (0.845655). Such divergence of modularity scores across closely related strains is likely to occur because of the loss of just very few central reactions, fragmenting the metabolic network and consequently altering modularity scores in a considerable manner. This hypothesis was examined by removing the three most central reactions (DNA (cytosine-5-)-methyltransferase, 5-formyltetrahydrofolate cycloligase and glutamine-fructose-6-phosphate transaminase) in Bacteroides fragilis YCH46 that are absent from B. fragilis NCTC9343. The modularity score of the network obtained after the removal of just these three central reactions of YCH46 was 0.846176, a very similar score to that of NCTC9343. The larger variance in modularity scores emanating from the loss of central reactions (compared with the loss of more peripheral reactions) was validated through simulations, where the effect of deleting reactions on network modularity was examined as a function of the centrality of these reactions (Methods and Fig. S2). Clearly, such loss of central reactions that affects major metabolic functions is probably detrimental and hence very rare. However, host-associated pathogens or commensals like B. fragilis are more likely to survive such loss because of the abundance of many metabolites in their growth environment. Reassuringly, one may note that such variation in modularity among strains is probably not just a result of varying annotation practices that bias the Kyoto Encyclopedia of Genes and Genomes (KEGG) data; this is exemplified by the genome of Agrobacterium tumefaciens that was sequenced and annotated by two independent consortia, but its different KEGG versions still show very similar modularity scores, as one would expect in this case.

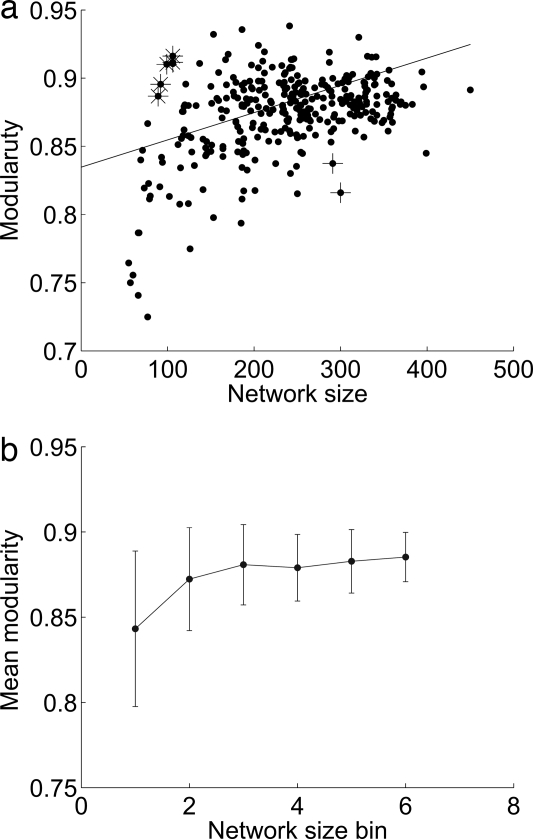
We next measured the correlation between different topological network properties and their modularity scores. One finding is an overall correlation between the size of the network (the number of enzymes it contains) and its modularity (r = 0.3151, P < 7·10⁻⁹, Spearman rank-correlation test, Fig. 3a). This test is valid because the modularity score of Newman used here is normalized for network size and is thus unbiased (23). However, this overall correlation is mainly derived from the differences between the smallest-size networks to the rest of the networks (Fig. 3b). Namely, the correlation resembles a saturation curve and networks of sizes larger than 109 nodes essentially do not differ in their modularity scores in a statistically significant manner. Additionally, we find a significant correlation between modularity and mean nodes (reactions) degree (r = 0.1223, P = 0.027, Spearman rank correlation) and between modularity and network centrality (r = 0.2079, P < 2·10⁻⁴, Spearman rank correlation). However, a partial correlation test of the contribution of these topological characteristics to modularity, given network size, results in the absence of any significant marginal contribution. In summary, there is an overall rather marked correlation between network size and modularity, but it mainly arises because of the significantly lower modularity scores of small-sized networks. Interestingly, no significant correlation was observed between bacterial growth rate (24) and modularity (r = −0.0842, P = 0.3796) despite the fact that network size is positively correlated with a faster growth rate (r = 0.3570, P < 1.25·10⁻⁴).

Fig. 3.

Modularity scores vs. network size. (a) Modularity vs. network size. Network size is measured as the number of enzymes in the network. The outliers noted by * represent very small networks that yet have high modularity scores, and the ones noted by + represent large networks that have low modularity scores. The solid line represents the linear regression curve, marking the correlation between modularity and network size. (b) Mean modularity and standard deviation as a function of network size. Each bin contains a similar number of networks (n = 54), with bin #1 including the smallest networks and bin #6 including the largest ones. The smallest networks (bin #1) have significantly smaller modularity scores than the networks in all other bins. (Wilcoxon rank sum test P values for bins 2–6 are 3.92·10⁻⁴, 2.55·10⁻⁶, 3.34·10⁻⁶, 1.37·10⁻⁷, and 1.76·10⁻⁸, correspondingly).

It is instructive to examine some of the outliers marked by an asterisk in Fig. 3a; specifically, a few species of Rickettsia and Borrelia have very small networks but high modularity scores. Although genetically very remote, these species have a shared lifestyle—they are obligate mammalian pathogens that are transmitted by parasitic insects such as fleas or ticks. This intricate life cycle requires a rapid and efficient shift between two very different environments, which probably dictated the emergence of niche-specific metabolic subsystems, increasing modularity. This may be an extreme example of the principle laid out by ref. 19, that environmental diversity promotes network modularity. Conversely, we could not find any evident common link between the outlier organisms with low modularity scores and large networks such as, e.g., the bioremediation agent Dechloromonas aromatica and the antibiotic producing Streptomyces avermitilis (marked by a plus sign in Fig. 3a).

After these specific observations, we examined the overall correlation between modularity and various environmental properties in our dataset. A recent study (20) has explored the link between modularity and environmental diversity, focusing on one environmental property (habitat diversity) in a smaller number of networks. The analysis of ref. 20 has relied on assignment of discrete environmental diversity scores to different habitats. Here, we take a different approach, analyzing different subsets of bacteria that are grouped by common habitat features (Methods). Comparisons of several habitat groups shows a statistically significant difference in their modularity scores (employing a Wilcoxon ranked-sum test). Evidently, host-associated bacteria have significantly lower modularity values than organisms in multiple (P = 0.00064), aquatic (P = 0.001), and terrestrial (P = 0.0067) environments, corresponding to the findings of ref. 20 that obligate host-associated organisms have the lowest modularity scores. This trend is probably due to the lifestyle of many of these organisms (best exemplified by the mycoplasmas)—dependence on a multitude of host-derived metabolites in different pathways, which results in smaller networks with overall lower modularity.

Interestingly, among the host-associated organisms, endosymbionts have miniscule metabolic networks (average size of 157 enzymes with mean modularity 0.8688 and SD 0.0353) but these networks are slightly more modular than those of commensals and pathogens (average size of 212 enzymes with mean modularity 0.8663 and SD 0.0177), which are more metabolically versatile (although this difference is not statistically significant). Furthermore, we find that thermophilic bacteria have significantly higher modularity scores than organisms in either mesophilic (P = 0.0495) or hyperthermophilic (P = 0.0464) environments, and facultative bacteria have lower modularity scores than aerobic bacteria (P = 0.0028) (after correcting for multiple hypotheses testing using the Bonferroni correction). However, the evolutionary forces that have shaped these differences remain unclear. Finally, we note that the genomic fraction of transporters and permeases, which may have been putatively thought to constitute a simple rough correlate of environmental diversity, does not manifest a significant correlation with network modularity.

We next examine the evolution of modularity since the last universal common ancestors of bacteria, by reconstructing the ancestral metabolic networks of the species that appear in the tree of life of (21) (Fig. 1) and computing their modularity scores (Methods). There is a significant negative correlation between the modularity scores of the ancestral networks and their distance from the root of the tree (−0.212, P < 0.0129, Spearman correlation test). Including the extant species (the leaves of the tree) in the test, results in a correlation of −0.196126 (P = 0.001). This overall trend, where ancestral modularity scores tend to be higher than those of the descendants, may be attributed to speciation and niche specialization of the organism and to the gradual addition of more peripheral metabolic pathways during evolution (25, 26). Indeed, the latter process of incremental, peripheral evolution is likely to decrease overall network modularity, as evident from the positive correlation between network centrality and modularity shown earlier.

An additional important force that has been assumed to effect the emergence of modularity in metabolic networks is HGT. HGT refers to several biological mechanisms by which one organism may transfer genetic material to another organism that is not its descendant and is a major evolutionary force in prokaryotes (27, 28). Accordingly, it has been hypothesized that HGT accelerates gene clustering and thus may potentially contribute to (and benefit from) network modularity (16). We explored the relationship between the extent of HGT and modularity using the data in ref. 29, which specifies the proportion of horizontally transferred genes in various organisms. The Spearman rank-correlation test between the extent of HGT and modularity in the 94 organisms that are included both in our dataset and in that of ref. 29 yields a correlation of r = 0.2863 (P = 0.0052). Taking into consideration that many transferred genes encode for cell-surface components and proteins of unknown function (29) that are clearly not represented in the metabolic network and that newly arrived genes may take time to adapt and integrate into existing networks (30), the magnitude of this correlation is indeed remarkable.

Discussion

Analyzing the modularity of metabolic networks of hundreds of bacterial species, we find that it is moderately concordant with organismal phylogeny along the tree of life. We also find that network size is a strong determinant of metabolic network modularity. Accordingly, endosymbiotic organisms that tend to have smaller networks have lower modularity scores than nonsymbiotic organisms. The modularity values of pathogens and commensals are generally as low or lower than those of endosymbionts. However, obligate mammalian pathogens that are transmitted by parasitic insect vectors provide a telling exception, having small networks but high modularity scores. Although some studies have found no evidence that varying environments are required for the evolution of modularity (31), our findings support the notion put forward by refs. 18–20 that the need to accommodate for different niches markedly enhances the evolution of modularity. An additional important force in the evolution of modularity is HGT, because the fraction of overall horizontally transferred genes is shown to significantly correlate with modularity scores across species, in congruence with the selfish-operon theory (16). Finally, examining the evolution of modularity across the a tree of life reveals a trend of decreasing modularity scores from ancestors to their descendants, which may result from niche specialization and the addition of peripheral metabolic pathways. This complex mixture of driving forces reinforces the notion that modularity can be thought of as a product of both the organism's past evolutionary heritage and its present adaptation to a certain lifestyle and to available niches. The determination of whether modularity is a converging vs. a genetic trait remains an open challenge.

Obviously, one should acknowledge that a study of the kind presented here suffers from a few methodological limitations. Primarily, the large scale KEGG data used is not free from noise and missing information, and the representation used lacks reactions' directionality, stoichiometry and more. However, the large scope of the data used permits a very large-scale investigation across hundreds of networks and leads to the identification of general relations that run across the data. Another potential concern may arise from the disconnected nature of the analyzed networks, a property that could affect modularity-score estimation to some extent. To this end, we repeated the analysis presented here while randomly connecting each network's components to form its closely connected analog, confirming the results reported in this article (see SI Text for details). Future studies could extend the approach presented here to investigate the modularity of metabolic networks of Archaebacteria and Eukarya to obtain a more comprehensive view of their evolution. As they become available for many species, it will be telling to explore the modularities of other kinds of biological networks like protein–protein interaction networks on an evolutionary scale. It remains to be seen whether the forces identified here in bacterial metabolic networks do play a similar or a different role in the evolution of modularity in other kinds of biological networks.

Methods

Construction of Species-Specific Metabolic Networks.

We constructed the metabolic networks of 325 bacterial organisms following the approach outlined in (32). Metabolic data were collected from KEGG (release 39, September 2006, ftp://ftp.genome.jp/pub/kegg). Parsing KEGG reactions, compounds and enzymes' data, we created a list of the existing reactions in each species in our collection, their products and substrates, and their directionality. Water, protons, and electron components were removed from the networks as in ref. 33. Highly connected metabolites that participate in >10 reactions were also removed, and reactions that have one of these compounds as their sole product or substrate were subsequently removed (analogous to the procedure used in ref. 34). A mapping associating metabolic enzymes to the reactions they catalyze was generated, based on the information in the KEGG database.

The metabolic network of each organism was generated from its list of reactions as follows: Each enzyme is represented as a node in the network. Let E₁ = {e₁¹, e₂¹, …, e_n¹} denote the set of enzymes that catalyze reaction R₁, and E₂ = {e₁², e₂², …, e_m²} denote the set of enzymes that catalyze reaction R₂. If a product of R₁ is a substrate of R₂, then edges are assigned between all nodes of E₁ and all nodes of E₂. Edges are also assigned within E₁ nodes and within E₂ nodes. Edges in the network are considered undirected. For each network, we computed the ratio between the number of metabolic enzymes and the overall number of genes in the genome of the pertaining species. Networks for which this ratio was <0.05 were considered as lacking sufficient data and were omitted from our analysis (overall 12 networks were filtered out, resulting in a total of 325 metabolic networks).

Identifying Topological Features of the Network.

For each metabolic network, we computed the network centrality measure and the mean degree of its nodes. A network's centrality is computed as follows: All pairwise shortest paths were determined, using the Floyd–Warshall algorithm (35), and for each node, its mean shortest-path distance to all other nodes in the network was computed, denoting the node's centrality. In cases where the network has more than one connected component, nodes from two different components are assumed to have a distance of twice the maximal distance obtained within the components. The node with the smallest mean shortest distance is considered the most central node, and its mean distance is defined as the network's centrality.

Computing Network Modularity.

The modularity score of each metabolic network is computed by using the algorithm presented in ref. 23. Newman's algorithm partitions the network into modules such that the number of edges between modules is significantly less than expected by chance. The algorithm provides a mathematical measure for modularity with network-size normalized values, ranging from 0 (low modularity) to 1 (maximum modularity). The use of Newman's algorithm provides a size-invariant modularity measure and thus enables us to study the role of network size on modularity as an independent, interesting topological variable [this is different from Parter et al. (20), which used a modified measure and examined equal size networks].

Characterizing Bacterial Environments.

We first used the number of transporter genes in a species' genome as a rough correlate of the diversity of the environment in which it resides. The number of transporter genes was computed by counting the number of appearances of the words “transporter” and “permease” in the pertinent.ent file of each organism in the KEGG database, describing the organism's genomic data: gene numbers, names, functional description, orthology, position, etc. A second, more refined characterization of the environment of each species was obtained from the prokaryotic attributes table of the National Center for Biotechnology Information Genome Project (www.ncbi.nlm.nih.gov/genomes/lproks.cgi). For each organism, we obtained four features: salinity, oxygen requirements, habitat, and temperature range. Each of these features is defined by discrete categories as follows: salinity: nonhalophilic, mesophilic, moderate halophile, or extreme halophile; oxygen requirements: aerobic, microaerophilic, facultative, or anaerobic; temperature range: cryophilic, psychrophilic, mesophilic, thermophilic, or hyper thermophilic; habitat: host-associated, aquatic, terrestrial, specialized, or multiple. This four-feature description of each organism's environment was then used to search for specific environmental characteristics that may influence metabolic modularity.

Phylogenetic Analysis and Reconstruction of Ancestral Metabolic Networks.

The tree of life generated in ref. 21 was used to identify the phylogenetic relations between the species studied in our analysis and for inferring ancestral metabolic networks along the tree. This tree includes a relatively large number of species, covering most of the taxonomic groups for which metabolic data are available. Specifically, this tree was used to measure the distance of each extant and ancestral species to the last universal common ancestors of bacteria and to calculate the species pairwise phylogenetic distances (measured as the sum of distances from the two species to their last common ancestor). The phylogenetic reconstruction part of our analysis was restricted to bacterial species that could be matched to those included in the reference tree, resulting in a total of 138 species. Using the presence/absence pattern of each enzyme across extant species and employing Fitch's small-parsimony algorithm to determine the presence/absence of each enzyme in every internal node (36), the ancestral metabolic networks (corresponding to internal nodes in the tree) were reconstructed.