Drug resistance in HIV-1 protease: Flexibility-assisted mechanism of compensatory mutations

Abstract

The emergence of drug-resistant variants is a serious side effect associated with acquired immune deficiency syndrome therapies based on inhibition of human immunodeficiency virus type 1 protease (HIV-1 PR). In these variants, compensatory mutations, usually located far from the active site, are able to affect the enzymatic activity via molecular mechanisms that have been related to differences in the conformational flexibility, although the detailed mechanistic aspects have not been clarified so far. Here, we perform multinanosecond molecular dynamics simulations on L63P HIV-1 PR, corresponding to the wild type, and one of its most frequently occurring compensatory mutations, M46I, complexed with the substrate and an enzymatic intermediate. The quality of the calculations is established by comparison with the available nuclear magnetic resonance data. Our calculations indicate that the dynamical fluctuations of the mutated enzyme differ from those in the wild type. These differences in the dynamic properties of the adducts with the substrate and with the gem-diol intermediate might be directly related to variations in the enzymatic activity and therefore offer an explanation of the observed changes in catalytic rate between wild type and mutated enzyme. We anticipate that this "flexibility-assisted" mechanism might be effective in the vast majority of compensatory mutations, which do not change the electrostatic properties of the enzyme.

The aspartyl protease from the human immunodeficiency virus type 1 (HIV-1 PR) is an enzyme essential for the viral metabolism (Wlodawer and Vondrasek 1998). Some of its inhibitors constitute the most powerful anti-acquired immune deficiency syndrome (AIDS) drugs and have been used in the clinics for several years. Unfortunately, the long-term efficiency of these antiviral agents is severely limited by the emergence of viral variants that display cross-resistance against HIV-1 PR inhibitors (Erickson and Burt 1996; Gulnik et al. 2000; Young and Kuritzkes 2001) (Fig. 1 ▶). Apparently, these variants are able to evolve resistance by complementary strategies: several active-site (Fig. 1 ▶, red) and nonactive-site (Fig.1 ▶, green) mutations reduce the affinity for both drugs and substrates. This may be achieved by disrupting favorable drug-protease interactions (Chen et al. 1995; Markowitz et al. 1995; Schaffer and Verkhivker 1998; Tawa et al. 1998; Mahalingam et al. 1999,2001; Rosin et al. 1999; Hong et al. 2000; Wang and Kollman 2001). In contrast, "compensatory mutations" (Fig. 1 ▶, blue) are able to enhance the protease activity that is decreased by the active-site mutations (Gulnik et al. 2000).

Fig. 1.

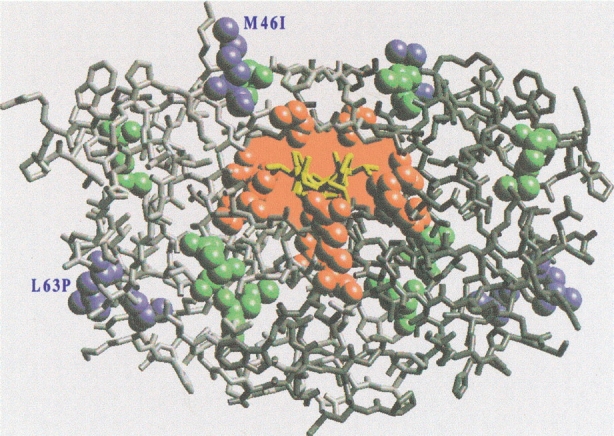
Inhibitor binding and drug resistance in human immunodeficiency virus type 1 protease (HIV-1 PR). The figure shows the complex between the protease (gray) and the A79285 inhibitor (yellow) (Wlodawer and Erickson 1993). The five U.S. Food and Drug Administration (FDA)-approved inhibitors for clinical use (saquinavir, indinavir, ritonavir, nelfinavir, and amprenavir) bind, like A79285, in the active site cavity (red) so as to compete with peptide substrate binding (Wlodawer and Erickson 1993). The figure also displays selected residues undergoing mutations associated with viral resistance to the FDA-approved drugs. Active-site mutations (red spheres) are located in direct contact with the protease inhibitors such as to disrupt favorable drug-enzyme interactions. Other mutations (green) are often located in close proximity of the active site and influence the energetics of binding through second-order effects. Compensatory mutations (blue) are located away from the active site and their role usually cannot be inferred from structural studies. M46I is a very common mutation associated with compensatory cross-resistance against four of the FDA-approved drugs (Condra et al. 1996; Mammano et al. 2000; Young and Kuritzkes 2001) and in combination with L63P, is found to increase the catalytic activity by 110–530% in a large wealth of diverse substrates (Pazhanisamy et al. 1996; Schock et al. 1996; Mahalingam et al. 1999). As other variants exhibiting compensatory resistance (L63P, I47V, A71T), this mutation is located away from the active site and does not involve charged residues.

The way these variants exert their catalytic role is not fully understood. Compensatory mutations are usually located away from the active site and do not involve charged residues. Thus, they cannot influence the enzymatic reactivity through long-range electrostatic interactions (Warshel 1978) and in fact they appear to have little effect on substrate and inhibitor binding (Pazhanisamy et al. 1996; Schock et al. 1996). Intriguingly, they also lead to only minor geometric rearrangements that cannot account for the marked increase in catalytic activity (Chen et al. 1995; Schock et al. 1996; Ridky et al. 1998).

In the last years, several laboratories have pointed to the difference in conformational flexibility between wild type and mutants as a possible key factor for the catalytic activity (Chen et al. 1995; Gulnik et al. 2000). This proposal is corroborated by X-ray crystallography and theoretical data. In fact, in the structures solved so far that contain compensatory mutations (K45I [Mahalingam et al. 2001], M46I [Chen et al. 1995], L90M [Hong et al. 2000]), the mutated enzymes turn out to be less flexible as indicated by lower B factors. The motion of the flap tips in the free HIV-1 PR has also been investigated with nuclear magnetic resonance (NMR) (Ishima et al. 1999; Freedberg et al. 2002) and molecular dynamics simulation (Scott and Schiffer 2000). These studies indicate that the flaps are highly mobile and can adopt a large number of conformations on the ns to ms timescale, thus suggesting that mutations in the flaps can be very important for the kinetics of substrate and inhibitor binding. A classical molecular dynamics (MD) study on wild type and M46I variant free enzyme, arguably the most common and representative compensatory mutation (Ho et al. 1994) (Fig. 1 ▶), has indicated that the two systems differ in their flexibility and, in particular, that this mutation appears to stabilize the closed conformation of the flaps (Collins et al. 1995). However, the M46I mutation appears to have little effect on the HIV-1 PR affinity for most of the inhibitors (Pazhanisamy et al. 1996; Schock et al. 1996), thus indicating that other factors, besides the binding affinity must play a role in this kind of mutation.

Our recent quantum chemical and MD calculations on the complex between L63P HIV-1 PR³ and a peptide substrate (SUB) have indicated that the overall flexibility of the enzyme/substrate complex is an essential ingredient for the enzymatic function (Piana et al. 2002). Specifically, large-scale motions of the enzyme have been found to be essential to drive the substrate in an appropriate position in which the catalytic cleavage can occur (Piana et al. 2002). Similar conclusions have been drawn for other enzymatic systems (Lau and Bruice 2000; Radkiewicz and Brooks 2000). This has led to the suggestion that conformational flexibility might play a role not only in substrate or inhibitor binding, but also for the increase in catalytic efficiency.

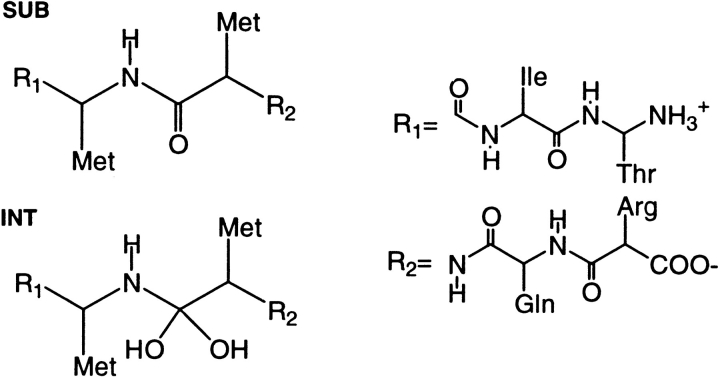
Here, we have used multi-ns MD on complexes of L63P enzyme (which can be considered as a representative of the wild type enzyme³) and the double mutant M46I-L63P to shed light on this issue. Specifically, we have prolonged our simulation of the L63P/SUB complex to 11 ns and performed simulations on the same time scale for the complex between L63P-M46I HIV-1 PR and SUB as well as with the corresponding gem-diol intermediate (INT) of the catalytic cycle (Hyland et al. 1991) (Chart 1 ▶).

Chart 1.

Our calculations suggest that while the MD-averaged structures of L63P/SUB and M46I-L63P/SUB turn out to be very similar, their flexibility differs distinctly, especially in the flap and substrate regions. Furthermore, the M46I mutation induces a displacement of the reaction intermediate toward the active site. This demonstrates that relatively small local changes in the protein structure can lead to alterations of the dynamical properties, which are intimately linked to the enzymatic activity (Piana et al. 2002). Both the induced change in substrate flexibility and intermediate conformation may account for the difference in catalytic rates between the two forms of the enzyme.

Results and Discussion

Structural features

The structures of all the complexes investigated here (L63P/SUB, L63P/INT, L63P-M46I/SUB, and L63P-M46I/INT) were stable over the time scale investigated (7–16 ns), as indicated by the small values of the root mean square deviation (rmsd) of the backbone atoms with respect to the starting structure (rmsd ∼1.0–1.4 Å) (Fig. 1 ▶SI of Supplemental Material). A comparison of the MD-averaged structures of the four complexes (Fig. 2S and 2 ▶SI of Supplemental Material) further confirms that the overall folding is well maintained in the four systems.

Fig. 2.

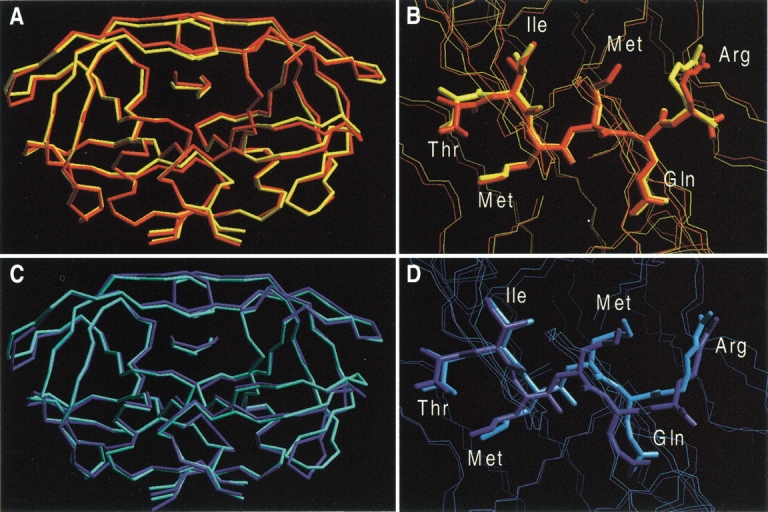
MD-averaged structures: Wild type/SUB complex (red); M46I PR/SUB complex (yellow); wild type/INT complex (blue); M46I/INT complex (cyan). (A) Wild type/SUB complexes and (B) active-site region. (C) Wild type/INT complexes and (D) active-site region. In A and C, only the backbone Cα, C, and N atoms are shown for clarity. Note the different binding modes adopted by Gln P2' in (C).

Overall, the four adducts share similar structural features. The largest differences between initial and MD-averaged structures of the four complexes are observed in the most flexible protein regions [residues 1(1')–4(4'), 16(16')– 18(18') 38(38')–42(42') and 68(68')–71(71')] and in the flap tips [residues 48(48')–51(51')]. In particular, the MD-averaged structural properties around site 46 are rather similar (see Table 1 and Table 2SI of Supplemental Material). This result is in line with previous MD calculations (Harte et al. 1992; Luo et al. 1998) and with experimental data (Chen et al. 1995).

Table 1.

Molecular dynamics-averaged values (degrees) of selected dihedral angles relative to residue 46(46')

Dihedral angle		WT/SUB	M46I/SUB	WT/INT	M46I/INT
46	φ	−127 (16)	−134 (10)	−128 (19)	−132 (12)
	ξ	134 (17)	135 (11)	145 (12)	139 (9)
46'	φ	−130 (13)	−133 (13)	−133 (12)	−135 (11)
	ξ	139 (15)	135 (13)	143 (11)	141 (9)
Cβ46-Cα46-N46-C45		110 (17)	99 (10)	107 (20)	102 (12)
Cβ46-Cα46-C46-N45		−104 (17)	−100 (11)	−91 (13)	−97 (9)
Cβ46'-Cα46'-N46'-C45'		107 (13)	99 (13)	104 (13)	99 (11)
Cβ46'-Cα46'-C46'-N45'		−99 (15)	−100 (12)	−95 (11)	−94 (9)

φ = C-N-Cα-C; ξ = N-Cα-C-N. Standard deviations are reported in parenthesis.

Table 2.

Hydrogen bonds between SUB (or INT) and HIV-1 PR

	Presence of the interaction (%)
Substrate-protein hydrogen bonds	4HVP	WT/SUB	M46I/SUB	WT/INT	M46I/INT
N-H1,2,3(P3). . .Oδ1,2(48)	100	30	100	99	100
N-H(29). . .O(P3)	100	27	95	97	100
N-H(P2). . .O(48)	100	100	99	93	100
O-H(wat_b). . .O(P2)	100	99	100	100	99
N-H(P1). . .O(27)	100	1	3	39	27
O-H(wat_b). . .O(P1')	100	98	99	100	99
N-H(P2'). . .O(27')	100	84	89	12	95
Nɛ-Hɛ1(P2'). . .O(30')	0	100	100	99	94
N-H(29'). . .Oɛ(P2')	0	81	90	25	79
N-H(P3'). . .O(48')	100	95	79	99	99
N-H(48). . .O1,2(P3')	0	9	20	100	100

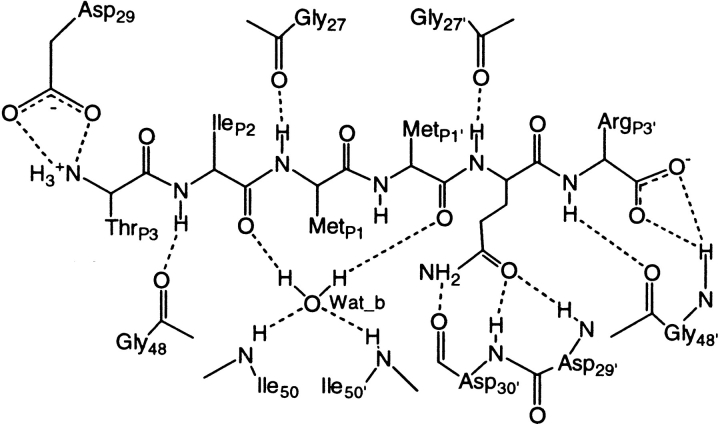
Labeling as in Chart 2 ▶. In the Table, the A-H. . .B H-bond is present at each step of the dynamics if d(H. . .A) < 3.0 Å and |nj(B-H. . .A) < 120°. 4HVP is the crystal structure of HIV-1 PR complexed with MVT101 (Miller et al. 1989). The overall agreement is fairly good, as most of the H-bonds present in the crystal structure are maintained in the molecular dynamics simulations. The few exceptions (presence < 50%) that are marked in bold face, are located at the cleavage site region. The largest discrepancy, which involves N-H_(P2'). . .O_(27'), could be a consequence of the structural differences between the MVT101 inhibitor (Miller et al. 1989) and SUB/INT (Rose et al. 1996). Other significant discrepancies are found for the two hydrogen bonds that restrain the P3 terminal substrate in wild type/SUB, indicating a large flexibility of this residue (Fig. 4B ▶) and for the two hydrogen bonds at the P2' site in wild type/INT. In this case, the side chain of GlnP2' adopts a different binding mode and there does not seem to be a large effect on the INT flexibility at the P2' site (Fig. 4C ▶).

Most of the hydrogen-bond interactions between SUB (or INT) and HIV-1 PR are maintained during the four simulations (Table 2); the few hydrogen bonds that are lost are located between SUB (or INT) and the cleavage site region. Interestingly, two different binding modes are observed for the side chain of Gln P2' (Fig. 2B,D), a residue that is important for HIV-1 PR activity (Poorman et al. 1991; Polgár et al. 1994; Szeltner and Polgár 1996). In the L63P/INT simulation the binding is the same as in the crystal structure; in the other three simulations the Oɛ of Gln P2' is hydrogen bonded to the backbone amide nitrogen of Asp 29'.

Finally, we note that the hydrogen bonds in the loops region are mostly preserved, although occasional local unfolding events are observed in the glycine-rich tip of the flap region (residues 49–52) (Table 1SI of Supplemental Material).

We conclude that the structural differences between L63P and the L63P-M46I MD-averaged structures are small. This agrees with a structural study on the M46I-L63P-V82T-I84V quadruple mutant (Chen et al. 1995), which is found to exhibit only a minor rearrangement of the flaps relative to wild type.

Dynamics: Local fluctuations

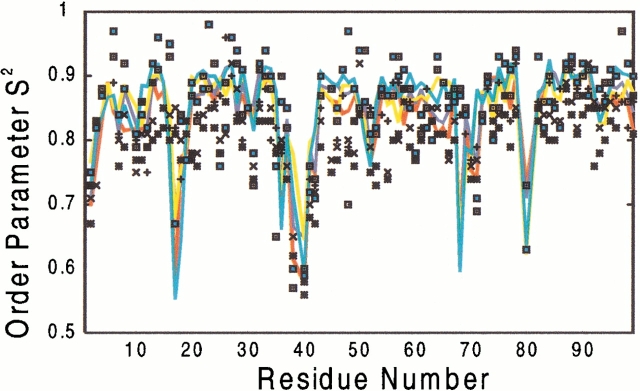
We now turn our attention to the flexibility of the protein, which is the main focus of this work. The conformational fluctuations of the adducts in the sub-ns time scale can be described in terms of generalized order parameters S² for which direct contact with NMR data (Lipari and Szabo 1982a) can be made (Lipari and Szabo 1982b; Luo et al. 1998). The calculated values (Fig. 3 ▶) turn out to be very similar in the four systems and are in excellent agreement with the available experimental data (Nicholson et al. 1995; Tjandra et al. 1996; Freedberg et al. 1998). The only residue that systematically exhibits large deviations is Gly 68(68') whose calculated order parameter (0.6) is much lower than the experimental values (0.85–0.9). This discrepancy might arise from the fact that Gly68(68') is part of the 68(68')–71(71') mobile loop. Indeed, this loop encompasses the solvent-exposed His69(69') which is very likely to be affected by proton exchange at the imidazole ring on time scales longer than the one simulated here. This proton exchange, which cannot be accounted for in our MD simulations, could influence the dynamics of the adjacent Gly 68 residue giving rise to the discrepancy in the order parameters.

Fig. 3.

Calculated generalized-order parameters (S²)(Lipari and Szabo 1982a,b) for the backbone amide groups. Wild type/SUB complex (red); M46I/SUB complex (yellow); wild type/INT complex (blue); M46I/INT complex (cyan). The experimental values measured for wild type complexed with KNI272 (Freedberg et al. 1998), P9941 (Nicholson et al. 1995), DMP323 (at 300Mhz)(Nicholson et al. 1995), DMP323 (2) (at 600Mhz) (Nicholson et al. 1995; Tjandra et al. 1996) inhibitors are represented as `+', `□', `x', `*', `▪', respectively. Only one of the two monomers is shown for clarity, the other monomer shares very similar patterns.

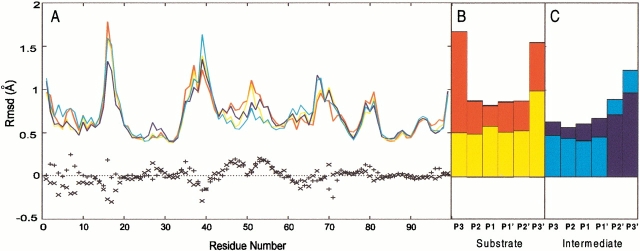
Further information about the local mobility of the protein can be obtained by a plot of the rmsd for each residue with respect to the MD-averaged structure (Fig. 4A–C ▶). In all four systems, the largest flexibility is observed in the regions characterized by the presence of one or more residues with a low order parameter (residues 16–18, 37–42, 68–71, and 78–82 in Fig. 3 and 4A ▶ ▶) (Nicholson et al. 1995; Tjandra et al. 1996; Freedberg et al. 1998), which mostly correspond to the protein loops. This result is in agreement with a recent study (Zoete et al. 2002) where 73 crystal structures of HIV-1 PR are compared; based on the differences in the crystal structures in combination with MD results, the authors conclude that these are the regions of largest flexibility.

Fig. 4.

Average root mean square deviation (rmsd) calculated on each residue of the protein (A), peptide substrate (SUB) (B), gem-diol intermediate (INT) (C) relative to the average molecular dynamics structure: Wild type/SUB complex (red); M46I/SUB complex (yellow); wild type/INT complex (blue); M46I/INT complex (cyan). The difference between the value calculated for the wild type and the M46I enzyme is reported as `+' for the human immunodeficiency virus type 1 protease (HIV-1 PR)/SUB complexes and as `x' for the HIV-1 PR/INT complexes.

The flap regions at the active site [the so-called "flap tips", corresponding to residues 45(45')–55(55')] are more mobile in the complexes with SUB than in those with INT. The difference is not surprising as this region is in close contact with the ligand and its conformation clearly influences binding (Baca and Kent 1993; Prabu-Jeyabalan et al. 2000). Indeed, in this area large differences are observed in the S² values for HIV-1 PR bound to different inhibitors (Nicholson et al. 1995; Freedberg et al.1998) and for the residues of the two HIV-1 PR subunits in presence of an asymmetric inhibitor (Freedberg et al. 1998).

Differences in flexibility are also observed between L63P and the L63P-M46I mutant in complex with either SUB or INT (Fig. 4A ▶). The flap elbows (residue 38–42) turn out to be more flexible in the double mutant. However, the rest of the flaps (residues 45–49 and 52–57), as well as SUB/INT (Fig. 4B,C ▶), are more flexible in the L63P enzyme. Accordingly, although the average conformation of residue 46(46') is very much the same in the four simulations (Table 1 and 2SI), the standard deviations of the torsional angles clearly indicate that SUB is more flexible than INT and L63P is more flexible than M46I-L63P. All these findings are in line with previous MD calculations of the free M46I enzyme in vacuum (Collins et al. 1995), which indicated that the M46I mutation strongly influences the dynamics of flap opening.

Thus, we conclude that the M46I mutation induces mostly a lower flexibility, although the MD-averaged structural properties are similar.

Dynamics: Large-scale motions

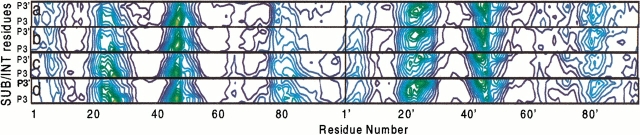
The overall flexibility of the system can be further analyzed in terms of correlations between the substrate and the protein motions (Fig. 5a–d ▶) (Harte et al. 1992; Radkiewicz and Brooks 2000; Piana et al. 2002). The corresponding dynamic cross-correlation matrix indicates that in all four systems the substrate motions are tightly coupled to fluctuations in the tip of the flaps (residue 48–51) and in the cleavage site (residues 25–30) (Fig. 5a–d ▶). This is consistent with the H-bond pattern described in Table 2, which shows that the hydrogen bonds between SUB (or INT) and the loops are fully maintained. To a lesser extent, motions of the substrate appear to be correlated with the 78–85 loop, which is crucial for substrate selectivity (Stebbins et al. 1997) and drug resistance (Gulnik et al. 2000).

Fig. 5.

Dynamic cross correlation matrix between the protein and peptide substrate (SUB) (or gem-diol intermediate [INT]). (a) Wild type/SUB; (b) MUT/SUB; (c) wild type/INT; (d) MUT/INT. The maps have been calculated for the Cα atoms from the molecular dynamics simulation. Coloring goes from red (+1) to green (+0.4) to blue (<−0.1). The map elements range between ±1. A value >+0.5 reflects a high correlation between the motions of a pair of Cα atoms.

Implications for the enzymatic activity and substrate selectivity

Our MD simulations of the enzyme/substrate and enzyme/intermediate complexes in aqueous solution have provided evidence for the lower conformational flexibility of the double mutant. This finding is in line with previous calculations of the free enzyme in vacuo (Collins et al. 1995) and with X-ray data (Miller et al. 1989).

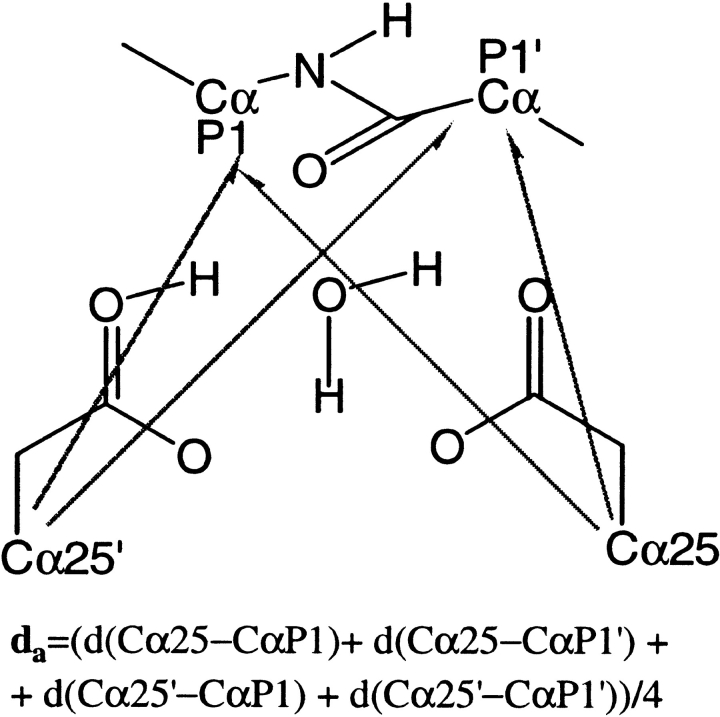
In this section, we attempt to relate the different dynamical properties of the ligand (either SUB or INT, Scheme 1) to the two steps of the enzymatic mechanism, namely the formation of INT and the subsequent cleavage of the C-N bond (Scheme 1). Previously, we have shown that the substrate/enzyme distance d_a (Scheme 3) is an appropriate reaction coordinate for the first step of the enzymatic reaction (Piana et al. 2002). In particular, the reactive wild type/SUB conformations have been shown to be characterized by short d_a values of d_a<d_min ∼7.5.

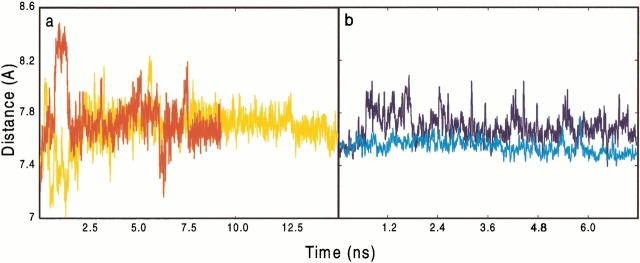
A plot of d_a as a function of time in both L63P and L63P-M46I/SUB complexes is presented in Fig. 6a ▶. The L63P HIV-PR samples often-reactive conformations (as defined by a critical distance d_a<7.5Å) for short times. However, in the mutant MD simulation d_a samples once a critical state for a long time. Such an event is observed only once in the simulation and could be an artifact because of the limited statistics. However, analysis of the d_a distance distribution indicates that while the average d_a in L63P (7.91 Å) and in the double mutant (7.89 Å) are very similar, because of the difference in flexibility, the standard deviation of the double mutant (0.20 Å) is smaller than that of the L63P enzyme (0.24 Å). The same difference in flexibility is obtained if only the first or second half of the simulations is considered (Table 3SI). We conclude that within the limits of the short timescale investigated, which is several orders of magnitude smaller than that relevant for the biological catalysis, the simulations indicate that substrate flexibility and sampling of the reactive conformation in the two cases could be different. The high sensitivity of the reaction free energy barrier on d_a (Piana et al. 2002), strongly suggests that even small differences in the probability distribution of d_a could account for the differences in catalytic activity between L63P and the double mutant (Schock et al. 1996).

Fig. 6.

Peptide substrate (SUB)- and gem-diol intermediate (INT)-Asp dyad distance (d_a) plotted as a function of time. (a) d_a for L63P/SUB (red); M46I-L63P/SUB (yellow). (b) d_a for L63P/INT (blue); M46I-L63P/INT (cyan).

Figure 6b ▶ shows the analogous plot for the adducts with INT. As for the substrate complex, the fluctuations of d_a are larger in L63P, consistent with the larger flexibility of L63P (Fig. 4B,C ▶). However, in this case INT is closer to the active site in the M46I-L63P mutant simulations (average d_a 7.5 Å) with respect to L63P (7.7 Å). The differences in structural and dynamical properties of INT at the active site might also be related to its reactivity. However, the direct implication of differences in INT flexibility and conformation on the catalytic activity has not yet firmly been established through a detailed quantum-mechanical study.

Such a flexibility-assisted catalysis mechanism may also provide a rationale for the strikingly different behavior of protease/peptide adducts. Indeed, peptides with similar affinity have been found to either act as inhibitors (Kotler et al. 1988) or to be hydrolyzed via rate-limiting chemical or physical steps (Polgár et al. 1994; Szeltner and Polgár 1996). This is rather surprising as the chemical characteristics of the peptide bond are expected to be very similar in all cases; therefore, HIV-1 PR-bound peptides might be expected to be cleaved in a similar way. In terms of the flexibility-assisted mechanism presented here, some peptides will form adducts with the protease which might not sample "reactive conformations" because of their particular flexibility properties and thus these ligands will act as inhibitors. Other peptide/protease adducts will easily achieve the proper conformation for cleavage and the rate-limiting step in these cases will be imposed by the chemical catalysis reaction itself. Finally, a third class of peptides will sample "reactive conformations" less often and eventually, achieving the proper conformation, will become rate limiting (i.e., a "physical" step).

Conclusions

We have presented multi-ns MD simulations on adducts between HIV-1 PR with the model substrate SUB (10–16 ns) and INT (7 ns).

Our calculations suggest that the small chemical changes in going from L63P to M46I-L63P, while not modifying the global structure of the complexes, can induce subtle differences in the dynamics of the protein (especially the flaps) and of the substrate itself. Most interestingly for the present discussion, the M46I mutation strongly affects the overall flexibility of the flaps that induce corresponding changes in the dynamic properties of SUB/INT.

The changes in conformational flexibility in the substrate complexes may play an important role for the enzymatic activity. Indeed, as this motion is crucial for modulating the activation free energy of the reaction (Piana et al. 2002), we propose that the difference in substrate mobility on passing from wild type to M46I is a crucial ingredient for the observed increase of k_cat upon mutation (Schock et al. 1996). This `flexibility-assisted catalysis' mechanism might also be effective in other compensatory mutations not involving charged residues (Fig. 1 ▶) and may provide a rationale for the different fate of adducts between the protease and a variety of peptides with similar affinity.

Materials and methods

The structural model of wild type/SUB (SUB = Thr-Ile-Met-Met-Gln-Arg) was built from the X-ray structure of HIV-1 PR complexed with MVT101 (Miller et al. 1989; Hyland et al. 1991) (entry 4HVP in the Protein Data Bank [PDB] [Berman et al. 2000]). This structure contains the L63P mutation. This mutation is a common polymorphism of HIV-1 PR and does not affect the viral fit (Martinez-Picado et al. 2000). The choice of SUB is based on the following facts: (i) its sequence corresponds to a natural cleavage site for HIV-1 PR (the so-called p2/NC site) (Ratner et al. 1985); (ii) kinetic measurements for cleavage of this substrate by the wild type and the L63P-M46I double mutant are available (Pazhanisamy et al. 1996; Schock et al. 1996). The complexes L63P-M46I/SUB, L63P-M46I/INT, and L63P/INT were constructed from the wild type/SUB equilibrated structure (see below). The M46I mutant was obtained by replacing the Met 46(46') side chain with Ile. The gem-diol INT (Piana et al. 2002) was obtained by replacing the carbonyl group of the P1-P1' peptide bond with the gem-diol group −C(OH)₂. In the INT complexes, the catalytic water molecule present in the SUB complexes, was eliminated and Asp25 was protonated (Piana et al. 2002). Note that the total number of atoms does not change in going from SUB to INT as the atoms that constitute the catalytic water molecule in the SUB complex are part of the gem-diol in the INT complex. Bond, angle, torsion, and Lennard-Johnes parameters for the gem-diol were derived from the AMBER force field (Cornell et al. 1995) as they were consistent with the ab-initio MD simulation of the active site of HIV-1 PR complexed with a gem-diol reaction INT (Piana et al. 2002). ESP charges for the INT nonstandard atoms were calculated as average from 10 snapshots of the ab-initio MD simulation of the gem-diol INT (Piana et al. 2002). Values of the charges for C, O, Ho, N, and Hn are 0.490, −0.550, 0.310, −0.463, and 0.252, respectively.

Protein residues belonging to subunit 1 were numbered from 1 to 99 and those belonging to subunit 2 from 1' to 99'. Substrate residues binding to subunit 1 (2) were numbered from P1 (P1') to P3 (P3') (Berger and Schechter 1970): Thr (P3)-Ile (P2)-Met (P1)-Met (P1')-Gln (P2')-Arg (P3'). Thus, the peptide bond to be cleaved by the enzyme belongs to residues P1 and P1' (Met-Met).

The HIV-1 PR/SUB complex was immersed in a 66.8 × 55.2 × 43.0 ų box containing 4170 water molecules. The positive charge of the HIV-1 PR peptide complex (+5) was neutralized by adding five chloride ions close to five positively charged groups not involved in salt bridges in the crystal structure of the enzyme. The total system was composed of 15,749 atoms.

The classical MD simulations were carried out using the AMBER suite of programs (Case et al. 1997). The force-field parameters of the protein, SUB and Cl⁻ were those of the AMBER force field (Cornell et al. 1995) whereas for water the TIP3P model was used.

Electrostatic interactions were calculated with the Ewald particle mesh method, using a 64 × 54 × 45 grid (Darden and York 1993; Essman et al. 1995; Weerasinghe et al. 1995; Duan and Killman 1999) and a cubic interpolation between the points. The motion of the center of mass was removed every 30 ps. Constant temperature and pressure conditions were achieved by coupling the system to a Berendsen's thermostat and barostat (Berendsen et al. 1984) with a relaxation time of 2.0 ps. Bonds involving hydrogen atoms were constrained to their equilibrium position with the SHAKE algorithm. The time step was 1.5 fs.

The system was heated to 150 K in 15 ps, then to 300 K in 15 ps. Subsequently, 1200 ps of equilibration at 300 K were carried out. Following Liu et al. 1996, we imposed position restraints in the cleavage site during the first 700 ps of the equilibration phase. Specifically we restrained the position of the Asp dyad with a harmonic restraint of 1.0 kcal Mol⁻¹ Ų and the HN_(Gly27,27') −O_(MetP1,P2') H-bonds (see Chart 2 ▶) with one of 0.5 kcal Mol⁻¹ Ų centered at 2.3 Å. These H-bonds are conserved in the complexes of HIV-1 PR with peptido-mimetic inhibitors for which the X-ray structure has been determined. On the other hand, previous MD studies reported difficulties in maintaining them (Liu et al. 1996). After 700 ps, these constraints were released and 500 ps of further equilibration were carried out.

Chart 2.

The simulations of L63P/SUB were performed for 11.2 ns at 300 K and 1 Atm. The last 10 ns were collected for analysis. The MD structure obtained after 1.2 ns of equilibration was used as a starting point to build L63P/INT, L63P-M46I/SUB, and L63P-M46I/INT. The structures were equilibrated by carrying out 15 ps of NPT MD simulation at 150 K and 1 Atm, followed by further 100 ps of NPT MD simulation at 300 K. The last 16, 7, and 7 ns, respectively, were collected for analysis.

Generalized order parameters (S²) were calculated according to the model-free formulation of Lipari and Szabo (Lipari and Szabo 1982a,b). The order parameters were calculated as MD averages calculated on windows of 100 ps taken along the entire trajectory.

The dynamical cross-correlation matrix C_ij of the Cα atoms i and j was calculated as (Harte et al. 1990):

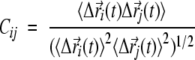where 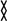denotes an MD-averaged quantity and the instantaneous displacement from the average MD position of atom i during a given time step. C_ij varies from −1.0 for completely anticorrelated motions to 1.0 for completely correlated motions.

Convergence of the residue rmsd and NMR order parameters were assessed by calculating these properties on different segments of the L63P-M46I/SUB simulation. The results of these control calculations are presented in the supplementary information and indicate that the residue rmsds converge on the 1 ns time scale, while a longer sampling (>5 ns) is required to achieve convergence of the NMR order parameters.

The SUB/INT-active site distance (d_a) was defined as the average distance (measured on the four Cαs) between the Asp dyad and the methionine residues of SUB/INT (Piana et al. 2002) (see Chart 3 ▶):

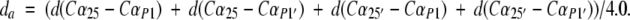Chart 3.

Electronic supplemental material

Supplemental materials are provided as Microsoft Word 97 file. Filename: suppmat.doc. They include: a table of selected distances in the loop region; a table of the loop dihedral angles; a table of the average d_a calculated for different parts of the simulation; a plot of the rmsd as a function of time in the four complexes; a picture of the average MD structure of the four complexes; a plot of the residue rmsd convergence as a function of the simulation time; a plot of the S² order parameters convergence as a function of time.