Signal processing by the HOG MAP kinase pathway

Abstract

Signaling pathways relay information about changes in the external environment so that cells can respond appropriately. How much information a pathway can carry depends on its bandwidth. We designed a microfluidic device to reliably change the environment of single cells over a range of frequencies. Using this device, we measured the bandwidth of the Saccharomyces cerevisiae signaling pathway that responds to high osmolarity. This prototypical pathway, the HOG pathway, is shown to act as a low-pass filter, integrating the signal when it changes rapidly and following it faithfully when it changes more slowly. We study the dependence of the pathway's bandwidth on its architecture. We measure previously unknown bounds on all of the in vivo reaction rates acting in this pathway. We find that the two-component Ssk1 branch of this pathway is capable of fast signal integration, whereas the kinase Ste11 branch is not. Our experimental techniques can be applied to other signaling pathways, allowing the measurement of their in vivo kinetics and the quantification of their information capacity.

For a signaling pathway to carry accurate information about its environment, the output of the pathway must closely follow the input. Pathways measuring stimuli that change more rapidly with time need to carry more information. The information capacity of a pathway, i.e., how much information can be transmitted through the pathway per unit time, is proportional to the bandwidth of the pathway (1). The larger the bandwidth of a signaling pathway, the shorter its response time and the more accurately it can follow a rapidly varying signal. Bandwidth measurements are routinely used to characterize communications systems. In this article, we present an experimental technique combined with a microfluidic device that allows measurement of signaling-pathway bandwidth. We use this technique to measure the in vivo bandwidth of the hyperosmolar signaling pathway (HOG) in the yeast Saccharomyces cerevisiae (Fig. 1A).

Fig. 1.

Analysis of a model pathway and the hyperosmolar response pathway in S. cerevisiae. (A) The hyperosmolar glycerol response HOG pathway consists of two input branches. The SLN1 phosphorelay represses the kinase Ssk1 under osmotically neutral conditions. Hyperosmotic stress results in deactivation of Sln1. The subsequent derepression of Ssk1 allows Ssk1 to activate the MAPKKKs Ssk2 and Ssk22, which in turn phosphorylate Pbs2. The SHO1 branch activates Pbs2 through the MAPKK Ste11. Activation of Hog1 by Pbs2 leads to its nuclear localization and a hyperosmolar transcriptional response. (B) A model three-level branched signaling cascade with both X*₁ and X′*₁ activating X₂, which in turn activates X₃. Each level of the cascade activates the next through phosphorylation consuming one molecule of ATP. (C) The steady-state level of X*₃ is plotted as a function of time. For an input oscillating slowly, the level of X*₃ (in red) oscillates between zero and a maximum value, following the input in time. For an input oscillating rapidly, the level of X*₃ (in green) oscillates with a very small amplitude and shows a response primarily to the time-averaged value of the input. (D) The amplitude of the oscillating response of X*₃ is plotted as a function of the frequency of the input signal oscillation. The points corresponding to the input frequencies in B are shown as a red square and a green square, respectively. This amplitude of the oscillatory response drops off sharply at a characteristic frequency ω_b of the input, which is the bandwidth of this model pathway. How fast information propagates through such a cascade is proportional to this pathway bandwidth ω_b.

Signaling pathways consist of cascades of proteins where each protein activates the next (2). A signaling cascade is triggered when a receptor is activated by an external stimulus. Often, the signals are transmitted through kinase-dependent phosphorylation (Fig. 1A). Information about the environment is then transmitted through the pathway, resulting in a response from the cell. The bandwidth of the pathway can be determined by measuring the response of the pathway to the input signal fluctuating at different frequencies. At frequencies up to the bandwidth, the pathway responds faithfully to the input stimulus. To understand how a signaling pathway responds to excitation over a range of frequencies, we numerically studied (3) the three-level branched signaling cascade shown in Fig. 1B and described in Box 1. When the input stimulus to this pathway oscillates at frequencies lower than the bandwidth ω_b, the output of the cascade measured by the levels of the activated enzyme X*₃ follows the input faithfully. When the input oscillates at frequencies higher than the bandwidth ω_b, the pathway integrates and, hence, averages over the input (Fig. 1C). Thus, the concentration of X*₃ shows a response to the mean level of the input and no response to the input oscillations. The pathway acts as a low-pass filter with a bandwidth ω_b (Fig. 1D). This model pathway can faithfully convey information about fluctuations in its stimulus that happen on time scales slower than τ_b ∼ 1/ω_b. For a linear pathway, the bandwidth ω_b is dominated by the slowest time scale in the cascade. Thus, all activation and deactivation rate constants in this cascade must be at least as large as ω_b for the cascade to respond faithfully to the inputs oscillating at frequencies lower than ω_b. For a branched pathway, the activation rate constant of the slower branch does not affect the bandwidth. However, the deactivation rate constants of both branches have to be at least as fast as the bandwidth.

To measure signaling pathway response in vivo over different input frequencies and, hence, the bandwidth, as it is usually done in engineering, we developed a microfluidic device that allows for rapid periodic changes in media (Fig. 2). Rapid changes in media are exceptionally difficult to achieve in conventional microfluidic devices. Our device has two fluids entering through different inlets of a Y-shaped flow chamber, as shown in Fig. 2A. The region of lateral diffusion and, hence, mixing scales as $\sqrt{Dx/u}$, with D representing the diffusion constant of the media, u the speed of the laminar flow, and x the distance from the point of union of the two fluids, measured along the direction of the flow. Near the point where the two fluids meet, mixing is minimal. By changing pressure difference between the fluids by using a computer-controlled switch, we can sweep the separation line across the width of the flow cell. This allows us to rapidly switch the conditions to which the cells in the flow chamber are exposed. The media can be changed as frequently as twice a second, i.e., at 2 Hz (Fig. 2) without perturbing cell adhesion. Appropriate alignment is achieved by observing the separation line in real time by using phase contrast microscopy [see supporting information (SI) Text and Movie S1 and Movie S2].

Fig. 2.

Microfluidic device for studying frequency response of single cells. (A) One of the input arms of a Y-shaped flow chamber is fed by a solution of 1 M sorbitol in SC medium (in red) from reservoir R3 at a hydrostatic pressure head at P₀. The other arm is fed by SC (in blue) from one of two reservoirs, R1 at a hydrostatic pressure head at P₊ and R2 at P₋. The choice between the two reservoirs, R1 or R2, is made by a programmable three-way electrovalve. When reservoir R2 is chosen, the fluid from reservoir R3 fills most of the chamber, whereas when R1 is chosen, the fluid from R1 fills the chamber. Periodic changes in the state of the electrovalve allow a change in the environment of the cells at a tunable period T. (B) To characterize the device, water was filled in reservoirs R1 and R2, and a dilute solution of fluorescein was filled in R3. The state of a cross-section of the flow chamber was imaged by fluorescent microscopy. This state is shown as a function of flow-cell width (along the x axis) and time (along the y axis) for both T = 1-s oscillations (Left) and T = 0.5-s oscillations (Right). The bright regions indicate fluorescein solution, and the dark regions indicate water. The sharp interfaces between the dark and bright regions show the efficiency of our device in changing conditions rapidly. (C) The fluorescence intensity for a typical point in the middle of the channel is shown for oscillation periods ranging from T = 0.5 s to T = 4 s. The curves have been offset along the y axis for clarity, and for each curve, time has been scaled by its input frequency ω. All the curves oscillate between the same minimum and maximum fluorescence intensities. The transition from one medium to the other gets less sharp as T = 0.5 s is approached, indicating the limit of resolution for our experimental device.

We used this device to measure the bandwidth of the hyper osmolar glycerol (HOG) pathway in S. cerevisiae single cells (Fig. 1A). This MAP kinase pathway (4) is used by S. cerevisiae and other fungi (5, 6) to sense osmolar pressure in the environment and maintain water homeostasis. Although the HOG pathway is well documented, its transduction kinetics and in vivo reaction rates have been only roughly estimated, and its filtering properties are unknown. The SLN1 (7, 8) and SHO1 (9, 10) branches, shown in Fig. 1A, are redundant for cell survival under conditions of moderate osmotic stress. However, the SLN1 branch seems more important for pathway response to low and very high osmotic stress (11–13). Additionally, it is known that in an ssk2Δ ssk22Δ strain, the maximal phosphorylation of Hog1 is delayed from 1 min to ≈3–5 min (11, 14). Once phosphorylated, Hog1 localizes to the nucleus (15–17), where it is recruited to target promoters and activates several transcription factors.

To determine the bandwidth of the HOG pathway, we followed the nuclear localization of Hog1 as a reporter of the output of the signaling activity of the cascade (Movie S3). We exposed yeast cells in the flow chamber to an osmolar shock oscillating between 0 and 1 M sorbitol over a range of frequencies. These measurements allowed us to extract dynamical signaling properties of the HOG pathway. We measured frequency-dependent colocalization of Hog1-GFP with the nuclear protein Htb2-mCherry (Fig. 3). Assuming a first-order linear filter, we could obtain the bandwidth of the Hog1-GFP localization response to be 4.6 × 10⁻³ ± 1.1 × 10⁻³ Hz (see Methods and Fig. S1). Thus cytoplasmic activity in the signal-transduction cascade results in the phosphorylation of Hog1 and its subsequent nuclear translocation upon the beginning of the input pulse and nuclear delocalization at the end of the input pulse, all in ≈220 seconds. At frequencies slower than 4.6 × 10⁻³ Hz, the nuclear level of Hog1-GFP faithfully follows the input (Fig. 3B). At frequencies higher than 4.6 × 10⁻³ Hz, the steady-state response of the signaling cascade to the oscillating input drops sharply.

Fig. 3.

The mechanical and Hog1 localization responses of the HOG pathway in S. cerevisiae behave as low-pass filters with distinct bandwidths. (A) The response of Hog1 localization to oscillating 1 M sorbitol input behaves like a low-pass filter with bandwidth ω_b = 4.6 × 10⁻³ ± 1.1 × 10⁻³ Hz. Each point represents the average response amplitude as measured by Hog1-GFP colocalization with Htb2-mCherry over, typically, 15 cells (391 cells total). Error bars denote one standard deviation from the mean. (B) At input frequencies below ω_b = 4.6 × 10⁻³ Hz, the pathway output faithfully records the input: Hog1-GFP localizes and delocalizes in phase with the ω = 1.25 × 10⁻³-Hz input oscillations (filled circles and red lines). (C) At input frequencies above the bandwidth (ω = 6.7 × 10⁻² Hz, ω = 3.3 × 10⁻² Hz, or ω = 1.4 × 10⁻² Hz), the pathway does not respond faithfully to the input oscillations but, rather, integrates the signal. The traces for response to a 1 M sorbitol (black line) and a 0.5 M sorbitol (red line) step shock show that for input at frequencies above the bandwidth, the pathway responds approximately to the mean change in input. (D) The transcriptional response of the HOG pathway, as reported by Gpd1-GFP, reflects its low-pass behavior. Below the bandwidth, (ω = 8 × 10⁻⁴ Hz, green line) the level of Gpd1-GFP follows the input faithfully by initiating a new round of transcription during each period. At input frequencies above ω_b (ω = 0.5 Hz, purple line) the transcriptional response of Gpd1-GFP integrates the signal and responds to the mean change in input. (E) The mechanical response of an S. cerevisiae cell to oscillating 1 M sorbitol input is measured as variation in cytoplasmic fluorescence and is plotted versus input frequency. Each point represents 5–10 cells. Error bars denote one standard deviation from the mean. Size response is a low-pass filter with a bandwidth ω_b = 0.033 ± 0.01 Hz. Comparison of the mechanical response of cells exposed to 1 M sorbitol (open squares) with the response of cells exposed to 2 M sorbitol (filled circles) scaled by a factor of 0.5 indicates that cell-size response is linear in the input magnitude. (F) At frequencies slower than ω_b (ω = 2.5 × 10⁻³ Hz, black line), the cell-size response follows the input faithfully. At frequencies higher than the bandwidth (ω = 0.33 Hz, red line) the magnitude of cell-size response drops dramatically. Time has been normalized by the input frequency, and fluorescence intensity variations are shown around their mean intensity.

As in our model (Fig. 1B, Box 1), the pathway transiently integrates the signal (Fig. 3C) before reaching an unresponsive steady-state at high frequencies. Integration is possible if the time scale of pathway deactivation is limiting for pathway bandwidth. When the time of the off-phase of the pulse (when there is no sorbitol in the medium) is less than the time for complete pathway deactivation, components of the pathway remain activated. Activated pathway components, and hence activated nuclear Hog1, accumulate during each on-phase of the pulse (when there is 1 M sorbitol in the medium), leading to integration. Deactivation time refers to the time required for the pathway to deactivate all components when confronted with the sorbitol signal turning off. This is not to be confused with the time scale for pathway adaptation, which is much slower. Our experiments show that the pathway integrates at high input frequencies, which suggests that the deactivation rate of the pathway may be limiting for pathway bandwidth.

To confirm HOG pathway activity and low-pass filtering behavior at the transcriptional level, we used Gpd1-GFP (glycerol-3-phosphate dehydrogenase), a gene that is strongly up-regulated by osmotic stress (18), as a transcriptional reporter of pathway activity. At low frequencies, as indicated by steadily increasing Gpd1-GFP levels, transcription begins during each osmotic input cycle (Fig. 3D), showing a faithful response to the input signal. At high frequencies, the transcriptional response is activated just once with subsequent adaptation. The transcriptional response at high frequencies mimics the response of the cell to a step shock of lower magnitude. Thus, we again see that at high frequencies, the cell effectively integrates the signal. Although transcription and translation are not fast reporters of HOG pathway activity, these results do allow us to confirm the Hog1 localization results at both very high and very low frequencies.

Pathway bandwidth could be set by the time scale of water export and/or the resulting size change after osmotic pulse. We measured the size response of the cells by again exposing yeast cells in the flow chamber to an osmolar shock oscillating between 0 and 1 M sorbitol over a range of frequencies. We monitored accurately the change in cell size on osmolar shock by measuring the change in the cell's mean fluorescent intensity in a strain with cytoplasmic fluorescent protein Ura1-GFP (Fig. S2). We also studied changes in cell size in Hog1-GFP strains in which PBS2 was deleted, rendering the HOG pathway inactive. By comparing cell-size response for 1 and 2 M sorbitol input over a range of frequencies, we found that the mechanical response of the cell is linear and acts as a low-pass filter (Fig. 3E) with a bandwidth of 0.033 ± 0.01 Hz. At higher frequencies, the size oscillations drop dramatically. At lower frequencies, the size oscillations follow the input (Fig. 3F). This, in turn, sets the typical time scale for water transport in and out of the cell at 30 ± 1 s, and the porosity of the cell wall to be of the order of 1.75 × 10⁻¹³ m·Pa⁻¹·sec⁻¹ (SI Text). The mechanical response of the cell occurs on time scales much faster than that of Hog1 localization and therefore cannot set the time scale of pathway activation.

Because the HOG pathway bandwidth is not constrained by the cell's mechanical responses, the 4.6 × 10⁻³-Hz bandwidth of the HOG signaling pathway must depend on the biochemical reaction rates during signaling. Following our model, the pathway time scale could be set at or below the level of Pbs2 where the two branches converge or by the faster of the two branches. To test the role of the Pbs2 protein, we studied signaling dynamics under conditions of extreme Pbs2 under- and overexpression. Under conditions where Pbs2 is underexpressed from the glucose-repressed GAL1 promoter, the response of the HOG pathway is drastically slowed (Fig. S3). When highly overexpressed by induction of the GAL1 promoter, Pbs2 does not significantly change the time scale of signaling through the HOG pathway (Fig. S3). This indicates that Pbs2 is not in limiting concentrations under wild-type conditions. We also measured the bandwidth in wild-type diploid cells and in pbs2Δ/PBS2 diploid cells. We found that the deletion of a single copy of PBS2 did not change the bandwidth of the diploid cell from that of the wild type (Figs. S4 and S5).

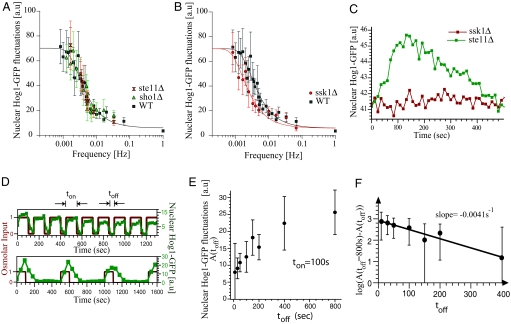
To understand whether either of the input branches set the bandwidth of the pathway, we studied the dynamics of Hog1-GFP in both ste11Δ and sho1Δ strains where activation of Pbs2 through the SHO1 branch is destroyed. The Hog1 localization response in these strains behaved identically to the wild-type strain (Fig. 4A). In striking contrast, blocking signaling from the SLN1 branch by deleting the SSK1 gene caused the Hog1 localization response to slow by almost 2-fold, to a bandwidth of 2.6 × 10⁻³ ± 0.4 × 10⁻³ Hz (Fig. 4B).

Fig. 4.

The SHO1 and SLN1 branches have different bandwidths. (A) Deletion of STE11 (red ) or SHO1 (▴) blocks input to Hog1 from the SHO1 branch. Strains with this branch blocked show no change in bandwidth compared with the wild-type strain. Time scales are in good agreement for wild type (ω_b = 4.6 × 10⁻³ ± 1.10 × 10⁻³ Hz), sho1Δ mutants (ω_b = 4.6 × 10⁻³ ± 0.9 × 10⁻³ Hz), and ste11Δ mutants (ω_b = 4.6 × 10⁻³ ± 1 × 10⁻³ Hz), indicating that the SSK1 branch dominates the activation dynamics of the HOG pathway. (B) Deletion of SSK1 (●) blocks input to Hog1 from the SLN1 branch. The ssk1Δ strains (ω_b = 2.6 × 10⁻³ ± 0.4 × ¹⁰⁻³ Hz) show close to 2-fold decrease in bandwidth compared with the wild-type strain (■, ω_b = 4.6 × 10⁻³ ± 1.1 × 10⁻³ Hz). Each point represents the amplitude of Hog1-GFP and Htb2-mCherry colocalization over, typically, 10 cells. The error bars represent one standard deviation from the mean. (C) The time course of nuclear Hog1-GFP levels for the input oscillating 0.2 Hz (larger than the pathway bandwidth) is shown for cells of ste11Δ (in green) and ssk1Δ (in red) strain backgrounds. At such high frequencies, the cells possessing only the Ssk1 branch (ste11Δ) integrate the input just as the wild type (see Fig. 3C), whereas the cells possessing just the Sho1 branch (ssk1Δ) do not respond at all. Thus it is the Ssk1 branch of the pathway that allows the cells to integrate fluctuating inputs from the environment. (D) Time course of nuclear Hog1::GFP intensity as a function of time shown for different temporally changing inputs. In both Upper and Lower graphs, the input amplitude (shown in red) oscillates between 0 and 1 M sorbitol starting at time t = 0 s. In Upper, the input stays at 1 M for t_on = 100 s and at 0 M for t_off = 50 s. In Lower, t_on = 100 s, whereas t_off = 400 s. The nuclear Hog1::GFP intensity oscillates according to the input. The amplitude of the oscillation for t_off = 400 is larger than for t_off = 50 s. (E) The amplitude of the oscillations in Hog1 nuclear intensity is plotted as a function of t_off for a fixed t_on = 100 s. With increasing t_off, the amplitude of Hog1::GFP oscillations in steady-state increase, reaching a maximum at and above t_off = 800 s. (F) The log of the difference in the amplitude of the oscillation at a given t_off (shown in D) from that at t_off = 800 s is plotted as a function of t_off. This plot gives an accurate measure of the rate constant for the turn off of the osmolar pathway when the osmolar input is turned off, and from the slope of this plot, we find it to be 0.0041 ± 0.0005 Hz, which corresponds to within error bars to the bandwidth of the Hog pathway shown in Fig. 3. This shows that the rate-limiting step is the turn off of the Hog pathway.

Additionally, we find that the SHO1 branch does not quickly integrate the high-frequency input signals, whereas the SLN1 branch does (Fig. 4C). The deactivation rate constants of the pathway in mutants without either the SSK1 or the SHO1 branch are the same (Fig. S6). That the SLN1 branch is faster is consistent with previous results (9). In wild-type cells, it is the SLN1 branch that integrates high-frequency signals leading to the wild-type response.

The SLN1 branch consists of a two-component system, common in prokaryotes, in which there is no enzymatic amplification of the signal. The SHO1 branch is an enzymatic kinase cascade of the type that constitutes most signaling pathways in eukaryotes. We find that signal transduction through the branch with the phospho-relay is more than twice as fast as the SHO1 branch employing an enzymatic cascade. Interestingly in some other yeasts and fungi, the Sho1 protein is not conserved or the SHO1 branch does not signal to the HOG pathway (6, 19–21). Furthermore, it is the faster SLN1 branch that is conserved in fungi.

The bandwidth of the HOG pathway could be set by the time for Hog1 to be activated and localize to the nucleus or the time for Hog1 to be deactivated and delocalize from the nucleus. The activation time includes the time to activate the SLN1 branch of the pathway, the time for this branch to activate Pbs2, or the time for Pbs2 to activate Hog1. The pathway deactivation time includes the time to deactivate one of the SLN1 or the SHO1 branch, the time to deactivate Pbs2, or the time to deactivate Hog1 and delocalize it from the nucleus. Consistent with the experimental evidence that the pathway is able to integrate the signal at high frequencies, the rate at which the HOG pathway turns off could be limiting for bandwidth. Accurately measuring the deactivation rate constant from nuclear Hog1 traces (such as Fig. S6) is difficult because the initial drop in intensity is due to the cell size suddenly increasing in response to a decreasing osmotic level in the environment. This is followed by nuclear Hog1 export and the nuclear signal decaying into measurement noise, leaving very few data points to fit to an exponential. To carefully measure the deactivation rate constant of the HOG pathway, we used asymmetric pulses of osmolar shock (Fig. 4C). When the off time of the pulse (t_off) is very short, the cell cannot tell independent pulses apart, responding as if to a step increase in sorbitol. When the pulses are very far apart (t_off is very large), the pathway responds to each pulse, and Hog1 oscillates in and out of the nucleus each time. The amplitude of this oscillation decreases with t_off, vanishing as t_off approaches zero. This amplitude scales as 1 − e^{−k_off t_off}, where k_off is the slowest deactivation rate constant in the pathway. The fit of the amplitude to this single exponential allowed us to extract the rate constant for the slowest deactivation rate to be 4.1 × 10⁻³ ± 0.5 ×10⁻³ Hz (Fig. 4E), which is equal to the measured bandwidth of the HOG pathway (Fig. 3) to within error bars. This, coupled with the fact that the deactivation rates in mutants with either a deactivated SHO1 branch or the SLN1 branch are identical to within error bars (Fig. S6), supports the argument that the deactivation rates of components at or downstream of Pbs2 must be limiting for pathway bandwidth. It is possible that the bandwidth of the HOG pathway is set by phosphatases responsible for deactivating Pbs2 and Hog1 (22). The study of phosphatases in controlling the signaling dynamics of the pathway is left to future work.

Our results indicate that the time scales of Hog1 localization in all strains are set by biochemical reaction rates. Time scales are not set by cell-wall mechanical response and water transport because these processes happen on a much faster time scale. The results from our experiments on wild-type and mutant strains indicate that the activation and deactivation rates of Pbs2, Hog1, and all of the components upstream of Pbs2 in the SLN1 branch must be ≥4.6 × 10⁻³ Hz. We also show that the deactivation rates of all components in the SHO1 branch must be ≥4.6 × 10⁻³ Hz, whereas the activation rates are significantly slower. As we saw in our model, the bandwidth of a pathway is set by the slowest time scale; thus, if any protein activation or deactivation rate were <4.6 × 10⁻³ Hz, the bandwidth of the HOG pathway in wild-type and sho1Δ strains would have to be <4.6 × 10⁻³ Hz. Similarly, the difference between the ssk1Δ and sho1Δ strains indicates that the activation rates of all proteins upstream of Pbs2 in the Sho1 branch must be ≥2.6 × 10⁻³ Hz. Our systems-level measurements of the HOG pathway put bounds on all of the rate constants in the signaling pathway in vivo.

Our microfluidic device allows for measurement of pathway bandwidth and elucidation of how bandwidth is set. Bandwidth measurement places bounds on all of the rate constants in the pathway. Similar experiments can help compare the design and dynamics of different signaling pathways within the same cell as well as the same pathway in different evolutionarily related species.

Methods

Box1: Model.

The proteins X₁ and X′₁ are directly activated by the input I (Fig. 1) to their excited form X*₁ and X′*₁ at rates given by

These proteins in turn excite X₂ to X*₂ at a rate

which in turn excites X₃ to X*₃ at a rate

k_a^js are the rate constant, K_Mjs are the Michaelis–Menten constants for the reactions activated by X*_j, and T_i is the lifetime of activated protein X*_i. For an input that fluctuates in time about a constant value Ī by a small δI(t), we can linearize the above equations in fluctuations in the concentrations of excited forms of the proteins about the steady-state. The Fourier transform of the fluctuations, δX*₃(ω) is found to be proportional to:

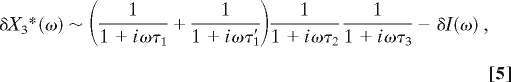where δI(ω) is the Fourier transform of the input and τ₁, τ′₁, τ₂, and τ₃ are the sum of the time scales of excitation and deexcitation of X₁, X′₁, X₂, and X₃, respectively. At high frequencies [ω > max(1/τ₁,1/τ′₁,1/τ₃)], the amplitude of the fluctuations in the excited proteins fall rapidly, and the linearization is valid. The bandwidth of the pathway ω_c ∼ max[min(1/τ₁,1/τ₂,1/τ₃),min(1/τ′₁,1/τ₂,1/τ₃)] and, similarly, the slowest time scale in the pathway τ_c ∼ min[max(τ₁,τ₂,τ₃),max(τ′₁,τ₂,τ₃)]. For excitations above this critical frequency ω_c, the pathway integrates the signal, whereas below it, the pathway follows the signal faithfully. It is important to note that all of the activation and deactivation times of all of the proteins in the pathway have to be faster than or equal to this slowest time scale.

Yeast Strains and Plasmids.

Yeast strains and plasmids were constructed by using standard molecular biology techniques. Table S1 contains the list of strains and plasmids used in this study

Yeast Growth Conditions.

Cells were grown overnight at 30°C in synthetic complete (SC) medium, reinoculated into fresh SC medium and grown at 30°C for 4–6 h before microscopy.

Microfluidic Chamber and Attachment of Yeast Cells.

Microfluidic chambers were made in PDMS (polydimethylsiloxane) by using classic soft lithography techniques and then adhered to a coverslip (24 × 60 × 1 mm) by using a plasma oven. Our device used a three-way electrovalve (The Lee Company) controlled by a computer. A saturated solution of Con A (25 mg/ml; Sigma–Aldrich) was added into the chamber, and after washing the chamber with fresh SC, yeast cells were injected and allowed 5–10 min to settle down and stick to the coverslip. Once started, the flow removed the unattached cells. The visual basic code for controlling the switch and flow cell design will be made freely available upon publication.

Microscopy and Image Processing.

The cells were observed by using a Zeiss 200M fluorescent microscope with an Orca-II-ER camera and a 100×/1.45 N.A. plan α fluar objective. Emission from GFP was visualized at 528 nm (38-nm bandwidth) upon excitation at 490 nm (20-nm bandwidth), and emission of mCherry was visualized at 617 nm (73-nm bandwidth) upon excitation at 555 nm (28-nm bandwidth). Cells were allowed to adapt to the oscillating conditions for up to 20 min before starting acquisition. Subsequently cells were photographed at regular intervals and faster than twice the frequency of the oscillations of the flowing media. Image analysis was done by using ImageJ (http://rsb.info.nih.gov/ij/). Localization of Hog1-GFP was obtained by measuring the GFP intensity colocalized with Htb2-mCherry. Cell size was measured as the variations of cytoplasmic fluorescently labeled proteins (HOG1 in the main text and URA1 in SI Text). When the cell volume changes, the concentration changes, and hence the fluorescent intensity per unit projected area of the cell changes. This method was more accurate at measuring cell-size fluctuations than the one by estimating the size of cells from the DIC image. Hog1 nuclear localization was measured in individual cells. The data points in all plots denote the means over cells, and the error bars denote standard deviation in the response of these cells.

Bandwidth Measurements.

Amplitude measurements as in Figs. 3 and 4 were fit to the classic low-pass filter form

with ω representing the frequency and τ the time scale of the filter. We also fit the measured amplitudes with the response of a model pathway with the slowest activation, k_on and the slowest deactivation rate k_off, to the periodic inputs of our flow cell. This leads to a fit of the amplitude χ of the form

with T representing the period of oscillation of the stimulus in the flow cell, A representing the gain of the system, and an offset value, δ, that takes into account the fact that, even at high frequencies, the amplitude of nuclear amplitude of the oscillatory signal is non-zero because of the autofluorescence intensity changes due to size variations. Both fits lead to consistent extraction of the slowest rate constant in the pathway.