Abstract
A large-scale brain network can be defined as a set of segregated and integrated regions, that is, distant regions that share strong anatomical connections and functional interactions. Data-driven investigation of such networks has recently received a great deal of attention in blood-oxygen-level-dependent (BOLD) functional magnetic resonance imaging (fMRI). We here review the rationale for such an investigation, the methods used, the results obtained, and also discuss some issues that have to be faced for an efficient exploration.
1. INTRODUCTION
Blood-oxygen-level-dependent (BOLD) functional magnetic resonance imaging (fMRI) is an imaging technique that makes it possible to dynamically and noninvasively track metabolic and hemodynamic changes in the brain [1, 2]. The early developments of BOLD fMRI data analysis have mostly relied on a method called general linear model (GLM), whose objective is to pinpoint the differential involvement of certain regions during various tasks [3–5]. Voxel clusters that exhibited such a behavior are declared “activated” and gathered into a so-called activation map that provides the output of the GLM approach; each map represents all regions that are significantly correlated with the stimulus time course. GLM-based methods have been extensively used in order to extract regions in a wide variety of conditions (see, e.g., [6] for a review of activation studies related to the premotor cortex).
The GLM, however, does not properly render the brain's intricate organization, which is believed to be based on two major principles: segregation and integration [7, 8]. According to these two principles, functional tasks are performed by specific collections of brain regions, also called networks, that are anatomically connected and can engage in complex interactions [9–11]. Even though the BOLD contrast is only remotely related to neuronal activity, it was first hypothesized, and then evidenced, that this imaging modality is able to reflect, at least to some extent, the strong constraints imposed on the brain by segregation and integration. This realization came from the investigation of the (misleadingly called) “rest” condition. First, studies showed that brain regions could still be correlated at rest, hinting for the existence of functional brain networks that could still be present and imaged even when no task was explicitly required from the subject [12, 13]. Network investigation also started with a closer examination of the “baseline,” that is, the signal measured when a subject is in the “rest” condition of a protocol, between two task conditions [14]. This approach was justified from the fact that, from an energetic perspective, the brain uses a significant part of the body's energy, independently of the presence or absence of a “task” [15, 16]. As methods of increasing complexity were developed and validated, the objective of many methodological developments shifted from GLM-related procedures to methods that were able to extract networks from BOLD fMRI data.
This paper is an attempt to review the latest advances in investigation of extended large-scale networks in fMRI from a methodological perspective, as well as the networks that have been found using these methods. This new methodology, if confirmed, has very deep implications in terms of methods that should be developed, and we discuss some of the issues that such methods will have to deal with in order to provide reliable and useful results.
2. LARGE-SCALE NETWORKS AS A CONSEQUENCE OF BRAIN ORGANIZATION
An extended large-scale functional brain network may be defined as a (potentially large) number of segregated regions (potentially spread over the whole brain) that interact in order to execute a coherent task. While Bressler and Tognoli [17] mostly consider “high-level brain functions of which cognition is comprised,” it is important to emphasize the fact that about any function that the brain is able to process is likely to have a network representation (see, e.g., Section 4 for a description of some low-level brain functions, such as vision and audition processing).
Large-scale networks share many important features. First, they are widely distributed over the brain. As a consequence of the segregation principle, it is hypothesized that they can be broken down into small brain regions, coined “nodes” by Mesulam [18], “units” by Marrelec et al. [19], and “local cortical area networks” by Bressler and Tognoli [17], each region being characterized by a consistent functional behavior. Such nodes can readily be identified in subcortical structures, which are often gathered into nuclei [20]. As to the cortex, despite cytoarchitectonic features (embodied, e.g., by the work of Brodmann [21] and his eponymous regions) that vary across its surface, its parcellation based on structural criteria alone remains globally a challenge. Nonetheless, local brain areas are also strongly characterized by their function [17]. For instance, primary sensory regions (e.g., visual) have been localized in a quite reproducible manner; within these regions, areas responding more specifically to certain types of inputs have been successfully identified (e.g., vertical versus horizontal lines in the primary visual cortex [22]). Still, even though various levels of specialization can usually be observed, there is a general agreement that most regions cannot be unambiguously associated with one specific function (see, e.g., [23] for Broca's area) and, in general, a region will exhibit a certain level of “multifunctionality” [17]: its contribution will not be limited to one task but will be allowed to vary within a given range of functions that it is able to implement.
As a consequence of the integration principle, large-scale networks are also characterized by potentially distant regions with strong (anatomical) connections and (functional) interactions. Whether top-down or bottom-up, serial or parallel, connections and interactions are quintessential of networks [18, 24, 25]. Anatomically, interregional connectivity is suspected to be rather sparse [26–30]. Even though most connections originating from one region are thought to re-enter the same region, axons are known to connect regions that are far apart from each other, for example, homologue regions [e.g., [31–33]]. Functionally, these connections have translations at all levels, from electrophysiology [34–38] to measures of the electromagnetic field [39] and of the BOLD signal [12, 13].
Whether coined “new phrenology” [40] or considered as being “beyond phrenology” [25], such an approach leads to a model of brain functions in which most functional tasks are subserved by functional brain networks, that is, collections of specialized regions that collaborate in order to generate a coherent behavior [11, 36]. In support of this approach, several networks have already been described and documented. Luria [10] refers to three blocks: one that “regulates the energy level and tone of the cortex,” another one that is strongly implicated in information processing, and a last one that is involved in higher, complex tasks, such as “the formation of intentions and programs for behavior.” Mesulam [18] proposed two distinct subdivisions of the brain. First, based on the co-occurrence of functions with similar features, the brain can be divided into five major “subtypes”: primary sensory-motor, unimodal association, heteromodal association, paralimbic, and limbic. There are also at least five large-scale networks, each dealing with a specific cognitive function: spatial awareness, language, explicit memory/emotion, face-object recognition, and working memory-executive function. These networks are not isolated from one another, but interact in very complex fashion, for example, through “transmodal” areas.
3. fMRI INVESTIGATION OF LARGE-SCALE NETWORKS
Relying on the assumption that BOLD fMRI is indeed able to image brain networks (see, e.g., [15] for a review of the neurophysiological substrate of neuroimaging), two categories of methods may be identified for such studies: approaches that make use of prior cognitive information and fully exploratory methods.
3.1. Using neurocognitive information
Correlational methods were historically the first ones to be applied to investigate large-scale networks in fMRI data analysis, in the form of functional connectivity studies and functional connectivity maps [12, 41–47]. Starting from a voxel or region—the so-called “seed” voxel/region—one extracts all voxels whose time courses are significantly correlated with that of the seed. Measures other than temporal correlation have also been used, such as coherence and partial coherence [48, 49]. Selection of the seed region is a key issue in studies of functional connectivity. First, a brain region is selected according to its function (e.g., cortical representation for hand movement, [47]). The corresponding seed is then obtained from either prior anatomical knowledge or functional manipulation. Anatomically, common approaches consist of using coordinates in a standardized space (Talairach or MNI) [44], or having an expert delineate the region on anatomical images [48]. Functionally, the seed can be obtained from an activation map, provided that the region of interest can be characterized by its implication in a specific task (e.g., the primary motor cortex in a simple movement) [41, 45, 47].
As opposed to effective connectivity—where Gonçlaves and Hall [50] showed that results of SEM analyses may vary depending on the choice of the seed voxel—robustness of functional connectivity maps with regard to the selection of the seed region and its spatial extent have barely been examined yet. Vincent et al. [51] showed that, for the visual or the somatomotor network, the resulting functional connectivity map was robust to the choice of the starting seed region. Many other parameters (e.g., design, size of each region) may have an influence on the outcome of the analysis, potentially leading to different spatial structures or correlation values between structures. Full exploration of a whole network (i.e., with many regions) would imply the recourse to several successive computations of functional connectivity maps, each map being used to select a region significantly correlated as seed voxel for the next step—a procedure that is lengthy, complex, and whose convergence is not assured. Wang and Xia [52] have recently proposed a method to perform this exploration in only one step.
3.2. Blind exploration
The goal of fully exploratory methods is to provide data-driven approaches of large-scale network detection in which no prior cognitive information is required for the methods to proceed. A number of such procedures have been proposed, most of them relying more or less closely on either of the two key features of large-scale networks, namely integration and segregation.
The vast majority of approaches proceed as follows. Based on a similarity measure, they gather voxels irrespective of their anatomical proximity (and, hence, of segregation) into separate classes that are strongly similar to each other and dissimilar from one another. For each class, the output is a map representative of the class and an associated time course. All methods have one or several parameters whose tuning affects the number of classes. Since each class tends to gather voxels that are strongly correlated, it is often univocally identified with a large-scale network. Blind approaches include methods based on eigenvalue decomposition, such as principal component analysis (PCA) [53–55], correlation clustering [56], Kendall's coefficient of concordance [57, 58], K-means [59, 60], fuzzy clustering methods [54, 56], self-organizing map algorithms [61], Kohonen clustering neural network and fuzzy C-means [62], hierarchical clustering [60, 63], integration and information-theoretic quantities [64, 65], and spatial independent component analysis (sICA) [66]. While most methods provide maps that are exclusive (a voxel can only belong to one map), a few (e.g., fuzzy clustering or ICA) provide an index of the plausibility for a voxel to belong to each of the different classes. Most methods also provide local criteria, calling for stepwise analyses, at the exception of PCA and ICA that use global measures and, consequently, are able to perform classification in one step.
Most approaches mentioned in the previous paragraph have only been used a limited number of time in fMRI data analysis so far. This can probably be accounted for by the complexity of their algorithms, which is commensurate with the difficulty of the task at hand. Outstandingly, sICA has been used quite a lot recently, with results that are rather promising. Regardless of its popularity, though, the network interpretation of the results obtained needs to be proved beyond simple criteria (these include, e.g., that voxels located close to each other or in homologue regions tend to belong to the same class). For instance, for PCA, Friston and Büchel [67] mention that the interpretation of the eigenimages in biological terms might be dubious, since they could be rotated in the data space and still be a solution to the problem (but see [68]). By contrast, components obtained through ICA can be more easily related to known physiological noises or functional processes [66, 69]. The methodological reasons for this success are, however, still not clear, and many explanations are plausible: the relevance of the assumption of spatial independence, the adequacy of the underlying mixing model, the efficiency of the global criterion/one-step discrimination approach, or some interesting feature of the information-theoretic optimization algorithm. In any case, the fact that its application simplifies the results to a maximum and produces a very limited number of widespread networks, making interpretation easier, clearly plays in its favor (compare, e.g., with [70, 71], or [72]). Its sensitivity, which is much higher than that of clustering methods, might also explain its success. Nevertheless, it must still be kept in mind that the assumptions underlying ICA (perfect synchrony within a network and spatial independence between networks) impose an extreme and unrealistic case of integration. While the simplification of several time courses into one is performed only once for ICA, the stepwise procedures implemented by other methods essentially go through the same approximation at each step, leading to an error that is probably far larger.
Unlike the numerous approaches to functional integration, few methods have specifically sought to extract segregated regions. Some methods decrease the complexity of the data by using predefined regions (e.g., according to the Tzourio-Mazoyer et al. [81] template). Approaches using predefinite regions do not check that all voxels within a region exhibit homogeneous bahaviors; they merely assume that it is the case. Average signals are then extracted from each region, on which any integration-based approach, such as hierarchical clustering [71, 72], can be applied. Intuitively, many clustering methods mentioned previously (e.g., K-means, hierarchical clustering, or information-theoretic measures) could easily be applied for the purpose of detecting segregated regions by incorporating a constraint of contiguity between voxels that could be merged. Among these, only the information-theoretic approach explicitly takes both within- and between-classes measures of similarity into account. Specifically, they optimize a so-called functional clustering index (FCI) that keeps a balance between region homogeneity (strong segregation) and sparseness of inter-regional interactions (low integration) [64, 65]—the latter constraint being hard to justify from a network perspective. As to other clustering methods, as noted by Goutte et al. [60] in accordance to Huygens' formula, maximizing a measure of the internal coherence of a class (associated with segregation) is often equivalent to minimizing the same measure of coherence but computed between classes (that could be associated with integration). As such, the behavior of such methods with regard to networks would again lead to questioning.
A tentative approach to consider simultaneously segregation and integration has been conducted by the large scale network identification (LSNI) method by Bellec et al. [80]. LSNI first clusters neighboring voxels into small regions using a region-growing algorithm [82] and then selects regions that exhibit a significant correlation with other distant regions. Such a procedure allows to define brain functional regions and networks in a purely data-driven way. While the sensitivity of the algorithm proposed was rather low, it had the great advantage to explicitly define and address the two principles of functional segregation and integration. So far, this method seems adapted for individual analyses; its extension to group studies seems limited due to the subject-dependent definition of regions.
4. TYPOLOGY OF NETWORKS EXTRACTED WITH fMRI
During the last decade, several brain systems have been studied in fMRI using functional connectivity-related approaches. These studies have revealed integrated systems, including primary systems and associative networks. Exploratory approaches have also allowed to extract several functional networks at once. Even if all brain areas are not included in a network, these networks involve many areas and constitute a possible functional parcellation of the brain.
The motor network was the first network studied through functional connectivity analyses. Biswal et al. [12] reported correlations in low-frequency resting-state fluctuations between left and right motor areas using single-slice fast-sampled acquisitions. This result was later reproduced with multislice acquisitions where an extended motor network was shown to correlate with a region in the primary motor cortex [44, 47]. Lowe et al. [44] showed that other functional networks could be detected using other seed regions, namely the visual network with a seed around the calcarine fissure and a limbic network with a seed in the amygdala. An auditory and a language systems were later extracted in the same way [41, 43]. Other networks were also studied using the seed-region functional connectivity approach, such as the default-mode network [83–86], the attentional networks [42, 83, 87], and memory networks [46, 88].
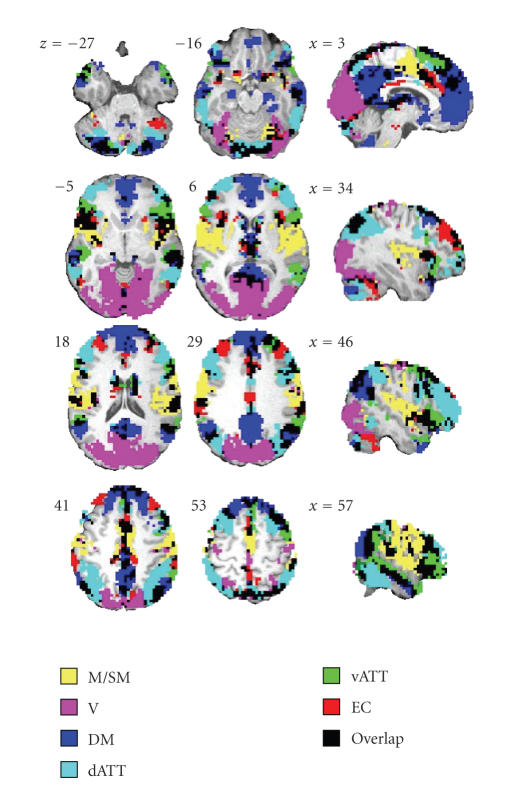
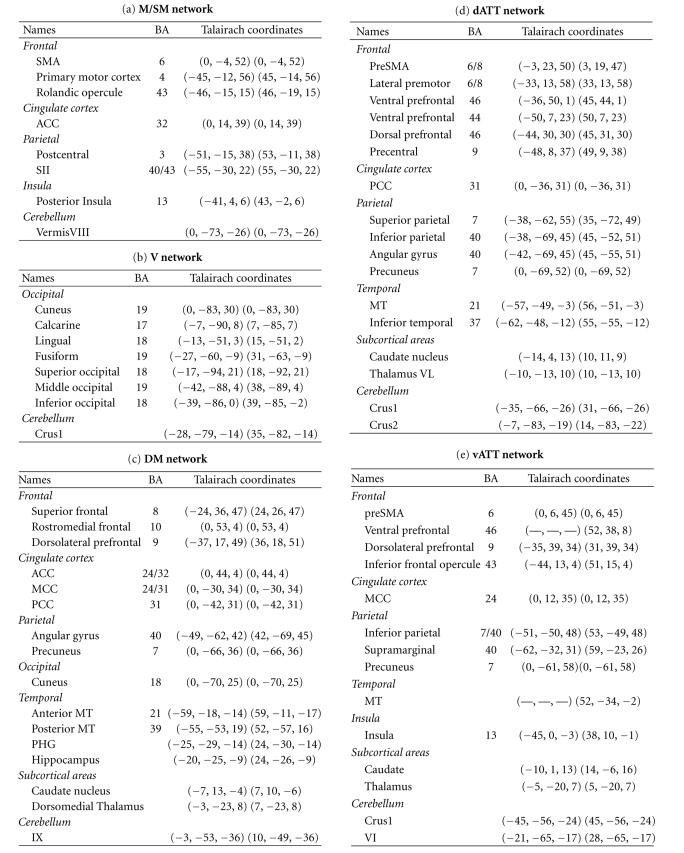
More recently, a larger number of functional networks were revealed using exploratory methods based on ICA [76–78]. Even if the number of extracted networks varied, their spatial organizations were reproducible across studies. For instance, all three studies just mentioned found functional networks involving the same systems that were sometimes split into different parts (e.g., left/right, rostral/caudal). Using group ICA studies of resting-state datasets [76–78], which were the most reproducible, we selected seven functional networks: a motor/sensorimotor system, a visual system, an auditory system, a default-mode network, a dorsal attentional network, a ventral attentional network, and an executive control network. Van de ven et al. [75] systematically studied the reproducibility of ICA results on individual datasets and the results using hierarchical clustering [63] and self-organizing map algorithm (SOM) [61] were presented on an individual level. The results from studies that provided a systematic description of all networks found are reported in Table 1. In Figure 1 and Table 2, we also reported results from a study on a population of 20 healthy subjects acquired at rest, where networks were extracted using spatial ICA and a hierarchical clustering approach similar to that of Esposito et al. [79].
Table 1.
Literature summary of the different networks found in network investigation of fMRI data. Methods—HC: hierarchical clustering, SOM: self-organizing map algorithm, ICA: independent component analysis. Networks—M/SM: motor/sensorimotor, V: visual, A: auditory, DM: default mode, dAtt: dorsal attentional, vAtt: ventral attentional, EC: executive control. Networks found are denoted by “X.” (*) In addition to primary cortices (sensorimotor, visual, and auditory), the clusters shown by Cordes et al. [63] were essentially bilateral single regions (thalami, fusiform gyri, and frontal gyri) which were parts of different networks of reference. (†) Except for the sensorimotor system, the networks identified by Peltier et al. [61] were not properly labeled; the spatial organizations of the maps shown seemed similar to the attentional networks. (‡) The results presented by Calhoun et al. [73] were partial, mentioning the extraction of other networks that they did not show neither comment; another study on similar datasets showed that the sensorimotor and the dorsal attentional networks might be detected too [74].
Figure 1.
Example of extended large-scale networks extracted in fMRI at rest. The six networks were identified using spatial ICA and a hierarchical clustering approach similar to that of [79] on a group of 20 healthy subjects acquired at rest. Networks—M/SM: motor/sensorimotor, V: visual, DM: default mode, dAtt: dorsal attentional, vAtt: ventral attentional, EC: executive control. The auditory network was not found as a separate network but some temporal regions of the primary auditory cortex are overlapped by other networks (in particular the M/SM network and the two attentional networks). The union of all networks does not add up to comprise the entire brain; for instance, some parts of the frontal cortex do not belong to any reported networks. By contrast, some brain regions simultaneously belong to several networks (in black).
Table 2.
Example of extended large-scale networks extracted in fMRI at rest. Peak foci corresponding to the six networks identified using spatial ICA and a hierarchical clustering approach similar to that of [79] on a group of 20 healthy subjects acquired at rest—M/SM: motor/sensorimotor, V: visual, DM: default mode, dAtt: dorsal attentional, vAtt: ventral attentional, EC: executive control.
|

|
The sensorimotor system involves at least the pre- and postcentral gyri (including the primary motor cortex and supplementary motor area). The visual system involves both medial striate and extrastriate regions (calcarine sulcus and lingual gyrus), as well as lateral occipital regions (nonprimary visual regions); these two visual networks (primary and associative) were identified separately by the three group-ICA studies. The auditory system involves principally lateral superior temporal gyri, the Heschl's gyrus and insular cortex. The so-called default-mode network involves the anterior and posterior cingulate cortices, the medial prefrontal cortex and lateral parietal regions [15, 89–91]. The dorsal attentional network involves lateral prefrontal and dorsal partietal cortex; these regions are involved in visio-spatial control [42, 92, 93]. The ventral attentional network involves inferior occipito-parietal regions and inferior lateral prefrontal regions; these regions are principally involved in new item recognition [42, 94]. Last, the executive control network involves superior and middle prefrontal cortices, ventrolateral prefrontal cortex and anterior cingulate gyrus [95].
Other studies have applied these exploratory approaches to extract integrated functional networks from fMRI datasets acquired during external stimulation [73, 79, 80]. The results of these three studies are also compiled in Table 1. These results showed that the detection of the functional networks not directly related to the stimulation were less sensitive than that without external stimulation.
5. FUTURE ISSUES
Tracking the presence of extended large-scale networks in BOLD fMRI data raises many issues. We have here focused on some aspects related to the neurocognitive aspects of networks, their identifiability by fMRI, and the methodological questions raised by network analyses.
5.1. Neurocognitive aspects
The major issue to be faced is arguably the very definition of an extended large-scale brain network. Indeed, even though the brain is far from being fully connected, any region is eventually connected to any other regions if one takes polysynaptic connections into account. Obviously, stating that the brain can be considered as one network is by no way satisfying, no more than it is to say that each macrocolumn forms a networks by itself. The strongly hierarchical nature of the brain's anatomical and structural organization induces similar characteristics at all levels. As the brain can be decomposed in networks, each network can in turn be further partitioned into subnetworks, subnetworks into subsubnetworks, and so on. Furthermore, even though there probably is a (potentially loose) relationship between anatomical and functional organizations, it is still unknown how functional integration and segregation are coded in anatomical terms. For the exact same structural organization, it has been shown that networks can be observed to break down as one discriminates different sets of functional tasks or behaviors with increasing precision. For instance, the visual system can be decomposed into a ventral and a dorsal stream [22]. These two subnetworks, albeit interacting, have very distinct functions [42, 92, 96]. Similarly, the motor system can be further separated into a cerebello-cortical and a basal-cortical loop with different patterns of involvement [97, 98]. The difficulty to define a network does not yield for primary networks only. For instance, it has been argued that the fronto-parietal network could be further partitioned into two subnetworks subserving attention and working memory, respectively, [99], while the working memory network itself could be further broken down in two, with one subnetwork mediating attentional selection and another one rather underlying language functions [100]. Networks are not exclusive from each other either. Mesulam [18] refers to transmodal nodes that connect various neurocognitive networks. For instance, activation of some fronto-parietal regions is observed during different cognitive tasks [101]; are these regions transmodal or part of a subnetwork that has a specific function? Similarly, the insular cortex is typically a multimodal association area that is not specifically activated by auditory stimuli. However, as reported in Section 4, recent papers have consistently classified it as belonging to a so-called auditory system. As evidenced by Figure 1, there are also some overlapping between networks, and voxels can be simultaneously classified as belonging to different networks. What is the function of such regions? Could this overlapping between networks be related to synchronization through distinct frequency-bands [35]—if such a phenomenon is indeed visible through fMRI BOLD imaging? Regarding the influence of a task on a network, an issue that has not received much attention yet, studies have shown that networks could indeed be influenced by the processing of a task, either during the task [86] or even after it [102]. It is hence not unrealistic to suspect that processing of a task might also modify the very structure of some networks.
Another cogent question is the relationship between networks as detected by fMRI data analyses and those mentioned in the literature. Networks extracted from fMRI are the consequence of the optimization of a mathematical criterion whose link to neuroscience is, at the very least, not obvious. While some results have been rather successfully related to the neurocognitive literature (e.g., attentional network), other results are more complex to interpret. Some networks extracted seem to share commonalities with some of the subtypes described by Mesulam [18] (e.g., the motor network; cf. Section 2), while others seem to be rather related to Mesulam [18]'s neurocognitive networks (e.g., the attentional network). Besides, the union of all reported networks (e.g., by sICA) does not include the whole brain. Some brain regions are then excluded from the functional networks organization of the brain. Why so? Globally, the criterion used for network extraction might make the methods sensitive to some functions or types of connections. For instance, top-down and bottom-up influences have distinct features [25, 34, 36–38]. Can they be detected equally well by existing methods?
Apart from these difficulties, there has also been evidence of variability across healthy subjects [80, 103] that could be explained by many factors, such as development and/or age [104, 105], and, in general, all forms of plasticity [106, 107]. Pathologies, for example, stroke [108, 109] or tumors [110–113], render the issue even more complex. Some studies have shown that certain pathologies can have network-specific effects: behavioral deficits in spatial neglects for the fronto-parietal network [114]; epilepsy [115] and Alzheimer's disease [116] for the default-mode network. Nonetheless, these results must be used with caution, for it is not clear yet whether they truly reflect a change in neuronal properties or, as, for example, in grade II glioma, a mere modification of the metabolic and vascular properties of the surrounding tissues.
5.2. BOLD fMRI imaging
Use of BOLD fMRI as a way to investigate large-scale networks relies on three successive assumptions, namely, that information exchanges between neurons is related to synchronies, synchronies to the BOLD contrast, and the BOLD contrast to the fMRI data effectively measured.
Synchronies are the blueprint of communication between regions [17, 39, 117–120] and, as such, should be strongly related to large-scale networks. A challenging issue is to determine the exact relationship between the spatial distribution and interaction pattern of regions within a large-scale network on the one hand and, on the other hand, the spatial and frequential distribution of oscillations.
Another issue is the connection between neuronal activity/synchrony and the appearance of a BOLD signal. While much still needs to be unraveled as to the connection between neuronal synchronies and the BOLD signal, it now seems more and more accepted that a sustained change in neuronal activity is likely to entail a relative change in the BOLD level [121–124], even though the exact relationship is expected to be rather complex [125].
Still, the BOLD signal is only a fraction of the total signal that is acquired in fMRI, a signal that is not exempt from many kinds of artifacts [126–128]. In particular, some physiological processes (e.g., cardiac, respiratory, or movement-related) induce spurious effects that contaminate the BOLD signal in the whole brain [129, 130]. Such artifacts are predominant in certain regions of the brain, such as the basal arteries for cardiac activity or the interfaces between cerebrospinal fluid pools and brain tissus for breathing and head movements. This origin-dependent predilection implies a spatial structure of the noise. Some network detection algorithms may hence recognize voxels influenced by the same spatially structured artifact as meeting the requirement for strong temporal coherence and, hence, assign them to a common structure. This feature has been successfully used by ICA techniques to provide efficient noise separation and removal techniques [66, 131, 132]. Yet, the issue arises when structures induced by noise are wrongly interpreted as functional networks; their detection and removal is hence of very high importance. The fundamental question, while examining spatial structures with a similar temporal behavior, is “do we measure neurally induced signal or consequences of physiological processes [133]?” Even though our understanding of the potential artifacts that can contaminate the BOLD fMRI signal improves, the consequences of many potential sources of structured noise have barely been mentioned, let alone investigated. For instance, it is believed that some mechanisms related to the regulation of blood flow (e.g., through the level of CO2 in the blood) could induce coherent changes in BOLD signal throughout the brain—giving birth to an effect likely to be identified as a functional network. In fact, such an effect has been used to explain the presence of the default-mode network in fMRI [134, 135]. Now, whether these regions are wrongfully classified as belonging to a common functional network because their voxels are corrupted by the same artifact, or whether they are actually regions that drive the physiological response is a matter that remains to be solved.
5.3. Data analysis
Many questions remain open regarding what methodologies to apply to extract functional networks. We here quickly discuss issues related to the choice of a model, the redundancy of fMRI signals, the necessity to provide both individual and group analyses, the importance of result representation, and the validation of fMRI results with other modalities.
Procedures used to investigate networks are usually based on mathematical methods that have been discovered independently of the field of fMRI data analysis. Their behavior is hence not guided by cognitive but mathematical considerations. While it can be accepted that most methods are general enough to be applied to a wide variety of problems, they still require a careful assessment of how best to adapt them to the issue at hand. We believe that the major point to cope with here is “how do methods code for segregation and integration? Does it make sense?” A relevant approach could be to try to derive out consistence requirements from cognitive consideration of what an “ideal” method should be able to do: quantify integration between voxels, regions, or networks using the same principled measure (such as the multiple correlation coefficient [136] or integration [7, 137]); differentiate between direct and indirect information exchanges (such as partial correlation [19, 72, 138–141]); discriminate causality from simple co-occurrence (such as Granger causality [138, 142–144]). Some methods are able to deal with one aspect of the problem, but none has been proposed to answer all these questions simultaneously.
Besides, investigation of large-scale networks face a very interesting problem, namely that of determining the spatial precision under which data should be considered as segregated and over which they should be said to be integrated. While it is obvious that neighboring voxels share a great deal of information, methods that model and summarize the behavior of a whole network with one single time course clearly oversimplify the problem and discard a lot of cogent information. Bellec et al. [80] proposed a statistical model that provides a critical distance that separates segregation and integration. Voxel clustering is another attempt to deal with that issue. However, the parameters that characterize the clustering coarseness are set a priori, when they should be determined by the intrinsic properties of the data and allowed to vary across the brain (e.g., between subcortical and cortical structures, which have distinct characteristic spatial extents). This step allows one also to reduce the dimensionality of the data. At least for this reason, it is a crucial step, because network investigation requires multivariate analyses that are computationally very demanding (the computational burden roughly exponentialy increase with the number of regions).
In neurocomputing, models investigating issues very similar to that of large-scale networks have already been developed [145–148]. However, most methods developed so far for effective connectivity, such as structural equation modeling (SEM) [149–152], dynamical causal modeling (DCM) [153–155], or generative models—including neural mass models [145, 156] and large-scale neural models [147, 157–159]—, have been of little use to the investigation of extended large-scale networks, since their intrinsic complexity prevent them from modeling systems with that many degrees of freedom (but see, [160]).
Methods originating from graph and/or network theories might prove more adapted to such problems [161–163], since they provide global quantification of structures that, besides from being ubiquitous [164, 165], are not unlike some models of brain networks. Using such methods, brain networks have been shown to exhibit small-world [70, 166–170] and scale-free [171, 172] features. The fact that networks simultaneously exhibit both properties has strong structural [104, 173] and functional [174, 175] implications.
Being able to devise methods that can deal with both individual and group analyses is also an important issue. At the individual level, it is essential to assess the significance of the different networks [80, 85, 176]. With procedures of increasing complexity, nonparametric resampling procedures [177], mostly used in the context of the GLM so far [178], might be appealing [179]. At the group level, one seeks to determine invariant networks across subjects. This has been done by either considering a model for the group [76] or solving the problem at an individual level and then performing clustering [79]. Validation of such methods have to be developed; a first step in this direction has been proposed by Calhoun et al. [180].
Once results have been produced, representing the results becomes a key issue. Consider for instance functional connectivity as measured by marginal correlation. Though computationally tractable on a large-scale network of N units, even for N large, such a method generates N(N−1)/2 correlation coefficients (e.g., 4950 for as few as 100 voxels/regions; 19900 for 200; 499 500 for 1000). Simply representing these on a graph as is commonly done [72, 140, 181] would prove impossible to read, let alone to interpret. Procedures that summarize the information have to be proposed; these can rely on PCA/MDS [71, 79, 182]; they could also use other representational techniques [183, 184].
Last, but not least, an essential point to validate and better understand the large-scale network approach in fMRI is the comparison with results form other imaging modalities or areas of neuroscience, such as electrophysiology [34–38], electroencephalography (EEG) or magnetoencephalography (MEG) [39, 125, 185, 186], and diffusion tensor imaging (DTI) [187–190]. To be able to efficiently compare results from different imaging modalities, it is essential to better understand how each modality images the activity of large-scale brain networks. In this perspective, providing a unified generative and/or statistical model for several of these modalities would be of the utmost importance, granting access to multimodal in vivo imaging of the brain in action.
ACKNOWLEDGMENTS
The authors would like to thank the guest editors for providing them with the opportunity to submit an invited paper to this special issue of the International Journal of Biomedical Imaging, as well as an anonymous referee for improving the quality of this manuscript. They are also grateful to Pierre Bellec, Jean Daunizeau, and Saâd Jbabdi for discussions regarding an early draft of this manuscript.
References
- 1.Chen W, Ogawa S. Principles of BOLD functional MRI. In: Moonen C, Bandettini P, editors. Functional MRI. Berlin, Germany: Springer; 1999. pp. 103–113. [Google Scholar]
- 2.Huettel SA, Song AW, McCarthy G. Functional Magnetic Resonance Imaging. Sunderland, Mass, USA: Sinauer Associates; 2004. [Google Scholar]
- 3.Friston KJ, Holmes AP, Poline J-B, et al. Analysis of fMRI time-series revisited. NeuroImage. 1995;2(1):45–53. doi: 10.1006/nimg.1995.1007. [DOI] [PubMed] [Google Scholar]
- 4.Friston KJ, Holmes AP, Worsley KJ, Poline J-P, Frith CD, Frackowiak RSJ. Statistical parametric maps in functional imaging: a general linear approach. Human Brain Mapping. 1994;2(4):189–210. [Google Scholar]
- 5.Friston KJ, Jezzard P, Turner R. Analysis of functional MRI time-series. Human Brain Mapping. 1993;1(2):153–171. [Google Scholar]
- 6.Picard N, Strick PL. Imaging the premotor areas. Current Opinion in Neurobiology. 2001;11(6):663–672. doi: 10.1016/s0959-4388(01)00266-5. [DOI] [PubMed] [Google Scholar]
- 7.Tononi G, Sporns O, Edelman GM. A measure for brain complexity: relating functional segregation and integration in the nervous system. Proceedings of the National Academy of Sciences of the United States of America. 1994;91(11):5033–5037. doi: 10.1073/pnas.91.11.5033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zeki S, Shipp S. The functional logic of cortical connections. Nature. 1988;335(6188):311–317. doi: 10.1038/335311a0. [DOI] [PubMed] [Google Scholar]
- 9.Hebb DO. The Organization of Behavior: A Neurophysiological Theory. New York, NY, USA: John Wiley & Sons; 1949. [Google Scholar]
- 10.Luria AR. The functional organization of the brain. Scientific American. 1970;222(3):66–78. doi: 10.1038/scientificamerican0370-66. [DOI] [PubMed] [Google Scholar]
- 11.Varela F, Lachaux J-P, Rodriguez E, Martinerie J. The brainweb: phase synchronization and large-scale integration. Nature Reviews Neuroscience. 2001;2(4):229–239. doi: 10.1038/35067550. [DOI] [PubMed] [Google Scholar]
- 12.Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magnetic Resonance in Medicine. 1995;34(4):537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- 13.Biswal BB, Van Kylen J, Hyde JS. Simultaneous assessment of flow and BOLD signals in resting-state functional connectivity maps. NMR in Biomedicine. 1997;10(4-5):165–170. doi: 10.1002/(sici)1099-1492(199706/08)10:4/5<165::aid-nbm454>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 14.Gusnard DA, Raichle ME. Searching for a baseline: functional imaging and the resting human brain. Nature Reviews Neuroscience. 2001;2(10):685–694. doi: 10.1038/35094500. [DOI] [PubMed] [Google Scholar]
- 15.Raichle ME, Mintun MA. Brain work and brain imaging. Annual Review of Neuroscience. 2006;29:449–476. doi: 10.1146/annurev.neuro.29.051605.112819. [DOI] [PubMed] [Google Scholar]
- 16.Shulman RG, Rothman DL, Behar KL, Hyder F. Energetic basis of brain activity: implications for neuroimaging. Trends in Neurosciences. 2004;27(8):489–495. doi: 10.1016/j.tins.2004.06.005. [DOI] [PubMed] [Google Scholar]
- 17.Bressler SL, Tognoli E. Operational principles of neurocognitive networks. International Journal of Psychophysiology. 2006;60(2):139–148. doi: 10.1016/j.ijpsycho.2005.12.008. [DOI] [PubMed] [Google Scholar]
- 18.Mesulam M-M. From sensation to cognition. Brain. 1998;121(6):1013–1052. doi: 10.1093/brain/121.6.1013. [DOI] [PubMed] [Google Scholar]
- 19.Marrelec G, Daunizeau J, Pélégrini-Issac M, Doyon J, Benali H. Conditional correlation as a measure of mediated interactivity in fMRI and MEG/EEG. IEEE Transactions on Signal Processing. 2005;53(9):3503–3516. [Google Scholar]
- 20.Kahle W. Atlas de Poche d'Anatomie. 3. Système nerveux et organes des sens. 3rd edition. Paris, France: Flammarion; 2002. [Google Scholar]
- 21.Brodmann K. Vergleichende Lokalisationslehre der Großhirnrinde in ihren Prinzipien dargestellt auf Grund des Zellenbaues. Leipzig, Germany: J. A. Barth; 1909. [Google Scholar]
- 22.Bear MF, Connors BW, Paradiso MA. Neuroscience: Exploring the Brain. 2nd edition. Baltimore, Md, USA: Lippincott Williams & Wilkins; 2001. [Google Scholar]
- 23.Poldrack RA. Can cognitive processes be inferred from neuroimaging data? Trends in Cognitive Sciences. 2006;10(2):59–63. doi: 10.1016/j.tics.2005.12.004. [DOI] [PubMed] [Google Scholar]
- 24.Bressler SL. Large-scale cortical networks and cognition. Brain Research Reviews. 1995;20(3):288–304. doi: 10.1016/0165-0173(94)00016-i. [DOI] [PubMed] [Google Scholar]
- 25.Friston K. Beyond phrenology: what can neuroimaging tell us about distributed circuitry? Annual Review of Neuroscience. 2002;25:221–250. doi: 10.1146/annurev.neuro.25.112701.142846. [DOI] [PubMed] [Google Scholar]
- 26.Felleman DJ, Van Essen DC. Distributed hierarchical processing in the primate cerebral cortex. Cerebral Cortex. 1991;1(1):1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- 27.Kötter R, Stephan KE. Network participation indices: characterizing component roles for information processing in neural networks. Neural Networks. 2003;16(9):1261–1275. doi: 10.1016/j.neunet.2003.06.002. [DOI] [PubMed] [Google Scholar]
- 28.Scannell JW, Burns GAPC, Hilgetag CC, O'Neil MA, Young MP. The connectional organization of the cortico-thalamic system of the cat. Cerebral Cortex. 1999;9(3):277–299. doi: 10.1093/cercor/9.3.277. [DOI] [PubMed] [Google Scholar]
- 29.Sporns O, Honey CJ, Kötter R. Identification and classification of hubs in brain networks. PLoS Biology. 2007;2(10):e1049. doi: 10.1371/journal.pone.0001049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Young MP. Objective analysis of the topological organization of the primate cortical visual system. Nature. 1992;358(6382):152–155. doi: 10.1038/358152a0. [DOI] [PubMed] [Google Scholar]
- 31.Hoshi E, Tremblay L, Féger J, Carras PL, Strick PL. The cerebellum communicates with the basal ganglia. Nature Neuroscience. 2005;8(11):1491–1493. doi: 10.1038/nn1544. [DOI] [PubMed] [Google Scholar]
- 32.Künzle H. An autoradiographic analysis of the efferent connections from premotor and adjacent prefrontal regions (areas 6 and 9) in macaca fascicularis. Brain, Behavior and Evolution. 1978;15(3):185–234. doi: 10.1159/000123779. [DOI] [PubMed] [Google Scholar]
- 33.Leichnetz GR. Afferent and efferent connections of the dorsolateral precentral gyrus (area 4, hand/arm region) in the macaque monkey, with comparisons to area 8. Journal of Comparative Neurology. 1986;254(4):460–492. doi: 10.1002/cne.902540403. [DOI] [PubMed] [Google Scholar]
- 34.Buschman TJ, Miller EK. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science. 2007;315(5820):1860–1864. doi: 10.1126/science.1138071. [DOI] [PubMed] [Google Scholar]
- 35.Buzsáki G, Draguhn A. Neuronal olscillations in cortical networks. Science. 2004;304(5679):1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- 36.Knight RT. Neural networks debunk phrenology. Science. 2007;316(5831):1578–1579. doi: 10.1126/science.1144677. [DOI] [PubMed] [Google Scholar]
- 37.Saalmann YB, Pigarev IN, Vidyasagar TR. Neural mechanisms of visual attention: how top-down feedback highlights relevant locations. Science. 2007;316(5831):1612–1615. doi: 10.1126/science.1139140. [DOI] [PubMed] [Google Scholar]
- 38.Womelsdorf T, Schoffelen J-M, Oostenveld R, et al. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316(5831):1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- 39.Başar E, Başar-Eroğlu C, Karakaş S, Schürmann M. Gamma, alpha, delta, and theta oscillations govern cognitive processes. International Journal of Psychophysiology. 2000;39(2–3):241–248. doi: 10.1016/s0167-8760(00)00145-8. [DOI] [PubMed] [Google Scholar]
- 40.Raichle ME. Modern phrenology: maps of human cortical function. Annals of the New York Academy of Sciences. 1999;882:107–118. doi: 10.1111/j.1749-6632.1999.tb08537.x. [DOI] [PubMed] [Google Scholar]
- 41.Cordes D, Haughton VM, Arfanakis K, et al. Mapping functionally related regions of brain with functional connectivity MR imaging. American Journal of Neuroradiology. 2000;21(9):1636–1644. [PMC free article] [PubMed] [Google Scholar]
- 42.Fox MD, Corbetta M, Snyder AZ, Vincent JL, Raichle ME. Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(26):10046–10051. doi: 10.1073/pnas.0604187103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hampson M, Peterson BS, Skudlarski P, Gatenby JC, Gore JC. Detection of functional connectivity using temporal correlations in MR images. Human Brain Mapping. 2002;15(4):247–262. doi: 10.1002/hbm.10022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lowe MJ, Mock BJ, Sorenson JA. Functional connectivity in single and multislice echoplanar imaging using resting-state fluctuations. NeuroImage. 1998;7(2):119–132. doi: 10.1006/nimg.1997.0315. [DOI] [PubMed] [Google Scholar]
- 45.Quigley M, Cordes D, Wendt G, et al. Effect of focal and nonfocal cerebral lesions on functional connectivity studied with MR imaging. American Journal of Neuroradiology. 2001;22(2):294–300. [PMC free article] [PubMed] [Google Scholar]
- 46.Vincent JL, Snyder AZ, Fox MD, et al. Coherent spontaneous activity identifies a hippocampal-parietal memory network. Journal of Neurophysiology. 2006;96(6):3517–3531. doi: 10.1152/jn.00048.2006. [DOI] [PubMed] [Google Scholar]
- 47.Xiong J, Parsons LM, Gao J-H, Fox PT. Interregional connectivity to primary motor cortex revealed using MRI resting state images. Human Brain Mapping. 1999;8(2–3):151–156. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<151::AID-HBM13>3.0.CO;2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sun FT, Miller LM, D'Esposito M. Measuring interregional functional connectivity using coherence and partial coherence analyses of fMRI data. NeuroImage. 2004;21(2):647–658. doi: 10.1016/j.neuroimage.2003.09.056. [DOI] [PubMed] [Google Scholar]
- 49.Sun FT, Miller LM, D'Esposito M. Measuring temporal dynamics of functional networks using phase spectrum of fMRI data. NeuroImage. 2005;28(1):227–237. doi: 10.1016/j.neuroimage.2005.05.043. [DOI] [PubMed] [Google Scholar]
- 50.Gonçalves MS, Hall DA. Connectivity analysis with structural equation modelling: an example of the effects of voxel selection. NeuroImage. 2003;20(3):1455–1467. doi: 10.1016/s1053-8119(03)00394-x. [DOI] [PubMed] [Google Scholar]
- 51.Vincent JL, Patel GH, Fox MD, et al. Intrinsic functional architecture in the anaesthetized monkey brain. Nature. 2007;447(7140):83–86. doi: 10.1038/nature05758. [DOI] [PubMed] [Google Scholar]
- 52.Wang YM, Xia J. Functional interactivity in fMRI using multiple seeds' correlation analyses—novel methods and comparisons. In: Karssemeijer N, Lelieveldt BPF, editors. In: Proceedings of the 20th International Conference on Information Processing in Medical Imaging (IPMI '07), vol. 4584; July 2007; Kerkrade, The Netherlands. Springer; pp. 147–159. [DOI] [PubMed] [Google Scholar]
- 53.Andersen AH, Gash DM, Avison MJ. Principal component analysis of the dynamic response measured by fMRI: a generalized linear systems framework. Magnetic Resonance Imaging. 1999;17(6):795–815. doi: 10.1016/s0730-725x(99)00028-4. [DOI] [PubMed] [Google Scholar]
- 54.Baumgartner R, Ryner L, Richter W, Summers R, Jarmasz M, Somorjai R. Comparison of two exploratory data analysis methods for fMRI: fuzzy clustering vs. principal component analysis. Magnetic Resonance Imaging. 2000;18(1):89–94. doi: 10.1016/s0730-725x(99)00102-2. [DOI] [PubMed] [Google Scholar]
- 55.Bullmore ET, Rabe-Hesketh S, Morris RG, et al. Functional magnetic resonance image analysis of a large-scale neurocognitive network. NeuroImage. 1996;4(1):16–33. doi: 10.1006/nimg.1996.0026. [DOI] [PubMed] [Google Scholar]
- 56.Baumgartner R, Windischberger C, Moser E. Quantification in functional magnetic resonance imaging: fuzzy clustering vs. correlation analysis. Magnetic Resonance Imaging. 1998;16(2):115–125. doi: 10.1016/s0730-725x(97)00277-4. [DOI] [PubMed] [Google Scholar]
- 57.Baumgartner R, Somorjai R, Summers R, Richter W. Assessment of cluster homogeneity in fMRI data using Kendall's coefficient of concordance. Magnetic Resonance Imaging. 1999;17(10):1525–1532. doi: 10.1016/s0730-725x(99)00101-0. [DOI] [PubMed] [Google Scholar]
- 58.Baumgartner R, Somorjai R, Summers R, Richter W, Ryner L. Correlator beware: correlation has limited selectivity for fMRI data analysis. NeuroImage. 2000;12(2):240–243. doi: 10.1006/nimg.2000.0605. [DOI] [PubMed] [Google Scholar]
- 59.Filzmoser P, Baumgartner R, Moser E. A hierarchical clustering method for analyzing functional MR images. Magnetic Resonance Imaging. 1999;17(6):817–826. doi: 10.1016/s0730-725x(99)00014-4. [DOI] [PubMed] [Google Scholar]
- 60.Goutte C, Toft P, Rostrup E, Nielsen FÅ, Hansen LK. On clustering fMRI time series. NeuroImage. 1999;9(3):298–310. doi: 10.1006/nimg.1998.0391. [DOI] [PubMed] [Google Scholar]
- 61.Peltier SJ, Polk TA, Noll DC. Detecting low-frequency functional connectivity in fMRI using a self-organizing map (SOM) algorithm. Human Brain Mapping. 2003;20(4):220–226. doi: 10.1002/hbm.10144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Chuang K-H, Chiu M-J, Lin C-C, Chen J-H. Model-free functional MRI analysis using Kohonen clustering neural network and fuzzy C-means. IEEE Transactions on Medical Imaging. 1999;18(12):1117–1128. doi: 10.1109/42.819322. [DOI] [PubMed] [Google Scholar]
- 63.Cordes D, Haughton V, Carew JD, Arfanakis K, Maravilla K. Hierarchical clustering to measure connectivity in fMRI resting-state data. Magnetic Resonance Imaging. 2002;20(4):305–317. doi: 10.1016/s0730-725x(02)00503-9. [DOI] [PubMed] [Google Scholar]
- 64.Foucher JR, Vidailhet P, Chanraud S, et al. Functional integration in schizophrenia: too little or too much? Preliminary results on fMRI data. NeuroImage. 2005;26(2):374–388. doi: 10.1016/j.neuroimage.2005.01.042. [DOI] [PubMed] [Google Scholar]
- 65.Tononi G, McIntosh AR, Russell DP, Edelman GM. Functional clustering: identifying strongly interactive brain regions in neuroimaging data. NeuroImage. 1998;7(2):133–149. doi: 10.1006/nimg.1997.0313. [DOI] [PubMed] [Google Scholar]
- 66.McKeown MJ, Makeig S, Brown GG, et al. Analysis of fMRI data by blind separation into independent spatial components. Human Brain Mapping. 1998;6(3):160–188. doi: 10.1002/(SICI)1097-0193(1998)6:3<160::AID-HBM5>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Friston KJ, Büchel C. Human Brain Function. San Diego, Calif, USA: Elsevier; 2004. Functional connectivity: eigenimages and multivariate analysis; pp. 999–1018. [Google Scholar]
- 68.Ecker C, Reynaud E, Williams SC, Brammer MJ. Detecting functional nodes in large-scale cortical networks with functional magnetic resonance imaging: a principal component analysis of the human visual system. Human Brain Mapping. 2007;28(9):817–834. doi: 10.1002/hbm.20311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Calhoun VD, Adali T, Pekar JJ, Pearlson GD. Latency (in)sensitive ICA: group independent component analysis of fMRI data in the temporal frequency domain. NeuroImage. 2003;20(3):1661–1669. doi: 10.1016/s1053-8119(03)00411-7. [DOI] [PubMed] [Google Scholar]
- 70.Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. Journal of Neuroscience. 2006;26(1):63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Salvador R, Suckling J, Coleman MR, Pickard JD, Menon D, Bullmore E. Neurophysiological architecture of functional magnetic resonance images of human brain. Cerebral Cortex. 2005;15(9):1332–2342. doi: 10.1093/cercor/bhi016. [DOI] [PubMed] [Google Scholar]
- 72.Salvador R, Suckling J, Schwarzbauer C, Bullmore E. Undirected graphs of frequency-dependent functional connectivity in whole brain networks. Philosophical Transactions of the Royal Society of London Series B. 2005;360(1457):937–946. doi: 10.1098/rstb.2005.1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Calhoun VD, Adali T, McGinty VB, Pekar JJ, Watson TD, Pearlson GD. fMRI activation in a visual-perception task: network of areas detected using the general linear model and independent components analysis. NeuroImage. 2001;14(5):1080–1088. doi: 10.1006/nimg.2001.0921. [DOI] [PubMed] [Google Scholar]
- 74.Calhoun VD, Adali T, Pearlson GD, Pekar JJ. A method for making group inferences from functional MRI data using independent component analysis. Human Brain Mapping. 2001;14(3):140–151. doi: 10.1002/hbm.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.van de Ven VG, Formisano E, Prvulovic D, Roeder CH, Linden DEJ. Functional connectivity as revealed by spatial independent component analysis of fMRI measurements during rest. Human Brain Mapping. 2004;22(3):165–178. doi: 10.1002/hbm.20022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. Philosophical Transactions of the Royal Society of London Series B. 2005;360(1457):1001–1013. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Damoiseaux JS, Rombouts SARB, Barkhof F, et al. Consistent resting-state networks across healthy subjects. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(37):13848–13853. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.De Luca M, Beckmann CF, De Stefano N, Matthews PM, Smith SM. fMRI resting state networks define distinct modes of long-distance interactions in the human brain. NeuroImage. 2006;29(4):1359–1367. doi: 10.1016/j.neuroimage.2005.08.035. [DOI] [PubMed] [Google Scholar]
- 79.Esposito F, Scarabino T, Hyvarinen A, et al. Independent component analysis of fMRI group studies by self-organizing clustering. NeuroImage. 2005;25(1):193–205. doi: 10.1016/j.neuroimage.2004.10.042. [DOI] [PubMed] [Google Scholar]
- 80.Bellec P, Perlbarg V, Jbabdi S, et al. Identification of large-scale networks in the brain using fMRI. NeuroImage. 2006;29(4):1231–1243. doi: 10.1016/j.neuroimage.2005.08.044. [DOI] [PubMed] [Google Scholar]
- 81.Tzourio-Mazoyer N, Landeau B, Papathanassiou D, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- 82.Lu Y, Jiang T, Zang Y. Region growing method for the analysis of functional MRI data. NeuroImage. 2003;20(1):455–465. doi: 10.1016/s1053-8119(03)00352-5. [DOI] [PubMed] [Google Scholar]
- 83.Fransson P. Spontaneous low-frequency BOLD signal fluctuations: an fMRI investigation of the resting-state default mode of brain function hypothesis. Human Brain Mapping. 2005;26(1):15–29. doi: 10.1002/hbm.20113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Fransson P. How default is the default mode of brain function? Further evidence from intrinsic BOLD signal fluctuations. Neuropsychologia. 2006;44(14):2836–2845. doi: 10.1016/j.neuropsychologia.2006.06.017. [DOI] [PubMed] [Google Scholar]
- 85.Greicius MD, Krasnow B, Reiss AL, Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proceedings of the National Academy of Sciences of the United States of America. 2003;100(1):253–258. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Greicius MD, Menon V. Default-mode activity during a passive sensory task: uncoupled from deactivation but impacting activation. Journal of Cognitive Neuroscience. 2004;16(9):1484–1492. doi: 10.1162/0898929042568532. [DOI] [PubMed] [Google Scholar]
- 87.Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Stein T, Moritz C, Quigley M, Cordes D, Haughton V, Meyerand E. Functional connectivity in the thalamus and hippocampus studied with functional MR imaging. American Journal of Neuroradiology. 2000;21(8):1397–1401. [PMC free article] [PubMed] [Google Scholar]
- 89.Mason MF, Norton MI, Van Horn JD, Wegner DM, Grafton ST, Macrae CN. Wandering minds: the default network and stimulus-independent thought. Science. 2007;315(5810):393–395. doi: 10.1126/science.1131295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Raichle ME. Neuroscience: the brain's dark energy. Science. 2006;314(5803):1249–1250. [PubMed] [Google Scholar]
- 91.Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proceedings of the National Academy of Sciences of the United States of America. 2001;98(2):676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Corbetta M, Shulman GL. Control of goal-directed and stimulus-driven attention in the brain. Nature Reviews Neuroscience. 2002;3(3):201–215. doi: 10.1038/nrn755. [DOI] [PubMed] [Google Scholar]
- 93.Ungerleider LG, Haxby JV. ‘What’ and ‘where’ in the human brain. Current Opinion in Neurobiology. 1994;4(2):157–165. doi: 10.1016/0959-4388(94)90066-3. [DOI] [PubMed] [Google Scholar]
- 94.Achim AM, Lepage M. Neural correlates of memory for items and for associations: an event-related functional magnetic resonance imaging study. Journal of Cognitive Neuroscience. 2005;17(4):652–667. doi: 10.1162/0898929053467578. [DOI] [PubMed] [Google Scholar]
- 95.Miller EK, Cohen JD. An integrative theory of prefrontal cortex function. Annual Review of Neuroscience. 2001;24:167–202. doi: 10.1146/annurev.neuro.24.1.167. [DOI] [PubMed] [Google Scholar]
- 96.Ungerleider LG, Courtney SM, Haxby JV. A neural system for human visual working memory. Proceedings of the National Academy of Sciences of the United States of America. 1998;95(3):883–890. doi: 10.1073/pnas.95.3.883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Doyon J, Benali H. Reorganization and plasticity in the adult brain during learning of motor skills. Current Opinion in Neurobiology. 2005;15(2):161–167. doi: 10.1016/j.conb.2005.03.004. [DOI] [PubMed] [Google Scholar]
- 98.Taniwaki T, Okayama A, Yoshiura T, et al. Functional network of the basal ganglia and cerebellar motor loops in vivo: different activation patterns between self-initiated and externally triggered movements. NeuroImage. 2006;31(2):745–753. doi: 10.1016/j.neuroimage.2005.12.032. [DOI] [PubMed] [Google Scholar]
- 99.Awh E, Vogel EK, Oh S-H. Interactions between attention and working memory. Neuroscience. 2006;139(1):201–208. doi: 10.1016/j.neuroscience.2005.08.023. [DOI] [PubMed] [Google Scholar]
- 100.Gruber O, Goschke T. Executive control emerging from dynamic interactions between brain systems mediating language, working memory and attentional processes. Acta Psychologica. 2004;115(2-3):105–121. doi: 10.1016/j.actpsy.2003.12.003. [DOI] [PubMed] [Google Scholar]
- 101.Naghavi HR, Nyberg L. Common fronto-parietal activity in attention, memory, and consciousness: shared demands on integration? Consciousness and Cognition. 2005;14(2):390–425. doi: 10.1016/j.concog.2004.10.003. [DOI] [PubMed] [Google Scholar]
- 102.Waites AB, Stanislavsky A, Abbott DF, Jackson GD. Effect of prior cognitive state on resting state networks measured with functional connectivity. Human Brain Mapping. 2005;24(1):59–68. doi: 10.1002/hbm.20069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Mechelli A, Penny WD, Price CJ, Gitelman DR, Friston KJ. Effective connectivity and intersubject variability: using a multisubject network to test differences and commonalities. NeuroImage. 2002;17(3):1459–1469. doi: 10.1006/nimg.2002.1231. [DOI] [PubMed] [Google Scholar]
- 104.Kaiser M, Hilgetag CC. Modelling the development of cortical systems networks. Neurocomputing. 2004;58–60:297–302. [Google Scholar]
- 105.Wu T, Zang Y, Wang L, et al. Aging influence on functional connectivity of the motor network in the resting state. Neuroscience Letters. 2007;422(3):164–168. doi: 10.1016/j.neulet.2007.06.011. [DOI] [PubMed] [Google Scholar]
- 106.Majewska AK, Sur M. Plasticity and specificity of cortical processing networks. Trends in Neurosciences. 2006;29(6):323–329. doi: 10.1016/j.tins.2006.04.002. [DOI] [PubMed] [Google Scholar]
- 107.Poldrack RA. Imaging brain plasticity: conceptual and methodological issues—a theoretical review. NeuroImage. 2000;12(1):1–13. doi: 10.1006/nimg.2000.0596. [DOI] [PubMed] [Google Scholar]
- 108.Calautti C, Baron J-C. Functional neuroimaging studies of motor recovery after stroke in adults: a review. Stroke. 2003;34(6):1553–1566. doi: 10.1161/01.STR.0000071761.36075.A6. [DOI] [PubMed] [Google Scholar]
- 109.Ward NS. Plasticity and the functional reorganization of the human brain. International Journal of Psychophysiology. 2005;58(2-3):158–161. doi: 10.1016/j.ijpsycho.2005.02.009. [DOI] [PubMed] [Google Scholar]
- 110.Duffau H. Lessons from brain mapping in surgery for low-grade glioma: insights into associations between tumour and brain plasticity. The Lancet Neurology. 2005;4(8):476–486. doi: 10.1016/S1474-4422(05)70140-X. [DOI] [PubMed] [Google Scholar]
- 111.Krainik A, Lehéricy S, Duffau H, et al. Postoperative speech disorder after medial frontal surgery: role of the supplementary motor area. Neurology. 2003;60(4):587–594. doi: 10.1212/01.wnl.0000048206.07837.59. [DOI] [PubMed] [Google Scholar]
- 112.Krainik A, Lehéricy S, Duffau H, et al. Role of the supplementary motor area in motor deficit following medial frontal lobe surgery. Neurology. 2001;57(5):871–878. doi: 10.1212/wnl.57.5.871. [DOI] [PubMed] [Google Scholar]
- 113.Thiel A, Herholz K, Koyuncu A, et al. Plasticity of language networks in patients with brain tumors: a positron emission tomography activation study. Annals of Neurology. 2001;50(5):620–629. doi: 10.1002/ana.1253. [DOI] [PubMed] [Google Scholar]
- 114.He BJ, Snyder AZ, Vincent JL, Epstein A, Shulman GL, Corbetta M. Breakdown of functional connectivity in frontoparietal networks underlies behavioral deficits in spatial neglect. Neuron. 2007;53(6):905–918. doi: 10.1016/j.neuron.2007.02.013. [DOI] [PubMed] [Google Scholar]
- 115.Gotman J, Grova C, Bagshaw A, Kobayashi E, Aghakhani Y, Dubeau F. Generalized epileptic discharges show thalamocortical activation and suspension of the default state of the brain. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(42):15236–15240. doi: 10.1073/pnas.0504935102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Buckner RL, Snyder AZ, Shannon BJ, et al. Molecular, structural, and functional characterization of Alzheimer's disease: evidence for a relationship between default activity, amyloid, and memory. Journal of Neuroscience. 2005;25(34):7709–7717. doi: 10.1523/JNEUROSCI.2177-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Başar E, Başar-Eroğlu C, Karakaş S, Schürmann M. Are cognitive processes manifested in event-related gamma, alpha, theta and delta oscillations in the EEG? Neuroscience Letters. 1999;259(3):165–168. doi: 10.1016/s0304-3940(98)00934-3. [DOI] [PubMed] [Google Scholar]
- 118.Başar E, Schürmann M, Sakowitz O. The selectively distributed theta system: functions. International Journal of Psychophysiology. 2000;39(2-3):197–212. doi: 10.1016/s0167-8760(00)00141-0. [DOI] [PubMed] [Google Scholar]
- 119.Karakaş S, Başar-Eroğlu C, Özesmi Ç, Kafadar H, Erzengin ÖÜ. Gamma response of the brain: a multifunctional oscillation that represents bottom-up with top-down processing. International Journal of Psychophysiology. 2000;39(2-3):137–150. doi: 10.1016/s0167-8760(00)00137-9. [DOI] [PubMed] [Google Scholar]
- 120.Schürmann M, Başar E. Functional aspects of alpha oscillations in the EEG. International Journal of Psychophysiology. 2000;39(2-3):151–158. doi: 10.1016/s0167-8760(00)00138-0. [DOI] [PubMed] [Google Scholar]
- 121.Leopold DA, Murayama Y, Logothetis NK. Very slow activity fluctuations in monkey visual cortex: implications for functional brain imaging. Cerebral Cortex. 2003;13(4):422–433. doi: 10.1093/cercor/13.4.422. [DOI] [PubMed] [Google Scholar]
- 122.Logothetis NK. The underpinnings of the BOLD functional magnetic resonance imaging signal. Journal of Neuroscience. 2003;23(10):3963–3971. doi: 10.1523/JNEUROSCI.23-10-03963.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Logothetis NK, Pauls J, Augath M, Trinath T, Oeltermann A. Neurophysiological investigation of the basis of the fMRI signal. Nature. 2001;412(6843):150–157. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
- 124.Logothetis NK, Pfeuffer J. On the nature of the BOLD fMRI contrast mechanism. Magnetic Resonance Imaging. 2004;22(10):1517–1531. doi: 10.1016/j.mri.2004.10.018. [DOI] [PubMed] [Google Scholar]
- 125.Winterer G, Carver FW, Musso F, Mattay V, Weinberger DR, Coppola R. Complex relationship between BOLD signal and synchronization/desynchronization of human brain MEG oscillations. Human Brain Mapping. 2007;28(9):805–816. doi: 10.1002/hbm.20322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Friston KJ, Williams S, Howard R, Frackowiak RSJ, Turner R. Movement-related effects in fMRI time-series. Magnetic Resonance in Medicine. 1996;35(3):346–355. doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- 127.Gretton A, Belitski A, Murayama Y, Schölkopf B, Logothetis N. The effect of artifacts on dependence measurement in fMRI. Magnetic Resonance Imaging. 2006;24(4):401–409. doi: 10.1016/j.mri.2005.12.036. [DOI] [PubMed] [Google Scholar]
- 128.Krüger G, Glover GH. Physiological noise in oxygenation-sensitive magnetic resonance imaging. Magnetic Resonance in Medicine. 2001;46(4):631–637. doi: 10.1002/mrm.1240. [DOI] [PubMed] [Google Scholar]
- 129.Dagli MS, Ingeholm JE, Haxby JV. Localization of cardiac-induced signal change in fMRI. NeuroImage. 1999;9(4):407–415. doi: 10.1006/nimg.1998.0424. [DOI] [PubMed] [Google Scholar]
- 130.Raj D, Anderson AW, Gore JC. Respiratory effects in human functional magnetic resonance imaging due to bulk susceptibility changes. Physics in Medicine and Biology. 2001;46(12):3331–3340. doi: 10.1088/0031-9155/46/12/318. [DOI] [PubMed] [Google Scholar]
- 131.Perlbarg V, Bellec P, Anton J-L, Pélégrini-Issac M, Doyon J, Benali H. CORSICA: correction of structured noise in fMRI by automatic identification of ICA components. Magnetic Resonance Imaging. 2007;25(1):35–46. doi: 10.1016/j.mri.2006.09.042. [DOI] [PubMed] [Google Scholar]
- 132.Thomas CG, Harshman RA, Menon RS. Noise reduction in BOLD-based fMRI using component analysis. NeuroImage. 2002;17(3):1521–1537. doi: 10.1006/nimg.2002.1200. [DOI] [PubMed] [Google Scholar]
- 133.Lund TE, Li S-J. fcMRI—mapping functional connectivity or correlating cardiac-induced noise? Magnetic Resonance in Medicine. 2001;46(3):628–628. doi: 10.1002/mrm.1238. [DOI] [PubMed] [Google Scholar]
- 134.Birn RM, Diamond JB, Smith MA, Bandettini PA. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. NeuroImage. 2006;31(4):1536–1548. doi: 10.1016/j.neuroimage.2006.02.048. [DOI] [PubMed] [Google Scholar]
- 135.Wise RG, Ide K, Poulin MJ, Tracey I. Resting fluctuations in arterial carbon dioxide induce significant low frequency variations in BOLD signal. NeuroImage. 2004;21(4):1652–1664. doi: 10.1016/j.neuroimage.2003.11.025. [DOI] [PubMed] [Google Scholar]
- 136.Anderson TW. An Introduction to Multivariate Statistical Analysis. New York, NY, USA: John Wiley & Sons; 1958. (Wiley Publications in Statistics). [Google Scholar]
- 137.Marrelec G, Bellec P, Duffau H, et al. Regions, systems, and the brain: hierarchical measures of functional integration in fMRI. doi: 10.1016/j.media.2008.02.002. to appear in Medical Image Analysis. [DOI] [PubMed] [Google Scholar]
- 138.Marrelec G, Bellec P, Benali H. Exploring large-scale brain networks in functional MRI. Journal of Physiology Paris. 2006;100(4):171–181. doi: 10.1016/j.jphysparis.2007.01.003. [DOI] [PubMed] [Google Scholar]
- 139.Marrelec G, Horwitz B, Kim J, Pélégrini-Issac M, Benali H, Doyon J. Using partial correlation to enhance structural equation modeling of functional MRI data. Magnetic Resonance Imaging. 2007;25(8):1181–1189. doi: 10.1016/j.mri.2007.02.012. [DOI] [PubMed] [Google Scholar]
- 140.Marrelec G, Krainik A, Duffau H, et al. Partial correlation for functional brain interactivity investigation in functional MRI. NeuroImage. 2006;32(1):228–237. doi: 10.1016/j.neuroimage.2005.12.057. [DOI] [PubMed] [Google Scholar]
- 141.Marrelec G, Kim J, Doyon J, Horwitz B. Large scale model validation of partial correlation analysis for effective connectivity Investigation in functional MRI. doi: 10.1002/hbm.20555. to appear in Human Brain Mapping. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Abler B, Roebroeck A, Goebel R, et al. Investigating directed influences between activated brain areas in a motor-response task using fMRI. Magnetic Resonance Imaging. 2006;24(2):181–185. doi: 10.1016/j.mri.2005.10.022. [DOI] [PubMed] [Google Scholar]
- 143.Goebel R, Roebroeck A, Kim D-S, Formisano E. Investigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magnetic Resonance Imaging. 2003;21(10):1251–1261. doi: 10.1016/j.mri.2003.08.026. [DOI] [PubMed] [Google Scholar]
- 144.Roebroeck A, Formisano E, Goebel R. Mapping directed influence over the brain using Granger causality and fMRI. NeuroImage. 2005;25(1):230–242. doi: 10.1016/j.neuroimage.2004.11.017. [DOI] [PubMed] [Google Scholar]
- 145.David O, Friston KJ. A neural mass model for MEG/EEG: coupling and neuronal dynamics. NeuroImage. 2003;20(3):1743–1755. doi: 10.1016/j.neuroimage.2003.07.015. [DOI] [PubMed] [Google Scholar]
- 146.Kötter R, Sommer FT. Global relationship between anatomical connectivity and activity propagation in the cerebral cortex. Philosophical Transactions of the Royal Society of London Series B. 2000;355(1393):127–134. doi: 10.1098/rstb.2000.0553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Tagamets M-A, Horwitz B. Integrating electrophysiological and anatomical experimental data to create a large-scale model that simulates a delayed match-to-sample human brain imaging study. Cerebral Cortex. 1998;8(4):310–320. doi: 10.1093/cercor/8.4.310. [DOI] [PubMed] [Google Scholar]
- 148.Tononi G, Sporns O, Edelman GM. Reentry and the problem of integrating multiple cortical areas: simulation of dynamic integration in the visual system. Cerebral Cortex. 1992;2(4):310–335. doi: 10.1093/cercor/2.4.310. [DOI] [PubMed] [Google Scholar]
- 149.Büchel C, Friston K. Assessing interactions among neuronal systems using functional neuroimaging. Neural Networks. 2000;13(8-9):871–882. doi: 10.1016/s0893-6080(00)00066-6. [DOI] [PubMed] [Google Scholar]
- 150.McIntosh AR. Towards a network theory of cognition. Neural Networks. 2000;13(8-9):861–870. doi: 10.1016/s0893-6080(00)00059-9. [DOI] [PubMed] [Google Scholar]
- 151.McIntosh AR, Gonzalez-Lima F. Structural equation modeling and its application to network analysis in functional brain imaging. Human Brain Mapping. 1994;2(1-2):2–22. [Google Scholar]
- 152.McIntosh AR, Grady CL, Ungerleider LG, Haxby JV, Rapoport SI, Horwitz B. Network analysis of cortical visual pathways mapped with PET. Journal of Neuroscience. 1994;14(2):655–666. doi: 10.1523/JNEUROSCI.14-02-00655.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Friston KJ, Harrison L, Penny W. Dynamic causal modelling. NeuroImage. 2003;19(4):1273–1302. doi: 10.1016/s1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- 154.Penny WD, Stephan KE, Mechelli A, Friston KJ. Comparing dynamic causal models. NeuroImage. 2004;22(3):1157–1172. doi: 10.1016/j.neuroimage.2004.03.026. [DOI] [PubMed] [Google Scholar]
- 155.Penny WD, Stephan KE, Mechelli A, Friston KJ. Modelling functional integration: a comparison of structural equation and dynamic causal models. NeuroImage. 2004;23(supplement 1):S264–S274. doi: 10.1016/j.neuroimage.2004.07.041. [DOI] [PubMed] [Google Scholar]
- 156.David O, Cosmelli D, Friston KJ. Evaluation of different measures of functional connectivity using a neural mass model. NeuroImage. 2004;21(2):659–673. doi: 10.1016/j.neuroimage.2003.10.006. [DOI] [PubMed] [Google Scholar]
- 157.Horwitz B. Relating fMRI and PET signals to neural activity by means of large-scale neural models. Neuroinformatics. 2004;2(2):251–266. doi: 10.1385/NI:2:2:251. [DOI] [PubMed] [Google Scholar]
- 158.Horwitz B, Braun AR. Brain network interactions in auditory, visual and linguistic processing. Brain and Language. 2004;89(2):377–384. doi: 10.1016/S0093-934X(03)00349-3. [DOI] [PubMed] [Google Scholar]
- 159.Husain FT, Tagamets M-A, Fromm SJ, Braun AR, Horwitz B. Relating neuronal dynamics for auditory object processing to neuroimaging activity: a computational modeling and an fMRI study. NeuroImage. 2004;21(4):1701–1720. doi: 10.1016/j.neuroimage.2003.11.012. [DOI] [PubMed] [Google Scholar]
- 160.Honey CJ, Kötter R, Breakspear M, Sporns O. Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(24):10240–10245. doi: 10.1073/pnas.0701519104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Gupte N, Singh BK, Janaki TM. Networks: structure, function and optimisation. Physica A. 2005;346(1-2):75–81. [Google Scholar]
- 162.Newman MEJ. The structure and function of complex networks. SIAM Review. 2003;45(2):167–256. [Google Scholar]
- 163.Strogatz SH. Exploring complex networks. Nature. 2001;410(6825):268–276. doi: 10.1038/35065725. [DOI] [PubMed] [Google Scholar]
- 164.Albert R, Barabási A-L. Statistical mechanics of complex networks. Reviews of Modern Physics. 2002;74(1):47–97. [Google Scholar]
- 165.Barabási A-L, Albert R. Emergence of scaring in random networks. Science. 1999;286(5439):509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 166.Achard S, Bullmore E. Efficiency and cost of economical brain functional networks. PLoS Computational Biology. 2007;3(2):e17. doi: 10.1371/journal.pcbi.0030017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Bassett DS, Bullmore E. Small-world brain networks. The Neuroscientist. 2006;12(6):512–523. doi: 10.1177/1073858406293182. [DOI] [PubMed] [Google Scholar]
- 168.Bassett DS, Meyer-Lindenberg A, Achard S, Duke T, Bullmore E. Adaptive reconfiguration of fractal small-world human brain functional networks. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(51):19518–19523. doi: 10.1073/pnas.0606005103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Sporns O, Zwi JD. The small world of the cerebral cortex. Neuroinformatics. 2004;2(2):145–162. doi: 10.1385/NI:2:2:145. [DOI] [PubMed] [Google Scholar]
- 170.Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 171.Chialvo DR. Critical brain networks. Physica A. 2004;340(4):756–765. [Google Scholar]
- 172.Eguíluz VM, Chialvo DR, Cecchi GA, Baliki M, Apkarian AV. Scale-free brain functional networks. Physical Review Letters. 2005;94(1):4 pages. doi: 10.1103/PhysRevLett.94.018102. Article ID 018102. [DOI] [PubMed] [Google Scholar]
- 173.Kaiser M, Martin R, Andras P, Young MP. Simulation of robustness against lesions of cortical networks. European Journal of Neuroscience. 2007;25(10):3185–3192. doi: 10.1111/j.1460-9568.2007.05574.x. [DOI] [PubMed] [Google Scholar]
- 174.Micheloyannis S, Pachou E, Stam CJ, et al. Small-world networks and disturbed functional connectivity in schizophrenia. Schizophrenia Research. 2006;87(1–3):60–66. doi: 10.1016/j.schres.2006.06.028. [DOI] [PubMed] [Google Scholar]
- 175.Shin C-W, Kim S. Self-organized criticality and scale-free properties in emergent functional neural networks. Physical Review E. 2006;74(4):4. doi: 10.1103/PhysRevE.74.045101.045101 [DOI] [PubMed] [Google Scholar]
- 176.Beckmann CF, Smith SM. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Transactions on Medical Imaging. 2004;23(2):137–152. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- 177.Himberg J, Hyvärinen A, Esposito F. Validating the independent components of neuroimaging time series via clustering and visualization. NeuroImage. 2004;22(3):1214–1222. doi: 10.1016/j.neuroimage.2004.03.027. [DOI] [PubMed] [Google Scholar]
- 178.Friman O, Westin C-F. Resampling fMRI time series. NeuroImage. 2005;25(3):859–867. doi: 10.1016/j.neuroimage.2004.11.046. [DOI] [PubMed] [Google Scholar]
- 179.Bellec P, Marrelec G, Benali H. A bootstrap test to investigate changes in brain connectivity for functional MRI. to appear in Statistica Sinica http://www3.stat.sinica.edu.tw/preprint/SS-07-138_1.pdf. [Google Scholar]
- 180.Calhoun VD, Adali T, Pekar JJ. A method for comparing group fMRI data using independent component analysis: application to visual, motor and visuomotor tasks. Magnetic Resonance Imaging. 2004;22(9):1181–1191. doi: 10.1016/j.mri.2004.09.004. [DOI] [PubMed] [Google Scholar]
- 181.Dodel S, Golestani N, Pallier C, ElKouby V, Le Bihan D, Poline J-B. Condition-dependent functional connectivity: syntax networks in bilinguals. Philosophical Transactions of the Royal Society of London Series B. 2005;360(1457):921–935. doi: 10.1098/rstb.2005.1653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182.Fristen KJ, Frith CD, Fletcher P, Liddle PF, Frackowiak RSJ. Functional topography: multidimensional scaling and functional connectivity in the brain. Cerebral Cortex. 1996;6(2):156–164. doi: 10.1093/cercor/6.2.156. [DOI] [PubMed] [Google Scholar]
- 183.Toro R, Burnod Y. Geometric atlas: modeling the cortex as an organized surface. NeuroImage. 2003;20(3):1468–1484. doi: 10.1016/j.neuroimage.2003.07.008. [DOI] [PubMed] [Google Scholar]
- 184.Unwin A, Theus M, Hofmann H. Graphics of Large Datasets. Visualizing A Million. New York, NY, USA: Springer; 2006. [Google Scholar]
- 185.Mizuhara H, Wang L-Q, Kobayashi K, Yamaguchi Y. Long-range EEG phase synchronization during an arithmetic task indexes a coherent cortical network simultaneously measured by fMRI. NeuroImage. 2005;27(3):553–563. doi: 10.1016/j.neuroimage.2005.04.030. [DOI] [PubMed] [Google Scholar]
- 186.Wheaton LA, Nolte G, Bohlhalter S, Fridman E, Hallett M. Synchronization of parietal and premotor areas during preparation and execution of praxis hand movements. Clinical Neurophysiology. 2005;116(6):1382–1390. doi: 10.1016/j.clinph.2005.01.008. [DOI] [PubMed] [Google Scholar]
- 187.Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. Journal of Magnetic Resonance, Series B. 1994;103(3):247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- 188.Behrens TEJ, Johansen-Berg H. Relating connectional architecture to grey matter function using diffusion imaging. Philosophical Transactions of the Royal Society of London Series B. 2005;360(1457):903–911. doi: 10.1098/rstb.2005.1640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 189.Behrens TEJ, Johansen-Berg H, Woolrich MW, et al. Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. Nature Neuroscience. 2003;6(7):750–757. doi: 10.1038/nn1075. [DOI] [PubMed] [Google Scholar]
- 190.Johansen-Berg H, Behrens TEJ, Robson MD, et al. Changes in connectivity profiles define functionally distinct regions in human medial frontal cortex. Proceedings of the National Academy of Sciences of the United States of America. 2004;101(36):13335–13340. doi: 10.1073/pnas.0403743101. [DOI] [PMC free article] [PubMed] [Google Scholar]