Abstract
Horizontal binocular disparities provide information about the distance of objects relative to the point of ocular fixation, and must be combined with an estimate of viewing distance in order to recover the egocentric distance of an object. Vergence angle and the gradient of vertical disparities across the visual field are thought to provide independent sources of viewing distance information, based on human behavioral studies. While the effect of vergence angle on horizontal disparity selectivity in early visual cortex has been examined (with mixed results), the effect of the vertical disparity field has not been explored. We manipulated the vertical disparities in a large random-dot stimulus to simulate different viewing distances, and we examined the effect of this manipulation on both the responses of neurons in the middle temporal (MT) area and on the psychophysical performance of the animal in a curvature discrimination task. We report here that alterations to the vertical disparity field have no effect on the horizontal disparity tuning of MT neurons. However, the same manipulation strongly and systematically biases the monkey's judgments of curvature, consistent with previous human studies. We conclude that monkeys, like humans, make use of the vertical disparity field to estimate viewing distance, but that the physiological mechanisms for this effect occur either downstream of MT or in a different pathway.
Introduction
An important task for the visual system is to estimate the three dimensional (3D) location of objects in the visual scene, so that we are able to effectively interact with our environment. For example, to reach quickly to an object in the field of view, the brain may need to compute the location of the target relative to the body (egocentric distance) so that an accurate reach can be planned.
Binocular vision provides important information for specifying 3D scene structure. The horizontal separation of the eyes produces binocular disparities, which typically have both a horizontal and a vertical component (Howard and Rogers 1995; 2002). Horizontal disparities provide precise information about the depth of objects relative to the point of ocular fixation. However, to compute the egocentric distance to a visual target, horizontal disparities must be combined with an estimate of the subject's viewing distance (the distance from the cyclopean eye to the point of fixation, e.g., Bishop 1989). What information is available to specify viewing distance? One obvious candidate is the vergence angle of the eyes. Either proprioceptive or efference copy signals regarding vergence angle could be used to specify viewing distance (accommodation signals could also contribute). Alternatively, theoretical work indicates that the pattern of vertical disparities across a large region of the visual field (Fig. 1) can also provide information about viewing distance (Bishop 1989; Mayhew 1982; Mayhew and Longuet-Higgins 1982).
Figure 1.
Schematic illustration of the vertical disparity field. A) An observer views a frontoparallel surface (checkerboard). The middle and bottom rows illustrate the left and right eye views for near and far viewing distances, respectively. Note that there are opposite gradients of vertical subtense in the two eyes' views, and that these gradients are larger for near viewing than far viewing. In this illustration, the gradients have been exaggerated for visual effect, and the left and right eye views have not been inverted (due to the lens). Due to the differential perspective of the two eyes, there is a horizontal gradient of vertical disparity between the two images. B) For symmetric convergence, the relationship between vertical disparity, visual field location, and viewing distance is given by: v(x,y) ≈ I x y / D, where v is the vertical disparity, I is the interocular separation, x and y are the horizontal (azimuth) and vertical (elevation) Fick angles to a point in space (in radians), and D is the viewing distance. This function is plotted as a color map, where the color of each point is related to the vertical disparity (computed based on the following values: I=3.0 cm, D = 57 cm). This relationship implies that the gradient of vertical disparity across space (e.g, the horizontal gradient at a fixed value of y) is inversely proportional to viewing distance. Note that vertical disparity will be zero for points along the vertical meridian (x = 0) or in the horizontal plane of regard (y = 0).
Previous human psychophysical studies have examined how vergence and vertical disparities modulate depth percepts based on horizontal disparities (Backus et al. 1999; Bradshaw et al. 1996; Cumming et al. 1991; Rogers and Bradshaw 1995; 1993; Sobel and Collett 1991). Both vergence and vertical disparities have been found to contribute to the viewing distance estimate used to interpret horizontal disparities, with the relative contributions of the two signals depending on the size of the visual display (Bradshaw et al. 1996). When the field of view is small, vergence angle dominates because vertical disparities are very small within the central visual field (see Fig. 1B) (Bradshaw et al. 1996; Cumming et al. 1991; Sobel and Collett 1991). When the field of view is large, vertical disparities contribute substantially and have even been reported to outweigh vergence angle in some tasks (Backus et al. 1999; Bradshaw et al. 1996).
Several previous studies have examined the effect of vergence angle on the horizontal disparity tuning of neurons in visual cortex, with somewhat mixed results. Some studies have reported that vergence angle modulates the gain of neural responses in primary visual cortex (V1) (Dobbins et al. 1998; Gonzalez and Perez 1998; Trotter et al. 1992; 1996), although others have found smaller effects (Cumming and Parker 1999, see Discussion). Studies of neurons at higher levels of processing also suggest that vergence angle can modify disparity selectivity (Dobbins et al. 1998; Roy et al. 1992). In contrast, the effect of the vertical disparity field on tuning for horizontal disparity has not been examined to our knowledge. We have addressed this issue in area MT, an extrastriate area that has been linked to depth perception in some tasks (DeAngelis et al. 1998; Dodd et al. 2001; Krug et al. 2004; Uka and DeAngelis 2004; 2006).
We have tested the hypothesis that manipulating the vertical disparity field to simulate different viewing distances will alter the tuning of MT neurons for horizontal disparities presented within the classical receptive field. The vertical disparity field could act to modify the gain of responses to horizontal disparities (as reported for vergence), or it could act to shift or broaden tuning curves along the horizontal disparity axis. For example, if neurons were to code egocentric distance, then their horizontal disparity tuning curves would be expected to shift systematically with changes in the vertical disparity field that simulate different viewing distances. We examined MT tuning curves for any of these possible changes. We have chosen to manipulate vertical disparities in a large region of the visual field that excludes the classical receptive field for two reasons. First, psychophysical studies indicate that the relevant vertical disparity signals are likely to arise from mechanisms that compute disparity gradients across a large area of the visual field (Kaneko and Howard 1996; 1997). Second, it is known that neurons as early as V1 are selective for both horizontal and vertical disparities presented within their classical receptive fields (Cumming 2002; Durand et al. 2006; Durand et al. 2002; Gonzalez et al. 1993; Trotter et al. 2004). To avoid confounds of local selectivity for vertical disparity, we therefore varied only horizontal disparities within the classical receptive field, whereas the remainder of the large-field display contained a gradient of vertical disparities that simulated different viewing distances (Fig. 2).
Figure 2.
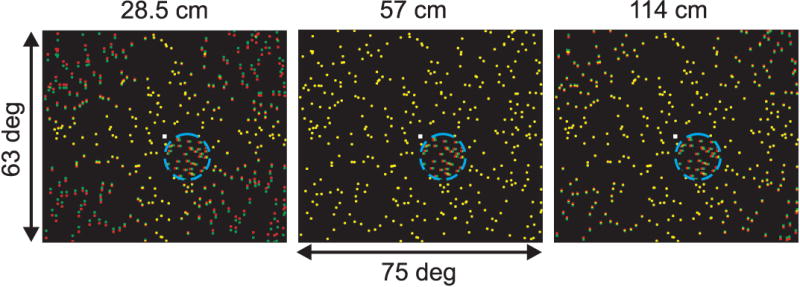
Illustration of the visual stimuli used to measure the effect of vertical disparities on horizontal disparity tuning in MT. Each panel shows a stimulus with a vertical disparity field that simulates a different viewing distance: 28.5, 57, and 114 cm (left to right). Red and green dots indicate the left and right half-images, respectively. The small white square is the fixation point, and the blue dashed circle (not visible in the actual display) indicates the boundary of the small dot patch that covers the MT receptive field. Dots within the receptive field have only a horizontal disparity and drift in the neurons preferred direction of motion. The horizontal disparity of the small patch of dots is varied across trials to measure disparity tuning curves for each simulated distance.
We report here that manipulating the vertical disparity field has no effect on the horizontal disparity tuning of MT neurons. In contrast, the same manipulation of vertical disparities was found to robustly modulate a monkey's depth percepts in a curvature discrimination task similar to that used in human studies (Rogers and Bradshaw 1995). Together, our findings indicate that monkeys (like humans) make use of vertical disparities to estimate viewing distance, but that the neural basis for this effect occurs either downstream of area MT or in a different pathway.
Methods
Subjects and surgery
Experiments were performed using three adult rhesus monkeys (Macaca mulatta) weighing between 5.4 and 9.4 kg. Two animals were used in single-unit recording experiments (monkeys L and R), and one animal was used in the psychophysical studies (monkey B). All animal care and experimental procedures were approved by the Institutional Animal Care and Use committee at Washington University, and were in accordance with NIH guidelines.
For each animal, a head restraint post was attached to the skull using cortical screws and cranioplastic cement. Eye coils were implanted under the conjunctiva of both eyes for monitoring changes in eye position, including both version and vergence (Judge et al. 1980). A cylindrical recording chamber was implanted over the occipital cortex (centered at 17mm lateral and 14mm dorsal to the occipital ridge) in each of the two monkeys that were used for single unit recordings. The long axis of the chamber was oriented in a parasaggital plane and was inclined 25° relative to the horizontal plane, such that area MT was accessed after passing through extrastriate visual areas in the lunate sulcus. All surgical procedures were performed under sterile conditions using gas inhalation anesthesia (isoflurane, 1-2%), as described previously (DeAngelis and Uka 2003; Uka and DeAngelis 2003).
Visual stimuli
Random-dot stereograms were programmed using the OpenGL graphics libraries under Microsoft Visual C++, and were generated by an OpenGL accelerator board (Oxygen GVX1 Pro or GVX420; 3DLabs, Milpitas, CA) that was housed in a dedicated, dual-CPU computer (see DeAngelis and Uka 2003 for details). Each dot in the stereogram subtended approximately 0.1°, and dots were rendered using the hardware anti-aliasing capability of the OpenGL board to provide sub-pixel resolution. The stimuli were viewed stereoscopically by the monkey through ferro-electric shutter glasses that were driven by the graphics board; this allowed frame-sequential presentation of stimuli to the two eyes. All stereograms consisted of red dots on a black background, with an average density of 64 dots per square degree per second.
In all physiological experiments and roughly half of the psychophysical experiments, the monkey viewed stimuli that were rear projected using a stereoscopic projector (100 Hz vertical refresh rate, 1280 X 1024 resolution; Mirage 2000; Christie Digital Systems, Cypress, CA) onto a large tangent screen placed at a viewing distance of 57cm. At this viewing distance, the screen subtended 75° × 63°. This 3-chip DLP projection system has essentially no visual persistence, and stereo crosstalk in this display setup was negligible. Roughly half of the psychophysical sessions were conducted in a different rig in which the monkey viewed stimuli presented on a 22″ CRT (Sony) viewed from a distance of 57 cm. This display subtended 40° × 30°, and stereo crosstalk was ∼3% in this system. We did not find any significant difference (ANCOVA, p > 0.1) between psychophysical results (Fig. 9) obtained in the two systems; hence the data have been pooled for presentation.
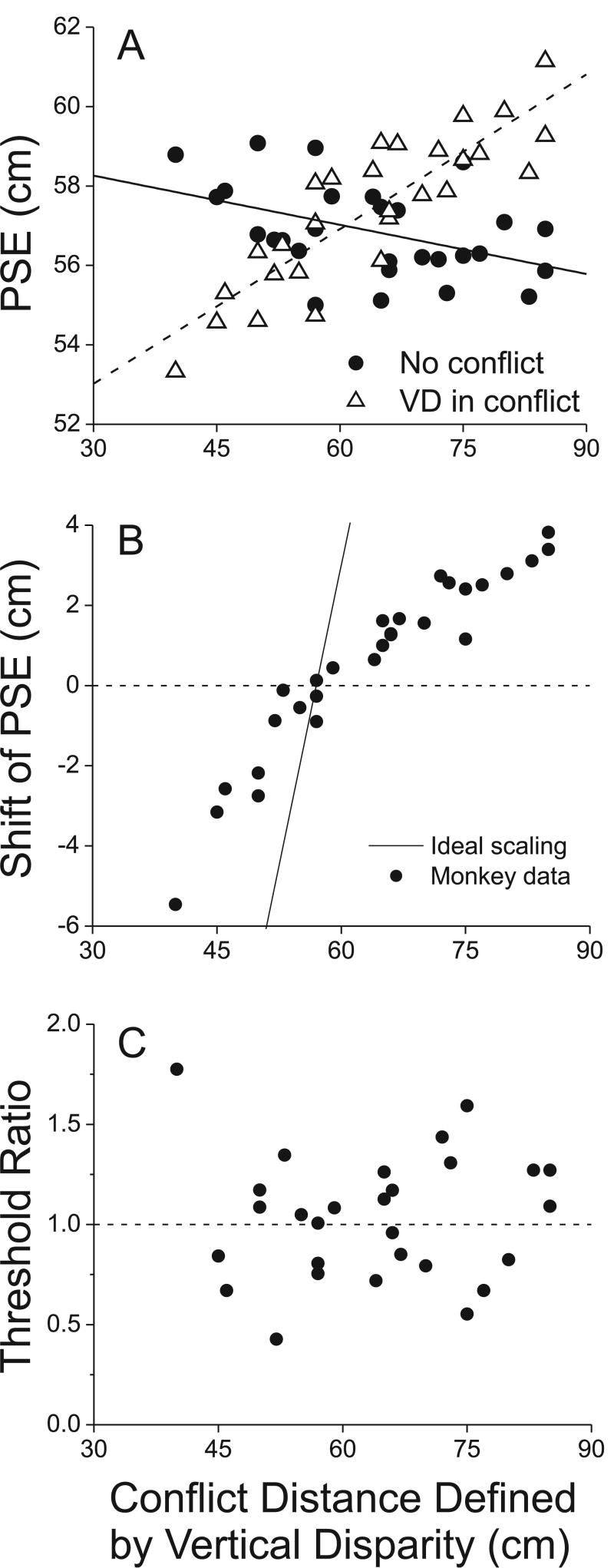
Figure 9.
Summary data showing that vertical disparity biases curvature judgments without affecting sensitivity (N=29 sessions). A) The PSE of the monkey is plotted as a function of the distance simulated by vertical disparities. Open triangles show the PSE from each session when the vertical disparity gradient simulated a viewing distance that was in conflict with the real physical distance of 57 cm (‘VD in conflict’). Filled circles show the PSE from each session when the vertical disparity field was consistent with the physical viewing distance (‘No conflict’). B) The shift of the PSE (horizontal offset between the two psychometric functions) is plotted against the simulated distance defined by the vertical disparity gradient. Note that when vertical disparities simulate a distance >57cm, the PSE shift is positive, whereas vertical disparities that simulated distances <57cm produce negative PSE shifts. B) The ratio of psychophysical thresholds (i.e., slopes of the psychometric functions around 57cm) between the cue-conflict and no-conflict conditions is plotted as a function of the conflict distance defined by vertical disparity. There is no systematic dependence of threshold on the distance simulated by vertical disparity.
In physiology experiments, the visual stimulus consisted of a small patch of drifting random dots that was tailored to the size and location of the classical receptive field of the recorded MT neuron. This small patch of dots was superimposed over a full-field random-dot background (see Fig. 2; note that the small patch occluded a portion of the background). The small patch of dots varied only in horizontal disparity, allowing us to measure the disparity tuning of the neuron. The full-field background stimulus was always presented with zero horizontal disparity (on the screen), such that it appeared to lie in the plane of the display screen when the vertical disparity was also zero (Fig. 2, middle). Across trials, a gradient of vertical disparity was applied to the background stimulus in order to simulate different viewing distances (Fig. 2, left and right panels). The computations used to generate these stimuli have been described previously (Wei et al. 2003, Appendix). It is well established that applying a gradient of vertical disparity to a large-field background stimulus induces a subtle percept of curvature (Rogers and Bradshaw 1995), and we take advantage of this fact in the psychophysical experiments described below.
Note that the horizontal and vertical disparities of the background stimulus were zero in the region immediately around the fixation point (Fig. 2), and that the small patch of dots never overlapped the fixation point. Thus, the stimulus did not drive vergence away from the plane of fixation, and monkeys were required to maintain their vergence angle within a 0.5° vergence window in most experiments. As a result, vergence was always maintained near the actual eye-to-screen distance of 57cm, even when vertical disparities simulated a larger or smaller distance. Therefore, our stimuli involved cue conflict between vertical disparities and vergence (and most likely also accommodation). This was intentional, as we sought to isolate the effects of vertical disparity in this study.
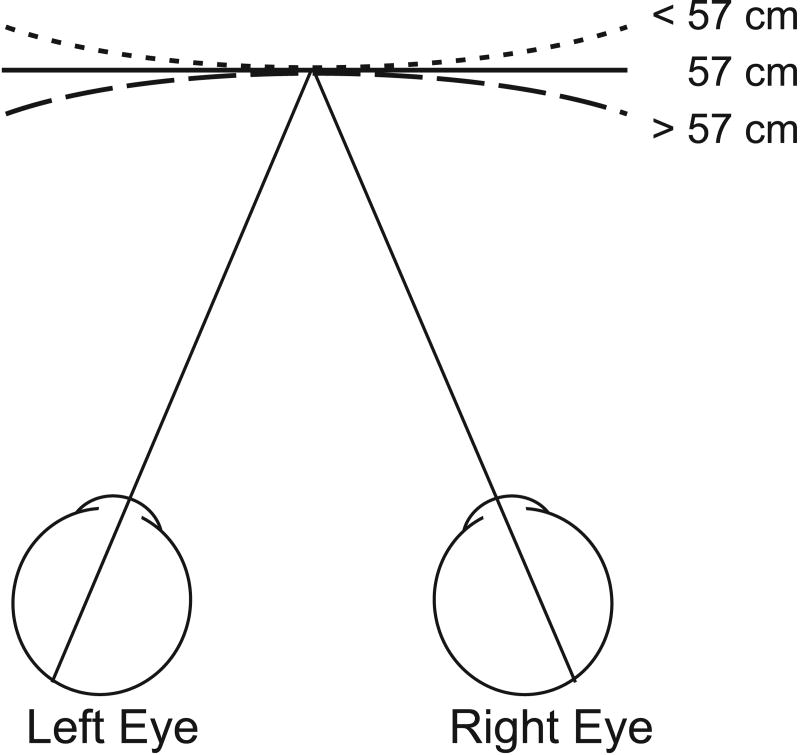
In the psychophysical experiments, the visual stimulus was a single full-field random dot pattern. A gradient of horizontal disparity was applied to the stimulus to simulate different viewing distances. When the horizontal disparity gradient simulated a distance >57cm, the random-dot surface appeared slightly concave, whereas a simulated distance <57cm made the surface appear slightly convex (Fig. 7). Thus, the horizontal disparity gradient was used to vary the curvature of the random-dot surface. This manipulation is based on the fact that the geometric horopter (Vieth-Muller circle) has a curvature that decreases with larger viewing distance. This stimulus allowed us to explore the effect of a gradient of vertical disparity on the perceived curvature of the surface, by measuring how the vertical disparity gradient biases the percept of curvature created by the horizontal disparity gradient (described further below). When both horizontal and vertical disparity gradients were applied, individual dots within the visual stimulus generally had both a horizontal and a vertical disparity component.
Figure 7.
Schematic illustration of the viewing situation in the curvature discrimination task. The monkey views a full-field random-dot stereogram that is made to appear curved (convex or concave) by addition of a horizontal disparity gradient that simulates different viewing distances. Simulated distances < 57 cm appear convex (short-dashed curve), > 57 cm appear concave (long-dashed curve), and 57 cm appears flat (solid line). At the end of each trial, the monkey makes a saccade to one of two targets to report his percept as ‘concave’ or ‘convex’. After the monkey was fully trained to discriminate the sign of curvature based on horizontal disparities, cue conflict conditions were introduced in which a vertical disparity gradient simulating a discrepant viewing distance was added to the display on half of the trials.
In the physiology experiment, the vertical disparity gradient of the background (on the large 75° × 63° display) generally did not extend through the portion of the display that covered the receptive field (except for a few neurons, see Discussion). In contrast, the display for the psychophysical experiment contained an uninterrupted vertical disparity gradient. This difference is very unlikely to be important, especially given that the psychophysical results were equally strong on the smaller (40° × 30°) display. Vertical disparities are most informative about viewing distance in the periphery (where they are large), and reducing the overall display size would be expected to have a much larger effect on the vertical disparity cue than interrupting the gradient within the small region over the receptive field.
Tasks and experimental protocols
Physiology experiments
Monkeys were trained through operant conditioning to maintain fixation within a small window (1.5-2.0° full width for version, 0.5° full width for vergence) in order to receive liquid rewards. In all physiology experiments, the monkey's task was simply to maintain fixation throughout the 1.5s stimulus presentation. Trials were aborted and data discarded when the monkey failed to maintain fixation. Correct trials were rewarded with a drop (0.1-0.15 ml) of water or juice.
Once the action potential of a single unit was isolated, the receptive field was first mapped manually using a computer-controlled search program. The center of the receptive field was localized carefully by moving a small patch of drifting random dots around the screen and observing a density map of the instantaneous firing rate of the neuron. This was taken as the center location for subsequent stimuli. Each neuron was then subject to a standard battery of preliminary tests as described in detail elsewhere (DeAngelis and Uka 2003). Direction tuning was measured by presenting 8 directions of motion, 45° apart, in a block of randomly interleaved trials. Speed tuning was measured by presenting a block of randomized trials with speeds of 0, 0.5, 1, 2, 4, 8, 16, and 32 deg/sec. Size tuning (area summation) was measured by presenting random dots patches having diameters of 0, 1, 2, 4, 8, 16, and 32°. The optimal direction, speed, and size of the random dot pattern were determined from these tests and were used in the subsequent measurements. For some cells, the receptive field was also mapped quantitatively by presenting small patches of dots (typically ¼ the receptive field size) at all locations on a 4×4 grid of positions that covered the receptive field. These quantitative receptive field maps were used to confirm accurate centering of the stimuli over the receptive field.
Following these preliminary tests, the horizontal disparity selectivity of each neuron was measured at each of 3 different simulated distances specified by vertical disparity (Fig. 2). Across trials, nine different horizontal disparities (typically 0°, ±0.4°, ±0.8°, ±1.2°, and ±1.6°), were presented in the small patch of dots that covered the classical receptive field of the MT neuron. This set of horizontal disparities was presented for each of three different simulated distances specified by the vertical disparity of the background dots: 28.5, 57, and 114 cm. All 27 stimulus conditions, plus a blank condition, were randomly interleaved in a single block of trials, and each distinct stimulus was typically presented at least 5 times. These data were used to construct a horizontal disparity tuning curve for each of the 3 simulated distances.
Psychophysical experiments
For the psychophysical experiments, monkey B was trained to perform a curvature discrimination task very similar to that used previously to study effects of vertical disparity gradients on human perception (Rogers and Bradshaw 1995). In this task, the monkey first fixated a point at the center of the display screen. A full-field random-dot pattern then appeared. The gradient of horizontal disparity in this stimulus was varied across trials to simulate different distances, resulting in different perceived surface curvatures (owing to the fact that the geometric horopter, or Vieth-Muller circle, has less curvature at larger viewing distances). When no horizontal disparity gradient was added to the stimulus (in screen coordinates), the random-dot surface appeared flat. When a horizontal disparity gradient was added to the stimulus to simulate a distance > 57cm (57 cm was the actual eye-to-screen distance), the random-dot field appeared slightly concave along the horizontal dimension (Fig. 7). A horizontal disparity gradient that simulated a distance < 57cm caused the surface to appear slightly convex. The monkey was trained to report whether the surface appeared concave or convex by making a saccade to one of two choice targets that appeared at the end of each trial when the random dot stimulus was extinguished. The two choice targets were located 5° left and right of the fixation point, and corresponded to convex and concave judgments, respectively.
Once the monkey learned to perform the task at > 80% correct for large curvatures, the simulated distances were varied across trials in a staircase procedure. As the simulated distance approaches 57cm from above or below, the random-dot surfaces appear closer to flat and performance of the animal approaches chance. Thus, by varying the simulated distance defined by the horizontal disparity gradient, we were able to measure a psychometric function for the monkey (see Fig. 8, filled symbols).
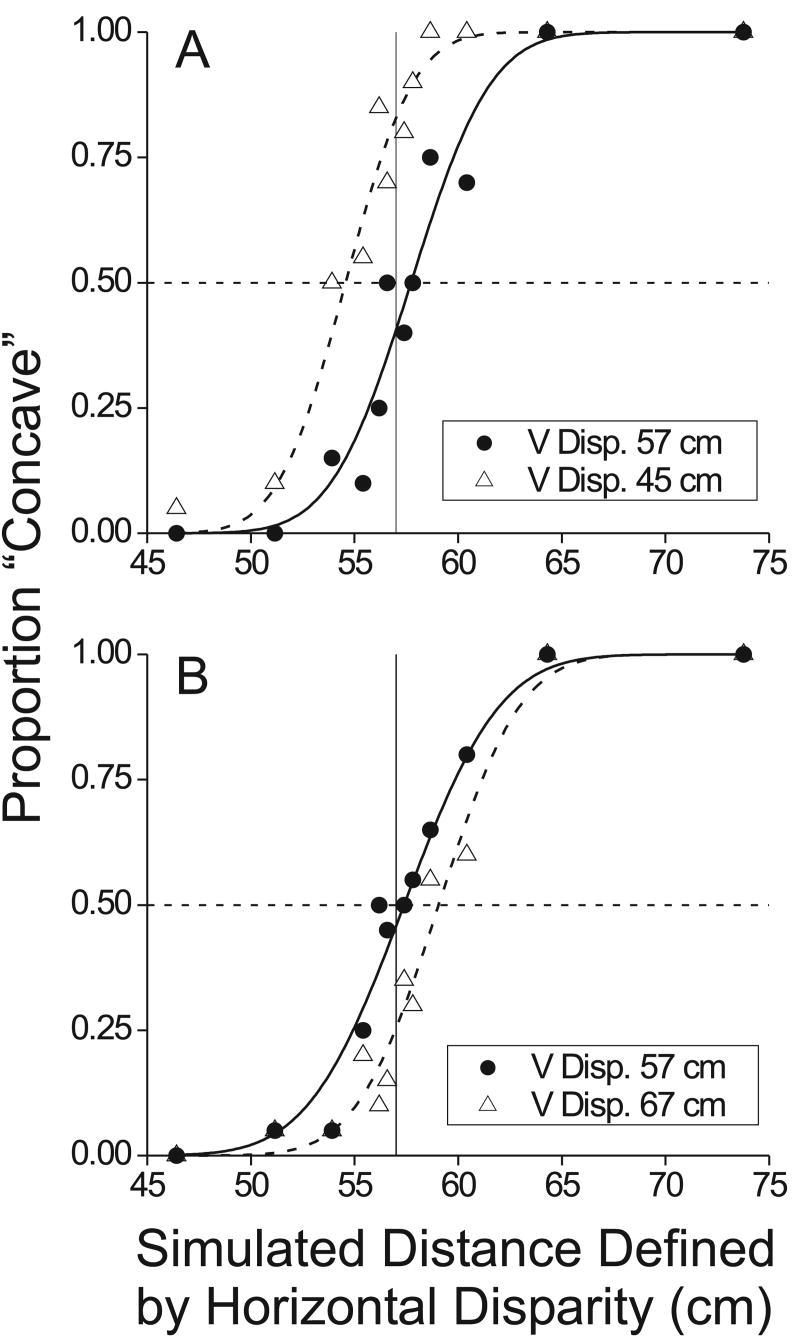
Figure 8.
Example psychophysical data from the curvature discrimination task performed by monkey B. In each panel, the proportion of “concave” decisions is plotted as a function of simulated distance defined by horizontal disparity. Smooth curves are fits of a cumulative Gaussian function. Filled symbols and solid curves indicate conditions in which the vertical disparity field was consistent with the actual viewing distance of 57cm. Open symbols and dashed curves indicate conditions in which vertical disparities simulate a different (discrepant) viewing distance. A) A vertical disparity gradient simulating a distance of 45cm causes a leftward shift of the psychometric function. As a result, the monkey's point of subjective equality (PSE) shifts toward smaller distances. B) A vertical disparity gradient simulating a distance of 67cm shifts the psychometric function (and the PSE) to the right.
Once psychophysical thresholds reached a plateau level of performance, we began to introduce ‘conflict’ trials in which the gradient of vertical disparities simulated a distance that was different from the actual eye-to-screen viewing distance of 57cm. In each session of data collection, the vertical disparity gradient simulated two viewing distances: 57cm (no conflict) and some other distance either less than or greater than this value. If the monkey uses the gradient of vertical disparity to estimate viewing distance and interpret horizontal disparities, then a vertical disparity gradient that simulates a distance of < 57cm should cause the monkey to perceive the surface as frontoparallel when the horizontal disparity gradient also simulates a distance of < 57cm. Thus, by measuring the change in the monkey's point of subjective equality (PSE) – equivalent to the horizontal shift of the psychometric function – we can quantify the effect of the vertical disparity gradient on the percept of surface curvature defined by horizontal disparities. Across sessions, different ‘conflict’ distances defined by the vertical disparity gradient were tested, with each block of trials containing one conflict distance and the non-conflict distance of 57 cm. The order of presentation of the different conflict distances was varied quasi-randomly across behavioral sessions.
It is important to note that the animal was always rewarded based on the curvature defined by the horizontal disparity cue (as though the conflicting vertical disparities were not present). As a result, a shift in the animal's PSE due to conflicting vertical disparities will tend to reduce the animals overall reward rate. It would, therefore, be in the animal's best interest to ignore the vertical disparity cue if this were possible. We adopt this conservative approach because we think it provides the strongest test of the hypothesis that the vertical disparity field alters the animal's percept of curvature based on horizontal disparities. A similar approach has been adopted in microstimulation studies (DeAngelis et al. 1998; Salzman et al. 1992).
Data acquisition
Extracellular activity of single neurons was recorded using tungsten microelectrodes (impedance typically 0.5-3.0 MΩ at 1 kHz, FHC, Inc.). The electrode was advanced into the cortex through a transdural guide tube, using a micromanipulator (MO 951C, Narishige, East Meadow, NY). Single units were isolated by using a conventional amplifier, bandpass filter (500-5000 Hz), and window discriminator (Bak Electronics, Mount Airy, MD). Times of occurrence of action potentials and trial events were stored to disk with 1 ms resolution. The positions of both eyes were sampled at 1 kHz and stored at 250 Hz. Behavioral and neural data acquisition was controlled by a commercially available software package (TEMPO, Reflective Computing, Olympia, WA).
Area MT was recognized on the basis of several anatomical and physiological criteria that have been described previously (DeAngelis and Newsome 1999; DeAngelis and Uka 2003). All data included in this study were derived from recordings that were assigned confidently to area MT. Recording sessions usually lasted for a duration of 3-5 hours, and animals typically performed between 600-1200 trials during this time.
Data analysis
Physiology experiments
For each correctly completed fixation trial, the response of the neuron was taken to be the mean firing rate over the 1.5 s stimulus period. Tuning curves were constructed by plotting the mean firing rate of the neuron (±se) as a function of the horizontal disparity of the small dot patch that covered the classical receptive field. One tuning curve was constructed for each of the 3 simulated distances specified by the vertical disparity gradient (see Fig. 4 for examples).
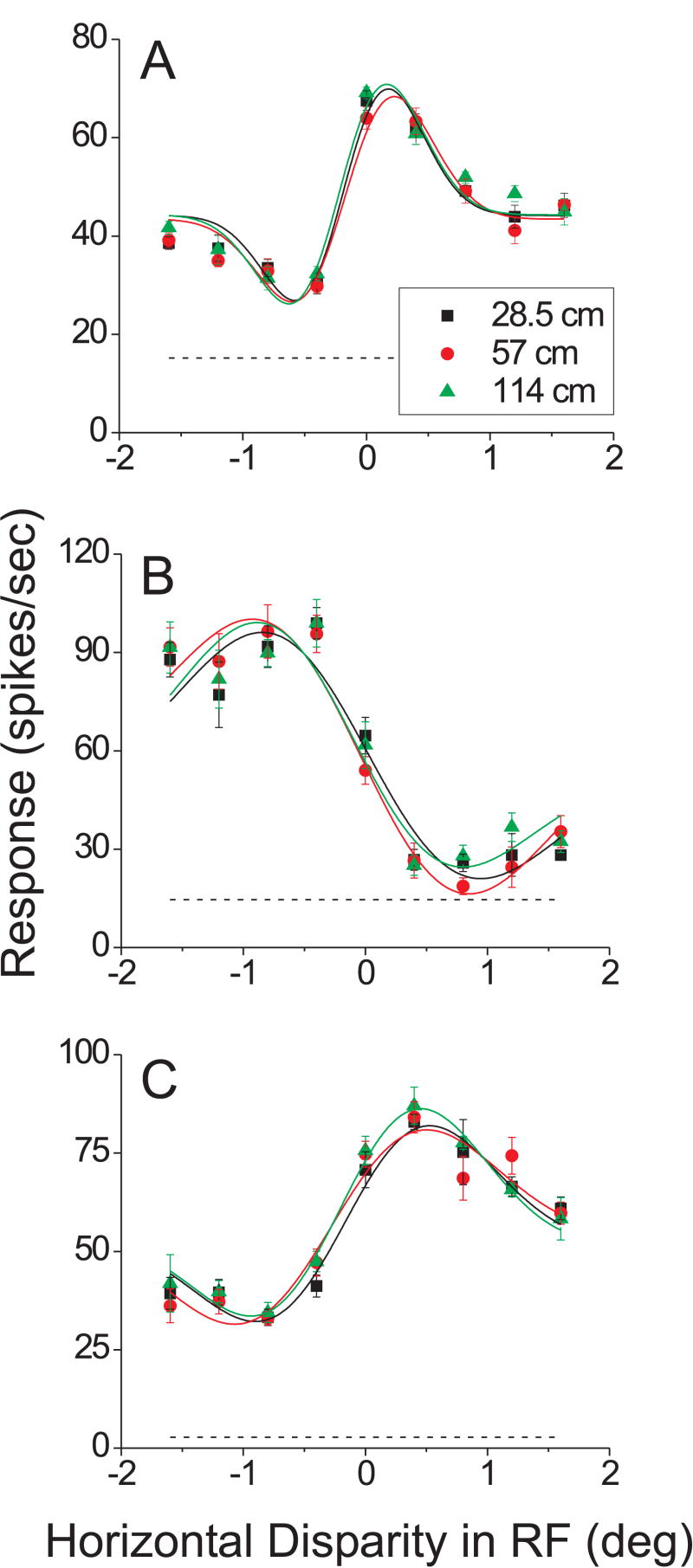
Figure 4.
Effect of vertical disparities on horizontal disparity tuning for 3 typical MT neurons. In each panel, horizontal disparity tuning curves are shown for three simulated viewing distances defined by vertical disparity gradients: 28.5 cm (black), 57 cm (red), and 114 cm (green). For each tuning curve, response strength (spikes/sec) is plotted as a function of the horizontal disparity of the patch of dots that covered the classical receptive field. Smooth curves are the best-fitting independent Gabor functions, and the dashed line indicates the level of spontaneous activity.
To quantify whether the vertical disparity gradient had a statistically significant effect on the horizontal disparity tuning of each MT neuron, we performed parametric analyses based on fitting Gabor functions to the disparity tuning curves (see DeAngelis and Uka 2003; Palanca and DeAngelis 2003 for additional details). Each disparity tuning curve was fit with a Gabor function of the form:
| (1) |
where d is the stimulus disparity, R0 is the baseline activity level, A is the amplitude, d0 is the center of the Gaussian envelope, σ is the standard deviation of the Gaussian, f is the frequency of the sinusoid, and Φ is the phase of the sinusoid (relative to the center of the Gaussian).
To test whether the viewing distance simulated by vertical disparity altered the tuning of a neuron for horizontal disparity, we asked whether the trio of tuning curves was significantly better fit by three independent Gabor functions than by a single Gabor function (identical for each simulated viewing distance). Thus, we compared the error of the independent Gabor fits to the error obtained when all 3 curves were fit with a single Gabor function, and we assessed the significance of the difference in error using a sequential F test. Since the Gabor function is not linear in its parameters, we first performed Monte Carlo simulations to determine that the sequential F-test worked properly in our application (see also Palanca and DeAngelis 2003). If the sequential F-test yielded a significant outcome (p < 0.05), we would conclude that the three different disparity tuning curves were not identical.
Psychophysical experiments
For the curvature discrimination task, we constructed psychometric functions by plotting the monkey's proportion of ‘concave’ reports as a function of the simulated distance defined by the horizontal disparity gradient (Fig. 8). The psychometric functions from each session were fit with cumulative Gaussian curves. The standard deviation of the cumulative Gaussian was taken as the psychophysical threshold of the animal (corresponding to 84% correct performance), and the offset of the underlying Gaussian was taken as the monkey's point of subjective equality (PSE). The PSE is the point where the psychometric function crosses 50% ‘concave’ decisions.
In each session of psychophysics, we determined both the threshold and PSE of the monkey's behavior for both of the distances simulated by vertical disparities (one distance was 57cm, the other was greater or less than 57cm). The difference in PSE between the two vertical disparity conditions was taken as the change in perceived curvature induced by application of the conflicting vertical disparity gradient.
Results
We present the results of this study in two parts. First, we describe how manipulating the vertical disparity field affects the tuning of MT neurons to horizontal disparities. Second, we describe how the same manipulation of the vertical disparity field affects a monkey's perceptual judgments of surface curvature.
Effect of vertical disparity gradient on MT responses
As illustrated in Figure 2, we constructed random-dot stereograms that allowed us to measure the influence of vertical disparities on the horizontal disparity tuning of MT neurons. A small patch of dots filled the classical receptive field of the MT neuron, and these dots varied in horizontal disparity (typically from -1.6° to 1.6° in steps of 0.4°) to characterize the conventional disparity tuning curve (DeAngelis and Uka 2003). The average size of the receptive field patch was 9.9° (±0.56° se; range: 4° to 30°) and the average eccentricity of the MT receptive fields was 8.7° (±0.46° se; range: 2.5° to 20.5°). The remainder of the large-field visual display was filled with dots that contained a gradient of vertical disparities that simulated one of three viewing distances: 28.5, 57, and 114 cm. All 27 combinations of horizontal disparities and simulated distances were randomly interleaved in a single block of trials, such that we simultaneously measured the horizontal disparity tuning of the neuron for each simulated viewing distance.
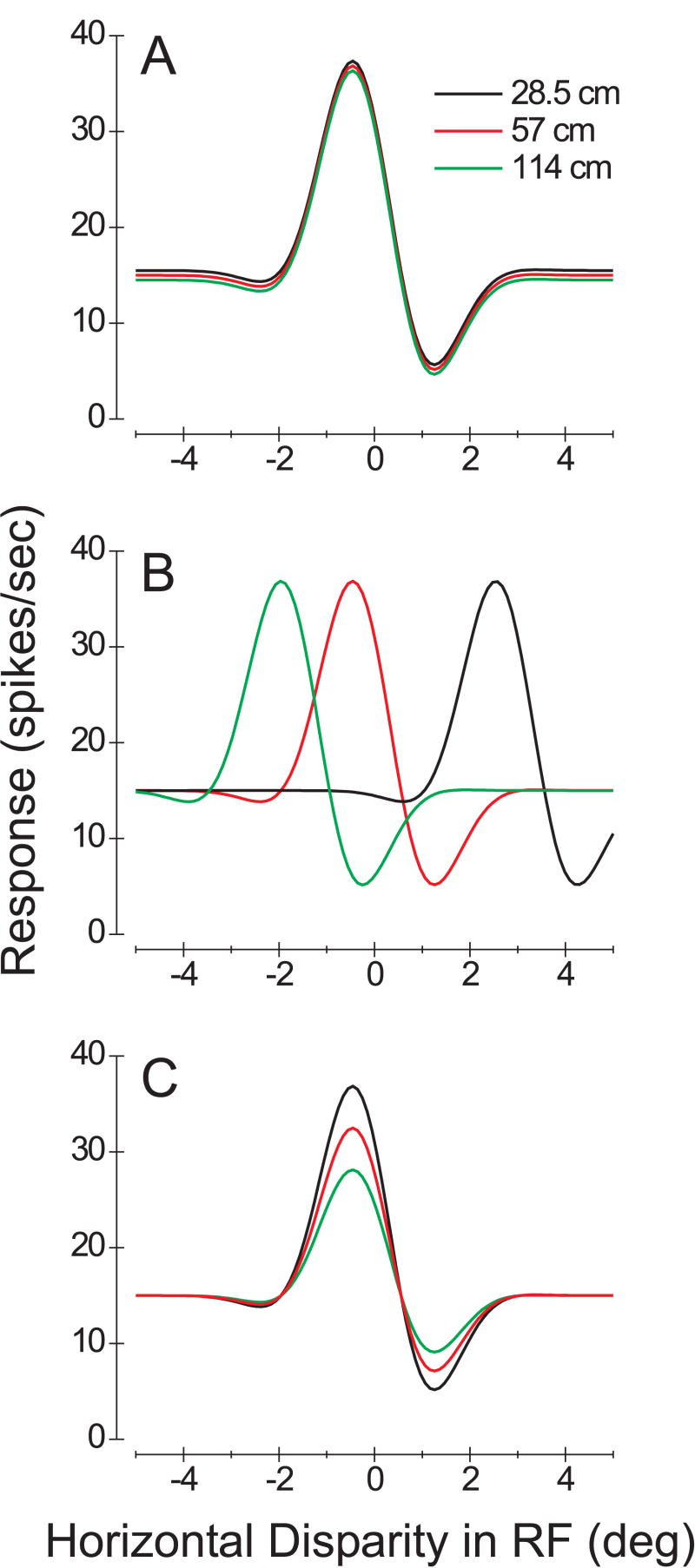
Figure 3 illustrates schematically some possible outcomes of this experiment. If an estimate of viewing distance based on vertical disparity has no effect on horizontal disparity coding in area MT, then the disparity tuning curves measured at the three simulated distances should be identical (Fig. 3A). Another extreme possibility is that MT neurons might be tuned for egocentric distance. In this case, the horizontal disparity tuning of the neuron would shift substantially with simulated viewing distance (Fig. 3B). Specifically, a simulated distance of 28.5cm would cause the horizontal disparity tuning curve to shift rightward by 3.0° (black curve), whereas a simulated distance of 114 cm would cause a leftward shift of 1.5° (green curve). These predictions assume an interocular distance of 3 cm, and that viewing distance is specified solely by the gradient of vertical disparity. Realistically, one would not expect shifts this large because vergence angle and accommodation are in conflict with vertical disparities in our experiment (by design). Nevertheless, if vertical disparities contribute to a computation of egocentric distance in MT, one should see tuning curves shift in the direction of the effects illustrated in Fig. 3B. A third possible outcome is that vertical disparities would change the response gain of MT neurons without shifting the tuning curve (Fig. 3C). This outcome would be akin to the effects of vergence angle on disparity tuning reported in some studies of V1 neurons (Gonzalez and Perez 1998; Trotter et al. 1992; 1996). Such a gain effect could also contribute to a coding of egocentric distance (Pouget and Sejnowski 1994). Our physiology experiment was designed to detect any of these possible outcomes, as well as others not listed here (such as changes in tuning width).
Figure 3.
Schematic illustration of some possible outcomes of the physiology experiment. Smooth curves are Gabor functions that represent the horizontal disparity tuning of a hypothetical neuron. The three color-coded curves in each panel represent viewing distances of 28.5 (black), 57 (red), and 114 (green) cm, as simulated by the gradient of vertical disparities. A) A situation in which the vertical disparity field has no effect on horizontal disparity tuning. B) A scenario in which the neuron codes for egocentric distance, such that its horizontal disparity tuning curve shifts according to the viewing distance simulated by vertical disparity. The predicted shifts are based on an interocular distance of 3.0 cm. C) A situation in which simulated distance modulates the gain of the neural response, without altering the shape or location of the tuning curve.
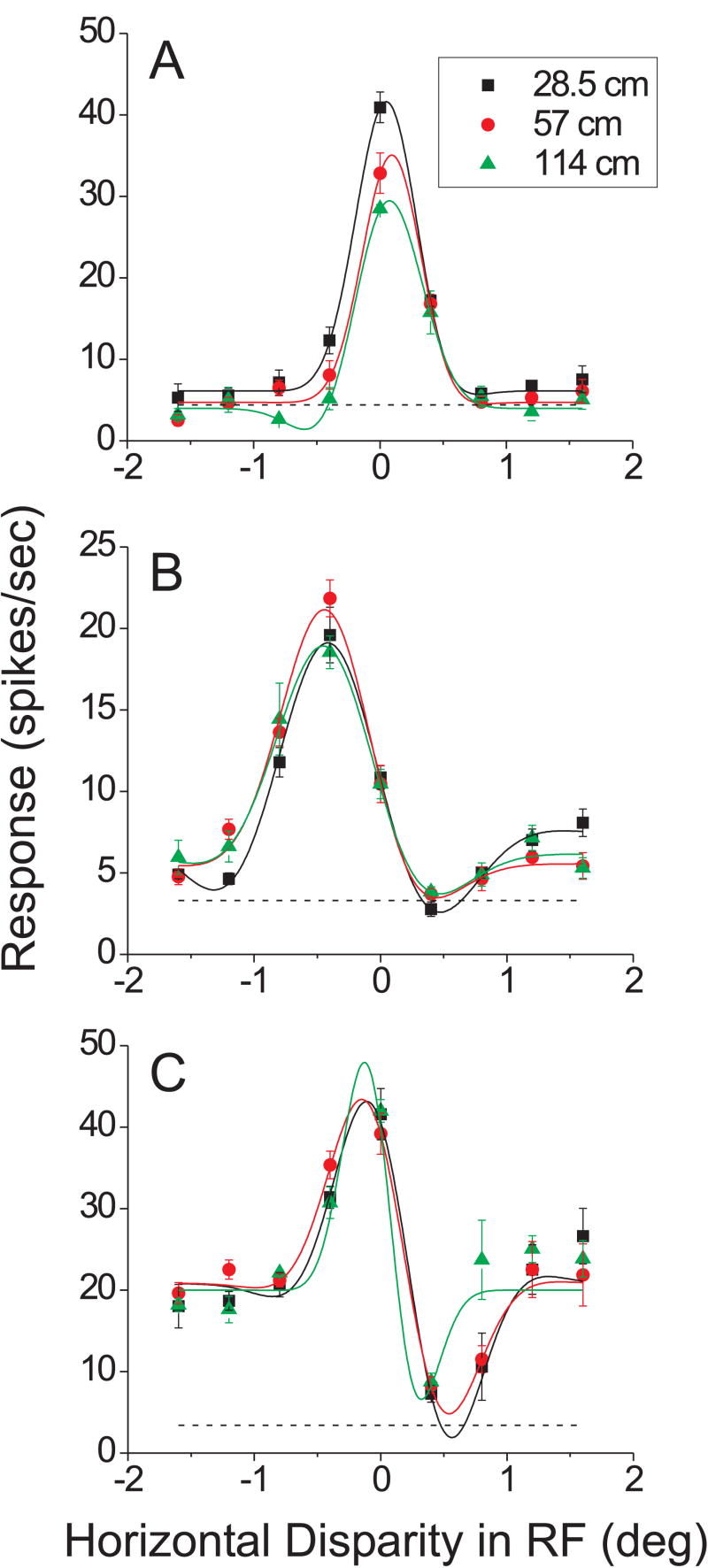
Figure 4 shows results from 3 MT neurons that were typical of the overall sample. For each neuron, the figure shows horizontal disparity tuning curves measured at the three simulated distances (color coded). For these example cells, altering the vertical disparity field outside of the neurons' classical receptive field had no clear effect on the horizontal disparity tuning curve. As described in Methods, we quantified the effect of vertical disparities for each neuron by fitting the set of tuning curves with two different models. In the ‘independent’ model, each curve was fit with a Gabor function having an independent set of parameters (18 parameters total). Smooth curves in Fig. 4 show the independent Gabor fits for the example neurons. In the ‘shared’ model, all three curves were fit with a single Gabor function (6 parameters). If the error for the shared model is not significantly larger than the error for the independent model, then we conclude that all three curves are essentially identical. This was determined using a sequential F-test (see Methods), and the result was non-significant for each of these example neurons (p = 0.99, 0.77, and 0.92, respectively).
We recorded responses from 73 isolated single units in two monkeys (37 from monkey R, 36 from monkey L). Among these, 62/73 showed significant horizontal disparity tuning at all three distances simulated by vertical disparity. We found that the vast majority of these selective cells (59/62, 95%) showed no significant effect of the vertical disparity field (sequential F-test, p > 0.05). Only 3 neurons (5%) passed the significance criterion, and the tuning curves for these three neurons are shown in Figure 5. The neuron in Fig. 5A showed the most highly significant effect of vertical disparity (p = 0.0003), which was manifest as a modest gain change across simulated viewing distances. The neurons in Fig. 5B and 5C both showed marginally significant effects of vertical disparity (p = 0.03 and 0.04, respectively) that were arguably expressed as small changes in the shapes of the tuning curves. We never saw any clear evidence for a shift in the horizontal disparity tuning curve as a function of simulated distance. This lack of significant effects of simulated distance was not a result of poor fits of the Gabor model. Consistent with previous work (DeAngelis and Uka 2003), the independent Gabor fits accounted for 93% (median) of the variance in the data across the population.
Figure 5.
Data from the 3 neurons (out of 62) that showed a statistically significant effect of vertical disparity on horizontal disparity tuning (sequential F-test, p < 0.05). Format as in Figure 4.
To validate the results of this model-based analysis, we also analyzed the data from each neuron using a two-way ANOVA, with horizontal disparity and simulated distance as factors. The three example neurons shown in Figure 5 all showed a significant main effect of simulated distance or a significant interaction between simulated distance and horizontal disparity (p < 0.05). In addition, three other MT neurons also showed weak, but significant effects of simulated distance in the ANOVA. For two neurons, this was expressed as a significant main effect of simulated distance (p = 0.032 and p = 0.023, respectively), whereas the remaining neuron showed a significant interaction (p = 0.033). For the remaining 56/62 neurons (90%), ANOVA showed no significant effect of distance simulated by vertical disparity. Thus, on a cell-by-cell basis, the two methods of analysis yielded quite similar results.
As the background dots containing the vertical disparity signal were statically presented during each trial, we considered the possibility that the vertical disparity field could have a transient effect on MT responses which might later be overcome by the conflicting vergence and accommodative state of the animal's eyes. If so, then vertical disparity effects might be larger in the early portion of the neural response, and this might have been missed by computing firing rates over the entire 1.5 second epoch. To address this issue, we also selected the first 100ms and 200ms of each neuron's response (starting 70ms after stimulus onset to account for typical MT response latencies), and again performed the two-way ANOVA. Over the first 100ms of response, 51/62 neurons still showed significant horizontal disparity tuning (main effect of horizontal disparity, p < 0.05). However, only 4/62 neurons showed a significant main effect of simulated distance, and only 2/62 neurons showed a significant interaction effect (p < 0.05). Over the first 200ms of response, 60/62 neurons showed a significant main effect of disparity, 2/62 showed a significant main effect of simulated distance, and 3/62 showed a significant interaction effect (p < 0.05). Thus, over the first 100 or 200ms of responses, effects of vertical disparity on horizontal disparity tuning are still at chance level, suggesting that vertical disparity did not have even a transient effect on MT responses.
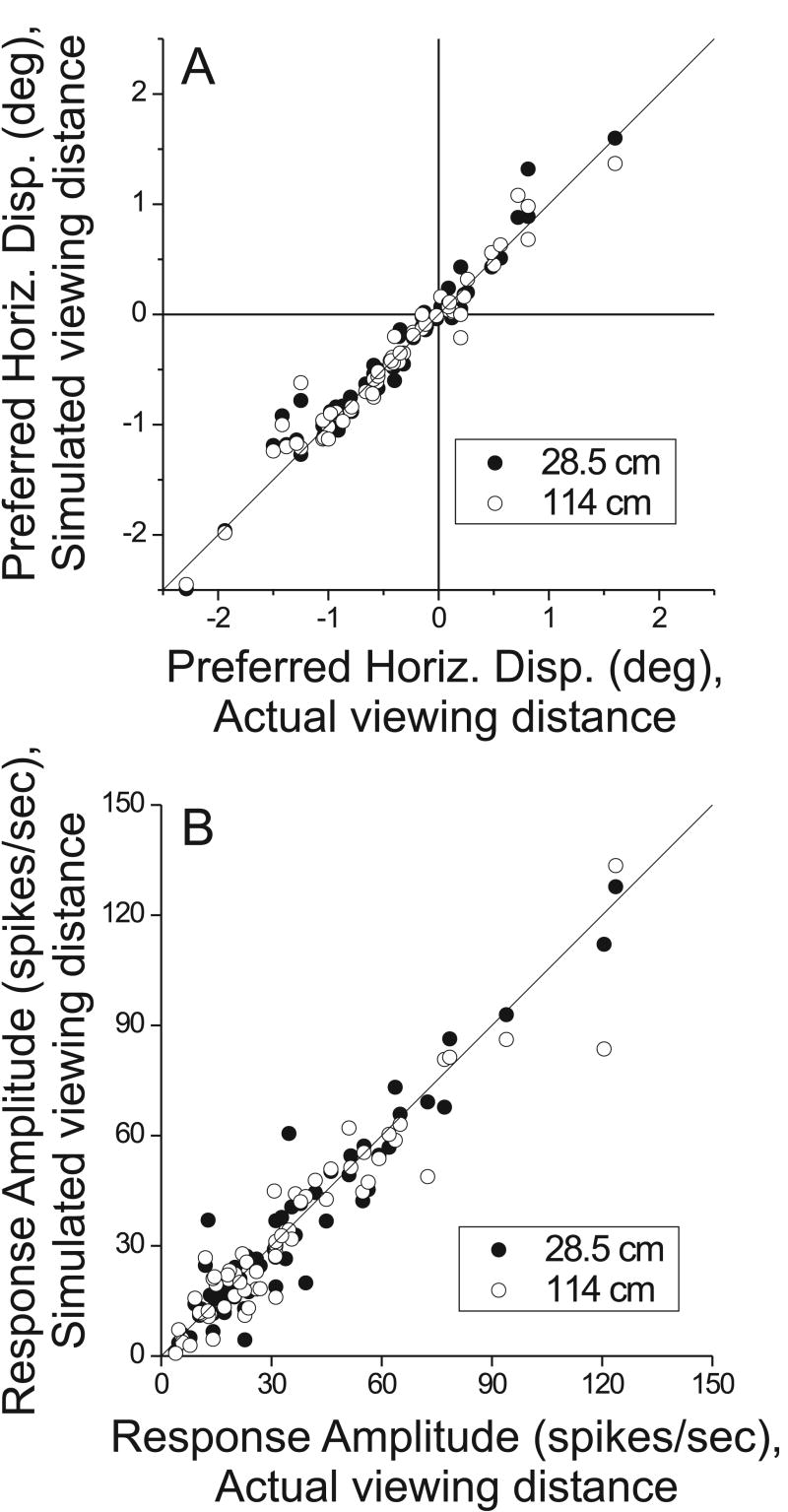
These analyses demonstrate that individual MT neurons generally showed little effect of the vertical disparity field on horizontal disparity tuning. To further probe for small effects at the population level, we compared parameters of the independent Gabor fits obtained for the simulated viewing distances of 28.5 and 114 cm against the Gabor parameters obtained at the actual viewing distance of 57cm. Fig. 6A shows this comparison for the preferred disparity (peak of the fitted Gabor function). Note that the data are clustered tightly around the unity-slope diagonal line, indicating that the preferred disparity at 28.5cm (filled symbols) or 114cm (open symbols) was very similar to that measured at the actual viewing distance of 57cm. Across the population, there were no significant differences in disparity preference between simulated distance conditions (paired t-test, p > 0.1 for each of the three pair-wise comparisons: 28.5 vs. 57cm, 114 vs. 57cm, and 28.5 vs. 114cm).
Figure 6.
Population summary of the effects of simulated distance on parameters of the horizontal disparity tuning curve. A) The preferred disparity of each neuron at simulated distances of 28.5 cm (filled symbols) and 114 cm (open symbols) is plotted against the disparity preference at the actual viewing distance of 57cm. Note that data cluster tightly around the unity slope diagonal for both simulated distances. B) Summary of results for the response gain of the horizontal disparity tuning curve (amplitude of the best-fitting Gabor function, see Methods). Format as in panel A. Again, the data for both near (filled symbols) and far (open symbols) simulated distances cluster tightly around the unity slope diagonal, indicating no effect of simulated distance on response gain.
Fig. 6B shows analogous data for the amplitude parameter (A) of the fitted Gabor function. Again, the data cluster tightly around the unity-slope diagonal, and there is no significant difference in response amplitude between simulated distances across the population (paired t-test, p > 0.2 for each of the three pair-wise comparisons). We carried out similar analyses for the other parameters of the fitted Gabor functions (Eqn. 1), and we found no significant differences across simulated distances for any of the Gabor parameters (paired t-tests, p > 0.05). Thus, even at the population level, there was no evidence that the vertical disparity field changed the horizontal disparity tuning of MT neurons.
Effect of the vertical disparity gradient on curvature perception
The results described above indicate that vertical disparities do not act at the level of area MT to modify the representation of horizontal disparities. These findings have two possible implications: 1) vertical disparities act downstream of area MT (or in a different pathway) to scale horizontal disparities, or 2) monkeys, unlike humans, do not make use of vertical disparity information when perceiving depth from horizontal disparities. To test the latter possibility, we trained one monkey to perform a curvature discrimination task very similar to that used previously to study the effects of vertical disparity and vergence on human perception (Rogers and Bradshaw 1995).
In this task, the monkey views a random-dot field that fills the entire display screen, and a gradient of horizontal disparities is applied to the dots to mimic a flat surface viewed from a variety of distances. When the distance simulated by horizontal disparity is less than the actual viewing distance (< 57cm), the random-dot surface appears to be curved away from the observer (convex, short-dashed curve in Fig. 7). When the distance simulated by horizontal disparity is > 57cm, the surface appears to be curved toward the observer (concave, long-dashed curve in Fig. 7). The monkey was trained to report whether the surface appeared convex or concave (see Methods).
Filled symbols in Fig. 8 show the performance of the monkey in two typical experiments. The abscissa shows the distance simulated by the horizontal disparity gradient, and the ordinate shows the proportion of trials in which the monkey reported the surface as “concave”. Note that the proportion of ‘concave’ reports was very close to 0.5 when the simulated distance was 57cm such that the random-dot surface appeared flat. In other words, the monkey's point of subjective equality (PSE) was close to 57cm when both horizontal and vertical disparities were consistent with the actual viewing distance of 57cm. Thus, the monkey was able to perform this task with little bias.
Having established this behavior, we could then ask whether changing the vertical disparity field would alter the monkey's PSE in this task. If monkeys make use of vertical disparities to estimate viewing distance, then altering the vertical disparity field to simulate a distance other than 57cm should cause the monkey to incorrectly perceive the curvature of the random-dot surface (Rogers and Bradshaw 1995). Specifically, if vertical disparities simulate a viewing distance < 57cm, then the monkey's PSE in judging the curvature defined by horizontal disparity should become lower. An example of this effect is shown in Fig. 8A. Open symbols show the situation in which the vertical disparity field simulates a viewing distance of 45cm. This produces a leftward shift of the psychometric function, such that the monkey's PSE is now 54.5cm (vs. 57.6cm when the vertical disparity field simulated 57cm, filled symbols). Analogously, Fig. 8B shows the effect of setting the vertical disparity field to simulate a viewing distance larger than 57cm (67cm). In this case, the psychometric function (open symbols) now shifts to the right, producing a PSE of 59.1cm (vs. 57.3 cm when vertical disparity simulated a distance of 57cm).
Fig. 9A summarizes the psychophysical results from 29 sessions performed on monkey B. Open triangles show the PSE obtained when vertical disparities specified a conflicting viewing distance, as given on the abscissa. Filled circles show the PSE obtained during interleaved trials in which there was no conflict (vertical disparities consistent with the physical viewing distance of 57cm). As expected from the examples described above, PSE values in the conflict case (open triangles) are strongly positively correlated with the conflict distance (r=0.86, p <<0.001). In the no-conflict conditions (filled circles), PSEs are weakly negatively correlated with conflict distance (r=-0.44, p=0.016). This latter result indicates that the psychometric function constructed from the interleaved no-conflict trials is often shifted slightly in the direction opposite to the curve constructed from the conflict trials. This likely results from the animal engaging in ‘probability matching’—he expects to make roughly equal numbers of choices to the two targets overall, so he compensates for the effect of conflicting vertical disparities by making more choices in the opposite direction on no-conflict trials. Similar effects have been frequently seen in microstimulation studies (DeAngelis et al. 1998; Salzman et al. 1992). As such, an unbiased PSE in the no-conflict situation does not mean that the animal has correctly estimated the viewing distance.
For each session, we computed the PSE shift as the difference in PSE between the conflict and no-conflict conditions. In the scatter plot of Fig. 9B, the PSE shift is plotted as a function of the viewing distance simulated by vertical disparities. There is a clear, orderly relationship in the data, such that simulated distances >57cm produce positive PSE shifts, and simulated distances <57cm produce negative PSE shifts. The two variables are highly correlated (r = 0.95, p << 0.001). Note, however, that the PSE shift produced by vertical disparity is much smaller than expected if vertical disparities alone were completely responsible for the estimate of viewing distance (diagonal line in Fig. 9B). This partial effect of vertical disparities is consistent with that seen in human studies (Backus et al. 1999; Bradshaw et al. 1996; Rogers and Bradshaw 1995), and can probably be attributed to the fact that both vergence and accommodation are in conflict with the viewing distance specified by vertical disparities.
We analyzed the vergence angle of the monkey, and found no significant dependence of vergence angle on the distance simulated by either horizontal or vertical disparities (ANCOVA, p> 0.2 for each session). This is not surprising given that the applied horizontal and vertical disparity gradients go to zero near the fixation point, such that all dots within a few degrees of the fixation point have negligible disparities. Thus, vergence was well anchored in the plane of the screen, and was therefore (along with accommodation) in conflict with vertical disparities. This cue conflict most likely accounts for the partial effect of vertical disparities in shifting the monkey's PSEs.
Finally, the PSE data of Fig. 9A, B may be difficult to interpret if the sensitivity of the monkey (psychophysical threshold) changes with the vertical disparity manipulation. Fig. 9C shows that this is not the case. The ordinate plots the ratio of the psychophysical threshold obtained at the conflict viewing distance (vertical disparities simulate a distance ≠ 57cm) to the threshold obtained at the actual viewing distance of 57cm. There is no significant correlation between this threshold ratio and the distance defined by vertical disparity (r = 0.04, p = 0.83). Thus, overall, the vertical disparity field produced a shift in the monkey's PSE without changing the slope of the psychometric function in the curvature task.
Discussion
It is well established that viewing distance information modulates depth perception in humans (Backus et al. 1999; Bradshaw et al. 1996; Cumming et al. 1991; Rogers and Bradshaw 1995; 1993; Sobel and Collett 1991), but the neural basis for this effect is poorly understood. Previous studies have examined the effect of vergence angle on disparity selectivity in visual cortex (Cumming and Parker 1999; Dobbins et al. 1998; Gonzalez and Perez 1998; Roy et al. 1992; Trotter et al. 1992; 1996), but to our knowledge no previous study has systematically examined the effect of the vertical disparity field on the representation of horizontal disparities by cortical neurons. Our physiological results establish clearly that the vertical disparity gradient does not modulate the horizontal disparity tuning of MT neurons. This implies either that vertical disparities act at some other locus in visual cortex, or that monkeys do not make use of vertical disparities in depth perception. Our monkey psychophysical results argue against the latter possibility, implying that vertical disparities should modulate horizontal disparity tuning at some other location in visual cortex. Further research will be needed to establish where this takes place.
We previously used the same stimulus manipulations to examine whether the vertical disparity field contributes to the estimate of viewing distance that is used to set the gain of the translational vestibulo-ocular reflex (TVOR) (Wei et al. 2003). In that study, we found no effect of changes in the vertical disparity field on TVOR gain. This indicates that the perceptual and oculomotor systems in monkeys may operate based on different neural estimates of viewing distance.
Vertical disparity signals in visual cortex
Our findings show that the gradient of vertical disparity across a large region of the visual field does not alter the local horizontal disparity tuning of MT neurons. However, this should not be taken to mean that vertical disparities are not represented in MT. Already at the level of primary visual cortex (V1), single neurons carry information about both horizontal and vertical disparities within their classical receptive fields (Cumming 2002; Durand et al. 2006; Durand et al. 2002; Gonzalez et al. 1993), as predicted by the disparity energy model (Cumming and DeAngelis 2001). It thus seems quite likely that MT neurons would also show selectivity to vertical disparities within their classical receptive field. Indeed, vertical disparity selectivity (in response to bar stimuli) was reported by Maunsell and Van Essen (1983) in anesthetized macaques, and we have observed vertical disparity tuning for a handful of MT neurons tested with random-dot stereograms in alert fixating macaques.
It was the very likely prospect that MT neurons would be selective for vertical disparities within the classical receptive field that led us to adopt an experimental design in which the vertical disparity field is modulated only outside of the classical receptive field. We did test a few neurons with stimuli in which the vertical disparity gradient passed through the classical receptive field, and we did not observe any difference in the results. Nevertheless, this could be dependent on eccentricity, as the vertical disparities in our stimuli were generally quite small in the central visual field.
Our decision to vary vertical disparities only outside the classical receptive field was also motivated by the results of psychophysical studies which indicate that the vertical disparity gradients used to estimate viewing distance are computed over a large region of the visual field (Kaneko and Howard 1996; 1997). It is conceivable that vertical disparities could be coded locally by neurons with small receptive fields and used to modulate horizontal disparity tuning, but this would not appear to be a robust computational strategy given that large local deviations in the vertical disparity field can be produced by occlusions (Farell 1998). Rather, the psychophysical data (Kaneko and Howard 1996; 1997) suggest that vertical disparity gradients are computed by neurons with large receptive fields. It is tempting to speculate that the vertical disparity gradient may be coded by the same neurons, found in both parietal and frontal cortex (Fukushima et al. 2002; Sakata et al. 1980), that show a monotonic dependence of response on vergence angle. If these neurons also have large receptive fields that are selective for vertical disparity gradients, they could potentially provide a unified signal related to viewing distance. This will be an interesting topic for future experiments.
Effects of viewing distance on horizontal disparity selectivity
If single binocular neurons in the visual system represent egocentric distance, then they should combine horizontal disparity signals with viewing distance information. One possibility is that horizontal disparity tuning curves shift with viewing distance such that individual neurons are tuned to a fixed egocentric distance (Fig. 3B). Alternatively, the response gain of disparity-selective neurons could vary with viewing distance (Fig. 3C), and a population of such gain-modulated neurons could form a distributed code for egocentric distance (Pouget and Sejnowski 1994).
A few previous studies have examined the effects of viewing distance on responses of neurons in early visual cortex, with somewhat mixed results. Two groups (Gonzalez and Perez 1998; Trotter et al. 1992; 1996) have reported that viewing distance modifies the response gain of neurons in V1, and these effects have been largely attributed to vergence angle because the field of view was relatively small. Similar modulations of response gain with viewing distance have also been reported for neurons in V2 and V4 (Dobbins et al. 1998), suggesting that gain modulations with viewing distance may be commonplace in early visual cortex. It should be noted, however, that vergence angle was not measured precisely nor enforced in these studies. In contrast, Cumming and Parker (1999) studied V1 responses under conditions in which vergence angle was controlled precisely, and found little effect of vergence angle on response gain (although their experiments covered a smaller range of vergence angles). Thus, although response gain may be modulated by vergence angle, the lack of precise monitoring and control of eye movements in some studies leaves the pervasiveness of these effects somewhat uncertain. In this regard, it is interesting to note that we did not observe any systematic effects of vertical disparity on response gain. If viewing distance modifies horizontal disparity signals through a population of gain-modulated neurons (Pouget and Sejnowski 1994), then one might expect to find variations in response gain with vertical disparity gradients.
It is also worth noting that, in previous studies reporting effects of vergence by changing the physical viewing distance (Dobbins et al. 1998; Trotter et al. 1992; 1996), the stimuli also contained changes in vertical disparity within the receptive field. It is unclear whether these vertical disparity changes contributed to the effects observed since the eccentricities of the receptive fields were quite small. On the other hand, V1 neurons have been shown to be quite sensitive to small variations in vertical disparity (Cumming 2002; Durand et al. 2002). In our approach, we have avoided confounds between the vertical disparity gradient and vergence, and have also avoided interactions between horizontal and vertical disparity within the classical receptive field.
Only one study has reported a shift in horizontal disparity tuning with viewing distance in visual cortex. Roy et al. (1992) describe a neuron in area MST that shows a horizontal shift in disparity preference with vergence angle. However, it is somewhat difficult to distinguish a horizontal shift in tuning from a vertical shift in response (gain effect) for this neuron because its disparity tuning curve was monotonic over the range tested. Thus, conclusive evidence for neurons in visual cortex that are explicitly tuned for egocentric distance is still lacking (but see Genovesio and Ferraina 2004 regarding parietal neurons).
In the absence of pictorial depth cues, vergence and vertical disparities (and perhaps also accommodation) are the main candidate sources of viewing distance information. Thus far, no study has systematically and quantitatively characterized the effects of both vergence and vertical disparities on the same set of neurons (but see Dobbins et al. 1998). It may be important to consider the effects of both vergence and vertical disparities, separately and together, as the two signals could combine in a nonlinear fashion to modulate horizontal disparity processing. Further work will be necessary to evaluate this possibility. Having established here that monkeys use vertical disparity signals in depth perception, it is important that future physiological studies of viewing distance modulation in visual cortex consider the contribution of vertical disparities.
Acknowledgments
We thank Amy McArdle, Heidi Loschen, and Donna Lalor for excellent training and care of animals, and for assistance with behavioral data collection. We thank Vinod Rao and Jacob Nadler for helpful comments on the manuscript. We also thank Yuqing Liu for assistance with neural recordings. This work was supported by a grant from the National Eye Institute (EY013644) and by a Searle Scholar award (to GCD) from the Kinship Foundation.
References
- Backus BT, Banks MS, van Ee R, Crowell JA. Horizontal and vertical disparity, eye position, and stereoscopic slant perception. Vision Res. 1999;39:1143–1170. doi: 10.1016/s0042-6989(98)00139-4. [DOI] [PubMed] [Google Scholar]
- Bishop PO. Vertical disparity, egocentric distance and stereoscopic depth constancy: a new interpretation. Proc R Soc Lond B. 1989;237:445–469. doi: 10.1098/rspb.1989.0059. [DOI] [PubMed] [Google Scholar]
- Bradshaw MF, Glennerster A, Rogers BJ. The effect of display size on disparity scaling from differential perspective and vergence cues. Vision Res. 1996;36:1255–1264. doi: 10.1016/0042-6989(95)00190-5. [DOI] [PubMed] [Google Scholar]
- Cumming BG. An unexpected specialization for horizontal disparity in primate primary visual cortex. Nature. 2002;418:633–636. doi: 10.1038/nature00909. [DOI] [PubMed] [Google Scholar]
- Cumming BG, DeAngelis GC. The physiology of stereopsis. Ann Review Neurosci. 2001 doi: 10.1146/annurev.neuro.24.1.203. In Press. [DOI] [PubMed] [Google Scholar]
- Cumming BG, Johnston EB, Parker AJ. Vertical disparities and perception of three-dimensional shape. Nature. 1991;349:411–413. doi: 10.1038/349411a0. [DOI] [PubMed] [Google Scholar]
- Cumming BG, Parker AJ. Binocular neurons in V1 of awake monkeys are selective for absolute, not relative, disparity. J Neurosci. 1999;19:5602–5618. doi: 10.1523/JNEUROSCI.19-13-05602.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeAngelis GC, Cumming BG, Newsome WT. Cortical area MT and the perception of stereoscopic depth. Nature. 1998;394:677–680. doi: 10.1038/29299. [DOI] [PubMed] [Google Scholar]
- DeAngelis GC, Newsome WT. Organization of disparity-selective neurons in macaque area MT. J Neurosci. 1999;19:1398–1415. doi: 10.1523/JNEUROSCI.19-04-01398.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeAngelis GC, Uka T. Coding of horizontal disparity and velocity by MT neurons in the alert macaque. J Neurophysiol. 2003;89:1094–1111. doi: 10.1152/jn.00717.2002. [DOI] [PubMed] [Google Scholar]
- Dobbins AC, Jeo RM, Fiser J, Allman JM. Distance modulation of neural activity in the visual cortex. Science. 1998;281:552–555. doi: 10.1126/science.281.5376.552. [DOI] [PubMed] [Google Scholar]
- Dodd JV, Krug K, Cumming BG, Parker AJ. Perceptually bistable three-dimensional figures evoke high choice probabilities in cortical area MT. J Neurosci. 2001;21:4809–4821. doi: 10.1523/JNEUROSCI.21-13-04809.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durand JB, Celebrini S, Trotter Y. Neural Bases of Stereopsis across Visual Field of the Alert Macaque Monkey. Cereb Cortex. 2006 doi: 10.1093/cercor/bhl050. In Press. [DOI] [PubMed] [Google Scholar]
- Durand JB, Zhu S, Celebrini S, Trotter Y. Neurons in parafoveal areas V1 and V2 encode vertical and horizontal disparities. J Neurophysiol. 2002;88:2874–2879. doi: 10.1152/jn.00291.2002. [DOI] [PubMed] [Google Scholar]
- Farell B. Two-dimensional matches from one-dimensional stimulus components in human stereopsis. Nature. 1998;395:689–693. doi: 10.1038/27192. [DOI] [PubMed] [Google Scholar]
- Fukushima K, Yamanobe T, Shinmei Y, Fukushima J, Kurkin S, Peterson BW. Coding of smooth eye movements in three-dimensional space by frontal cortex. Nature. 2002;419:157–162. doi: 10.1038/nature00953. [DOI] [PubMed] [Google Scholar]
- Genovesio A, Ferraina S. Integration of retinal disparity and fixation-distance related signals toward an egocentric coding of distance in the posterior parietal cortex of primates. J Neurophysiol. 2004;91:2670–2684. doi: 10.1152/jn.00712.2003. [DOI] [PubMed] [Google Scholar]
- Gonzalez F, Perez R. Modulation of cell responses to horizontal disparities by ocular vergence in the visual cortex of the awake Macaca mulatta monkey. Neurosci Lett. 1998;245:101–104. doi: 10.1016/s0304-3940(98)00191-8. [DOI] [PubMed] [Google Scholar]
- Gonzalez F, Relova JL, Perez R, Acuña C, Alonso JM. Cell responses to vertical and horizontal retinal disparities in the monkey visual cortex. Neurosci Lett. 1993;160:167–170. doi: 10.1016/0304-3940(93)90405-a. [DOI] [PubMed] [Google Scholar]
- Howard IP, Rogers BJ. Binocular vision and stereopsis. New York: Oxford University Press; 1995. [Google Scholar]
- Howard IP, Rogers BJ. Seeing in Depth. Volume 2: Depth Perception. Toronto: I. Porteus; 2002. [Google Scholar]
- Judge SJ, Richmond BJ, Chu FC. Implantation of magnetic search coils for measurement of eye position: an improved method. Vision Research. 1980;20:535–538. doi: 10.1016/0042-6989(80)90128-5. [DOI] [PubMed] [Google Scholar]
- Kaneko H, Howard IP. Relative size disparities and the perception of surface slant. Vision Res. 1996;36:1919–1930. doi: 10.1016/0042-6989(95)00258-8. [DOI] [PubMed] [Google Scholar]
- Kaneko H, Howard IP. Spatial limitation of vertical-size disparity processing. Vision Res. 1997;37:2871–2878. doi: 10.1016/s0042-6989(97)00099-0. [DOI] [PubMed] [Google Scholar]
- Krug K, Cumming BG, Parker AJ. Comparing perceptual signals of single V5/MT neurons in two binocular depth tasks. J Neurophysiol. 2004;92:1586–1596. doi: 10.1152/jn.00851.2003. [DOI] [PubMed] [Google Scholar]
- Maunsell JH, Van Essen DC. Functional properties of neurons in middle temporal visual area of the macaque monkey. II. Binocular interactions and sensitivity to binocular disparity. J Neurophysiol. 1983;49:1148–1167. doi: 10.1152/jn.1983.49.5.1148. [DOI] [PubMed] [Google Scholar]
- Mayhew J. The interpretation of stereo-disparity information: the computation of surface orientation and depth. Perception. 1982;11:387–403. doi: 10.1068/p110387. [DOI] [PubMed] [Google Scholar]
- Mayhew JE, Longuet-Higgins HC. A computational model of binocular depth perception. Nature. 1982;297:376–378. doi: 10.1038/297376a0. [DOI] [PubMed] [Google Scholar]
- Palanca BJ, DeAngelis GC. Macaque middle temporal neurons signal depth in the absence of motion. J Neurosci. 2003;23:7647–7658. doi: 10.1523/JNEUROSCI.23-20-07647.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouget A, Sejnowski TJ. A neural model of the cortical representation of egocentric distance. Cerebral Cortex. 1994;4:314–329. doi: 10.1093/cercor/4.3.314. [DOI] [PubMed] [Google Scholar]
- Rogers BJ, Bradshaw MF. Disparity scaling and the perception of frontoparallel surfaces. Perception. 1995;24:155–179. doi: 10.1068/p240155. [DOI] [PubMed] [Google Scholar]
- Rogers BJ, Bradshaw MF. Vertical disparities, differential perspective and binocular stereopsis. Nature. 1993;361:253–255. doi: 10.1038/361253a0. [DOI] [PubMed] [Google Scholar]
- Roy JP, Komatsu H, Wurtz RH. Disparity sensitivity of neurons in monkey extrastriate area MST. J Neurosci. 1992;12:2478–2492. doi: 10.1523/JNEUROSCI.12-07-02478.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakata H, Shibutani H, Kawano K. Spatial properties of visual fixation neurons in posterior parietal association cortex of the monkey. J Neurophysiol. 1980;43:1654–1672. doi: 10.1152/jn.1980.43.6.1654. [DOI] [PubMed] [Google Scholar]
- Salzman CD, Murasugi CM, Britten KH, Newsome WT. Microstimulation in visual area MT: effects on direction discrimination performance. J Neurosci. 1992;12:2331–2355. doi: 10.1523/JNEUROSCI.12-06-02331.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobel EC, Collett TS. Does vertical disparity scale the perception of stereoscopic depth? Proc R Soc Lond B. 1991;244:87–90. doi: 10.1098/rspb.1991.0055. [DOI] [PubMed] [Google Scholar]
- Trotter Y, Celebrini S, Durand JB. Evidence for implication of primate area V1 in neural 3-D spatial localization processing. J Physiol Paris. 2004;98:125–134. doi: 10.1016/j.jphysparis.2004.03.004. [DOI] [PubMed] [Google Scholar]
- Trotter Y, Celebrini S, Stricanne B, Thorpe S, Imbert M. Modulation of neural stereoscopic processing in primate area V1 by the viewing distance. Science. 1992;257:1279–1281. doi: 10.1126/science.1519066. [DOI] [PubMed] [Google Scholar]
- Trotter Y, Celebrini S, Stricanne B, Thorpe S, Imbert M. Neural processing of stereopsis as a function of viewing distance in primate visual cortical area V1. J Neurophysiol. 1996;76:2872–2885. doi: 10.1152/jn.1996.76.5.2872. [DOI] [PubMed] [Google Scholar]
- Uka T, DeAngelis GC. Contribution of area MT to stereoscopic depth perception: choice-related response modulations reflect task strategy. Neuron. 2004;42:297–310. doi: 10.1016/s0896-6273(04)00186-2. [DOI] [PubMed] [Google Scholar]
- Uka T, DeAngelis GC. Contribution of middle temporal area to coarse depth discrimination: comparison of neuronal and psychophysical sensitivity. J Neurosci. 2003;23:3515–3530. doi: 10.1523/JNEUROSCI.23-08-03515.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uka T, DeAngelis GC. Linking neural representation to function in stereoscopic depth perception: roles of the middle temporal area in coarse versus fine disparity discrimination. J Neurosci. 2006;26:6791–6802. doi: 10.1523/JNEUROSCI.5435-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei M, DeAngelis GC, Angelaki DE. Do visual cues contribute to the neural estimate of viewing distance used by the oculomotor system? J Neurosci. 2003;23:8340–8350. doi: 10.1523/JNEUROSCI.23-23-08340.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]