Individually Programmable Cell Stretching Microwell Arrays Actuated by a Braille Display

Abstract

Cell culture systems are often static and are therefore nonphysiological. In vivo, many cells are exposed to dynamic surroundings that stimulate cellular responses in a process known as mechanotransduction. To recreate this environment, stretchable cell culture substrate systems have been developed, however these systems are limited by being macroscopic and low throughput. We have developed a device consisting of 24 miniature cell stretching chambers with flexible bottom membranes that are deformed using the computer-controlled, piezoelectrically actuated pins of a Braille display. We have also developed efficient image capture and analysis protocols to quantify morphological responses of the cells to applied strain. Human dermal microvascular endothelial cells (HDMECs) were found to show increasing degrees of alignment and elongation perpendicular to the radial strain in response to cyclic stretch at increasing frequencies of 0.2, 1, and 5 Hz, after 2, 4, and 12 hours. Mouse myogenic C2C12 cells were also found to align in response to the stretch, while A549 human lung adenocarcinoma epithelial cells did not respond to stretch.

1. Introduction

In the body, cells are continuously exposed to mechanical deformation originating from processes such as muscle movement, respiration, and the pulsatile nature of blood flow. The ability of cells to sense and respond to mechanical strain is important in many tissues including the vasculature, lung alveoli, and skeletal muscle [1–3]. The process by which cells convert mechanical signals into biochemical responses is known as mechanotranduction. Extracellular forces are transduced across the cell membrane to effect intracellular biochemical events such as proliferation, differentiation, and alignment. To study such events, cell culture systems designed to replicate in vivo situations, where cells are exposed to mechanical stimuli, are useful to better represent physiological conditions.

To apply mechanical strain to cells in vitro, a variety of stretchable cell culture substrate systems have been developed. The majority of devices consist of cells cultured on a membrane (either a circular one held about its periphery, or a rectangular membrane held at opposite ends) and stretch applied either multiaxially, where there is a nonuniform strain through two axes (radial and circumferential) [4], or uniaxially where there is a single axis of uniform tensile strain with a small magnitude of compression [2]. Multiaxial strain can be applied to circular membranes by injection of air or liquid into a chamber beneath the membrane [5–7] or direct displacement with an indentor [8,9]. Uniaxial strain is often applied by fixing one end of a rectangular membrane while the other end is attached to a motor-driven movable frame [2,10].

These devices have demonstrated the value of in vitro stretching systems for a wide range of cellular studies. Existing cell stretching systems, however, are macroscopic and low throughput. Typically one cell type is exposed to one stretching condition per device. Commonly used devices have between 6 and 24 cell stretching wells but expose all wells to the same stretching condition [9]. What would enhance many in vitro studies and cellular screening assays would be the ability to test multiple conditions and cell types in parallel. Additionally, as the number of cellular samples that are exposed to different stretching conditions increases, the use of fewer cells and reagents, as well as the development of software algorithms to automate analysis of cellular responses to stretch in these array based systems would be required. A readily observed cellular response to mechanical strain is cell alignment. For example, upon cyclic stretching certain cells orient perpendicular to the direction of stretch including endothelial cells [10–13], fibroblasts [14], smooth muscle cells [15,16], cardiac myocytes [17], avian skeletal muscle cells [9], and mesangial cells [18].

Here, we describe a device with an array of miniature cell stretching chambers that enables efficient study of the effects of mechanical strain in vitro in a parallel manner amenable for higher throughput screening. The system uses microwells with flexible bottom membranes that are placed over the computer-controlled, piezoelectrically actuated pins of a refreshable Braille display (Figure 1a). Each pin is independently controlled according to a computer program to push against the flexible bottom membrane of the microwells and apply a cyclical radial strain to cells cultured on the membrane (Figure 1b). Computer control allows modification of parameters such as the frequency and duration of stretch, while an alteration in fabrication allows modification of the magnitude of stretch. Advantages of this device include the ability to create a microscale environment for cell culture and to run multiple experiments in parallel. The Braille device contains multiple independent pins, each of which can be actuated at varying frequencies. Commercially available Braille displays typically have between 320 and 1536 pins. We constructed a custom setup [19] that is more compact and has the potential to test up to 48 conditions with one display. We also developed image capture and automated image processing protocols to enable efficient analysis of morphological cellular responses across the multiple microwells. For biological validation we tested the response of three different cell types expected to behave differently in terms of cell alignment to mechanical stretch: (i) human dermal microvascular endothelial cells (Figure 1c,d) (HDMECs), (ii) A549 human lung adenocarcinoma epithelial cells, and (iii) mouse myogenic C2C12 cells.

Figure 1.

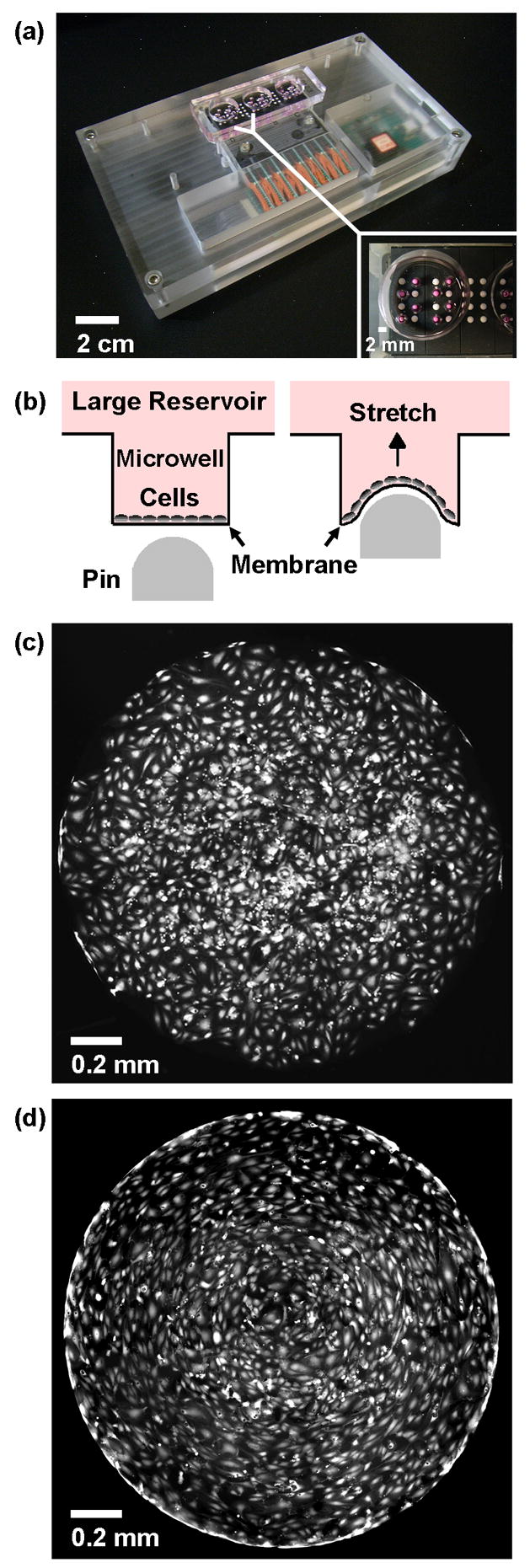
(a) PDMS device with 24 millimeter-sized cell stretching wells placed over a pin actuator array. The 24 microwells are divided into 3 larger reservoirs with 8 microwells each (inset). (b) Schematic figure of how cells are cultured on flexible membranes at the bottom of the microwells. When the pin moves upwards, it deforms the membrane and applies strain to the cells. Fluorescence micrographs of endothelial cells cultured in the wells, unstretched (c) and after application of cyclic stretch at 5 Hz for 12 hours (d). The diameter of the microwells is 1.7 mm.

2. Materials and Methods

2.1 Cells and growth media

Mouse myogenic cell line C2C12 cells and the human lung adenocarcinoma epithelial cell line A549 cells were obtained from American Tissue Type Culture Collection (ATCC, Manassas, VA). Growth medium for the C2C12 cells consisted of Dulbecco’s Modified Eagle Medium (DMEM, Invitrogen, Calsbad, CA) supplemented with 10% fetal bovine serum (FBS, Invitrogen) and 1% antibiotic/antimycotic (Invitrogen). Growth media for the A549 cells consisted of Ham’s F12K medium (ATCC) with 10% FBS (Invitrogen) and 1% antibiotic/antimycotic (Invitrogen). Human dermal microvascular endothelial cells (HDMECs) were obtained from Cambrex (East Rutherford, NJ) and cultured in microvascular endothelial growth medium-2 (EGM-2MV, Cambrex).

2.2 Cell stretching device

2.2.1 ANSYS Finite Element Analysis (FEA)

In order to estimate the strain generated on an elastomeric PDMS membrane top surface while the membrane is deformed by Braille pin movement, we performed simulations using finite element analysis (FEA) software, ANSYS 10.0 (ANSYS Inc., Southpointe, PA). To reduce the computational time, a 2-D model with an axis symmetric boundary condition was constructed (Figure 2a). The model was composed of a flat membrane and a curved Braille pin structure, where the pin structure was assumed to be rigid. Contact analysis was performed to simulate the interaction between the two objects. Contact and target elements, CONTA172 and TARGE169, were assigned on the Braille pin and the membrane bottom surface to simulate the surface-to-surface contact. The membrane was simulated using triangular 2-D elements, PLANE2. The axis symmetric boundary condition was assigned along the Y-axis, and one end of the membrane was assigned the fixed boundary condition. The displacement boundary condition, which was measured experimentally (Figure 2b), was assigned to the Braille pin. To simulate the large deformation of the PDMS membrane, non-linear, large deformation static analysis was performed. For all simulations, a Young’s Modulus of 750 kPa and a Poisson’s Ratio of 0.49 for the membrane were used (Dow Corning, Midland, MI). Although the 2-D finite element model dramatically reduced the time required for computations, the model cannot be utilized to estimate the membrane surface strain distribution while the membranes and Braille pins are not perfectly aligned, as may be the case in the actual experiments. Such discrepancy may cause errors in estimating the strains that the cells are exposed to during stretching.

Figure 2.

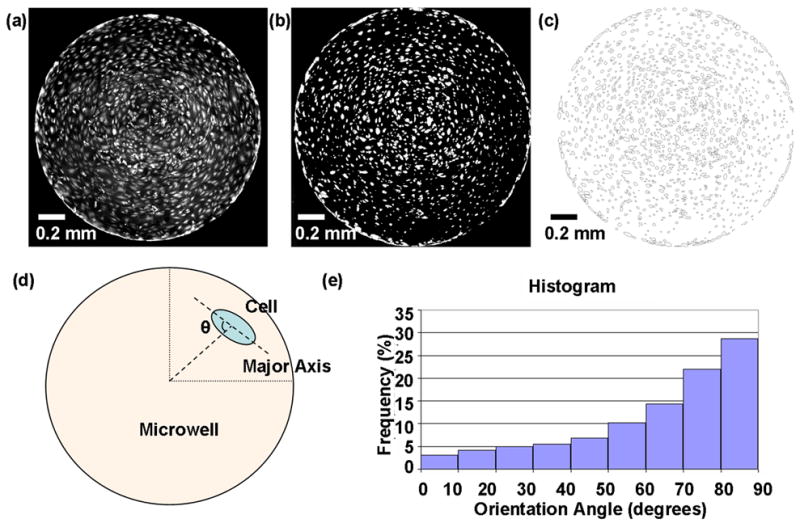
Automated image analysis using ImageJ (NIH). (a) Original fluorescence micrograph of endothelial cells subjected to stretch at 5 Hz for 12 hrs and stained with calcein AM. During processing, images were thresholded to create a binary black and white image (b) and ellipses were automatically fitted around each cell (c). The orientation angle (θ) was calculated as the angle between the major axis of the ellipse and a line extending from the center of the well to the ellipse centroid (d). (e) Alignment histogram with the distribution of cell orientation angles.

2.2.2 Fabrication of chip and preparation for experiments

The three layer stretch chips were fabricated using the elastomer poly(dimethylsiloxane) (PDMS, Sylgard 184, Dow Corning, Midland, MI) and standard soft lithographic procedures [20]. Briefly, for the top layer, three large reservoirs of 1.5 cm diameter were punched into a cured slab of PDMS (10:1 prepolymer to curing agent) (dimensions: 7 cm × 2 cm × 0.5 cm height). For the middle layer, 24 microwells (1.7 mm diameter each) were punched into another PDMS slab of the same dimensions. The bottom layer consisted of a 100 μm thick PDMS membrane formed by spin coating prepolymer onto a 4 inch diameter silanized silicon wafer and curing for 30 minutes in a 120°C oven. Strict control over the thickness of the membrane was achieved by keeping constant during the fabrication process: the ratio of PDMS to prepolymer, curing times in the oven, spin coating programs for the bottom membrane, and by sealing multiple devices onto the same spin coated PDMS membrane. This was critical to ensure reproducibility. The top two layers were sealed using a PDMS glue mixture (2:3 PDMS prepolymer: toluene ratio) and cured in a 120°C oven for 20 minutes [21]. The bottom two layers were sealed irreversibly by treating both surfaces with plasma oxygen (SPI Supplies, West Chester, PA) for 30 seconds at 500 mtorr, and placed in a 120°C oven for 20 minutes post-sealing.

After fabrication, the microwells were each filled with 10 μl of 50 μg/ml fibronectin (Invitrogen) solution in growth media and placed under UV sterilization for 30 minutes. The microwells were then washed twice with phosphate-buffered saline (PBS, Invitrogen). After removing the PBS, the microwells were then filled, along with each large reservoir, with 0.5 ml of cell culture media

2.2.3 Culture of cells in PDMS microwells

At subconfluence, C2C12 and A549 cells were trypsinized using 0.25% trypsin/EDTA (Invitrogen) from 100 mm diameter tissue culture plates. The trypsin was removed using centrifugation and the supernatant aspirated leaving a pellet of cells. After resuspending the cells in 8 ml of growth media, 100 μl of the cell solutions was pipetted into each large reservoir. HDMECs were grown in T-25 culture flasks and were washed and detached using 0.25% trypsin/EDTA (Invitrogen). After resuspension in growth media, the cells were seeded at a density of 200,000 cells/ml. Each of the three cells types (ECs, A549, and C2C12 cells) were seeded into 4 separate stretching chips, one cell type per chip, for a total of 12 chips. All cells were left to attach overnight in a humidified 5% CO₂ incubator.

2.3 Cell stretching experiments

2.3.1 Braille display

The stretching was provided through the multiple, computer-controlled, piezoelectrically actuated pins of a refreshable Braille display. Each pin can be independently shifted upwards at specified frequencies to push against the flexible bottom membranes of the PDMS microwells. The PDMS chip was aligned over the Braille pin and held in place using a glass slide placed over the large reservoirs and a weight.

2.3.2 Stretching of cells

After incubating overnight, the chips were examined under a brightfield microscope to verify cell attachment and uniformity of cell coating on the bottom of the microwell. Three custom Braille displays were used for each set of experiments (one each for 2 hrs, 4 hrs, and 12 hrs). On each Braille display, three stretching chips (one per cell type) were carefully aligned over the pins and secured in place using a glass slide held down by a weight and placed in the incubator. Experimentally, we observed that when the alignment is off, the “center” as observed by cell morphology also shifts slightly. Errors were also minimized by designing chips with multiple microwells to ensure the minimal misalignment with the Braille pins.

The remaining three chips were kept off the device as the controls and were stained for analysis immediately after beginning the experiments. The computer program to begin pin movement was then started for all devices, this being time 0 hrs. Chips on each Braille display were removed either at 2 hrs, 4 hrs, or 12 hrs for concurrent staining and imaging. A total of 12 chips were used for the experiments.

2.3.3 Fluorescence cell staining

Cells were stained using the LIVE/DEAD Viability/Cytotoxicity kit for mammalian cells (Invitrogen). Upon entering live cells, Calcein AM is converted into its green fluorescent form (ex/em 495 nm/515 nm) and is retained within the cell. 5 μl of 4mM Calcein AM in anhydrous DMSO (ATCC) was diluted into 495 μl of growth media. 100 μl of this solution was then pipetted into each of the large reservoirs and allowed to incubate for 15 minutes. Afterwards, the liquid inside the large reservoirs was aspirated out and the wells were imaged. At time 0, 2, 4, and 12 hours, one set of chips was removed from the Braille setup and stained for imaging.

All images were taken using Simple PCI imaging software (Compix Inc. Cranberry Township, PA) connected to a CCD camera (Hamamatsu Orca-ER) mounted on an inverted phase contrast/fluorescence microscope (TE-300, Nikon, Tokyo) using the 4x and 10x objectives.

2.3.4 Quantification of alignment and elongation

Morphological changes were quantified using two variables; orientation angle and elongation ratio. All cells located in each microwell (on average 1000–2000 cells/microwell) were included in the analysis. Fluorescence images of cells stained with calcein AM, taken using a 4x objective (2 images per microwell) were processed using a semi-automated program created in ImageJ (NIH). The program was designed to process each grayscale image automatically by subtracting the background, thresholding to create a binary image where each pixel was either black or white, and performing watershedding (an algorithm within ImageJ that automatically separates particles that touch to better separate overlapping cells). Watershed segmentation is a way of automatically separating or cutting apart particles that touch. It starts with a binary image, and creates a Euclidean distance map of the image to find the fattest parts of the object (the peaks or local maxima of the distance map). Objects are then eroded until only the peaks or maximal erosion points (MEPs) remains. ImageJ then dilates the image from each of these MEPs as far as possible - either until the edge of the object is reached, or the edge of the region of another (growing) MEP. In the case of reaching the edge or another MEP, a one pixel wide boundary of background color separates the object into 2 [22]. After fitting ellipses around each cell, and then removing background noise by ignoring ellipses too large or too small to represent a cell (Figure 3a,b,c), a data set was then generated including information such as the number of ellipses in a microwell, and, for each ellipse, the location of its centroid, the orientation angle, and the lengths along the major and minor axis to calculate the elongation ratio. Each orientation angle was recalculated with respect to the center of the microwell as the center of the coordinate system (Figure 3d). Any angles over 90° were subtracted from 180° so that all angles lay between 0 and 90°. For each cell, based upon its radial distance from the center of the microwell, cells located within 30% and outside of 90% of the radius were eliminated from the data set. This still represented over 70% of the total area within the well. Cumulative frequencies of cells located between 30 and 90% of the radius were then plotted versus orientation. Randomly oriented cells would result in a straight line of the plots (see Supporting Information), while cells that orient perpendicular to stretch would result in a histogram skewed towards 90 degrees (Figure 3e). Cells with orientation angles between 80 and 90° were considered aligned and the percentage of aligned cells for each condition were calculated and plotted. Assuming the cell has an elliptical shape, the elongation ratio for the endothelial cells was calculated as the ratio of cell lengths along the major and minor axis.

Figure 3.

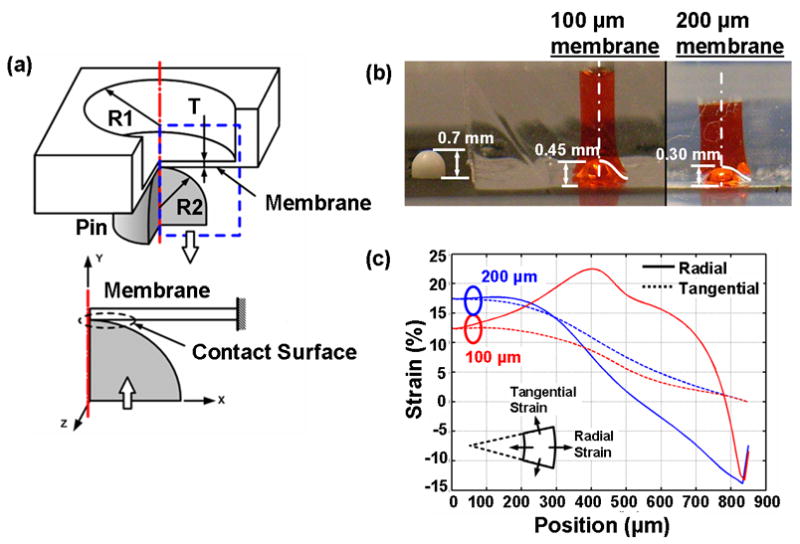
ANSYS Finite Element Analysis simulation of membrane stretching. (a) 2-D model for pin (radius R2) contacting a microwell (radius R1) with a flexible bottom membrane (thickness T). (b) Experimental results of Braille pin pushing upwards with no load (far left), pushing against PDMS membranes of thickness 100 μm (center) and 200 μm (far right). (c) Simulated radial and tangential strains on membranes of different thicknesses.

2.3.5 Statistical Analysis

Results for the alignment analysis are presented as percentages of cells taken from duplicate wells. Standard errors of means for the averages are included in Supporting Information. Results for the elongation measurements are presented as means ± standard deviation. Elongation data was compared using a two-sample t-test assuming equal variances with a p < 0.05 considered significant.

3. Results

3.1 Membrane thickness

Side view images of the Braille pin were taken under three conditions (Figure 2b): (i) without any load, the Braille pin extends a distance of 0.7 mm. (ii) When placed below a PDMS microwell with a bottom membrane of thickness 100 μm, the pin moves up 0.45 mm. (iii) For a thicker membrane (200 μm), the pin pushes upwards a distance of 0.3 mm. In each case, the Braille pin pushes up with a force (0.18 N initially, and decreasing nonlinearly until maximum extension) against the stiffness of the membrane. Assuming a constant Young’s Modulus, the deformation of the membrane is a result of its thickness. Figure 2c shows the results of the finite element analysis simulation for radial and tangential strains across the radius of the microwell.

In general, the membrane bending rigidity will increase along with the increase of the membrane thickness, which will result in a smaller displacement when applying same amount of force. This leads to smaller strains generated in the membrane. In contrast, with the same radius of curvature of deformed membranes, a thicker membrane will yield higher surface strain due to the longer distance between the neutral plane and the surface. Due to the combination of these effects, it is difficult to predict the strain field on the membrane surface without advanced analysis. Therefore, the non-linear FEA simulation performed in this paper is critical for us when designing the membrane thickness in our experiments.

3.2 Cell orientation angle and elongation ratio

Representative fluorescence images of unstretched cells (Figure 4a,c,e) and cells cyclically stretched at 5 Hz for 12 hrs (Figure 4b,d,f) are shown for the 3 cell types used in this study. Figure 5 shows the results obtained from the automated analysis of duplicate microwells for each condition and cell type. All cells within a microwell were analyzed for orientation angle relative to the center of the microwell and distance of its centroid from the center. Alignment was expected to occur perpendicular to the radial direction, which was the predominant strain direction. A cell angle between 80 and 90° corresponded to circumferential alignment. The percentage of cells that aligned were calculated and plotted versus each of the 5 conditions (Figure 5a). The elongation ratios (ratio of lengths along the major axis and minor axis of the cell) for the endothelial cells were also plotted (see Supporting Information).

Figure 4.

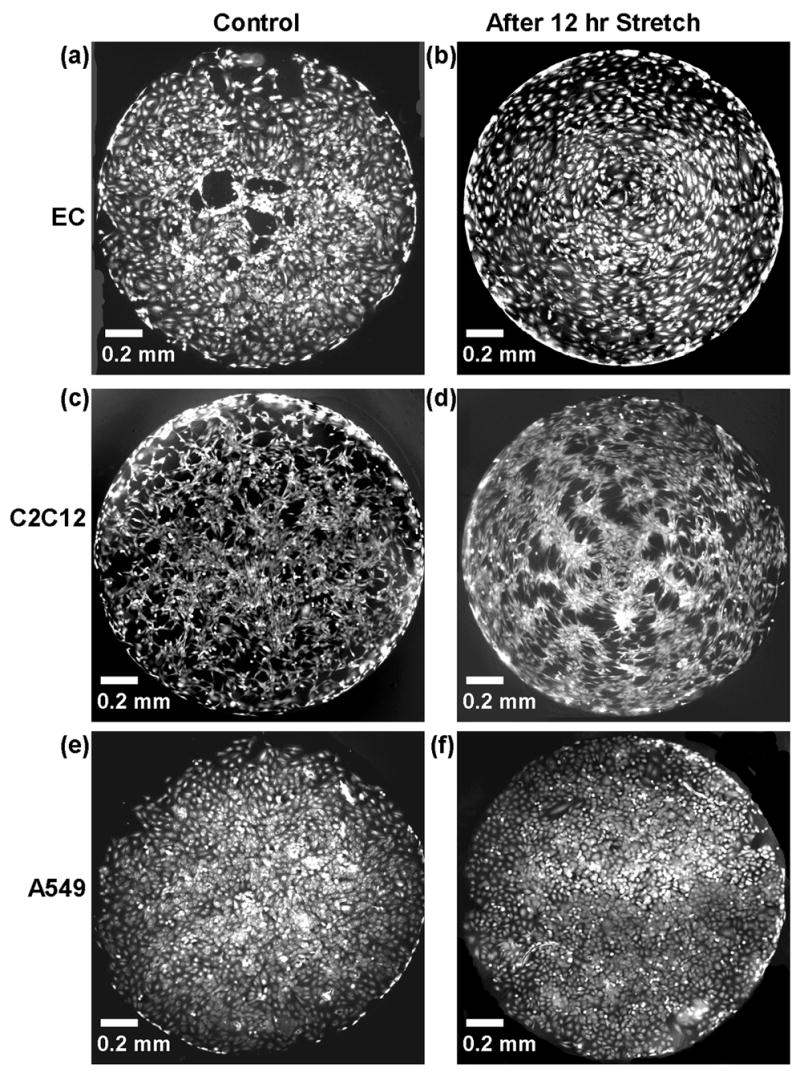
Fluorescent images of cells stained with calcein AM before stretch (left column) and after cyclically stretching at 5Hz for 12 hrs (right column). Three cell types (a) Endothelial cells, (b) C2C12 myoblast cells, and (c) A549 alveolar epithelial cells were used.

Figure 5.

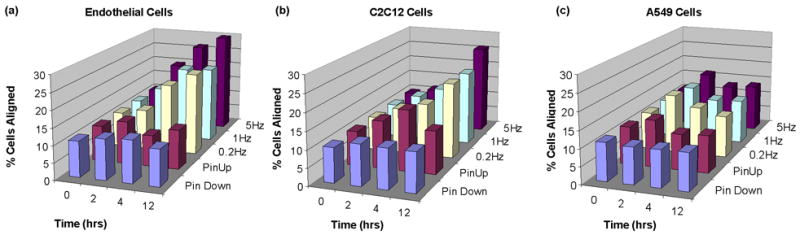
Percentage of cells within 30 and 90% of the radius with orientation angles between 80–90°, with 90° considered perfect alignment. Data shown as averages between duplicates for endothelial cells (a), C2C12 cells (b), and A549 cells (c). For standard error of means, see Supporting Information.

4. Discussion

A dynamic environment for cells is often crucial to their growth, development, function, and even in the development of disease. It would therefore benefit many in vitro studies to recreate this biomechanical environment.

To study the response of cultured cells to strain, various stretchable cell culture substrate systems have been developed. Early methods used a vacuum to pull down an elastic circular membrane [23]. Currently the most widely used apparatus to deliver controlled in vitro strain to cultured cells is the Flexercell Strain Unit (Flexcell Corp, McKeesport, PA). Adherent cells are cultured on flexible silicone membranes which are stretched over a loading post by applying negative vacuum pressure. Biaxial strain can be applied by using a circular loading post, while uniaxial strain is applied using an oblong-shaped post. The substrate can be elongated up to 30% and the computer-controlled vacuum can apply defined, controlled, static, or cyclic deformation in varying frequencies, amplitudes, and waveforms. Another version created by Flexercell is the strain unit (FX-2000) where circular silicone rubber surfaces form the bottom of 6-well culture plates. Application of a computer-controlled vacuum pressure deflects the surfaces downward [23,24]. Limitations to this and other similar systems include the macroscopic dimensions and low throughput. The device described here overcomes these limitations with the capability of simultaneously applying radial cyclic stretch to 24 microwells at different frequencies.

The 64 pins of the Braille display are independently controlled with a computer program able to manipulate each pin’s movement at a set frequency. Microwells with flexible PDMS bottom membranes are placed over the pin and deflected with the pin’s upward movement. By combining a FEA simulation and experimental observations, the thickness of the PDMS membrane was selected to generate a biaxial strain where the radial strain is significantly larger than the tangential (azimuthal) strain level. Previous studies have shown that endothelial cells undergo a 15% oscillation in its external diameter due to blood pulsation [25], and alveolar epithelial cells experience mechanical strain levels of 8–12% normally and 17–22% in pathophysiological conditions due to respiratory cycles [26]. In the present study, in order to generate radial strains greater than 15% on the membrane surface, the dimensions (microwell diameter and PDMS membrane thickness) of the chip was selected to provide a high radial/tangential strain ratio when stretched. As seen in Figure 2c, a 100 μm thick membrane with a microwell of 1.7 mm diameter, when stretched by the pin can provide 20–25% maximal strain in the radial direction while the tangential strain is kept below 12%. As shown in Figure 2c, the radial strain is dominant over the tangential strain at each position in the microwell except for in the center where the strain is biaxial. Maximum radial strain occurs in a concentric circle halfway to the radius of the microwell and drops off near the outer edges. Under these conditions, the increase in surface area in the stretched state compared to the relaxed state is 17.2% over the total surface of the microwell and 20.9% between 30 and 90% of the radius. For the thicker membrane (200 μm), simulation results show nearly equal levels of radial and tangential strain throughout the microwell (Figure 2c).

All cell types were seeded at a density averaging approximately 1000 cells/microwell. The effects of cell density on alignment were not further studied, however high cell densities were avoided to prevent the formation of large aggregates of cells, which can obstruct the imaging and analysis of substrate attached cells as well as prevent some cells from responding to the surface strain due to crowding. With endothelial cells, too low a cell density caused many cells to die (data not shown). Endothelial cells and C2C12 cells, when cyclically stretched, have been shown to align perpendicular to the radial strain [10–11, 27–33]. In this case, the cells would be expected to align in a concentric pattern around the center of the microwell.

Each microwell contained a range of 500–2000 cells and we performed experiments with hundreds of microwells. Thus, it became prudent to perform morphological analysis using automated processing. A plugin using ImageJ (NIH) analysis software was developed which allowed us to take each image, convert all cells into ellipses, then compute the angle of orientation, lengths along the major and minor axis, and location of the cell. Cells located at the center and edges of the microwell (less than 30% and greater than 90% of the radius) were eliminated from the data set. To justify this step, the percentage of cells aligned in radial segments of 10% (between 0–10%, 10–20%, etc) was calculated and plotted versus the simulated difference in radial and tangential strains (see Supporting Information). The 30%–90% radius region is where the difference in radial to tangential stretch is largest and most cell alignment due to stretching is expected and observed. Another area where the most cells aligned occurred between 90–100% of the radius. This was a region where the cells may have aligned due to their proximity to the edge rather than as a physiological response to stretching. In this region, the radial strain is also negative, hence the cells were being compressed rather than stretched (Figure 2c). Cells within 30% of the radius were also eliminated because of the smaller difference in radial to tangential strains. There are ways to potentially alter the substrate strains that the cells are exposed to. To have a more evenly stretched cell population, it is possible to limit cell attachment to certain areas of the membrane using selective cell seeding and patterning of the membrane [34]. Although not explored in the present study, a method to alter the strain fields in the membrane is to use materials with a different stiffness value. PDMS is ideal since it has a relatively low Young's Modulus (~750kPa) which allows for highly directional surface strains in the radial direction as estimated using the constructed finite element model.

Previous studies, using a circular substrate for cell culture, have analyzed cell alignment by either choosing random areas on the membrane, or by focusing on three main regions (the center, middle, and periphery) [3]. The automated processing described here, allows one to analyze all cells in the microwell and is time efficient, eliminates user bias, and can be easily adapted for a variety of other measurements. Image capture is also done quickly, with 2 images taken using the 4x objective per microwell. While ideal for analyzing EC and A549 cells, this analysis was limited in analyzing the C2C12 cells due to their shape and density. For the C2C12 cells it was necessary to manually inspect each ellipse image and if necessary, separate cells in areas with a large overlap of cells by manually drawing fine lines to separate individual cells.

In the present experiments, the alignment of cells perpendicular to the radial strain can be discussed in view of physiological conditions. Frequencies of 0.2 Hz and 1 Hz were chosen to be representative of a normal resting respiration rate and average heart rate respectively, while 5 Hz represents an abnormally high frequency that is observed during situations such as muscle fibrillation. Both endothelial cells and C2C12 cells are known to align when exposed to mechanical strain in vivo.

In vivo, endothelial cells appear spindle-like and align longitudinally on the luminal surface of a blood vessel. They are exposed continuously to mechanical stimulation such as fluid shear stress from the circulating blood, but also periodic stretching and relaxing caused by blood pulsation. The pulsatile nature of this blood flow along with its pressure waveform acts on the compliance of the arterial wall to produce circumferential stretching of the wall. In response, endothelial cells align to form the most efficient functional configuration, orienting roughly parallel to the longitudinal axis [3]. Previous studies have shown that ECs subject to cyclical deformation ranging from 10 to 20% elongate and reorient perpendicular to the stretch direction [10,11,28–32]. In our device, endothelial cells were shown to align in response to radial strain, with the greatest percentage of aligned cells (31.1%) occurring at a pin frequency of 5 Hz after 12 hrs versus the control unstretched cells (10.8%) (Figure 5a). The EC cells also elongated in response to both stretch frequency and time (Figure 5b) with the greatest elongation change occurring at 12 hours after stretch at 5Hz (1.86 ± 0.64 versus the unstretched 1.65 ± 0.47, P < 0.05).

Mechanical stimuli are believed to also significantly influence skeletal muscle which experiences several types of loads in vivo such as longitudinal load during developmental bone growth and cyclic loading during exercise and movement [1]. Akimoto et al. found that after growing C2C12 cells in the Flexcell system and exposing them to 20% cyclic stretch for 24 hrs, the cells oriented at an oblique angle on either side of the stretching plane [33]. In our studies, C2C12 cells aligned perpendicular to the radial direction (Figure 5a), with the greatest percentage of aligned cells (26.0% versus the control at 11.3%) occurring after 12 hrs of stretch at 5 Hz. The data, in this case, is not as clear as the EC cells due to the difficulty in automatically analyzing the orientation angles. C2C12 cells have a spindle-like morphology and cytoplasmic extensions, which make it difficult to fit ellipses around each cell and had to be manually separated.

Physical forces also play an important role in regulating the structure, function, and metabolism of the lung [2]. The alveolar epithelium, comprised of Type I and Type II cells, lines the alveolar air sacs of the lung and experiences cyclical mechanical deformation due to respiratory cycles. Type II alveolar epithelial cells that cover 3–7% of the alveolar surface, are small, cuboidal cells (diameter 10 μm) predominantly located in the corners of alveoli. In vivo Type II cells serve as the progenitor of the Type I cells, transdifferentiating into the squamous Type I cells [35]. The A549 cell line, representative of the Type II cells, maintains a similar cuboidal shape in culture, however does not undergo morphological changes to differentiate into the elongated Type I-like cells [36]. In response to mechanical stimulation the A549 cell line is thus not expected to elongate or align. Our results show that, in contrast to endothelial cells, the A549 alveolar epithelial cells were shown to have little response morphologically to cyclic stretch. As shown in Figure 5, A549 cells had little change in orientation angle (10.8% cells aligned in control versus 13.8% after stretching at 5Hz for 12 hrs) due to stretching conditions.

One of the drawbacks to the Braille based system is the inability to control the first time derivative of the mechanical strain amplitude: the strain rate. The rate at which a strain is applied is a fundamental component of a mechanical stimulus and changes with blood pressure, heart rate, and other factors [37]. In the present system, due to the digitized movement of the Braille pins (positioned either up or down), the maximum strain and its rate cannot be controlled independently. The maximum strain can be altered by varying the PDMS membrane thickness, while the average strain is set to be the strain divided by the pin movement time. In the future, to study the effect of strain rate on cellular behavior, a customized advanced Braille system can be developed that is connected to a variable voltage circuit rather than the current circuit that uses a 0V to 200V switch.

5. Conclusions

The system described here is a fast and easy-to-fabricate device to expose cells to cyclical stretch at different frequencies. Endothelial and C2C12 cells align perpendicularly in response to the radial strain. From the simulation results, it is shown that the radial and tangential strain field across the surface of the microwell is nonuniform but adjustable depending on specific needs. The thickness of the membrane is a significant factor in the strains generated. The well size and shape can also be manipulated to alter strain fields. Another possibility to manipulate the strain fields that has not been explored here is to alter the shape of the Braille pin. The pin can also be shaped to have minimal contact with the membrane, for example with a pointed end. Future work will focus on increasing the throughput of the device, by the addition of more microwells. The device is also amenable to the study of other cell types and their responses to strain. Although this paper focused mainly on cell alignment, the present device has the potential to be also used to study other effects of cyclic stretch on cells such as the disruption of the basement membrane of epithelial cells leading to increased barrier permeability and cell death [26], cytoskeletal rearrangements like actin remodeling [11], activation of changes in gene expression [27,28,39], and the release of factors such as cytokines and growth factors [40]. Although our system used flat membranes, one can also envision the use of micropatterned membranes. Such systems would allow efficient analysis of the combined effect of cell patterning with cell stretching [41–44]. With its ease of fabrication and quick image capture and analysis protocols, this cell stretching device is ideal for studying the responses of cultured cells to mechanical strain and will benefit in vitro studies of mechanotransduction.

Figure 1s. Average elongation ratio for endothelial cells for each condition. Elongation ratio is defined as the length of the cell along the major axis divided by the length along the minor axis.

Figure 2s. Top: From simulation results, the difference between radial and tangential strain (%) across the membrane. Bottom: For one experiment of endothelial cells stretched at 5 Hz for 12 hrs, the percentage of cells aligned (between 80–90°) for each radial segment.

Figure 3s. Average percentage of cells within 30 and 90% of the radius with orientation angles between 80–90°, with 90° considered perfect alignment with standard error of means.

Figure 4s. Automated image analysis using ImageJ (NIH). (a) Original fluorescence micrograph of endothelial cells subjected to stretch at 5 Hz for 12 hrs and stained with calcein AM. During processing, images were thresholded to create a binary black and white image (b) and ellipses were automatically fitted around each cell (c). The orientation angle (θ) was calculated as the angle between the major axis of the ellipse and a line extending from the center of the well to the ellipse centroid (d). (e) Alignment histogram with the distribution of cell orientation angles.