Abstract
Atrial natriuretic factor (ANF) is a peptide hormone that increases renal NaCl and water excretion. Several renal sites of ANF action have been identified, but general agreement has not been reached concerning the quantitative contribution of each action to the natriuresis and diuresis. Using a five-nephron central core model of NaCl, urea, KCl, and water transport in the rat kidney, we have quantitatively evaluated the hypothetical effects on whole kidney function of three experimentally observed ANF actions: 1) inhibition of active NaCl absorption in the collecting duct, 2) inhibition of osmotic water permeability in the collecting duct, and 3) increased NaCl and water delivery out of the proximal convoluted tubule simulating an increase in glomerular filtration rate. The simulations show that inhibition of collecting duct active NaCl absorption by ≥50% can increase NaCl and water excretion to levels that match experimental values. In addition, the model predicted that the urinary sodium concentration will increase to greater than plasma levels as observed experimentally. Simulated decreases in collecting duct water permeability predicted an in- crease in water excretion with little change in NaCl excretion. Simulated 2.5−5% increases in glomerular filtration rate also increased simulated NaCl and water excretion rates to experimentally observed levels in response to ANF. However, this action was less effective than inhibition of collecting duct active NaCl absorption in increasing the urinary NaCl concentration. We conclude that a combination of several actions are likely to account for the overall renal effect of ANF.
Keywords: concentrating mechanism, glomerular filtration rate, collecting duct, sodium chloride, water, urea, mathematical model
ATRIAL NATRIURETIC FACTOR (ANF) is a circulating peptide, secreted by cardiac atria, that induces a marked increase in renal NaCl and water excretion when its circulating level rises. A unique aspect of this response (vis-a-vis other factors that cause a natriuresis) is that the urinary NaCl concentration increases to levels well in excess of the plasma NaCl concentration (1). Several renal sites of ANF action have been identified, but general agreement has not been reached concerning the quantitative contribution of each action to the natriuresis and diuresis.
The renal excretion of any substance is determined by the relative rates of its filtration by the glomerulus, its tubular reabsorption, and its tubular secretion. In theory, ANF could affect NaCl and water excretion by altering any of these processes, individually or in combination. Evidence for each of these possibilities has been presented in the literature.
Several studies have provided evidence that ANF increases glomerular filtration rate (GFR) (1, 21, 26). Normally, delivery of NaCl and fluid to the distal tubule is stabilized by the tubuloglomerular feedback mechanism. However, ANF blunts tubuloglomerular feedback (5,14), an effect that can potentially allow increases in the filtered load of NaCl to increase distal NaCl delivery and to increase NaCl excretion.
In vivo micropuncture and microcatherization studies support the view that ANF directly inhibits NaCl and water reabsorption in the collecting duct system (4, 5, 9, 37,38,47). These have demonstrated that ANF decreases the capacity for NaCl reabsorption in the inner medullary portion of the collecting duct. However, ANF also markedly increases the delivery to the beginning of the inner medullary collecting duct (IMCD), indicating that it must have some effect upstream from the IMCD.
Additional evidence for a tubular effect of ANF comes from in vitro studies. ANF has been shown to increase cyclic GMP accumulation in microdissected IMCD and cortical collecting duct (CCD) segments (27). ANF inhibited vasopressin-stimulated osmotic water permeability in isolated perfused rabbit CCD (8) and in isolated perfused rat IMCD segments (28). ANF directly inhibited active NaCl absorption in isolated perfused rat CCD (29). Furthermore, Zeidel and co-workers have shown that ANF inhibits ouabain-sensitive oxygen consumption (49) and 22Na uptake (48) in suspensions of rabbit IMCD cells.
Theoretically, ANF could also act by stimulating tubular NaCl secretion. In micropuncture studies in rats, Fried et al. (9) found that ANF increased Cl delivery to the early IMCD to a level well in excess of the Cl delivery to the late distal tubule of superficial nephrons. They suggested that this observation could have resulted from ANF-induced NaCl secretion in the collecting ducts or from preferential inhibition of NaCl absorption in the deep nephrons. However, similar studies by Sonnenberg et al. (37) did not show a rise in Na delivery between the late distal tubule and the beginning of the IMCD in response to ANF.
In summary, there are at least two hypotheses for the renal mechanism of ANF action: the “GFR” hypothesis and the “renal tubule” hypothesis. These hypotheses are not mutually exclusive. Through the use of a central core model of NaCl, urea, KCl, and water transport in the rat kidney, we sought to assess quantitatively the hypothetical contribution to NaCl and water excretion that would result from the experimentally observed ANF effects on either tubular transport or GFR.
METHODS
Description of Mathematical Model
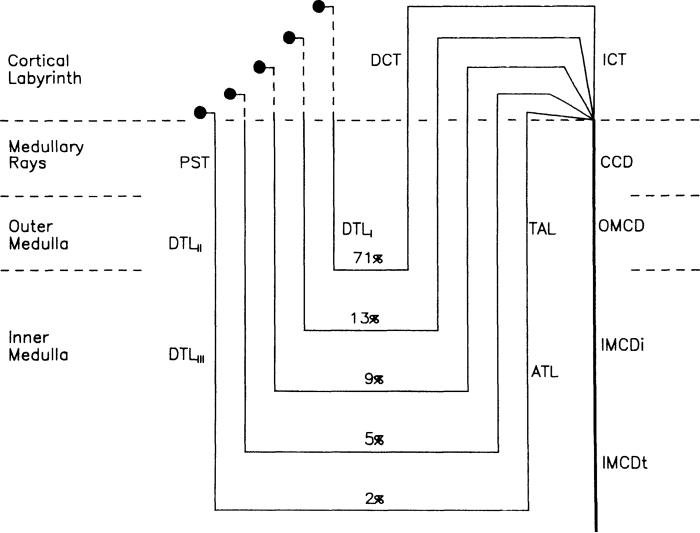
The mathematical model is based on the central core model of Stephenson (41, 42) and a multinephron, multisolute model of the mammalian kidney described by Mejia and Stephenson (25). The model is shown schematically in Fig. 1 and is described in detail in the APPENDIX. It consists of equations of motion and balance equations for solute mass and volume flow in the cortex and the medulla. Five populations of nephrons (based on loop length) are assumed in order to approximate the entire distribution of nephrons (Fig. 1). Individual nephron segments described include the proximal straight tubules (PST), descending and ascending limbs of Henle, distal convoluted tubules (DCT), initial collecting tubules (ICT), and collecting ducts. The function of the proximal convoluted tubule is not explicitly simulated.
FIG. 1.
Schematic diagram of mathematical model showing 5 nephron populations (1 superficial and 4 juxtamedullary) and percent of nephrons that they represent. All nephrons empty into a common collecting duct at junction of cortical labyrinth and medullary rays. See text for definitions of abbreviations.
Rather the aggregate function of the glomerulus and proximal convoluted tubule are simulated by specifying the input to the PST as 40% of the GFR. In the medullary rays and in the medulla the vasculature is merged with the interstitium to form a medullary central core that is homogeneous at each medullary depth. In the cortical labyrinth the interstitium and the blood vessels are merged into a well-mixed compartment. Conservation equations are then solved along each nephron segment and at each axial position of the core.
Protocols
The model parameters and transport rates were estimated from experimental measurements (Tables 1-3). Whenever possible, data from studies in rats were used. Where experimental data were not available, the model parameters were chosen to match experimentally measured water, urea, and salt concentrations both within the kidney and in the urine, as described below. These parameters defined the control condition for this study. The hypothetical effects of ANF in the kidney were simulated with the model by increasing the volume flow rate to the PST or by changing a specific transport parameter in the appropriate tubule segment. The use of a model with a central core configuration allowed us to study these effects independently of possible hemodynamic actions of ANF. Solution of the model yielded values of the mass flow rate and concentration profiles for NaCl, urea, and water as a function of depth from the cortex to the papillary tip for the tubule segments and the central core. Specifically, three questions were addressed by model simulations with specific parameter changes.
TABLE 1.
Collecting duct transport parameters
| Segment | Pf, μm/s | Purea, × 105 cm/s | VmaxNaCl, pmol·mm−1·min−1 | KmNaCl, mM |
|---|---|---|---|---|
| CCD | 900a | 0e | 48h | 28j |
| OMCD | 900b | 0f | 0i | 28j |
| IMCDi | 510c | 0f | 0j | 28j |
| IMCDt | 510d | 75g | 46j | 28j |
Pf, water permeability; Purea, urea permeability; VmaxNaCl, maximum rate of NaCl transport; KmNaCl, Michaelis constant for NaCl. OMCD, outer medullary collecting duct; IMCDi and IMCDt, initial and terminal inner medullary collecting ducts, respectively.
Matched to CCD.
Matched to IMCDt.
From Ref. 28.
From Ref. 16.
From Ref. 35.
From Ref. 36.
From Ref. 45.
From Ref. 44.
Chosen to match in vivo data (see METHODS).
TABLE 3.
Distal tubule transport parameters
| Segment | Nephron Population No. | Pf, μm/s | PKCl, × 105 cm/s | VmaxNaCl, pmol·mm−1·min−1 | KmNaCl, mM |
|---|---|---|---|---|---|
| DCT | 1 | 3.25 | 24 | 50 | |
| 2−5 | 3.25 | 18 | 50 | ||
| ICT | 1 | 170 | 3.25 | 24 | 50 |
| 2−5 | 170 | 3.25 | 18 | 50 |
Parameters were chosen to match in vivo conditions as described in METHODS. See Table 1 for definitions of abbreviations.
Question 1
What are the hypothetical effects on NaCl, water, and urea excretion of inhibition of active sodium transport, both in the CCD (29) and the IMCD (4,9, 38, 47, 48)?
Question 2
What are the hypothetical effects on NaCl, water, and urea excretion of inhibition of osmotic water permeability, both in the terminal inner medullary collecting duct (IMCDt (28) and in the CCD (8, 29)?
Question 3
What are the hypothetical effects on NaCl, water, and urea excretion of an increase in fluid delivery out of the proximal convoluted tubule due either to an increase in GFR or a decrease in proximal tubule fluid reabsorption?
Transport Parameters
The transport parameters used in the control simulations were chosen from the in vitro perfusion literature or assigned to satisfy criteria based on in vivo and tissue slice measurements. Reflection coefficients for all solutes were chosen equal to 1.0, and relatively small permeabilities were set equal to zero. NaCl permeabilities were uniformly set equal to zero, and active NaCl transport was assumed to obey Michaelis-Menten kinetics. The maximum rate of NaCl transport (Vmax) and the Michaelis constant (Km) for the CCD and the IMCDt (Table 1) were chosen so that excreted NaCl concentration in the control experiment is 42 mM and collecting duct NaCl concentration at the beginning of the IMCDt is ∼1.3 times plasma (7).
For the control simulations the solute (k) diffusion coefficients in the central core (DOk) which reflect the efficiency of the idealized vascular exchange, were specified as 1 × 10−6 cm2/s, a low value. The effect of hydrostatic pressure on the simulations was negligible, so hydrostatic pressure was held constant by setting the resistance to flow, Ri, equal to zero.
The transport parameters in the other nephron segments are given in Tables 2 and 3. Water and urea permeabilities in the PST and descending limb of Henle's loop and active NaCl transport parameters in the ascending limb of Henle's loop were adjusted so that 1) the total solute concentration in the central core at the papillary tip is ∼5 times plasma with ∼70% NaCl and ∼30% urea (3, 30), and 2) the osmolality in the core at the junction of the inner and outer medulla is ∼2.5 times plasma (12). To obtain realistic axial NaCl osmolality gradients in the inner medulla, we assumed active NaCl transport in the thin ascending limb. This choice was made because the mechanism of NaCl accumulation in the inner medulla remains an unresolved issue (18), and active NaCl transport was the simplest means of generating the inner medullary environment to which the IMCDs are exposed in vivo. The conclusions of this study do not depend on this assumption. Water and active transport parameters for NaCl in the cortical thick ascending limb (TAL), DCT, and in the ICT were adjusted so that 1) luminal fluid NaCl concentration is ∼50 mM entering the DC (10), and 2) luminal fluid entering the CCD at the medullary rays is isotonic with plasma (11) and the tubular fluid-to-plasma ratio of inulin (TF/P) is ∼10 (9). To account for the osmotic effects of KC1 in the collecting ducts, we assumed that KC1 is secreted into the DCT and ICT, so that ∼20 mM KC1 was delivered to the CCD. We found it convenient to do this by allowing passive influx, although the secretory mechanism in vivo is active. These features are consistent with data for animals during antidiuresis.
TABLE 2.
Tubule transport parameters
| Segment | Nephron Population No. | Pf, μm/s | Purea, × 105 cm/s | VmaxNaCl, pmol·mm−1·min−1 | KmNaCl, mM |
|---|---|---|---|---|---|
| PST | 1 | 141 | |||
| 2−3 | 106 | ||||
| 4−5 | 109 | ||||
| DTLI,II | 1 | 141 | |||
| 2−3 | 106 | ||||
| 4−5 | 109 | ||||
| DTLIII | 2−3 | 106 | 90 | ||
| 4−5 | 109 | 90 | |||
| ATL | 2 | 541 | 50 | ||
| 3 | 90 | 386 | 50 | ||
| 4 | 90 | 300 | 50 | ||
| 5 | 90 | 246 | 50 | ||
| TAL (OM) | 1 | 897 | 50 | ||
| 2 | 541 | 50 | |||
| 3 | 386 | 50 | |||
| 4 | 300 | 50 | |||
| 5 | 246 | 50 | |||
| TAL (MR) | 1−5 | 12 | 50 |
Parameters were chosen to match in vivo conditions as described in METHODS. DTLI,II and DTLIII, descending thin limb segments I and II and segment III, respectively; ATL, ascending thin limb; TAL (OM), thick ascending limb in outer medulla; TAL (MR), thick ascending limb in medullary rays. See Table 1 for definitions of other abbreviations.
The whole kidney GFR was assumed to be 0.95 ml/ min distributed uniformly to 38,000 nephrons. Solute concentrations in systemic plasma were assumed to be 150 mM Na and 6.5 mM urea. The input to the PST was assumed to have a composition identical to plasma, except that the urea concentration was increased to 1.5 times plasma (19).
Geometric Parameters
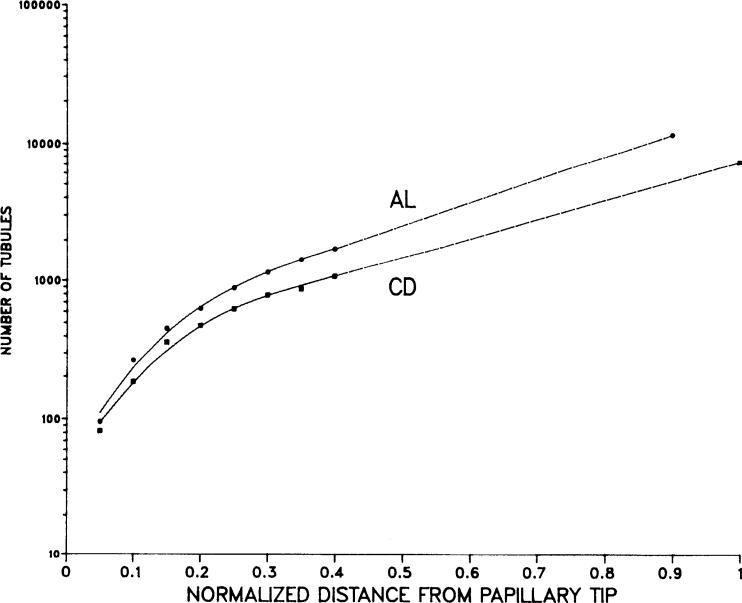
The total number of ascending limbs of Henle and of collecting ducts is shown vs. normalized distance from the papillary tip in Fig. 2. These values were obtained by multiplying the number of tubules per unit cross-sectional area determined experimentally (17) by the measured cross-sectional areas (Knepper, unpublished data). The depth of the medulla from the medullary rays to the papilla is ∼8 mm, with the medullary rays and the outer stripe of the outer medulla 1.5 mm in depth, the inner stripe of the outer medulla 1.5 mm, and the inner medulla 5.0 mm. Five nephron populations are considered to represent a total of 38,000 individual nephrons (17). As shown in Fig. 1, the 71% of all descending limbs of Henle that turn within the outer medulla define the short-looped nephron population (39). Four long-looped nephron populations include 13% that turn in the next 1.25 mm, 9% that turn in the next 1.25 mm, 5% that turn in the next 1.25 mm, and 2% that turn in the final 1.25 mm to approximate the nephron distribution in the rat kidney. The length of the distal tubules is taken to be 1.6 mm, and the ICT was assigned to be 1.6 mm in length. The radii for individual tubule segments are (in μm) 10 PST, 8 descending thin limb (DTL); 7.5 ascending thin limb (ATL); 13.5 thick ascending limb (TAL); 20 DCT; 12 ICT, CCD, and outer medullary collecting duct (OMCD); and 16 IMCD. The cross-sectional area of the central core is estimated from the volume fraction of vascular structures, interstitium, and nephron segments at each depth in the medulla (17).
FIG . 2.
Total number of ascending of limbs of Henle (AL) and of collecting ducts (CD) in rat's inner medulla is shown vs. normalized distance from papillary tip. • and ■, mean values for 3 rats. Curve fit is nonlinear in inner 0.4 and linear in outer 0.6.
Numerical Methods
Differential equations describing the model are stated in the APPENDIX. To obtain the concentration of each solute and the volume flow in each renal tubule segment and in the central core, the equations are discretized and solved numerically using the boundary conditions given in the APPENDIX. To satisfy water and mass balance, the volume and solute flux out of the tubes must equal the volume and solute flux into the core. A second-order box scheme is used to approximate space derivatives, and an implicit first-order integration scheme is used in time (24). Domain decomposition is used to partition the model for solution, and symbolic algebra is used to optimize the calculation of pressures, flows, and solute concentrations in the nephrons (25). Parameter continuation is performed until the solution with the desired parameter set is obtained (23). We thus obtain time-stable steady-state solutions of the model. Simulations were performed on a CRAY X-MP computer at the National Cancer Institute's Frederick Cancer Research Center.
RESULTS
Control Simulations
With the parameters given in Tables 1-3, a control simulation was performed. Figure 3, A and B, shows the mass flow and concentration of NaCl in the collecting duct as a function of medullary depth from the cortex to the papilla for the control simulation (solid lines). Table 4A shows the composition of the outflow from the distal convoluted tubules of the superficial nephrons, the composition of the mixed tubule fluid entering the CCD, and the urinary composition.
FIG. 3.
A: axial profile of NaCl mass flow in collecting duct as fraction of filtered load for control experiment (solid line), for 50% reduction (long dashes), and for 90% reduction (short dashes) in maximum rate of NaCl absorption in CCD. B: axial profile of NaCl concentration in collecting duct for control experiment (solid line), for 50% reduction (long dashes), and for 90% reduction (short dashes) in maximum rate of NaCl absorption in CCD.
TABLE 4.
Composition for control and other simulations
| Water |
NaCl |
Urea |
Total Osmolality, mosmol/kgH2O | ||||
|---|---|---|---|---|---|---|---|
| FFL, ×100 | V, nl/min | FFL, ×100 | Concn, mM | FFL, ×100 | Concn, mM | ||
| A. Control | |||||||
| DCT out | 19.74 | 4.94 | 6.11 | 46 | 55.4 | 18 | 130 |
| CCD in | 9.59 | 2.40 | 5.37 | 84 | 149.1 | 101 | 311 |
| CD out | 0.96 | 0.24 | 0.27 | 42 | 46.9 | 318 | 822 |
| B. 50% | |||||||
| DCT out | 19.66 | 4.92 | 6.08 | 46 | 55.4 | 18 | 130 |
| CCD in | 9.17 | 2.29 | 5.30 | 87 | 130.8 | 93 | 309 |
| CD out | 1.14 | 0.28 | 0.84 | 111 | 46.7 | 266 | 835 |
| C. 10% | |||||||
| DCT out | 19.64 | 4.91 | 6.08 | 46 | 55.4 | 18 | 130 |
| CCD in | 8.89 | 2.22 | 5.26 | 89 | 117.9 | 86 | 308 |
| CD out | 1.32 | 0.33 | 1.41 | 159 | 46.7 | 229 | 843 |
| D. 50% | |||||||
| DCT out | 19.81 | 4.95 | 6.13 | 46 | 55.4 | 18 | 130 |
| CCD in | 8.67 | 2.17 | 5.31 | 92 | 102.8 | 77 | 306 |
| CD out | 1.68 | 0.42 | 2.60 | 232 | 48.5 | 187 | 883 |
| E. 10% | |||||||
| DCT out | 20.14 | 5.04 | 6.23 | 46 | 55.4 | 18 | 129 |
| CCD in | 8.47 | 2.12 | 5.40 | 96 | 84.7 | 65 | 302 |
| CD out | 2.47 | 0.62 | 4.85 | 294 | 49.9 | 131 | 878 |
| F. 50% Pf, IMCDt | |||||||
| DCT out | 19.58 | 4.89 | 6.06 | 46 | 55.4 | 18 | 130 |
| CCD in | 9.20 | 2.30 | 5.24 | 86 | 137.2 | 97 | 311 |
| CD out | 1.02 | 0.26 | 0.20 | 29 | 46.9 | 299 | 745 |
| G. 20% Pf, IMCDt | |||||||
| DCT out | 19.34 | 4.83 | 5.98 | 46 | 55.4 | 19 | 131 |
| CCD in | 8.60 | 2.15 | 5.05 | 88 | 118.7 | 90 | 310 |
| CD out | 1.12 | 0.28 | 0.11 | 15 | 47.0 | 272 | 643 |
| H. 50% Pf, CD | |||||||
| DCT out | 20.27 | 5.07 | 6.27 | 46 | 55.4 | 18 | 129 |
| CCD in | 9.35 | 2.34 | 5.43 | 87 | 128.5 | 89 | 307 |
| CD out | 1.14 | 0.29 | 0.35 | 46 | 47.0 | 267 | 712 |
| I. 20% Pf, CD | |||||||
| DCT out | 20.67 | 5.17 | 6.38 | 46 | 55.4 | 17 | 128 |
| CCD in | 8.86 | 2.22 | 5.47 | 93 | 95.7 | 70 | 301 |
| CD out | 1.76 | 0.44 | 0.52 | 44 | 46.7 | 173 | 490 |
| J. 20% Pf, CD and 50% | |||||||
| DCT out | 20.83 | 5.21 | 6.43 | 46 | 55.4 | 17 | 128 |
| CCD in | 8.72 | 2.18 | 5.56 | 96 | 81.4 | 61 | 298 |
| CD out | 2.54 | 0.64 | 2.93 | 173 | 48.3 | 123 | 626 |
| K. 20% Pf, CD and 10% | |||||||
| DCT out | 21.06 | 5.26 | 6.50 | 46 | 55.4 | 17 | 128 |
| CCD in | 8.81 | 2.20 | 5.70 | 97 | 75.2 | 56 | 296 |
| CD out | 3.35 | 0.84 | 5.17 | 231 | 49.7 | 96 | 680 |
| L. 1.025 VPST (0) | |||||||
| DCT out | 20.29 | 5.20 | 6.83 | 50 | 55.4 | 18 | 137 |
| CCD in | 10.01 | 2.57 | 6.04 | 90 | 126.9 | 82 | 305 |
| CD out | 1.23 | 0.32 | 0.89 | 108 | 47.1 | 248 | 800 |
| M. 1.05 VPST (0) | |||||||
| DCT out | 20.92 | 5.49 | 7.57 | 54 | 55.4 | 17 | 144 |
| CCD in | 10.58 | 2.78 | 6.75 | 96 | 110.1 | 68 | 299 |
| CD out | 1.57 | 0.41 | 1.64 | 156 | 47.3 | 196 | 778 |
The following refer to value assigned in control experiment: is maximum rate of NaCl transport in cortical collecting duct, is maximum rate of NaCl transport in collecting duct, Pf, IMCDt is osmotic water permeability of terminal segment of inner medullary collecting duct, Pf, CD is osmotic water permeability of collecting duct, VPST (0) is volume flow entering proximal straight tubules. Flow rates (V) in collecting ducts are normalized by total number of glomerulotubular units in rat kidney (38,000). Therefore, to obtain total flow in collecting ducts, values should be multiplied by 38,000. FFL, fraction of filtered load. DCT values are for population 1 (superficial) nephrons only.
Hypothetical Effects of Inhibition of Active NaCl Transport
CCD. Nonoguchi et al. (29) reported that ANF caused a 90% inhibition of net NaCl absorption in the CCD of rats and a 50% inhibition of vasopressin-stimulated net fluid absorption. Therefore we examined the hypothetical effects of both a 50 and a 90% inhibition of active NaCl absorption in the CCD (Table 4, B and C). Figure 3, A and B, shows mass flow rate and concentration of NaCl in the collecting duct (dashed lines). Hypothetical reductions in CCD NaCl transport increased the NaCl delivery to the IMCD, increasing the NaCl reabsorption rate in the terminal segment and increasing the NaCl excretion. A hypothetical decrease in NaCl transport in the CCD also predicted increased water excretion but no change in urea excretion (Table 4, B and C).
Complete collecting duct
Several studies have provided evidence for an inhibition of net NaCl absorption in the IMCD (4,9,38,47–49). Therefore we next examined the effect of a 50 and a 90% inhibition of net NaCl absorption in the entire collecting duct system (Table 4, D and E). The reduction in active NaCl absorption increased simulated NaCl and water excretion above levels found in the previous simulations. Simulated fractional NaCl excretion rose to 2.6% of the filtered load with 50% inhibition and 4.85% with 90% inhibition, values comparable to those seen in micropuncture studies of ANF action (5, 9,38,47). The urinary NaCl concentration was predicted to increase above plasma NaCl concentration, as has been demonstrated experimentally (1, 6, 32, 34).
Hypothetical Effects of Inhibition of Osmotic Water Permeability
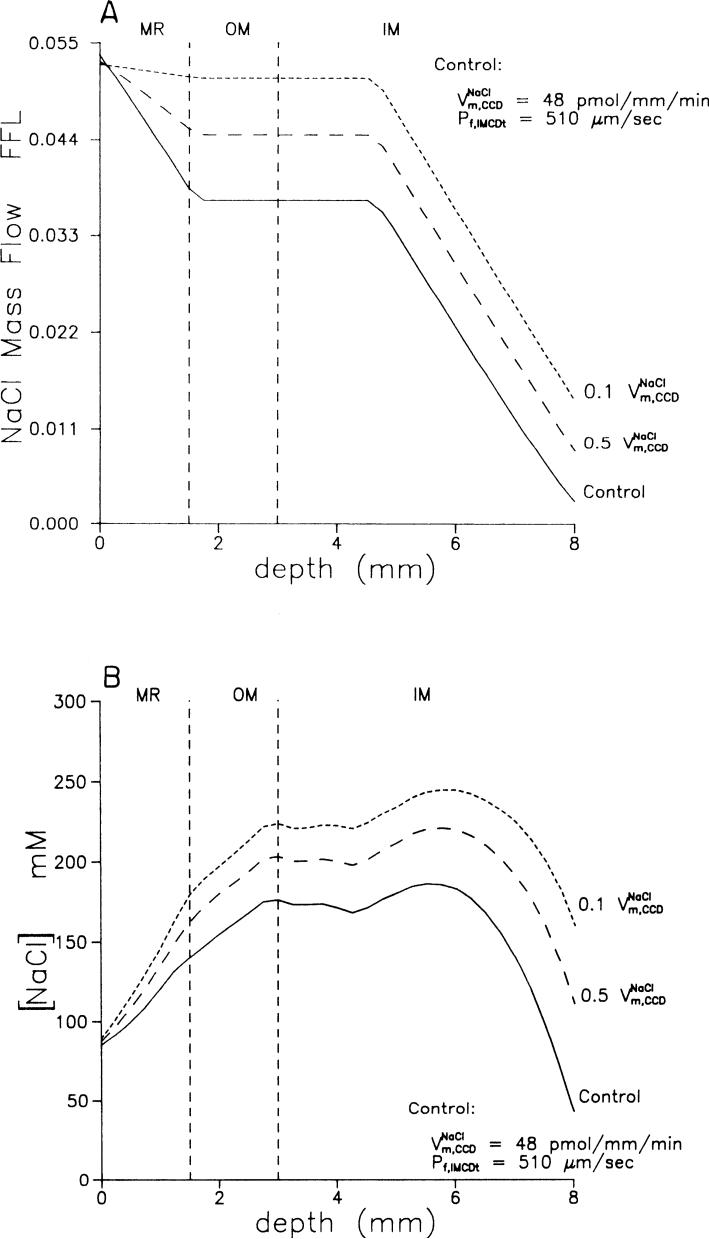
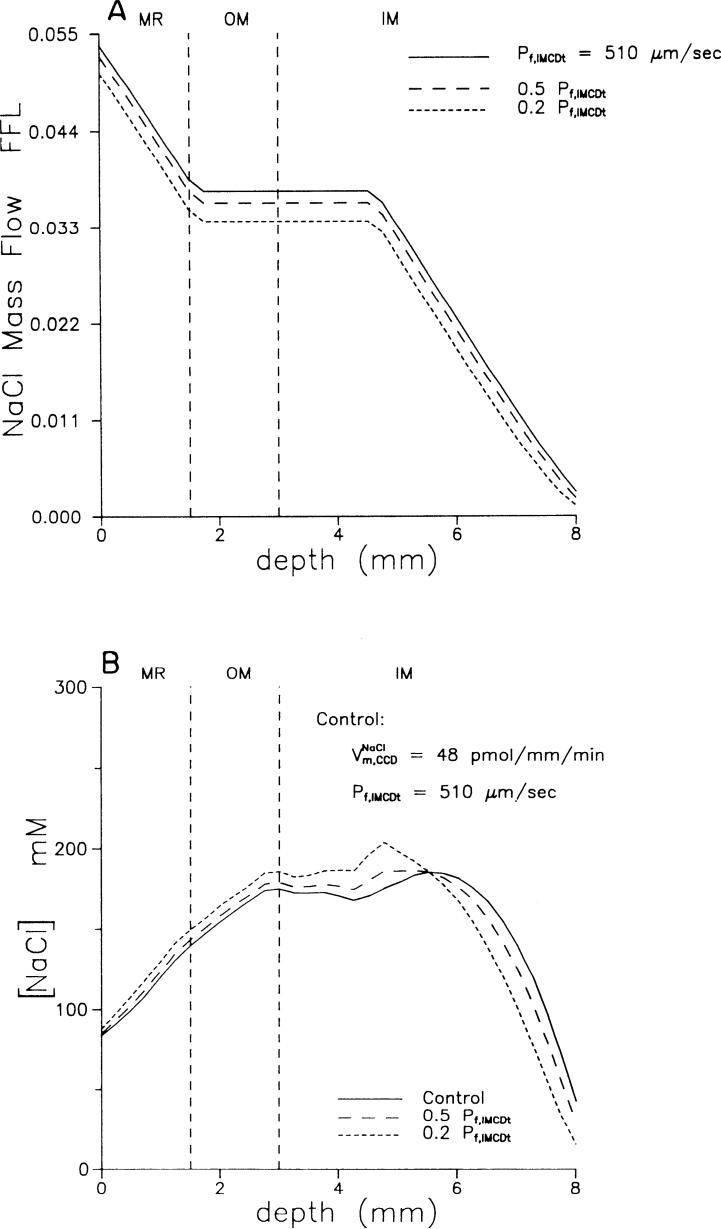
IMCD. ANF inhibits vasopressin-stimulated osmotic water permeability in IMCDt (28). We examined the hypothetical effects of a 50 and an 80% inhibition of osmotic water permeability in IMCDt (Table 4, F and G). Figure 4, A and B, shows NaCl mass flow and concentration along the collecting duct. Changes in NaCl and water excretion were small compared with those seen with inhibition of active NaCl transport. As osmotic water excretion increased slightly and NaCl excretion decreased slightly relative to the control. Simulated urea excretion was unchanged. The major effect was a reduction in simulated urinary osmolality due to incomplete osmotic equilibration with the medullary interstitium.
FIG. 4.
A: axial profile of NaCl mass flow in collecting duct for control experiment (solid line), for 50% inhibition (long dashes), and for 80% inhibition (short dashes) in osmotic water permeability of IMCDt. B: axial profile of NaCl concentration in collecting duct for control experiment (solid line), for 50% inhibition (long dashes), and for 80% inhibition (short dashes) in osmotic water permeability of IMCDt.
Complete collecting duct
Dillingham and Anderson (8) demonstrated that ANF inhibits vasopressin-stimulated osmotic water permeability in CCDs. Therefore we also examined the effect of inhibition of osmotic water permeability along the entire collecting duct system (Table 4, H and 1). A simulated reduction in osmotic water permeability increased water excretion and, as in the previous simulations, did not affect urea excretion. It produced a modest increase in NaCl excretion. Because water excretion was increased out of proportion to the increase in solute excretion, there was a marked decrease in urine osmolality.
Combined Effects of an Inhibition of Active NaCl Absorption and Osmotic Water Permeability
We next studied the combined effects of a simulated decrease in both active NaCl absorption and osmotic water permeability throughout the collecting duct (Table 4, J and K). Compared with the results with inhibition of active NaCl transport alone (Table 4, D and E), the main effects of the simulated decrease in osmotic water permeability were a modulation of the elevated urinary NaCl concentration and a decrease in the predicted urinary osmolality.
Hypothetical Effects of an Increase in NaCl and Fluid Delivery to PST
Several studies have provided evidence for an effect of ANF on GFR as reviewed by Ballermann and Brenner (1), Needleman and Greenwald (26), and Maack (21). Therefore we next studied the effect of increasing fluid delivery out of the proximal convoluted tubule. This would simulate an increase in GFR, assuming glomerulotubular balance. Table 4, L and M shows results for a 2.5 and 5% increase in fluid delivery to the PST, which can be compared with the control simulation (Table 4A). Increased delivery to the PST is associated with increased NaCl and water excretion but no change in fractional urea excretion. The urinary NaCl concentration increased to a level close to the plasma concentration. Simulated water flow out of the DCT of superficial nephrons increased by over 11% for a 5% increase in delivery to the PST.
DISCUSSION
In this paper, we have used a five-nephron, central core mathematical model of the rat kidney to assess the hypothetical steady-state effects on renal excretion of several specific local actions of ANF, namely, inhibition of active NaCl absorption in the collecting duct system, inhibition of water permeability in the collecting duct system, and increased GFR. Among these actions, it was found that either inhibition of collecting duct NaCl transport or increased GFR could account for the observed steady-state increases in NaCl excretion in response to ANF. All three of the proposed local actions of ANF have predicted effects on the pattern of renal solute and water excretion and/or solute and water delivery to micropuncture-accessible sites that appear to match various aspects of the observed renal response to ANF in vivo. On the basis of the observations in this paper, we propose that the overall renal effect of an increase in circulating ANF levels is due to multiple actions of ANF in the kidney that integrate to produce a more effective regulatory response than any single action could produce. In this section, we discuss the basis of this conclusion.
Mathematical Modeling Approach
Assumptions and Simplifications
The mathematical modeling approach employed here is based on the view that the extensive knowledge gained over the years concerning the function of individual nephron segments and their topologic organization in the kidney can be utilized to evaluate the feasibility of specific hypotheses, in this case concerning the action of ANF in the kidney. The model incorporates this knowledge in its overall structure (Fig. 1) and in its geometric and transport parameters. The ideal model is an isomorphic model, i.e., a model that has a structure that precisely represents the structure of the kidney and that has parameters that are all estimated by independent experimental measurements. Obviously, this ideal is not attainable. A numerical solution using a discretized approximation to the differential equations is necessary. The size of the discretized model, i.e., the number of nonlinear algebraic equations that can be solved simultaneously, is bounded, even with the advent of supercomputers. Furthermore, we are still studying the functions of individual nephron segments, and therefore the appropriate transport parameters for the model are not fully defined. In view of these limitations, it was necessary to introduce a number of simplifications and assumptions to reduce the mathematical complexity of the model and to eliminate any dependence on parameters that do not play a critical role in answering the specific questions posed. In the following, we review these simplifications and assumptions along with their rationales.
Steady-state assumption
For this paper, we chose to simulate only the steady-state behavior of the kidney. This was a practical choice based on numerical simplicity, cost, and the central core configuration. We recognize that much of the data available in the literature concerning the effects of ANF on the kidney describe the transient or dynamic responses to the peptide rather than the steady-state response. In terms of NaCl and water excretion, the transient response has been found experimentally to be substantially larger than the steady-state response. Because our simulations describe only the steady state, we cannot presently evaluate whether any of the proposed local actions of ANF can explain the large transient increases in NaCl and water excretion.
Rat anatomy
We chose to base the model on the anatomy of the rat, because much of the in vivo data that is available concerning the effects of ANF are from studies in rats. Therefore we can compare our simulation results with in vivo data without concern that “species difference” could account for possible discrepancies. Previously transport parameter values were available chiefly from in vitro microperfusion studies in rabbits. Consequently mathematical models using these parameters reflected the behavior of the rabbit kidney. Recently rapid progress has been made in the acquisition of adequate data from isolated rat nephron segments, allowing us to eliminate substantial dependence on data from the rabbit.
Central core
For this model, we chose to assume the central core configuration of Stephenson (40, 41), which idealizes nephrovascular coupling in the renal medulla. This simplification lumps the renal medullary vasculature and interstitium into a single compartment, the composition of which varies only as a function of distance along the medullary axis and with vascular efficiency determined by the diffusion of solutes in the core. This assumption precludes any explicit treatment of the consequences of ANF effects on medullary blood flow. Consequently, the full evaluation of the effects of changes in medullary blood flow and/or medullary hydrostatic pressure on renal sodium excretion must await the development of a more detailed dynamic model.
Glomerulus and proximal tubule
For model simplicity, we chose not to simulate explicitly the function of the glomerulus or the proximal convoluted tubule. Rather an input flow was assumed into the PST where NaCl concentration was assumed to be the same as that of the glomerular filtrate and where volume flow rate was assumed to be 40% of the GFR. Changes in GFR in response to ANF were assumed to result in proportionate changes in delivery to the PST. That is, glomerulotubular balance was assumed. In this paper, we did not consider explicitly possible actions of ANF to inhibit NaCl reabsorption in the proximal convoluted tubule (13), which remain controversial. However, it is evident that this model does not discriminate between effects on glomerular filtration and proximal convoluted tubule transport, since both would affect delivery to the PST in the same way.
Loop of Henle
Controversy exists regarding the mechanism by which the inner medullary interstitial osmolality gradient is formed (18). The basis of the controversy is a discrepancy that exists between the measured properties of renal medullary tubule segments and the renal tubule properties that are required for the proposed models to work. Because this controversy is not germane to the present physiological question, we chose to bypass the issue by selecting loop of Henle transport parameters arbitrarily to match measured in vivo solute gradients in the inner medulla rather than on the basis of isolated perfused tubule data (Table 2). Specifically, we chose to assume active NaCl transport throughout the length of the ascending limb of Henle's loop to create a “single effect” for countercurrent multiplication throughout the renal medulla. This allows possible effects of ANF on the collecting duct to be evaluated in the context of the appropriate solute gradients. Although there is some evidence for ANF effects on NaCl transport in the loop of Henle (5, 46), there is also evidence against this possibility (20, 31). Pending more direct evidence for an effect of ANF in the loop of Henle, we have chosen not to evaluate such a possibility with our model.
Medullary rays
The medullary rays are fingerlike extensions of the outer stripe of the outer medulla into the cortex. In this model, we have incorporated the medullary rays into the model structure. Many previous models have ignored the medullary rays and, in so doing, have ignored the renal tubule segments contained in the rays: the PST, the cortical TAL, and the CCD. Because all three of these segments are thought to play important roles in the regulation of NaCl and water balance, the incorporation of the medullary rays into the model was a necessity.
Quantitative anatomy of the renal inner medulla
The renal inner medulla is a cone-shaped structure, the inner two-thirds of which is the renal papilla. The tapered structure of the inner medulla is due to the decreasing numbers of loops of Henle and collecting ducts that reach progressively deeper levels. The loops of Henle decrease in number toward the papillary tip because loop bends occur along the entire inner medullary axis. The collecting ducts decrease in number because of dichotomous junctions that occur throughout the inner medulla. Because net transport in the kidney depends not only on the transport parameters of individual renal tubule segments but also on the surface areas of the transporting epithelia, an accurate quantitative description of the medulla depends critically on accurate estimates of the numbers of loops of Henle and collecting ducts at each medullary level. Our model incorporates the appropriate distributions that account for the tapered structure of the inner medulla. In this paper (Fig. 2), we report previously unpublished data describing the quantitative distribution of loops of Henle and collecting ducts in the renal medulla.
Interpretation of Simulation Results
The simulations showed that the hypothetical inhibition of active NaCl absorption by ANF in the collecting duct can account for the steady-state effect of ANF administration on urinary NaCl excretion. The fractional delivery of NaCl to the distal tubule under control conditions is 5<6%, and fractional sodium excretion is generally <0.5% (5, 37). (In our control simulation, the fractional delivery of NaCl to the distal tubule was 5.4%, and the fractional excretion of NaCl was 0.3%.) The steady-state fractional excretion of NaCl after ANF increased to 1.5−4% (5, 37). The simulations show that 50% inhibition of active NaCl absorption along the entire collecting duct is sufficient to produce this increase in fractional NaCl excretion (Table 4D). ANF has been reported in several studies to increase urinary sodium concentration to a level higher than the plasma sodium concentration (1). Typical urinary sodium concentrations have been ∼200 mM (6, 32, 34). No other natriuretic substance is known to produce a rise in urinary sodium concentration to above the plasma level. In light of this observation, it is of interest that simulations assuming ANF-mediated inhibition of active NaCl transport in the collecting duct predicted a rise in urinary sodium concentration to >200 mM (Table 4, D and E). Thus we conclude that inhibition of active NaCl transport in the collecting ducts can account quantitatively and qualitatively for the observed in vivo response to ANF.
Simulated inhibition of the osmotic water permeability of the collecting duct had a relatively small effect on the predicted urinary NaCl excretion rate (Table 4, H and I). Thus we conclude that effects of ANF on osmotic water permeability alone cannot account for findings in animal studies. However, inhibition of osmotic water permeability in the collecting ducts when combined in simulations with decreased active NaCl transport had interesting effects that could be construed as providing a physiological advantage. Specifically, a decrease of water permeability blunted the predicted rise in urinary sodium concentration and decreased the predicted urinary osmolality (cf. Table 4, J and K with D and E). This is an advantage because sustained natriuresis with a high urinary NaCl concentration and a high osmolality would result in systemic hyponatremia and hypotonicity.
Increases in GFR can also increase urinary sodium excretion. Although some studies have demonstrated increases in urinary sodium excretion in response to low doses of ANF without a measurable effect on GFR, it could be argued that increases in GFR too small to measure could account for observed increases in NaCl excretion. Accordingly, we simulated the effects of small increases in GFR (2.5 and 5%) that may escape detection by the usual clearance methodology. These simulations confirmed that increases of this magnitude could account for steady-state increases in NaCl excretion similar to those seen in response to ANF. For example, the simulated fractional NaCl excretion was 1.64% with a 5% increase in GFR (Table 4M). Interestingly, the predicted urinary sodium concentration also rose to a level slightly above the plasma level when a 5% increase in GFR was assumed (156 mM in the urine vs. 150 mM in the plasma). Nevertheless, it appears that increases in glomerular filtration in this range cannot account for urinary concentrations as high as the 200 mM level observed experimentally (see above).
The modeling results provide an explanation for the observed increase in urinary sodium concentration to above plasma levels in response to ANF. The urinary NaCl concentration can be viewed as the product of the urinary osmolality and the fraction of the total urinary osmolality that is due to NaCl. The urinary osmolality is determined by the medullary interstitial osmolality, because osmotic equilibration occurs across the medullary collecting ducts. The fraction of the total urinary osmolality due to NaCl is simply the ratio (RNaCl) of the mass flow rate of sodium plus chloride to the mass flow rate of total osmotically active particles. In the simulations, both a decrease in NaCl reabsorption and an increase in GFR markedly increased RNaCl. Both actions, however, had relatively small effects on interstitial osmolality and consequently did not markedly decrease simulated urinary osmolality, since osmotic equilibration across the collecting ducts persisted. Therefore both actions of ANF increased the simulated urinary NaCl concentration. Thus a rise in urinary NaCl concentration above plasma levels does not imply any specific effect on NaCl transport in the collecting duct. All it requires is that osmotic equilibration with a hypertonic interstitium persists while at the same time the mole fraction of NaCl in the collecting duct luminal fluid is increased.
As may be expected, simulations of increases in glomerular filtration predict an increase in the absolute and fractional delivery of NaCl to the superficial distal convoluted tubule (Table 4, L and M), whereas simulations of decreased collecting duct NaCl absorption do not predict such a change (Table 4, B–E). Theoretically, this difference could be used experimentally to discriminate the site of action of ANF. Attempts to do this (5, 9, 37) have led to variable results. A statistically significant effect of ANF on NaCl delivery to the superficial distal tubule was found in only one of the three studies (5). For the other studies, it could be argued that small physiologically important changes may not be technically resolvable. Alternatively, increases in delivery to the distal tubule may only occur in deep nephron populations that are not accessible from the surface of the renal cortex (9). The late portion of the micropuncture-accessible distal tubule is morphologically the ICT (22). This segment is morphologically similar (if not identical) to the CCD. If ANF inhibits NaCl reabsorption in the ICT as it inhibits NaCl reabsorption in the CCD (29), such an effect could be experimentally detectable by comparing the function at early and late distal micropuncture sites.
In summary, none of the individual actions of ANF that we considered in this study appears to account for all of the whole kidney actions of ANF when considered alone. Consequently, we propose that the overall effect of ANF on the kidney may be dependent on ANF actions at several renal sites. In the following, we present a rationale for this view.
Integrated Effects of ANF in the Kidney
Many hormones involved in the precise control of NaCl excretion act by regulating NaCl transport in the collecting duct system (15). Regulation at the collecting duct level allows NaCl excretion to be controlled independent of the excretion of other solutes and of water. Alterations in NaCl concentration and NaCl delivery early in the nephron would be expected to interfere with other regulatory mechanisms, because the transport of water and many solutes are dependent on NaCl transport (15). In fact, potent regulatory mechanisms normally maintain a relatively constant delivery of NaCl to the distal nephron, specifically glomerulotubular balance and tubuloglomerular feedback. Maintenance of a stable rate of NaCl delivery to the distal nephron allows precise control of NaCl excretion through regulation of NaCl transport in the collecting ducts and DCT. However, because of the relatively small amount of NaCl reabsorbed in the collecting duct system, control mechanisms at this site can only mediate relatively small changes in the NaCl excretion rate. Consequently, large increases in NaCl excretion, such as may be required in response to pathological increases in extracellular fluid volume, can be produced only by inhibition of proximal NaCl transport or by increases in GFR, presumably at the expense of distal mechanisms responsible for the fine control of NaCl excretion.
On the basis of this general view, the following model of ANF action in the kidney can be proposed: the regulation of NaCl excretion by ANF may involve several local actions in the kidney. At the lowest plasma ANF concentrations, a variable inhibition of active NaCl reabsorption in the collecting ducts may occur, possibly contributing to the day-to-day control of NaCl excretion. At higher ANF concentrations, renal tubular transport may be affected at other nephron sites, either directly or possibly indirectly as a result of hemodynamic effects of the peptides that alter local driving forces for net NaCl and fluid transport (1, 2). Finally, at the highest concentrations, changes in GFR may occur and produce very high NaCl excretion rates. Such a hierarchy of local ANF actions is supported by dose-response studies of ANF-stimulated cyclic GMP accumulation, demonstrating that the threshold for ANF stimulation of cyclic GMP accumulation occurred at lower ANF concentrations in IMCD segments than in isolated glomeruli (27). This model could account for the observations that although ANF-mediated increases in NaCl excretion are associated with increases in the GFR in some studies, increases in renal NaCl excretion could occur without increases in GFR in other studies, particularly those in which ANF was administered at relatively low doses (see above).
APPENDIX
A central core model of the mammalian kidney (40-42) is characterized by a central vascular core consisting of vasa recta, assumed so highly permeable that the core functions as a single compartment, merged with the interstitium. The differential equations that describe solute and water movement in the ith tubular segment (43) are as follows
| (A1) |
| (A2) |
| (A3) |
where I is the total number of tubule segments and K is the total number of solutes; for 0 ≤ i ≤ I, 1 ≤ k ≤ K; x is the axial distance along a tube; 0 ≤ x ≤ Li is the length of the ith segment; and Cik is the concentration of the kth solute in the ith tube. The volume flow in the axial direction in the ith tube is Fiv;Ai is the cross-sectional area of the ith tube; Dik is the diffusion coefficient of the kth solute in the ith tube; Jik and Jiv, are the outward fluxes of solute and volume from the ith tube; t is time; Pi is the hydrostatic pressure; and Ri is the resistance to flow.
The transmural fluxes are as follow
| (A4) |
and
| (A5) |
where ρi is the radius of the ith tube, Pf, i; is the osmotic water permeability of tube i, Vw, is the partial molar volume of water, R is the gas constant, T is absolute temperature, the subscript q indicates a central core value (q = c for the cortex, and q = 0 for the medulla); αk is the osmotic coefficient of the kth solute; and σik is the Staverman reflection coefficient of the wall of the ith tube for the kth solute. The first term of Eq. A5 defines passive transport of the kth solute from the ith tube, where Pik is the solute permeability. The second term accounts for solvent drag, and the last term defines the metabolically driven transport, which is assumed to obey Michaelis-Menten kinetics with a maximum rate of transport , and Michaelis constant .
For the purpose of these simulations we ignore compliance of the tubules, so that Ai = Ai(x) is independent of time. We also assume that Dik = 0 for 0 < i ≤ I and all k.
Equations A1-A3 are integrated along each tube in the direction of flow with boundary conditions specified at the proximal end of each segment so that for t ≥ 0
| (A6) |
where the superscript o indicates a specified value and
| (A7) |
for 1 ≤ k ≤ K
| (A8) |
| (A9) |
for 1 < i ≤ Ih is the number of tube segments in population h; and subscripts ip and id specify the proximal and distal end of tube i, respectively. We define volume flow toward the papilla to be positive and toward the cortex to be negative, so that at a turning point Eq. A8 takes the negative sign.
In the cortex, the central core is considered to be a well-mixed bath with the concentration of each solute equal to its concentration in plasma (superscript p), namely
| (A10) |
for 1 ≤ k ≤ K, and the hydrostatic perssure is described as
| (A11) |
In the medulla and the medullary rays, the central core is treated as a tube, closed at the papilla and open at the border with the cortical labyrinth, through which the other tubes exchange solutes and water. Hence Eqs. A1-A3 apply, and the boundary conditions for the medullary core are
| (A12) |
| (A13) |
| (A14) |
for 1 ≤ k ≤ K and . Volume and mass conservation require that
| (A15) |
and
| (A16) |
for 0 ≤ x ≤ L and all solutes k, where the sums are taken over the tubes that extend to medullary depth x.
Initial conditions are defined to be
| (A17) |
for 0 ≤ i ≤ I, 1 ≤ k ≤ K and axial positions x.
The finite difference method used to discretize differential Eqs. A1-A3 to be solved with boundary conditions (A6-A14) and initial conditions (A17) is described in detail in Ref. 25. A second-order accurate box scheme is used to obtain a numerically stable and accurate approximation to the differential equations (24). The time stability of steady-state solutions has been verified by solution of the time-dependent equations near the steady state as described in Ref. 25. Continuation of steady-state solutions as a function of transport parameters is done under the control of a path-following algorithm described in Ref. 23.
Footnotes
Computations were performed on the CRAY X-MP supercomputer at the Advanced Scientific Computing Facility of the National Cancer Institute.
REFERENCES
- 1.Ballermann BJ, Brenner BM. Biologically active atrial peptides. J. Clin. Invest. 1985;76:2041–2048. doi: 10.1172/JCI112206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ballermann BJ, Brenner BM. Role of atrial peptides in body fluid homeostasis. Circ. Res. 1986;58:619–630. doi: 10.1161/01.res.58.5.619. [DOI] [PubMed] [Google Scholar]
- 3.Battilana CA, Dobyan DC, Lacy FB, Bhattacharya J, Johnston PA, Jamison RL. Effect of chronic potassium loading on potassium secretion by the pars recta or descending limb of the juxtamedullary nephron in the rat. J. Clin. Invest. 1978;62:1093–1103. doi: 10.1172/JCI109215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Briggs JP, Soejima H, Schnermann J. Effect of atrial natriuretic peptide (ANP) on Cl absorption along papillary collecting ducts (PCD) (Abstract). Proc. Int. Congr. Nephrol. 10th London July 1987. :207. [Google Scholar]
- 5.Briggs JP, Steipe B, Schubert G, Schnermann J. Micropuncture studies of renal effects of atrial natriuretic substance. Pfluegers Arch. 1982;395:271–276. doi: 10.1007/BF00580789. [DOI] [PubMed] [Google Scholar]
- 6.Camargo MJF, Atlas SA, Maack T. Role of increased glomerular filtration rate in atrial natriuretic factor-induced natriuresis in the rat. Life Sci. 1986;38:2397–2404. doi: 10.1016/0024-3205(86)90608-9. [DOI] [PubMed] [Google Scholar]
- 7.Diezi J, Michoud P, Aceves J, Giebisch G. Micropuncture study of electrolyte transport across papillary collecting duct of the rat. Am. J. Physiol. 1973;224:623–631. doi: 10.1152/ajplegacy.1973.224.3.623. [DOI] [PubMed] [Google Scholar]
- 8.Dillingham MA, Anderson RJ. Inhibition of vasopressin action by atrial natriuretic factor. Science Wash. DC. 1986;231:1572–1573. doi: 10.1126/science.3006248. [DOI] [PubMed] [Google Scholar]
- 9.Fried TA, Osgood RW, Stein JH. Tubular site(s) of action of atrial natriuretic peptide in the rat. Am. J. Physiol. 1988;255:F313–F316. doi: 10.1152/ajprenal.1988.255.2.F313. (Renal Fluid Electrolyte Physiol. 24) [DOI] [PubMed] [Google Scholar]
- 10.Giebisch G, Windhager E. Renal tubular transfer of sodium, chloride, and potassium. Am. J. Med. 1964;36:643–669. doi: 10.1016/0002-9343(64)90178-0. [DOI] [PubMed] [Google Scholar]
- 11.Gottschalk CW, Mylle M. Micropuncture study of the mammalian urinary concentrating mechanism: evidence for the countercurrent hypothesis. Am. J. Physiol. 1959;196:927–936. doi: 10.1152/ajplegacy.1959.196.4.927. [DOI] [PubMed] [Google Scholar]
- 12.Hai MA, Thomas S. Influence of prehydration on the changes in renal tissue composition induced by water diuresis in the rat. J. Physiol. Lond. 1969;205:599–618. doi: 10.1113/jphysiol.1969.sp008985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Harris PJ, Thomas D, Morgan T0. Atrial natriuretic peptide inhibits angiotensin-stimulated proximal tubular sodium and water reabsorption. Nature Lond. 1987;326:697–698. doi: 10.1038/326697a0. [DOI] [PubMed] [Google Scholar]
- 14.Huang C-L, Cogan MG. Atrial natriuretic factor inhibits maximal tubuloglomerular feedback response. Am. J. Physiol. 1987;252:F825–F828. doi: 10.1152/ajprenal.1987.252.5.F825. (Renal Fluid Electrolyte Physiol. 21) [DOI] [PubMed] [Google Scholar]
- 15.Knepper M, Burg M. Organization of nephron function. Am. J. Physiol. 1983;244:F579–F589. doi: 10.1152/ajprenal.1983.244.6.F579. (Renal Fluid Electrolyte Physiol. 13) [DOI] [PubMed] [Google Scholar]
- 16.Knepper MA. Urea transport in isolated thick ascending limbs and collecting ducts from rats. Am. J. Physiol. 1983;245:F634–F639. doi: 10.1152/ajprenal.1983.245.5.F634. (Renal Fluid Electrolyte Physiol. 14) [DOI] [PubMed] [Google Scholar]
- 17.Knepper MA, Danielson RA, Saidel GM, Post RS. Quantitative analysis of renal medullary anatomy in rats and rabbits. Kidney Int. 1977;12:313–323. doi: 10.1038/ki.1977.118. [DOI] [PubMed] [Google Scholar]
- 18.Knepper MA, Stephenson JL. Urinary concentrating and diluting processes. In: Andreoli TF, editor. Physiology of Membrane Disorders. Plenum; New York: 1986. pp. 713–726. [Google Scholar]
- 19.Lassiter WE, Gottschalk CW, Mylle M. Micropuncture study of net transtubular movement of water and urea in nondiuretic mammalian kidney. Am. J. Physiol. 1961;200:1139–1146. doi: 10.1152/ajplegacy.1961.200.6.1139. [DOI] [PubMed] [Google Scholar]
- 20.Kondo Y, Imai M, Kangawa K, Matsuo H. Lack of direct action of α-human atrial natriuretic polypeptide on the in vitro perfused segments of Henle's loop isolated from rabbit kidney. Pfluegers Arch. 1986;406:273–278. doi: 10.1007/BF00640913. [DOI] [PubMed] [Google Scholar]
- 21.Maack T, Camargo MJF, Kleinert HD, Laragh JH, Atlas SA. Atrial natriuretic factor: structure and functional properties. Kidney Int. 1985;27:607–615. doi: 10.1038/ki.1985.54. [DOI] [PubMed] [Google Scholar]
- 22.Madsen KM, Tisher CC. Structural-functional relationships along the distal nephron. Am. J. Physiol. 1986;250:F1–F15. doi: 10.1152/ajprenal.1986.250.1.F1. (Renal Fluid Electrolyte Physiol. 19) [DOI] [PubMed] [Google Scholar]
- 23.Mejia R. CONKUB: a conversational path-follower for systems of nonlinear equations. J. Computational Phys. 1986;63:67–84. [Google Scholar]
- 24.Mejia R, Kellogg RB, Stephenson JL. Comparison of numerical methods for renal network flows. J. Computational Phys. 1977;23:53–62. [Google Scholar]
- 25.Mejia R, Stephenson JL. Solution of a multinephron, multisolute model of the mammalian kidney by Newton and continuation methods. Math. Biosci. 1984;68:279–298. [Google Scholar]
- 26.Needleman P, Greenwald JE. Atriopeptin: a cardiac hormone intimately involved in fluid, electrolyte, and blood-pressure homeostasis. N. Engl. J. Med. 1986;314:828–834. doi: 10.1056/NEJM198603273141306. [DOI] [PubMed] [Google Scholar]
- 27.Nonoguchi H, Knepper MA, Manganiello VC. Effects of atrial natriuretic factor on cyclic guanosine monophosphate and cyclic adenosine monophosphate accumulation in microdissected nephron segments from rats. J. Clin. Invest. 1987;79:500–507. doi: 10.1172/JCI112840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nonoguchi H, Sands JM, Knepper MA. Atrial natriuretic factor inhibits vasopressin-stimulated osmotic water permeability in rat inner medullary collecting duct. J. Clin. Invest. 1988;82:1383–1390. doi: 10.1172/JCI113742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nonoguchi H, Sands JM, Knepper MA. ANF inhibits NaCl and fluid absorption in cortical collecting duct of rat kidney. Am. J. Physiol. 1989;256:F179–F186. doi: 10.1152/ajprenal.1989.256.1.F179. (Renal Fluid Electrolyte Physiol. 25) [DOI] [PubMed] [Google Scholar]
- 30.Pennell JP, Lacy FB, Jamison RL. An in vivo study of the concentrating process in the descending limb of Henle's loop. Kidney Int. 1974;5:337–347. doi: 10.1038/ki.1974.49. [DOI] [PubMed] [Google Scholar]
- 31.Peterson LN, DeRouffignac C, Sonnenberg H, Levine DZ. Thick ascending limb response to dDAVP and atrial natriuretic factor in vivo. Am. J. Physiol. 1987;252:F374–F381. doi: 10.1152/ajprenal.1987.252.3.F374. (Renal Fluid Electrolyte Physiol. 21) [DOI] [PubMed] [Google Scholar]
- 32.Pollack DM, Arendshorst WJ. Effect of atrial natriuretic factor on renal hemodynamics in the rat. Am. J. Physiol. 1986;251:F795–F801. doi: 10.1152/ajprenal.1986.251.5.F795. (Renal Fluid Electrolyte Physiol. 20) [DOI] [PubMed] [Google Scholar]
- 33.Reif MC, Troutman SL, Schafer JA. Sustained response to vasopressin in isolated rat cortical collecting tubule. Kidney Int. 1984;26:725–732. doi: 10.1038/ki.1984.208. [DOI] [PubMed] [Google Scholar]
- 34.Roy DR. Effect of synthetic ANP on renal and loop of Henle functions in the young rat. Am. J. Physiol. 1986;251:F220–F225. doi: 10.1152/ajprenal.1986.251.2.F220. (Renal Fluid Electrolyte Physiol. 20) [DOI] [PubMed] [Google Scholar]
- 35.Sands JM, Knepper MA. Urea permeability of mammalian inner medullary collecting duct system and papillary surface epithelium. J. Clin. Invest. 1987;79:138–147. doi: 10.1172/JCI112774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sands JM, Nonoguchi H, Knepper MA. Vasopressin effects on urea and H2O transport in inner medullary collecting ducts. Am. J. Physiol. 1987;253:F823–F832. doi: 10.1152/ajprenal.1987.253.5.F823. (Renal Fluid Electrolyte Physiol. 22) [DOI] [PubMed] [Google Scholar]
- 37.Sonnenberg H, Cupples WA, DeBold AJ, Veress AT. Intrarenal localization of the natriuretic effect of cardiac atrial extract. Can. J. Physiol. Pharmacol. 1982;60:1149–1152. doi: 10.1139/y82-166. [DOI] [PubMed] [Google Scholar]
- 38.Sonnenberg H, Honrath U, Chong CK, Wilson DR. Atrial natriuretic factor inhibits sodium transport in medullary collecting duct. Am. J. Physiol. 1986;250:F963–F966. doi: 10.1152/ajprenal.1986.250.6.F963. (Renal Fluid Electrolyte Physiol. 19) [DOI] [PubMed] [Google Scholar]
- 39.Sperber I. Studies on the mammalian kidney. Zool. Bidr. Uppsala. 1944;22:249–431. [Google Scholar]
- 40.Stephenson JL. Concentration of urine in a central core model of the renal counterflow system. Kidney Int. 1972;2:85–94. doi: 10.1038/ki.1972.75. [DOI] [PubMed] [Google Scholar]
- 41.Stephenson JL. Concentrating engines and the kidney. II. Multisolute central core systems. Biophys. J. 1973;13:546–567. doi: 10.1016/S0006-3495(73)86006-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Stephenson JL. Concentrating engines and the kidney. III. Canonical mass balance equation for multinephron models of the renal medulla. Biophys. J. 1976;16:1273–1286. doi: 10.1016/S0006-3495(76)85773-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Stephenson JL, Mejia R, Tewarson RP. Model of solute and water movement in the kidney. Proc. Natl. Acad. Sci. USA. 1976;73:252–256. doi: 10.1073/pnas.73.1.252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stokes JB. Ion transport by the cortical and outer medullary collecting tubule. Kidney Int. 1982;22:473–484. doi: 10.1038/ki.1982.200. [DOI] [PubMed] [Google Scholar]
- 45.Tomita K, Pisano JJ, Knepper MA. Control of sodium and potassium transport in the cortical collecting duct of the rat. J. Clin. Invest. 1985;76:132–136. doi: 10.1172/JCI111935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Van de Stolpe A, Blouch K, Jamison RL. Effect of atrial natriuretic peptide (ANP) on the superficial proximal tubule and loop of Henle (Abstract). Kidney Int. 1988;33:289. [Google Scholar]
- 47.Van de Stolpe A, Jamison RL. Micropuncture study of the effect of ANP on the papillary collecting duct in the rat. Am. J. Physiol. 1988;254:F477–F483. doi: 10.1152/ajprenal.1988.254.4.F477. (Renal Fluid Electrolyte Physiol. 23) [DOI] [PubMed] [Google Scholar]
- 48.Zeidel ML, Kikeri D, Burrows M, Silva P, Brenner BM. Atrial natriuretic peptide (ANP) inhibits 22Na uptake in rabbit inner medullary collecting duct (IMCD) cells (Abstract). Kidney Int. 1988;33:291. [Google Scholar]
- 49.Zeidel ML, Seifter JL, Lear S, Brenner BM, Silva P. Atrial peptides inhibit oxygen consumption in kidney medullary collecting duct cells. Am. J. Physiol. 1986;251:F379–F383. doi: 10.1152/ajprenal.1986.251.2.F379. (Renal Fluid Electrolyte Physiol. 20) [DOI] [PubMed] [Google Scholar]