Abstract
Enthalpy arrays enable label-free, solution-based calorimetric detection of molecular interactions in a 96-detector array format. The combination of the small size of the detectors and ability to perform measurements in parallel results in a significant reduction of sample volume and measurement time compared with conventional calorimetry. We have made significant improvements in the technology by reducing the temperature noise of the detectors and improving the fabrication materials and methods. In combination with an automated measurement system, the advances in device performance and data analysis have allowed us to develop basic enzyme assays for substrate specificity and inhibitor activity. We have also performed a full titration of 18-crown-6 with barium chloride. These results point to future applications for enthalpy array technology, include fragment-based screening, secondary assays, and thermodynamic characterization of leads in drug discovery.
Keywords: nanocalorimetry, enzyme assay, binding assay, label-free assay
Introduction
Enthalpy arrays, which are arrays of nanocalorimeters, allow scientists to measure thermodynamics and kinetics of molecular interactions using small sample volumes and short measurement times [1]. The measurements do not require immobilization or labeling of reactants, an attractive feature compared with surface-based methods such as Surface Plasmon Resonance and photometric methods requiring tagging. Like commercially available calorimeters, such as Isothermal Titration Calorimetry (ITC) instruments from Microcal® or TA Instruments2, enthalpy arrays detect the heat from reactions, but they do so with an array of miniaturized detectors. Note that enthalpy arrays achieve miniaturization and arrayed detectors by sacrificing some of the accuracy and capability of ITC instruments.
ITC can be used to characterize the thermodynamics of biomolecular interactions [2; 3; 4; 5]. In a titration, one simultaneously determines the enthalpy, affinity, and stoichiometry of the reaction of interest, which is a hallmark of ITC. A titration is usually performed by adding aliquots of ligand at high concentration to a biomacromolecule sample, although the inverse titration is sometimes performed if the solubility of the ligand is low and the solubility of the biomacromolecule is high enough. While ITC is used in drug discovery and basic sciences, the level of use is severely hampered by the need for large samples (≈1.5 mL) and long measurement times (typically 1.5-2 hrs). In addition to titrations, ITC instruments have been used to monitor enzyme reactions [6; 7; 8; 9; 10]. As steady-state turnover of substrate to product generates heat over an extended period of time, the required concentration of enzyme is generally much lower than required concentrations of proteins for titration experiments. Nonetheless, in general the titrations and enzymatic measurements require quantities of reactants that are considered quite large in biochemical studies, making high throughput measurements or measurements with limited amounts of material unfeasible. Enthalpy array technology addresses this problem by enabling measurements with 250 nL drops that only take a few minutes. For assays in which sample size and measurement time are of primary importance, enthalpy arrays are an attractive technology.
Each site in the enthalpy array consists of two identical detector regions, providing a differential temperature measurement between a sample and reference specimen. Each region has its own electrodes for electrostatically-driven isothermal mixing. After mixing, the detector measures temperature changes of the sample relative to a simultaneous mixing of similar but non-reacting materials in the reference region. This relative measurement subtracts out common-mode changes in temperature, thereby improving sensitivity.
Previously, we demonstrated that enthalpy arrays could be used to measure enthalpies of binding reactions at a single ligand concentration [1]. In addition, we demonstrated an enzyme-substrate interaction at a substrate concentration that allowed a very short reaction.
Here we describe how improvements in device sensitivity have enabled the enthalpy arrays to be used for enzyme assays of substrate specificity and inhibitor activity, as well as for a titration of an interaction having a reported Kd = 0.16 mM.
Material and methods
Device fabrication
Fabrication of devices with n+ amorphous silicon thermistors on a polyimide membrane was described previously [1]. The device improvements we describe here were achieved by changing the thermistor material to vanadium oxide (VOx) and fabricating the detectors on a polyethylene naphthalate (PEN) membrane. Each detector is on a portion of the 25 μm thick PEN membrane suspended over a cavity in a rigid stainless-steel support plate. The center region of each detector contains two rectangular thermal equilibration areas, defined by 8 μm thick copper islands on the back side of the membrane. The highly sensitive thin-film VOx sensors are fabricated on the front side of these regions.
A detector consists of two identical sensing elements: one measurement and one reference site. The reduction of common-mode changes in temperature is obtained by connecting the thermistors on both sites in a Wheatstone bridge configuration. Electrical contacts to the detectors in the array are made using an array of gold coated and spring-loaded contact pins (‘pogo-pins’).
More details on the fabrication and characterization of the VOx thermistors can be found in De Bruyker, et al. [11].
Measurement protocols
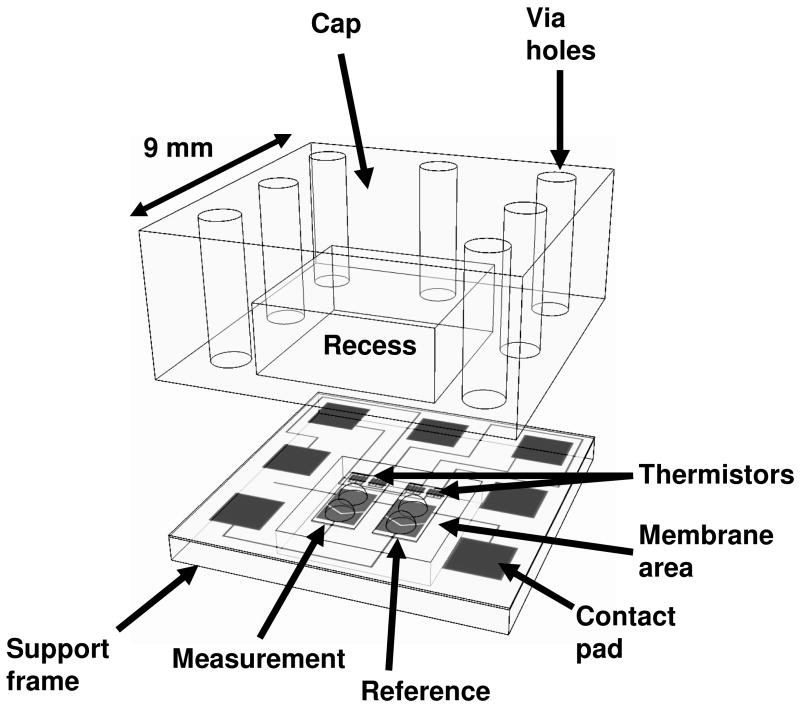
All measurements were performed at 21°C. Drops (≈250 nl) containing enzyme, substrate, barium chloride, 18-crown-6, or buffer were deposited on the appropriate location of the detector region using a Deerac spot-on™ liquid handling system (Deerac Fluidics, Dublin, Ireland). The liquid handling system is capable of delivering drops with a volume CV≤6%. The array was placed in a temperature-controlled measurement chamber and a polymer cap was applied to the array in order to minimize drop evaporation. The cap contained recessed cavities that encapsulated and sealed corresponding detectors (Figure 1).
Figure 1.
Schematic view of an individual detector. The measurement and reference regions are identical and are designated based on the reagents in the drops. The figure shows two drops in both regions (2 measurement drops + 2 reference drops), representing the configuration before merging of drops.
The drops were allowed to come to thermal equilibrium (approximately 3 minutes) prior to initiating the reaction. Initiation consisted of applying a voltage (180V) across the merging electrodes to electrostatically merge the two drops of interest on a detector region (measurement region). At the same time, two similar nonreacting drops on the reference region were electrostatically merged using the same voltage pulse. The nonreacting drops provided a reference for the differential measurement. The output voltage of the Wheatstone bridge was typically recorded for 30 seconds prior to the merge time and 3.5 minutes following initiation of the reaction.
Enzyme assays
Trypsin (EC 3.4.21.4) hydrolysis of benzoylarginine ethyl ester (BAEE) was measured at 21°C in 200 mM Tris–HCl, pH 8.0, 50 mM CaCl2, and 0.2% PEG-8000 [7]. The measurement region materials consisted of a drop of trypsin (92.8 μM, 6.79 BAEE units) and a drop of substrate solution (0.5-10 mM BAEE). The reference region used a drop of buffer and a drop of the same substrate solution (0.5-10 mM BAEE) used in the measurement region. The combined drops in the measurement region contained 46.4 μM trypsin (6.79 BAEE units) and 0.25 to 5.0 mM BAEE. Reactions with trypsin inhibitors were performed as above, except that the inhibitor was mixed with trypsin and incubated at room temperature for 15 minutes prior to drop deposition. All reagents were obtained from Sigma-Aldrich and used without further purification.
Hexokinase (EC 2.7.1.1) phosphorylation of glucose was measured at 21°C in 50 mM Tris-HCl, pH 7.8, and 10 mM MgCl2. ATP was the limiting substrate in all reactions. The measurement region materials consisted of a drop containing hexokinase (200 U/ml, ≈2.1 μM) and ATP present at various concentrations between 0.125 mM and 1.84 mM and a drop of glucose (20 mM) and ATP at the same concentration present in the hexokinase drop. The reference region used a drop of buffer and a drop of 20 mM glucose, each with ATP present at the same concentration used in the measurement region. The combined drops in the measurement region contained ≈1.1 μM hexokinase (0.05 U), 10 mM glucose, and ATP at the initial drop concentration. The hexokinase concentration was calculated assuming the enzyme is a dimer (110 kDa) with a maximum specific activity of 900 U/mg [12]. Substrate specificity measurements were performed at a single ATP concentration (1 mM) with 10 mM putative sugar substrate.
Titration
Titration of 18-crown-6 with barium chloride was performed at 21°C in unbuffered water. Performing “titrations” using enthalpy arrays differs from a conventional titration in that multiple measurements at varying concentrations are performed on multiple detectors rather than injecting multiple aliquots into a single volume. To perform the titration, a series of measurements was performed by merging 250 nl drops of 4 mM 18-crown-6 with 250 nl drops containing BaCl2 at various concentrations between 1.25 and 50 mM. The reference region of each measurement contained a 250 nl drop of BaCl2 at the same concentration used on the measurement region and a 250 nl drop of water. A minimum of four measurements was performed at each concentration of BaCl2.
Data analysis
For each measurement we record the differential temperature as a function of time (e.g. Figure 2A). We need to convert this information into an enthalpy, and we do so by deconvoluting Q(τ) from the equation
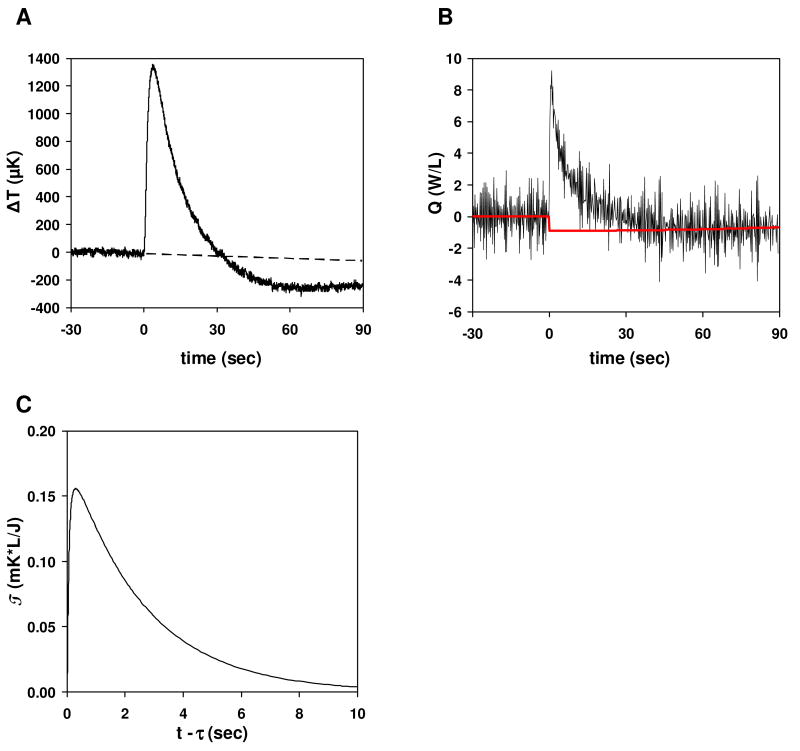
Figure 2.
Trypsin catalyzed hydrolysis of BAEE. Reactions contained 46.4 μM trypsin and 2.5 mM BAEE. The drops were merged at t=0. (A) Plot of temperature difference vs. time. The dashed line is the baseline based on the pre-merge data. (B) Plot of power (Q) vs. time for the reaction shown in (A). The red solid line is the baseline fit. Note the shift at t=0 from the baseline before the merge to the final baseline. Q is integrated relative to the red baseline. (C) Impulse response.
| [1] |
In this equation, T(t) is the temperature change (T) as a function of time (t) relative to the baseline temperature, Q(τ) is the rate of heat generation (e.g. due to a biochemical reaction) as a function of time, and T(t-τ), the “impulse response”, is the temperature rise that would occur at a time t given a Dirac delta function impulse of heat at time τ (Figure 2C). To obtain Q(τ) from T(t), we need to know T(t-τ) a priori. In this work, we used COMSOL® (COMSOL, Inc.) simulations of our nanocalorimeters to determine T(t-τ) [13]3. To deconvolute Q(τ), we approximate Q(τ) as a piece-wise linear continuous function and use a least-squares regression to determine the fitting coefficients. Each linear piece spanned 30/128 sec, covering 30 of the temperature points that were recorded every 1/128 sec. Figure 2B shows an example of such a fit. Following calculation of Q(τ), we integrate Q(τ) over time to obtain the total enthalpy. For Figure 2B, the integrated value was 92.0 J/L, equivalent to 46.0 μJ for the 500 nL drop.
As evident from Figure 2B, Q(τ) as calculated is more noisy than the temperature data. Because Q(τ) is in the integrand of the above equation, it is analogous to the derivative of the temperature data with respect to amplification of noise; calculating derivates of data point-by-point generally gives results that are more noisy than the data itself. One could use a smoothing algorithm to achieve less noisy Q(τ) results, but it is not necessary for the present purposes because the integral of Q(τ) is ultimately the quantity of interest.
The calculation of enthalpy requires subtracting a baseline from the data. In the case of a linear baseline before the merge and return of the signal to the same baseline after the heat has dissipated, subtraction of the baseline is trivial. However, in most cases the baseline does not return to the same level, resulting in a “baseline shift”. In Figure 2A the baseline shift is about 250 μK, which is typical for the current technology. The correction for these shifts is most important when the signal from a reaction is of a comparable magnitude.
This baseline shift occurs because energy transport from the drops changes when the drops merge. At steady state, the drops attain a temperature at which heating from the thermistor power is balanced by heat dissipation due to conduction and evaporation, and after merging this balance changes. Hence, the steady-state temperatures change. The change is not necessarily the same for both the sample and reference drops, which results in a shift of the differential temperature measured by the detectors. It is important to note that this difference for the sample side would cancel with the difference for the reference side for any one detector if common-mode rejection were perfect, but our simulations show how effects such as very small amounts of water vapor escaping from underneath the caps make it very difficult to attain such a level of common-mode rejection [13].
Thus, we need to remove the effects of thermal baseline shifts from our results. This requires knowledge of the time dependence of these shifts. Either a model for this behavior or experimental measurements could in principle be used. We chose to use a simple model that captures the essential physics to first order, leaving it for future work to use COMSOL simulations and experiments for more careful fitting and removal of baseline shifts.
In our simple model, thermal baseline shifts manifest themselves as sudden shifts in Q(t) resulting from the sudden change in drop configuration due to merging., To put this model into practice, Q(t) is deconvoluted from the integral representation of T(t) as discussed previously without worrying about thermal baseline shifts, and then the shift, if any, in the baseline of Q(t) from times before merging to times after completion of the reaction(s) of interest is simply subtracted from the Q(t>tmerge) data (Figure 2B).
In addition to baseline shifts, the baseline often drifts slowly over time due to imperfect thermal stabilization of the array (≈1 μK/sec is typical). We used a quadratic fit of the baseline before and after the reaction of interest to account for such drifts.
To determine ΔH, the enthalpy per mole of reaction, and Kd, the dissociation equilibrium constant, from titration results, we fit the titration data (measured enthalpy vs. concentration) to the equation
| [2] |
We use the weighted nonlinear least-squares routine in Origin (OriginLab Corporation, Northampton, MA) to compute ΔH, Kd, and n, n being the number of binding sites per B molecule. The weights are calculated from the standard errors measured at each concentration. A0 and B0 are the initial concentrations in the merged drop of the two species undergoing a reaction, which in our case are BaCl2 and 18-crown-6, respectively. Equation 2 corresponds to the standard “Single Set of Identical Sites” model used to fit ITC data (ITC Data Analysis in Origin® Tutorial Guide, version 7.0, 2004). Measurements are done in which the initial concentration of BaCl2 is varied while the concentration of 18-crown-6 is held constant. Note that the enthalpy ΔH is the enthalpy per mole of binding sites, and there are nB0 binding sites per unit volume.
Results
The improvements in consistent device performance have allowed us to perform a larger number of measurements that have enabled the titration and enzyme assays discussed below. We previously presented data in which the measurements were performed one at a time with manual deposition of the sample drops using a syringe [1]. We now typically perform measurements with automated deposition and data capture. The previous work demonstrated that thermistors made from n+ amorphous silicon have noise of ≈80 μK and could detect 250 ncal heat from a 500 nl reaction at signal-to-noise ratio of 6 (2.1 J/L signal at S:N of 6, [1]). The VOx detectors used for the measurements we report here have noise as low as 10 μK, translating to an improvement of a factor of 8 in noise of the thermistors.
We use pre-characterized devices where the intrinsic device noise and Wheatstone bridge offset are low. The intrinsic device noise is the noise observed at the output of the thermistor bridge during measurement of a baseline, and it can be expressed as a noise equivalent temperature difference (NETD, in Kelvin) by using NETD = 2Vnoise / (αVbridge), with Vnoise being the output noise voltage of the bridge, α=-1/R(dR/dT) the temperature coefficient of resistance (TCR) of the thermistors, R the resistance of the thermistors, and Vbridge the bridge supply voltage. The temperature response of the devices is calibrated by measuring the TCR of each array. Based on measurements of over two dozen arrays, the VOx thermistors have a TCR of 0.0270 (±0.0008) °C-1.
We also need to validate the calculation of heat from the temperature. The heat values determined from Eq. 1 were validated by using special devices having thin-film resistive heaters fabricated on the merging electrodes. Each array had a small number of such devices. To perform a heater measurement, 500 nl buffer drops were placed on the measurement and reference regions of a device and an electrically generated pulse (25 μW) was applied to one of the two drops through the heater. The pulse (30 seconds) was long enough to allow the system to reach a steady state, and the temperature rise recorded. The values for four qualified arrays that we tested were 851 to 914 μK/μW, with an average value of 890 μK/μW. Qualified arrays were arrays that passed quality control checks for alignment of features, thickness of the back-plane copper, and low noise and offset of sites. From Eq. 1 and the impulse function shown in Figure 2C, a heater is calculated to give a temperature rise of 985 μK/μW, in good agreement with these measured results. From array to array there is some variability in the fabrication that can cause the heater results to vary, especially if characteristics like the thickness of the back-plane copper vary from the design point. Consequently, all arrays were calibrated using the result from a heater measurement on that array. The uncalibrated temperature rises were all in the range of 700 μK/μW to 1000 μK/μW, and calibration adjusted the values to 1000 μK/μW.
For the current VOx thermistors, the lowest intrinsic device noise observed is about 10 μK over a measurement bandwidth of 0.1 Hz to 4 Hz, which is well below other sources of noise, as discussed in the subsequent section. Intrinsic device noise below 30 μK is hence considered to be acceptable. Bridge offsets need to be below 1% in order to maintain good common-mode rejection and to allow the sensor interface to perform low-noise amplification. In best-of-class arrays, 95% of the devices meet our intrinsic noise and offset criteria.
Another source of improved performance is the polymer cap. The polymer cap provides evaporation control, which is critical to maximize the thermal dissipation time constant and to minimize common-mode artifacts. Previously, we reported a thermal dissipation time of ≈1.3 sec [1]. For signal-to-noise ratios, a longer time would be better. With the current measurement environment, a thermal dissipation time constant of ≈2.0 sec was obtained. This time constant was determined using heater measurements as described above and the thermal time constant was measured from the time dependence of the temperature decay at the end of the pulse. We expect future improvements to increase the thermal dissipation time constant by a factor of 2-3.
Enzyme substrate and inhibitor assays
For an enzyme-catalyzed reaction, the differential temperature signal is directly related to the rate of conversion of substrate to product by the enzyme. Since the magnitude of the temperature signal is proportional to kcat·[E]·ΔHapp, the enzyme concentration can be adjusted to obtain a sufficient signal-to-noise ratio for the reaction of interest. To produce a measurable signal, the reaction must evolve heat faster than the thermal dissipation time constant of the enthalpy array detector. Total integrated heat is proportional to amount of substrate converted to product.
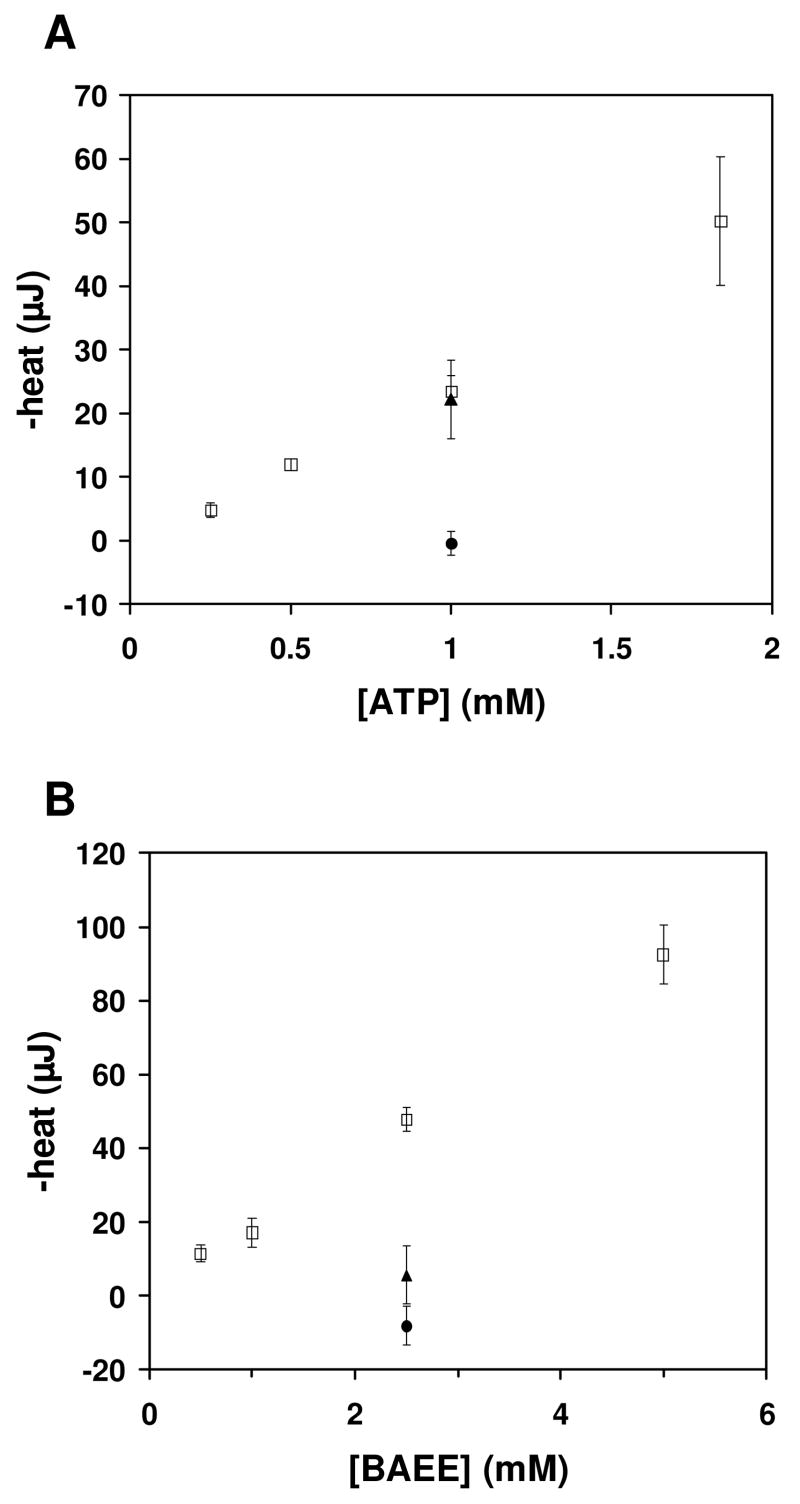
Figure 3A shows hexokinase phosphorylation of glucose. In these experiments, ATP was the limiting substrate and the reaction was initiated by combining a drop containing both hexokinase and ATP with a drop containing glucose and ATP. The total heat increases linearly with the total ATP concentration, as expected. The ΔHapp was -11.2 (±1.6) kcal/mol at 21 °C, compared to ΔHapp ≈-14 kcal/mol reported at 25 °C (at pH 7.6) [14]. We observed a good signal-to-noise ratio at 0.5 mM and 1 mM ATP. Hexokinase will specifically phosphorylate 6-carbon sugars [15]. To demonstrate that we could discriminate phosphorylation of true hexokinase substrates, we monitored the reaction when 10 mM fructose (6-carbon sugar) or 10 mM xylose (5-carbon sugar) were added instead of 10 mM glucose. We observed a signal for fructose that was nearly identical to that observed with glucose, and we did not observe a signal for xylose, as expected.
Figure 3.
Enzyme assays. (A) Hexokinase substrate specificity assay. Reactions were performed as described in the methods. ATP was the limiting substrate in all reactions. Error bars indicate the 95% confidence interval of the mean of each set of measurements at a given [ATP]. ΔHapp = -11.2 (± 1.6) kcal/mol. (□) 10 mM glucose, (▲) 10 mM fructose, (●) 10 mM xylose. (B) Trypsin inhibitor assay. Reactions were performed as described in the methods. Trypsin was present at 46.4 μM in the combined drop. BAEE was present at the concentration indicated. Error bars indicate the 95% confidence interval of the mean of each set of measurements at a given [BAEE]. ΔHapp = -9.3 (± 1.2) kcal/mol. (□) no inhibitor, (▲) 50 μM leupeptin, (●) 250 μM antipain.
Figure 3B shows trypsin hydrolysis of BAEE as a function of substrate concentration. As expected, the integrated heat increases linearly with the concentration of substrate. The ΔHapp was -9.3 (±1.2) kcal/mol at 21 °C, compared to ΔHapp =-11.45 kcal/mol reported at 25 °C [7]. We obtained a good signal-to-noise ratio at 2.5 mM BAEE, and this substrate concentration was used to test the effects of two known trypsin inhibitors. Leupeptin and antipain produced significant inhibition of BAEE hydrolysis by trypsin when either was added at a concentration equal to or greater than the trypsin concentration, as expected.
Barium chloride/18-crown-6 titration
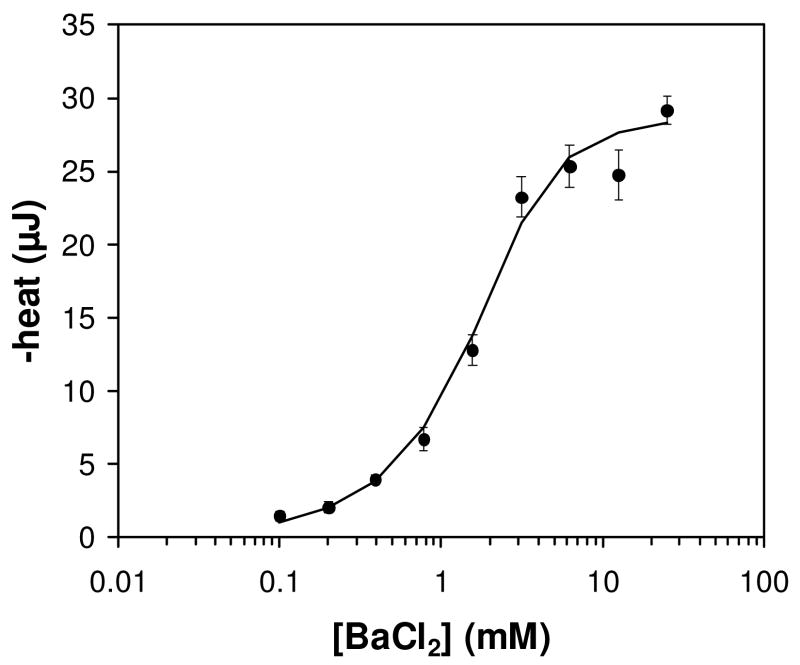
To investigate the potential of enthalpy arrays for thermodynamic characterization of binding reactions, a full titration of barium chloride with 18-crown-6 was performed. To achieve a high signal-to-noise ratio, 18-crown-6 was present at 2 mM in the titration. Rather than measuring the heat evolved by addition of several aliquots of barium chloride to a single sample of 18-crown-6 as is done in a titration experiment performed with a commercial titration microcalorimeter, separate measurements were performed at each concentration of barium chloride. A total of nine different concentrations of barium chloride in a two-fold serial dilution series were measured. A minimum of four measurements at each barium chloride concentration were performed. Figure 4 shows the binding isotherm for titration of 2 mM 18-crown-6 with barium chloride. The data were fit as described in the methods, yielding Kd = 0.47 mM (±0.30 mM), ΔH = -6.92 kcal/mol binding sites (±1.24 kcal/mol), and n=1.19 (±0.19).
Figure 4.
Titration of 18-crown-6 titration with barium chloride. Points represent average values at each concentration of BaCl2. Error bars represent the standard error of the mean for each BaCl2 concentration. The solid black line represents the nonlinear least-squares fit of the data using equation 2 in the methods and allowing the value of n to float. Least-squares fitted parameters: Kd = 0.47 mM, ΔH = -28.9 kJ/mol (-6.9 kcal/mol) 18-crown-6, n=1.2.
Discussion
For enzymatic reactions, we have presented examples of assays for substrate identification and inhibitor identification. These assays could be used on a large number of putative substrates for an enzyme of interest, enabling screening using the integrated heat as a criterion for a valid substrate. The limited calorimetric data available indicates that the enthalpy for a specific type of reaction (phosphorylation, peptide bond cleavage) performed under the same conditions (buffer, pH, temperature) will be similar even with minor modifications in the substrate. For example, an identical enthalpy is observed for cleavage of a peptide bond by HIV-1 protease with two different peptide substrates (-1.1 kcal/mol)[7]. Therefore, the number of false negatives in a substrate identification assay should remain low.
Screening inhibitors will probably require that separate samples of enzyme mixed with each inhibitor be made and incubated prior to the enthalpy array measurement of the reaction with substrate, which is not ideal for a higher-throughput primary screen. Although one could try to perform the experiment by merging a drop of enzyme with a drop of substrate plus inhibitor directly on the detector, the kinetics of inhibitor binding relative to the turnover number may result in some substrate turnover before the inhibitor acts, even for a tightly binding inhibitor. The outcome would be an observed enthalpy of reaction, even for a potent inhibitor, reducing the apparent potency. On the other hand, pre-mixing enzyme and inhibitor could be feasible for a secondary assay used to verify and further elucidate hits from a previous screen. Thus, enthalpy array measurements could become a useful tool for such secondary assays.
The sensitivity of the inhibitor assay is directly related to the concentration of enzyme that must be used to obtain a good signal-to-noise ratio. Antipain has an IC50 of 0.26 μg/ml (≈400 nM) against trypsin [16], and leupeptin has a reported Ki of 130 nM [17]. As expected, a high degree of inhibition was only observed when the concentration of antipain or leupeptin was greater than or equal to the trypsin concentration (46.4 μM), as there needs to be an inhibitor molecule for each enzyme molecule. Thus, at the higher enzyme concentrations needed to achieve a reasonable signal, it is not possible to measure an IC50 when the value is below [E].
For the barium chloride/18-crown-6 titration, the Kd measured using enthalpy arrays (0.47 mM) was higher than previously reported values measured at 20°C (0.16 mM) and 25°C (0.18 to 0.2 mM) using isothermal titration calorimetry [18; 19; 20]. Note, however, that the signal minus the error (0.47 mM - 0.3 mM = 0.17 mM) falls in the range of the previously reported values. The value for ΔH per mole of 18-crown-6 obtained by enthalpy array was slightly lower than other reports in the literature (ΔH=-6.9 kcal/mol vs. -7.5 to −7.9 kcal/mol).
The data presented here demonstrate the current sensitivity of the enthalpy array technology, which, as a developing technology, has not yet reached its sensitivity limits. Based on linear regression of the BaCl2 titration data standard errors, noise from all sources is currently equal to 0.05* Signal (in J/L) + 0.7 J/L. The current sensitivity is not limited by thermistor noise, as there are additional sources of “noise” (i.e. scatter) that exceed the temperature noise of the VOx detectors. These additional noise sources include baseline shifts and drop volume variation. Mixing variability may also be present and is worthy of investigation, as mixing is a known issue in the field of microfluidics [21; 22]. When drops merge, fluidic mixing occurs down to some length scale that is difficult to measure, and beyond that point the detectors rely on diffusion to finish the job of mixing reactants. For our system, a mixing length of 50 μm is a rough estimate based on scaling analysis of the shear forces and mass*acceleration of a drop from high-speed video of drop merging. For a typical small molecule (500 Da) diffusivity of 3×10-6 cm2/sec in water [23], an estimate of the characteristic diffusion time of 8 sec follows. Compared with the thermal dissipation time of ≈2 sec for our detectors, diffusion over 50 μm is not particularly fast, even though the dimension is rather small. Further research on mixing in the merged drops will reveal whether there is an opportunity for improvement with enthalpy array detectors.
Given the potential issues with baseline shifts and the above method for handling them, their effect on noise was studied by further examining the BaCl2 titration data. For each BaCl2 concentration, the deviations of the individual replicate measurements from the mean at that BaCl2 concentration were compiled, and a linear regression of all the deviations for all BaCl2 concentrations against the fitted baseline shift for each measurement was performed. The root-mean-square (rms) average of the deviations (the “average noise”) and the rms average of the differences of the deviations from the linear fit were compared, providing an estimate of the fraction of the noise attributable to baseline shifts. Statistical analysis of 2000 bootstrapped replicates [24] of the deviation vs. baseline shift data revealed the noise due to baseline shifts to be ≤10% of the total noise at the 95% confidence level. In absolute terms, the average noise is 4.7 J/L and the contribution from non-zero baseline shifts is estimated to be ≤0.47 J/L, after accounting for the shifts as described above.
The measurements presented here were enabled by the better and more consistent device performance and our movement toward more automated measurements. The automated drop deposition reduces the time to deposit a set of four drops to about 4 seconds, compared to well over 2 minutes for our previously reported data using syringes for manual deposition [1]. The speed and consistency of drop deposition using the automated device reduces variation due to unequal evaporation of drops prior to application of the polymer cap.
Improvements in the thermal dissipation time constant, and perhaps in mixing consistency, will result in increased signal-to-noise ratio beyond what is reported here. These improvements will enable a direct measure of kcat and KM for enzyme reactions and extend the limits for Kd determination in the future.
Based on our current estimates of the limits of the enthalpy array technology, it should be possible to measure enzyme reactions with a kcat of 0.5 sec-1 or greater. Recalling the relationship Signal ∝ kcat·[E]·ΔHapp, at the lower limit of the detectable turnover number, assuming an average ΔH of ±5 kcal/mol, it would require approximately 20 μM enzyme (10 pmol per measurement) to produce a sufficient signal from a 60 second reaction in a 500 nl combined drop to yield approximately 15-fold signal over noise including all noise sources. Enzyme reactions with a higher turnover number and/or higher enthalpy will use a correspondingly lower concentration of enzyme to obtain an equivalent signal. In performing enzyme inhibition assays, the limit of detection for non-competitive inhibitors will equal the enzyme concentration required to obtain a sufficient signal-to-noise ratio.
For titration experiments, the limitation on Kd determination is generally considered to be ≈0.05x the concentration of receptor. The lower limit for receptor concentration is currently 100 μM for our devices, assuming ΔH ±10 kcal/mol. The signal at saturation corresponds to a 10-fold signal over noise including all noise sources. This translates to a Kd determination limit of 5μM. It should be noted that one can also determine binding stoichiometry from a titration, even if the binding affinity is too strong to measure accurately. In some applications, determining stoichiometry in itself is valuable.
Thus, as the sensitivity of enthalpy array technology is improved, the low material requirements compared to other calorimetric techniques and the rapid measurements enabled by parallel data collection should make enthalpy arrays attractive for a variety of applications. For example, measuring Kd in the 0.1 to 5 mM range is important in fragment-based drug discovery [25], and calorimetric measurements can be useful in secondary hit validation and lead characterization in drug discovery.
Acknowledgments
The authors thank Lai Wong, Vicki Geluz-Aguilar and Mary Anne Rosenthal for their assistance in device fabrication and David Goldberg for assistance with statistical analysis.
Footnotes
This work was supported by NIH grant 1R01GM077435-01, NIH Contract # HHSN 266200400058C and grant SFP-1543. This is TSRI manuscript 19187.
TA Instruments acquired Calorimetry Sciences Corporation in 2007.
Full presentation available at: http://www.parc.com/research/publications/files/6277.pdf
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Torres FE, Kuhn P, De Bruyker D, Bell AG, Wolkin MV, Peeters E, Williamson JR, Anderson GB, Schmitz GP, Recht MI, Schweizer S, Scott LG, Ho JH, Elrod SA, Schultz PG, Lerner RA, Bruce RH. Enthalpy arrays. Proc Natl Acad Sci U S A. 2004;101:9517–22. doi: 10.1073/pnas.0403573101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Velazquez-Campoy A, Leavitt SA, Freire E. Characterization of protein-protein interactions by isothermal titration calorimetry. Methods Mol Biol. 2004;261:35–54. doi: 10.1385/1-59259-762-9:035. [DOI] [PubMed] [Google Scholar]
- 3.Leavitt S, Freire E. Direct measurement of protein binding energetics by isothermal titration calorimetry. Curr Opin Struct Biol. 2001;11:560–6. doi: 10.1016/s0959-440x(00)00248-7. [DOI] [PubMed] [Google Scholar]
- 4.Feig AL. Applications of isothermal titration calorimetry in RNA biochemistry and biophysics. Biopolymers. 2007 doi: 10.1002/bip.20816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wiseman T, Williston S, Brandts JF, Lin LN. Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal Biochem. 1989;179:131–7. doi: 10.1016/0003-2697(89)90213-3. [DOI] [PubMed] [Google Scholar]
- 6.Bianconi ML. Calorimetry of enzyme-catalyzed reactions. Biophys Chem. 2007;126:59–64. doi: 10.1016/j.bpc.2006.05.017. [DOI] [PubMed] [Google Scholar]
- 7.Todd MJ, Gomez J. Enzyme kinetics determined using calorimetry: a general assay for enzyme activity? Anal Biochem. 2001;296:179–87. doi: 10.1006/abio.2001.5218. [DOI] [PubMed] [Google Scholar]
- 8.Morin PE, Freire E. Direct calorimetric analysis of the enzymatic activity of yeast cytochrome c oxidase. Biochemistry. 1991;30:8494–500. doi: 10.1021/bi00098a030. [DOI] [PubMed] [Google Scholar]
- 9.Williams BA, Toone EJ. Calorimetric evaluation of enzyme kinetic parameters. J Org Chem. 1993;58:3507–3510. [Google Scholar]
- 10.Olsen SN. Applications of isothermal titration calorimetry to measure enzyme kinetics and activity in complex solutions. Thermochimica Acta. 2006;448:12–18. [Google Scholar]
- 11.De Bruyker D, Wolkin MV, Recht MI, Torres FE, Bell AG, Anderson GB, Peeters E, Kolatkar A, Kuhn P, Bruce RH. MEMS-based enthalpy arrays, Transducers 2007 -2007 international conference on solid-state sensors, actuators and microsystems. IEEE; New York City, NY: 2007. pp. 1757–1760. [Google Scholar]
- 12.Barnard EA. Hexokinases from yeast. Methods Enzymol. 1975;42:6–20. doi: 10.1016/0076-6879(75)42085-7. [DOI] [PubMed] [Google Scholar]
- 13.Torres FE, Recht MI, Bell AG, De Bruyker D, Wolkin MV, Peeters E, Anderson GB, Kuhn P, Bruce RH. Modeling the PARC nanocalorimeter using COMSOL. COMSOL User’s Conference; Las Vegas, NV: 2006. [Google Scholar]
- 14.Bianconi ML. Calorimetric determination of thermodynamic parameters of reaction reveals different enthalpic compensations of the yeast hexokinase isozymes. J Biol Chem. 2003;278:18709–13. doi: 10.1074/jbc.M211103200. [DOI] [PubMed] [Google Scholar]
- 15.Darrow RA, Colowick SP. Hexokinase from Baker’s yeast: ATP+Hexose-->ADP+Hexose-6-phosphate+H+ Methods Enzymol. 1962;5:226. [Google Scholar]
- 16.Umezawa H. Structures and activities of protease inhibitors of microbial origin. Methods Enzymol. 1976;45:678–95. doi: 10.1016/s0076-6879(76)45058-9. [DOI] [PubMed] [Google Scholar]
- 17.Umezawa H. Low-molecular-weight enzyme inhibitors of microbial origin. Annu Rev Microbiol. 1982;36:75–99. doi: 10.1146/annurev.mi.36.100182.000451. [DOI] [PubMed] [Google Scholar]
- 18.Mizoue LS, Tellinghuisen J. Calorimetric vs. van’t Hoff binding enthalpies from isothermal titration calorimetry: Ba2+-crown ether complexation. Biophys Chem. 2004;110:15–24. doi: 10.1016/j.bpc.2003.12.011. [DOI] [PubMed] [Google Scholar]
- 19.Horn JR, Russell D, Lewis EA, Murphy KP. Van’t Hoff and calorimetric enthalpies from isothermal titration calorimetry: are there significant discrepancies? Biochemistry. 2001;40:1774–8. doi: 10.1021/bi002408e. [DOI] [PubMed] [Google Scholar]
- 20.Liu Y, Sturtevant JM. Significant discrepancies between van’t Hoff and calorimetric enthalpies. II. Protein Sci. 1995;4:2559–61. doi: 10.1002/pro.5560041212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Squires TM, Quake SR. Microfluidics: Fluid physics at the nanoliter scale. Reviews of Modern Physics. 2005;77:977. [Google Scholar]
- 22.Stone HA, Stroock AD, Ajdari A. ENGINEERING FLOWS IN SMALL DEVICES Microfluidics Toward a Lab-on-a-Chip. Annual Review of Fluid Mechanics. 2004;36:381–411. [Google Scholar]
- 23.Yaws CL. Yaws’ Handbook of Thermodynamic and Physical Properties of Chemical Compounds. Knovel; 2003. [Google Scholar]
- 24.Efron B, Tibshirani R. An introduction to the bootstrap. Chapman & Hall; New York: 1993. [Google Scholar]
- 25.Erlanson DA, McDowell RS, O’Brien T. Fragment-based drug discovery. J Med Chem. 2004;47:3463–82. doi: 10.1021/jm040031v. [DOI] [PubMed] [Google Scholar]