Visual stimuli induce waves of electrical activity in turtle cortex

Abstract

The computations involved in the processing of a visual scene invariably involve the interactions among neurons throughout all of visual cortex. One hypothesis is that the timing of neuronal activity, as well as the amplitude of activity, provides a means to encode features of objects. The experimental data from studies on cat [Gray, C. M., Konig, P., Engel, A. K. & Singer, W. (1989) Nature (London) 338, 334–337] support a view in which only synchronous (no phase lags) activity carries information about the visual scene. In contrast, theoretical studies suggest, on the one hand, the utility of multiple phases within a population of neurons as a means to encode independent visual features and, on the other hand, the likely existence of timing differences solely on the basis of network dynamics. Here we use widefield imaging in conjunction with voltage-sensitive dyes to record electrical activity from the virtually intact, unanesthetized turtle brain. Our data consist of single-trial measurements. We analyze our data in the frequency domain to isolate coherent events that lie in different frequency bands. Low frequency oscillations (<5 Hz) are seen in both ongoing activity and activity induced by visual stimuli. These oscillations propagate parallel to the afferent input. Higher frequency activity, with spectral peaks near 10 and 20 Hz, is seen solely in response to stimulation. This activity consists of plane waves and spiral-like waves, as well as more complex patterns. The plane waves have an average phase gradient of ≈π/2 radians/mm and propagate orthogonally to the low frequency waves. Our results show that large-scale differences in neuronal timing are present and persistent during visual processing.

The flow of visual information through the retinogeniculocortical pathway in turtles projects to a rostral area of its dorsal cortex (1, 2), whose cellular and synaptic physiology share basic features with mammalian neocortex (3, 4). Anatomical studies indicate that the geniculocortical afferents traverse the lateral part of this area of dorsal cortex with few collaterals, and their ending defines the border between a lateral, solely visual area (D2) and a medial area (D1) that receives input from multiple sensory modalities (2, 5) (Fig. 1a). These afferents, along with widely distributed intrinsic fibers (6), form an extensively interconnected lattice that is reminiscent of an association area. This organization is consistent with the finding that single neurons in the visual cortex respond to stimuli in all quadrants of the visual field (7) and that visual stimulation leads to oscillations in the local field potential (LFP) throughout all of visual cortex (8, 9). The frequency content of the oscillations is state dependent; a band near 20 Hz appears to be specific to visual stimuli, whereas lower-frequency bands depend more generally on arousal (8).

Figure 1.

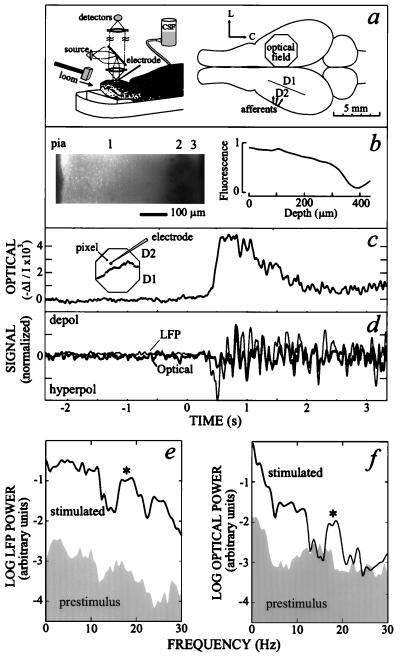
Experimental procedure (a and b) and the response from single cortical locations (c–f). (a) Schematic of the set-up. A 3.5-mm-diameter region of stained cortex that encompasses parts of lateral (D2) and medial (D1) dorsal cortex was imaged onto an array of photodiodes (135 μm/pixel). The focal plane was typically ≈200 μm below the pial surface. A metal electrode was used to measure the LFP. (b) Fluorescent micrograph of a thin section of stained turtle cortex, prepared as in ref. 10, along with the normalized emission from the section as a function of depth below the pial surface. (c) The optical signal after low-pass filtering at 40 Hz. The large depolarization appears ≈400 ms after stimulus onset of the loom (t = 0). Insert shows the approximate location of the pixel relative to the reconstructed D1/D2 border (Methods). (d) Overlay of the optical signal at one pixel and the adjacent LFP, as indicated in Insert in c. The large depolarization in the optical signal was removed with a median filter (400 ms wide), and the relative amplitudes of the two signals were adjusted to give the maximal overlap during the stimulus interval. (e) Spectral power (logarithmic scale) in the LFP during the 1- to 2-s epoch prior to stimulation and the 1- to 2-s epoch after the onset of stimulation (2WT = 5.0; K = 3). Note the emergence of a broad peak at 18 Hz (∗) during stimulation. (f) Spectral power in the optical signal during the 1- to 2-s epoch prior to stimulation and the 1- to 2-s epoch after the onset.

METHODS

Preparation.

Pond turtles (Pseudemys scripta) of both sexes with carapace lengths between 12 and 16 cm were maintained in aquaria (20° to 25°C). Use of the animals were under the guidelines of local institutional animal care and use committees and the National Institutes of Health (Bethesda, MD). Under anesthesia by cold narcosis, the dorsal aspect of the telencephalon was exposed as described (9) (Fig. 1a). For all optical measurements, the brain was partially isolated by sectioning the spinal cord and cranial nerves IV–XII from a ventral approach. The innominate artery was catheterized and the animal was continuously perfused with an oxygenated artificial cerebrospinal fluid (CSF) that consisted of 96.5 mM NaCl/2.6 mM KCl/4.0 mM CaCl₂/2.0 mM MgCl₂/31.5 mM NaHCO₃/10 mM dextrose/1.5% (wt/vol) 60–90 kDa dextran, and was saturated with 5% (vol/vol) CO₂ in O₂, pH 7.4. The pial surface of the brain was stained for 15 min with 0.02–0.08% (wt/vol) solutions of voltage-sensitive dye (JPW1114 or RH795; Molecular Probes) in CSF. The dye was observed to stain tissue throughout the entire depth of dorsal cortex (Fig. 1b).

At the end of each experiment the animal was injected with a lethal dose of sodium pentobarbital; we recorded the response from the resulting isoelectric brain as a measure of the noise level. Further, the exposed surface of the turtle cortex was labeled with pin holes at the center of the optical field; these marks and the LFP electrode locus served as fiducials for the location of the D1/D2 border. The brain was subsequently sectioned at 30 μm and stained with cresyl violet; the D1/D2 border is defined by differences in cell packing and the width of the deep neuropil (layer 2) (2).

Optical Recording.

A 3.5-mm-diameter region that encompassed most of rostral dorsal cortex was imaged with a 0.5 numerical aperture epi-illumination system (10) onto an octagonal array of photodiodes whose individual outputs were band-limited (0.3 Hz single-pole high-pass and 300 Hz 4-pole Bessel low-pass filters) (11) and digitized at 1010 Hz for 8 s epochs under the control of NeuroPlex acquisition software (Universal Imaging, Media, PA). The intensity of emitted light at time t for a pixel centered at (x,y) is denoted I(x,y,t). The spatially averaged change in transmembrane potential within the field of each pixel is linearly proportional to the fractional change in emitted light, i.e., ΔV(x, y, t) ∝ ΔI(x, y, t)/I(x, y) where ΔI(x, y, t) = I(x, y, t) − I(x, y) is the filtered signal and I(x, y) is the value prior to acquisition of the sequence. Defective optical channels are ignored, and the final data contain 447 spatial measurements.

Electrophysiology.

Data from an epipial field electrode were acquired (1 Hz single-pole high-pass filter) concurrently with the optical images. The location of the electrode was marked by electrodepositing iron from the electrode at the end of each experiment.

Stimuli.

The loom was a white brick, 9 × 12 cm, that was mechanically moved toward the contralateral eye on a 45° azimuth from midline. The total excursion was from 30 cm (10° subtended angle) to 5 cm (60°) at a speed of 8 cm/s. An alternate stimulus was a step illumination provided by a red (620 nm) light-emitting diode; the light was diffused by covering the eye with moistened tissue paper.

Data Reduction.

Five numerical procedures were performed with the data.

Spectral estimation.

For a given time series, denoted V(t), the power spectrum was obtained with a direct multitaper estimate (12) given by

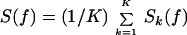1

where

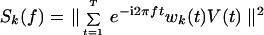2

is the discrete Fourier transform of V(t) multiplied by the k-th Slepian taper, denoted w_k(t). The tapers form an orthogonal basis and are characterized by a bandwidth parameter, denoted W; there are K + 1 = 2WT such functions that are concentrated spectrally in the full bandwidth 2W, where T is the record length. The concentration reduces bias in the spectral estimate, and the average over spectral estimates reduces the variance of the power spectrum. The bandwidth is chosen to achieve smoothing while preserving relevant spectral structure.

Denoising.

The presence of shot-noise in the optical signal makes direct visualization of the space–time data difficult. As the desired signal is correlated in space and time, filtering can be used to improve the signal-to-noise ratio. Temporal filtering is appropriate since the frequency spectrum contains peaks; however, spatial frequency filtering will blur sharp spatial features that are present in the data. Superior results to conventional smoothing or filtering methods were obtained by truncating a space–time singular value decomposition (SVD) of the data V(x, y, t). The standard SVD is applied to the two-dimensional data matrix obtained by collapsing the spatial dimensions into a single index, denoted x [i.e., V(x, y, t) → V(x, t)]. The decomposition is given by

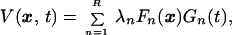3

where the spatial modes F_n(x) and the temporal modes G_n(t) each form an orthogonal basis, and R is the rank of the matrix V. The singular values λ_n are presumed to be in descending order. The data from an active brain were empirically found to be characterized by a few large singular values and a long tail of values; that from the pentobarbital-perfused animal contained only the tail of the distribution. This result can be quantitatively explained by assuming that the data for an active brain are a low-rank matrix corrupted by shot noise (A. M. Sengupta and P. P. Mitra, unpublished work). We thus truncated the SVD to keep a number of modes, R_max, consistent with the estimated shot noise to obtain a denoised matrix

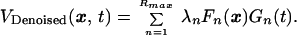4

In practice, R = 447 and R_max < 40.

Temporal filtering.

Projection filters (13) based on Slepian functions provide optimal frequency isolation and were used for purposes of temporal filtering. For a given length of time series, (i.e., V(t) with t ∈ [1, T]), the projection operator P has matrix entries P_k,t = e^−i2πftw_k(t). The Slepian functions w_k(t) are characterized by a bandwidth W (see above); the choice k < 2WT projects the spectral energy into a frequency band [f − W, f + W]. The projected or filtered time series is given by V_filtered = P^T PV.

Spatial coherence.

To examine the spatial patterns of coherence corresponding to peaks in the frequency spectra, a space–frequency SVD (14) was used. In this method, the space–time data are first projected into a local temporal frequency domain using the projection operator defined above, i.e.,

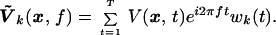5

Here the index k effectively defines a local frequency index in the band [f − W, f + W] with k < 2WT. For a fixed frequency, f, an SVD is performed on the complex matrix Ṽ_k(x, f) to yield

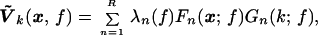6

where R is the rank of Ṽ_k, typically set by 2WT. If the fluctuations were completely coherent in the given frequency band, only one of the singular values would be non-zero. A measure of coherence is then given by the ratio of the power of the leading mode to the total power, i.e.,

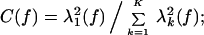7

for a completely coherent response C(f) = 1, and for a uniform random process C(f) ≈ K⁻¹. Where C(f) has a peak, it is useful to examine the largest spatial mode, Ṽ₁(x, f). The magnitude of this complex image gives the spatial distribution of coherence at that frequency, and gradients in the phase of the complex image indicate the local direction of propagation.

Demodulation.

Slow changes in the magnitude and phase of the oscillatory response near a particular frequency were found by complex demodulation of the denoised data. We formed Ṽ_f(x, y, t) = e^i2πft V(x, y, t), so that in temporal frequency space the origin is now shifted to the center frequency f, and low-pass filtered the time series at each spatial location (see above).

RESULTS

Basic Response.

We measured the change in fluorescence from cortex stained with voltage-sensitive dye (15) together with measurements of the LFP (Fig. 1a). The optical measurements provide a means to record the average transmembrane potential at ≈450 neighboring sites with an intrinsic spatial resolution of ≈150 μm per site (10, 15). The optical signal at a single location atop dorsal cortex shows a large depolarization upon onset of a loom (Fig. 1c), a behaviorally relevant stimulus (16), consistent with previous results (17). Superimposed on the depolarization are relatively fast oscillations (Fig. 1c) whose timing is correlated with those seen in the LFP sampled at an adjacent location (Fig. 1d; correlation coefficient = 0.6). We detected no significant changes in the intrinsic optical properties of the preparation upon stimulation.

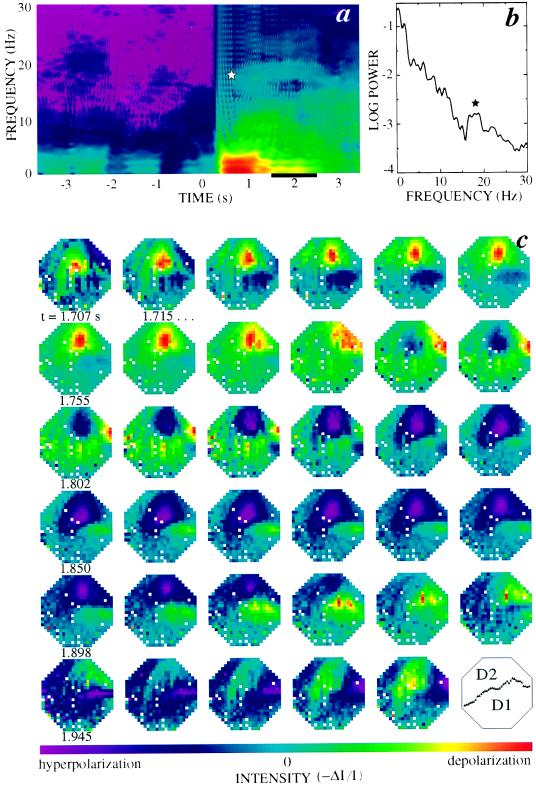
Both the LFP and the optical signal show weak spectral features prior to stimulation (Fig. 1 e and f). In the presence of a visual stimulus the power is enhanced at all frequencies and a significant peak emerges near 18 Hz (∗ in Fig. 1 e and f). The average spectrum across all strongly activated sites in the optical field (Fig. 2 a and b) is similar to that seen at the previous single location (Fig. 1f); a band centered at 18 Hz appears within 0.5 s of the onset of stimulation and lasts for nearly 2 s of the 3-s stimulation period (Fig. 2a). Similar results are observed in all preparations with the loom (n = 7).

Figure 2.

The spatiotemporal optical signal. (a) The average of the power spectra for 72 pixels over the most active part of cortex, computed over sliding 1-s intervals (2WT = 4.0; K = 2). The logarithm of the data is false colored, with red corresponding to the maximum and purple corresponding to minimum values. The transition near 0.3 s reflects the onset of stimulus-induced activity. The star indicates the stimulus-induced band at 18 Hz. (b) The spectrum for a particular 1-s interval (bar in a). (c) The broad-band filtered optical data. We plotted every eighth frame (126 Hz) of the single-trial response. The data were spatially denoised and low-pass filtered at 60 Hz (Methods), and the large stimulus-induced depolarization was removed with a median filter (400 ms width). The color scale for each frame was separately normalized by the magnitude of the largest optical signal within that frame. Note that the vertical stripes apparent in some images are a motion artifact whose frequency content lies below 1 Hz and thus does not effect subsequent analysis of the data. Orientation and size of the optical field are as in Fig. 1a.

As a control, we tested whether our preparative procedures distorted the spectral content of the LFP. First, we compared the stimulus-induced LFP from intact preparations with preparations in which the brain was isolated from nociceptive and nonvisual sensory inputs. The spectral content of the LFP was essentially unchanged. Further, we observed that the spectral content was unchanged by vascular perfusion, a procedure that removed a systematic source of optical noise. Last, we checked for pharmacological effects of the voltage-sensitive dye. Dye concentrations of 0.08% (wt/vol) or more decreased the magnitude of the “20 Hz” band in the LFP by 10%; concentrations at twice this level had a more pronounced effect. Thus, our images may contain suppressed high-frequency activity, although other sources of distortion, such as anesthetics or anticholinergic paralytics, are absent from the preparation.

Large-Scale Dynamics.

Are the stimulus-induced oscillations in different regions of turtle visual cortex coherent with each other? The “raw” image data was denoised (Methods) and a front of depolarization (Fig. 1c) that propagates along the direction of the afferents (17) was subtracted. The resultant sequence of images exhibits spatial patterns that evolve over time. For the sequence of Fig. 2c, we observed depolarization and hyperpolarization that travel in the caudal direction, consistent with low-resolution LFP measurements (18), as well as swirls of polarization. This examination shows that the spatial and temporal aspects of the response are coupled. However the images appeared complex, not surprisingly in light of the broad spectral content of the response, and were dominated by the larger amplitudes of the low-frequency activity.

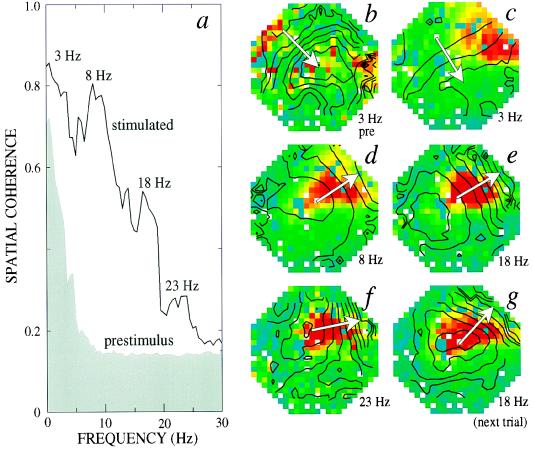
As a means to probe for a simple spatiotemporal structure that might underlie the response, we determined whether the observed cortical signal exhibits a dominant pattern of spatial coherence within separate frequency bands. We considered the response over 3-s intervals before and during stimulation (Methods); the magnitude of calculated coherence for each pixel in the dominant pattern reports the stability of the oscillation and the phase reports the relative timing of the oscillation during the 3-s interval. Before stimulation, significant coherence was limited to frequencies less than ≈5 Hz (Fig. 3a). The magnitude of the coherence was dispersed (false color plot, Fig. 3b), but the phase gradient lay in the laterorostral to mediocaudal direction (contour plot, Fig. 3b); this axis lies parallel to the thalamocortical input tract (Fig. 1 a) (19). The presence of a stimulus caused the spatial coherence at low frequencies to apparently coalesce (Fig. 3c), while the phase gradient remained congruent to that seen prior to stimulation (cf. Fig. 3 b and c). Further, the stimulus elicited spatial coherence in bands centered near the higher frequencies of 8, 18, and 23 Hz (Fig. 3a). The peak magnitude of the coherence for each of these additional bands were colocalized. Their phase gradients lay in the mediorostral to laterocaudal direction (Fig. 3 d–f); this axis lies parallel to the D1/D2 border and was perpendicular to the gradient of the ongoing low-frequency activity (cf. Fig. 3 c and e). Repetition of the stimulus led to a dominant pattern with a similar spatial localization and phase gradient (cf. Fig. 3 e and g).

Figure 3.

The magnitude and phase of the spatial coherence of the optical signal from a space–frequency SVD analysis (Methods). (a) The coherence averaged over a T = 3 s interval both prior to and subsequent to the onset of stimulation. In the latter case the interval encompassed the entire epoch of significant spectral power in the band at 18 Hz (Fig. 2a). The coherence was estimated at successive frequency bins (2WT = 3.0; K = 7); a value of C(f) ≅ 0.14 indicates the lack of significant coherence. (b) Phase (contour lines) and amplitude (false color) of the coherence at f = 3 Hz prior to stimulation. The image formed by the magnitude of Ṽ₁(x, y, f = 3) defines the spatial distribution of coherence, and the phase of Ṽ₁(x, y, 3) defines the temporal delays between different regions. The relative magnitude is false colored with red for maximum and blue/green for zero, and the phase is overlaid as a contour plot with π/12 radians per contour. The arrow indicates the dominant direction of the gradient. (c–f) Phase and amplitude at f = 3, 8, 18, and 22 Hz, respectively, during stimulation by a loom. (g) Phase and amplitude at 18 Hz for the next trial with the same animal. Orientation of the optical field is as in Fig. 1a.

The three essential features of the response discussed above were seen in all trials (seven animals, three to four trials per animal), namely, (i) the low-frequency activity propagates predominantly along the direction of the afferent fiber tract, (ii) the high-frequency activity propagates predominantly orthogonal to that at low frequency, and (iii) stimulus-induced coherent activity is localized. The variability in the direction of propagation for the dominant component was 25° (SD) for frequencies below ≈5 Hz and 15° for frequencies ≥8 Hz; for the 18-Hz band the variability dropped to 5°. The direction of this phase gradient did not significantly change when the axis of the loom was shifted by 90° in the horizontal plane or when the oscillations were induced by a step of illumination rather than a loom (n = 3); thus, the direction appears to be intrinsic to cortex. The gradient across the region of highest spatial coherence was 1.4 ± 0.2 radians/mm (mean ± SD) for frequencies between 8 and 12 Hz and 1.6 ± 0.3 radians/mm for frequencies between 16 and 20 Hz. The inferred propagation speeds were 0.05 and 0.09 mm/ms, respectively; such slow speeds have been reported for fibers in turtle cortex (20).

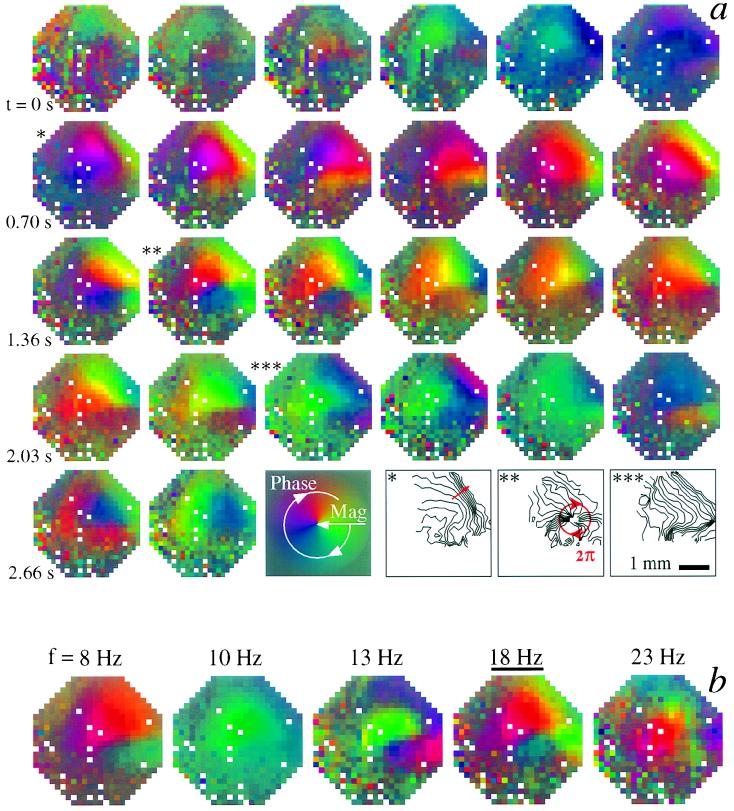
Spatial events that are short-lived or whose pattern drifts will not survive the averaging used to determine the dominant pattern (Fig. 3). To address this possibility, we focused on the temporal evolution of the stimulus-induced response within the 18-Hz band; demodulation (Methods) of the data provides a means to isolate the magnitude (color saturation; Fig. 4) and phase (color hue; Fig. 4) of the response. The phase was poorly defined at the onset of stimulation and showed an initial coherent response that corresponded to plane waves (∗ in Fig. 4a) that run in the caudolateral direction, as was seen in the dominant mode of the coherence (Fig. 3e). At later times we observed the onset of a phase singularity and circular waves (∗∗ in Fig. 4a), followed by a return to plane waves (∗∗∗ in Fig. 4a). The singularity lay near the D1/D2 border but did not correspond to any presently known anatomical feature or to injury. The epicenter wandered as the response progressed; this partly accounts for the absence of a circular component in the dominant mode over the 3-s stimulation period, which is described above (Fig. 3e). Lastly, the presence of a circular wave at 18 Hz persisted when the demodulate was averaged over independent time intervals (four cycles; Fig. 4b). Consistent with a lifetime of at least four periods, the circular wave at 18 Hz was not accompanied by similar waves at neighboring frequencies (14 and 23 Hz; Fig. 4b).

Figure 4.

Temporal evolution of the band-limited electrical activity from a demodulation procedure. (a) The magnitude and phase of the optical response centered at 18 Hz as a function of time, beginning with the onset of the loom. We plotted the demodulate, Ṽ_f(x, y, t), as a sequence of false-colored images with the magnitude of the demodulate coded by the saturation level and the phase of the demodulate coded by the hue; a single normalization is used for the entire sequence. Note the presence of approximately linear (∗ and ∗∗∗) and circular (∗∗) phase shifts. Each frame corresponds to an independent sample (9 Hz); a phase shift of 2π radians corresponds to a cycling through the chromatic scale (e.g., red → green → blue → red). The final row includes contour maps of the phase only at times t = 0.68 s (∗), t = 1.45 s (∗∗), and t = 2.22 s (∗∗∗); each contour corresponds to π/12 radians. Orientation of the optical field is as in Fig. 1a. (b) The magnitude and phase of the demodulate centered at f = 8, 10, 13, 18, and 23 Hz, filtered at W = f/4 (2WT = 2; K = 1), and averaged over a period of four cycles. The center time of the interval was t = 1.51 s (∗∗ in a).

DISCUSSION

The observed phase gradient for the high-frequency bands is likely to be mediated by intrinsic cortical connectivity since it lies orthogonal to the geniculocortical afferents. However, the known short- and long-range horizontal connectivity exhibit no obvious orientation (6). Thus, the direction of the gradient at high frequencies is likely to emerge from the dynamics of the underlying neuronal oscillators and their connections (21, 22).

The phase gradients seen here (Figs. 3 and 4) and those reported for other central structures (23–31) do not exceed 2π radians. This suggests that the oscillatory component of the spike train of different neurons in cortex have an unambiguous phase, as opposed to the case where the shifts exceed 2π. For example, spiral waves in networks of weakly coupled oscillators may exhibit phase singularities that are multiples of 2π (32). Gradients with unambiguous phase provide a unique label that may be used to segment (33) or categorize (34, 35) the visual scene in the temporal domain.

The wave phenomena reported here are likely to modulate the computations performed by the turtle’s nervous system, although currently there is no evidence to relate such spatiotemporal patterns to behavior in a causal fashion. A similar situation holds for the visually induced “40 Hz” oscillations (36–39) and the thalamocortical spindle oscillations (40) in mammalian cortex. Although both of these oscillations are believed to be spatially uniform (but see ref. 27), high-resolution imaging of the mammalian cortex may reveal features similar to those reported here (Figs. 3 and 4).

ABBREVIATIONS

LFP

local field potential

SVD

singular value decomposition