Equilibrium distributions of topological states in circular DNA: Interplay of supercoiling and knotting

Abstract

Two variables define the topological state of closed double-stranded DNA: the knot type, K, and ΔLk, the linking number difference from relaxed DNA. The equilibrium distribution of probabilities of these states, P(ΔLk, K), is related to two conditional distributions: P(ΔLk|K), the distribution of ΔLk for a particular K, and P(K|ΔLk) and also to two simple distributions: P(ΔLk), the distribution of ΔLk irrespective of K, and P(K). We explored the relationships between these distributions. P(ΔLk, K), P(ΔLk), and P(K|ΔLk) were calculated from the simulated distributions of P(ΔLk|K) and of P(K). The calculated distributions agreed with previous experimental and theoretical results and greatly advanced on them. Our major focus was on P(K|ΔLk), the distribution of knot types for a particular value of ΔLk, which had not been evaluated previously. We found that unknotted circular DNA is not the most probable state beyond small values of ΔLk. Highly chiral knotted DNA has a lower free energy because it has less torsional deformation. Surprisingly, even at |ΔLk| > 12, only one or two knot types dominate the P(K|ΔLk) distribution despite the huge number of knots of comparable complexity. A large fraction of the knots found belong to the small family of torus knots. The relationship between supercoiling and knotting in vivo is discussed.

Topological properties of DNA are essential for life. It is simplest to consider the topological properties of circular DNA in which both strands are intact, called closed circular DNA, but linear DNA in vivo is also topologically constrained (1, 2). The topological state of closed circular DNA can be described by two variables. One is the knot type, K, formed by the double helix axis. In particular, a molecule may be unknotted (unknot, trivial knot) or form a non-trivial knot. The second variable, the linking number of the complementary strands, Lk, describes the winding of the strands of the double helix about each other. It is more convenient to use the difference between Lk and that of relaxed DNA (Lk_o), ΔLk = Lk − Lk_o, than Lk itself. Circular DNA extracted from cells has negative ΔLk (3).

Random cyclization of linear DNA molecules results in an equilibrium distribution of topological states, P(ΔLk, K). Studies of the components of this distribution have greatly advanced our understanding of DNA conformational properties. The measurement in 1975 of the equilibrium distribution of ΔLk for unknotted circular DNAs, the conditional distribution P(ΔLk|Unknot), led to elegant determinations of the free energy of supercoiling (4, 5). These textbook experiments were elaborated later to include the effect of DNA length, solvent, temperature, and ionic conditions (6–10). A theoretical analysis of P(ΔLk|Unknot) allowed the determination of the torsional rigidity of DNA (11–15). The conditional distribution for the simplest knot, P(ΔLk|Trefoil), has also been studied theoretically (16) and experimentally (17).

The value of Lk is not defined in nicked circular DNA, whose topological state is specified by knot type only. The corresponding equilibrium distribution of knots in torsionally unstressed molecules, P(K), has been the subject of many theoretical studies (16, 18–23). Experimental measurements of P(K) for different DNA lengths were performed for the first time in 1993 and allowed an accurate determination of the electrostatic repulsion between DNA segments under different ionic conditions (10, 17, 24).

To provide a more complete description of DNA topology, we evaluated the general relationships between P(ΔLk, K) and the four derivative distributions, P(ΔLk|K), P(K|ΔLk), P(K), and P(ΔLk). There is no known method for measuring P(ΔLk, K) directly, but it can be calculated from a pair of derivative distributions that can be measured or simulated, P(K) and P(ΔLk|K). P(ΔLk, K) can also be simulated directly.

We focused particularly on the conditional distribution P(K|ΔLk), the equilibrium distribution of knot types in DNA molecules with a particular value of ΔLk. We computed P(K|ΔLk) in two different ways and obtained the same distributions. These computations showed, in agreement with (25), that beyond very small values of ΔLk, the lowest energy form of DNA for a particular ΔLk is knotted and not plectonemically supercoiled. This preference arises because formation of highly chiral knots minimizes torsional deformation of DNA. Unexpectedly, we found that only a few knots dominated the distribution for a particular ΔLk value and a large fraction of these knots belongs to the small family of torus knots. We discuss the relationship between supercoiling and knot formation inside the cell.

Methods of Calculations

DNA Model.

We modeled DNA as a discrete analog of a worm-like chain and accounted for intersegment electrostatic repulsion. A DNA molecule composed of n Kuhn statistical lengths is modeled as a closed chain of kn rigid cylinders of equal length. Replacement of a continuous worm-like chain with kn hinged rigid segments is an approximation that improves as k increases. The bending energy of the chain, E_b, is given by

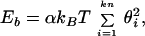1

where the summation extends over all the joints between the elementary segments, θ_i is the angular displacement of segment i relative to segment i − 1, α is the bending rigidity constant, k_B is the Boltzmann constant, and T is the absolute temperature. The value of α is defined so that the Kuhn statistical length corresponds to k rigid segments (12). We used k = 10, which has been shown to be large enough to obtain accurate results for supercoiled DNA (26). The Kuhn length was set equal to 100 nm (27).

In the simulation of closed circular DNA, we also accounted for the energy of torsional deformation, E_t:

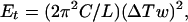2

where C is the torsional rigidity constant of DNA, L is the length of the DNA chain, and ΔTw is the difference in double helical twist from relaxed DNA (26). The value of ΔTw was not specified in the model directly but was calculated for each conformation using White’s equation (28–30), which connects ΔLk and writhe of the DNA axis, Wr, to ΔTw:

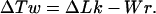3

Eq. 3 allows us to use our DNA model to simulate the properties of closed circular DNA with a specified value of ΔLk. The calculation of Wr for a particular conformation was based on Le Bret’s algorithm (16).

The excluded volume effect and the electrostatic interactions between DNA segments are taken into account in the model via the concept of effective diameter, d. This is the actual diameter of the impenetrable cylindrical segments of the model chain. We used d = 5 nm throughout this work, which corresponds to a NaCl concentration of 0.2 M (24, 31).

Monte Carlo Simulation Procedure.

We used the Metropolis Monte Carlo procedure (32) to generate an equilibrium set of conformations as described in detail elsewhere (33).

Control of Topological Variables.

Since the chain segments are allowed to pass through each other during successive deformations in the Metropolis procedure, the knot type of the chain can change. The constructed equilibrium set of chain conformations specifies the equilibrium distributions of knots, P(K). To calculate P(K), one needs only to know the topology of each conformation. In the simulations, this is done by calculating the value of the Alexander polynomial, Δ(t) at t = −1 and t = −2 (18). Although the values of Δ(−1) and Δ(−2) distinguish all knots obtained in this work, to identify complex knots, we also calculated the more powerful invariant, the Jones polynomial (see ref. 34, for example), using a program written by Jenkins (35).

To calculate P(ΔLk|K), we prevented a change of knot type during the simulation by rejecting trial conformations for which the values of Δ(−1) or Δ(−2) had changed. We calculated first P(Wr|K), the distribution of Wr for a particular knot type. The torsional and bending deformations of DNA are independent to a good approximation (36). This allowed us to calculate P(ΔLk|K) as a convolution of P(Wr|K) and the distribution of the torsional fluctuations, P(ΔTw). Namely,

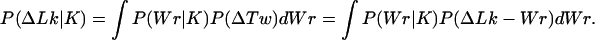4

We assumed that P(ΔTw) is specified by a Gaussian distribution with variance 〈(ΔTw)²〉 given by ref. 15:

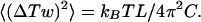5

We used a value of 3⋅10⁻¹⁹ erg⋅cm (1 erg = 0.1 μJ) for C (10, 15, 27). This way of calculating P(ΔLk|K) was first suggested by Benham (37) and was realized in ref. 11.

Results

Definitions of Lk and ΔLk, and the Classification of Knots.

We consider here the equilibrium probability distributions of the linking number difference, ΔLk, and knot type, K. The value of Lk for two closed contours C₁ and C₂ can be defined as (30, 38):

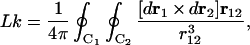6

where r₁ and r₂ are vectors that start at a point O and move, upon integration, over C₁ and C₂, respectively; r₁₂ = r₁ − r₂. This definition using the Gauss integral can be applied equally to knotted and unknotted contours. ΔLk can be calculated as

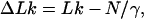7

where N is the number of base pairs in the DNA and γ is the number of base pairs per turn of the unstressed double helix. Because the value of N/γ is not integral, it is more convenient to consider ΔLk as a continuous variable even though for any particular DNA its value can differ only in integral amounts. The distribution of discrete values of ΔLk is obtained from the corresponding continuous distribution by simple renormalization. Although most of our calculations were for negative ΔLk, there is no internal chirality in the DNA model used in the simulations, and thus the results can be easily generalized to positive values of ΔLk.

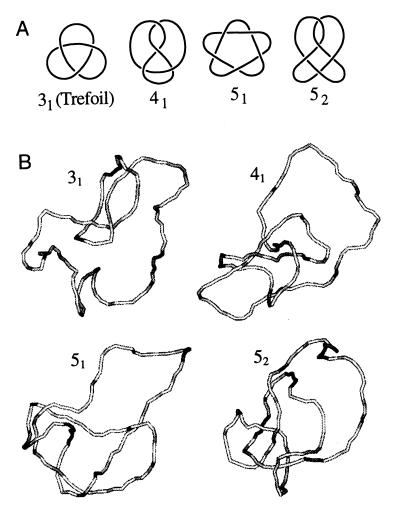
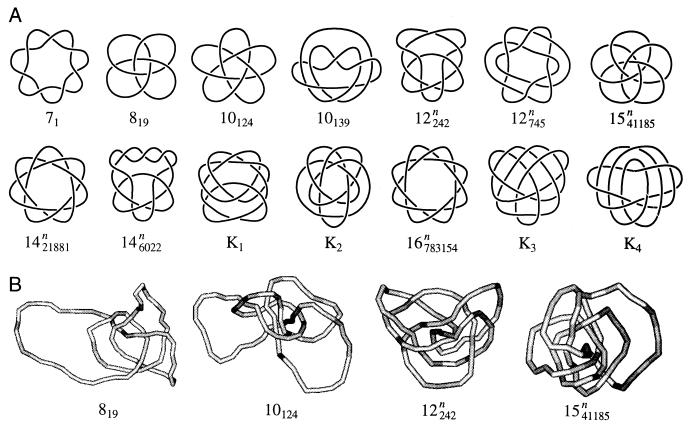
Knots are classified according to the minimum number of intersections in their plane projection. We will refer to such presentation of knots as standard forms. The simplest knot has three intersections in standard form, and there are only four different types of knots with less than six intersections (Fig. 1A). As the number of intersections in the standard form increases, the number of knot types grows very fast: there are 1,701,936 knots with less than 17 crossings (39). A knot and its mirror image are rarely topologically equivalent (only the knot 4₁ is equivalent to its mirror image among the four simplest knots shown in Fig. 1A), but only one representative of a pair is accounted in the classification (see ref. 34, for example, for more details).

Figure 1.

Simple knots. (A) Shown are the standard forms of knots that can be presented with less than six crossings in plane projection. The chiral knots 3₁, 5₁, and 5₂ are represented by only one mirror image. (B) Typical simulated knotted conformations of nicked circular DNA, 4 kb in length.

General Relationships Between P(ΔLk, K) and the Derivative Distributions.

We use in our calculations four general relationships among P(ΔLk, K) and the derivative distributions P(ΔLk|K), P(K|ΔLk), P(K), and P(ΔLk). These relationships, valid for any two-dimensional distribution, are:

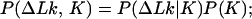8

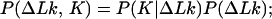9

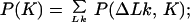10

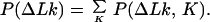11

The Distribution of Knots and ΔLk, P(ΔLk, K).

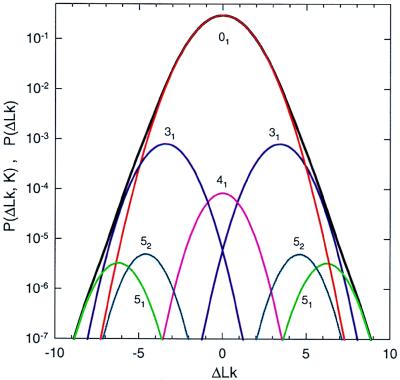
Fig. 1B illustrates typical conformations of the simplest knots obtained in the simulation of DNA molecules 4 kb in length. We calculated the equilibrium distribution, P(ΔLk, K), using Eq. 8 and simulated distributions of P(ΔLk|K) and P(K) (Fig. 2). Because P(K) decreases sharply as knot complexity grows, we were able to calculate P(K) with reasonable accuracy only for the four simplest knots, 3₁, 4₁, 5₁, and 5₂. Knots 3₁, 5₁, and 5₂ are chiral, and therefore both of their mirror images are presented in Fig. 2; knot 4₁ is achiral. The values of P(K) are shown in Table 1. In agreement with experimental data (4, 5, 17), we found that for all these knots P(ΔLk|K) is approximated well by the Gaussian distribution:

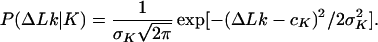12

The values of the distribution variance, σ_K², and of c_K are shown in Table 1. The simulation data did not deviate by more than 15% from the best fitted Gaussian curve in the interval (−4σ_K, 4σ_K). The values of c_K correspond to the average values of writhe, 〈Wr〉, over the distribution of equilibrium conformations of nicked circular DNA forming a knot K. Our values of c_K are in full agreement with those calculated by Katritch et al. (40).

Figure 2.

Simulated distributions of P(ΔLk, K) and P(ΔLk). The distribution P(ΔLk, K) is represented by separate peaks that correspond to different knots: 0₁ (unknotted circles) (red), 3₁ (blue), 4₁ (pink), 5₁ (light green), and 5₂ (turquoise). Contributions from both mirror images of the chiral knots 3₁, 5₁, and 5₂ are shown. Each peak is a Gaussian distribution over ΔLk. The distribution P(ΔLk), the sum of P(ΔLk, K) over K, is shown by the black line. The simulations were performed for DNA molecules 4 kb in length.

Table 1.

Properties of the simplest knots

Knot type, K	cK	σK2	P(K)
01	0	1.59	0.995324
31	−3.42	1.21	0.002210
41	0	1.08	0.000204
51	−6.23	1.00	0.000008
52	−4.59	0.99	0.000012

The parameters of the distribution P(ΔLk|K), specified by Eq. 12, were computed for DNA molecules 4 kb in length. c_K equals the average value of writhe, 〈Wr〉, of a torsionally unstressed DNA molecule forming the knot K. For chiral knots, the values of c_K for negative knots are shown. 

The Distribution P(K|ΔLk).

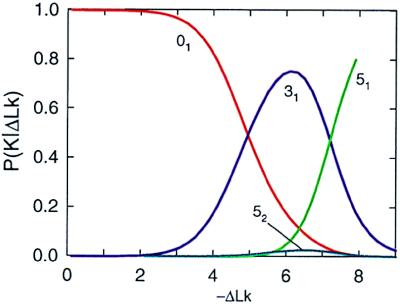
Without extra simulation, two other derivative distributions, P(K|ΔLk) and P(ΔLk), can be obtained from P(ΔLk, K) by using Eqs. 9 and 11. P(K|ΔLk), the calculated distribution of knots as a function of ΔLk, is shown in Fig. 3. Although only unknotted circular molecules (0₁) and four knots, 3₁, 4₁, 5₁, and 5₂, were taken into account during the calculation, further results showed (see Fig. 4) that only these knots compete for appearance in the range of ΔLk between 0 and −7.5. It is easy to understand why the knot 4₁ does not appear in this distribution. The average value of Wr for the amphichiral 4₁ equals zero, and thus it competes for appearance with the trivial knot in the range of ΔLk around zero but loses out because P(ΔLk, 0₁) ≫ P(ΔLk, 4₁). It is more interesting that there is a very small amount of the knot 5₂ in Fig. 3. This is because P(ΔLk, 3₁) ≫ P(ΔLk, 5₂), even though the absolute value of 〈Wr〉 is lower for 3₁ than for 5₂ (see Fig. 2), for all values of −ΔLk less than 8. For −ΔLk > 7.2, knot 5₁ makes a major contribution to the conditional distribution.

Figure 3.

Simulated distribution of P(K|ΔLk) for 4-kb DNA. The distribution was obtained by using Eqs. 9 and 10 and the data from Table 1. Each curve corresponds to a particular knot: 0₁ (red), 3₁ (blue), 5₁ (light green), and 5₂ (turquoise).

Figure 4.

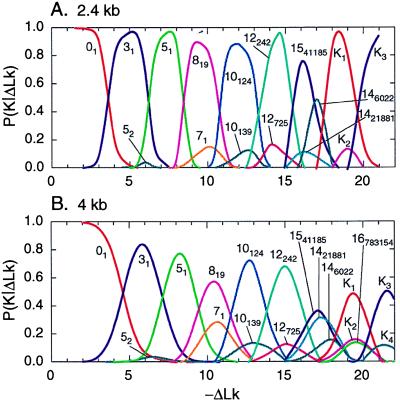
Simulated distribution of P(K|ΔLk) for 2.4-kb (A) and 4-kb (B) DNAs. The data were obtained by direct simulation of this conditional distribution. Each curve corresponds to a particular knot. Curves are shown only for those knots for which P(K|ΔLk) exceeds 0.1 (with the exception of knot 5₂). The standard form of these knots is shown in Fig. 5, and some of their features are listed in Table 2.

It is difficult to obtain P(K|ΔLk) for larger values of ΔLk using Eqs. 9 and 11, because we are not able to calculate P(K) for more complex knots. We can, however, simulate P(K|ΔLk) directly for a range of values of ΔLk. The algorithm we use allows us to restrict the equilibrium set of conformations to certain values of K or ΔLk or to remove one or both of these restrictions (see Methods of Calculations). To calculate P(K|ΔLk), we constructed equilibrium sets of conformations for particular values of ΔLk but allowed any change of knot type during the simulation.

The distributions P(K|ΔLk) obtained by direct simulation for two DNA lengths, 2.4 and 4 kb, are shown in Fig. 4. The distribution for 4-kb DNA in Fig. 4B is nearly identical with the calculated distribution in Fig. 3 over the same range of ΔLk and for DNA of the same size. This agreement demonstrates the consistency of the computations. A remarkable feature of the distribution is readily seen in Fig. 4: for any particular value of ΔLk, only very few knots dominate. Indeed, there are 1,701,936 different knots with less than 17 crossings in their standard form (39), but only 12 of them appear in the conditional distributions with probability more than 0.1! Four other knots that appear in Fig. 4 have more than 16 crossings in the standard form and therefore are not among these 1,701,936. Comparison of the distributions calculated for the two DNA lengths shows that the same knots make the major contributions in both cases, although they appear at slightly different values of ΔLk. Also slightly more knots contribute to the distribution for longer DNA. This weak dependence of P(K|ΔLk) on DNA length is due to the fact that the average Wr of knotted molecules is nearly length-independent (16, 40). The knots that make the major contribution to P(K|ΔLk) are shown in Fig. 5A in standard form. Typical conformations for some of these knots are shown in Fig. 5B; they are quite similar to the standard presentations and contain barely any extraneous crossings.

Figure 5.

Knots that make the major contributions to P(K|ΔLk). Shown are the standard forms of these knots (A) and four examples of simulated conformations of knots (B). Knot notations are explained in the legend to Table 2.

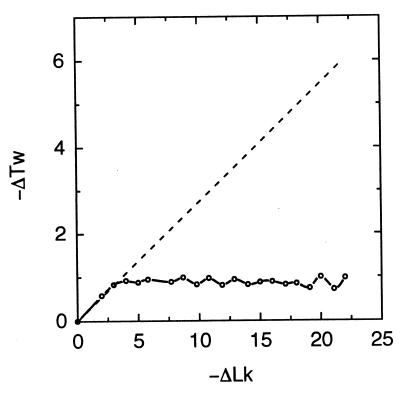
Why do so few knots make the major contribution to P(K|ΔLk)? To address this question, we calculated the average Wr for these knots in the absence of the torsional stress. The results presented in Table 2 show that the values of |〈Wr〉| of the represented knots are very large and exceed the number of crossings in their standard form. When 〈Wr〉 is near ΔLk, the torsional deformation, ΔTw, of the double helix is minimized. This in turn decreases the free energy of torsionally stressed DNA and makes the appearance of the knots thermodynamically favorable. We monitored the average values of ΔTw during the calculation of P(K|ΔLk) and found that it does not increase over a wide range of ΔLk (Fig. 6). This is very different from the properties of unknotted supercoiled DNA, for which torsional deformation grows linearly with ΔLk (Fig. 6 and ref. 41). Thus, it seems clear that high chirality, that is a high value of |〈Wr〉| in the torsionally unstressed state, is a necessary condition for the appearance of a knot in the distribution. This high chirality is manifested for the knots shown in Fig. 5 by the fact that all the crossings in standard form have the same sign. High chirality is not sufficient, however. For example, knot 9₁ is not present in the distribution, although the absolute value of its average writhe equals 12.07 (40), and all nine of its crossings have the same sign. There are at least two other chiral knots, 10₁₂₄ (in the notation of ref. 42) and 12₂₄₂ⁿ (in the notation of ref. 39), for which P(K|ΔLk) is larger in the corresponding range of ΔLk (Fig. 4).

Table 2.

Knots that make the major contributions to P(K|ΔLk)

Knot type	Alexander polynomial, |Δ(−1)|, |Δ(−2)|	〈Wr〉	p, q for torus knots
31	3, 7	−3.42	−3, 2
51	5, 31	−6.23	−2, 5
71	7, 127	−9.03	−2, 7
819	3, 91	−8.59	−3, 4
10124	1, 331	−11.17	−3, 5
10139	3, 259	−11.38
12242n	1, 1291	−13.57
12725n	5, 1147	−13.68
1541185n	5, 6355	−15.74	−4, 5
1421881n	1, 5419	−15.93	−3, 7
146022n	3, 5131	−16.14
K1	11, 26611	−18.07
K2	19, 29059	−18.24
16783154n	3, 21931	−18.39	−3, 8
K3	13, 106483	−20.37
K4	21, 115843	−20.50

Notations for knots 3₁, 5₁, 7₁, 8₁₉, 10₁₂₄, and 10₁₃₉ are explained in ref. 42; those for 12₂₄₂ⁿ, 12₇₂₅ⁿ, 15₄₁₁₈₅ⁿ, 14₆₀₂₂ⁿ, 14₂₁₈₈₁ⁿ, and 16₇₈₃₁₅₄ⁿ are presented in ref. 39. Knots K₁–K₄ have more crossings than knots in any tables available to us; their structure is shown in Fig. 5. The largest odd numbers that divide |Δ(−2)| rather than the values of |Δ(−2)| themselves are shown in the table. 

Figure 6.

Dependence of the average torsional deformation, ΔTw, of DNA on ΔLk. Points connected by the solid line are derived from the knot distributions shown in Fig. 4B. The dependence of ΔTw on ΔLk for unknotted supercoiled DNA is shown by the dashed line for comparison (41).

Another surprising result is that a large fraction of these knots belong to the family of torus knots (see Table 2). These knots can be drawn without intersection on the surface of a torus and can be specified by two integer variables, p and q, the numbers of intersections of the torus meridian and longitude (34). Torus knots can be readily identified by their Jones polynomial (43), V(t), since, for these knots,

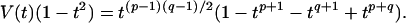13

We calculated V(t) for the knots appearing in P(K|ΔLk) and identified torus knots by trying to fit V(t) to Eq. 13. The values of p and q for the obtained torus knots are shown in Table 2. The majority of torus knots with less than 17 crossings are in the table. Only the knots with p = −2 and q = 9, 11, 13, or 15 are absent. Certainly, all torus knots are highly chiral, and this is why they appear so prominently in the distribution. It seems that, in the interval of ΔLk studied, there are few other knots with similar values of 〈Wr〉 to compete for appearance in P(K|ΔLk) with the tiny group of torus knots. It is possible that the other knots presented in P(K|ΔLk) can be obtained from corresponding torus knots by only a few stand-passages (44).

Discussion

We considered the equilibrium distribution of ΔLk and K that define the topological state of closed circular DNA. Using computer simulation, we calculated P(ΔLk, K) and four derivative distributions: P(ΔLk|K), P(K|ΔLk), P(K), and P(ΔLk). We found that P(ΔLk|K) is approximated well by a Gaussian distribution. This fact has a simple explanation. We can express the free energy of a knot K, G_K(ΔLk), as the Taylor expansion:

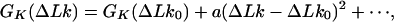14

where ΔLk₀ is the value of ΔLk when G_K(ΔLk) has its minimum value. P(ΔLk|K) will have a Gaussian distribution if the terms in Eq. 14 after the quadratic term are small in comparison with the quadratic one. The simulation results show that this is the case. The variance of the distribution diminishes as knot complexity grows (Table 1). For achiral knots, the distribution maximum is at a ΔLk = 0. For the two mirror image forms of a chiral knot, the distributions of P(ΔLk|K) are symmetrical, and their maxima are well separated (Fig. 2). We found that, for DNA molecules a few kilobases in length, P(K) decreases very rapidly with increasing knot complexity. Our results for P(ΔLk|K) and P(K) extend the data obtained in earlier studies (15, 16, 24).

The most interesting and most unexpected results were obtained for the conditional distribution P(K|ΔLk). The simulations showed that only a few highly chiral knots make a major contribution to the distribution at any particular value of ΔLk. Only 12 of more than 1.7 million knots with fewer then 17 crossings in standard form appear in the distribution with probability larger than 0.1, but for these knots the probability approaches 1 at particular values of ΔLk (Fig. 4). The major feature of these knots is a high value of average Wr when torsionally unstressed. A large fraction of the knots belongs to the torus family, although not all torus knots contribute to the distribution. Increasing the DNA length from 2.4 to 4 kb does not change P(K|ΔLk) substantially.

In the simulations, we used only one particular value of DNA torsional rigidity, C, but a wide range of values for C have been reported (8, 15, 25, 45–47). The effect of the torsional rigidity on the distributions studied is rather simple, as long as the torsional and bending deformations in DNA are energetically independent. In this case, P(ΔLk, K) can be expressed as a convolution of the twist distribution, P(ΔTw) and the distribution of writhe and knot types, P(Wr, K), similar to Eq. 4. Since P(Wr, K) gives the distribution for nicked circular DNA, it does not depend on C. Thus, the dependence of P(ΔLk, K) on C depends only on P(ΔTw). P(ΔTw) is a Gaussian distribution centered at ΔTw = 0 that broadens as C decreases (see Eq. 5). The conclusion of this analysis is that lowering C will not change the knots that appear in P(K|ΔLk), but particular knots will be found at higher values of ΔLk (see Fig. 4) and the peaks will be broader. We confirmed this. In a special simulation in which C = 1⋅10⁻¹⁹ erg⋅cm, P(K|ΔLk) was shifted by 2 in comparison with the results in Fig. 4B, which was calculated by using C = 3⋅10⁻¹⁹ erg⋅cm.

It is important to emphasize that the distributions P(ΔLk|K) and P(K) can be measured experimentally and that all other distributions, P(ΔLk, K), P(K|ΔLk), and P(ΔLk), can be calculated from the measured ones. The distribution P(K) can be generated by cyclization of linear DNA molecules via cohesive ends (17, 24). Separation of knots by gel electrophoresis and measurement of their relative amounts allows the evaluation of P(K). The equilibrium distribution of ΔLk for a particular knot P(ΔLk|K) can be obtained by ligation of nicks in these knots (17) and measurement of the distribution of ΔLk topoisomers by gel electrophoresis. Recombinases, topoisomerases, and DNA replication can also be used to obtain specific knot types for similar analyses (48).

The distribution P(ΔLk|K) has been studied in great detail for unknotted molecules (4–10), and there is very good agreement between these measurements and the results of computer simulation for all DNA lengths and ionic conditions studied (10, 15). P(ΔLk|K) was also measured for trefoils (17) and is in good agreement with our simulation results (Table 1). Both the experimental data and simulation indicate that the distribution variance, σ_K², for trefoils is 1.3× smaller than for unknotted DNA of the same length. There is also very good agreement between measured and simulated results for P(K) (17, 24). We conclude that the simulations reliably describe the equilibrium distributions of topological variables in circular DNA. The simulated results have the advantages over experimental measurements covering a much greater range of DNA size, ΔLk, and topological complexity, and some of the distributions cannot as yet be measured at all.

It has been observed that, under certain conditions, supercoiling strongly promotes knot formation by type II topoisomerases (49, 50). All these experiments, however, used very high concentrations of enzyme, so that DNA-bound enzyme molecules promote knotting. Does supercoiling promote knot formation at low enzyme concentrations, where DNA conformations are minimally disturbed by enzyme binding? This question is important for understanding knotting inside the cell, and it is interesting to analyze it in terms of the current study.

Let us consider the free energy of circular DNA, which is a function of its topological state, G(ΔLk, K). This energy can be calculated as

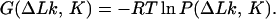15

Since P(ΔLk, K) has a global maximum at unknotted DNA with ΔLk = 0 (this is the most probable state for DNA molecules <100 kb in length), G(ΔLk, K) reaches the global minimum for DNA in this topological state. Therefore, a circular DNA must relax to this or close to this state when at equilibrium. Very often, however, topological equilibrium cannot be reached. If DNA is in closed form and no topoisomerases are present, its topology cannot be changed at all.

If a type I topoisomerase is added, ΔLk but not knot type can change. The result will be an equilibrium distribution over ΔLk for each knot present. The molecules relax to the states that correspond to the minimum G(ΔLk, K) under the condition that K is constant. This minimum is not, in general, a local minimum of G(ΔLk, K). Relaxation is restricted by a particular value of K due to the topological constraint.

In our computation of P(K|ΔLk), we restricted topological relaxation in a reciprocal fashion and kept the value of ΔLk constant but allowed K to change. The most probable states found in this computer experiment correspond to the minima of G(ΔLk, K), under the condition that ΔLk is constant. Again, these minima are not, in general, the local minima of G(ΔLk, K).

What would happen if we added a type II topoisomerase to closed circular DNA? These enzymes can change both topological variables, ΔLk and K, by catalyzing the passages of one double-stranded segment through another. We might expect that these enzymes will yield unknotted molecules with ΔLk ≈ 0, corresponding to the global minimum of G(ΔLk, K). The situation is more complex, however. DNA gyrase introduces negative supercoils in circular DNA (51), and other type II topoisomerases untie knots in DNA molecules below equilibrium level (52). This is possible because the strand passage reactions catalyzed by the enzymes are coupled to ATP hydrolysis, which serves as a source of energy. Thus, it is difficult to predict the distribution of topological states of circular DNA in the presence of type II topoisomerases. The presence of type I topoisomerases inside prokaryotic cells, which relax negative supercoils, makes this dynamic picture even more complex.

We know that DNA molecules inside of cells adopt plectonemically supercoiled unknotted conformations [see review (41) and references therein]. This is certainly the desired result for the cell because plectonemic (−) supercoils perform essential work in promoting double-helix opening and DNA compaction. The equilibrium distribution of topological states studied in this work shows that this result is far from obvious, because for DNA with even a modest ΔLk the free energy of highly chiral knots is lower than that of an unknotted plectonemic superhelix. It is possible that changing the amounts and/or activity of topoisomerases or other DNA ligands could result in knotting of circular DNA in vivo.