From residue matching patterns to protein folding topographies: General model and bovine pancreatic trypsin inhibitor

Abstract

A coarse-grained model for protein-folding dynamics is introduced based on a discretized representation of torsional modes. The model, based on the Ramachandran map of the local torsional potential surface and the class (hydrophobic/polar/neutral) of each residue, recognizes patterns of both torsional conformations and hydrophobic-polar contacts, with tolerance for imperfect patterns. It incorporates empirical rates for formation of secondary and tertiary structure. The method yields a topological representation of the evolving local torsional configuration of the folding protein, modulo the basins of the Ramachandran map. The folding process is modeled as a sequence of transitions from one contact pattern to another, as the torsional patterns evolve. We test the model by applying it to the folding process of bovine pancreatic trypsin inhibitor, obtaining a kinetic description of the transitions between the contact patterns visited by the protein along the dominant folding pathway. The kinetics and detailed balance make it possible to invert the result to obtain a coarse topographic description of the potential energy surface along the dominant folding pathway, in effect to go backward or forward between a topological representation of the chain conformation and a topographical description of the potential energy surface governing the folding process. As a result, the strong structure-seeking character of bovine pancreatic trypsin inhibitor and the principal features of its folding pathway are reproduced in a reasonably quantitative way.

The discretized folding model we introduce here is a computational tool based on topology, pattern recognition, and general characteristics of protein folding kinetics. Topology here implies information about pattern but not about specific geometric structure. Only the minimum-energy locations of the backbone torsion angles Φ and Ψ, the hydrophobic-hydrophilic natures of the residues, and the conformational constraints of the type of side group of each residue on the backbone conformation enter into this description. We construct a local topological matrix (LTM), a time-dependent, 2 × N matrix for an N-residue protein, in which the first row denotes the class of a residue, hydrophobic, hydrophilic (polar), or neutral. The second row specifies the torsional configuration at a specific time, discretized according to the basins of the Ramachandran map (R-map) of the torsional energy associated with the two angles Φ and Ψ that may assume wide ranges of values during the folding process. [The R-map is a representation of the potential energy surface (PES) of the residues, as a function of only the two dihedral angles Ψ, torsion around the carboxyl-C^α bond, and Φ, torsion about the C^α-N bond.] We introduce an integer variable R(y,n) appropriate for residue n, and a variable y whose values specify the residue’s configuration in the overall chain configuration y; R(y,n) has allowable values determined by which of four kinds of discretized R-maps (1) corresponds to that residue. The four types are: l-alanine-like, glycine, proline, and any residue preceding proline. The first, l-alanyl-like residues, may lie in any of three basins in its R-map so R(1,n) may be 1, 2, or 3. Glycyl residues may be in any of the (maximum of) four basins, so for glycine, R(1,n) may be 1, 2, 3, or 4. Proline may lie in only basins 1 or 3, and any residue preceding proline, in basins 1 or 2. The description of the system’s torsional dynamics follows from the fact that R(y,n) = 1 is compatible with the incorporation of the yth residue into a β-sheet, R(y,n) = 2 with either a β-bend or a left-handed helix, and R(y,n) = 3 with a β-bend or with a right-handed α-helix.

Within such a coarse local description, which gives considerable latitude to the values that the dihedral angles may take within any given Ramachandran basin, the precise, instantaneous geometry of the chain becomes immaterial; the description becomes topological, rather than geometric. Thus, for example, a β-turn with zero pitch becomes indistinguishable from a turn of an α-helix, until we introduce other information, such as the pattern of hydrophobic-hydrophobic contacts, to resolve the ambiguity, yet both correspond to formation of a pattern implying secondary structure. This discrete codification of the local torsional states for the peptide chain requires that the principal topological features of the R-maps, as we may call the representations based on the allowed values of R(y,n), remain invariant during the folding process, all the way to the fully folded state. That this is valid with at least 92% probability has been established by the (Φ,Ψ) plots of more than 163 protein structures resolved to 2 Å or better (2), and by theoretical calculations that show that the type of R-map for each residue is determined primarily by local interactions. These data imply that long-range interactions contributing to the potential energy only mildly perturb locally optimized geometries and do not have a major effect on the topology of the chain, which is governed primarily by the R-map. Hence we may have confidence in the level of coarse graining introduced here.

The LTM at each new time step is shaken or transformed by imposition of torsional transitions between the discrete basins of the R-map. The likelihood of such transitions is governed by a set of fixed Gaussian distributions of transition probabilities, including some determined by structures already established. Then, at fixed intervals, we examine the full structure of the LTM to identify sequences or windows of sequences of torsional states that exhibit consensus patterns that we can identify with particular structures, secondary or tertiary. When any such pattern appears, the interbasin transition rates drop for the residues in that pattern, to reflect the formation and stability of the structure associated with that pattern. This is tantamount to assuming that if a structure-forming pattern of dihedrals occurs, the corresponding structure will form as soon as the pattern is recognized. The emerging pattern may be encoded in the form of a contact matrix as soon as any of the above-mentioned structural ambiguity has been removed by the evolving participants in the pattern and their neighbors. If an ambiguity is not resolved soon after it occurs, the information about its topology is stored and later retrieved as further structural compatibilities are established, at which time the ambiguities can be resolved.

Denaturation or dismantling of stable structural elements occurs when a consecutive set of residues constituting at least 30% of a previous consensus window or structured pattern no longer match the pattern required for that structural motif. When dismantling occurs, the transition rates return from the slower to the faster range of values. This percentage criterion implies that the larger is the consensus window or assembled structure, the less likely it is to dismantle. Regions of disassembling residues are bubbles in ordered regions. The size of the critical bubbles that lead to dismantling of an entire consensus window has been established in computer simulations mimicking the kinetics of this process (3).

The time evolution of the contact matrix not only allows us to track the emerging patterns; it also reveals the renormalization of the time scales of the chain dynamics by exhibiting the regimes of flipping rates of the residues. Residues involved in no secondary structure move among the Ramachandran basins at a mean rate of 10¹¹ sec⁻¹ (4); we call these class I residues. Residues engaged in α-helical or β-sheet patterns have mean jump rates of 10⁷ sec⁻¹ (5–8) and are called class II residues. Class III residues are those in tertiary structures; these are assigned rates centered about 10³ s⁻¹ (3, 9, 10). The widths of the Gaussian distributions of these rates are temperature dependent. For class II residues, this width is estimated empirically as 10⁸ s⁻¹. For a typical, experimentally determined denaturation temperature of 313 K, the dispersion should be sufficiently broad that from one reading of the LTM to the next, i.e., within 64 ps, we should find a 50% probability that a 30% nonconforming bubble forms in a preexisting pattern. Thus the width to be used to represent the Gaussian distribution of interbasin hopping rates should become broad enough to produce this denaturation, as expressed by roughly 50% likelihood of appearance of a 30% nonconforming bubble, at 313 K. With this premise, we estimate the proportionality constant for the temperature dependence of the Gaussian SD to be 3.2 × 10⁻¹⁹ s²⋅K⁻¹.

Each step in the discretized evolution of the protein requires a new set of assignments of the Ramachandran basins of all of the residues, not only those in secondary or tertiary structures. The minimum time for such a transition in a single residue at 298 K is t′ = 6 ps (4). Hence, because each search that invokes a change in conformation of a class I residue has two possible new assignments, and six such residues is the minimum number to form the pattern of a stable helix turn or β-bend, the appropriate time between scans of the LTM for appearance of new patterns is 2⁶/6 × 6 ps or 64 ps (6, 9, 11). The time or rate associated with secondary and tertiary structures are the times that govern the rates at which these may dismantle, once formed. This value is obtained from the Gaussian width required to form consensus bubbles of at least 30% of the consensus length of a pattern. Such bubbles or sequences of consecutive, out-of-pattern residues have been determined empirically to be sufficient to trigger dismantling of existing patterns. Hence, above a critical temperature (or temperature range, because they are small, finite systems), such bubbles should form frequently within two successive evaluations of the LTM.

Frustration or Mismatch Tolerance

If the requirements for pattern formation apply strictly, then, as the example below illustrates, the system can never find its way to a stable, organized structure, much less a native structure. Consequently there must be some tolerance for error in establishing contact patterns (CPs). In particular, tolerance is necessary toward uncorrectible mismatches of neighboring hydrophobic, polar, and neutral residues, mismatches that constitute a form of frustration (4, 10, 12). However this tolerance cannot be too high; if it is, then again, the system floats among a wide range of structures and never finds a native structure as a well-organized resting place.

The rates of movement among Ramachandran basins depend on the extent of the recognized contact patterns and the determination of what constitutes a contact pattern depends on the tolerance level. From forward and backward rates of motion, we may establish the conditions for microscopic reversibility and, from these, infer the local topography of the potential surface for adjoining minima and the saddles linking them. These two together imply that a semiquantitative link can be made, for each level of frustration tolerance, between topology as revealed through the evolution of CPs and topography, at least of an average dominant folding pathway. The topography so inferred is by no means a complete, detailed topography. The pathway found this way may be considered representative of a vast number of specific pathways from crater rims to native structures.

From Topology to Topography: The Dominant Folding Pathway

The kinetic data from the coarse dynamical model described above can be inverted by using the detailed balance principle to obtain topographic information about the PES of bovine pancreatic trypsin inhibitor (BPTI), at least along a kind of mean dominant folding pathway. The topography is represented as a sequence of minima, with energies U_i, U_j, … , connected by effective saddle points k with energies U_ij^k. If there is more than one saddle between minima i and j, their combined effect may be represented as a single effective, temperature-dependent saddle. It is more convenient and precise to retain the full description until aggregation of the information becomes mandatory; in the process we describe here, of moving from a topological pattern to an effective topography, only an effective surface can be constructed. Inferring the topography from the topological data is achievable by application of the principle of detailed balance, which dictates that forward and backward rates, scaled by the corresponding equilibrium probabilities, must be equal across any barrier or set of barriers, for a system in equilibrium. At the level of coarse graining of this approach, the rate coefficients for pattern formation may be taken as mean-first-passage rate coefficients (11). This presumption is the basis for our inferences of the coarse topography of the PES.

The specifics of this process of inference are as follows: We let the function P(i, j, F, X) represent the tolerance to mismatches by giving the probability that CP_i forms in the presence of F torsional mismatches and X hydrophobic/polar mismatches; this probability is 1 if F = X = 0. Then the forward rate for formation of CP_i from a predecessor CP_j is

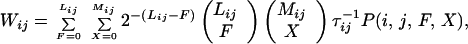1

where L_ij is the number of residues that must make an interbasin transition to take the system from CP_j to CP_i, τ_ij⁻¹ is the rate of hopping for the residues that take the system from CP_j to CP_i, and 2^−(Lij−F) is the probability that there be L_ij − F residues whose Ramachandran patterns are compatible with CP_i. The first binomial factor gives the number of available distributions of F residues torsionally incompatible with the contact pattern, among L_ij residues; the second is the number of ways of having X mismatches of the hydrophobic and polar contacts among M_ij total contacts. Initial simulations used the logistic function to model P(i, j, F, X). One natural course of investigation described in the next section is the dependence of W_ij and the topography on the form of P(i, j, F, X). For our chosen critical size of a dismantling bubble of a sequence of 30% of the residues in the CP, the rate of the reverse transition, that of the dismantling process from CP_j to CP_i, is

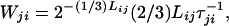2

if the frustration tolerance is zero. (The factor of 2L_ij/3 arises because this is the number of positions of the critical sequence of size L_ij/3 along the window of length L_ij.) In practice, we have found it most practical to estimate the dismantling rate from simulations. Detailed balance requires that at equilibrium,

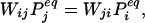3

where the equilibrium probability is the Boltzmann value, incorporating the degeneracy D_i, the partition function Z = Σ_jD_je^−βUj, and the inverse temperature β = 1/kT:

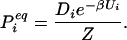4

The degeneracy D_i is the number of Ramachandran basins q_n(i) available to N_f free residues in the contact pattern CP_i, just the product

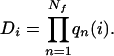5

From these, we infer the energy difference between contact patterns CP_i and CP_j as

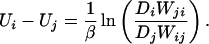6

The effective barriers ΔU*_ij then can be inferred by assuming that the rate coefficients for inter-well passages have Arrhenius forms, k_ij = Aexp(−β ΔU*_ij), and finding these rates from simulations.

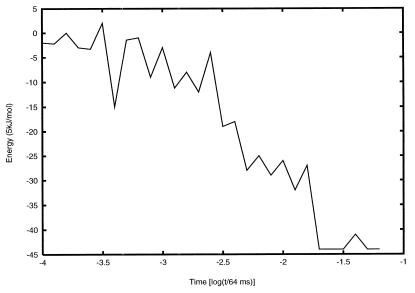
Fig. 1 presents the topography implied by the topological simulation for the dominant folding pathway of BPTI as it evolves from a random coil initial state. This particular pathway is derived from a tolerance level of 22%. This topography is significantly more conducive to folding than one based on a lower or zero tolerance level. A much higher tolerance level yields a topography that is too flat and not conducive to structure seeking. The effective pathway shown in Fig. 1 displays an overall monotonic decrease in energy with a large number of staircase-like steps, a clear signature of a good structure seeker. Initially a series of misfolded states is formed and dismantled with no discernible pattern. Subsequently, a series of staircase-like transitions lead to a native-like intermediate with low energy. This intermediate exists for an appreciable amount of time as it undergoes structural refinements, which eventually result in the formation of the native structure of BPTI accompanied by a large drop in energy.

Figure 1.

The effective PES inferred from the topological pattern formation process for BPTI, with a tolerance level of 22%.

A more complete understanding of the folding process requires knowledge of the alternative folding pathways accessible to a protein. One measure of the availability of alternative pathways as folding proceeds is the Shannon entropy, σ(t), associated with the time-dependent probability distribution over the ensemble of CPs (3, 8). Such entropy σ(t) is maximum if there is equal probability for the occurrence of all CPs, and zero if only one state is populated. This information-dependent criterion reinforces the importance of a multipath or funnel conceptualization of protein folding, which has largely replaced the earlier paradigm of unique folding pathways.

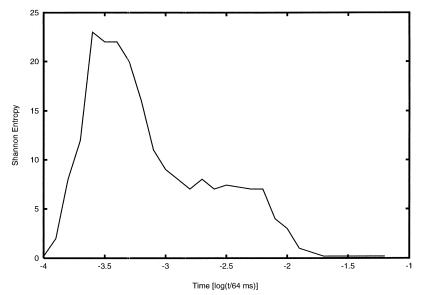
The complementary analysis of the PES topography and the Shannon entropy suggest that the folding of this BPTI model proceeds in several stages. Initially σ(t) is very large, indicating that the multitude of the possible folding pathways may dominate over the most probable one. Fig. 2 shows the time evolution of the Shannon entropy for a tolerance level for mismatches of 22%. Fig. 2 was generated from an ensemble of 98 pathways that led to pattern formation, following the digitized feedback algorithm (3, 7, 8). Fig. 2 shows that even on the coarse-grained scale of these time intervals, the folding process requires a multiplicity of pathways. In the next stage, the dismantling of misfolded states and consequent formation of structure is accompanied by a large reduction of σ(t). Eventually the protein finds its way downhill through a series of staircase transitions on the PES, forming in the process a native-like intermediate with constant σ(t). In the last stage, the structure of the intermediate is refined to form the native structure while the Shannon entropy drops to zero, consistent with a convergence of alternative folding pathways.

Figure 2.

The time dependence of the Shannon entropy during the topologically simulated folding process of BPTI, for a contact mismatch tolerance level of 22%.

Frustration Dependence of the Folding Pathways

Two types of mismatches may lead to frustration: torsional mismatches in which the torsional state of a residue differs from the consensus of the contact pattern and contact mismatches of the hydrophobic and polar residues. Here, for BPTI, we study only the influence of the latter type of frustration. As discussed above, the limit of zero-frustration tolerance requires perfect matching of all hydrophobic/hydrophobic contacts to allow the formation of a CP and the corresponding renormalization of the transition frequencies of its residues. The simulations carried out with this model fail to reach the native state of BPTI. Instead, partially folded states form and dismantle periodically as evidenced by periodic high-lying minima in the energy and σ(t). Clearly, imposition of overly rigid requirements for CP formation leads to a dramatic reduction in the number of correct pathways available to the protein. Making correct downhill steps toward the native structure requires exhaustive conformational searches and any secondary structure motifs that may form have a high probability of dismantling before they can grow or combine with other motifs to form tertiary structure.

The other limit of allowing an arbitrary amount of frustration is equally unacceptable because too many states are accessible and every conformation becomes equally likely. The amount of frustration that represents the behavior of a real protein must lie between these two limits. We have studied the folding properties of BPTI under our coarse-grained model at several intermediate levels of frustration tolerance to hydrophobic/polar contact mismatches. Two important conclusions emerge from these studies. First, the folding behavior of BPTI is insensitive to the specific functional expression for the frustration-dependent probability for a transition between two contact patterns as long as this probability is set to zero at some threshold level of frustration. Second, the folding of BPTI is reproducible and expeditious only within a narrow interval of frustration tolerance as expressed by the fraction of total contacts that represent hydrophobic/polar mismatches. Simulations with less than 20% tolerance show behavior qualitatively similar to that exhibited by the zero-frustration algorithm. Efficient and robust folding is achieved only if the frustration level is between approximately 20% and 30%.

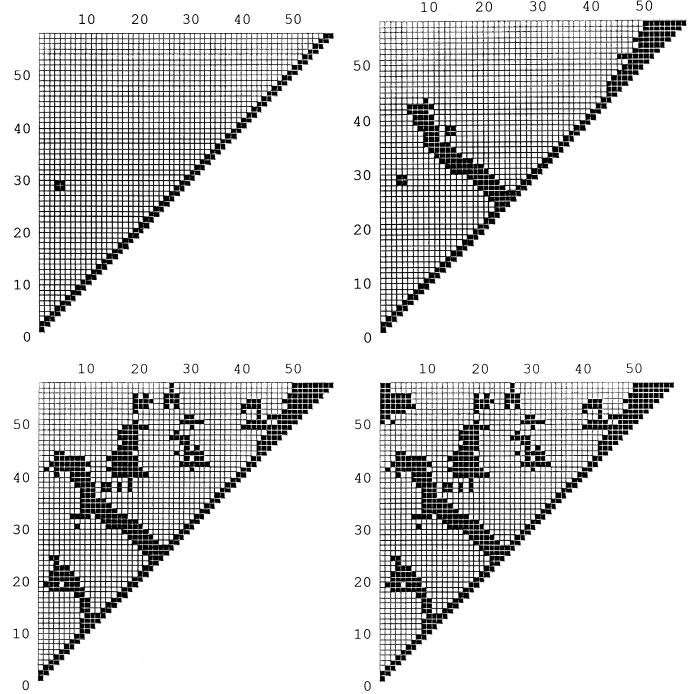
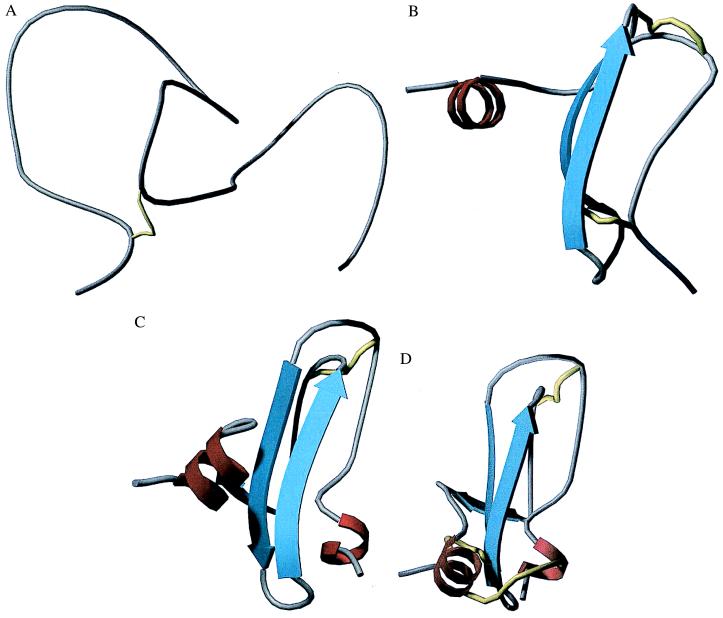
Fig. 3 shows a typical sequence of contact patterns, Fig. 4 shows the corresponding structures of intermediates along the dominant folding pathway of BPTI, for a tolerance level of 22%. All the patterns shown persisted for at least 100 pattern-recognition steps. The times at which these were taken, measured from initiation of folding, were 3.2 × 10⁻⁴ s, 1.3 × 10⁻³ s, 1.3 × 10⁻³ + 3.2 × 10⁻⁷ s, and 1.3 × 10⁻³ + 3.2 × 10⁻⁷ + 5 × 10⁻³ s. The structures shown were determined from local optimization, i.e., adoption of the local minima of the Ramachandran basins but without consideration of long-range nonbonded interactions. Although these structures, members of the class represented by the corresponding contact pattern, are made unique by local energy minimization, full global optimization, including all the long-range interactions, may yield multiple solutions. For example, basin 3, with a single minimum deriving from the local interactions, still is consistent with both a right-handed α-helical turn and a β-turn. The energetic distinction between these local motifs can be made only when the long-range interactions are included. The final contact pattern, the last in Fig. 3 (Lower Right), reproduces all the important features of the native folded structure, when it is compared with the structures retrieved from the Protein Data Bank.

Figure 3.

A typical sequence of contact patterns of structures along the dominant folding pathway of BPTI, at times given in the text, 3.2 × 10⁻⁴ s, 1.3 × 10⁻³ s, 1.3 × 10⁻³ + 3.2 × 10⁻⁷ s, and 1.3 × 10⁻³ + 3.2 × 10⁻⁷ + 5 × 10⁻³ s. This sequence was constructed with a tolerance level of 22%.

Figure 4.

Representations of the structures of BPTI at the four stages shown in Fig. 3. (A) Completely unfolded. (B) One β-sheet (represented by the strong counter-diagonal of Fig. 3, Upper Right) and a helical region (the upper right thick pattern in Fig. 3, Upper Right). (C) A nearly assembled structure. (D) The native structure, with the (5,55) disulfide bond formed.

Increasing the hydrophobic/polar mismatch tolerance dramatically transforms the PES landscape. On one hand, the choice of the tolerance limit affects to a different extent the forward and backward rates for transitions between the CPs and hence through the detailed balance principle affects the energy differences between the states on the landscape. On the other hand, the number of possible CPs greatly increases as new structural motifs with imperfect contact matching become possible. Therefore, the CP energies of runs with different levels of frustration are not directly comparable.

In the range of 30% to 40% hydrophobic/polar contact mismatches the active structure of BPTI is reached, but at a substantially slower rate because of the longer initial period of formation of misfolded structures. For tolerance levels higher than 40% no single final state can be reached reproducibly. Different runs reach different final states, frequently with energies lower than that of the native structure. Preliminary results of a detailed analysis of the compact states reached at high frustration levels suggest that some of these states are characterized by the formation of a non-native (5,30) disulfide bond with the concurrent breaking of the (30,51) and (5,55) disulfide bonds (made possible by the reducing solvent conditions implicit in this study). This flexibility allows the movement of the C-terminal helix, which then forms a tertiary interaction with the β-sheet region. The oblate native state thus is transformed into a globular structure, although the lower energy of the latter is likely an artifact of the model, and particularly of the topography implicit in the level of tolerance to frustrated hydrophobic/polar matches.

Thus, too low a tolerance level implies a topography with barriers so high that the system cannot move toward its native structure. Too high a tolerance level implies a topography too flat to focus the system toward a native structure. Between these limits lies a tolerance band within which the implicit topography has enough staircase character, with low enough barriers, to bring the system successfully to a native structure, and in fact at a rate consistent with those found from experiment.

The concept of a band or range of tolerance levels consistent with successful folding, and an associated range of topographies, carries with it a suggestion, possibly even an implication, regarding the relation between structure and function of proteins. The suggestion, by no means new here (13, 14), is that real proteins, by analogy with the model, have a range of structures that all can function adequately in an organism, albeit in ref. 13 on a finer scale of energies than here. This inference is entirely consistent with experiments that show a range of rates of activity for different samples of an enzyme (15, 16) and with variations among samples of myoglobin. It does caution us to avoid becoming locked to any concept of uniqueness of native structures.

This combination of methods will be described in full detail, with algorithms for their execution, in subsequent publications.

Abbreviations

BPTI

bovine pancreatic trypsin inhibitor

LTM

local topological matrix

R-map

Ramachandran map

CP

contact pattern

PES

potential energy surface