A model-based approach for assessing in vivo combination therapy interactions

Abstract

We present an approach for evaluating the efficacy of combination antitumor agent schedules that accounts for order and timing of drug administration. Our model-based approach compares in vivo tumor volume data over a time course and offers a quantitative definition for additivity of drug effects, relative to which synergism and antagonism are interpreted. We begin by fitting data from individual mice receiving at most one drug to a differential equation tumor growth/drug effect model and combine individual parameter estimates to obtain population statistics. Using two null hypotheses: (i) combination therapy is consistent with additivity or (ii) combination therapy is equivalent to treating with the more effective single agent alone, we compute predicted tumor growth trajectories and their distribution for combination treated animals. We illustrate this approach by comparing entire observed and expected tumor volume trajectories for a data set in which HER-2/neu-overexpressing MCF-7 human breast cancer xenografts are treated with a humanized, anti-HER-2 monoclonal antibody (rhuMAb HER-2), doxorubicin, or one of five proposed combination therapy schedules.

Assessing the efficacy of a combination of antitumor agents by analyzing in vivo tumor growth is an increasingly popular experimental design. However, analyses of tumor growth curves and of drug interactions are both complex statistical problems. Many methods for assessing growth address only a univariate summary, such as doubling time or tumor volume at an arbitrary endpoint, and either lack power or inflate the type I error rate (1). Multivariate methods that use the entire nonlinear growth curve are preferred (1, 2), but most published methods have been limited to linear growth models that may not be appropriate for long time courses or multiple-drug administration. No method of which we are aware has incorporated differences in drug administration time and/or order of drug administration in a statistical analysis comparing treatment schedules.

Another stumbling block in evaluating combination therapy is clearly defining additivity or summation of effect (also referred to as “independence”) (3). Antagonism or synergism is generally interpreted as an outcome that falls short of or exceeds, respectively, the effect expected from a purely additive interaction of individual drugs. There is, however, much debate as to how these quantities are to be calculated (4), and their definitions are often context and model dependent, particularly for nonlinear dose-effect relationships. Some definitions focus on addition of effects, whereas others consider the combinations of doses necessary to reach a preset effect. These definitions are not equivalent except, perhaps, when the system is linear. Consequently, there is no consensus on a quantitative definition of synergism and antagonism. Finally, most classical methods for assessing drug additivity (4–7) are designed only for a univariate measure of drug effectiveness and require experimental data at multiple doses to define the dose-effect relationship for each drug alone and their mixtures.

We present a model-based method to analyze the interaction of two drugs that uses tumor volume data in vivo over the complete time course of an experiment. We demonstrate our approach on data from a study in which 12 groups of mice with HER-2/neu-overexpressing MCF-7 breast carcinoma xenografts were treated with a single dose of rhuMAb HER-2, a humanized monoclonal antibody directed against HER-2 (8–10); a single dose of doxorubicin; or a combination of these agents given simultaneously or 1 or 4 days apart (see Table 1 for the schedule). Tumor volumes were followed for 28 days. With this experimental design, the time of administration and the order in which a combination is given, not the dosages, are critical features. Also, the “effect” measure for these data is not a single endpoint, as assumed by other methods, but rather a trajectory of tumor volumes (i.e., tumor volume over the entire 28-day follow-up period).

Table 1.

Treatment schedule

Group no.	Group code	Time of 1.0 mg/kg rhu MAb HER-2 administration, days	Time of 5.0 mg/kg doxorubicin administration, days
1	C	—	—
2	H0	0	—
3	H1	1	—
4	H4	4	—
5	D0	—	0
6	D1	—	1
7	D4	—	4
8	H0D0	0	0
9	H0D1	0	1
10	H0D4	0	4
11	H1D0	1	0
12	H4D0	4	0

Day 0 is 14 days after xenograft implantation. There were seven mice per group. 

Our approach is similar in spirit to work by Heitjan (2) in the use of a parameterized model for tumor growth and timing of a treatment effect coupled with statistical methods for fitting the growth model to population data. In our formulation, each drug’s effect on tumor growth is represented by an independent, additive term in a differential equation growth model. This representation leads to an unambiguous definition of additivity of effects, allowing for a direct method for detecting nonadditivity in the context of this model. We fit the growth model to data from each mouse receiving either a control solution or one drug alone (rhuMAb HER-2 or doxorubicin). We combine parameter estimates from these individual fits to develop population-based estimates for the effect of each drug alone on tumor growth. Using this population profile and our model, we predict the distribution of tumor volumes in mice receiving combination therapy under the null hypothesis of additivity. We assess statistically the differences between observed and expected growth trajectories over the complete time course of the experiment by using a novel distance measure.

Materials and Methods

MCF-7 human breast carcinoma cells, expressing wild-type levels of the HER-2/neu gene, were transfected with full-length cDNA of the human HER-2/neu gene as described (8), with the replication defective retroviral expression vector pLXSN into which the HER-2/neu cDNA was ligated. Stable HER-2/neu transfectants were selected for high-level HER-2/neu overexpression by using fluorescence-activated cell sorting with indirect immunofluorescence labeling mediated by murine monoclonal antibody 4D5 (Genentech) and anti-mouse IgG/FITC (Caltag, South San Francisco, CA).

HER-2/neu vector-infected MCF-7 cells were injected subcutaneously (s.c.) (1 × 10⁷ cells per xenograft) in the mid-back region of 4- to 6-week-old, female CD-1 (nu/nu) mice (Charles River Laboratories). One week before xenograft injection, all mice were primed with 17B-estradiol (Innovative Research of America) applied s.c. in a biodegradable sustained-release carrier binder (1.7 mg of estradiol per pellet) to promote tumor cell growth. Tumor volumes, calculated as the product of length, width, and depth in millimeters, were assessed twice weekly by serial micrometer measurements by a single observer. Fourteen days after tumor cell inoculation, when objectively measurable xenografts were confirmed, mice were randomly assigned to treatment groups (Table 1). There was no statistically significant difference in mean tumor volumes or mouse weights among groups at the start of treatment (single factor ANOVA). Doxorubicin (5 mg/kg; Cetus) and monoclonal antibodies (rhuMAb HER-2 and control solution IgG-1, provided by Mark Sliwkowski, Genentech) were given by i.p. injection (Table 1). Doses were based on individual mouse weights determined immediately before injection. Doxorubicin and rhuMAb HER-2 doses were based on independent dose-finding experiments conducted in our laboratory. The doxorubicin dose is near the MTD (maximal tolerated dose) for this strain of female athymic mice.

Growth/Drug Effect Model

We assume that tumors grow in accordance with a Gompertzian growth model (11). This is often used to model nonexponential growth of solid tumors for which relative growth rate decreases with increasing tumor size. In the absence of drug, tumor growth is given by the differential equation

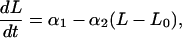1

where t is time, L is the natural logarithm of tumor volume, and L₀ is the logarithm of tumor volume when t = 0. In our application, the first measurement of tumor volume occurs 14 days after xenograft implantation, a time defined as t = 0. Parameter α₁ is the relative growth rate dL/dt when L = L₀, and α₂ is the nonnegative Gompertzian parameter governing the extent to which growth departs from simple exponential growth. When α₂ = 0, growth is purely exponential with rate constant α₁. When α₂ > 0, relative tumor growth decreases with increasing tumor size. Eq. 1 proved to be numerically more stable for estimating parameters in individual mice than the alternate parameterization dL/dt = α̃₁ − α₂L (where α̃₁ = α₁ + α₂L₀), as the correlation of regression estimates between α̃₁ and α₂ tended to be very high.

To account for each drug’s effect on tumor growth, the equation for unperturbed growth is augmented by a two-parameter negative “effect term” that decreases the relative growth rate starting at the time of the drug’s administration. When rhuMAB HER-2 alone is given at time t_h, the differential equation for time t ≥ t_h is represented by

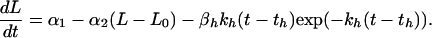2

The third term on the right-hand side starts at zero when t = t_h, reaches its greatest magnitude (proportional to β_h) at time 1/k_h after administration (i.e., at time t_h + 1/k_h), and then decays to zero near exponentially at rate constant k_h. In our application, this mimicking of the gradual onset of drug effect followed by an exponential washout was found to be somewhat superior to a model in which the drug’s maximal effect is at the time of its administration. There was no evidence to suggest a more complicated three-parameter model (e.g., a difference of two exponentials) would provide further improvement. If doxorubicin is given alone at time t_d, the differential equation for t ≥ t_d is

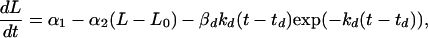3

with β_d and k_d the corresponding parameters for the magnitude and rate constant for the doxorubicin effect term. An analysis of preliminary dose-response data (not shown) indicated that β_h and β_d were roughly proportional to drug dose over the range of 1.0–3.3 mg/kg for rhuMAb HER-2 and 1.0–5.0 mg/kg for doxorubicin.

Our final model when both drugs are given is:

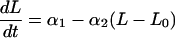4

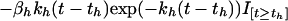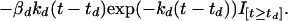Expressing the combined effect as the sum of the effect terms for Eqs. 2 and 3 defines our null hypothesis of additivity. This equation is shorthand for a set of discontinuous differential equations in which each drug effect term enters the equation at the time of that drug’s administration. Here, I is an indicator function, which is zero before an agent is given and unity after being given.

Statistical Methods

Parameter Estimates For Individual Mice.

We begin by obtaining estimates of model parameters for each individual mouse receiving at most one drug. For each mouse in groups 1–7, we fit the appropriate differential equation model to the logarithm of tumor volume by using the nonlinear least squares program bmdpar (12), constraining all parameters to be nonnegative. Data from each of the seven mice in group 1 were used to fit Eq. 1, yielding seven estimates of the three-parameter vector (L₀, α₁, α₂) and an asymptotic covariance matrix (i.e., the inverse of the information matrix) for each of these estimates. Eqs. 2 and 3 were fit to data from mice in groups 2–4 (rhuMAB HER-2 alone) and 5–7 (doxorubicin alone), respectively, yielding 21 estimates of the five-parameter vector (L₀, α₁, α₂, β_h, k_h), and 21 of (L₀, α₁, α₂, β_d, k_d) along with their corresponding 5 × 5 covariance matrices. We note that none of these mice yielded information on all seven of the parameters that comprise the complete model for combination therapy. As preliminary analysis of residuals for the fits of individual mice had suggested constant variance errors, we used unweighted least squares and estimated the mean squared error (MSE) for each mouse by the residual sum of squares divided by degrees of freedom.

Population Distribution of Model Parameters and Expected Trajectories.

To obtain the population distribution of parameters (i.e., the mean and covariance matrix for the full set of seven parameters), we combined individual parameter estimates from mice receiving control solution or one drug alone (groups 1–7) by using a suitably modified global two-stage (GTS) method (13). The iterative GTS method combines individual parameter estimates, weighting each individual estimate by a function of its covariance matrix. This method is more accurate than naïve data averaging or averaging of individual parameter estimates and is comparable to other approaches for the analysis of nonlinear mixed effect models (14), but it normally requires estimates for all of the parameters for each mouse. Our modification permits combining parameter estimates even when each mouse provides an estimate of only a subset of the full parameter vector. We were able to use the individual estimates of L̂₀, α̂₁, α̂₂ from all mice in groups 1–7, estimates of β̂_h and k̂_h from only those mice receiving rhuMAb HER-2 alone, and β̂_d and k̂_d from mice receiving doxorubicin alone to obtain the population distribution for all seven parameters in the growth model. Because inverses of covariance matrices (i.e., information matrices) are used to revise GTS population estimates, we augmented the original 3 × 3 (group 1) or 5 × 5 (groups 2–7) information matrices for each mouse to a full 7 × 7 matrix by setting to zero those rows and columns of the information matrix corresponding to the inestimable parameters. As calculations of the GTS algorithm are insensitive to the actual values of inestimable components of the parameter vector, we assigned a “placeholder” value of zero to parameters that were inestimable for a given mouse.

Using the population distribution of our model parameters calculated in this way, we obtained the population distribution of trajectories for tumor growth for each of the 12 groups. We approximated an expected response trajectory for each group (i.e., by the trajectory predicted by the model using the parameter vector evaluated at the population mean) and the population variability of trajectories as detailed below. For groups receiving combination therapy, we predicted the expected trajectory and population variability under the null hypothesis.

Distance Measure between Observed and Predicted Trajectories.

We developed a distance measure to assess the difference between the observed and expected trajectory for each mouse. For mice receiving at most one drug (groups 1–7), this distance is used as a measure of goodness-of-fit of the growth model. For combination-treated mice (groups 8–12), the distance is used as a statistical test for null hypotheses. We assume that tumor growth and response to the tested drugs follow the differential equation model in all mice, with mice differing only in their realization of the parameter vector, θ ≡ (L₀, α₁, α₂, β_h, κ_h, β_d, κ_d). The measured log tumor volume at the ith observation time t_i, is given by z_i = L(t_i, θ) + ɛ_i, where L(t_i, θ) is the true logarithm of tumor volume at time t_i and the measurement errors ɛ_i are assumed independent and identically distributed with mean zero and variance σ². Denoting the trajectory of N observations by z ≡ (z₁, … , z_N)^T, we define a nonnegative scalar distance measure between z and the predicted (expected) trajectory E(z):

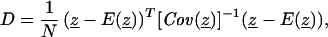5

where Cov(z) is the covariance matrix of z. Qualitatively, D is the average squared deviation between observed and predicted log tumor volumes for a mouse, weighted inversely by combined population and measurement variability. Letting y(θ) ≡ (L(t₁, θ), … , L(t_N, θ))^T and μ̂ and Ĉ denote the estimated population mean and covariance matrix of θ, respectively, we used y(μ̂) as the first order Taylor approximation for E(z) and (dy/dθ) Ĉ(dy/dθ)^T + σ²I as the approximation for Cov(z). σ² was estimated by averaging the MSE’s for mice in groups 1–7. Under the assumption of correct specification of the growth model and distribution of z, the expected value of D is 1, and D⋅N asymptotically follows a χ² distribution with N degrees of freedom (df). As a large D does not indicate whether tumor volumes tended to be much larger or smaller than expected, we used a signed distance measure (D_s) for graphical purposes. A (+) or (−) sign was assigned to D depending on whether the majority of observed trajectory points were, respectively, greater or less than their expected value. In all cases, we could make an unambiguous assignment of sign, as the number of observations above and below the predictions were unequal. When the D value was sufficiently large to reject additivity (see below) the number of observations above and below differed by at least 3. In the majority of these cases all or all but one of the observations for a mouse were on the same side of the expected trajectory.

For each mouse receiving combination therapy (groups 8–12), we calculated a D value, comparing that mouse’s observed data to the expected trajectory for its group under the null hypothesis of additivity. We calculated an additional D value comparing observed tumor volumes to the expected effect had the more effective agent (rhuMAb HER-2) been given alone. For this second hypothesis, the predicted trajectory for groups 8, 9, and 10 is identical to the predicted trajectory for group 2, as each of these groups received rhuMAb HER-2 on day 0. Similarly, the predicted trajectory for groups 11 and 12 is equivalent to the trajectory for groups 3 and 4, respectively, matching groups based on the time they received rhuMAb HER-2. For either null hypothesis, a distance greater than the 95th percentile of the χ²/df distribution provides evidence to reject the tested null hypothesis at the 0.05 level of significance for that mouse. For a trajectory sampled at N = 9 times (as was the case for all but 1 mouse), this critical region is D_s ≤ −1.88 (evidence for superadditivity or synergy of drug effect) or D_s ≥ 1.88 (evidence for subadditivity).

To combine individual statistics into a single hypothesis test, we summed D⋅N values for all mice in each group and compared this sum to a χ² distribution with df equal to the sum of the individual df values. This approach yielded group P-values comparable to those obtained by Fisher’s method (15) for combining tests of the individual D_s values. We note that a significant group P-value simply indicates that the set of trajectories is not consistent with the null hypothesis. This could be attributed to heterogeneity of response in which subsets of mice have patterns of deviation different from the expected distribution of trajectories. The use of a group P-value is particularly advantageous when trajectories show the extremes of heterogeneity, as it avoids such anomalies as combining a significantly positive D_s and a significantly negative D_s value and incorrectly concluding a nonsignificant result from the average D_s. A cross-validation check was performed to assess the fits for groups 1–7 and the empirical distribution of D values. The cross-validation D value for each mouse in a group was based on the reestimated population mean and covariance matrix (μ̂ and Ĉ) and pooled estimate of σ² using individual fits of mice only from the remaining 6 groups.

Results

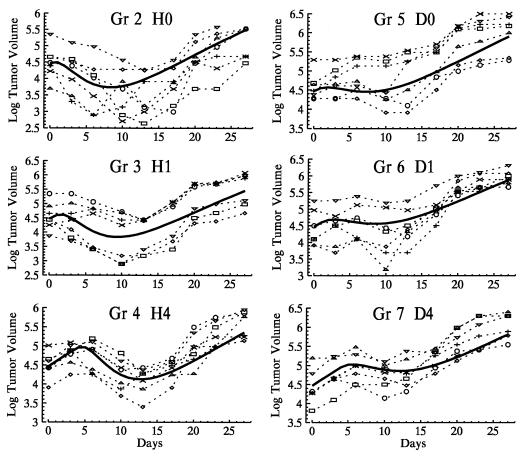
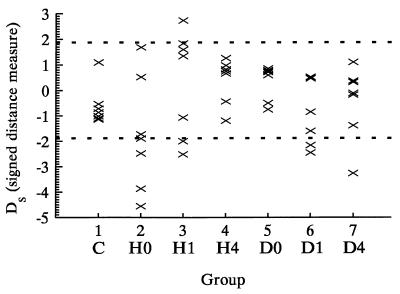
Fig. 1 shows the observed and expected trajectories of the logarithm of tumor volumes for mice receiving one drug (groups 2–7). Each expected trajectory captures the characteristics of the observed trajectories, and the generally small signed distance measures between observed and mean trajectories under cross-validation (Fig. 2) suggest a close fit of the model and adequacy of our first order approximations. The empirical distribution of the cross-validated D⋅N statistics for groups 1–7 was slightly shifted to the right of the asymptotic theory χ² distribution (1-sided P = 0.04, Kolmogorov test). This discrepancy appeared to be due primarily to group 2 (Kolmogorov test P = 0.4 with group 2 removed). Analyses with and without group 2 included were similar and qualitative conclusions were identical. Inclusion of group 2 tended to produce more conservative results (larger P-values), and only these analyses are reported.

Figure 1.

Tumor volumes for groups receiving the single agents doxorubicin or rhuMAb HER-2 at the times indicated in Table 1 (groups 2–7). Symbols connected by dashed lines are the observed natural log tumor volumes for each mouse. The solid line is the expected trajectory for the group predicted by the growth/drug effect model using the population mean parameter vector.

Figure 2.

Signed distance measure D_s for the deviation between individual observed tumor volume trajectories and the expected model-based trajectory for groups 1–7 under cross-validation. The dashed lines are the boundary of the α = 0.05 critical region for D based on a χ²/df statistic with 9 df.

The estimated mean for our Gompertzian parameter α₂ was statistically greater than zero (Table 2), indicating that the tumors show slight departures from purely exponential growth, with relative growth decreasing with increasing tumor volume. The proportionality constants for the effect of rhuMAb HER-2, β_h, and doxorubicin, β_d, are both significantly greater than zero, indicating that each agent alone has an effect on tumor volume. Furthermore, the population mean ± SE for β_h/β_d is 1.88 ± 0.1, showing that peak strength of the rhuMAb HER-2 effect on tumor volume is almost twice that of doxorubicin at doses used here. The population means for k_h and k_d are close, indicating that these agents have comparable durations of action, with peak rhuMAb HER-2 effect at a mean of 3.0 ± 0.2 days after administration, compared to 4.1 ± 0.2 days for doxorubicin.

Table 2.

Estimates of population parameters

Parameter	Population mean (asymptotic SE)	Population SD
L0	4.4691 (0.0626)	0.4158
α1 (days−1)	0.1274 (0.0077)	0.0391
α2 (days−1)	0.0235 (0.0046)	0.0106
βh	0.8124 (0.0433)	0.1483
kh (days−1)	0.3279 (0.0203)	0.0945
βd	0.4311 (0.0311)	0.1589
kd (days−1)	0.2453 (0.0131)	0.0499

Pooled estimated of σ² was 0.04907. 

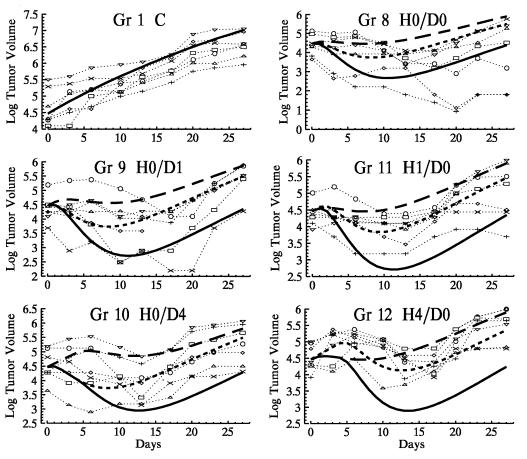
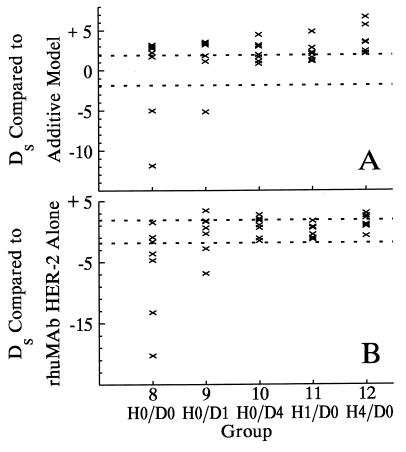
Fig. 3 shows observed trajectories for mice receiving combination therapy, along with the expected trajectories predicted by the model for combination therapy under the null hypothesis of additivity. The expected trajectories had each drug been given alone (and at the same time as it was given as part of the combination therapy) are shown for comparison. D_s values calculated by comparing observed trajectories in groups 8–12 to the mean trajectories predicted for combination therapy under additivity are given in Fig. 4A. From our group statistic, the null hypothesis of additivity can be rejected for each of groups 8 through 12 (each P < 0.0001). Fig. 4A shows that for group 8, this rejection of additivity is due to heterogeneity of response, as two tumors are significantly smaller than expected (i.e., superadditive drug effects), whereas four of the remaining five are significantly larger than expected, showing subadditivity. Group 9 also shows some heterogeneity of response, with one tumor significantly smaller than predicted under additivity, three consistent with additivity, and three larger than expected. Compared to additivity, all mice in groups 10–12 have positive D_s values, indicating larger than predicted xenografts and providing evidence for subadditivity.

Figure 3.

The symbols connected by dotted lines are the observed trajectories for mice receiving combination therapy (groups 8–12). The solid line is the expected tumor volume trajectory for combination therapy under the null hypothesis of additivity. The upper long-dashed line is the expected effect had doxorubicin been given alone; the short-dashed line is the expected effect had rhuMAb HER-2 been given alone. Observed trajectories and the expected trajectory for the control group (group 1) are shown for reference.

Figure 4.

D_s values reflecting the deviation between individual observed tumor volume trajectories for mice receiving combination therapy and the expected trajectory under the hypotheses of an additive model (A) or if rhuMAb HER-2 had been given alone (B). Positive or negative values indicate the majority of observations for a particular mouse are greater than or less than, respectively, the expected trajectory for that hypothesis. Individual D_s values outside the inner region marked by the horizontal dashed lines are significant at the α = 0.05 level.

This evidence for subadditivity does not necessarily exclude the possibility that combination therapy may still be more effective than treatment with a single agent. We therefore compared the observed trajectories from mice receiving combination therapy to the expected trajectories had the single more effective agent (rhuMAb HER-2) been given alone (Fig. 4B). From group statistics, groups 8 (P < 0.0001), 9 (P < 0.0001), 10 (P = 0.003), and 12 (P = 0.0009) are significantly different from treatment with rhuMAb HER-2 alone, whereas group 11 cannot be distinguished from rhuMAb HER-2 alone (P = 0.6).

From both analyses, we see that when both agents are administered simultaneously (group 8), two tumors respond superadditively, two are smaller than expected had rhuMAb HER-2 been given alone, and three are consistent with rhuMAb HER-2 alone. When rhuMAb HER-2 is given 1 day before doxorubicin (group 9), one tumor shows a superadditive response, one is smaller than expected had rhuMAb HER-2 been given alone, four are consistent with rhuMAb HER-2 alone, and one is significantly larger than expected from either null hypothesis. When doxorubicin is given 1 day before rhuMAb HER-2 (group 11), the effect of combination therapy cannot be distinguished from the effect of rhuMAb HER-2 alone. In groups 10 and 12, where the time between rhuMAb HER-2 and doxorubicin administration is maximal, drug subadditivity may be strong enough in five mice to obscure even the action of rhuMAb HER-2.

Discussion

Finding the optimal combination therapy treatment schedule from in vivo tumor volume data when drugs are given at different times and in various orders encompasses two distinct statistical issues. The first issue is how to compare entire tumor volume curves (trajectories) in a manner that takes the time and order of administration into account. The second arises in determining the nature of the interaction between the combined drugs. In particular, one needs to define what it means for two drugs to act independently (i.e., additivity), so that synergism and antagonism can be clearly interpreted. Our combined modeling and statistical methodology addresses both of these issues and potentially has broad application for the analysis of in vivo drug combination data in a variety of fields.

The model-based approach accounts for differences in timing and order of drug administration, both when individual mice are fit and when expected trajectories are predicted for a group. The advantages offered by our method for comparing entire individual growth curves using the group statistic and individual D_s statistics include (i) increased power over methods that use only univariate summaries of data, (ii) avoiding problems associated with naïve pooling of data across mice (13, 14), (iii) providing a means for recognizing heterogeneity of responses, and (iv) permitting the use of mice with missing data points (such mice still yield individual parameter estimates, though the fits may be less informative for the population summary). As demonstrated, our method also allows comparison of responses to several null hypotheses, i.e., additivity versus equivalence to one drug alone.

The use of a combined growth and drug effect model provides a formal means for defining additivity of response to drug combinations, relative to which synergism and antagonism can be interpreted. Central to our approach is the underlying differential equation growth model in the absence of treatment (Eq. 1) and evidence from fits to groups 2–7 and dose-response data that growth in the presence of each drug alone is well represented by the addition of a single drug effect term to the tumor growth model (Eq. 2 or Eq. 3). For combination therapy, the use of the additive drug effect term for each agent defines the null hypothesis of additivity or independence between agents. Significant departures from this model provide evidence for a drug interaction beyond simple summation, with tumors generally smaller than expected indicating superadditive responses and tumors larger than expected showing subadditive responses. In our example, there was little ambiguity in assigning a sign to D_s for large D values as nearly all observed points were on the same side of the expected curve. However, other applications may require alternate means of categorization, e.g., greater weighting of terminal points in determination of sign.

The terms describing each of the two drug’s effects have an onset period, rise to a maximum effect, and then wear off. As this is an empirical formulation, it would be premature to lend a pharmacokinetic or mechanistic interpretation to this aspect of the model. The observed lag between the time of drug administration and peak tumor effect might be due to a variety of nonpharmacokinetic factors, for example, receptor and signalling kinetics or time needed for resorption of killed tumor cells.

The observed heterogeneity of response to treatment might be missed by approaches that only look at group statistics. Though the null hypothesis of additivity was rejected for each combination therapy group in this study, consideration of individual mice demonstrates a wide range of tumor responses, particularly when both agents are given simultaneously. The trends we observed considering both individual and group responses strongly suggest that timing and order of administration are both crucial, with simultaneous coadministration being optimal in this case.

Although superadditivity is straightforward to interpret as a synergistic response (i.e., drug effect greater than expected from additivity), the results in Fig. 4 highlight the complexity of interpreting subadditivity. Subadditivity simply means a failure to reach a response that is fully additive and does not preclude the possibility that the combination is clinically more beneficial than one drug alone. However, if the subadditivity is severe enough to block the response expected from the more effective single agent alone (e.g., as seen in some mice in groups 9, 10, and 12), then interpretation as an antagonistic interaction may be justified.

Our methodology is a way of comparing time course data while accounting for the time and order of drug administration and may have wider applicability for quantifying drug interactions in vivo. The addition of drug effect terms to a Gompertzian growth model has the potential to represent a broad class of in vivo responses (2). Although our model was derived empirically for dose/response kinetics consistent with data for two specific agents, it may be applicable directly to other drug combinations, perhaps only with adjustment of the form of the drug effect terms. However, the basic method of modeling tumor growth in the presence of control or one drug alone for each individual, combining parameter estimates to obtain group statistics and then comparing observed and predicted responses using the methods developed here may be a generally useful tool for analyzing combination therapy. The assumptions and definitions underlying this model-based approach are potentially testable, and this may allow for clearer quantification and interpretation of the complex concepts of synergism, additivity, and antagonism for in vivo tumor models.

Abbreviation

GTS

global two-stage