Population Structure and Inbreeding From Pedigree Analysis of Purebred Dogs

Abstract

Dogs are of increasing interest as models for human diseases, and many canine population-association studies are beginning to emerge. The choice of breeds for such studies should be informed by a knowledge of factors such as inbreeding, genetic diversity, and population structure, which are likely to depend on breed-specific selective breeding patterns. To address the lack of such studies we have exploited one of the world's most extensive resources for canine population-genetics studies: the United Kingdom (UK) Kennel Club registration database. We chose 10 representative breeds and analyzed their pedigrees since electronic records were established around 1970, corresponding to about eight generations before present. We find extremely inbred dogs in each breed except the greyhound and estimate an inbreeding effective population size between 40 and 80 for all but 2 breeds. For all but 3 breeds, >90% of unique genetic variants are lost over six generations, indicating a dramatic effect of breeding patterns on genetic diversity. We introduce a novel index Ψ for measuring population structure directly from the pedigree and use it to identify subpopulations in several breeds. As well as informing the design of canine population genetics studies, our results have implications for breeding practices to enhance canine welfare.

THE domestic dog (Canis lupus familiaris) is important for many economic and social reasons and has recently become increasingly prominant as a model species for human disease. Purebred dogs have been successfully used as models for human Mendelian disorders, such as narcolepsy (Lin et al. 1999; Boehmer et al. 2004) and hereditary kidney cancer (Nickerson et al. 2002; Comstock et al. 2004). Advantages of dogs as models for human disease include substantial genomic homology with humans: although dogs are further from humans than mice on a phylogenetic tree, they are nevertheless genomically more similar because of their larger generation time. Dogs in population studies are often exposed to similar environments to those of their human owners and, like humans, they can be studied using population case–control designs, without the expense and ethical concerns raised by keeping study animals in laboratories. Many diseases affecting dogs have high prevalence in one or a few breeds, such as Addison's disease, common in Portuguese water dogs (Chase et al. 2006), interstitial lung disease in West Highland white terriers (Norris et al. 2005), and dermoid sinus in ridgeback dogs (Salmon Hillbertz et al. 2007). This raises the hope that causal variants that are rare overall may be concentrated in specific breeds and thus easier to map than the corresponding human variant. For these reasons, dogs have been proposed as a model for a number of complex human diseases, such as autoinflammatory diseases (Puppo et al. 2006), cancer (Khanna et al. 2006), and retinitis pigmentosa (Guyon et al. 2007).

Following the canine genome sequence (Lindblad-Toh et al. 2005), two single-nucleotide polymorphism (SNP) chips have recently been commercially released, each representing a set of ∼26,000 SNPs chosen for accuracy and uniform genome coverage (Lindblad-Toh 2007). The first genomewide population association study in dogs has now emerged (Karlsson et al. 2007) and many more are expected.

Population structure is an important factor in genetic association studies and can lead to spurious associations (Cardon and Palmer 2003; Marchini et al. 2004; Clayton et al. 2005). Although methods are now available to diagnose and correct for population stratification from genomewide marker data, it is desirable for researchers to be aware of potential stratification before embarking on such studies. The breed structure of dogs is well recognized, but the extent to which there might be additional population structure within dog breeds has not been extensively investigated. The breeding programs implemented by dog breeders, including use of “popular” sires, could lead to cryptic population structure. In many species, population structure is studied at a geographic level: for example, allele frequencies are compared in different lakes or valleys or in regions or nations. Dog breeding patterns, however, can be driven by stud value assessed by behavior when shown and by conformance to breed standards. Because of such factors, together with artificial insemination and international dog shows, geography may be less relevant for purebred dogs than for other species. Population structure is a property of the underlying pedigree, whether observed or not and whether or not it is aligned with geographical units. We develop novel approaches for investigating population structure directly, without genotyping.

Some studies of canine pedigrees have appeared (Cole et al. 2004; Leroy et al. 2006), but we propose a more extensive study in terms of both pedigree size and analyses adopted, particularly the novel analyses of population structure. We use pedigrees from the United Kingdom (UK) Kennel Club (KC), the oldest dog fanciers club in the world. Since its foundation in 1873, the KC has compiled a dog registration database, which has become the most comprehensive record of UK dog breeds and is among the largest canine pedigree records internationally. Registration records are available in electronic form since about 1970, and we analyze these for a selection of 10 breeds, to assess levels of inbreeding and population structure. Since this database has not been described elsewhere in the scientific literature, we also analyze demographic parameters such as offspring counts and generational imbalance between mates and compare these across breeds.

METHODS

Data:

The electronically recorded part of the KC database includes 5.7 million dogs from 207 breeds registered up to the end of 2006, with a median of 3443 dogs per breed. We chose 10 breeds for analysis (Table 1), including at least two representatives of the four main breed groups identified from genetic analysis (Parker et al. 2004; Parker and Ostrander 2005). We also sought to include the most popular breeds in the UK and major breeds that originated in the UK. Greyhounds are a special case, because the KC database does not include most greyhounds bred for racing. The Akita Inu is also special in that the breed was introduced into the UK since the advent of electronic records, and so the pedigree analyzed here spans the entire history of the breed in the UK.

TABLE 1.

Breeds included in the study, with pedigree size and the numbers of sires, dams, and founders

Breed	Breed group	No. dogs	No. sires (% of males)	No. dams (% of females)	No. founders
Akita Inu	Oriental	21,155	1,329 (13)	2,115 (20)	223
Boxer	Mastiff	195,358	8,518 (9)	24,601 (25)	4,032
English bulldog	Mastiff	46,420	2,175 (11)	7,660 (36)	882
Chow chow	Oriental	18,386	928 (11)	2,597 (27)	1,012
Rough collie	Shepherd	83,864	4,190 (11)	13,232 (30)	5,285
Golden retriever	Hunting	317,527	7,752 (5)	28,963 (18)	6,932
Greyhound	Shepherd	1,060	103 (21)	159 (28)	81
German shepherd dog	Shepherd	474,078	21,629 (9)	48,108 (20)	15,843
Labrador retriever	Hunting	703,566	26,830 (8)	70,541 (20)	15,064
English springer spaniel	Hunting	276,179	17,471 (13)	34,252 (24)	9,718

The breed group refers to the four groups identified by Parker et al. (2004).

The database records for each dog its registration number, the registration number of both parents, the date of birth, the number of littermates born and the number subsequently registered, and the coat color. Only the registration numbers of dog and parents are used in the present analyses. Four dogs, all Labrador retrievers, were recorded both as a sire and as a dam and have been eliminated from our analyses. Individuals with both sire and dam missing are assumed to be founders, but 0.05% of dogs have exactly one parent recorded, which unequivocally indicates missing data. This proportion is highest in the chow chow and the collie (0.13% in each case).

Generation number:

The generation number (GN) of an individual has been defined (Thompson 1986) as one plus the maximum GN of its parents, with founders assigned GN = 0. However, because dog pedigrees have many overlapping generations, we prefer to follow Brinks et al. (1962) and define the GN of the ith nonfounder in each breed to be

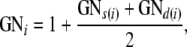where s(i) and d(i) denote the sire and dam of i. Thus, when parental GN values differ by more than two, which holds for >5% of matings in our pedigrees, the offspring GN will be less than the GN of one of the parents. We round GN to integer values where convenient. If only one parent is missing, that parent is assumed to have GN = 0.

Inbreeding and diversity:

The inbreeding coefficient f_i for the ith dog is the probability that its two alleles at a locus descend from the same ancestral allele within the pedigree. It also equals (Cannings and Thomas 2007) the kinship coefficient of s(i) and d(i). The value of f_i depends on the available pedigree: common ancestors of s(i) and d(i) not recorded in the pedigree do not contribute to f_i. In effect, all founders are assumed to have f = 0, which is unrealistic because the history of most breeds extends beyond the founders in the KC database. The dependence of f_i on the available pedigree is undesirable in general, for example, because different dogs may have the same underlying level of inbreeding but have different f-values because of different numbers of ancestors recorded in the pedigree. However, this problem is minimal for the KC pedigrees studied here, which have few missing data and are of relatively uniform depth. To minimize the effect of pedigree time depth, we report average f values only for dogs in generations 6 and 7.

We used “Meuw” in the Pedig package (Boichard 2002) to calculate f_i, which implements the algorithm of Meuwissen and Luo (1992), on the basis of the formula of Wright (1922),

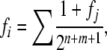(1)

where the sum is over all inbreeding loops in the pedigree of i. An inbreeding loop consists of a pair of nonoverlapping ancestral lineages from s(i) and d(i), respectively, up to a common ancestor j, and n and m are the numbers of meioses in the lineages from s(i) and d(i) to j.

In a random-mating population of N/2 male and N/2 female breeding adults, the average inbreeding coefficient is expected to increase by ∼1/N in each generation after the first. We use this relationship, together with the average increase in f per generation up to generation 5, to compute an inbreeding effective population size (N_e) for each breed.

We compare the average inbreeding coefficient f with the kinship coefficient, also computed using Pedig (Boichard 2002), averaged over all pairs of individuals in the final two generations represented in each breed. Under random mating, average kinship and average f are similar. Any discrepancy between the two reflects a difference between the relatedness of mate pairs from that expected under random mating and hence provides a measure of the tendency to consanguinous matings within a breed.

The genetic diversity among founders that is retained over the time depth of the pedigree is also reported, which is equivalent to the ratio of effective to actual numbers of founders (Lacy 1989). Specifically, we estimate from simulations the probability that an allele chosen at random from a founder would be represented by a copy in generation 6. We found through simulations that for a random-mating population with a large, constant size, this probability is close to 25%. A low proportion of genetic diversity is retained under strong inbreeding or when reproductive success is highly variable across individuals.

Population structure:

Informally, population structure corresponds to disjoint sets of ancestors having less overlap in their corresponding sets of descendants than would be expected under panmixia. The most extreme case would arise if there exist sets of ancestors that have no descendants in common: this would correspond to completely isolated subbreeds. Below, we use “descendant” to mean an individual having no recorded offspring and whose GN value is within two of the maximum GN for the breed. In addition, we consider only one member of any (full) sibship. We use “ancestor” to mean a founder with at least one descendant.

The ancestor–descendant relationships within a breed can be represented by a bipartite graph, with sets of nodes A and D corresponding to ancestors and descendants and arcs from A to D representing their relationships. Population structure corresponds to subsets A′ ⊂ A and D′ ⊂ D such that there are many arcs from A′ to D′ and few arcs from A′ to D\D′ or from A\A′ to D′, where “many” and “few” are relative to expectations under random mating. Methods for identifying “community structure,” that is, tightly linked components of general graphs that are partly isolated from the rest of the graph, have been reported in the study of social networks (Girvan and Newman 2002, 2004). These methods are not appropriate for the special features of pedigree analysis, in particular the need to assess relatively weak population structure, and we explore here some novel approaches.

First we considered some graphical methods of identifying within-breed population structure. We applied principal-components analysis on the basis of the ancestor/descendant incidence matrix that has 1 in row i and column j if j is an ancestor of descendant i and 0 otherwise. Thus, the descendants are treated as individuals and the ancestors as binary variates. Informally, the first few principal components correspond to sets of ancestors such that descendants tend to have either many or few ancestors in each set. We also applied multidimensional scaling, which is a related technique that tries to find the best representation of distances between all pairs of descendants; we used one minus the kinship coefficient to measure the “distance” between two individuals. Both these techniques lead to plots that can be inspected visually for apparent population structure.

To obtain a quantitative measure of population structure, we applied K-means clustering to identify K = 2 clusters of descendants having maximal common ancestry. We used the kmeans algorithm in R ( R Development Core Team 2007). For each cluster, the mean value for ancestor j is the proportion of descendants in the cluster having j as an ancestor. Strong population structuring corresponds to widely separated mean values in different clusters, so that each cluster has a very different pattern of ancestry.

To quantify the level of clustering, after the K-means algorithm converged, we assumed that the vector of counts of descendants of ancestor j in each cluster has the beta-binomial distribution with parameters N_j, λp, and λ(1 − p), where N_j denotes the total number of descendants of j, and p is the proportion of all descendants that are in the first cluster. This distribution has

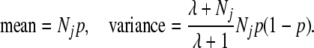The beta binomial reduces to the binomial in the special case λ = ∞, which corresponds to the descendants of j being allocated independently to clusters, with probability proportional to cluster size. Finite values of λ correspond to a positive correlation in the cluster memberships of different descendants. Thus, λ measures the effect of population structure and is the focus of our interest. We estimate λ via maximum likelihood (Balding 2003), treating the cluster memberships of descendants of different ancestors as independent. Because mates can have many descendants in common, we performed analyses separately for male and female ancestors. However, the independence assumption may still not be strictly valid, so that the 95% credible intervals reported below, based on a uniform prior, should be regarded as approximate.

By implementing the transformation

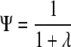we obtain a value between zero and one that we call the “pedigree structure index.” Ψ is analogous to F_st, the classical measure of population differentiation (Excoffier 2007). The value Ψ = 1 means that different clusters of descendants have no ancestors in common, while Ψ ≈ 0 indicates that the overlap in the ancestors of different clusters could have arisen from a random assignment of ancestors to descendants. Since the K-means clustering algorithm can by chance identify some apparent clustering, even in the absence of population structure, we very rarely obtain Ψ = 0. To investigate this effect, we randomly permuted the columns of the ancestor/descendant incidence matrix for the smallest and largest breeds (greyhound and Labrador retriever), each 1000 times, and estimated Ψ for each resulting data set. Thus, Ψ should be small, but it will be nonzero because the K-means algorithm may identify some apparent clustering. We also tested our algorithm by applying it to two distinct breeds analyzed as if a single breed.

RESULTS

Pedigree size and complexity:

A total of 2.1 million dogs were studied in 10 breeds (Table 1), ranging in size from the greyhound (∼1000) to the Labrador retriever (∼700,000). The maximum GN value ranged from 5.9 in greyhounds up to 9.0 in the German shepherd, with an average over the 10 breeds of 8.0. A measure of the complexity of pedigrees is given by the number of cross-generation matings and the magnitude of the generational differences. In 19% of Akita Inu matings, and 16% of bulldog matings, the GN of the mates differs by ≥2, and in 7% of matings in both breeds the GN difference between mates was ≥3. The lowest rate of GN imbalance among mates was in the golden retriever, with 4% of mates having GN differing by ≥2. In every breed, the GN of the dam on average exceeds that of the sire (i.e., the dam tends to be younger), but there were also many instances of the sire having a larger GN than the dam. The greatest mean difference in the GN of mates is just over 0.5, in the Akita Inu.

Offspring distribution:

Around 20% of dogs have a recorded offspring (Table 2). Popular sires (defined here as >100 recorded offspring) are evident in all breeds except greyhound. Golden retrievers have the largest proportion of popular sires (10%) and conversely the lowest proportion (5%) of male dogs that are sires (Table 1). Other than the greyhound, the Akita Inu has the most even distribution of reproductive success: the lowest proportion of popular sires (1%) and the highest proportion (13%) of male dogs that are sires. Highly prolific dams (>40 offspring) are concentrated in three breeds: German shepherd, golden retriever, and Labrador retriever. Most dams have just one litter recorded.

TABLE 2.

Distribution of numbers of offspring per sire and per dam, numbers of popular sires (≥100 offspring) and popular dams (≥40 offspring), and percentage of all sires and dams that are “popular”

	Sire offspring		Popular sires		Dam offspring		Popular dams
Breed	Maximum	Median	No.	%	Maximum	Median	No.	%
Akita Inu	306	9	16	1	52	8	4	0.0
Boxer	1101	8	372	4	49	6	25	0.0
English bulldog	430	9	77	4	36	5	0
Chow chow	212	8	22	2	35	5	0
Rough collie	775	7	128	3	39	5	0
Golden retriever	1386	10	792	10	59	8	328	1
Greyhound	45	7	0		17	5	0
German shepherd dog	1479	8	851	4	67	7	509	1
Labrador retriever	1911	9	1338	5	72	8	639	1
English springer spaniel	2538	7	271	2	62	6	89	0.3

Inbreeding and diversity:

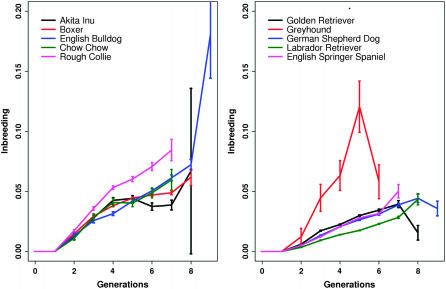
Figure 1 shows average values of the pedigree inbreeding coefficient f over generations. As GN increases, there are additional generations of ancestors recorded and so f tends to increase. All breeds show a roughly constant increase over generations, indicating little change in mating patterns, except for the final generation that may be atypical because most eventual members of this generation are not yet recorded.

Figure 1.—

Inbreeding coefficients averaged over dogs with the same GN value, rounded to the nearest integer. The vertical bars represent ±1 standard error of the mean.

Greyhounds have a high average value of f up to generation 5, but there are no highly inbred greyhounds (Table 3). Further, the average kinship is also high, so that the high average f can be largely attributed to small population size rather than a practice of consanguinous matings. Since there are only 16 greyhounds in generations 6 and 7, we ignore them in the following discussion.

TABLE 3.

Inbreeding, kinship, and effective population

	Dogs in generations 6 and 7
Breed	N	Mean f	% > 0.1	Maximum f	Ne	Mean kinship	% survival 6 generations
Akita Inu	2,864	0.038	9.0	0.32	45	0.023	30
Boxer	44,521	0.048	16	0.50	45	0.017	11
English bulldog	12,396	0.057	18	0.41	48	0.038	17
Chow chow	1,747	0.051	19	0.38	50	0.028	6.2
Rough collie	4,650	0.073	29	0.38	33	0.020	2.9
Golden retriever	31,259	0.035	8.2	0.39	67	0.013	6.3
Greyhound	16	0.058	0	0.08	17	0.072	6.5
German shepherd dog	43,488	0.033	12	0.47	76	0.014	5.6
Labrador retriever	97,884	0.024	5.2	0.39	114	0.012	9.2
English springer spaniel	23,721	0.033	6.0	0.38	72	0.017	8.0

Columns 2–4 describe the pedigree-based inbreeding coefficient f of dogs in generations 6 and 7 (5.5 ≤ GN ≤ 7.5): number of dogs, mean f, and percentage of dogs with f > 0.1. Column 5, maximum f over all dogs in breed; column 6, inbreeding effective population size of breed calculated from the average increase in f over generations 1–5; column 7, average kinship over all pairs of dogs in the final two generations represented in each breed; column 8, percentage of singleton founder alleles expected to survive until generation 6.

Every other breed includes some highly inbred dogs, the most inbred being four boxers each with f = 0.5 (Figure 2). Bulldogs have an extremely high mean f in generation 9 (Figure 1), but most breeds do not have a ninth generation for comparison. When averaged over generations 6 and 7 (Table 3), f is highest in collies, with almost 30% of collies in these generations being highly inbred (f > 0.1). Mean kinship among collies is not elevated, at 0.020, and so the high level of inbreeding appears to represent a pattern of consanguinous matings in the collie. In contrast, the Akita Inus have a higher mean kinship at 0.023, reflecting their small population size, yet this breed has relatively low values of f, which could reflect a pattern of inbreeding avoidance by Akita breeders.

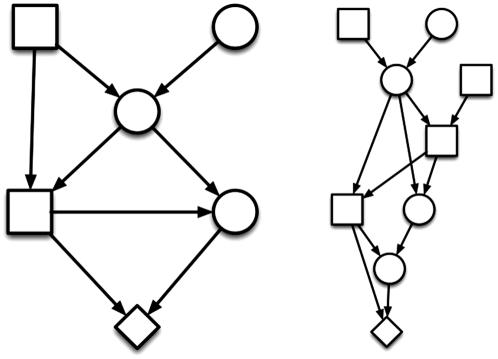
Figure 2.—

Pedigrees of two highly inbred boxer dogs (represented by diamonds), each with f = 0.5. Squares represent sires and circles represent dams.

There is overall a negative correlation between average f and breed size: the four lowest average f values all occur in large breeds. The largest breed, Labrador retriever, has the lowest average f as well as the lowest mean kinship. The boxer is an outlier, being one of the larger breeds but with average f close to 5%, and 16% of boxers have f > 0.1.

The inbreeding effective population sizes (N_e) range from 17 to 114 (Table 3). They are thus relatively uniform across breeds and much smaller than, though strongly correlated with, census sizes (Table 1). Akita Inu and chow chow have a higher N_e than would be predicted from census size, whereas collies have a relatively small N_e. The Akita Inu has the same N_e as the boxer, a much larger breed.

The Akita Inu preserves 30% of the founders' unique genetic variants up to generation 6, more than expected under random mating (25%). The boxer and the bulldog also score highly on this index, which is surprising in view of the high average f in both breeds. In the case of the bulldog, this may be attributed to having the highest proportion of bitches that are dams (36%). It is striking that seven breeds retain <10% of genetic variants up to generation 6, indicating a severe effect of breeding patterns on total genetic variation.

Population structure:

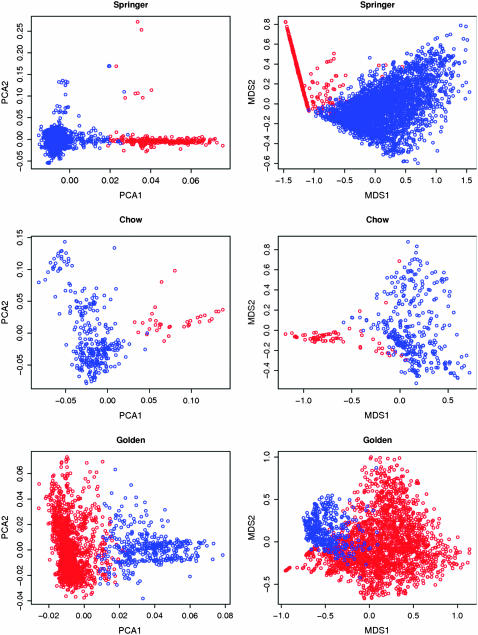
Principal-component and multidimensional scaling plots show strong signs of systematic structure in the springer spaniel and to a lesser extent in the golden retriever and chow chow (Figure 3). In the spaniels, there appears to be a subpopulation engaging in a distinct breeding pattern leading to linear structure in both plots, and this corresponds to the minority cluster identified by two-means clustering. This cluster of dogs has in total 266 ancestors among the springer spaniel founders, 175 (66%) of which have descendants only among dogs in this line, which thus appears to represent a subpopulation of springer spaniels with a distinct pattern of ancestry. Moreover, the mean kinship of dogs in the line is 0.034, double the mean kinship over the whole breed.

Figure 3.—

Dogs in the final two generations for (top) springer spaniel, (center) chow chow, and (bottom) golden retriever are plotted according to (left) the first two principal components based on their ancestors in the founding generation and (right) multidimensional scaling based on pairwise kinship coefficients. The red and blue circles indicate the two clusters identified using two-means clustering based on founder ancestry.

Our novel measure of population structure, Ψ, revealed in each of the 10 breeds a moderate to strong level of clustering of current-generation dogs according to their founder ancestors, both sires and dams (Table 4). The estimate of Ψ ranged from 0.10 in Akita Inu to 0.55 in springer spaniel, in both cases obtained when analyzing ancestral sires. For comparison, F_st among three widely separated human populations investigated in the International Hap Map project was estimated at 0.12. Our clustering step can exaggerate the apparent population structure relative to a situation in which subpopulations are defined a priori, for example, by geography. However, from randomized data sets (Table 5), we found that the Ψ-values are concentrated near 1% for the large breed and range up to ∼8% for the small breed, which indicates that Ψ is significantly different from zero in every breed and suggests that the inflation in its estimated value due to the effect of our clustering is modest. When applying the algorithm to 2 distinct breeds analyzed as if a single breed, the clustering algorithm correctly partitioned all the dogs into the 2 breeds, with no ancestors in common, and hence Ψ = 1.

TABLE 4.

Pedigree structure index Ψ

Breed	Sires (95% C.I.)	Dams (95% C.I.)
Akita Inu	0.10 (0.07–0.17)	0.13 (0.09–0.20)
Boxer	0.36 (0.33–0.40)	0.40 (0.38–0.43)
English bulldog	0.15 (0.12–0.19)	0.14 (0.12–0.17)
Chow chow	0.43 (0.36–0.50)	0.45 (0.39–0.53)
Rough collie	0.34 (0.29–0.40)	0.38 (0.34–0.42)
Golden retriever	0.37 (0.33–0.40)	0.43 (0.41–0.46)
Greyhound	0.40 (0.20–0.65)	0.34 (0.17–0.57)
German shepherd	0.41 (0.37–0.43)	0.35 (0.33–0.38)
Labrador retriever	0.22 (0.20–0.24)	0.33 (0.31–0.35)
English springer spaniel	0.55 (0.51–0.58)	0.28 (0.26–0.30)

TABLE 5.

Distribution of Ψ for 1000 randomized data sets

Breed	2.5 percentile	Median	97.5 percentile
Greyhound	0.007	0.037	0.078
Labrador retriever	0.008	0.010	0.012

Inspection of the clustering results for springer spaniels reveals further information about the springer spaniel subpopulation evident from Figure 3. Among springer ancestral sires, 8% have overall 86% of their descendants in the minority cluster, whereas the remaining 92% of ancestral sires have <2% of their descendants in this cluster. Another striking feature of the springer spaniel is that the strong structuring evident among ancestral sires is almost absent among ancestral dams: only 2 of our 10 breeds give a smaller value of Ψ for ancestral dams. Thus, the current generation of Springer spaniels shows a clear pattern of ancestral sires but not of ancestral dams. In other breeds, the value of Ψ is similar between ancestral sires and dams, except for the Labrador retriever but in this case it is the dams that show greater population structure.

The Akita Inu, a relatively rare breed that has been imported into the UK starting from the 1970s, shows Ψ = 0.10 and Ψ = 0.13 among sires and dams, in each case the lowest among the breeds studied. Chow chow, another imported breed but that is longer established in the UK, has Ψ = 0.43 and Ψ = 0.45, second highest and highest values among sires and dams, respectively.

DISCUSSION

Population structure corresponds to a pattern of preferential mating within a subgroup of the population. For many species it is natural to identify the subgroups with a geographical terrain, but this is less natural for purebred dog populations and in any case is not necessary: population structure is fundamentally a property of the pedigree, irrespective of geography. Directly studying population structure from a pedigree allows it to be measured without genotyping. Just as inbreeding can be studied either via excess homozygosity in genotype data or by pedigree analysis, so population structure can be studied in both ways, but to our knowledge there has been no systematic previous attempt to study population structure by analyzing pedigrees. Thus, our pedigree structure index Ψ appears to be the first proposal for a method to measure it.

Using Ψ, and the pedigree-based inbreeding coefficient f, we found evidence of population structure and inbreeding in all breeds. The springer spaniel shows low levels of inbreeding but strong population structure, apparently due to systematic choice of sires in a subpopulation representing ∼10% of the breed. Collies and bulldogs show high levels of inbreeding, but population structure is low in the bulldog and only modest in the collie. The Akita Inu showed the least evidence of population structure and also a low level of inbreeding relative to its small size. Popular sires are evident in all breeds except the greyhound and are most common in the golden retriever.

Those designing population-based gene-mapping experiments in purebred dogs might wish to avoid breeds with high levels of population structure, such as the springer spaniel, if at all possible. When no realistic choice of breed is available, for example, because the disease is concentrated in one breed, pedigree analysis could help inform sampling strategy. Whatever breed is chosen, some account should be taken of the effects of within-breed population structure on the association analyses. Inbreeding, on the other hand, can be advantageous for gene mapping because it generates more minor allele homozygotes, which can assist power, particularly for recessive phenotypes. Thus, the bulldog, with its high level of inbreeding but low level of population structure, might make a suitable choice.

Dog breeds are required to conform to a breed standard, the pursuit of which often involves intensive inbreeding: the inbreeding effective population size of most breeds considered here is orders of magnitude smaller than the census size and exceeds 100 only in the Labrador retriever. This has adverse consequences in terms of loss of genetic variability and high prevalence of recessive genetic disorders. These features make purebred dogs attractive for the study of genetic disorders, but raise concerns about canine welfare.

Dog registration rules have been rigidly enforced only for ∼50 years; prior to that occasional outcrossing was still possible. Anecdotal evidence suggests that loss of genetic variation and high levels of inbreeding have adverse consequences for canine health and fertility. We have found that the loss of genetic diversity is very high, with many breeds losing >90% of singleton variants in just six generations. On the basis of these results, we concur with Leroy et al. (2006) that remedial action to maintain or increase genetic diversity should now be a high priority in the interests of the health of purebred dogs. Possible remedial action includes limits on the use of popular sires, encouragement of matings across national and continental boundaries, and even the relaxation of breed rules to permit controlled outcrossing.

In addition to dog breeds, extensive pedigree records that can inform gene-mapping studies are available for a number of economically important species, such as cattle. Several human populations—many of them the focus of interest for gene-mapping efforts—have detailed pedigree information available, ranging from isolated religious groups, such as the Amish (Hurd 1983; Agarwala et al. 1998) and the Hutterites (Chapman et al. 2001), to 2.2 million living and deceased residents of Utah (Maul et al. 2006). Several European populations have extensive pedigrees recorded in the marriage certificates of parish churches and have already been used for demographic studies (Boattini et al. 2006). Our population structure index Ψ could be useful in rapidly assessing population structure in advance of genotyping in such populations, as well as to help select individuals for genotyping.