Sex and Deleterious Mutations

Abstract

The evolutionary advantage of sexual reproduction has been considered as one of the most pressing questions in evolutionary biology. While a pluralistic view of the evolution of sex and recombination has been suggested by some, here we take a simpler view and try to quantify the conditions under which sex can evolve given a set of minimal assumptions. Since real populations are finite and also subject to recurrent deleterious mutations, this minimal model should apply generally to all populations. We show that the maximum advantage of recombination occurs for an intermediate value of the deleterious effect of mutations. Furthermore we show that the conditions under which the biggest advantage of sex is achieved are those that produce the fastest fitness decline in the corresponding asexual population and are therefore the conditions for which Muller's ratchet has the strongest effect. We also show that the selective advantage of a modifier of the recombination rate depends on its strength. The quantification of the range of selective effects that favors recombination then leads us to suggest that, if in stressful environments the effect of deleterious mutations is enhanced, a connection between sex and stress could be expected, as it is found in several species.

SEXUAL reproduction involves exchange of genetic information between individuals of a given species. Why this should be advantageous remains a matter of debate (Barton and Charlesworth 1998; Agrawal 2006). The number of theories to explain the prevalence of sex in the natural world has been increasing over several decades and a pluralistic view of the evolution of sex has been suggested by some (West et al. 1999). From the population genetics perspective one of the major consequences of sex and recombination is that it can break down linkage disequilibrium created in natural populations by selection and/or genetic drift (Felsenstein 1974). Linkage disequilibrium has therefore been considered the key for understanding the maintenance of sexual reproduction. Here we take a simple view and try to quantify the minimal conditions under which sex can evolve. The minimal model we study here has been the target of recent studies (Keightley and Otto 2006) and here we explore it further. It is based on the hypothesis put forward by H. J. Muller that sexual populations are more efficient at eliminating deleterious mutations and that in asexual populations a ratchet mechanism can operate (Felsenstein 1974). Muller's ratchet is the accumulation of slightly deleterious mutations in an asexual population and its continuous genetic degeneration by the stochastic loss of its best-fit individuals. The relevant evolutionary forces in question when studying the ratchet are mutation, purifying selection, and random genetic drift. Muller's ratchet is a particular case of the more general Hill–Robertson effect, which states that selection at one locus affects the efficacy of selection at other linked loci (Hill and Robertson 1966; Felsenstein 1974; Comeron et al. 2008). The key force generating negative linkage disequilibrium required for an advantage of recombination in the Hill–Robertson effect is genetic drift due to the finiteness of populations.

But before considering drift, let us consider the fitness distribution in an effectively infinite population subject to the deterministic forces of mutation and purifying selection. If new mutations occur in an individual according to a Poisson with mean U_d, their effect on fitness is s_d and if we further assume that there are no epistatic interactions between two or more mutations, then the equilibrium distribution of deleterious mutations in an asexual population is a Poisson with mean U_d/s_d (Haigh 1978; Gordo and Dionisio 2005). Above we have assumed that each individual comprises a sufficiently large genome and the selection coefficient is not very small, such that back-mutations are reasonably rare and thus can be ignored. Interestingly, under sexual reproduction and assuming free recombination, the distribution of mutations will also be a Poisson. To see why, consider first the equilibrium frequency of a slightly deleterious mutation in a gene. If μ_d is the mutation rate per gene and if we assume that μ_d < < s_d, as seen in the vast majority of biological scenarios, then the expected equilibrium frequency of a deleterious mutation in a given gene is μ_d/s_d (Crow and Kimura 1970). So in a genome with G genes, the probability that a given individual, in a freely recombining population, has k mutated genes (F(k)) follows a binomial distribution with parameter p = μ_d/s_d; i.e.,

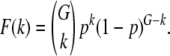(1)

Since G is large and per gene mutation rates are generally small, this distribution tends to a Poisson with mean μ_dG/s_d = U_d/s_d. So, under the assumption of multiplicative fitness, the expected number of individuals free of deleterious mutations, the best class, is n₀ = N exp(−U_d/s_d). In any finite sexual or asexual population this Poisson distribution will be a good approximation to the distribution of fitnesses in the population when 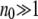(Gessler 1995). If this condition is not met then neither type of population is at mutation–selection balance. For asexuals this implies an extremely rapid accumulation of deleterious mutations and continuous fitness decline and can lead to their extinction (Lynch and Gabriel 1990). For sexuals this accumulation is either not existent or extremely slow (Charlesworth et al. 1993).

The operation of Muller's ratchet has been considered as a possible hypothesis for an advantage of sex and recombination, but at the same time unlikely to be sufficient for explaining the maintenance of high rates of recombination (Barton and Charlesworth 1998). This is because the ratchet is thought to be stopped with very small amounts of recombination (Barton and Charlesworth 1998), and it is thought to operate in only relatively small populations (Keightley and Otto 2006). It is in fact the case that recombination slows down the ratchet (Maynard-Smith 1978; Charlesworth et al. 1993), but there is still no comprehensive study nor any reasonable approximation to express how much recombination is needed to stop it. Surely whenever there is recombination the ratchet cannot turn irreversibly, but it may effectively still turn.

Here we address the conditions under which a new allele that is a modifier of the recombination rate can spread and fix in an asexual population that undergoes mutation accumulation by the ratchet. We further study whether such an allele has the potential to reduce the rate of deleterious mutation accumulation and thus release the population from a fast fitness decline. The use of modifier alleles, such as modifiers of the recombination rate or of the mutation rate, has a long history in understanding the key evolutionary forces that explain genetic systems (Felsenstein 1974; Dawson 1999; Keightley and Otto 2006; Van Cleve and Feldman 2007).

SIMULATION MODEL

We consider a homogeneous population of N haploid individuals that evolves according to the standard Wright–Fisher model. The likelihood of generating descendants is proportional to the individual's fitness. Each individual is represented by an infinitely large genome S = (s₁, s₂, …), where s_a denotes the nucleotide state in position a that can be in state 0 (original state) or 1 (means that a mutation has occurred). This corresponds to the infinite-sites model, and so there is no back-mutation. The fitness landscape is multiplicative, and so the fitness of an individual with k deleterious mutations is determined by ω_k = (1 − s_d)^k, where s_d is the selection coefficient of a given deleterious mutation. In most of the simulations we have assumed a constant value of s_d, although we also studied the case where the effect of deleterious mutations follows a gamma distribution. Deleterious mutations occur at a constant rate U_d, and the number of deleterious mutations that a given individual acquires per generation is Poisson distributed. For each new mutation, we ascribe a position in the genome that is a random number in the interval (0, 1]. The population evolves according to the following life cycle: reproduction, mutation, and selection. Recombination, when it occurs, happens at reproduction. At the start of each simulation, every individual in the population is mutation free and the modifier of the recombination allele is inactive. We then let the population evolve during N generations in such a way to reach an approximate mutation–selection equilibrium. At this time, we randomly choose an individual at which a modifier recombination allele becomes activated. At the recombination stage, we randomly arrange N/2 pairs of individuals. For each pair, if only one carries the modifier allele, recombination occurs with probability r/2. In the case that both individuals share the modifier allele, then they recombine with probability r. When a recombination event occurs, we randomly generate a real number in the interval (0, 1] that corresponds to the position for the exchange. This position divides the genome into two segments that will be exchanged between the individuals; i.e., if before recombination we have genome A with segment 1 and segment 2 and genome B with segment 1 and segment 2, then the result of recombination is two new genomes A′ and B′, where A′ is composed of segment 1 of genome A and segment 2 of genome B and B′ is composed of segment 1 of genome B and segment 2 of genome A. If mutations at the same position exist in both genomes, then recombination will not lead to any change. The population then evolves up to fixation or loss of the modifier recombination allele in the population. Thousands of runs are then performed to estimate the probability of fixation of the modifier recombination allele, P_fix. This probability is then compared with the neutral expectation, P_neu, so that the relative probability of fixation, P_fix/P_neu is quantified.

RESULTS

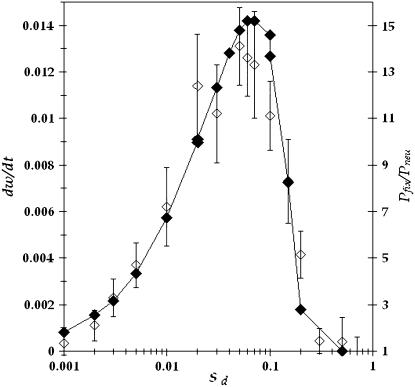
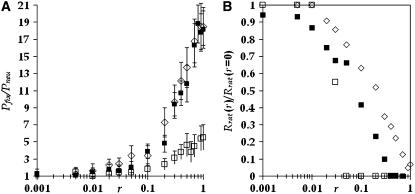
For a given population of effective size N and genomic deleterious mutation rate U_d we have studied how the effect of each deleterious mutation s_d affects the advantage of sex. In Figure 1 we show the probability of fixation of the modifier allele for recombination relative to the neutral case as a function of the selection coefficient against deleterious mutations s_d. In the neutral case the probability of fixation of the modifier allele is 1/N. From Figure 1, we clearly note that the probability of fixation of the modifier allele is maximized for intermediate values of the parameter s_d, which means that for low and high values of s_d recombination does not bring any preeminent advantage to the population. For extremely low values of s_d, mutations accumulate at a rate (R_rat) close to that expected under neutrality (i.e., R_rat ≈ U_d), and they behave as effectively neutral in all except extremely large populations. In these circumstances there is no selection for increments in the rate of recombination. In fact, we observe that an advantage of recombination can be observed only when Ns_d ≥ 1. For values of s_d above this, the advantage of recombination increases with increasing population size. An increase in the advantage of sex with population size has been previously observed (Keightley and Otto 2006). Increasing further the effect of deleterious mutations above a critical value leads to a drastic reduction in the advantage of recombination. In fact, we have ascertained that the reduction starts to occur when n₀ = N exp(−U_d/s_d) ≈ 1. As mentioned before, n₀ is the expected number of individuals free of deleterious mutations under a balance between mutation and selection. To clarify this point, in Figure 2 we plot the relative probability of fixation of the modifier allele together with the value of n₀, for two populations with different values of U_d. For U_d = 1, the value of s_d above which n₀ > 1 is 0.15, for U_d = 0.5 the value of s_d is 0.11. From Figure 2 we note that in the region where n₀ rapidly grows above 1, P_fix/P_neu starts to exhibit a fast decline. For U = 0.5 this happens at a smaller s_d value (∼0.08) than for U = 1 (where the decline is observed for s_d values between 0.1 and 0.2). More precisely, we see that the reduction in the advantage of sex starts to occur when N exp(−U_d/s_d) ≈ 1 and that the advantage disappears when Ns_dexp(−U_d/s_d) ≈ 1. The latter condition occurs at s_d ≈ 0.2 for U_d = 1 and s_d ≈ 0.11 for U_d = 0.5 (see Figure 2). This can be understood in the context of the expected equilibrium distribution of mutations and in the context of some theoretical results on the speed and effects of Muller's ratchet (Gessler 1995; Gessler and Xu 1999; Gordo and Charlesworth 2000; Gordo et al. 2002; Loewe 2006). It was previously found that the ratchet would turn at an exceedingly slow pace when 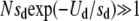. In fact, when it does not turn, we have not observed any increase in the probability of fixation of the modifier allele above what is expected for a neutral mutation (1/N). It was also found that the reduction of genetic diversity at a neutral locus (which is proportional to the effective population size) due to the ratchet was maximal for intermediate values of s_d (Gordo et al. 2002). To put these results in the present context we show in Figure 3 how the decline in mean fitness of an asexual population (left scale on the graph) changes with increasing s_d. There is a clear relation between the set of parameters under which the maximal decline in fitness occurs and those that create a maximal advantage for the modifier allele (right scale on the graph). So, Figure 3 corroborates that the advantage of sex is maximal when the speed at which the ratchet causes fitness decline, in the corresponding asexual population, is maximal. Furthermore we can see from Figure 4 that the reduction in effective population size is maximal for intermediate values of s_d and that is higher in the larger populations. This reduction is measured at a neutral locus that is completely linked to the deleterious background where mutations are accumulating. The reduction in effective size has been considered one of the major signatures of the Hill–Robertson effect (Comeron et al. 2008).

Figure 1.—

The probability of fixation of a recombination modifier allele (relative to the neutral case −1/N). U_d = 1 is the genomic deleterious mutation rate and s_d is the effect of each deleterious mutation. Population size values from top to bottom are N = 10,000 (solid diamonds), 2000 (solid squares), 500 (open squares), and 100 (open diamonds).

Figure 2.—

The probability of fixation of a recombination modifier allele (relative to the neutral case −1/N) (left scale) and the expected number of individuals free of deleterious mutations, n₀ = N exp(−U_d/s_d) (right scale). Solid symbols correspond to U_d = 1 and open symbols to U_d = 0.5. r = 0.5 and N = 1000 in all simulations. The dashed line corresponds to the value of n₀ for U_d = 0.5 and the solid line to n₀ for U_d = 1.

Figure 3.—

The relative probability of fixation of a recombination modifier allele (open symbols with 95% C.I. and right scale) and the decline in mean population fitness, dw/dt, caused by the ratchet in a nonrecombining population (solid symbols and left scale). The parameters are N = 1000, U_d = 1, and r = 0.5.

Figure 4.—

The reduction in effective population size at a neutral locus in the absence of recombination. Mutation rate is U_d = 1 and population sizes are N = 100 (open diamonds), N = 500 (open squares), and N = 2000 (solid squares).

One question still remains: How are the previous scenarios dependent on the strength of the modifier allele? We now study how the strength of the modifier allele influences its evolutionary fate. Figure 5 (left) shows that strong modifiers that increase the recombination rate substantially have a much higher advantage than modifiers of intermediate strength that increase the recombination rate only by a small amount over asexuality. In fact, for very weak modifiers no advantage is observed. Therefore these simulations point out that, for a wide range of s_d values, it is not only sex but also the right amount of sex that is selected for. From comparing both graphs in Figure 5, we can see that for those modifier alleles whose strength is insufficient to significantly reduce the rate of mutation accumulation there is no advantage. An advantage starts to be observed for values of r for which a substantial decline in rate of the ratchet is observed. As we can observe in Figure 5 this occurs for r ≈ 0.01. Above this value of r the advantage of the modifier starts to increase with its strength and that advantage is higher for the smaller s_d values. For r > 0.01 we clearly see that the modifier starts to cause a substantial reduction in the rate of the ratchet. For the smaller s_d values the ratchet is stopped only by stronger modifiers whereas for s_d = 0.2 we see, as expected, that the ratchet can be stopped by weaker modifiers. Interestingly, for the larger value of s_d considered we can observe that the advantage of modifiers with strength >0.1 is significantly higher than that observed for modifiers with r = 0.1, which are able to stop deleterious mutation accumulation (see Figure 5, right). In fact, what we observe in these cases is that the number of mutations in the least loaded class after the modifier gets fixed tends to be smaller than what it was at the time of appearance of the modifier. So, in these cases the advantage is not only to stop the ratchet but also to restore classes with a higher fitness.

Figure 5.—

(Left) The relative probability of fixation of a modifier allele that changes the recombination rate from 0 to r for different values of s_d. (Right) The decrease in the rate of the ratchet caused by the fixation of the modifier allele. In both graphs U_d = 1 and N = 1000; solid squares correspond to s_d = 0.1, open squares to s_d = 0.2, and open diamonds to s_d = 0.05.

DISCUSSION

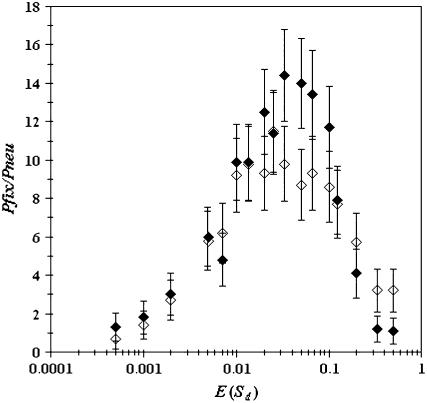
Natural populations are surely more complex than the simple populations we have simulated. But the simple scenario studied here together with the multitude of experiments, demonstrating that deleterious mutations are far more common than advantageous mutations, leads us to conclude that the results are likely to be important in natural populations. Nevertheless, two important assumptions made in this model deserve special consideration: (1) that all deleterious mutations have the same fitness effect and (2) that populations have no spatial structure. The first assumption will most likely be incorrect, although we are still far from having a reasonable amount of knowledge on the distribution of fitness effects of mutations in natural environments or even in many different laboratory environments (Bataillon 2000). However, whatever the true distribution of deleterious effects is, from Figure 1, we may expect a slightly smaller advantage of recombination in a model where mutations occur at rate U_d and have variable effects. This is because with variable effects some mutations will be effectively neutral and some almost lethal, so the effective mutation rate for those mutations of intermediate size will be smaller. In Figure 6 we show how variation in selective effects of deleterious mutations affects the probability of fixation of the modifier allele. As we can observe, the effect of the distribution is small. With an exponential distribution of deleterious mutations we see that, for large mean values of s_d, the fixation probability tends to be slightly larger, whereas for intermediate values of s_d it becomes slightly smaller. Nevertheless the overall picture is robust to variation in selection coefficients. The second assumption of a constant size, unstructured population will also not hold in the vast majority of natural populations. But we can predict, in the face of the results in Figure 3, that the advantage of the modifier will be larger when considering a model that includes population structure. This is because the speed of the ratchet is higher in populations with spatial structure (Combadao et al. 2007). Because the two assumptions lead us to suggest outcomes in different directions, investigations of a more complex model, which incorporates both mutations of variable effect and population structure, will be desirable in the future.

Figure 6.—

The effect of variation in mutation effects, assumed to be gamma distributed. Parameters considered are U_d = 1, r = 0.5, and N = 1000; solid diamonds correspond to a gamma distribution with shape parameter α = 10 and open diamonds to an exponential distribution (α = 1).

Another possibly important feature of natural populations is that the environments they inhabit are not homogeneous and constant but fluctuate in time and space. An observation done in several organisms is that they engage in sexual reproduction when the environmental conditions are stressful. This occurs, for example, in the yeast Saccharomyces cerevisiae, where meiotic recombination frequencies increase with nutrient stress (Abdullah and Borts 2001), and in other fungi collected from the soil (Grishkan et al. 2003). We can expect that the effect of each deleterious mutation on fitness may depend on the environmental conditions. It could be unchanged, enhanced, or even reduced under environmental stress. In fact, some experiments of the effects of mutations in different environmental conditions (Vassilieva et al. 2000; Szafraniec et al. 2001) suggest that in stressful environments the effect of deleterious mutations is enhanced. Putting these observations in the context of the model studied, if we assume that a population lives in an environment that fluctuates between benign and stressful, and that most deleterious mutations have small effects in the benign environment that become stronger in the stressful one, then in the face of the results in Figure 1 we predict that a relation between sex and stress could have evolved. Such a relation appears to be happening in the organisms referred to above, i.e., those populations respond to stress through genetic shuffling of their genes.