Gene-Centric Genomewide Association Study via Entropy

Abstract

Genes are the functional units in most organisms. Compared to genetic variants located outside genes, genic variants are more likely to affect disease risk. The development of the human HapMap project provides an unprecedented opportunity for genetic association studies at the genomewide level for elucidating disease etiology. Currently, most association studies at the single-nucleotide polymorphism (SNP) or the haplotype level rely on the linkage information between SNP markers and disease variants, with which association findings are difficult to replicate. Moreover, variants in genes might not be sufficiently covered by currently available methods. In this article, we present a gene-centric approach via entropy statistics for a genomewide association study to identify disease genes. The new entropy-based approach considers genic variants within one gene simultaneously and is developed on the basis of a joint genotype distribution among genetic variants for an association test. A grouping algorithm based on a penalized entropy measure is proposed to reduce the dimension of the test statistic. Type I error rates and power of the entropy test are evaluated through extensive simulation studies. The results indicate that the entropy test has stable power under different disease models with a reasonable sample size. Compared to single SNP-based analysis, the gene-centric approach has greater power, especially when there is more than one disease variant in a gene. As the genomewide genic SNPs become available, our entropy-based gene-centric approach would provide a robust and computationally efficient way for gene-based genomewide association study.

THE family-based linkage study has been the traditional means of disease gene discovery followed by a variety of fine-mapping techniques. For finer resolution, larger pedigrees are required, which largely restricts its utility, especially for identifying multiple low-penetrance variants involved in common diseases (Boehnke 1994). In the past decade, population-based association mapping, as an alternative for disease gene discovery, has been rapidly developed either at the single-variant or at the candidate gene level. Risch and Merikangas (1996) first showed that an association study has comparatively greater power than the linkage analysis in detecting disease variants with minor or modest effect size. Therefore genomewide association (GWA) studies are feasible. With the development of recent high-throughput genotyping technologies, it is now possible to conduct a disease gene search with millions of single-nucleotide polymorphism (SNP) markers covering the whole human genome (International Hapmap Consortium 2005). This rapid escalation in disease gene search from a family-based linkage scan to a population-based association study has greatly facilitated the process of disease gene discovery.

The analysis of association has been historically focused on alleles and the association has been primarily referred to as allelic association. With the high-density SNP markers generated by human HapMap and the availability of empirical linkage disequilibrium (LD) information across the genome, the haplotype-based association study is gaining popularity. However, both types of association studies at the SNP or the haplotype level have potential pitfalls in the context of replication (Neale and Sham 2004). Due to population histories and evolutionary forces, there has been inconsistency between different studies, caused by aberrant LD patterns across marker loci, different allele frequencies, and LD patterns across populations (Morton and Collins 1998; Pritchard and Przeworski 2001; Stephens et al. 2001; Freedman et al. 2004). There also has been controversy concerning statistical analysis and interpretation of association findings (Neale and Sham 2004). In a recent comprehensive review, Neale and Sham (2004) pointed out common problems associated with the single SNP and the haplotype-based analysis and proposed the prospects of a gene-based association study. To reduce reproducibility error, a shift to a gene-based analysis is necessary (Neale and Sham 2004).

With reduced genotyping costs, recent GWA studies have produced promising results (Ozaki et al. 2002; Klein et al. 2005; Maraganore et al. 2005; Skol et al. 2006; Hunter et al. 2007; Yeager et al. 2007). With limited prior knowledge of genomic regions harboring disease genes, a genomewide blind search for an association signal appears to be the most powerful approach in disease gene hunting. Most association mapping approaches based on either single SNP or haplotype can be applied in a GWA study with an appropriate genomewide multiple-testing adjustment. However, in a recent investigation of the HapMap ENCODE data, Jorgenson and Witte (2006) found that variants in genes are not sufficiently covered by the existing GWA approach. The authors raised their concerns about the coverage of the current GWA study. Some functionally important variants in genes might be missed due to the limitation of the existing SNP genotyping technology. Results in an age-related macular degeneration study also indicated that some genetic risk factors identified through a candidate gene-based approach were missed by the GWA approach (Conley et al. 2005; Rivera et al. 2005). Apparently, there is a lack of efficient coverage of functional variants by the current GWA approach, which could consequently result in missing association signals. With limited resources, a gene-centric GWA approach by focusing only on those SNPs located within a gene should be preferred as an alternative to the current GWA approach (Jorgenson and Witte 2006).

It is well known that genes are the functional units in most organisms. Genic variants are more likely to alter gene function and affect disease risk than those that occur outside genes (Jorgenson and Witte 2006). The sequence information and function of genes are highly consistent across diverse populations, which makes the gene-based association study more robust in terms of replication compared to the single SNP analysis (Neale and Sham 2004). Moreover, multiple testing has been a major statistical issue for the single SNP-based analysis. While haplotype tagging can potentially reduce the dimension of multiple testing, there are potential risks of missing association signals due to the limitations of SNP tagging. In contrast, the multiple-testing problem can be greatly alleviated with a gene-based analysis by conveniently dividing it into two stages, dealing first with the multiple variants within a gene and then with the multiple genes in the genome (Neale and Sham 2004).

Given the feasibility for a gene-centric genomewide association study, there are pressing needs for developing appropriate statistical approaches under this framework. By treating genes as testing units, any approach developed should consider the multilocus LD information simultaneously in a gene to produce sufficient association signals to be detected by a powerful statistical test. Recently, Zhao et al. (2005) showed the power of a nonlinear transformation of haplotype frequencies through an entropy-based haplotype-scoring approach for a genomewide association study. This approach can be extended for a gene-centric GWA study. However, since their approach relies on the information of haplotype frequencies, it needs an extra step to estimate haplotype phases and frequencies beyond the association testing step. Given the potentially large numbers of “genic” SNPs involved, the haplotype-scoring approach is computationally infeasible, especially for a large-scale genomewide study.

Relaxing the assumption of phase information for a haplotype-scoring approach, in this article, we propose an alternative approach by directly utilizing joint genotype information of genic SNPs in a gene. The joint genotypes within one gene could be considered as “pseudoalleles.” Following the argument of Zhao et al. (2005), we propose a nonlinear transformation of joint genotype frequencies through an entropy measure to amplify the genotype frequencies between cases and controls. The functional information for a gene is then compared between cases and controls through the entropy measure. To reduce the degrees of freedom of the entropy-based test and increase the efficiency and power of an association test, we propose a grouping algorithm to cluster rare joint genotypes to common ones with maximum similarity. An information-based penalized entropy measure is proposed to determine the clustering threshold. Extensive simulation studies are conducted to demonstrate the performance of this new entropy-based statistic. The type I error rate and the power of the entropy-based nonlinear test are compared with the single SNP analysis, considering different data generation schemes. The entropy test is then extended to the genomewide level and the performance of the gene-centric GWA approach is compared with the single SNP-based GWA study. Both real data and simulations confirm the powerfulness of the proposed approach.

METHODS

Entropy-based statistic:

In information theory, entropy measures the uncertainty of a random variable (Cover and Thomas 1991). One commonly used entropy measure is Shannon entropy (Shannon 1948). It can be used to measure the genetic diversity in DNA variation and has been applied to extract the maximal amount of information for a set of genetic loci (Hampe et al. 2003). Therefore, Shannon entropy provides a natural way to quantify relevant information gain or loss for a set of SNP markers within a gene related to certain diseases. The entropy of a discrete random variable or a system X is defined in general as

where p(x_t) = Prob(X = x_t), and x_t denotes the tth individual element in a system. The system X represents a gene with joint genotype x_t as an individual element in the following model derivation.

As a functional unit, a gene contains one or more functional variants that jointly function in a coordinated manner to develop a disease phenotype. A gene can thus be defined as a genetic locus system with jointly acting networks of functional units to maintain human homeostasis. Any systematic deviations from the homeostasis due to the perturbations of the underlying genetic variants could result in potential disease signals representing a change of the underlying locus information. This information change, when measured in genotype frequency in cases and controls, can be amplified and captured by a properly defined entropy measure.

Assume a sample of n unrelated individuals collected from a population with n₁ affected and n₂ unaffected. In this sample, a large number of genes across the genome are selected for genotyping. Within each gene, a number of SNPs are genotyped, which are defined as the genic SNPs. The goal of this study is to identify which genes are associated with the genetic disease of interest in a genomewide scale. For simplicity, we start with one gene. An extension to genomewide is given later. Consider N_i genic SNPs each with two alleles for the ith gene. Following the definition of Jorgenson and Witte (2006), genic SNPs include those that are synonymous and nonsynonymous coding SNPs and SNPs in 5′- and 3′-untranslated regions. At each locus, there are three possible genotypes coded as 0, 1, or 2 with 0 and 2 representing homozygote and 1 representing heterozygote. For the ith gene with N_i genic SNPs, there are a total of possible genotype combinations. In reality, there are fewer joint genotypes at one gene because of LD among SNPs within a gene. We define the combination of multilocus genotypes as a genetic locus system with each joint genotype as one single element within the system.

We denote the number of observed joint genotypes for the ith gene as m_i (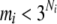). Let c_ij be the jth joint genotype of m_i observed joint genotypes at the ith gene. We deal with each joint genotype as one element within the locus system and each joint genotype captures the underlying multilocus LD information. Let 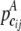and 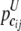be the frequency of the joint genotype c_ij in cases and controls, respectively. The entropies of the joint genotype c_ij in cases and controls are then defined as 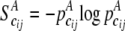and , respectively. Through this nonlinear transformation of the entropy measure, the joint genotype frequencies between cases and controls are amplified and the frequency difference is easier to detect than that in the original scale (Zhao et al. 2005).

Let 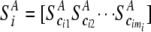and 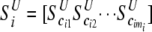be vectors of the entropy measure for the observed joint genotypes in cases and controls, respectively. Assuming independence among individuals, the number of joint genotypes at one gene follows a multinomial distribution. It can be shown that the variance–covariance matrices of joint genotypes in cases and controls are and 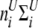, where and are the numbers of cases and controls for the ith gene, respectively, and 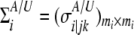with

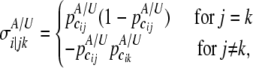where j and k (j, k = 1, · · ·, m_i) denote the jth column and the kth row of the covariance matrix .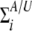

Denote the first partial derivatives of the joint genotype entropy with respect to the joint genotype frequency 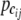for the ith gene in cases and controls as 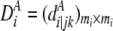and , where

Then, the entropy-based statistic for an association test between the ith gene and the disease is defined as

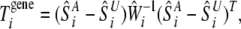(1)

where 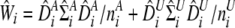, and the circumflex refers to estimated values.

When the frequencies of joint genotypes are not zeros, it can be shown that T_i^gene has an asymptotical central 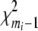distribution under the null hypothesis of no association between the ith gene and disease (Lehmann 1983; Zhao et al. 2005). When the matrix 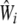is not invertible, we use the spectral decomposition to get 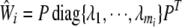, where are eigenvalues of and P is an orthogonal matrix. In the singular case, assume the rank of is ℓ (ℓ < m_i); then we use the matrix

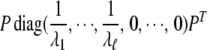to replace 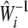in Equation 1. Under the alterative hypothesis that there is an association between the ith gene and disease, T_i^gene follows a noncentral distribution with the noncentrality parameter given as

When dealing with genotypes, the computation burden for estimating haplotype frequencies for a haplotype-based approach such as the one proposed by Zhao et al. (2005) can be alleviated. However, the large number of observable joint genotypes and hence the large degrees of freedom for an association test could affect the power of test. To overcome this difficulty, we propose an information-based grouping algorithm to cluster rare genotypes into common ones.

Genotype grouping via penalized entropy:

When the number of SNPs is large, the high dimensionality of the parameter space could reduce the power and efficiency of the proposed entropy approach. For a haplotype-based analysis, the same dimensionality problem also exists (Zhao et al. 2005). Dimension reduction is essential before conducting an association test. A number of studies have focused on haplotype dimension reduction either through excess haplotype sharing (Yu et al. 2004) or through haplotype grouping (Durrant et al. 2004; Tzeng 2005). To ensure the parameter space (𝒢) containing an appropriate set of joint genotypes, a predetermined frequency cutoff, termed a hard threshold, can be set intuitively. Genotypes with frequency less than the threshold are excluded. The so-called truncated method could result in a low-dimensional space 𝒢 that consists of high-frequency components that can reduce the degrees of freedom and increase the test efficiency. The risk is loss of detailed local information, leading to a consequence of power loss in detecting the difference between two distributions (Fan 1996).

To achieve an optimal balance between information and dimensionality, instead of discarding rare genotypes by setting a hard threshold, a more objective way is to group rare joint genotypes with the most similar ones by choosing a soft threshold based on data. By soft threshold, we mean a threshold determined by data itself according to a certain selection criterion, not based on a predetermined value. Here we introduce an information criterion based on the Shannon entropy to select the cutoff point with the goal to find a set of common joint genotypes that are parsimonious enough yet containing the maximal amount of information for the tested gene. The selected soft threshold is gene dependent and is more objective. The underlying rationale is that genotypes associated with disease should share close evolutionary character states. By assigning rare genotypes to a common cluster or group, one expects that genotypes within a cluster will preserve the original multilocus LD information and contain as much as possible the polymorphism information and, hence, might have similar effects on disease predisposition. From the evolutionary point of view, common genotypes reflect more of the history and, hence, should be preserved in the new clustered genotype space (𝒢). From the statistics point of view, common genotypes represent nonsparse components, which reveals the majority of information of a multinomial distribution (Zhao et al. 2005).

To incorporate both case and control information into the entropy measure, we combine cases and controls with the same joint genotype together before grouping. Consider a set of joint genotypes 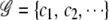for gene i. For simplicity, we drop the gene index subscript i. Each category c_j contains 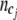joint genotypes with frequency , and c_j represents the joint genotype after combining cases and controls together. The Shannon entropy of each genotype category c_j is defined as 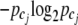(Shannon 1948). The base 2 logarithm is for information measurement in binary units (Tzeng 2005). The overall entropy is the sum over all categories, 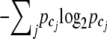. As the number of joint genotype categories increases, this information measure monotonically increases. Maximum information is achieved when all joint genotype categories are included. However, this does not serve our purpose of dimension reduction. To balance between information and dimension, we introduce a penalty function following Tzeng (2005) to penalize the information increase caused by adding more genotype categories in the parameter space 𝒢. The penalized entropy measure (PEM) is given as

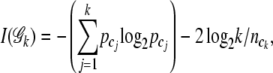(2)

where log₂k is the total number of bits needed to describe the outcome (MacKay 2003). The Akaike information criterion-like penalty term 2 log₂k is divided by the sample size of c_k to reflect the marginal cost of including the c_k category (Tzeng 2005). The penalty term 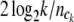penalizes the monotone increase of the entropy measure by adding new terms. Thus the one with the maximum PEM (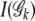) corresponds to the optimal parameter space. To do so, we first sort all joint genotypes according to their frequencies. Then for each truncated genotype set 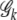, , 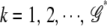we calculate the PEM (). The optimal dimension 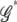that maximizes the PEM () contains k joint genotypes.

Once the grouping threshold is determined, we can proceed to group those joint genotypes with frequency less than the threshold with common ones. To preserve the maximum information for those rare joint genotypes after grouping, we first calculate the similarity (Equation 3) between those rare joint genotypes and those with frequencies larger than the grouping threshold. Each rare joint genotype is then grouped together with the common one having the largest similarity. To illustrate the idea, we consider one gene with 10 SNPs. Denote the genotype vector at the 10 SNP loci for one rare joint genotype with frequency less than the grouping threshold as 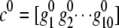, and denote the genotype vector for any one of the joint genotypes with frequency greater than the grouping threshold as 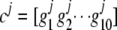, where 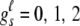, s = 1, 2, · · ·, 10, and ℓ ∈ {0, j(j ≥ 1)}. We define a similarity measure between these two joint genotypes as

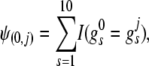(3)

where

is an indicator function. For each rare joint genotype to be grouped, a similarity score will be calculated against all common joint genotypes. This rare joint genotype will be grouped with the common one with the largest similarity.

The penalized entropy measure accommodates the increase of the joint genotype dimension and maintains the parsimony of the grouping parameter space. Figure 1 illustrates how the information measure PEM changes as the number of joint genotype changes. Figure 1A shows the bar plot of the sorted joint genotype frequencies with a case–control combined sample. The solid horizontal line indicates the grouping threshold. Figure 1D displays the PEM for each truncated distribution 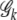, k = 1, 2, · · · . We can clearly see a concave curve with the peak indicating that six is the optimal number of dimension, i.e., six common joint genotypes after grouping. As sample size increases gradually, we see the same concave pattern for the PEM and the grouped dimension gradually increases (data not shown). Figure 1, B and C, shows the bar plots of the joint genotype distribution before grouping for cases and controls, respectively. The corresponding joint genotype distributions after grouping are shown in Figure 1, E and F, respectively. The data are simulated under the null hypothesis of no disease gene association. We can see that the joint genotype distributions in cases and controls are very similar before and after grouping. The common distribution pattern is preserved in both cases and controls after grouping.

Figure 1.—

Examples of joint genotype distributions of cases and controls within one gene under the null hypothesis of no association. (A) The bar plots of sorted joint genotype frequencies in both cases and controls. Categories with frequencies below the horizontal line will be grouped. (B) Joint genotype distribution in cases. (C) Joint genotype distribution in controls. (D) Plot of the penalized entropy measure (PEM) against the threshold. The horizontal line in A labels the categories to be retained when the maximal amount of PEM is achieved. (E and F) The grouped joint genotype distributions in cases and controls, respectively. Here, the numbers on the x-axis represent the categories of joint genotypes. Data are generated using the MS program with sample size 200.

Gene-centric genomewide significance:

For the single SNP-based GWA study, the significance level for multiple testings is adjusted on the order of ≥10⁵. Traditional Bonferroni adjustment is too conservative to detect the true effects. In past decades, a false discovery rate (FDR)-controlling approach has been widely used for multiple-testing adjustment (e.g., Benjamini and Hochberg 1995). As several studies have reported the problem of replicating certain genetic findings (reviewed by Neale and Sham 2004), people tend to use more stringent criteria to avoid false discoveries. This, however, could potentially result in false negatives too. The trade-off between false discovery and false negative has not been well established in a GWA study.

While the single SNP-based analysis has potential multiple-testing problems, a gene-based approach can greatly alleviate the multiple-testing burden by dealing with multiple variants within a gene as a testing unit and then dealing with multiple genes across the genome (Neale and Sham 2004). We know that the total number of genes in the whole human genome is estimated at ∼30,000 and these genes are likely to represent largely functional units. By focusing on each gene as a unit, we can potentially reduce the false positives and false negatives without suffering too much from power loss due to stringent criteria. Given the large number of tested genes, the Bonferroni or FDR adjustment procedure could still be too stringent to test moderate effects. Actually, for most common diseases, even though a search for disease factors is run with thousands of genes, we know that only a small proportion of genes will trigger true effects. The large number of association tests therefore confers a considerable risk of false discoveries. In reality, if the appropriate genotyping approach is used, scientists are more interested in detecting the proportion of true effects than controlling the false discovery rate. Incorporating certain prior knowledge about the proportion of true effects, therefore, would certainly lead to a more efficient error control. From a Bayesian point of view, this prior information can be updated in a multiple-testing adjustment approach. Van Den Oord and Sullivan (2003) proposed an optimizing approach by eliminating and controlling false discoveries to achieve a balance of true and false positives. Following Van Den Oord and Sullivan (2003), for a gene to be significant at the genomewide significance level, we have

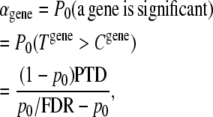(4)

where PTD is the expected proportion of genes with true effects to be detected, i.e., the average power of an association test; p₀ is the expected proportion of genes with no effect; and FDR is the false discovery rate. This approach can be applied for either a dependent or an independent test. A prior knowledge of 0.5% true effective genes and an average 85% association test power would lead to α_gene ≈ 2.2 × 10⁻⁴ with an FDR of 0.05. Therefore, a genewide significance of ∼2.2 × 10⁻⁴ would be considered to be genomewide significant.

The power of the gene-centric GWA approach can be calculated accordingly. If we know the genomewide significant threshold value C^gene, then the probability of selecting a disease gene under the alternative hypothesis is given by

where the C^gene value can be found through solving Equation 4.

SIMULATION STUDY

Simulation design:

Monte Carlo simulations are performed to evaluate the statistical property of the proposed approach. We use two methods to simulate the genotype data. The first method is based on the MS program developed by Hudson (2002), which simulates SNP haplotypes under a coalescent model where the recombination rate varies across the SNP sequence. This method cannot control the pairwise LD pattern across multiple SNPs within a gene. The second method generates SNP genotype data on the basis of a conditional distribution of current genotype data given on the distribution of previous genotype data. Thus the pairwise LD pattern can be easily controlled. We call the second method LD-based simulation. The details for the two methods are given as follows.

MS program:

We use the MS program developed by Hudson (2002) to simulate haplotypes for each individual to form individual genotype data. The main parameters under the coalescent model for generating haplotypes are set as follows: (1) the effective diploid population size n_e is 1 × 10⁴; (2) the scaled recombination rate for the whole region of interest, ρ = 4n_eγ/bp, is 4 × 10⁻³, where the parameter γ is the probability of crossover per generation between the ends of the haplotype locus being simulated; (3) the scaled mutation rate for the simulated haplotype region, 4n_eμ/bp, is set to be 5.6 × 10⁻⁴ for the region of simulated haplotypes; and (4) the length of sequence within the region of simulated haplotypes, n sites, is 10 kb. Similar parameter settings can be found in other studies (e.g., Hudson 2002; Tzeng 2005). We set the number of SNP sequences in the simulated sample to 100 for each gene and run the MS program to generate the haplotype sample on the basis of these parameter settings. Then we randomly select a segment of 10 adjacent SNPs as a haplotype. The next two haplotypes are randomly drawn from the simulated sample containing 100 10-SNP haplotypes and are paired to form an individual genotype.

LD-based simulation:

Under this scenario, SNP genotypes are generated according to the conditional distribution of current genotypes given in the previous genotype data. Suppose the frequencies of two adjacent SNPs with risk alleles A and B are p and q and the linkage disequilibrium between them is δ. Then the frequencies of four haplotypes are p_ab = (1 − p)(1 − q) + δ, p_Ab = p(1 − q) − δ, p_aB = (1 − p)q − δ, and p_AB = pq + δ. Given the allele frequency for A at locus 1 and assuming Hardy–Weinberg equilibrium, the SNP genotype data can be obtained at that locus assuming a multinomial distribution with genotype frequencies of p², 2p(1 − p), and (1 − p)² for genotypes AA, Aa, and aa, respectively. To simulate genotype data for SNP2 conditional on SNP1, we need to derive the conditional distribution P(SNP2 | SNP1). To illustrate the idea, consider the simple case P(BB | AA). By Bayes theorem,

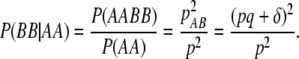Similarly, we can get the conditional distribution of other genotypes at SNP2 given in the genotype data at SNP1. A detailed conditional distribution is tabulated in Table 1. The pairwise LD pattern between adjacent SNPs can be easily controlled with this simulation method.

TABLE 1.

Conditional genotype probability of SNP2 given on SNP1 (P(SNP2 | SNP1))

	bb	bB	BB
aa		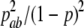2pabpaB/(1 − p)2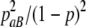
aA	pabpAb/p(1 − p)		pABpaB/p(1 − p)
AA		2pAbpAB/p2

Phenotype simulation:

Given the nature of the difficulty to know the true functional mechanism for a given gene, it is difficult to simulate the true functional variants and the true functional mechanism within a gene. Thus, we evaluate the performance of the entropy approach by considering different scenarios to mimic the situation of a complex disease for a given gene. Three situations are considered in the simulation study. The first scenario considers only one functional disease variant within a gene. The second one considers two disease variants where there are interactions between these two variants. The third one considers three disease variants and there are complex interactions among these three variants. The simulated data are then subjected to the entropy test and single SNP analysis.

Here we briefly illustrate how the disease phenotypes are simulated. Consider the first scenario in which there is only one disease variant. Let f_i be the penetrance function, which is defined as the probability of being affected given possession of i copies of disease alleles (i = 0, 1, 2). Denote λ = f₁/f₀ as the genotype relative risk (GRR). Let p be the disease allele frequency. Then the penetrance function for the three genotypes at a single locus, f₀, f₁, f₂, can be defined for an additive and a multiplicative model (Table 2). Once f_i is determined, the disease status for that particular individual is simulated according to a Bernoulli distribution with the probability of success f_i. The same process is repeated until n cases and n controls are generated.

TABLE 2.

Single-locus disease model

	f0	f1	f2
Additive		λf0	2λf0 − f0
Multiplicative		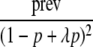λf0	λ2f0

prev, the population prevalence; λ, the genotype relative risk.

For a disease model with two interacting disease loci, we follow the settings given in Marchini et al. (2005). Two models are considered (Table 3). In model 1, the odds increase multiplicatively with genotype both within and between loci. In model 2, the odds of a disease have a baseline value (γ) and the odds increase multiplicatively both within and between genotypes once there is at least one disease allele at each disease locus.

TABLE 3.

Two-locus interaction disease model

	BB	Bb	bb
Model 1
AA	γ(1+θ)4	γ(1+θ)3	γ(1+θ)2
Aa	γ(1+θ)3	γ(1+θ)3	γ(1+θ)
aa	γ(1+θ)2	γ(1+θ)	γ
Model 2
AA	γ(1+θ)4	γ(1+θ)2	γ
Aa	γ(1+θ)2	γ(1+θ)	γ
aa	γ	γ	γ

γ, the baseline effect; θ, the genotypic effect.

For the three-locus interaction disease model, we denote the three-locus genotypes as (G_A, G_B, G_C) ∈ 0, 1, 2, which represents the number of risk alleles at each disease locus A, B, and C. Following Table 3, we generalize the two-locus disease model to the three-locus interaction disease model as

(5)

Once the disease loci are determined, the case–control disease status can then be simulated according to a multinomial distribution conditional on the observed genotype data.

Property of the new statistic:

Null distribution:

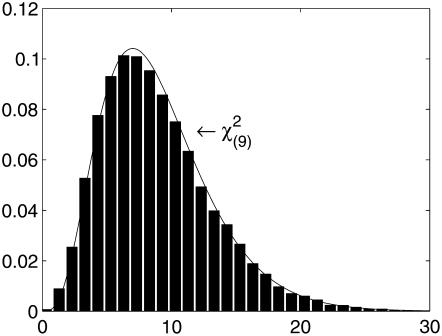
Under the assumption of large sample size under the null hypothesis, the entropy-based statistic T^gene has an asymptotic χ²-distribution. To examine whether the asymptotic results of the entropy-based statistic T^gene still hold for a small sample size under the null hypothesis of no association, we generated 200 cases and 200 controls for one gene containing 10 SNPs with 10 joint genotypes. Figure 2 plots the histogram of the test statistic T^gene. The distribution of T^gene is very similar to a χ²-distribution with 9 d.f.

Figure 2.—

Null distributions of the test statistic T^gene from the simulated 200 cases and 200 controls with 10 joint genotypes in a gene. 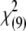indicates a 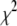-distribution with 9 d.f.

Type I error:

We evaluate the type I error rate for the new entropy statistics on the basis of the two genotype-generating schemes, the MS program and the LD-based simulation. Data are simulated under the null hypothesis of no association with 10 SNPs for a gene. A total of 1000 simulation runs are conducted under different sample sizes. The pattern of LD varies among SNPs when data are simulated using the MS program. To evaluate the extreme case, we use the LD-based simulation method to generate genotype data assuming high LD among SNPs (r² = 0.9). The simulated data are subjected to both the entropy test and single SNP analysis to compare their performance. The single SNP analysis is based on a genotype χ²-test with 2 d.f. Since our attention is focused on genes, for the single SNP analysis, a gene is declared to be significant if it contains at least one significant SNP. The significant level for each SNP within a gene is adjusted first with the Bonferroni correction. Results are summarized in Table 4. As we can see, the error rates are reasonably estimated for data simulated with both approaches. The disease allele frequency has no remarkable effect on type I error. Compared to the entropy test, the single SNP analysis underestimates the type I error in all scenarios. Therefore, when focused on a gene-based analysis, our approach has better error control than the single SNP analysis.

TABLE 4.

Type I error rates of the association test based on statistic T^gene at the 0.05 nominal level

		LD based
n	MS program	PD = 0.1	PD = 0.3	PD = 0.5
100	0.081 (0.025)	0.046 (0.022)	0.061 (0.025)	0.043 (0.030)
200	0.073 (0.038)	0.066 (0.015)	0.047 (0.025)	0.046 (0.025)
400	0.052 (0.027)	0.060 (0.030)	0.046 (0.027)	0.045 (0.032)

Data are simulated with the MS program and the LD-based approach. The type I error for the single SNP analysis is given in parentheses. P_D refers to disease allele frequency.

Power analysis:

Up to now the functional mechanism of most disease-related genes has not been comprehensively understood. For a gene to be associated with a disease phenotype, there must be complex functional mechanisms among multiple variants within the gene. The physical location and alignment pattern of SNPs within a gene, the up- and downstream signaling among SNPs, and the complex functional interactions among SNPs could result in potential functional variation and eventually lead to a disease signal. It is, therefore, difficult to simulate the true functional mechanism of a disease gene. To compare with the single SNP analysis, we simulate a disease gene by assuming one, two, or three disease loci within the gene. These scenarios represent approximations of true functional mechanisms of a disease gene.

The one-locus, two-locus, and three-locus disease models are given in Table 2, Table 3, and Equation 5, respectively. The simulation results for these three models are summarized in Tables 5, 6, and 7, respectively. We assume 10 SNPs on average for a simulated gene and use two simulation schemes, the MS program and LD-based simulation. Table 5 shows the power results under the additive and multiplicative disease model assuming one disease locus within a gene. The power for the single SNP analysis is given in parentheses. As can be seen, the power of the association test based on the statistic T^gene increases as sample size increases. For data simulated with the MS program, we observe a slightly smaller power of the entropy test than that of the single SNP analysis. As sample size increases from 200 to 400, the difference vanishes and the two approaches are comparable. For data simulated with the LD-based approach assuming r² = 0.9, we observe consistently higher power of the entropy test than that of the single SNP analysis. Also, the power is affected by the genotype relative risk. Different allele frequency has no remarkable effect on testing power and hence is omitted.

TABLE 5.

Power of the association test based on statistic T^gene assuming one disease locus in a tested gene under different sample sizes and different simulation schemes. The power for the single SNP analysis is given in parenthesis

		MS program		LD based (r2 = 0.9)
Disease model	(prev, GRR)	n = 200	n = 400	n = 200	n = 400
Additive	(0.1, 1.4)	0.370 (0.255)	0.588 (0.607)	0.438 (0.305)	0.766 (0.651)
	(0.1, 1.6)	0.602 (0.555)	0.897 (0.902)	0.681 (0.577)	0.943 (0.934)
Multiplicative	(0.1, 1.4)	0.402 (0.367)	0.735 (0.752)	0.521 (0.384)	0.808 (0.751)
	(0.1, 1.6)	0.751 (0.687)	0.960 (0.953)	0.812 (0.743)	0.970 (0.974)

prev, population prevalence; GRR, genotype relative risk. For both simulation schemes, we set the third SNP as the disease locus. The disease allele frequency for the LD-based simulation is set as P_D = 0.3. The significance level is 0.05.

TABLE 6.

Power of the association test based on the statistic T^gene assuming two interacting disease loci within one gene under different sample sizes and different simulation schemes

		MS program		LD based (r2 = 0.9)
Disease model	(BL, GE)	n = 200	n = 400	n = 200	n = 400
Model 1	(1, 0.7)	0.379 (0.160)	0.564 (0.385)	0.816 (0.709)	0.994 (0.822)
	(1, 0.9)	0.708 (0.272)	0.874 (0.595)	0.909 (0.817)	1.000 (0.827)
Model 2	(1, 0.7)	0.269 (0.152)	0.455 (0.387)	0.468 (0.349)	0.835 (0.641)
	(1, 0.9)	0.458 (0.232)	0.658 (0.559)	0.621 (0.426)	0.938 (0.733)

The power for the single SNP analysis is given in parentheses. BL, baseline effect; GE, genotypic effect. For the MS program, we set the fourth and ninth SNPs as the two interacting loci. For the LD-based simulation, we simulate two LD blocks, one containing six SNPs and the other containing four SNPs, with pairwise r² = 0.9 for SNPs within each block. Two interacting disease loci are from each block with allele frequency P_D = 0.3. The significance level is 0.05. Models 1 and 2 are defined in Table 3.

TABLE 7.

Power of the association test based on the statistic T^gene assuming three interacting disease loci within one gene under different sample sizes and different simulation schemes

		MS program		LD based (r2 = 0.9)
Disease model	(BL, GE)	n = 200	n = 400	n = 200	n = 400
Model 1	(1, 0.7)	0.465 (0.271)	0.658 (0.685)	0.866 (0.782)	0.992 (0.857)
	(1, 0.9)	0.802 (0.481)	0.925 (0.918)	0.956 (0.867)	1.000 (0.861)
Model 2	(1, 0.7)	0.471 (0.299)	0.629 (0.689)	0.858 (0.774)	0.994 (0.853)
	(1, 0.9)	0.808 (0.487)	0.927 (0.876)	0.960 (0.867)	1.000 (0.876)

The power for the single SNP analysis is given in parentheses. BL, baseline effect; GE, genotypic effect. For the MS program, we set the first, fifth, and ninth SNPs as the three interacting loci. For the LD-based simulation, we simulate three LD blocks, one containing five SNPs, one containing three SNPs, and the other one containing two SNPs, with pairwise r² = 0.9 for SNPs within each block. Three interacting disease loci are from each block with allele frequency P_D = 0.3. The significance level is 0.05. Models 1 and 2 are defined in Equation 5.

When the number of disease loci increases within a tested gene, we observe significant differences of the two approaches under the two data-simulation schemes. For the two-locus disease model, Table 6 shows that the power increases as the genotypic effect (GE) and sample size increase. As we expected, model 1 has higher power than model 2 due to the difference of the two models (Table 3). Note that the entropy-based test uniformly outperforms the single SNP analysis in all the simulation scenarios. Depending on the underlying gene action mode and linkage information among SNPs, a large sample size (>400, say) is always preferred.

The results for the three-locus disease model are very similar to those for the two-locus model under different sample sizes and different GEs (Table 7). It is worth noting that when the number of disease loci increases from two to three, the power of the entropy test has a remarkable increase. For example, when data are simulated assuming model 2 using the LD-based simulation approach, the power of the two-locus model (Table 3) is only 0.621. We observe a dramatic power increase from 0.621 to 0.960 when the number of functional disease loci increase to three (Equation 5) for fixed GE and sample size. A similar trend holds in general as the number of functional variants increases in a gene.

In summary, under different simulation scenarios, the results confirm that the entropy-based test outperforms the single SNP analysis in general when the unit of interest is focused on a gene. The results also indicate that we may need a large sample size (>400, say) to obtain reasonable power to detect the disease–gene association. As the number of functional variants within a gene increases (i.e., the functional mechanism of a gene becomes more complex), the power of the entropy test to detect the association also increases.

Power of genomewide association studies:

To check the performance of the entropy-based test on a genomewide scale analysis, we simulate 1000 genes. Even though 1000 genes do not represent a genomewide level (∼30,000 genes), extension to a genomewide scale is straightforward. For a gene to be significant at the genomewide scale, a genewide significance level is calculated on the basis of Equation 4. Assume there are 10 genes contributing to a disease phenotype in 1000 genes; i.e., p₀ = 0.99 and each gene contains 10 SNPs on average. If we further assume a minimum 80% power to detect an association (PTD = 0.8) and an FDR of 0.05, then α_gene ≈ 0.000425. This means that a gene significant at the 4.25 × 10⁻⁴ level would be considered to be genomewidely significant.

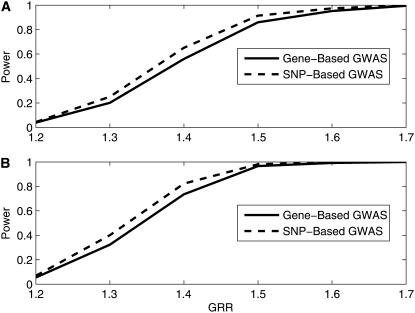
We randomly simulate 800 cases and 800 controls using the MS program. Figures 3–5 plot the genomewide power analysis of the entropy test for one-locus, two-locus, and three-locus disease models, respectively. In all three figures, the solid and the dashed lines represent the power curves for the entropy-based analysis and the single SNP analysis, respectively. The power as a function of the GRR for the one-locus disease model is plotted in Figure 3, A (additive model) and B (multiplicative model). We can see that the single SNP analysis slightly dominates the entropy test with moderate GRR. As GRR increases to 1.7, both tests converge to 100% power. The power as a function of GE is plotted in Figures 4 and 5 for the two-locus and three-locus disease models, respectively. The entropy test has consistently higher genomewide power than the single SNP analysis under two-gene action modes with moderate GE. The power difference decreases as the GE increases.

Figure 3.—

Power comparison of gene-based and SNP-based genomewide association studies as a function of genotype relative risk (GRR) under two single-locus disease models, the additive model (A) and the multiplicative model (B). The risk allele frequencies at both loci are 0.30, and the numbers of individuals in both cases and controls are 800, genotyped on 1000 genes with a population prevalence of 0.1.

Figure 4.—

Power comparison of gene-based and SNP-based genomewide association studies as a function of genotypic effect (GE) under two two-locus disease models, model 1 (A) and model 2 (B) defined in Table 3. The numbers of individuals in both cases and controls are 800, genotyped on 1000 genes.

Figure 5.—

Power comparison of gene-based and SNP-based genomewide association studies as a function of genotypic effect (GE) under two three-locus disease models, model 1 (A) and model 2 (B) defined in Equation 5. The numbers of individuals in both cases and controls are 800, genotyped on 1000 genes.

Note that the power for the single SNP test is adjusted within a gene using the Bonferroni correction and then is corrected in the genewide significance level calculated in Equation 4 as the familywise error rate for that gene. Therefore, in the single SNP analysis, a gene is declared to be significant if the smallest P-value of any single SNP test is <4.25 × 10⁻⁴/10. Compared to a SNP-wide significance level of 5 × 10⁻⁶ if we apply the genomewide Bonferroni correction for all SNPs, this threshold is less restrictive. However, if we use the restrictive genomewide Bonferroni correction, the power for the single SNP-based analysis would be much smaller compared to the gene-centric approach.

A CASE STUDY

Until now, a complete set of genomewide genic SNPs has not been fully developed (Jorgenson and Witte 2006). Hence no real data are available to test the method. To show the utility of the proposed approach, we apply our method to a large-scale candidate gene study. The data set contains 190 candidate genes in a genetic association study of preeclampsia (PE). PE typically occurs after 20 weeks gestation with a syndrome of hypertension and proteinuria. The disorder is a leading cause of maternal mortality and affects at least 5–7% of all pregnancies (Kaunitz et al. 1985). A previous study showed that genetic factors may contribute >50% of the variability in liability to PE (Esplin et al. 2001). In this study, subjects were recruited at the Sotero del Rio Hospital, in Puente Alto, Chile. Eligible mothers were enrolled in a longitudinal cohort study designed to predict either the subsequent development of PE or the existence of PE at the time of admission to the hospital. For a detailed data description, please refer to Goddard et al. (2007). After elimination of SNPs with minor allele frequency <5%, 819 SNPs were subjected to both the single SNP and the gene-centric association study. The data set contains a total of 225 cases and 585 controls.

If we assume a prior knowledge of 19 significant genes that would be associated with PE on the basis of previous studies (Goddard et al. 2007), the parameter p₀ takes a value of 19/190. If we further assume the power for a single-gene test is PTD = 85%, following Equation 4 with a false discovery rate of FDR = 0.05, a gene that is significant at the 0.005 level would be claimed to be significant at the “genomewide” level. Similarly, we can apply the same significance criterion to the single SNP-based analysis. On the basis of the report in Goddard et al. (2007), we assume a prior number of 21 significant SNPs of total 819 SNPs and a power of 0.85 for any single SNP test. Then a SNP is declared significant at the genomewide level if the P-value for that single test is <0.0012. Alternatively, if we focus on a gene-based unit, we can use the genewide significance level of 0.005 as the familywise significance level for one gene and apply the Bonferroni correction by dividing it by the number of SNPs in that gene to get the significance threshold for that particular gene. For example, if a gene contains 4 SNPs, then the gene is declared to be significant if the smallest P-value for any single SNP test is <0.005/4 = 1.25 × 10⁻³. In this case, the genewide significance level would be different for different genes.

Table 8 lists the P-values for both significant genes and SNPs. The significant genes and SNPs are underlined. For comparison, we also listed the smallest P-values of SNPs in which the corresponding gene is significant based on the gene-based test as well as the P-value for gene-based analysis if that gene contains at least one significant SNP. The test results show that the gene-based analysis detected 7 significant genes of 190 genes. The single SNP-based test detected three significant SNPs, and hence 3 significant genes, even though the significance level is much less stringent than the Bonferroni correction or FDR-based adjustment. Among the significant genes identified, only gene F13B is consistently picked up by both the gene-based and the SNP-based tests. Two polymorphisms in genes F2 and FGF4 also show marginal significance. The fact that those genes were detected by the gene-based entropy test but missed by the single SNP analysis indicates that complex functional interactions might exist among SNPs in those genes. It is not surprising that the complex systematic interactions among SNPs in those genes may not be detected by less powerful single SNP analysis by testing each SNP separately.

TABLE 8.

Analysis of the PE data set based on the gene-based entropy test and the single SNP-based χ²-test

Gene (SNP no.)	Gene-based P-value	SNPa	SNP-based P-value
APOB (9)	0.0019	rs5456814	0.0165
F13B (4)	0.0025	rs28787657	0.0010
F2 (7)	0.0016	rs28886771	0.0021
FGF4 (3)	0.0033	rs634043464	0.0067
IGF1R (7)	0.3600	rs40893937	0.0006
IGF2R (14)	0.0004	rs41410456	0.0330
MMP10 (8)	0.0009	rs634850223	0.0280
NOS2A (10)	0.0258	rs9678181	0.0001
PDGFC (2)	0.0044	rs634820282	0.0320

The number of SNPs in each gene is given in parentheses. Significant and nonsignificant P-values are underlined and in italics, respectively.

^aOnly SNPs with the smallest P-values within the corresponding genes are listed.

DISCUSSION

The development of the human HapMap provides an unprecedented opportunity for unraveling the disease etiology of complex human diseases with appropriate statistical analysis on a genomewide scale. The advancement of whole-genome genotyping technology and relatively reduced genotyping cost in recent years have made it possible to detect genomewide disease variants in thousands of individuals, with an aim to find variants with modest contributions to disease risk. Traditional single SNP-based analysis approaches find regions associated with a disease on the basis of differences in allele or genotype frequencies of the SNPs in regions between cases and controls. The methods find variants in LD with SNPs and are not comprehensive in the characterization of variation in the regions. In contrast to the SNP-based approaches, the gene-based analysis is less susceptible to erroneous findings due to genetic differences between populations (Neale and Sham 2004). Also a gene-centric approach should be more complete with regard to the coverage of genes, which is crucial to detecting causal variants (Jorgenson and Witte 2006). However, a genomewide genic SNP set has not been well established (Jorgenson and Witte 2006). Given the radical breakthrough in recent biotechnology, it will be made available to the public shortly. Therefore, the proposed gene-centric GWA approach in this article represents a timely effort to contribute to the identification of disease genes on a genomewide scale.

Increasing evidence has shown that complex interaction of genes performed in a coordinated manner is essential for normal function of any organism (Gibson 1996; Szathmary et al. 2001; Moore 2003; Hartwell 2004). The jointly acting network of functional variants, termed the genetic locus system, is crucial to maintain the system homeostasis. Any systematic deviations from the homeostasis could result in a potential disease signal. The overall disease signal resulting from multiple interacting disease variants for a particular gene can be more efficiently amplified and captured by considering all variants in a gene simultaneously by the proposed entropy test statistic. Compared to the single SNP analysis of testing each variant separately and hence tending to ignore the complex interaction mechanism among SNPs within a gene, the gene-centric approach is statistically more powerful and biologically more relevant. Moreover, the entropy approach considers the genic variants within a gene as a testing unit, which is in agreement with the conception that the gene is the functional unit of most organisms. By capturing the difference of the joint genotype distributions between cases and controls through nonlinear transformation of joint genotype frequencies, the entropy-based test shows appropriate type I error and good power in detecting disease-associated genes. Simulations also confirm the powerfulness of the gene-based test, especially when the underlying testing gene is functionally complex, for instance, containing two or more interacting disease variants.

The proposed entropy-based test considers the joint genotype distribution and is simple and easy to implement. The nonlinear transformation of the joint genotype frequencies amplifies the difference between cases and controls and hence increases the testing power. Unlike the haplotype-based entropy test (Zhao et al. 2005), the calculation of joint genotype frequency ismuch faster and simpler without estimating linkage phases as the haplotype-based approach does. The computation gain is even more significant when the number of genic SNPs is large. Intensive computation in estimating haplotype frequencies makes the haplotype-based approach practically infeasible to implement on a large genomewide scale.

Given the large number of possible joint genotypes compared to possible haplotypes, one of the disadvantages of genotype-focused analysis is the large number of degrees of freedom. One possible solution is to discard those rare joint genotypes with frequency less than a prespecified hard threshold. This, however, will largely reduce the sample size and hence the power of the association test. Without sacrificing sample size, the problem of large degrees of freedom is overcome by an efficient grouping algorithm. To balance the trade-off between informativeness and dimensionality, we have proposed a penalized entropy measure to determine a soft threshold. Rare joint genotypes are then grouped with common ones to reconstruct a lower-dimensional distribution from the original distribution. Simulations confirm the validity of the grouping approach.

The powerfulness of the proposed gene-centric approach on a genomewide scale is also confirmed by simulations (Figures 3–5). As revealed by the genomewide simulation studies, the gene-based approach has more power than the single SNP test when there is more than one functional disease variant in a gene (Figures 4 and 5). The proposed approach is not only restricted to a genomewide application; it also fits a candidate gene study with an appropriately defined SNP set for a candidate gene. The real example shown in this article indicates that the gene-centric approach detects more genes than the single SNP analysis and hence is more powerful than the single SNP-based analysis. Some genes identified by the gene-based approach but missed by the single SNP analysis have been shown in the literature. For example, genes APOB, FGF4, and F2 are detected by the gene-based analysis but are missed by the single SNP test. These genes were previously reported to be associated with PE (Anteby et al. 2004; Kosmas et al. 2004; Sarandöl et al. 2004). The fact that these genes are missed by the single SNP analysis but detected by the gene-based analysis may be due to higher-order complex interactions among disease variants. However, when there is only one disease variant in a gene, the single SNP test slightly beats the gene-based approach by simulation (Figure 3). As little is known about the nature of the true functional mechanism of a gene, our conservative recommendation is to report genes detected by both approaches.

By focusing on each gene as a separate module or unit, a gene-centric association study can be designed using a “direct” or “sequence-based” approach by examining candidate genes with known biological function or can be studied using an “indirect” or “map-based” approach taking advantage of LD among variants (Jorgenson and Witte 2006). Currently, the direct approach is limited by incomplete knowledge about functional variation of a gene. The indirect approach with reliance on the information of LD among variants is preferred instead. The developed entropy approach considers the joint multilocus LD information for a given gene in an association test and fits this mission well. Also, for SNPs in evolutionarily conserved regions, once genotyped, they can be defined as a functional unit and then an entropy-based test can be performed to identify possible cis enhancers to cover all functionally important variants. Due to reduced genotyping burden with a small number of genic SNPs, a gene-centric GWA approach would be a first choice to implement as an efficient initial genomewide association scan for targeting biologically plausible genomic regions with reduced multiple-testing burden.