Violations of transitivity under fitness maximization

Abstract

We present a novel demonstration that violations of transitive choice can result from decision strategies that maximize fitness. Our results depend on how the available options, including options not currently chosen, influence a decision-maker's expectations about the future. In particular, they depend on how the presence of an option may act as an insurance against a run of bad luck in the future.

1. Introduction

The principle of transitivity is one of the cornerstones of economic theories of rational choice (Edwards 1954, 1961; Luce & Suppes 1965; Grether & Plott 1979; Kacelnik 2006; Rieskamp et al. 2006). Given three options A, B and C, transitivity means that if an animal prefers B to A and C to B, then it prefers C to A. Transitivity is expected to hold if choices are based on a single scale, such as when fitness is maximized. In such a context, intransitivity is associated with irrational behaviour. However, intransitive choices have been reported relatively regularly from both humans and other animals (Tversky 1969; Temkin 1993; Rieskamp et al. 2006; Bateson & Healy 2005). We show that if a decision-maker is concerned not only with current gains but also with future gains, then intransitive decisions can emerge from optimal behaviour. This is relevant to a wide range of studies of human and animal choice.

Schuck-Paim et al. (2004) show that some apparent instances of intransitive choice can be explained by uncontrolled variations in the test subjects' state. If experiments are not carefully designed, animals in different treatments may accumulate different quantities of food during the experiment and hence differ in state. It is well established that choice depends on state, and so a valid test of transitivity must be based on choices made in the same state. We now show how decisions that violate transitivity may occur even when an animal's choice is measured in the same state. To obtain this, we assume that the options currently present may still be available in the future. Thus, current options influence future expectations and hence the value of a current action depends on the other available actions.

2. Intransitivity and long-term survival

We first consider an animal that is facing the dangers of starvation and predation during a long non-reproductive period such as winter. During this time, the animal dies of starvation if its energy reserves, x, fall to x=0. There is also a maximum energy storage capacity. At each of the discrete times t=0, 1, 2, …, the animal chooses between foraging options that differ in terms of mean energetic intake and risk of predation. Option i offers a reward of mean energetic content 2 with probability p_i and incurs predation risk μ_i. Under each option, one unit of energy reserves is required for metabolic expenditure in each time unit. A strategy for the animal specifies how the animal's choice of foraging option depends on its current energy reserves. Using dynamic programming (Houston & McNamara 1999; Clark & Mangel 2000), we find the state-dependent strategy that maximizes the animal's probability of overwinter survival. We focus on behaviour when there is a fairly long time to go before the end of the winter. In this case, the optimal strategy is independent of time (e.g. Houston & McNamara 1999; Clark & Mangel 2000). This optimal strategy always involves taking fewer risks in terms of predation as reserves increase (e.g. McNamara 1990).

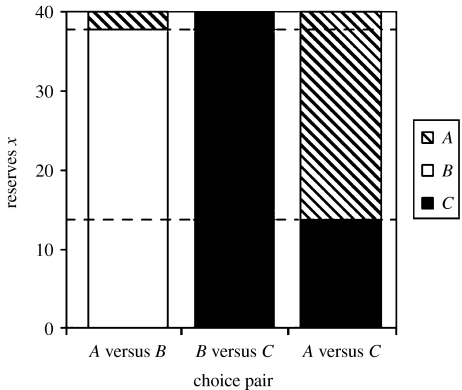
To show that transitivity can be violated, we find the optimal strategy in three environments (figure 1). In each environment, the animal can choose between two of the options given in table 1. The maximum level of energy reserves is 40. In the first environment, options A and B are available. The optimal strategy is to choose option B for reserves less than or equal to 38 and to choose option A for higher reserves. Option A (safe, but with a low intake) is used when energy reserves are high. When reserves are low, the animal should take a risk in order to obtain a higher energy intake and so chooses option B. In the second environment, options B and C are available and the optimal strategy is to choose option C at all levels of reserves because this option has the same predation risk as option B but a higher probability of obtaining food. In the third environment, options A and C are available. The optimal strategy is to choose option C for reserves less than or equal to 14 and to choose option A for higher reserves. To understand why the critical level of reserves at which choice changes is lower in this environment than in the first environment, note that option C has a higher mean intake than option B, and hence acts as a better insurance against starvation. The animal can thus afford to allow its reserves to fall to a lower threshold before using the risky option when option C is present rather than option B.

Figure 1.

The optimal reserve-dependent strategy in each of three environments when the animal is maximizing survival. In each environment, two of the three options given in table 1 are available. The maximum energy storage capacity is x=40. The dotted lines indicate the range of reserves between which intransitive choice is predicted.

Table 1.

The foraging options characterized by p, the probability that a food item of mean energy content 2 (actual content 1, 2 or 3 with probabilities 0.25, 0.50 and 0.25, respectively) is available, and μ, the predation risk.

option	p	μ
A	0.50	0
B	0.55	0.00001
C	0.75	0.00001

Now consider an experiment in which an animal with reserves x is given a single choice between two options. For reserves between x=15 and x=38, B is chosen from A and B, C is chosen from B and C and A is chosen from A and C, i.e. transitivity is violated.

3. Intransitivity and reproduction

In our second example, the animal is attempting to build up its reserves to a level at which it can reproduce. While doing so, the animal dies of starvation if its energy reserves, x, fall to x=0. At each of the discrete times t=0, 1, 2, …, the animal chooses between foraging options that differ in terms of mean and variance in energy intake. All options incur the same predation risk. We use dynamic programming to find the state-dependent strategy that maximizes the probability that the animal survives until it reaches the level of reserves required for reproduction.

For given variance in food intake, high mean intake is advantageous for two reasons. It helps to avoid starvation and it also improves the chances of reaching the level required for reproduction before the animal is killed by the background predation risk. For given mean intake, low variance is advantageous at low reserves because it reduces the chance that the animal will starve owing to a run of bad luck. On the other hand, high variance is advantageous at all levels of reserves because the background predation makes it worth an animal gambling on getting to high reserves quickly (Houston & McNamara 1990). This means that if there is a state-dependent switch between a low-variance and a high-variance option, then the low-variance option is chosen at low reserves and the high-variance option is chosen at high reserves (McNamara et al. 1991).

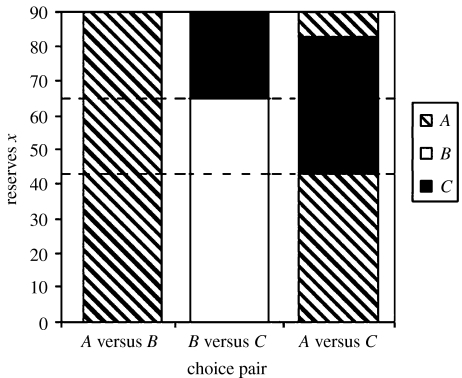
Again the animal makes decisions in three environments, each environment offering a choice between two of the three options given in table 2. Under each option, one unit of energy reserves is required for metabolic expenditure in each time unit. Option A has a mean intake between that of B and C and the lowest variance in intake. Option B has the lowest mean and intermediate variance. Option C has the highest mean and variance. Optimal strategies are shown in figure 2. When options A and B are available, it is always optimal to choose option A, since the possible benefits of choosing the riskier option (B) at high reserve levels are not great enough to outweigh the higher mean intake associated with option A. When options B and C are available, it is optimal to avoid variability when x<65 and choose B, but if x≥65 then the optimal strategy is to prefer variability and choose C. Similarly, a preference switch is observed when options A and C are available, but the level of reserves where the switch occurs in this environment is at x=43. Option C has high variance and is therefore an unsuitable choice at low reserves owing to the danger of starvation. When option C is paired with one of the other options, the other option acts as insurance when reserves are low. Option B has a lower mean and higher variance than option A and is therefore less good as an insurance. It follows that the animal has to switch to option B at higher reserves than it switches to option A if the insurance is to be effective in preventing starvation.

Table 2.

The foraging options characterized by p, the probability that a food item is available, and e, the mean energy content of the item (actual content e−1, e or e+1 with probabilities 0.25, 0.50 and 0.25, respectively). Background predation=0.00006.

option	p	e	mean	var
A	0.570	2	0.14	0.9804
B	0.271	4	0.084	3.1609
C	0.145	8	0.16	7.9344

Figure 2.

The optimal reserve-dependent strategy in each of three environments when the animal is building up reserves for reproduction. In each environment, two of the three options given in table 2 are available. The threshold value of reserves needed for reproduction is x=90. (When options A and C are available, the optimal strategy is to switch back to A when x goes above 83 since energy that would take the reserves above the threshold for reproduction is lost.) The dotted lines indicate the range of reserves between which intransitive choice is predicted.

Consider an experiment in which an animal with reserves x is given a single choice between two options. For reserves between 43 and 64, it will prefer A to B, B to C and C to A; we have again shown optimal strategies producing intransitive choice, this time within the context of an animal that is building up its reserves in order to reproduce.

4. Discussion

In the models that we present, the optimization procedure finds the best reserve-dependent strategy in each environment. In terms of these strategies, there is no violation of transitivity. For each environment, there is a unique best strategy and this strategy specifies how behaviour should depend on the animal's reserves. Decisions appear to violate transitivity if an observer interprets a single choice by an animal with given reserves as indicating a straightforward preference for one option over another, instead of viewing the choice as a consequence of following the optimal reserve-dependent strategy.

Our results are based on the animal being able to make repeated choices between options. Even if experiments do not involve such repeated choices, animals may use rules that evolved to cope with environments in which the options that are available to a decision-maker will persist into the future. This idea is plausible in many contexts. There is evidence to suggest that migrating birds use current food availability to predict future food availability (Houston 1998; Weber et al. 1999). Humans may behave as if interactions will be repeated (e.g. Hagen & Hammerstein 2006). Houston (1997) uses the idea of persistence to demonstrate violations of transitivity when there are cost-dependent errors in decision-making. These errors mean that future expectations are based on all available options, not just on the preferred option. In our current approach, decisions are not subject to errors but the animal's state can change over time and the action that should be taken in future states influences current optimal actions (cf. Kacelnik 2006; Kacelnik et al. 2006). Thus, even though reproductive value provides a common currency for decisions (McNamara & Houston 1986), value is not fixed, but depends on context. The option that is available but not currently chosen changes the future possibilities and hence the reproductive value.

We have shown that optimal state-dependent behavioural strategies can include intransitive choice patterns under certain circumstances. Although we have presented our effect in two particular contexts, it seems reasonable to suggest that the effect may be found if animals expect current options persist into the future and future circumstances are different from current circumstances. Under these conditions, current options influence prospects.