The mechanical power requirements of avian flight

Abstract

A major goal of flight research has been to establish the relationship between the mechanical power requirements of flight and flight speed. This relationship is central to our understanding of the ecology and evolution of bird flight behaviour. Current approaches to determining flight power have relied on a variety of indirect measurements and led to a controversy over the shape of the power–speed relationship and a lack of quantitative agreement between the different techniques. We have used a new approach to determine flight power at a range of speeds based on the performance of the pectoralis muscles. As such, our measurements provide a unique dataset for comparison with other methods. Here we show that in budgerigars (Melopsittacus undulatus) and zebra finches (Taenopygia guttata) power is modulated with flight speed, resulting in U-shaped power–speed relationship. Our measured muscle powers agreed well with a range of powers predicted using an aerodynamic model. Assessing the accuracy of mechanical power calculated using such models is essential as they are the basis for determining flight efficiency when compared to measurements of flight metabolic rate and for predicting minimum power and maximum range speeds, key determinants of optimal flight behaviour in the field.

1. Introduction

The relationship between the power that must be generated by the flight muscles and speed is central to understanding the ecology and evolution of bird flight behaviour and determining the limits to performance. Direct measurements of flight muscle power output are difficult to obtain and therefore previous approaches have relied on indirect measurements and assumptions. Indirect mechanical power estimates have been based on aerodynamic theory (Pennycuick 1975; Rayner 1979), derived from measurements of metabolic rate (Tucker 1973; Ward et al. 1999), or based on measurements of bone strain as an index of muscle force (Biewener et al. 1992; Dial et al. 1997; Hedrick et al. 2003). These approaches have produced power–speed relationships that vary both qualitatively and quantitatively. Consequently, the shape of the avian flight power–speed relationship has remained controversial (Tobalske et al. 2003). We have used a new approach to estimate the avian power–speed relationships based on physiological measurements of the flight muscles themselves.

2. Material and methods

Power was measured in a fascicle bundle excised from budgerigar (Melopsittacus undulatus) and zebra finch (Taenopygia guttata) pectoralis muscle. This muscle powers the downstroke and is the main mechanical power source during flight. In both species, the pectoralis muscles contain a single muscle fibre type, fast-oxidative glycolytic (Rosser & George 1986) and a single myosin heavy chain isoform (Rosser et al. 1996). Therefore, their power output is likely to be determined entirely by muscle activity and strain trajectory, rather than recruitment of motor units with different contractile properties as in many other vertebrate muscle systems.

(a) Animals

Budgerigars (N=18) and zebra finches (N=13) were trained to fly in a variable-speed wind tunnel (electronic supplementary material).

(b) Sonomicrometry and electromyography

For each experiment, two sonomicrometry transducers, two bipolar EMG electrodes and a single ground wire were implanted into the superficial facia of the pars sternobrachialis region of the pectoralis muscle under isoflurane-induced anaesthesia (electronic supplementary material). Muscle length and activity data were recorded in budgerigars (N=7) and zebra finches (N=6) flying at speeds ranging from 4 to 16 m s⁻¹ and 0 to 12 m s⁻¹, respectively. The average EMG intensity of muscle activity during the flight was calculated (electronic supplementary material).

(c) Muscle physiology

An intact bundle of fascicles was dissected from a set of trained birds, under terminal isoflurane-induced anaesthesia (budgerigars, N=11; and zebra finches, N=7) from the same region of the pectoralis muscle where sonomicrometry and electromyography recordings were made (§2b). The fascicles were transferred to a muscle chamber through which oxygenated Krebs–Henseleit Ringer's solution at 40°C was circulated. The muscle fascicle bundle was anchored proximally by a small section of the sternum to the base of the chamber and attached via the distal tendon to a muscle ergometer (Aurora Scientific, model 300B). Custom written software controlled the muscle ergometer and a stimulator (Grass model S4) and was used to impose on the muscle fascicles the simulated in vivo strain trajectories and activity patterns measured during flight following Askew & Marsh (2001). For each flight speed, a third-order Fourier series was fit to the in vivo strain data in a series of four to seven consecutive wing strokes. The Fourier coefficients from individual birds were averaged and a composite strain wave was reconstructed from the mean coefficients. The fascicles were subjected to the reconstructed strain trajectory and stimulated to contract by applying a supramaximal voltage via parallel, platinum electrodes (frequency 275 Hz zebra finch, 200 Hz budgerigar; pulse width 0.2 ms). Muscle force and length were recorded onto a personal computer at 5 kHz via a data acquisition card (Keithley Instruments model DAS1801AO). The positive power output during shortening (equivalent to the downstroke) was calculated from the force and differentiated strain trajectory of the fascicles. Measured in vitro power was corrected for in vivo recruitment by multiplying the power by relative intensity (assuming a direct link between EMG intensity and work; see Adams et al. 1992; Roberts et al. 1997). We also accounted for the birds' use of intermittent flight by multiplying the powers by the proportion of time spent flapping at each flight speed. Flight power was estimated by assuming that all of the mechanical power is generated by the pectoralis muscle and that the power generated by the fascicle bundle is representative of the whole pectoralis muscle.

(d) Kinematics and aerodynamic model

During flight, instrumented birds were videoed using a high-speed camera (Kodak MotionCorder) operating at a frame rate of 125 fps and shuttered at 1/5000 s. Wing and body kinematics were obtained by digitizing the recorded images (VideoPoint v.2.5). An aerodynamic analysis was carried out to calculate the total aerodynamic power (based on Wakeling & Ellington 1997; Askew et al. 2001; electronic supplementary material). The calculations require values to be assumed for the induced power factor k, the profile drag (C_D,pro) and parasite drag (C_D,par) coefficients, and body frontal area (S_b). We used the minimum and a typical range of values for the coefficients previously reported in the literature (electronic supplementary material).

3. Results and discussion

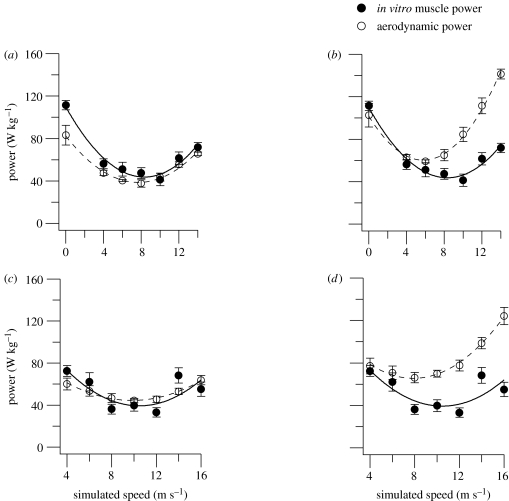
The mechanical performance of the pectoralis muscle fascicles operating under simulated in vivo conditions, corrected for speed-related changes in muscle activity and the birds' use of intermittent flight (§2c), is shown in figure 1. Mechanical power output of pectoralis muscle had an approximately U-shaped relationship with simulated speed in both species (figure 2).

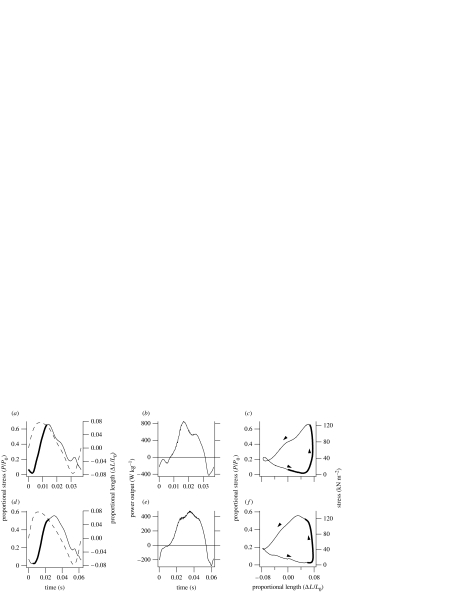
Figure 1.

Mechanical performance of pectoralis muscle fascicles in vitro. (a,d) The imposed strain trajectory(dashed line), stimulus and resulting force production(solid line), relative to peak isometric tetanic force, P₀. The bold line indicates the period of stimulation. (b,e) Instantaneous power output. (c,f) The force–length relationship or ‘work loop’. The work loops are anticlockwise (indicated by the arrows) and therefore represent net positive work. Data are typical examples obtained from (a–c) zebra finch and (d–f), budgerigar pectoralis muscle.

Figure 2.

Pectoralis muscle power output and its relationship with flight speed. Power output was calculated using an aerodynamic model for a range ((a,c) minimum: C_D,par 0.05 (Tucker, 2000), C_D,pro 0.01 (Tobalske et al., 2003), k 1.0; S_b=0.00813M_b^0.666 (Pennycuick et al., 1988); and (b,d) typical: C_D,par 0.13 (Rayner, 1999), C_D,pro 0.02 (Rayner, 1979), k 1.2 (Pennycuick, 1975), S_b=0.00813M_b^0.666 (Pennycuick et al., 1988)) of aerodynamic coefficients from the literature and is compared with pectoralis muscle power output (mean±s.e.m.) determined in vitro, corrected for recruitment and intermittent flight. Data are from (a,b) zebra finch and (c,d) budgerigar pectoralis muscle. In vitro muscle power data are presented as mean±s.e.m. (budgerigars N=11, 9, 9, 6, 9, 5, 7 for speeds 4, 6, 8, 10, 12, 14, 16 m s⁻¹, respectively; zebra finches N=7, 6, 3, 5, 4, 4, 7 for speeds 0, 4, 6, 8, 10, 12, 14 m s⁻¹, respectively). Aerodynamic modelling was carried out on seven budgerigars at all speeds except 4 and 16 m s⁻¹ where data are from four and six individuals, respectively. In zebra finches, modelling was performed on six individuals at all speeds, except 4 and 14 m s⁻¹ where data are from four individuals.

It is essential to determine the reliability of our muscle power measurements if they are to be compared with powers calculated using aerodynamic models. Measurements of isometric stress and mean stress difference during cyclical contractions indicate that the pectoralis muscle fascicles achieved a level of mechanical performance expected from muscle tissue of this type (electronic supplementary material). Therefore, we can have confidence in the reliability of our measured power outputs and the validity of our approach.

Previous measurements of pectoralis muscle function in birds have used tensile bone strain on the deltopectoral crest of the humerus as an index of muscle force (Biewener et al. 1992; Dial et al. 1997; Hedrick et al. 2003). This was thought to provide an independent measure of flight muscle power. Unfortunately, a reliable quantitative link between bone strain and pectoralis muscle force is difficult to establish (Hedrick et al. 2003). In recognition of these problems, power estimates obtained by this method have been calibrated with reference to aerodynamic estimates of power (Hedrick et al. 2003; Tobalske et al. 2003), limiting the utility of this approach as an independent, quantitative measure of pectoralis muscle power output.

Aerodynamic power estimates also have inherent uncertainties. Aerodynamic calculations of flight power are typically based on a three-component model (Pennycuick 1975; Rayner 1979). The induced power component is highest at low speeds and falls with increasing speed, whereas both the parasite and profile power components increase with speed. The relationship between total mechanical power and speed should therefore be U-shaped, at least qualitatively (Rayner 1999). The uncertainty lies in making quantitative power predictions. The absolute values calculated for both the parasite and profile power components are dictated by the drag coefficients used. Induced power calculations include a correction factor to account for energy losses and non-uniformity of airflow. Empirical data to indicate the correct values for these coefficients are scarce. This has led to the adoption of a wide range of values, generating an equally wide range of power estimates.

Given the uncertainty regarding the magnitude of powers calculated using aerodynamic theory, we compared our measurements of muscle power with a range of aerodynamic power estimates. These aerodynamic power estimates are based on the minimum and a set of typically used values for constants and drag coefficients previously suggested in the literature (§2). Overall, the minimum constant and coefficient values produce the closest match between the aerodynamic and in vitro power measurements (figure 2a,c). For an induced power factor (k) of 1.0, the induced power approaches that for an ideal helicopter and is physically very unlikely. It is therefore reassuring that in both species, k=1.0 underestimates flight power at low speeds. At low speeds, the agreement between the typical aerodynamic model and the in vitro power measurements suggests that an induced power factor of 1.2 is appropriate (figure 2b,d). Both profile and parasite powers dominate the total power requirements at higher speeds. The typical profile and parasite drag coefficients overestimate the mechanical power requirements of flight at intermediate and higher speeds in both species (figure 2b,d). The minimum profile and parasite drag coefficients produce a much closer match between the aerodynamic and in vitro muscle powers (figure 2a,c). In both species, a combination of a standard induced power factor of 1.2 and profile and parasite drag coefficients from the lower end of the range previously used in the literature provides the closest match between calculated aerodynamic power and measured muscle power output. Our data suggest that the use of typical drag coefficients in aerodynamic models should be re-evaluated, particularly when applied to high flight speeds.

Supplementary Material

The Mechanical Power Requirements of Avian Flight

Additional details of the methodology and analysis