Ab initio RNA folding by discrete molecular dynamics: From structure prediction to folding mechanisms

Abstract

RNA molecules with novel functions have revived interest in the accurate prediction of RNA three-dimensional (3D) structure and folding dynamics. However, existing methods are inefficient in automated 3D structure prediction. Here, we report a robust computational approach for rapid folding of RNA molecules. We develop a simplified RNA model for discrete molecular dynamics (DMD) simulations, incorporating base-pairing and base-stacking interactions. We demonstrate correct folding of 150 structurally diverse RNA sequences. The majority of DMD-predicted 3D structures have <4 Å deviations from experimental structures. The secondary structures corresponding to the predicted 3D structures consist of 94% native base-pair interactions. Folding thermodynamics and kinetics of tRNA^Phe, pseudoknots, and mRNA fragments in DMD simulations are in agreement with previous experimental findings. Folding of RNA molecules features transient, non-native conformations, suggesting non-hierarchical RNA folding. Our method allows rapid conformational sampling of RNA folding, with computational time increasing linearly with RNA length. We envision this approach as a promising tool for RNA structural and functional analyses.

INTRODUCTION

The central dogma of molecular biology ascribed fundamental importance to RNA molecules in transcription and translation. Both coding and noncoding RNA molecules are now known to possess much greater variety of biological functions (Eddy 2001; Huttenhofer and Schattner 2006) than what was suggested by the central dogma. During the last two decades, significant developments have lead to new insights in the importance of RNA in many post-transcriptional and post-translational processes. Discoveries of ribozymes and a variety of small RNAs with novel biological functions have highlighted RNA as a ubiquitous molecule in cellular processes (Doherty and Doudna 2001). To perform their biological functions, many RNA molecules adopt well-defined tertiary structures. The RNA conformational dynamics determines how often these functionally important conformations appear in the course of RNA's life and, therefore, modulate its functional activity. Hence, there is a rejuvenated interest in accurate ab initio prediction of three-dimensional (3D) structure and dynamics of RNAs (Shapiro et al. 2007).

Currently, RNA folding tools are mainly focused on predicting RNA secondary structure (Mathews 2006). Computational tools for RNA secondary structure prediction, such as Mfold (Zuker 2003) and Vienna RNA (Hofacker 2003), are successful in predicting the RNA base pairing loci, thereby predicting the secondary structure organization. Using a dynamic programming approach (Eddy 2004), secondary structures are inferred by scoring nearest-neighbor stacking interactions with adjacent base pairs (Mathews 2006). However, these analyses based on base-pairing and base-stacking interactions ignore 3D steric hindrances in scoring putative secondary structures of RNA. The explicit modeling of the 3D structure might prohibit unfeasible tertiary structures of RNA. Cao and Chen designed a simplified diamond-lattice model for predicting folded structure and thermodynamics of RNA pseudoknots (Cao and Chen 2006). This approach quantitatively predicts the free energy landscape for sequence-dependent folding of RNA pseudoknots, in agreement with experimental observations (Cao and Chen 2006). However, due to the lattice constraints and the dynamic issues associated with predefined Monte Carlo moves (Baumgartner 1987), this approach is inadequate to study the folding dynamics of RNAs. Several other computational tools were developed for RNA 3D structure prediction (for review, see Shapiro et al. 2007). These methods either use comparative modeling of RNA sequences with known structures or utilize known secondary and tertiary structural information from experiments in interactive modeling (Major et al. 1991, 1993; Shapiro et al. 2007). Therefore, novel automated computational tools are required to accurately predict the tertiary structure and dynamics of RNA molecules. Recently developed knowledge-based approaches using assembly of trinucleotide torsion-angle libraries (Das and Baker 2007) are successful in predicting RNA structures for small globular RNA fragments (∼30 nucleotides [nt]). However, RNA molecules often do not adopt globular topologies, such as the L-shaped tRNA. Enhanced prediction accuracy for longer RNA molecules is attainable by using physically principled energy functions and using an accurate sampling of RNA conformations.

Here, we introduce a discrete molecular dynamics (DMD) (Ding and Dokholyan 2005) approach toward ab initio 3D RNA structure predictions and characterization of RNA folding dynamics using simplified structural models. In contrast to the traditional molecular dynamics simulations, which are computation-intensive and hence expensive in probing RNA folding dynamics over long time scales, the DMD algorithm provides rapid conformational sampling (Ding and Dokholyan 2005). It is demonstrated in numerous studies that the DMD method is suitable for studying various properties of protein folding (Chen et al. 2008) and protein aggregation (Ding and Dokholyan 2005), and for probing different biomolecular mechanisms (Ding and Dokholyan 2005; Sharma et al. 2006, 2007). Here, we extend this methodology to the RNA folding problem. We simplify the RNA structural model by using a “bead-on-a-string” model polymer with three coarse-grained beads—phosphate, sugar, and base—representing each nucleotide (see Materials and Methods; Fig. 1). We include the base-pairing, base-stacking, and hydrophobic interactions, the parameters of which are obtained from experiments. The coarse-grained nature of the model, as well as the efficiency of the conformational sampling algorithm, enables us to rapidly explore the possible conformational space of RNA molecules.

FIGURE 1.

Coarse-grained structural model of RNA employed in DMD simulations. (A) Three consecutive nucleotides, indexed i − 1, i, i + 1, are shown. Beads in the RNA: sugar (S), phosphate (P), and base (B). (Thick lines) Covalent interactions, (dashed lines) angular constraints, (dashed–dotted lines) dihedral constraints. Additional steric constraints are used to model base stacking. (B) Hydrogen bonding in RNA base pairing. (Dashed lines) The base-pairing contacts between bases B _{i − 1}:B_{j + 1} and B _i:B _j. A reaction algorithm is used (see Materials and Methods) for modeling the hydrogen bonding interaction between specific nucleotide base pairs.

RESULTS

Large-scale benchmark test of DMD-based ab initio RNA structure prediction on 153 RNA sequences

We test the predictive power of the DMD-based RNA folding approach by selecting a set of intermediate-length RNA sequences, whose experimentally derived structures are available at the Nucleic Acid Database (NDB, http://ndbserver.rutgers.edu), and compare our predictions with experimentally derived structures and folding dynamics. We restrict our study to RNA molecules having a length greater than 10 nucleotides (nt) and shorter than 100 nt. Short RNA molecules lack well-formed tertiary structures and were excluded from this study. All simulated RNA molecules (153 in total) are listed in Supplemental Table 1. Notably, this set of 153 molecules spans a range of tertiary structural motifs: cloverleaf-like structures, L-shaped tRNAs, hairpins, and pseudoknots.

For each RNA molecule, we first generate a linear conformation using the nucleotide sequence. Starting from this extended conformation, we perform replica exchange simulations at different temperatures (see Materials and Methods). The three-dimensional conformation corresponding to the lowest free energy is predicted as the putative structure of the RNA molecule, assuming that the corresponding native structure is unknown. The extent of native structure formation in simulations is measured by computing the Q-values (akin to protein folding experiments [Sali et al. 1994], see Materials and Methods), defined as the fraction of native base pairs present in a given RNA conformation. We compute Q-values for the lowest free energy states (i.e., predicted putative structures) and also the maximum Q-values sampled during the course of simulations (Fig. 2A; Supplemental Table 1). For a majority of the simulated RNA sequences, the lowest free-energy structures from simulations have predicted Q-values close to unity, suggesting the correct formation of native base pairs in simulations. The average Q-value for all 153 RNA molecules under study is 94%. For comparison with available secondary structure prediction methods, we also compute the Q-values using Mfold (Fig. 2A; Supplemental Table 1), and the average Q-value is 91%. The DMD-based RNA folding approach shows improvement over the Mfold method in predicting the native base pairs, especially for pseudoknots (Supplemental Table 1).

FIGURE 2.

Ab initio RNA folding using DMD. (A) Fraction of native base pairs (Q-values) present in the predicted RNA 3D structure. The maximum Q-values during the course of simulations are also shown, which depict the conformational sampling efficiency of the DMD algorithm to reach the native states. We also show the Mfold predicted Q-values. (B) Scatter plots of RMSD for the final folded conformation with respect to the experimentally derived native structure as a function of RNA size. Large RNA molecules have increased fluctuations due to larger conformational freedom and consequently have greater RMSD from the native conformation. (C) Normalized histogram of predicted and least RMSD to the native RNA structure.

Out of 153 RNA molecules studied, there are three cases (NDB codes: 1P5O, 1P5M, and 2AP5) where the predicted and maximum Q-values as well as the Q-value from the Mfold prediction are small. Additionally, there are a few cases where the predicted Q-values are not unity while the maximum Q-values are unity (Fig. 2A). This suggests that our simulations are able to sample the native state, but the force field cannot capture it. Therefore, further optimization of the force field parameters is necessary.

The objective of this work is toward ab initio tertiary structure prediction. Toward this goal, we evaluate our predicted tertiary structures by computing their root-mean-square deviation (RMSD) from corresponding native structures, excluding the three RNA molecules where the secondary structures are not correctly formed (Fig. 2B,C). The RMSD value is computed based on the backbone phosphate atoms. We notice that the predicted lowest free energy structure usually does not have the lowest RMSD with respect to the corresponding crystal structure (Fig. 2B,C; Supplemental Table 1), possibly due to inaccuracy of the force field and the coarse-grained nature of the simplified RNA model. Despite these approximations, the method features striking predictive power. We observe that for the RNA molecules with nucleotide length <50, the predicted RMSD are <6 Å. Longer RNA molecules exhibit larger RMSD due to the highly flexible nature of RNA molecules. Among the 153 sequences simulated, 84% of the predicted tertiary structures have an RMSD of <4 Å with respect to the experimentally derived native RNA structure. Many functionally important RNA molecules have short sequences, e.g., pre-miRNA is typically 70–100 nt long, suggesting a potential for DMD-based RNA folding for de novo structure prediction of functional RNA molecules.

Folding dynamics in DMD simulations

We analyze the folding thermodynamics and kinetics for several nontrivial RNA motifs, the pseudoknot and tRNA. We also study the folding thermodynamics of B-RNA (Escherichia coli 23S rRNA, G1051-C1109) (Laing and Draper 1994), 72 RNA (E. coli α-operon mRNA fragment G16-A72) and its mutants: 72-C RNA (G16-A72, G51→C) and 72-14 RNA (G16-A72, AA44→CC, UU54→GG) (Gluick and Draper 1994), and compare our simulations with corresponding experimental measurements.

Pseudoknot folding

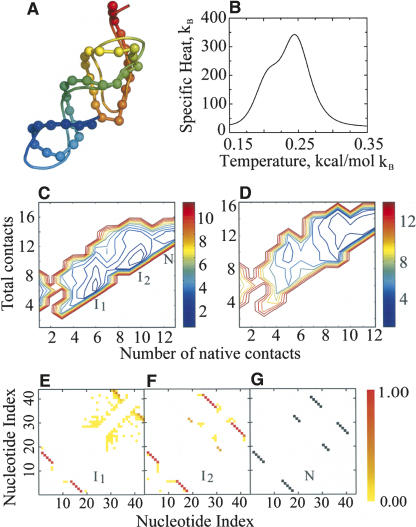
The RNA pseudoknot structure has non-nested base pairing and minimally consists of base-pairing between a loop region and a downstream RNA segment. Pseudoknots serve diverse biological functions, including formation of protein recognition sites mediating replication and translational initiation, self-cleaving ribozyme catalysis, and inducing frameshifts in ribosomes (Staple and Butcher 2005). We study pseudoknot folding dynamics by selecting a 44-nt-long representative pseudoknot whose structure is available at high resolution (NDB code: 1A60) (Fig. 3A). This pseudoknot represents the T-arm and acceptor stem of the turnip yellow mosaic virus (TYMV) and has structural similarity with TYMV genomic tRNA (Kolk et al. 1998). The model pseudoknot is stabilized by the hairpin loop formed at the 5′ end of RNA, and by the interactions with the loops of the pseudoknot in the 3′ end.

FIGURE 3.

Ab initio folding kinetics and energetics of a model pseudoknot RNA. (A) Superposition of experimental pseudoknot structure (NDB code: 1A60, ribbon) against DMD prediction (ribbon backbone trace with backbone spheres). Backbone ribbons are colored blue (N terminus) to red (C terminus). (B) Graph of specific heat of the pseudoknot molecule as a function of simulation temperature. (C) Two-dimensional potential of mean force 2D-PMF for pseudoknot folding at T* = 0.245 (corresponds to the major peak in the specific heat). (I₁, I₂) The two intermediate states, (N) native state. (D) The 2D-PMF plot at T* = 0.21. (E) Internucleotide base-pairing contact frequencies at the first folding intermediate (I₁) corresponding to the state where the 5′ hairpin is folded. (F) Internucleotide base-pairing contact frequencies at the second intermediate state (I₂) corresponding to the formation of the major groove helix stem of the 3′ pseudoknots. (G) Contact map of the native state (N) as observed in the experimental structure (NDB code: 1A60).

We calculate the folding thermodynamics using the weighted histogram analysis method (WHAM) (see Materials and Methods). The specific heat (Fig. 3B) has one peak centered at temperature T* = 0.245 and a shoulder near T* = 0.21 (temperature expressed in reduced units, see Materials and Methods), suggesting the presence of intermediate states in the folding pathway (Fig. 3B). The thermodynamic folding intermediate species is characterized by computing the two-dimensional potential of mean force (2D-PMF) as a function of total number of base pairs (N) and the number of native base pairs (NN). The 2D-PMF plots at temperatures corresponding to the two peaks in the specific heat (Fig. 3C,D) show two intermediate states with distinct free energy basins: The first intermediate state corresponds to the folded 5′ hairpin, while the second intermediate corresponds to the formation of one of the helix stems for the 3′ pseudoknot. For example, the 2D-PMF plot at T* = 0.21 (Fig. 3D) shows that the shoulder in the specific heat plot corresponds to the formation of the second intermediate state. The basins corresponding to the two intermediate states have a weak barrier, resulting in a lower height in the specific heat plot. Contact frequencies at the folding intermediates and the native state contact map (Fig. 3E–G) demonstrate the progress in the pseudoknot folding pathway.

tRNA folding

The transfer RNA (tRNA) molecules serve as information transducers, linking the amino acid sequence of a protein and the information in DNA, thereby, decoding the information in DNA. Crystallographic studies of tRNA molecules reveal a distinct L-shaped 3D structure (Fig. 4A). Here, we study the folding of a yeast phenylalanine tRNA (NDB code: 1evv). For the tRNA molecule, the predicted Q-value is ∼0.87. We find that the RMSD of the putative structure is ∼7.20 Å with respect to the crystal structure, while the lowest RMSD in the simulation is ∼5.2 Å (Supplemental Table 1). The predicted structure misses the tertiary contacts between the TΨC-loop and D-loop (Fig. 4A); such long-range contacts are stabilized by metal ion coordination as shown in high-resolution X-ray crystallography structures (Fig. 4A). Since our model does not include nucleotide metal ion coordination effects, such tertiary contacts mediated by metal coordination are not expected to form during the DMD simulations. However, this methodology is still able to recapitulate all other tertiary contacts, including the long-range helix between the 5′ and 3′ ends and co-stacking between the terminal helix and D-helix, and between the TΨC-helix and anticodon helix (Fig. 4B). The specific heat of tRNA exhibits a single peak at T* = 0.22 (Fig. 4C). However, a single peak in the specific heat does not guarantee the absence of folding intermediates (Dixon et al. 2004). We first compute the 2D-PMF as the function of the total number of contacts and the number of native contacts at T* = 0.22 (Fig. 4D). We observe two major basins: one corresponding to the unfolded/misfolded states (NN = 0 and N ≥ 0), and the other corresponding to a state that has NN ∼ 6. There are minor basins corresponding to states with NN ranging from 10 to 18 and the native state with NN ∼22.

FIGURE 4.

Ab initio folding kinetics and energetics of a model tRNA. (A) Mg²⁺ binding site (sphere) in the tRNA. (B) Superposition of experimental tRNA structure (NDB code: 1EVV, ribbon) against DMD prediction (ribbon backbone trace with backbone spheres). Backbone ribbons are colored blue (N terminus) to red (C terminus). D loop, TΨC loop, anticodon loop, and acceptor loop are indicated with color representing their position in the tRNA secondary structure. (C) The specific heat of the tRNA molecule as the function of simulation temperature. (D) The 2D-PMF as the function of the total number of contacts and the number of native contacts at T* = 0.22. (I₁, I₂, I₃) Folding intermediates, (N) native conformation. (E,F) Folding events in the trajectories of tRNA replica exchange simulation. Two folding events in corresponding different replicas are observed out of eight replicas. (G–I) Internucleotide base-pairing contact frequencies at the threefolding intermediate states, I₁, I₂, and I₃, respectively. (J) Contact map of the native conformation (N) as observed in the experimental structure (NDB code: 1EVV).

We examine the folding trajectories in simulations (Fig. 4E,F) and observe that the tRNA folding process is not cooperative and follows multiple folding pathways. The twofolding trajectories (Fig. 4E,F) consist of distinct folding intermediates populated along the successful folding pathway. While the rest of the folding pathways are different in the twofolding events, common to the two folding events is the initial formation of the anticodon helix, suggesting that these intermediate states (NN ranging from 10 to 18; Fig. 4G–J) have similar free energies. Sorin and coworkers investigated the folding mechanism of tRNA using all-atom molecular dynamics simulations with Gō model (Sorin et al. 2004). These investigators observed that the tRNA folds via multiple folding pathways with distinct intermediates populated upon folding. This observation is consistent with our studies. The advantage of our methodology is that we do not impose the native structure bias in the simulations.

Folding of ribosomal and messenger RNA fragments

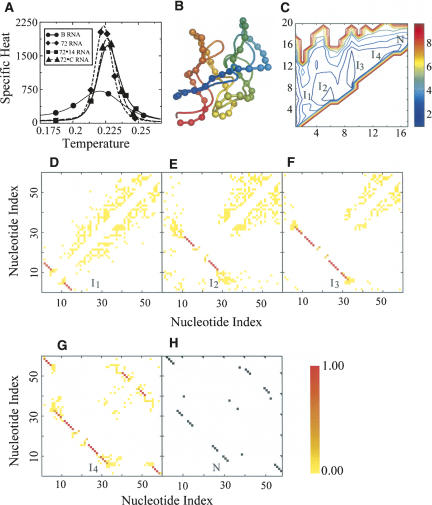
We compare our predictions with experimental data by studying the thermodynamics of four RNA sequences: B-RNA (E. coli 23S rRNA, G1051-C1109) (Laing and Draper 1994), 72 RNA (E. coli α-operon mRNA fragment G16-A72), and the 72-C RNA (G16-A72, G51→C), 72-14 RNA (G16-A72, AA44→CC, UU54→GG) mutants (Gluick and Draper 1994). The 72 RNA fragment contains a coding RNA sequence, suggesting functional implication of folding thermodynamics associated with translational regulation (Gluick and Draper 1994). Gluick and Draper (1994) have measured the melting curves of wild-type and mutant 72 RNA. Mutations at key 72-RNA nucleotides resulting in the 72-C RNA, 72-14 RNA sequences were engineered to probe significant events in 72-RNA folding thermodynamics (Gluick and Draper 1994). We compute the temperature dependence of specific heat of wild-type and mutant 72 RNA sequences from simulations (Fig. 5A). The predicted specific heat curves show a single dominant peak for each of the three 72 RNA sequences. We observe a shoulder at the higher temperature regime of 72-14 RNA, suggesting a convolution of multiple small transitions in 72-14 RNA folding. Notably, in 72-14 RNA, the peak of specific heat, corresponding to the experimentally measured melting temperature T_m, is shifted to the higher temperature regime, suggesting that the mutation AA44→CC, UU54→GG stabilizes the RNA. The predicted changes of T_m for 72-14 RNA and 72-C RNA with respect to wild-type 72-RNA are in agreement with the experimental measurements (Gluick and Draper 1994).

FIGURE 5.

Thermodynamics of B-RNA and 72 RNA variants. (A) Specific heat: (circles) B-RNA, (diamonds) 72-RNA, (squares) 72-C RNA, (triangles) 72-14 RNA (shown in DMD units). (B) Superposition of experimental B-RNA structure (ribbon) against DMD prediction (ribbon with backbone spheres). Backbone ribbons are colored blue (N terminus) to red (C terminus). (C) 2D-PMF of B-RNA as the function of the number of total base pairs and native base pairs. We find that there are three major basins in the 2D-PMF corresponding to intermediate states I₁, I₂, and I₃. (I₄) Near-native intermediate conformation, (N) native conformation. (D) Internucleotide contact frequencies at the intermediate state with about zero native contacts (i.e., non-native state I₁). (E) Internucleotide contact frequencies at the B-RNA folding intermediate state with about five native contacts, (non-native state I₂). (F) Internucleotide contact frequencies at the B-RNA folding intermediate state I₃ with about nine native contacts. (G) Internucleotide contact frequencies at the B-RNA folding intermediate state I₄ at near-native conformation. (H) Contact map in the native state (N) observed in the experimental structure (NDB code: 1C2W).

B-RNA represents the highly conserved 59-nt fragment (G1051-C1109) of E. coli 23S rRNA, serving as a recognition site for two structurally different ligands: ribosomal protein L11 and thiostrpton (a class of thiazole-containing antibiotics) (Laing and Draper 1994). Laing and Draper (1994) have experimentally measured the melting curves of B-RNA in 100 mM KCl, 0.1 mM MgCl₂. For B-RNA, we find that the specific heat profile has a broader peak (T* = 0.22) than that of 72-RNA and its mutants (Fig. 5A). We also observe that the magnitudes of specific heat of B-RNA at different temperatures are significantly smaller, as compared with that of the 72 RNA variants. The peak of specific heat for B-RNA is shifted toward the low-temperature regime, relative to 72-RNA, suggesting that B-RNA has lower stability than 72-RNA (Fig. 5A). These observations are consistent with calorimetric experiments of Laing and Draper (1994) and Gluick and Draper (1994). Also, the predicted B-RNA structure is in agreement with experimental observations (Fig. 5B). The corresponding experimental structure is taken from the 23S rRNA structure (NDB code: 1C2W), which is reconstructed from cryo-electron microscopy. We find that our predicted structure with the lowest free energy state agrees with the cryo-electron microscopic structure with a backbone RMSD of 6.2 Å.

There is also a broad shoulder in the B-RNA specific heat at the low-temperature regime. The flattened as well as skewed melting curve suggests a possible convolution of multiple folding transitions between intermediate states as observed in experiments (Laing and Draper 1994). The 2D-PMF of B-RNA at T* = 0.22 shows twofolding intermediates and one non-native state (Fig. 5C–F). Internucleotide contact frequencies in the near-native state are in agreement with the folded RNA state (Fig. 5G,H). Such accord between the predicted folding thermodynamics and experimental observations suggests that this approach is suitable for probing thermodynamics of RNA folding.

DISCUSSION

DMD-based RNA folding is rapid and potentially applicable for a number of molecular biotechnology and molecular biology-related applications. Rapid and accurate prediction of RNA tertiary structure is the core of the RNA folding problem. For small RNA molecules, ab initio predictions developed in this work have yielded significantly accurate structures. The available conformational space increases exponentially with increasing length of the simulated RNA. For example, we observed large structural flexibility for longer RNAs in DMD simulations. The complexity of adequately sampling conformational space through DMD simulations also increases significantly for large RNA molecules. We suggest that the hierarchical organization of RNA secondary and tertiary structures may be exploited to predict the structure of complex RNA molecules. Additionally, experimentally derived constraints, such as base pairs from SHAPE chemistry (Wilkinson et al. 2006), proximity information from hydroxyl radical experiments, and size measurements from small-angle X-ray scattering (SAXS), can help the structure determination of large RNA molecules. We can use biased interaction potential to guide simulations and generate RNA structures consistent with experimental measurements.

Two alternative scenarios for the time-course of RNA folding are possible: (1) the sequential hierarchical folding, where the secondary structure forms first, then tertiary contacts finally shape a specific tertiary structure (Tinoco and Bustamante 1999); and (2) the mutually dependent interplay of RNA secondary and tertiary interactions, where substantial rearrangement of folding intermediates successively takes place (Silverman et al. 1999). We posit that using simplified models for folding RNA is apt for investigating RNA folding mechanisms in de novo RNA fragments, as no assumptions regarding the folding mechanisms are made a priori. For the folding of the pseudoknot, the folding intermediate I₁ forms a weak non-native stem (contacts between nucleotides 32 and 42; see Fig. 3E), while intermediate I₂ does not have this but does have native stems (see Fig. 3F). The correct folding requires the disruption of the non-native stems. Similarly, the folding trajectories of tRNA (Fig. 4E,F) suggest that the folding of the RNA always accompanies the formation of non-native base pairs, with the total number of base pairs larger than the number of native base pairs. Therefore, our simulations suggest that RNA folds in a non-hierarchical manner, with nonnative conformations accumulated during the folding as observed in experiments (Wilkinson et al. 2005; Figs. 3, 4).

RNA folding has been investigated experimentally using single-molecule fluorescence spectroscopy (Zhuang 2005). These experiments conclude that RNA folding proceeds via a highly frustrated energy landscape, and adequate sampling of the RNA conformational ensemble is necessary for predicting RNA folding kinetics. The agreement of the thermodynamics between simulation predictions and experiments for B-RNA, 72-RNA, and its mutants encourages the efficacy of this method to qualitatively study folding thermodynamics of RNA molecules.

The coarse-graining process might alter the conformational entropy of molecules. To circumvent this coarse-graining artifact, the entropic contribution of loop formation is effectively modeled by estimating the loop free energies in simulations. The predicted structures correspond to the lowest free energy state, which is the result of an intricate interplay between enthalpy and entropy. We compute the effective loop free energies during simulations and introduced a stochastic approach to evaluate the formation of each base pair, corresponding to changes in loop lengths or formation/disruption of loops (see Materials and Methods). We find that this procedure is crucial for the correct prediction of the RNA structures: without taking the loop entropy into account, the simulation maximizes the number of base pairs but does not penalize the formation of additional loops, resulting in non-native RNA structures (data not shown).

One of the salient features of our approach is the rapid conformational sampling efficiency of DMD. We have previously reported estimates of experimental time scales accessible by DMD simulations (Ding and Dokholyan 2005). Typically, DMD simulations performed on a single processor can span time scales of the order of microseconds. Because of parallelization of replica exchange methodology, much larger time scales are accessible with short simulations. We perform the replica exchange method to rapidly sample the conformational space available to RNA. Folding simulation of a 36-nt-long RNA sequence for 2 × 10⁶ DMD time units took ∼5 h of wall-clock time utilizing eight 3.6-GHz Intel Xeon compute nodes, communicating over MPI. Within the 2 × 10⁶ time units of simulations, multiple folding transition events were observed. Since the DMD codes are highly optimized, we found that the computational time scales linearly with respect to the system size (Supplemental Fig. 1). After completion of this work, Das and Baker (2007) have reported the prediction of tertiary structures of RNA molecules with lengths of ∼30 nt. This approach utilizes assembly of short RNA fragments using Monte Carlo sampling with a knowledge-based energy function to predict putative RNA conformations. The DMD-based RNA folding approach is able to predict folding for longer RNA molecules having better agreement with the corresponding native structures. Generating 50,000 fragments with 45 sec per fragment would require 625 CPU-hours of computation, as opposed to 33 CPU-hours for a 30-nt-long RNA. Our method is fully automated, since a unique tertiary structure is predicted, corresponding to the least free energy conformation. In addition, replica exchange DMD simulations also offer probing the mechanistic features, (e.g., folding kinetics and thermodynamics) of the RNA folding process. Due to the computational efficiency of the DMD-based RNA folding prediction, we are able to test a larger set of RNA molecules than is accessible using the fragment-based approach. Finally, the web-based DMD simulation tool iFold (http://ifold.dokhlab.org) (Sharma et al. 2006) may be extended for predicting the folded structure and probing the folding dynamics of de novo RNAs.

MATERIALS AND METHODS

Discrete molecular dynamics

A detailed description of the DMD algorithm can be found elsewhere (Dokholyan et al. 1998). Briefly, interatomic interactions in DMD are governed by stepwise potential functions. Neighboring interactions, such as bonds, bond angles, and dihedrals, are modeled by infinitely high square well potentials. During a simulation, an atom's velocity remains constant until a potential step is encountered, where it changes instantaneously according to the conservations of energy, momentum, and angular momentum. Simulations proceed as a series of such collisions with a rapid sorting algorithm employed at each step to determine the following collision.

The simplified RNA model

We approximate the single-stranded RNA molecule as a “beads-on-a-string” polymer, with each bead corresponding to either sugar (S), phosphate (P), or nucleo-base (B) moieties, thus making three beads for each nucleotide (Fig. 1). Beads P and S are positioned at the center of mass of the corresponding phosphate group and the five-atom ring sugar. For both purines (adenine and guanine) and pyrimidines (uracil and cytosine), we represent the base bead (B) as the center of the six-atom ring. The neighboring beads, which are either inter- or intranucleotides, are constrained to mimic the chain connectivity and the local chain geometry (Fig. 1). The types of constraints include bonds (solid lines), bond angles (dashed lines), and dihedrals (dot–dashed lines). The parameters for the bonded interactions mimic the folded RNA structure and are derived from a high-resolution RNA structure database (Murray et al. 2003; Supplemental Table 2). The nonbonded interactions are crucial to model the folding dynamics of RNA molecules. In our model, we include the base-pairing (A–U, G–C, and U–G), base-stacking, short-range phosphate–phosphate repulsion, and hydrophobic interactions, which are described below as well as in the parameterization procedure.

Base pairing

In the folding of RNA molecules, the complementary hydrogen bonding interactions between nucleotides, base pairing, are the key interactions. We use the “reaction” algorithm to model the hydrogen-bonding interaction between specific nucleotide base pairs. The details of the algorithm can be found in Ding et al. (2003). Briefly, to mimic the orientation-dependent hydrogen-bond interaction, we introduce auxiliary interaction beside the distance-dependent interaction between donor and acceptor (Fig. 1). For example, once the two nucleotides (e.g., A–U, G–C, or U–G, represented as B_i and B_j in Fig. 1) approach the interaction range, we evaluate the distances between S_iB_j and S_jB_i, which define the orientations between these two nucleotides. If the distances satisfy the predetermined range, we allow the hydrogen bond to be formed, and forbid its formation otherwise. The parameters used for modeling base-pairing interactions are listed in Supplemental Table S3.

Phosphate–phosphate repulsion

Phosphates are negatively charged and usually repel each other. To account for the repulsion, we assign repulsion between phosphate groups. Due to the strong screening effect of water and ions, we use the Debye–Hückel model to account for the electrostatic repulsion between phosphates. We discretize the continuous potential with a step-wise function with a step of 1 Å and the cutoff distance of 10 Å.

Hydrophobic interactions

Buried inside the double-helix, the bases are hydrophobic in nature. We include a general attraction between all bases. Due to the coarse-graining feature of our model, the assignment of attraction between bases results in overpacking (e.g., the symmetrically attractive tends to form close packing). In order to avoid this artifact, we introduce an effect energy term to penalize the overpacking of bases: E _overpack = dEΘ(n_c − n_max). Here, Θ(x) is a step function, which adapts the value of x if x is positive and zero; otherwise, n_c is number of contacts, and n_max is the maximum number of contacts; dE is the repulsion coefficient. Using a cutoff of 6.5 Å, we sample the available RNA structures from NDB and find that n_max corresponds to 4.2.

Base stacking

A close examination of stacking interactions from available crystal structures suggests the following salient features: (1) Stacking interactions are usually short-ranged as in close packing; (2) each base has a stacking valence of 2; i.e., a base does not make more than two stacking interactions; (3) three consecutively stacked bases align approximately linearly. We include the above features into our model. We compute the distance distributions of stacked bases from available RNA structures. We find that distribution depends on the types (purine or pyrimidine), and we identify the stacking cutoff distances: 4.65 Å between purines, 4.60 Å between pyrimidines, and 3.80 Å between purine and pyrimidine. To approximately model the linearity of the stacking interactions, we penalize two bases, which form stacking interactions to the same base, from coming closer than 6.5 Å. As a result, these three bases effectively form an obtuse angle. Next, we discuss the energy parameterization of the base-stacking interaction, base pair, and hydrophobic interactions.

Parametrization of the hydrogen-bond, base-stacking, and hydrophobic interactions

In order to determine the pairwise interaction parameters for the stacking and hydrophobic interactions for all pairs of the bases, we decompose the sequence-dependent free energy parameters for individual nearest-neighbor hydrogen-bond model (INN-HB) (Mathews et al. 1999). We assume that the interaction of neighboring base pairs in INN-HB is the sum of the hydrogen-bond, base-stacking, and hydrophobic interactions. In a nearest neighboring base-pair configuration (Fig. 1), B_i+1 and B_i (B_j-1 and B_j) usually stack on top of each other. However, if both bases B_i+1 and B_j are purines, we find that they tend to stack instead. The bases B_i and B_j-1 are usually farther than the cutoff distance of 6.5 Å. Therefore, we use the following equation to estimate the pairwise interactions:

Here, E ^Stack, E^HB, and E ^Hydrophobic are the interaction strengths of stacking, base-pair, and hydrophobic interactions, respectively. Given the experimentally tabulated energy between all possible neighboring base pairs (Mathews et al. 1999), we are able to determine the values of E^{S tack}, E^HB, and E ^Hydrophobic, which are consistent with the experimental measurements using singular value decomposition. The interaction parameters are listed in Supplemental Tables 3 and 4.

Loop entropy

The loop entropy plays a pivotal role in RNA folding kinetics and thermodynamics (Tinoco and Bustamante 1999). Hence, an RNA folding prediction method should take the entropic effect into account, either implicitly (in all-atom MD simulations [Sorin et al. 2004]) or explicitly (Monte Carlo or dynamic programming methods [Rivas and Eddy 1999; Mathews 2006]). However, due to the reduction of the degrees of freedom in our simplified RNA model, the entropy is often underestimated in our DMD simulations. For example, we often observe that the RNA molecule forms long loops readily and is kept trapped in a nonnative conformation for a long simulation time. To overcome such an artifact due to the coarse-graining process, we develop a simple approach in the DMD simulation to model the loop entropy explicitly. We use the experimentally tabulated free energies for different types of loops, including hairpin, bulge, and internal loops (Mathews et al. 1999). The free energy of a loop depends on its size and type (hairpin, bulge, or internal loops). We compute the effective loop free energy in DMD simulations based on the set of base pairs formed in simulations. Upon the formation or breaking of each base pair, the total loop free energy changes. We estimate the loop–free energy difference ΔG^loop for each base pair formation during the simulation and determine the probability to form such a base pair by coupling to a Monte Carlo procedure using a Metropolis algorithm with a probability, p = exp(−βΔG^loop). If it is possible to form the base pair after the stochastic estimation, the particular base pair will form only if the kinetics energy is enough to overcome the possible potential difference before and after the base pair formation. Upon breaking of a base pair, the stochastic procedure is not invoked, since it is always entropically favorable to break the base pair. The breaking of the base pair is only governed by the conservation of momentum, energy, and angular momentum before and after the base pair breakage.

Replica exchange DMD simulations

We use DMD (Dokholyan et al. 1998) simulations to investigate the dynamics of RNA folding. Efficient exploration of the potential energy landscape of molecular systems is the central theme of most molecular modeling applications. Sampling efficiency at a given temperature is governed by the ruggedness and the slope toward the energy minimum in the landscape. Although passage out of local minima is accelerated at higher temperatures, the free energy landscape is altered due to larger entropic contributions. To efficiently overcome energy barriers while maintaining conformational sampling corresponding to a relevant free energy surface, we utilize the replica exchange sampling scheme. In replica exchange computing, multiple simulations or replicas of the same system are performed in parallel at different temperatures. Individual simulations are coupled through Monte Carlo-based exchanges of simulation temperatures between replicas at periodic time intervals. Temperatures are exchanged between two replicas, i and j, maintained at temperatures T_i and T_j and with energies E_i and E_j according to the canonical Metropolis criterion with the exchange probability p = 1 if Δ = (1/k_BT_i − 1/k_BT_j)(E_j − E_i) ≤ 0, and p = exp(−Δ), if Δ > 0. We perform the replica exchange method to rapidly sample the conformational space available to RNA. For simplicity, we use the set of eight temperatures in all the replica exchange simulations: 0.200, 0.208, 0.214, 0.220, 0.225, 0.230, 0.235, and 0.240. The temperature is in the abstract unit of kcal/(mol k_B). Note that we approximate the pairwise potential energy between the coarse-grained beads with the experimentally determined free energy of nearest neighboring base pairs, instead of the actual enthalpy. As a result, the temperature does not directly correspond to the physical temperatures. In DMD, constant temperature simulation is achieved by the Andersen thermostat (Andersen 1980). Folding simulation of a 36-nt-long RNA sequence (median size of RNA chains in the sample) for 2 × 10⁶ DMD time units took ∼5 h of wall-clock time utilizing eight 3.6-GHz Intel Xeon compute nodes, communicating over the Message Passing Interface library (http://www-unix.mcs.anl.gov/mpi).

Q-value of a putative RNA structure

We use the fraction of the total number of native base pairs, the Q-value, as one criterion to evaluate the accuracy of a putative RNA structure predicted from simulations. As used in protein folding studies (Sali et al. 1994), the Q-value quantifies the extent of native-likeness of a putative structure with respect to the native structure. To compute the Q-value of a putative RNA structure, the native structure or at least the native secondary structure must be known. If a Q-value equals 1, the putative structure correctly predicts the native base pairs and features all native secondary structures. If the Q-value is close to zero, the corresponding structure does not resemble the native state.

Weighted histogram analysis method

The weighted histogram analysis method (Kumar et al. 1992) was used to analyze the thermodynamics of RNA folding. The MMTSB toolset (Feig et al. 2004) was used to perform WHAM on replica exchange trajectories. Since our simulations are started from a fully extended conformation, we exclude the first 5 × 10⁵ time units of the simulation trajectories and use the last 1.5 × 10⁶ time units of simulation trajectory for performing the WHAM analysis.

SUPPLEMENTAL DATA

Supplemental material can be found at http://www.rnajournal.org.