Simultaneous Spatial and Temporal Focusing in Nonlinear Microscopy

Abstract

Simultaneous spatial and temporal focusing (SSTF), when combined with nonlinear microscopy, can improve the axial excitation confinement of wide-field and line-scanning imaging. Because two-photon excited fluorescence depends inversely on the pulse width of the excitation beam, SSTF decreases the background excitation of the sample outside of the focal volume by broadening the pulse width everywhere but at the geometric focus of the objective lens. This review theoretically describes the beam propagation within the sample using Fresnel diffraction in the frequency domain, deriving an analytical expression for the pulse evolution. SSTF can scan the temporal focal plane axially by adjusting the GVD in the excitation beam path. We theoretically define the axial confinement for line-scanning SSTF imaging using a time-domain understanding and conclude that line-scanning SSTF is similar to the temporally-decorrelated multifocal multiphoton imaging technique. Recent experiments on the temporal focusing effect and its axial confinement, as well as the axial scanning of the temporal focus by tuning the GVD, are presented. We further discuss this technique for axial-scanning multiphoton fluorescence fiber probes without any moving parts at the distal end. The temporal focusing effect in SSTF essentially replaces the focusing of one spatial dimension in conventional wide-field and line-scanning imaging. Although the best axial confinement achieved by SSTF cannot surpass that of a regular point-scanning system, this trade-off between spatial and temporal focusing can provide significant advantages in applications such as high-speed imaging and remote axial scanning in an endoscopic fiber probe.

1. Introduction

Multiphoton microscopy (MPM) has become a powerful tool for imaging biological samples due to its ability to perform optical sectioning [1, 2]. In two-photon excited fluorescence (TPEF) microscopy, for example, the signal depends quadratically on the excitation intensity, thus substantially decreasing the out-of-focus background [1, 3]. TPEF also depends inversely on the temporal pulse width of the excitation pulse, but in standard TPEF microscopy, the temporal pulse width is a constant throughout the sample. Thus, the spatial focusing due to the objective lens determines the axial confinement achieved in conventional TPEF microscopy.

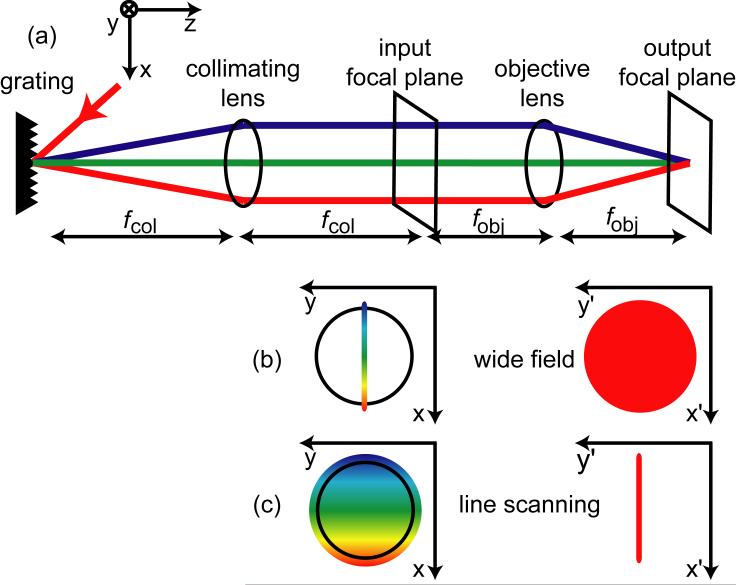
Recent papers have proposed and demonstrated simultaneous spatial and temporal focusing (SSTF) as a way of further enhancing the axial confinement in MPM [4, 5]. An extra degree of confinement can be obtained by creating a temporal focus where the shortest pulse width is only achieved at the focal point. SSTF works by spatially separating the frequencies of a short pulse with a grating [4, 5], collimating these beams with a lens, and then recombining them with an objective lens (Figure 1). A temporal focus occurs because the different frequency components only overlap within the focal region of the objective lens, and thus the pulse width is shortest only at the focal plane. In an alternative explanation, the grating is imaged at the focal plane of the objective lens [4]. By Fermat’s principle, the light rays emerging from different points on the grating travel the same optical path length to the focal plane, and so a short pulse at the grating will be imaged as a short pulse at the focus. This is not true for points outside of the focus, however, for different rays will follow paths of different lengths, thus broadening the pulse [4, 6].

Figure 1.

(a) A typical SSTF setup. (b) Beam profile for wide field SSTF. On the left is a cross-section at the input focal plane of the objective. On the right represents the beam shape at the focal plane. (c) Beam profile for line scanning SSTF.

In this paper, we review the derivation of the beam propagation to the focal volume in wide-field SSTF using Fresnel diffraction in the frequency domain (Section 2.1). In Section 2.2, we show that changing the GVD of the system results in axial scanning of the temporal focal plane. In Section 2.3, we present a new derivation for the axial confinement of line-scanning SSTF in the time domain. In Sections 3.1 and 3.2, we review experimental results of the temporal focusing effect as well as the capability of scanning the temporal focus axially by tuning the GVD. In Section 3.3, we present new experimental results on the axial confinement of SSTF. In Section 4, we discuss in detail the axial confinement of SSTF in an MPM setup and the possibility of a multiphoton fiber probe with remote axial scanning capability.

2. Theoretical Analysis of SSTF

Figure 1 shows a schematic of a typical SSTF setup. There are two imaging modalities for SSTF: wide field and line scanning. In conventional wide-field imaging, the beam incident upon the input focal plane of the objective lens is small, resulting in a loosely focused spot at the focal plane. In the SSTF wide-field case, however, the beam shape at the input focal plane of the objective is a thin line, where the width in the x-direction is the spreading of the monochromatic components due to the grating, and the height in the y-direction is the monochromatic beam size s (See Figure 1). Wide-field illumination in SSTF is achieved by using a spherical lens as the collimating lens (Figure 1) to focus the spatially-chirped beam to a small height s in the y-dimension at the input focal plane of the objective lens. Because the radius s of each monochromatic beam is small, the objective lens will not focus the monochromatic beams tightly, creating a large spot at the focal plane (Figure 1(b)). In contrast with conventional imaging, however, wide-field imaging with SSTF allows for optical sectioning due to the evolution of the temporal pulse width within the sample. In the SSTF line-scanning case, the beam has a circular cross-section at the input focal plane of the objective lens, such that the y-component of each monochromatic beam is large, but the x-component of each monochromatic beam remains the small width s. Thus, each monochromatic beam will focus to a large x-dimension but a small y-dimension, forming a line at the focus of the objective lens (Figure 1(c)). By using a 1-D scanner to sweep the line across the sample, 2D images can be obtained [7].

2.1 Temporal pulse-width evolution

The theoretical understanding of SSTF follows closely the published theory for wide-field SSTF with a chirped incident pulse [8]. Our frequency-domain analytical model uses Gaussian beam propagation under the paraxial limit [9]. We assume that the input beam profile, A₁(x,ω), at the input focal plane of the objective lens can be written as a superposition of many monochromatic, spatially transform-limited Gaussian beams whose center positions are linearly displaced according to their wavelengths. We further assume that the optical spectrum of the input waveform has a second-order chirp and has a Gaussian spectral profile. For one monochromatic beam with frequency ω, the beam amplitude at the input focal plane of the objective lens is:

$$A_1(x,\omega )=A_0{e}^{-\frac{{\omega }^2}{{\Omega }^2}}{e}^{-\frac{{(x-\alpha \omega )}^2}{s^2}}{e}^{i\beta {\omega }^2}$$ (1)

where A₀ is a normalization constant, $\sqrt{2\ln 2}\cdot \Omega$ is the full-width half maximum (FWHM) of the frequency spectrum of the pulse, $\sqrt{2\ln 2}\cdot s$ is the FWHM of each monochromatic beam in space, α is a constant proportional to the groove density of the grating and the focal length of the collimating lens [10], αω is the linear displacement of the monochromatic beam of frequency ω, and 2β is the GVD. The imaginary term in Eq. (1) represents the second-order chirp (quadratic spectral phase) of the input pulse.

In order to analytically describe the field at the output, we follow the paraxial approximation used in Ref. [9] to propagate the beam to the focal volume (for detailed calculations, see the Appendix in Ref. [8]). The spatially-chirped beam, A₁(x,ω), is incident upon the input focal plane of the objective lens. First, the Fresnel diffraction formula is applied to A₁ to propagate the beam to the objective lens. After adding the quadratic phase due to the objective lens, the Fresnel diffraction formula is used again to propagate it a distance z toward the focal plane. Fourier transforming back into the time domain, the field distribution at the focal volume is:

$$A_2(x,z,t)=\kappa \cdot e^{-\frac{x^2}{s_2^2}}{e}^{-\frac{{\Omega }^2}{4(1+\chi )}{(t+\gamma x)}^2}$$ (2)

where

$$\begin{array}{c}\hfill \kappa =A_0\Omega \sqrt{\frac{i\pi f}{z_M}}\frac{1}{{\left[\beta {\Omega }^2\frac{f-z}{z_M}-1+i\left(\frac{f-z}{z_R}+\beta {\Omega }^2\right)\right]}^{\frac{1}{2}}},\hfill \\ \hfill \gamma =\frac{k_0\alpha ∕f}{1+i(z-f)∕z_M},\hfill \\ \hfill \chi =\frac{i(z-f)∕z_B}{1+i(z-f)∕z_M}-i\beta {\Omega }^2,\hfill \\ \hfill s_2^2=\frac{4f_2}{k_0^2{s}^2}+i\frac{2(z-f)}{k_0},\hfill \\ \hfill z_M=\frac{2f^2}{k_0{s}^2},z_R=\frac{2f^2∕k_0}{s^2+{\alpha }^2{\Omega }^2},\text{and}{z}_B=\frac{2f^2}{k_0{\alpha }^2{\Omega }^2}.\hfill \end{array}$$

In Eqs. (2), f is the focal length of the objective lens, and z is the distance along the optical axis from the objective lens. To simplify calculations, we assume in the derivation of Eq. (2) that the wavevector k for each frequency is approximately k₀, the wavevector of the center wavelength of the pulse, which is valid for pulse widths on the order of 100 fs. In the case where the initial chirp (2β) is zero, the FWHM pulse width τ depends only on the propagation distance z:

$$\tau \left(z\right)=\frac{2\sqrt{2\ln 2}}{\Omega }.{\left[1+\frac{z_M}{z_B}\frac{{(f-z)}^2}{{(f-z)}^2+z_M{z}_R}\right]}^{\frac{1}{2}}.$$ (3)

Clearly, the pulse width will be shortest at the geometric focal plane of the objective lens. Note that the FWHM pulse width of $2\sqrt{2\ln 2}∕\Omega$ at the focus is the transform-limited value for a Gaussian pulse with a FWHM bandwidth of $\sqrt{2\ln 2}\cdot \Omega$, indicating that the pulse at the focal point is chirp free. At positions outside of the focus, the temporal pulse width increases quickly, demonstrating the effect of temporal focusing.

2.2 Axial scanning with GVD tuning

For non-zero dispersion (i.e., β ≠ 0), the temporal focus will be displaced along the optical axis from the geometric focus. Thus, changing the GVD effectively scans the temporal focal plane axially. Axial scanning in an SSTF system by tuning the amount of GVD in the beam path can be intuitively understood by following the wavefront of the pulse as it propagates through the system. After diffracting off the grating and being collimated by a lens (Figure 1), the beam becomes a spread of individual monochromatic beams, creating a one-to-one correspondence between the spectral frequency ω and the transverse position x. Thus, any curvature in the spectral phase will directly translate into a curvature of the wavefront in space. The wavefront is flat for a chirp-free pulse, but if there is any second-order chirp, this quadratic spectral phase will result in a quadratically-curved wavefront. This is equivalent to adding an extra lens in space to the system. Adjusting the amount of GVD is analogous to changing the curvature of the lens, thus shifting the position of the focal plane.

Continuing the derivation in Section 2.1 for wide-field SSTF with a chirped input, the dependence of the position of the temporal focal plane on dispersion can be analyzed. Using Eq. (2) for the field within the focal volume, integrating the squared intensity I (i.e., |A₂|⁴) over time and the transverse direction x yields the total two-photon excitation (TPE) signal at an axial plane at position z:

$$\begin{array}{cc}\hfill TPE\left(z\right)=& {\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{I}^2(x,z,t)dxdt\hfill \\ \hfill & =\frac{C_1}{{\left[{\left(1+\beta {\Omega }^2\frac{z-f}{z_M}\right)}^2+{\left(\frac{f-z+\beta {\Omega }^2{z}_R}{z_R}\right)}^2\right]}^{\frac{1}{2}}},\hfill \end{array}$$ (4)

where C₁ is a constant independent of z. If βΩ² is small, then Eq. (4) can be approximated as:

$$TPE\left(z\right)\approx \frac{C_1}{{\left[1+{\left(\frac{f-z+\beta {\Omega }^2{z}_R}{z_R}\right)}^2\right]}^{\frac{1}{2}}}.$$ (5)

As seen in Eq. (5), the axial response TPE(z) has a peak of constant value C₁, i.e., independent of GVD, at the temporal focal plane position z = f + βΩ² z_R. The FWHM of $TPE\left(z\right)(2\sqrt{3}\cdot z_R)$ defines the axial resolution. Eq. (5) also shows that the shift of the focal plane position has a linear dependence on GVD when βΩ² is small:

$$\Delta z_{\text{shift}}=\beta {\Omega }^2{z}_R.$$ (6)

The pulse width at the temporal focus can also be obtained (see Appendix in Ref. [8]) as:

$$\tau ={\tau }_0\cdot {\left[1+{\left(\beta {\Omega }^2\right)}^2\frac{z_R}{z_M}\right]}^{\frac{1}{2}}.$$ (7)

A small z_R is needed to obtain high axial resolution, but to achieve the desired axial scan range (Δz_shift), the dispersion value β must be increased when z_R decreases (Eq. (6)). There will be a limit, however, to the amount of shift that GVD can produce before the assumption that βΩ² is small is no longer valid. Thus, the exact expression of TPE(z) in Eq. (4) must be used to predict the behavior of TPE(z) when βΩ² is large. In this regime, the maximum value of TPE(z) is no longer a constant and decreases with increasing GVD. Intuitively, the monochromatic beams fail to overlap completely as the temporal focal plane is shifted a large distance away from the geometric focus, therefore broadening the pulse as well as increasing the lateral spot size (Figure 2). We define the onset of broadening as when the maximum value of TPE(z) in Eq. (4) is reduced to half its value when GVD is zero. Using the approximate peak position as z = f + βΩ² z_R and setting Eq. (4) equal to C₁/2, we determine the maximum amount of βΩ² possible without broadening to be:

$$\beta {\Omega }^2{\mid }_{\max }={\left(\frac{z_M}{z_R}\right)}^{\frac{1}{2}}={\left(\frac{s^2+{\alpha }^2{\Omega }^2}{s^2}\right)}^{\frac{1}{2}}\approx \frac{\alpha \Omega }{s}.$$ (8)

Substituting Eq. (8) into our expression for the pulse width (Eq. (7)), the pulse width at the temporal focus can be expressed as:

$$\tau ={\tau }_0\cdot {\left[1+{\left(\frac{\beta {\Omega }^2}{\beta {\Omega }^2{\mid }_{\max }}\right)}^2\right]}^{\frac{1}{2}}.$$ (9)

As seen in Eq. (9), the onset of broadening has been defined as when the pulse width at the temporal focal plane is $\tau =\sqrt{2}{\tau }_0$. Combining Eq. (6) and Eq. (8), the maximum shift allowed by SSTF is:

$$\Delta z_{\max }=\beta {\Omega }^2{\mid }_{\max }\cdot z_R={\left(z_M{z}_R\right)}^{\frac{1}{2}}\approx \frac{\alpha \Omega }{s}{z}_R.$$ (10)

Equation (10) shows that the number of resolvable z-sections (∼Δz_max/z_R) is simply the ratio between the widths of the spatially chirped beam (∼αΩ) and the monochromatic beam (s) at the input focal plane of the objective lens. In practice, the axial resolution (proportional to z_R) and maximum shift (Δz_max) can be scaled for a particular application. For example, a higher z-resolution (smaller z_R) will be possible if the maximum scanning range (Δz_max) is sacrificed.

Figure 2.

A ray-tracing representation of the focal volume shows intuitively the fundamental scanning limit, where s is the lateral spot size of a monochromatic beam and z_max is the length of the geometrical overlap.

2.3 Axial confinement

Rigorous treatment of the focusing characteristics of pulsed input illumination should be done in the frequency domain. However, under the condition that the input pulse spectrum is narrow, it is well known that the frequency-domain theory can be replaced by that in the time domain, owing to the fact that the difference between the diffraction patterns for different frequencies inside the focal volume is negligible. In this section, an understanding of SSTF axial confinement is developed in the time domain, unifying the ray-optics and wave-optics description of SSTF. This time-domain treatment also provides direct comparison between SSTF and conventional imaging.

We consider line-scanning SSTF and assume that there is no initial chirp, and the beam at the input focal plane of the objective lens is circular in cross-section. When a grating is used to spatially separate the individual frequency components of the beam, their center positions are laterally displaced according to their offset frequency measured from the spectrum center. Following the treatment of Martinez [10, 11], when diffraction is taken into account and assuming a chirp-free Gaussian spectral profile, a fast-rotating and a both temporally and spatially-stretched wavefront is formed at the output focal plane of the collimating lens (i.e., the input focal plane of the objective lens, see Figure 1). The profile of the beam at the input focal plane of the objective can be calculated in the time-domain by taking the Fourier transform of Eq. (1) with the added y-component for a line-scanning SSTF setup:

$$\begin{array}{cc}\hfill B_1(x,y,t)=& D_0{\int }_{-\infty }^{\infty }{e}^{-\frac{{(x-\alpha \omega )}^2}{s^2}}{e}^{-\frac{y^2}{s^2+{\alpha }^2{\Omega }^2}}{e}^{-\frac{{\omega }^2}{{\Omega }^2}}{e}^{-i\omega t}d\omega \hfill \\ \hfill =& D_1{e}^{-\frac{x^2+y^2}{s^2+{\alpha }^2{\Omega }^2}}{e}^{-\frac{t^2}{2{\tau }_0^2\left(1+\frac{{\alpha }^2{\Omega }^2}{s^2}\right)}}{e}^{i\frac{\alpha {\Omega }^2\cdot t\cdot x}{s^2+{\alpha }^2{\Omega }^2}},\hfill \end{array}$$ (11)

where D₀ is a normalization constant, D₁ is a constant independent of the time and transverse spatial coordinates, ${\tau }_0=\sqrt{2}∕\Omega$ describes the temporal pulse width. Note that when compared to the case where the stretching of the beam is absent (i.e., α = 0), both the spatial width and temporal width of the incident beam are now stretched by a factor of $\sqrt{1+{\alpha }^2{\Omega }^2∕s^2}$.

In the time-domain approach, the system temporal response to the input field is instantaneous, i.e. in the reference frame that travels with the pulse (the retarded frame), the spatial output pattern of the system at time t is uniquely determined by its spatial input pattern at the input focal plane of the objective at the same time t. This implies that the spectral response of the spatial focusing does not vary across the pulse bandwidth. We propagate the field at the input focal plane of the objective, B₁(x,y,t), to the output focal plane following the same Fresnel diffraction method used in Section 2.1 except with an additional pupil function [12]. The field distribution inside the focal volume can then be expressed as:

$$B_2(x,y,z,t)\approx D_2{e}^{-\frac{t^2}{{\tau }_{\text{sweep}}^2}}h(x+{\nu }_{\text{sweep}}t,y,z),$$ (12)

where

$$\begin{array}{c}h(x,y,z)=\underset{\infty }{\int \int }P(x^{\prime },y^{\prime })e^{-\frac{{x^{\prime }}^2+y^{{\prime }^2}}{s^2+{\alpha }^2{\Omega }^2}}{e}^{i{k}_0\left(\frac{x{x}^{\prime }+y{y}^{\prime }}{f}+z\frac{x^{{\prime }^2}+y^{{\prime }^2}}{2f^2}\right)}d{x}^{\prime }d{y}^{\prime },\hfill \\ {\nu }_{\text{sweep}}=\frac{f}{k_0}\frac{\alpha {\Omega }^2}{s^2+{\alpha }^2{\Omega }^2},\hfill \\ {\tau }_{\text{sweep}}={\tau }_0\cdot \sqrt{1+\frac{{\alpha }^2{\Omega }^2}{s^2}}.\hfill \end{array}$$ (13)

Here, D₂ is a constant independent of the time and spatial coordinates, and P(x’,y’) is the pupil function of the objective. We note that h(x,y,z) defined in Eq. (13) is the standard point-spread function but with the back aperture partially filled due to the effect of the finite size of the spatially-chirped beam.

Equation (12) presents a clear physical picture of the SSTF technique. At the focal plane, the field distribution measured at any instantaneous time t is a focused point that is determined by the point-spread function h(x,y,z) associated with a finite beam size $\sim \sqrt{s^2+{\alpha }^2{\Omega }^2}$ at the input focal plane of the objective. Different from a regular point-focusing system, however, this focused point sweeps rapidly at the speed ν_sweep along the x-direction. This ultrafast point-sweeping process will complete in a time duration of ∼τ_sweep, which corresponds to the temporal stretching of the spatially-chirped beam at the input focal plane of the objective lens. Intuitively, this is the result of different incident rays hitting the grating at different times because the illumination of the grating is tilted [4, 13]. By simply taking the product between the sweeping speed (ν_sweep) and the total sweeping time (τ_sweep), the length of the scanned line can be estimated to be λ₀ · f / s, which is the focused beam size corresponding to an individual monochromatic beam. Note that the sweeping speed is ultrafast. As an example, for a typical Ti:Sapphire laser where λ₀∼800nm and Δλ∼10nm, if the back aperture of the objective is approximately filled by the spatially-chirped beam (i.e., with a NA∼0.5 and f∼αΩ), we estimate that ν_sweep ∼ 5 × 10⁶ m/s.

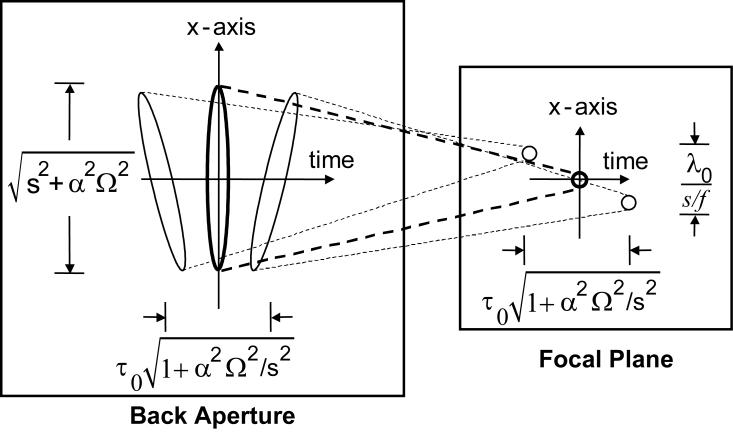
In Figure 3, an intuitive ray/wave optics understanding of this point-sweeping process in line-scanning SSTF is illustrated. At the input focal plane of the objective, the input short pulse (pulse width ∼τ₀) is first stretched into a long pulse (pulse width $\sim {\tau }_0\sqrt{1+{\alpha }^2{\Omega }^2∕s^2}$) due to the separation of spectral components. This long pulse can be virtually decomposed into $\sqrt{1+{\alpha }^2{\Omega }^2∕s^2}$ copies of spatially-overlapped but temporally-separated short pulses. Because of the ultrafast wavefront rotation caused by the spreading effect of the grating (see Eq.(11)), different copies of the short pulse will have different wavefront pointing directions, and therefore are focused to different lateral positions along the x-direction, forming a line that corresponds to $\sqrt{1+{\alpha }^2{\Omega }^2∕s^2}$ number of point pixels in line-scanning mode.

Figure 3.

Intuitive understanding of SSTF in the time domain. The wavefront of the illumination is rapidly rotating, causing the focused spot to sweep along the x-direction and forming a line illumination with a width of λ₀ /(s /f), where s/f represents the NA corresponding to an individual monochromatic beam. The total sweeping process takes ${\tau }_0\sqrt{1+{\alpha }^2{\Omega }^2∕s^2}$ to complete. Note that the horizontal axis represents time and the vertical axis represents x.

For the application of SSTF to TPEF microscopy, a theoretical understanding of the axial confinement is important. Mathematically, this can be done by evaluating the total two-photon excited signal on a perpendicular plane placed at position z from the objective. Because the TPE signal is proportional to the fourth power of the focused field, by using the expression in Eq. (12), we have:

$$TPE\left(z\right)=\underset{\infty }{\int \int \int }{\mid B_2(x,y,z,t)\mid }^{4}dxdydt=C_2\cdot \underset{\infty }{\int \int }{\mid h(x,y,z)\mid }^{4}dxdy,$$ (14)

where C₂ is a constant independent of z. Equation (14) shows that the axial confinement is completely determined by the characteristics of the point-spread function of the objective lens h(x,y,z). We thus conclude that it is the spatial profile of the spatially-chirped beam at the input focal plane of the objective that determines the axial confinement.

The above analysis focuses on the case of line-scanning operation of SSTF. For wide-field operation of SSTF, a similar method based on the paraxial approximation can also be used to evaluate the performance of SSTF. In wide-field SSTF, the beam is only stretched along one dimension. As a result, a line-shaped beam is formed at the input focal plane of the objective. To establish a quantitative time-domain understanding for wide-field operation of SSTF, Eqs. (12)-(14) can be modified by simply eliminating the y-variable. Thus, for wide-field SSTF with a Gaussian spectrum, the point spread function in Eqs. (12)-(14) should be replaced by:

$$h(x,z)={\int }_{-\infty }^{\infty }P\left(x^{\prime }\right)e^{-\frac{x^{{\prime }^2}}{s^2+{\alpha }^2{\Omega }^2}}{e}^{i{k}_0\left(\frac{x{x}^{\prime }}{f}+z\frac{x^{{\prime }^2}}{2f^2}\right)}d{x}^{\prime }.$$ (15)

We will discuss the implications of the axial confinement in wide-field SSTF in Section 4.1.

3. Experiments

3.1 Experiment on temporal pulse-width evolution

To demonstrate the temporal focusing effect, we employ the wide-field SSTF experimental setup shown in Figure 4. A ruled diffraction grating (groove density 1200 lines/mm) decomposes the beam from a mode-locked Ti:Sapphire laser (λ₀ = 800 nm, Δλ = 8 nm) into its monochromatic components, which are then collimated using a spherical lens. Note that the geometric dispersion caused by the grating is automatically cancelled after collimation, and therefore the spread of beams is chirp free in spectrum. The simultaneous spatial and temporal focusing effect is then realized by passing the beams through an objective lens. To collect the fluorescence signal, a dichroic mirror reflects the TPEF signal onto a PMT (Hamamatsu HC125-02) through filters that further remove the excitation light.

Figure 4.

SSTF experimental setup. BS: beam splitter. DM: dichroic mirror. OBJ: objective lens. A mode-locked Ti:Sapphire laser (Tsunami, Spectra-Physics) serves as the excitation source.

We measure the evolution of the temporal pulse width along the propagation direction in an interferometric second-order autocorrelator, which uses TPEF from a thin Rhodamine sample as the nonlinear element [8]. The autocorrelation traces at the focal plane and far away from the focus are shown in Figure 5(a) and (b), respectively. At 275 μm away from the focus (Figure 5(b)), a 1.64-ps pulse was measured and the characteristics of the interferometric autocorrelation trace were indicative of a highly chirped pulse. At the focal plane of the objective lens, however, a nearly chirp-free pulse is obtained, and the measured 84-fs pulse width (Figure 5(a)) is close to the original laser output. Figure 6 shows the measured temporal pulse width (solid squares) at various distances away from the focal plane by translating the thin Rhodamine B sample. Our measurements indicate that a value of 25 for the pulse width stretching factor (PWSF), which is defined as the ratio between the pulse width measured at the input focal plane of the objective lens and the pulse width measured at the focal point, could be achieved using the current setup. Note that in wide-field SSTF, this PWSF is critical for suppressing the background TPEF signal and performing optical sectioning. Using the model described in the Section 2.1, a fitting curve for the pulse width (Eq. (4)) is plotted in Figure 6 (solid line). Good agreement between the calculated and measured data is obtained.

Figure 5.

Autocorrelation traces of the measured pulse at different sample positions: (a) at the focal plane of the objective, (b) when moved 275 μm away from focal plane.

Figure 6.

Measured (solid squares) and theoretical (line) pulse width as a function of sample position. The location of the focal plane of the objective lens is set to zero.

3.2 Experiment on axial scanning with GVD tuning

In order to observe the displacement of the temporal focus caused by non-zero GVD, we measure TPE(z) traces (defined in Eq. (4)) by scanning a Rhodamine B film sample on a translation stage. A prism pair changes the GVD in the system by adjusting the amount of glass in the beam path. A beam shrinker composed of two plano-convex lenses controls the monochromatic beam size s. We perform these axial scans at different GVD values and record the peak position, i.e., the position of the temporal focal plane. Figure 7(a) shows the temporal focal plane position as a function of GVD. A linear relationship is observed between GVD and the displacement of the focal plane, in agreement with the theory (Eq. (6)). We are able to shift the temporal focus by more than 130 μm, limited by the thickness of the prisms. Despite the addition of extra dispersion, a nearly transform-limited pulse width is recovered for each of these data points (triangles in Figure 7(b)). The measured ratio αΩ/s in our experiment is ∼22. For a 65 fs pulse width (bandwidth Ω of 3.8×10¹³ Hz), the recovered pulses are expected to broaden near a GVD value of 3.0×10⁴ fs² (Eq. (8)), corresponding to a maximum shift of 0.5 mm.

Figure 7.

(a) The shift of the temporal focal plane position is plotted versus GVD varied by adjusting the prism pair. The squares represent peak positions of axial traces taken for various prism positions. The solid line is the expected linear relationship. In (b), the data points represent the pulse width at the sample for various GVD values. The triangles demonstrate the recovery of the pulse width for a 1200 lines per millimeter grating and a 4x beam shrinker. The squares show that the pulse broadens with added GVD when the grating is changed to 600 lines per millimeter and the beam shrinker is reduced to 2x. The solid red line is the predicted pulse width for the broadening case.

To demonstrate the broadening of the pulse when the shifting of the focal plane becomes large, we measure the pulse width at the sample using a different set of experimental parameters. Using the same GVD tuning range, we reduce the ratio αΩ/s to 5 by using a grating with only 600 lines/mm, a 2x beam shrinker, and a slightly shorter initial pulse width of 60 fs (Figure 7(b)). Pulse broadening now occurs at a GVD value of 6.7×10³ fs² yielding a shift of 350 μm. As seen in Figure 7(b), our experimental results agree reasonably well with the theoretical prediction (Eq. (8) and (9)).

The main advantage of shifting the focal plane by tuning the GVD in SSTF is the ability to perform remote axial scanning in a fiber delivery system. To demonstrate such a capability, we insert ∼1 m of large mode area fiber (core diameter 25 μm, Crystal Fibre) between the laser and the grating. This fiber was chosen due to its low nonlinearity even at high input power [14]. Using a #1 cover glass coated on both sides with a thin film of Rhodamine B, we scan the sample stage through the focal plane at a constant GVD value (solid line in Figure 8). Then, with the sample fixed, we scan through both the front and back films of the slide by adjusting the dispersion in the system (dots in Figure 8). An extra prism pair is added to the setup in Figure 4 to increase the GVD tuning range. Thus, we were able to shift the temporal focal plane by 200 μm when z_R is 11.5 μm, revealing both the front and back films of the cover glass. The axial scans obtained by translating the sample and by adjusting the dispersion are nearly identical, demonstrating the capability of remote scanning of the focal plane by adjusting the GVD. We note that the z values corresponding to points within the cover glass have been scaled by 1.5 to take into account refraction due to the air-glass interface. The different peak values from the front and back surfaces of the slide are due to a combination of the absorption of the TPEF signal of the back film by the front film and the distinct thicknesses of the two films.

Figure 8.

Scanning of a #1 cover glass coated on both sides with a thin Rhodamine B film. The solid line is an axial trace obtained by scanning the sample with a translation stage. The circles represent axial scan data taken by tuning the GVD at a fixed sample position.

In addition, the ability of SSTF to recover a transform-limited pulse width despite the presence of large chirp negates the need for any dispersion pre-compensation in a fiber delivery system (typically by using a grating pair). For example, when an 87 fs pulse is launched into the large mode area fiber, the pulse broadens to 1.27 ps at the output of the fiber due to its large dispersion (Figure 9(a)). At the temporal focus, a nearly chirp-free 99 fs pulse width is recovered (Figure 9(b)) without any dispersion pre-compensation. The 10% pulse broadening is predicted by our theory using the calculated GVD value of the fiber as 3.5×10⁴ fs². In essence, the SSTF setup acts as a post-dispersion compensation device, automatically removing the chirp of the pulse at the temporal focus. Although fibers have been engineered to exhibit both low nonlinearities and zero dispersion within a specific wavelength range [15], this technique allows short pulses to be delivered to the sample over a broad spectral range without any pre-compensation of dispersion.

Figure 9.

Autocorrelation traces for a system without dispersion compensation where the pulse has propagated through one meter of large mode area fiber. The laser has a center wavelength of 775 nm and a spectral width of 8 nm. In plot (a), the pulse is at the output of the large mode area fiber, and in (b), at the temporal focal plane of the SSTF setup.

3.3 Experiment on axial confinement

In this section, we experimentally measure the axial confinement of wide-field SSTF as well as the peak TPEF signal counts. In this experiment (Figure 4), the center wavelength of the Ti:Sapphire laser is 775 nm, the FWHM of the spectrum is 8.2 nm, and the groove density of the grating is 1200 lines/mm. The objective used in this experiment has a NA of 0.45. An aperture with radius 2.5 mm is placed in front of the objective back aperture in order to observe the finite back-aperture size effect easily. To vary the beam size, a set of collimating lenses with different focal lengths are used.

We define the axial confinement as the FWHM of the TPE(z) traces (from Eq. (14)) obtained by scanning a thin Rhodamine slide through the focal plane. The axial confinement and the TPEF counts generated from the peak position are measured for each focal length of the collimating lens. The results are plotted in Figure 10(a) and Figure 10(b) (solid squares). Note that the beam size is linearly proportional to the focal length of the collimating lens. We show in this experiment that the axial confinement is determined by the beam size at the input focal plane of the objective. Also shown in Figure 10 are the values calculated using the time-domain theory (solid lines), i.e. Eq. (12) and Eq. (14) but with Eq. (15) as the point spread function. Note that in order to get the best fit, a sech-squared spectrum profile is used instead of a Gaussian spectrum in Eq. (15). The measured data agrees well with the theoretical analysis.

Figure 10.

Experimental measurement (squares) and theory (lines) for wide-field SSTF (a) FWHM of the axial confinement function TPE(z) and (b) normalized signal power of the TPEF generated by a thin fluorescence film placed at the focal plane.

4. Discussion

4.1 Axial confinement enhancement

It has been shown that the axial characteristics of SSTF in TPEF are determined by the input spatial profile. It is therefore straightforward to compare the focusing in the SSTF regime to that of regular imaging (see Table 1). In wide-field SSTF, the beam is stretched only along one dimension to form a line-shape illumination at the input focal plane of the objective (see Figure 1). This is equivalent to the beam profile in a regular line-scanning setup, and thus the axial confinement of wide-field SSTF and a conventional line-scanning system are the same. In line-scanning SSTF, the beam has a circular cross-section at the input focal plane of the objective, and therefore its axial confinement will be equivalent to that of a regular point-scanning system [7]. Thus, SSTF provides an improved axial confinement when compared to conventional systems in the same imaging configuration (wide field or line scanning). Intuitively, the temporal focusing in SSTF replaces the focusing of one spatial dimension in a conventional imaging system. The best axial confinement achieved by SSTF (i.e., line scanning) cannot surpass that of a regular point-scanning TPEF system.

Table 1.

Comparison between different conventional imaging systems with those of SSTF. For conventional imaging, Gaussian beam propagation in the paraxial limit is used, where z_R represents the Rayleigh range of the beam. In SSTF imaging, z_R represents the Rayleigh range of the spatially-chirped beam as defined in Eq. (2). In both cases, Δz refers to the displacement from the focus.

	Point scan	Line scanning	Wide field
Conventional Imaging	$\sim {\left[1+{\left(\frac{\Delta z}{z_R}\right)}^2\right]}^{-1}$	$\sim {\left[1+{\left(\frac{\Delta z}{z_R}\right)}^2\right]}^{-\frac{1}{2}}$	N/A
SSTF Imaging	N/A	$\sim {\left[1+{\left(\frac{\Delta z}{z_R}\right)}^2\right]}^{-1}$	$\sim {\left[1+{\left(\frac{\Delta z}{z_R}\right)}^2\right]}^{-\frac{1}{2}}$

In practice, the axial resolution and the TPEF signal of SSTF microscopy are important design issues. Based on Eq. (14), it is apparent that these parameters for SSTF should follow exactly that of the regular TPEF microscopy, i.e. achieving higher resolution by further expanding the spatially-chirped beam at the input focal plane of the objective, although at the cost of less signal generated at the sample. These concepts are expressed in the experimental data found in Section 3.2 for wide-field SSTF (Figure 10). When the spatially-chirped beam is large (corresponding to a collimating lens with a long focal length), the FWHM of the axial confinement approaches that of a regular line-scanning system (Figure 10(a)). The generated TPEF signal, however, is low. On the other hand, when the size of the spatially-chirped beam is reduced, the FWHM of the axial confinement increases monotonically while the TPEF at the focal plane first increases, reaches a maximum, and then decreases. The initial increase is due to the improved power transmission of the monochromatic beams, which simultaneously increases the excitation power and shortens the temporal pulse width. The latter decrease is due to the lack of spatial focusing when the back aperture is underfilled. The same behavior is found with regular TPEF microscopy, indicating once again that it is the shape of the spatially-chirped beam at the input focal plane of the objective that determines the axial confinement for SSTF.

In the time-domain understanding of SSTF, as illustrated by Figure 3, the total nonlinear signal in the focal volume is the sum of the contribution of many short pulses, which are obtained after virtually decomposing the stretched long pulse into many short pulses delayed in time. We can make two observations at the output focal plane of the objective. First, there is no spatial overlapping of the focused spots since different short pulses are focused to different lateral positions. Second, there is no temporal overlapping of the pulse arrival time simply because of the long pulse decomposition. It is thus clear that SSTF is similar to the temporally-decorrelated multifocal multiphoton imaging technique [16, 17], but implemented in a continuous fashion and without the need to generate multiple beamlets.

The spatial and temporal trade-off in SSTF leads to a number of advantages. One of them is scanningless wide-field imaging [4]. Because the entire sample is illuminated, wide-field SSTF allows more excitation peak power to be directed onto the sample. In contrast to conventional wide-field imaging, wide-field SSTF provides optical sectioning. Imaging of biological tissues has been performed with wide-field SSTF [4], but the image acquisition time was long (∼30 seconds). The use of a regenerative amplifier or a specially-engineered dye with a greater two-photon cross-section could substantially decrease the image acquisition time, providing the possibility of the ultimate time resolution of one pulse per image.

4.2 Axial Scanning with GVD tuning

In this section, we discuss another exciting application enabled by the spatial and temporal trade-off of the SSTF technique: remote axial scanning. Multiphoton microscopy is the preferred technique for fluorescence imaging in thick biological tissues [2]. However, the application of MPM to a flexible fiber endoscope has been slow due to the difficulty in miniaturizing mechanical scanning components [18]. Transverse scanning has been performed on the proximal end of a fiber bundle in both one-photon confocal [19-21] and two-photon microscopy [22], but focusing and axial scanning invariably requires mechanical motion on the distal end of an endoscope [23, 24]. As seen in recent reports of multiphoton endoscopes [18, 25] and miniature microscopes [26, 27], these mechanical scanning devices are the main limitation in the fabrication of a flexible and compact endoscope, characteristics that are crucial to make multiphoton imaging compatible with existing endoscopes. As mentioned in Section 2.1, the addition of GVD to an SSTF system displaces the temporal focus from the geometric focus of the objective lens [4, 8, 28]. This technique of shifting the temporal focus allows fiber probes to perform remote axial scanning in a fiber delivery system, i.e. the scanning mechanism is at the proximal end of the fiber.

In an SSTF axial scanning setup, the z-resolution (proportional to z_R), lateral spot size (inversely proportional to s), and maximum shift (Δz_max) can be scaled for a particular application. For example, a larger lateral spot size (i.e., smaller s) will provide a larger scan range for a given z-resolution. As an example, a 10 μm z-resolution (z_R=3 μm) with a spot size of 150 μm can scan 435 μm before the pulse begins to broaden. Alternatively, an improved z-resolution is possible if we sacrifice the maximum scanning range. Tal et al. achieved a 1.5 μm z-resolution with temporal focusing for video-rate imaging [7]. For this z-resolution with a 35 μm spot size, the axial scanning range would be 40 μm. Experimentally, the scaling of the z-resolution, lateral spot size, and the maximum scanning range is readily achieved by choosing the right combinations of the focal lengths for the objective and collimating lenses, the groove density of the grating, and the input beam size.

We neglected the vertical dimension in our derivation in Section 2.2 because we treated the case of wide-field SSTF, where the beam shape is a thin line in the x-direction at the input focal plane of the objective lens. The line-scanning case results in two peaks when the geometrical and temporal foci do not overlap because TPEF is inversely proportional to both the illuminated area and pulse width. To demonstrate this effect experimentally, we expand the y-component of the beam with a cylindrical lens pair. As seen in Figure 11, changing the dispersion moves the temporal focus, but a stationary peak from the geometric focus remains. Because of the double peak formed in line-scanning SSTF, axial scanning of the temporal focal plane by tuning the GVD works best in the wide-field SSTF configuration.

Figure 11.

Axial scan data obtained by GVD tuning for (a) wide-field and (b) line-scanning SSTF.

As opposed to conventional imaging, wide-field imaging with SSTF provides optical sectioning as well as axial scanning using GVD tuning. In practice, the wide-field image is captured on a CCD camera [4]. As the focal plane scans, the camera must be moved correspondingly into focus for each temporal focus position. For in vivo endoscopic imaging, however, having a moving camera at the distal end of the fiber would be difficult. We believe that the demonstrated remote axial scanning technique is best suited in a passive, flexible fiber probe for multiphoton excitation of z-resolved fluorescence or harmonics, bridging the gap between imaging optical endoscopes and non-imaging fiber optic probes. It has all the desirable attributes of a passive fiber probe but with added z-sectioning capability over an axial scan range of hundreds of microns. As shown previously in tissue spectroscopy and imaging [29-31], the addition of z-sectioning to a conventional fiber probe will undoubtedly improve its capability in medical detection and diagnostics.

Fast and electronically-controlled GVD scanning is desirable for remote axial scanning. In our preliminary experiments, translating a pair of prisms into the beam path adjusts the GVD in the system. Although sufficient for demonstrating the concept of remote axial scanning, it is quite slow because mechanical translation of a bulky prism is necessary. Faster GVD scanning can be realized based on the same principle except by scanning the optical beam instead of moving the prisms. A regular scan mirror positioned at the focal point of a lens can quickly (up to kHz) redirect the excitation beam so that the amount of glass in the beam path varies, changing the GVD and the chirp of the pulse. An alternative method would be to manipulate the phase of the beam after the grating using an SLM [6, 32-34], allowing for fast non-mechanical scanning of the focal plane.

We have demonstrated axial scanning with SSTF, but its inherent lateral-scanning capability can also be potentially exploited. Because the beam sweeps along the x-direction on the order of one picosecond, SSTF can perform high-speed non-mechanical one-dimensional lateral scanning when the nonlinear response is ultrafast, e.g. second harmonic generation (SHG). When combined with axial scanning by tuning the GVD, a possible application of SSTF is performing non-mechanical 2D scanning in both a microscope and endoscope setting.

5. Conclusion

Simultaneous spatial and temporal focusing of femtosecond pulses improves the axial confinement in wide-field and line-scanning imaging systems. We have reviewed analytical expressions that describe the evolution of the pulse width within a TPEF sample. It is found that the axial confinement of SSTF nonlinear microscopy is determined by the spatial profile at the input focal plane of the objective. Thus, SSTF provides an improved axial confinement when compared to conventional wide-field and line-scanning systems, but the best axial confinement achieved by SSTF is the same as a regular point-scanning system. We also derive and show experimentally that SSTF can scan the temporal focal plane axially by adjusting the GVD in the excitation beam path. Because the temporal focusing in SSTF essentially replaces the focusing of one spatial dimension in a conventional system, this trade-off between spatial and temporal focusing can provide significant advantages in applications such as high-speed imaging and remote axial scanning in an endoscopic fiber probe.