Lattice Boltzmann simulation of blood flow in digitized vessel networks

Abstract

Efficient flow of red blood cells (RBCs) and white blood cells (WBCs) through the microcirculation is necessary for oxygen and nutrient delivery as well as immune cell function. Because blood is a dense particulate suspension, consisting of 40% RBCs by volume, it is difficult to analyze the physical mechanisms by which individual blood cells contribute to the bulk flow properties of blood. Both experimental and computational approaches are hindered by these non-Newtonian properties, and predicting macroscopic blood flow characteristics such as viscosity has historically been an empirical process. In order to examine the effect of the individual cells on macroscopic blood rheology, we developed a lattice Boltzmann model that considers the blood as a suspension of particles in plasma, accounting explicitly for cell-cell and cell-wall interactions. Previous studies have concluded that the abundance of leukocyte rolling in postcapillary venules is due to interactions between red blood cells and leukocytes as they enter postcapillary expansions. Similar fluid dynamics may be involved in the initiation of rolling at branch points, a phenomenon linked to atherosclerosis. The lattice Boltzmann approach is used to analyze the interactions of red and white blood cells as they flow through vascular networks digitized from normal and tumor tissue. A major advantage of the lattice-Boltzmann method is the ability to simulate particulate flow dynamically and in any geometry. Using this approach, we can accurately determine RBC-WBC forces, particle trajectories, the pressure changes in each segment that accompany cellular traffic in the network, and the forces felt by the vessel wall at any location. In this technique, intravital imaging using vascular contrast agents produces the network outline that is fed to the lattice-Boltzmann model. This powerful and flexible model can be used to predict blood flow properties in any vessel geometry and with any blood composition.

1 Introduction

Distribution of blood flow through the many parallel, small vessels of the microcirculation is of vital importance for organ function. The microcirculation network is the major site of the resistance to blood flow. Flow resistance is influenced by the complicated architecture of the microvascular network and the rheology of individual blood components. Blood is a two-phase suspension of red blood cells (RBCs), white blood cells (WBCs), and platelets suspended in an aqueous solution of organic molecules, proteins, and salts called plasma. RBCs (approximately 40% of blood volume) are the primary cell species influencing blood viscosity. The apparent viscosity of blood depends on the existing shear rate (i.e. blood behaves as a non-Newtonian fluid) and is determined by hematocrit, plasma viscosity, RBC aggregation, and microvascular geometry. Because of the complicated microvasculature and physiological properties of the blood components, blood flow exhibits interesting and unique dynamics in microcirculation.

Fahraeus effect

The Fahraeus effect[1] indicates that the hematocrit of blood in a narrow tube (tube hematocrit H_T ) of less than 200 μm is lower than the discharge hematocrit (H_D) exiting from the tube, i.e., H_T < H_D. This is due to the fact that RBCs move faster than the suspending medium in narrow tubes. The velocity difference originates from RBC migration away from the wall to the center of the tube, where velocities are higher. The ratio of particle velocity to suspending medium velocity depends on the ratio of particle diameter to tube diameter. A simple mass balance analysis links the hematocrit ratio to the velocity ratio: H_T/H_D = U/U_C, where U is the mean velocity of the whole suspension (cells plus plasma) and U_C is the cell mean velocity. The migration of RBCs to the tube axis creates a cell-free plasma layer along the wall and a cell-rich central core. This results in two other important blood flow anomalies: the Fahraeus-Lindqvist effect and plasma skimming.

Fahraeus-Lindqvist effect

The Fahraeus-Lindqvist effect[2] describes the decrease in apparent viscosity with decreasing microvessel diameter, with a minimum in the diameter range between 5 and 7 μm, corresponding to the size of capillaries. Further decreasing vessel diameter increases apparent viscosity because the tube becomes smaller than the blood cells. The effects of diameter and hematocrit on blood viscosity in tube flow have been extensively characterized using narrow glass tubes[3]. The Fahraeus-Lindqvist effect is observed in narrow tubes less than 300 μm, and it is enhanced at high hematocrit. In microvessels, the cell-free layer along the wall (Fahraeus effect) is important in reducing the friction between RBCs and endothelial cells and thus the flow resistance.

Plasma skimming

In vivo microvascular networks are composed of many vessel segments linked by frequent bifurcations. This architecture has a dramatic effect on hemodynamics and network perfusion, causing not only a substantial increase in vascular resistance, but also a significant degree of flow heterogeneity. A specific mechanism generating heterogeneity with respect to hematocrit distribution within microvascular networks results from the Fahraeus effect. At individual branch points in the network, the cell-free plasma layer along the wall in the mother vessel leads to an uneven distribution of cell and plasma flow into the two daughter branches. In general, larger daughter vessels with higher volume flow exhibit increased hematocrit at the expense of smaller ones with lower volume flow. For very uneven flow distributions, small vessels may even be perfused by plasma void of any red cells (plasma skimming).

RBC aggregation

RBCs are deformable biconcave disks, and this physical property facilitates blood flow both under bulk flow conditions and in the microcirculation. The tendency of RBCs to undergo reversible aggregation is an important determinant of apparent viscosity. The size of RBC aggregates is inversely proportional to the magnitude of shear forces; the aggregates are dispersed with increasing shear forces, then reform under low-flow or static conditions. RBC aggregation is mainly determined by plasma protein composition and surface properties of RBCs, with increased plasma concentrations of acute phase reactants in inflammatory disorders a common cause of increased RBC aggregation. RBC aggregation directly influences leukocyte adhesion[4], blood rheology[5], and oxygen transport[6]. RBC aggregation also affects the in vivo rheology of blood, especially in the low-shear regions of the circulatory system. Impairment of blood fluidity may significantly affect tissue perfusion and result in functional deteriorations[7], especially if disease processes also disturb vascular properties.

WBC adhesion

Although WBCs are less abundant (about 1 WBC for every 1000 RBCs), they are important for immune system and have important effects on microcirculation dynamics. WBCs adhere to the vascular endothelium in inflammation and in tissue injury. The leukocyte-endothelial interaction is well understood at the molecular and biophysical levels. WBCs may have a significant effect on venous resistance during physiologic and pathophysiologic states. It has been shown that leukocytes obstructing the passage of flow through an arteriole during hemorrhage may increase intravascular resistance by as much as 75% from control values[8]. WBC dynamics, i.e., margination, rolling, and adhesion to the vessel wall, are greatly influenced by the RBCs and RBC aggregation.

Although the behavior of blood microcirculation summarized above has been widely recognized after extensive investigations both in vitro and in vivo, a rigorous, quantitative description of these effects has been elusive. A variety of models have been developed for the quantification of specific effects of blood flow in microvasculature. The non-Newtonian rheology is largely due to the plasma-rich zone that forms near the wall. The Fahraeus effect and Fahraeus-Lindqvist effect were considered in two-phase continuum models where the Newtonian viscous fluid represents the RBC core and an annular concentric layer of a less viscous Newtonian fluid represents the cell-depleted layer[9; 10]. Computational fluid dynamics models of single cells have been developed to analyze RBC deformation[11] or leukocyte rolling[12; 13] in response to the shear flow. But considering the difficulty in simulating individual RBCs, these approaches are not easily extended to multiparticle systems with physiological numbers of particles. Therefore, these studies did not address the overall changes in bulk blood rheology due to interactions of individual cells, not to mention the Fahraeus effect and Fahraeus-Lindqvist effect.

Previously, we developed a mathematical model using a lattice Boltzmann method to characterize the interactions and estimate the forces involved as individual RBCs (modeled as capsules or ellipses) and WBCs interact in capillaries[14] and in postcapillary expansions[15]. This model is also ideally suited for analyzing the rheological properties of concentrated cell suspensions[16] which can reproduce the Fahraeus and Fahraeus-Lindqvist effects by explicitly accounting for the particulate nature of blood. This represents a first step toward achieving a fundamental understanding of the complex fluid dynamics of blood. The objective of the present paper is to introduce a lattice Boltzmann method that can predict various effects of blood flow in complex microvascular networks by explicitly accounting for RBC aggregation, leukocyte-endothelium interactions, and cell-cell interactions.

2 Methods

Fluid and particle dynamics

A lattice Boltzmann method (LBM) is used to calculate the unsteady flow field and the blood cell motions. The RBCs are represented by two-dimensional (2-D) capsules (rectangles with superimposed half-circles at the ends) and the WBC is modeled as a disk with ligands distributed around the circumference. The lattice Boltzmann equations are solved on a square lattice with nine directions for the fluid phase, which is coupled with the Newtonian rotation and translation of solid particles suspended in the fluid through solid-fluid interactions. The LBM solves a discretized BGK[17] form of the Boltzmann equation for the particle density distribution:

$$f_j(\overrightarrow{x}+{\overrightarrow{c}}_j\mathrm{\Delta }t,t+\mathrm{\Delta }t)=f_j(\overrightarrow{x},t)+{\mathrm{\Omega }}_j,$$ (1)

where ${\mathrm{\Omega }}_j=[f_j^{eq}(\overrightarrow{x},t)-f_j(\overrightarrow{x},t)]/\tau$. Ω_j is the BGK collision operator, τ is a relaxation time, x⃗ is the location of the lattice node, and c⃗_j is the particle velocity, $f_j^{eq}$ is the equilibrium distribution that is determined by the fluid density and momentum (see[18] for definition of $f_j^{eq}$).

Once the particle density distribution is known, we calculate the fluid density and momentum using: ρ= Σmf_j, ρ v⃗ = Σ m f_j c⃗_j.

The fluid density and velocity obtained using this approach are equivalent to those obtained using the following rigorous Navier-Stokes equations for Newtonian fluids[19; 20; 21]. The calculation of the cell motion is based on the approach of impermeable particle suspensions by Aidun et al.[18] and Ladd[22], where the Newton’s law applied:

$$\frac{d{\overrightarrow{u}}_p}{dt}=\frac{\overrightarrow{F}}{m_p};I\frac{d{\omega }_p}{dt}=T$$ (2)

where u⃗_p is the velocity of the cell, ω_p is the angular velocity, T is the torque, m_p is the mass, I is inertia and F⃗ is the net force acting on the cell. For RBCs, F⃗ consists of the hydrodynamic force and the aggregation binding force F⃗_a which acts between RBCs if they are close enough to each other, (described in the following subsections). For leukocytes, F⃗ includes the hydrodynamic force and the ligand force F⃗_L acting between the leukocyte and the vessel wall as defined in the following.

Leukocyte-endothelium (L-E) adhesion

The L-E adhesive dynamics approach has been extensively developed[23; 24; 25; 26] to describe cell attachment, rolling, and firm adhesion in flow (see Fig. 1). As in our previous work[15; 14; 16], the receptor-ligand bonds are modeled as springs providing a force along the bond direction: f_L = σ(L − λ), where L is the bond length, λ is the equilibrium bond length and σ is the spring constant. The forces contributed by individual ligand-receptor bonds are summed to determine the total bond force and the torque acting on the cell during the period Δt. If the receptor-ligand distance Y_l is less than a critical value H_c (40 nm), a new bond can form with a finite probability P_f = 1 − exp(−k_onΔt), if Y_l ≤ H_c, where k_on = k_f N_L, k_f is the forward reaction rate and N_L is the ligand density.

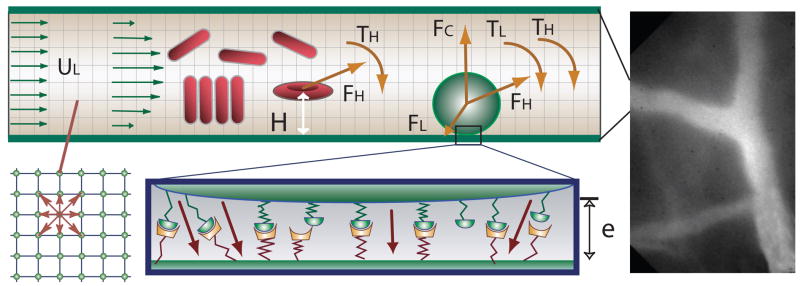
Fig. 1.

The right panel is an image of in vivo microvessels in the mouse skin (dorsal window) which is binarized and used in LBM simulations. Left panel illustrates the blood flow models in the microvessels. A disk representing a leukocyte rolls on the wall of a vessel. The leukocyte interacts with the wall through receptor-ligand interactions and a non-specific repulsive force. The forces and torques of individual bonds are summed (F⃗_L, T_L) and applied to the leukocyte together with the hydrodynamic forces and the torque (F⃗_H, T_H). RBCs may form an aggregate through the bridging molecules on their surfaces. Fluid particle velocities of a 2-D lattice Boltzmann model with nine velocities are illustrated at the left lower corner.

A preexisting bond is disassociated with a reverse probability P_r: P_r = 1 − exp (−k_rΔt), where k_r = k_r0 exp [(σ − σ*)(L − λ)²/(2k_bT)], k_b is the Boltzmann constant, T is the temperature, k_r0 is the reverse reaction rate and σ* is the transition state spring constant (see[15] for the constants). The probability P_r increases with the current load of the bond.

RBC aggregation

In normal blood at stasis, or flowing at low-shear rates, RBCs spontaneously aggregate, forming long linear stacks (known as “rouleaux”) and larger three-dimensional structures. RBC aggregation depends on high-molecular weight proteins in the plasma. Studies have shown that Dextrans of molecular weight lower than 50,000 prevent aggregation whereas higher molecular weight Dextrans increase the degree of red cell aggregation[27]. A recent study suggests that the influence of a nonionic polymer or plasma protein on RBC aggregation is simply a consequence of its size in an aqueous environment, and that the specific type of macromolecule is of minor importance[28]. Two hypotheses exist currently to explain how red cells overcome the repulsive electrostatic membrane charges of apposing red cells and the shearing forces caused by blood flow during aggregation. The bridging hypothesis proposes that long macromolecules in the plasma reversibly attach to the RBC membranes, forming bridges between apposing cells which are strong enough to counter electrostatic repulsion. The other hypothesis of red cell aggregation rests on the theory that the concentration of plasma proteins is less in the microscopic surface layer surrounding the red cell than in the bulk plasma, and an osmotic gradient brings cells together.

In the previous aggregation model[29], we assumed that when the surfaces of two RBCs are sufficiently close, bridges are formed by the long molecules evenly distributed on the RBC surfaces, inducing a binding force: F_a = σ_a(L_a − λ_a), if λ_a < L_a < L₀, where σ_a is a spring constant, L_a is the bridge length, L₀ is the maximum length, and λ_a is the equilibrium bridge length.

3 Results

A major advantage of the lattice Boltzmann method is the ability to simulate particulate flow dynamically and in arbitrary geometry. Using this approach, we are able to accurately determine RBC-WBC forces, the trajectories of these particles, the pressure changes in each segment due to cellular traffic, and the forces felt by the vessel wall at any location. The in vivo micro vessels in the mouse skin from a dorsal window (right panel of Fig. 1) are binarized and used in the present LBM simulation. The vessel diameters are 14 μm and 22 μm at the two inlets and are 27 μm and 23.4 μm at the two outlets. The computational domain is of 800×400 lattice nodes, where one lattice unit is 0.3 μm. A bounce-back boundary condition is imposed at the walls, corresponding to a non-slip wall boundary condition. The flow velocities at the inlets are imposed according to the flow velocities measured in the segments from intravital video. Constant pressures are imposed at the two outlets. As a preliminary test of the model for the complicated micro vessels, the leukocyte-endothelium binding and the RBC aggregation are not activated.

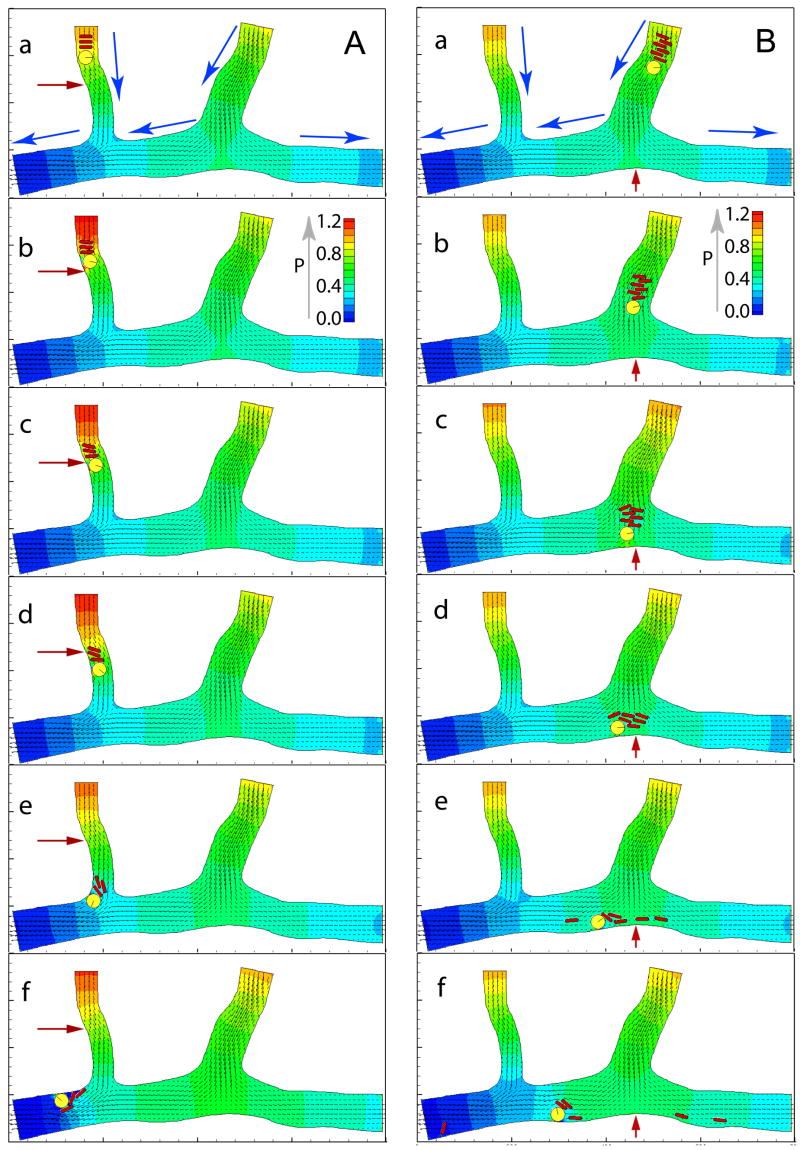
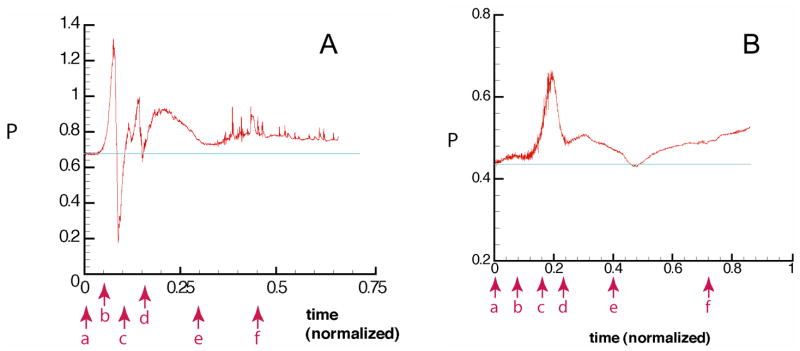
In the simulations, the pressure and velocity profiles at any location can be measured simultaneously with particle dynamics, and the model accurately predicts pressure changes in individual vessel segments due to the presence of flowing cells. The pressure is nondimensionalized by the pressure drop between the left entry at the top and the left exit at the bottom of the channel (see fig. 2) which is obtained by flowing the plasma without cells. Figure 2 shows three RBCs following a WBC through the left, smaller vessel (panel A) and six RBCs following a WBC through the right, larger vessel. The pressure and velocity fields at the initial time when the cells are placed in the vessels (the frames a) are the steady plasma flow fields without any cells. The rolling WBC and the RBC stack induce a large pressure perturbation in the left branch, especially near the curved wall marked by the red arrows in Fig. 2A, panels b–d (see Fig. 3A for the temporal pressure changes at this location). The right branch has a bifurcation at the bottom where the temporal changes in pressure at a stagnation point shows that the cells in blood produce large fluctuations in force in this region (see Fig. 2B). The flowing cells produce changes in the fluid velocity near the stagnation point, resulting in perturbations in shear stress at this location. Figure 3B shows the temporal pressure changes at the stagnation point. The fluctuations in normal and shear forces at the vessel wall may relate directly to the formation of atherogenesis in vivo.

Fig. 2.

Flow fields and cell positions at various times. Lattice: 800×400. One grid point unit is equal to 0.3 μm. Total time of 0.3 seconds is normalized to 1. The pressure field is represented by colors and the velocity field is represented by arrows. Panel A: simulation of L-E interactions in the left branch. Time sequence of three RBCs following a WBC into a larger venule is shown in a–f. Blue arrows in (a) give flow direction. Panel B: simulation of six RBCs following a WBC into the right branch with diverging flow.

Fig. 3.

Panel A: Normalized pressure, P, at the wall position marked by the red arrows in Fig. 2A indicates sequential time points correspond to panels a–f in Fig. 2A. Note the large fluctuation in pressure at the wall as the WBC passes (b–c), and then the RBCs pass (c–d). The pressure drop in this vessel segment decreases as the cells exit (e); then there is an elevated pressure (compared to baseline (a) due to the obstruction of flow in the exiting vessel by the cells (f). The “noise” in the region of (f) is due to collisions between the cells, which disturbs flow in the fluid phase, and thus the pressure. Panel B: Normalized pressure, P, at the wall position indicated by the red arrow in Fig. 2B. The pressure at the stagnation point increases significantly as the cells approach (a–d). The increase in pressure near the end of the simulation is due to the flow restriction produced by the cells.

4 Discussion and Conclusion

Our simulations show that the cells significantly increase the pressure and shear stress near the vessel wall as they pass by, especially at the curved segment and at the bifurcation point. This implies that the flowing cells induce higher flow resistance at these locations than in straight, non-branched segments of the network. Previously we quantified the impact of cells on the apparent viscosity in straight micro channels[16]. The present simulations indicate that curvature and bifurcations may produce additional increases in the relative apparent viscosity in real vessel networks. These results may have implications for atherogenesis at stagnation points. It is well known that the endothelial cells are nicely organized under constant shear stress, but they become disordered under oscillating shear stress, and therefore are more easily disrupted[30]. Our simulations suggest that a group of flowing cells may induce significant perturbations in pressure and shear stress near bifurcations where the shear stress is usually low. These perturbations may be important determinants of endothelial biology and the formation of the atherosclerosis. Since atherosclerosis is more common in larger arteries, further investigation is needed to determine the effect of this local perturbation on the endothelial cell and whether it facilitates atherosclerosis.

L-E binding and aggregation are not active in the present simulations. It is well known that red cell aggregation is a major factor in changing venous resistance during variations in blood flow. Aggregates flatten the velocity profile, increase the shear rate in the plasma layer near the vessel wall, and in turn, increase venous resistance[31]. Leukocytes may also have a significant effect on venous resistance in physiologic and pathophysiologic states. In previous studies, we have shown that leukocyte adhesion to the vessel has a significant effect on venous resistance in straight vessels[16] and RBC aggregation increases both leukocyte adhesion and flow resistance in postcapillary expansions[29]. Compared with individual RBCs, an aggregate interacts more strongly with a rolling WBC and therefore, transmits more force to the vessel wall through the WBC. Activation of the L-E binding and the aggregation will not only increase the relative apparent viscosity resulting from vessel curvature and bifurcation, but also amplify the stress oscillation at the bifurcation location which promotes atherogenesis.

In summary, we have adapted an LBM to simulate blood flow in a complex, real, microvascular network. This approach may be used to identify rheological and geometric determinants of interactions between blood cells and endothelium in various vascular beds. The preliminary simulations indicate that vessel curvature and bifurcations result in significant increases in the relative apparent viscosity, and that the flowing blood cells impose strong perturbations in stress near the stagnation locations, which may be related to the atherogenesis formation.