Phase Matching considerations in Second Harmonic Generation from tissues: Effects on emission directionality, conversion efficiency and observed morphology

1. Introduction

In the last several years, Second Harmonic Generation (SHG) has emerged as a powerful nonlinear optical contrast mechanism for tissue imaging applications. The majority of the recent reports have focused on visualizing collagen fibers in natural tissues including skin, tendon, blood vessels, and cornea(1–12). A smaller body of publications has described SHG imaging of acto-myosin complexes in muscle(13, 14) as well as microtubule-based structures in live cells(13, 15). A particularly strong attribute driving these efforts is that the SHG contrast is produced purely from the endogenous proteins without the need for exogenous dyes. Furthermore, SHG signals arise from an induced polarization rather than from absorption and this leads to substantially reduced photobleaching and phototoxicity relative to fluorescence methods (including multiphoton).

Since SHG is a second-order nonlinear optical process, it can arise only from media lacking a center of symmetry. This condition is met by the protein species listed above because these molecules possess permanent dipole moments which align in a highly ordered fashion. Additionally, the inherent chirality of the helices increases the overall asymmetry of the assembly and thus increases the second order response. While this symmetry constraint may appear limiting in general applicability, it allows SHG to be a direct sensor of supramolecular structure. This is because many diseases are characterized by defects or changes in the assembly of collagen in the respective tissue and we thus suggest that the SHG imaging modality has great potential as a clinical diagnostic tool. For example, the connective tissue disorder Osteogenesis Imperfecta (OI) is characterized by abnormal collagen assembly and we have shown that SHG can reveal differences in the morphology not possible by other optical methods(16). Additionally, SHG has also shown early promise in imaging cancer since malignant tumors often have abnormal collagen assembly relative to normal tissue (9, 17).

An additional enabling property for potential diagnostic imaging applications arises from the (quasi)coherent nature of the SHG process. Unlike the incoherent process of fluorescence which is emitted over 4π steradians, SHG has a phase (and spatial) relationship with the laser excitation. As we will discuss in detail in a latter section, this coherence is manifested in the initial directionality of the emission, which in part underlies the observed contrast in the forward and backward channels. In previous reports the forward/backward ratio has been ascribed to the fibril size(4, 11). Additionally, smaller, segmented features can be better visualized in the backwards signal, where this effect has recently been observed for collagen in tendon, skin, and cornea by Williams et al,(4) Tai(1) and Han et al(11), respectively and by us in cellulose(18). However, examination of the collective findings of these papers does not yield a unified relationship between SHG directionality, fibril morphology, and fibril size, suggesting fibril size considerations alone are insufficient for complete SHG image interpretation. Developing a thorough description of the SHG creation is an essential step for this imaging modality to become a useful clinical diagnostic tool for monitoring disease severity and progression. To solve this problem, here we present a new heuristic model which provides a mathematical framework leading to the necessary insight to enable a thorough understanding of the relationship between fibril size, and assembly to the SHG response.

The SHG creation model is based upon relaxed phase matching conditions which account for axial momentum contributions from the media, and includes a simple mathematical treatment which relates SHG conversion efficiency to fibril diameter and packing through the inclusion of potential intensity amplification resulting from quasi-phase matching (QPM). The basic premise of QPM is that the intensity builds up over the course of multiple fibrils domains allowing waves to build up intensities larger than that pertaining to a single domain, being maximized when the size and spacing are on the order of the coherence length. A direct consequence of this theory is that SHG in biological tissues is not strictly a coherent process, as dispersion, axial momentum contributions from the lattice, as well as randomness of the protein assembly all act to degrade coherence which has direct ramifications on the obtained SHG image in terms of the conversion efficiency, directionality, and observed morphology. Through this consideration, we will show (section 4.1) that the conversion efficiency associated with backward SHG creation within a single fibril is small and that only through QPM are appreciable intensities realized.

Using this theory we show that the emission directionality and also conversion efficiency depend collectively on the fibril diameter, the randomness of the inter-fibril packing structure, and that treatments that are only based on fibril size cannot adequately describe all SHG image characteristics. For example, in several reports, segmented fibrils have been observed exclusively in the backward channel, while these same fibrils appear to be continuous in the forward direction. While various descriptions have been suggested, we show here that these observations are consistent with the difference in the effective coherence lengths of the forward and backward components arising from the relaxed phase conditions appropriate for biological tissues. We further demonstrate the applicability of the model principles in comparing the SHG response in normal and Osteogenesis Imperfecta (OI) skin. We show that the observed directionality and decreased relative intensity in the diseased state is consistent with the relaxed phase matching conditions and QPM intensity contributions arising from the decreased fibril size and more random assembly. In its entirety this heuristic model provides the necessary insight to relate SHG emission characteristics to actual tissue morphology. Moreover, this treatment, when coupled with subsequent propagation models based upon bulk optical properties of the turbid media (19)a to account for subsequent photon/tissue interactions, forms a complete picture useful in interpreting the contrast between healthy and diseased SHG images for diagnostic applications.

2. Introduction to SHG creation in biological tissues

Due to the underlying polycrystalline nature of most collagenous tissues(20), these materials contribute axial momentum, altering the traditional phase matching conditions used to characterize strictly coherent processes, i.e. Δk=k_2ω−2k_ω=0, where k_2ω is the wave vector for SHG photon and k_ω is the wave vector for the incident photon. Accordingly, the fibrillar packing density and randomness alter the conservation of momentum establishing a quasi-coherent process. Due to the inherent differences in required axial momentum for forward and backward (F_SHG and B_SHG, respectively), this quasi-coherency is directionality dependent. In general, strict phase matching conditions are not applicable in this case where F_SHG created is mainly governed dispersion, (n_2ω ≠ n _ω) and where B_SHG requires axial momentum contributions from the media if the SHG created photon is to travel in the opposite direction of the incident photons. The SHG conversion efficiency is then determined by the phase mis-match, by axial momentum contributions from the media, as well as decreased by the randomness inherent to biological tissues.

Previously using antenna theory, Mertz demonstrated that spatial inhomogeneities (axially periodic and spherically localized distributions) are capable of contributing such momentum to the phase matching condition and, under appropriate conditions, can account for the creation of backwards SHG(21). In related work, Mertz also demonstrated a double peaked forward SHG profile with essentially no backwards component for dye molecules in membrane.(22) This poses a question as to how tissues contribute sufficient axial momentum to create B_SHG. Through our model we will demonstrate that only through QPM can appreciable B_SHG be produced by intensity buildup along multiple fibrils. Moreover, this treatment explains why backward SHG creation is not appreciably observed in the membrane case due to lack of distributive amplification along its very thin axial extent (~ 4nm). As Mertz’s treatment only considered a single scattering cluster (i.e. individual dye molecules) and neglected dispersion and randomness, this theory is not appropriate for consideration of the SHG directionality and conversion efficiency in tissues, where axially adjacent fibrils are packed sufficiently close (on the order of the coherence length) to interact and contribute to the overall SHG response.

To describe SHG creation in fibrillar collagen we build upon and expand Mertz’s formalism, where our treatment includes QPM and additional phase mis-match due to dispersion and randomness all of which lead to allows for the creation of partially-coherent SHG in both the forward and backward directions. QPM allows the buildup of SHG intensity between anisotropic domains (here either fibrils or assembly of small fibrils) without the need for strict phase matching conditions, with maximum effect when the domains size and spacing are on the order of the coherence length of radiation. For example, this theory has been utilized to describe the buildup of SHG in ferroelectric crystals, (23) and has been used to design efficient backwards SHG producing periodically poled “engineered” crystals (24). We note that while periodically poled crystals utilize periodic structures designed to maximize conversion efficiencies, similar, although less efficient, effects are present in tissues. Structural variations, dispersion and randomness inherent to biological tissues all act to decrease the coupling efficiency associated with QPM. Therefore it is instructive to associate the high QPM conversion performance characteristic of periodic poled crystals with a completely periodic collagenous structure and on the other extreme, low QPM conversion efficiency consistent with a totally random structure. The physiological case will lie somewhere in between these limits where the conversion efficiency is dependent upon the fibrillar diameter, inter-fibrillar spacing and randomness of the tissue assembly. In Section 4.2, we treat these structural aspects by presenting relaxed phase matching conditions which incorporate axial momentum contributions from the distribution of SHG radiators (i.e. collagen fibrils) and includes a term (Δk) pertaining to phase mis-match due to dispersion and randomness and, where this inclusion inherently implies the partially coherent nature of the created SHG signal. We note that in addition to SHG amplification within a single domain, distributed amplification is possible between domains which are separated by a distance comparable to the coherence length, L_c =2π/Δk. Due to the complexity of biological tissues SHG creation is possible in both configurations. Thus for comparison, throughout this work we will associate the total SHG signal with an effective Δk which maps the overall SHG intensity to that produced within a single normalized domain.

3. Quasicoherent and incoherent SHG components from fibrillar tissues

The overarching goal of our SHG imaging work is to develop metrics for diagnostic imaging, and to achieve this we need a complete picture of all the factors that govern the observed contrast in a tissue imaging measurement. These include contributions from both SH creation and subsequent propagation in the turbid media which produces both quasi-coherent and incoherent components, respectively, together forming the observed SHG images (25). In highly scattering tissues this latter component will become significant at SHG depths exceeding one mean free path (MFP) or ~1/μ_s of the matrix. This multiple scattering causes off-axis propagation and is responsible for the incoherent components in both the forward and backwards directions. In general Monte Carlo techniques are utilized to describe the effects of propagation through such turbid media. To accurately describe the actual image from tissue both the creation and subsequent propagation must be analyzed separately. Differentiating these components is an important consideration for clinical applications as diseased states may have smaller and more randomly packed fibrils which affect the initial generation directionality. Such tissues may also have different bulk optical parameters, governing the subsequent photon propagation (19).

We have recently examined the mixing of the quasi-coherent and incoherent contributions in fibrillar cellulose(18) as well as in OI and normal murine skin(19) and found the relative component weights are highly dependent upon SHG creation depth. Experimentally, we measured the SHG forward to backward ratio (F/B) which results from both components, as a function of the excitation depth into the tissue. The experimental data for oim and WT skin are shown in Fig 1a. In these measurements, the NA was 0.8, with a measured PSF of ~12 microns (due to under-filling of the lens). These slices were ~200 microns thick and containing the epidermis, dermis, and adipose layers. We have shown in another publication that the scattering coefficients for the oim and wild type tissues were 200 and 300 cm⁻¹, respectively. We observe that for both tissues the measured F/B increases with increasing depth into the tissue. This result is consistent in the framework of photon diffusion theory, where at least one MFP is required between the location of the emitted photon to the forward boundary of the specimen for efficient multiple scattering to occur(26). To analyze the incoherent scattering component, we performed Monte Carlo simulations of the photon propagation based on our measured bulk optical properties at both the fundamental and SHG wavelengths.(19) Simulations assuming 100% forward generation reproduced the measured trends but overestimated the detected F/B at all depths. Based on previous reports, (4, 18) this is not a realistic scenario since for small fibrils a significant backward coherent component will exist. Through SEM analysis the skin fibrils are ~λ_SHG/5 in diameter (70 and 100 nm) for the oim and WT, respectively. To estimate the initial F_SHG/B_SHG value, we ran simulations varying the ratio of the initial emission directionality. The results for a 75%–25% forward and backward distribution (both tissues) are shown in the bottom panel of Figure 1. These plots in Fig 1 approach the experimental data and this Monte Carlo method provides an estimate of the creation ratio. However, to fully interpret (or predict) the SHG response, we still need a general model to relate the relative conversion efficiency and initial emission directionality to the physical assembly of the matrix.

Fig. 1.

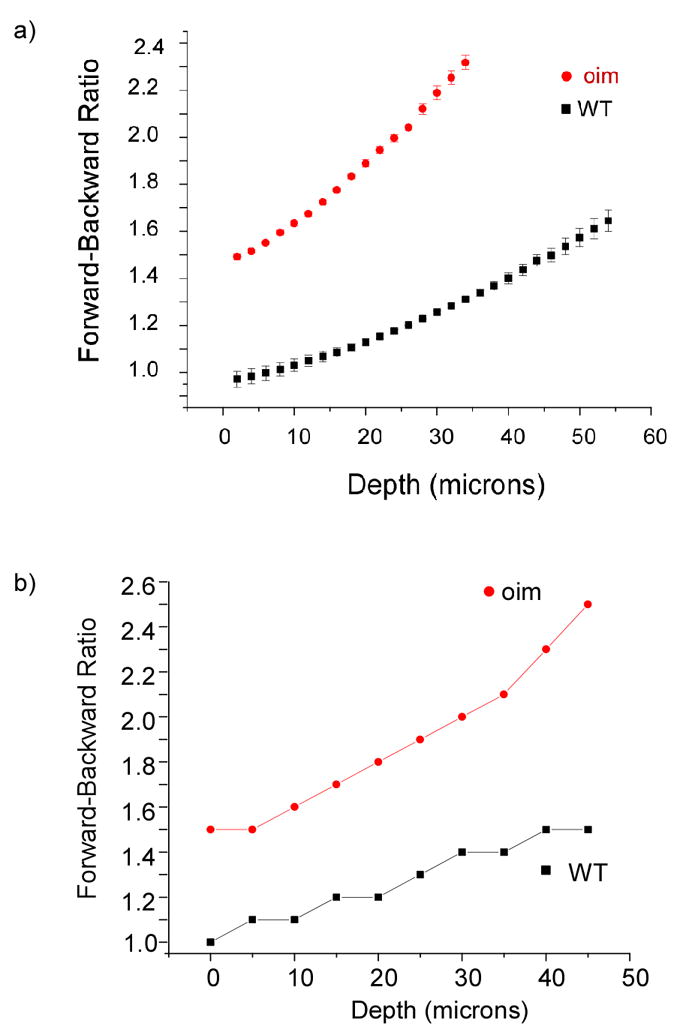
Experiment (a) and simulated (b) forward/backward intensities plotted as a function of excitation depth in WT and oim skin. The simulation used scattering parameters determined through diffuse reflectance and transmittance measurements and assumed an initial 75% and 25% distribution of (quasi)coherent forward and backward components.

In one approach, Williams et al(4) estimated the F_SHG and B_SHG ratio in tendon based only on fibril size, where this approach works due to the high degree of regularity in terms of the diameter and packing. However, most tissues, such as skin, bone, cornea, do not possess such regularity, and the randomness may be further increased in diseased states. Below, using relaxed phase matching considerations, we present a more general treatment of the generation step that explicitly relates fibril diameter and packing assembly to conversion efficiency, emission directionality, and observed morphology all within same framework of partial coherence and the corresponding different coherence lengths for the F_SHG and B_SHG. We show that this treatment is consistent with our experimental measurements on skin (oim disease model) and fibrillar cellulose as well as other reports in the literature.

4. Heuristic model for SHG creation

4.1 General phase matching considerations

To explicitly examine the impact of the relaxed phase matching conditions including axial contributions from the media, and a mis-match term Δk pertaining to dispersion and randomness contributions on SHG conversion efficiency and directionality, we begin by first considering the simple case of the propagation of a plane wave moving through a nonlinear media in the direction of its k → vector. Even though this is not a strictly accurate description of the actual case, which involves focused excitation (NA=0.8), we argue that general inferences may be obtained for the case where the focused beam length (in the axial direction) and the coherence length of the incident laser are longer than the coherence length of SHG radiation. In our experiment, both of these conditions are satisfied, as the measured axial point spread function is ~12 microns FWHM, the coherence length of the ti:sapphire laser is ~ 30 microns, whereas the maximum forward coherence length of collagenous tissues based on dispersion is ~7 microns. Furthermore we will account for the Guoy phase shift due to focusing through an effective reduction in axial propagation vector as employed by Mertz et al (21).

By following the coupled wave treatment of Munn (27) utilizing the slowly varying field approximation, the distributed amplification of the second harmonic within a homogeneous region or domain is given by the following equation:

$$\frac{dE(2\omega )}{dz}=-\frac{i\omega }{n_{2\omega }c}{d}_{\mathit{eff}}{E}^2(\omega )exp(i\mathrm{\Delta }kz)$$ (1)

where the effective SHG coefficient d_eff (2ω) is proportional to the second order susceptibility χ² n_2ω is the index of refraction for the second harmonic wavelength, c is the speed of light, and Δk=k_2ω−2k_ω is the magnitude of wave vector mismatch between the incident and second harmonic waves.

Assuming propagation in the z direction and neglecting walk-off (22), the total second harmonic radiation at length L (domain length) is the vector sum of all the intermediate constituents (taking into consideration their respective phases) from lengths 0<z<L, and, utilizing the boundary condition [E(2ω,z=0)=0], can be expressed by:

$$E(2\omega ,z=L)=\kappa E^2(\omega )\left[\frac{1-exp(i(\mathrm{\Delta }k))L}{-i\mathrm{\Delta }k}\right]exp(i(2\omega t-k_{2\omega }L))$$ (2)

with the coupling coefficient $\kappa =\frac{\omega d_{\mathit{eff}}}{nc}$. This equation includes the phase matching term Δk=k_2ω−2k_ω which when equal to zero produces the maximum conversion.

For non-zero Δks, the second harmonic amplitude E_2ω (z) at a position L along the propagation direction is given by:

$$E_{2\omega }=\kappa E_{\omega }^2\frac{sin(\mathrm{\Delta }kL/2)}{\mathrm{\Delta }kL/2}.$$ (3)

A plot illustrating the normalized conversion as a function of Δk is given in Fig. 2. In biological tissues the minimum phase mismatch is governed by dispersion and is denoted by Δk₁. Two values (Δk₁ and 2Δk₁, where Δk₁ is the wave vector mismatch due to change in index of refraction between the incident and second harmonic frequency) are shown to demonstrate the decrease in intensity for increasing values of Δk for relatively small mis-matches. Theoretically, the SHG conversion is maximized at the phase matched condition Δk=0 and decreasing conversion occurs for non-zero levels of Δk. Unlike birefringent crystals with Δk=0 at a specific incident angles of excitation for phase matching ordinary and extraordinary waves,(28) axial momentum contributions from the media (which are non-singular due to randomness) and dispersion inherent in biological tissues results in a large distribution of Δk values, where the overall SHG intensity includes contributions from this entire assembly. Furthermore we relate increased randomness with even wider distributions of Δk values, where signals corresponding to higher Δk values possess shorter coherence lengths and lower conversion efficiencies. It will be shown that the dominant Δk values contributing to the overall SHG conversion efficiency are determined both by the Δk distribution and domain size, whereas SHG directionality is a function of Δk distribution, domain size and inter-domain spacing. In a following section (4.3) we will explicitly show this to be the case in the oim disease model.

Fig. 2.

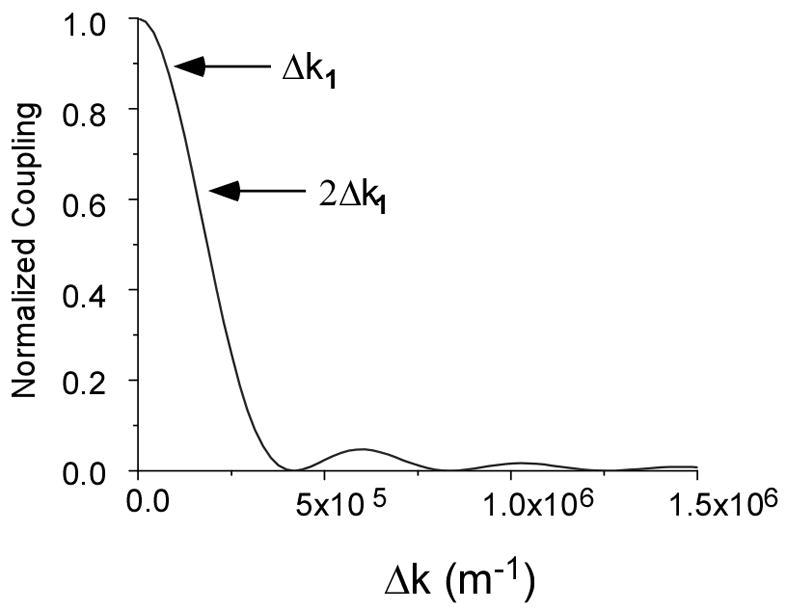
Normalized SHG coupling as function of Δk for values of Δk₁ and 2Δk₁. The increased phase mismatch of the wave vector results in relative decreased SHG conversion efficiency.

In other treatments it has been shown that the initial emission directionality is dependent upon the fibril diameter, where in general forward signals are associated with fibril diameters on the order of λ_SHG and F_SHG/B_SHG~1 for diameters of λ_SHG/10(11). Here we present the more general case of a SHG conversion within a domain, which we define as a local source or distributed collection of SHG radiators which in tissues can be either single fibrils or smaller fibrils packed closely together. For a given effective phase matching condition (Δk) the incremental conversion amplitude along the propagation direction is approximated by Eq. 1 assuming a homogeneous domain of length L. Due to the randomness associated with biological tissues we cannot measure actual Δk values, but utilize multiples of the mis-match due to dispersion (Δk₁) to investigate trends associated with higher mismatch. Figure 3 illustrates the normalized build up of the second harmonic with a phase mismatch of Δk₁ (for an Δn=.02) over the course of one normalized coherence length L_c1=2π/Δk₁. Analogous curves are also given for the distributive buildup of higher mismatched conditions given by mΔk (m is an integer) for multiples of Δk₁. We note that maximal SHG conversion efficiency will occur for small Δk values and interaction lengths L (or domains) on the order of L_c. For illustrative purposes the respective coherence lengths for the two largest (m=1&2) are depicted parallel to the x axis. We see that for each phase matching condition, the conversion scales as sin(mΔk L/2) and is therefore domain length dependant, reaching its first maximum at the respective L_c which is normalized by L_c1 in this figure. If the propagation lengths exceed the respective coherence length the amplitude oscillates sinusoidally (as depicted by the curves associated with larger Δk values). This suggests that for domains on the order of the coherence length, fields with relatively small Δk values will dominate, while fields associated with larger Δk values will be characterized by less-efficient SHG conversion at is maximum value. In sum, we associate large Δk values with lower SHG conversion efficiency. Next we will continue this analysis by associating large Δk values with backward SHG emission through relaxed phase matching conditions.

Fig. 3.

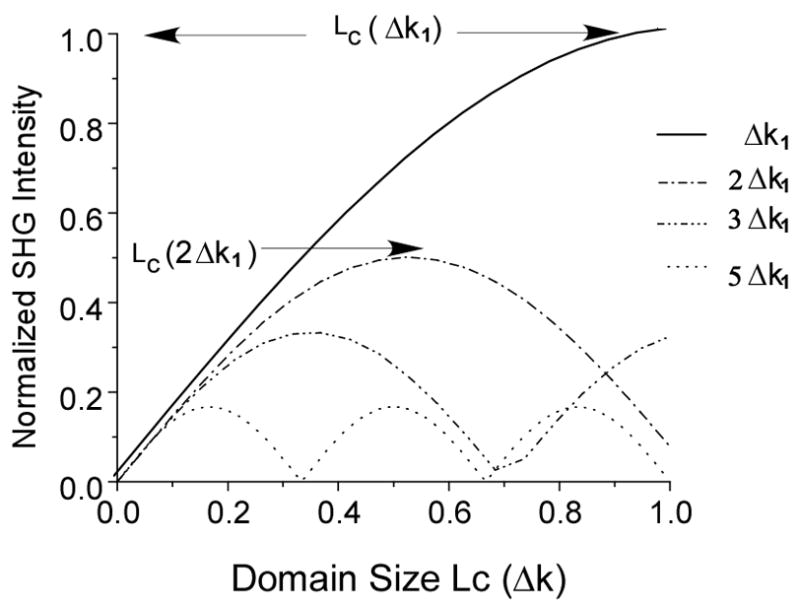
Normalized SHG buildup as functions of Δk₁ and domain size. The conversion oscillates as sin(Δk L/2) and domain length, L, reaching its first maximum at the respective coherence length. The respective coherence lengths for the two largest (m=1&2) are denoted by arrows.

4.2 Relaxed phase matching conditions and SHG directionality

Here we consider respective phase matching conditions for forward and backward SHG and how these relate to fibrillar domains in collagenous tissues. As pointed by Mertz, backward emission arises when the SHG producing assembly provides axial momentum, K, which alters the direction of the created photon(21). We stress here that this is specific to the creation step and is un-related to subsequent multiple scattering of the forward signal in tissue. Due to the fibrillar hierarchy of collagen (often described as polycrystalline in nature) and measured dispersion (Δn=n(2ω)-n(ω)=0.02) we assume that Δk values will exist such that the coherence length of the created SHG is on the order of the inter-fibrillar spacing thus allowing for the possibility of QPM. This then results in the following relaxed phase conditions.

$$\mathrm{\Delta }{k}_f=K_f-(k_{2\omega }-2k_{\omega })$$ (4)

and

$$\mathrm{\Delta }{k}_b=K_b-(k_{2\omega }+2k_{\omega })$$ (5)

where Δk_f and Δk_b are the phase mismatches for the forward and backward SHG creation, respectively, K_b and K_f are the axial momentum contributions to the backward and forward SHG creation, respectively. These equations are identical to those given by Canalias(24) used to describe periodically poled crystals, here we do not associate K with a single grating wave vector but an assembly of values (due to inherent randomness of collagenous tissues) provided by the medium. Backward SHG creation implies that in terms of magnitude that K_b >K_f. and therefore Δk_b> Δk_f., resulting in a distribution of “lower” efficiency SHG components making up the overall B_SHG. Consequently, shorter coherence lengths are associated with this component. These equations can be modified to account for focused initial radiation by replacing k_ωby ζk_ωwhere ζ is the effective reduction in axial propagation vector due to the Guoy phase shift(22). The description that follows below holds for the case where the axial spread of the focused spot is comparable or larger to 1/Δk_1, i.e. the material coherence length based on dispersion. As shown above, this condition is valid for our image acquisition performed at medium NA.

Forward SHG will be dominated by phase matching with smaller Δk_f values for domains on the order of Lc=2π/Δk_f, corresponding to small K_f values. Although the overall forward SHG signal is a summation of all the Δk terms, the lower Δk terms will dominate due to their relatively high conversion efficiency (see Fig. 2). Thus, we associate forward SHG with Δk₁ (i.e the maximum coherence length). By contrast, backward SHG is entirely dependent upon axial momentum provided by the lattice to redirect the created wave. Thus for significant (on the order of F_SHG ) backward SHG intensity the domain size should be less than the coherence length of the forward field (pertaining to the linear region of Figure 3) and the inter-fibrillar spacing must be on the order of the coherence length associated with the backward field. Thus, phase matching conditions support the association of B_SHG with relatively larger Δk values. We note that randomness increases the distribution of K values contributed by the medium and therefore the distribution of both Δk_f and Δk_b which effects the overall distribution of SHG creation. Thus we cannot specify the coherence lengths but state that the F_SHG has an upper bound limited by the material dispersion and as a consequence of Eq, 4 and 5, is characterized by longer L_c than that for B_SHG.

As we cannot measure the absolute Δk values, for comparative computational analysis we will associate F_SHG and Δk_f =Δk₁ and B_SHG with larger multiples of Δk₁ values (assigned values Δk_b= mΔk₁, where m is an integer and pertains to effective mis-match within a single domain). Doing so, one can predict the %F_SHG as a function of normalized domain (normalized to L_c1=2π/Δk₁) by dividing the SHG intensity of Δk₁ over the sum of itself and the respective mΔk₁ term (calculated from Fig. 3). Figure 4 shows the resulting % F_SHG for m=2–4. Utilizing superposition of these curves, this calculation shows that domains with values close to Lc₁ will support predominantly forward emission, while smaller domains will produce essentially even distributions. The emission directionality is highly sensitive to both the domain size and magnitude of Δk, where larger Δk values result in increased sensitivities and support steeper transitions to higher F_SHG. Based upon arguments made above we also attribute increased randomness with higher Δk values (i.e. shorter L_c) and lower conversion efficiency within a single domain. This analysis demonstrates that both domain size and randomness play an integral part in SHG emission directionality and that considerations based solely on fibril size do not form a complete description of the process. We will demonstrate this explicitly for the OI disease model in the next section.

Fig. 4.

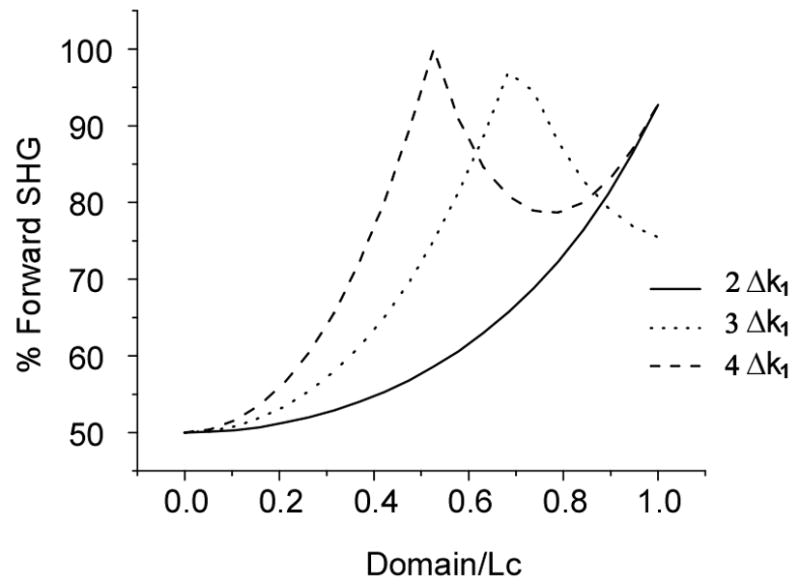
Calculated % F_SHG as a function of normalized domain size for several phase matching conditions. This calculation shows that domains with values close to Lc₁ will support predominantly forward emission, while smaller domains will produce essentially 50%-50% forward and backward distributions.

It is illustrative to relate the normalized domain used in Figure 3 to λ_SHG to associate these simulations with experimental observations that fibrils on the order of λ_SHG/10 produce creation ratios F_SHG/B_SHG~1. We point out that based on Eq. 4, the forward emission coherence length is affected by both K and Δk (which is at least Δk₁₎. To justify a forward coherence length on this order we note that the maximum coherence length as limited by dispersion is on the order of 7 μm and any axial momentum contribution from the medium acts to decrease this value, potentially by an order of magnitude. Thus by normalizing the domain to the SHG coherence length, we observe that for domains on the order of λ_SHG/10 (normalized to 0.1 in Fig. 3), the %F_SHG is close to 50%, as suggested by other work(4, 11) and increases to approximately 100% F_SHG for domains on the order of λ_SHG (normalized to 1 in Fig. 3).

It is important to note that the F_SHG/B_SHG ratio takes into consideration the quasi-coherent interactions associated with fibril diameter, packing density and randomness in the fibrillar matrix. Thus given the preceding theory, we predict large F_SHG/B_SHG ratios from collagen matrixes possessing relatively large fibril diameters (approximately λ_SHG, independent of the packing arrangement) and also from small fibrils (< < λ_SHG) if the fibril packing is very dense (essentially forming an effective domain), or for small fibrils which are sparsely packed compared to the backward coherence length. In contrast a F_SHG/B_SHG~1 can be expected for fibril diameters on the order of λ_SHG/10 for inter-fibril spacing on the order of the backwards coherence length.

4.3 OI vs WT Domains

We now apply the theoretical findings of the previous section to comparing the SHG response in the oim murine model for OI. As a point of reference Fig 5a, and 5b show representative SHG images of WT and oim skin. These images were taken with the experimental conditions described for the plots shown in Figure 1 (i.e. 900 nm and 0.8 NA). By inspection we note that the fibrils are more organized in the WT tissue, whereas the oim has a higher degree of randomness. In the data shown in Fig 1 we estimated the F_SHG/B_SHG creation ratio to be approximately 3:1 for both WT and oim skin. Now using the calculations shown for the general cases in Figs 3 and 4, we interpret the directionality and conversion efficiency in terms of the fibril size and randomness of the assembly.

Fig. 5.

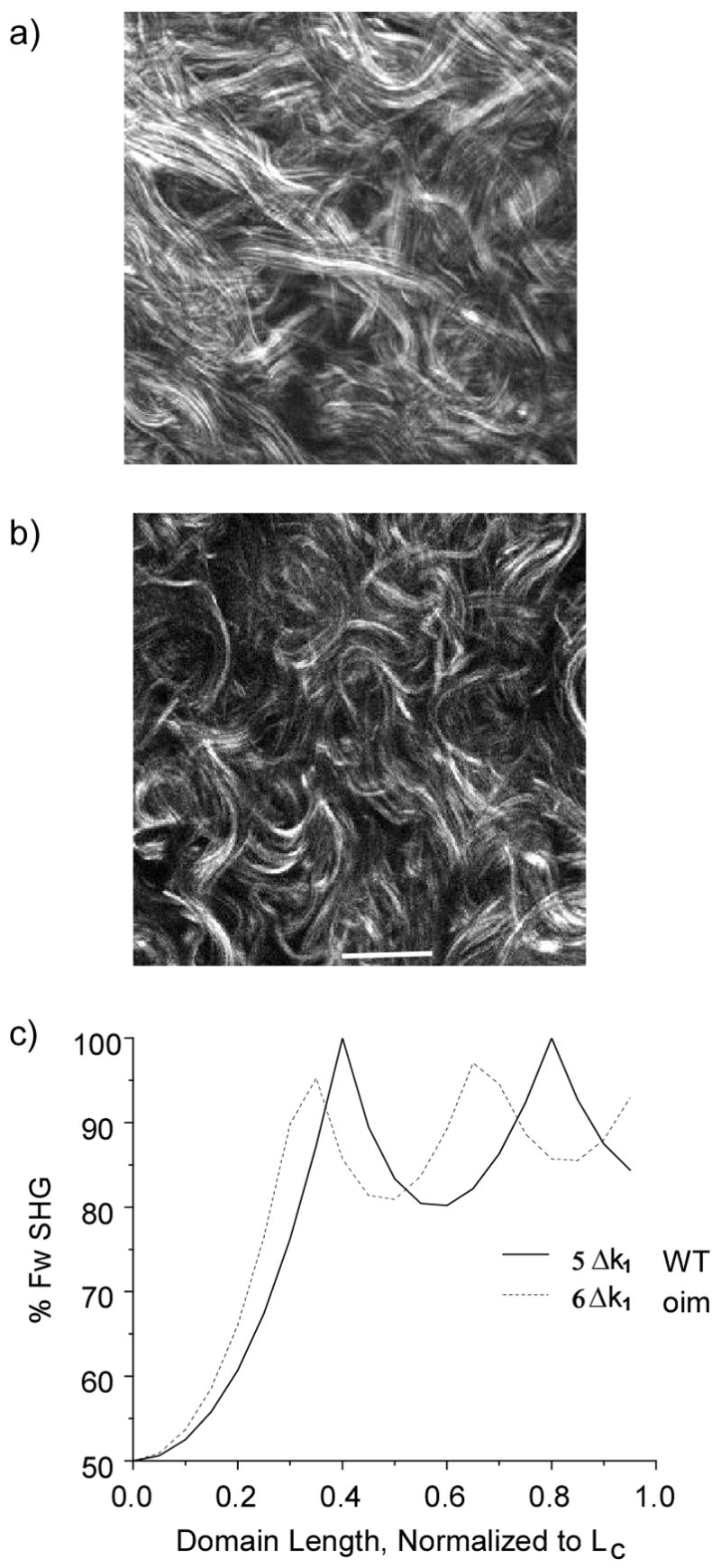
SHG images of WT and oim skin are shown in (a) and (b), respectively (Scale bar =20 microns). The oim has more random assembly. 5(c) shows the calculated %F_SHG for the corresponding relative Δk values for the WT and oim skin.

Using SEM imaging, we measured the average fibril diameters for these tissues and found average values of 70 and 100 nm for the oim and WT, respectively. Based solely on size, one might expect that the F_SHG//B_SHG from the WT should be larger than that of the oim skin. To explain the observed similar creation ratios we must also consider that the F_SHG/B_SHG is a function of Δk as demonstrated in Figure 4. In order to utilize these figures as a descriptive aid we must consider the effective domain size D = nL̄/λ_SHG (i.e. normalized to λ_SHG ) where ( L̄ ) is the average fibril diameter. Using these domain sizes and assuming Δk_f=Δk₁ we can then estimate effective Δk_b values that produce 75% F_SHG for both oim and WT skin. This results in ~20% higher value for oim over that of WT (with effective values of 6Δk₁ and 5Δk₁ respectively). The predicted forward SHG percentages for the WT and oim tissue are shown in Fig. 5c. By this description one can make the connection that larger Δk_b values are associated with a higher degree of randomness in the collagen matrix, as is evidenced in the oim SHG image relative to the WT (Fig. 5 b and 5a, respectively). The increased randomness of the oim tissue decreases the QPM contribution to the overall SHG, thus the emission is more forward directed (although with lower conversion efficiency) compared to more regularly packed fibrils of the same size. Thus the fact that the same F_SHG/B_SHG occurs for the WT and oim is a coincidence that arises from offsetting contributions from the larger fibril size in the WT and increased randomness in the oim skin. This example further shows that a treatment based solely on fibril size is insufficient to describe the emission direction.

The above analysis assumes that the distributive domain was equal to the respective coherence length. From the measured fibril diameters we set the domain to the respective average fibril diameter (which is smaller than these lengths) to determine a more appropriate value. For WT, with an average diameter of 100 nm and based on our measures values of Δk₁ the effective domain is approximately equal to L_c(5Δk₁)/10 and that of OI (average diameter~70 nm) is L_c(6Δk₁)/18. In Fig. 6, we now plot (using Eq 3 and as in Figure 3), the relative intensities for both oim and WT over their respective normalized domains. We note that this plot appears linear as it corresponds to the beginning region on Fig. 3, where for small angles sinθ≈θ. This analysis predicts that the WT will result in SHG intensities which are approximately 2.2 times that supported by oim. Experimentally we observed this trend and measured a ratio of approximately 2.5.(16) This demonstrates that phase matching considerations based on domain size and randomness can be used to make comparisons of the relative emission intensities in different tissues.

Fig. 6.

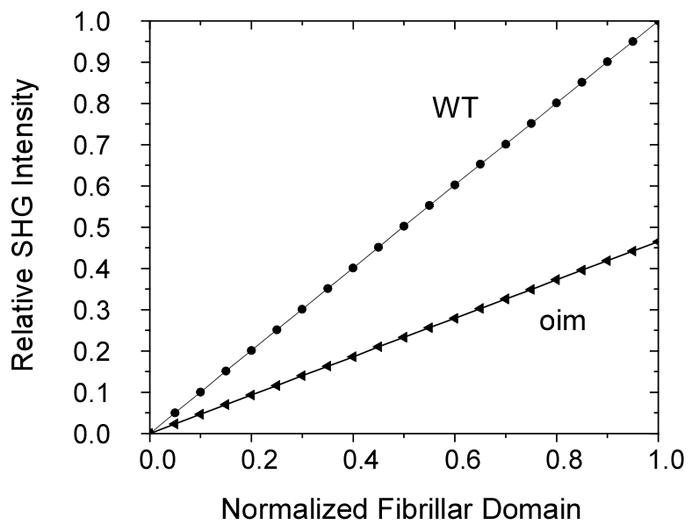
The relative SHG intensities (normalized to the maximum amplitude for WT) for both oim and WT over their respective normalized domains are calculated using the Δk values from Fig. 5. The plot appears linear as it corresponds to the beginning region on Fig. 3, where sinθ≈θ. This calculation shows that the WT will result in SHG intensities which are approximately 2.2 times larger than the oim. The experimentally ratio is approximately 2.5.

4.4 Fibrillar morphology and coherence lengths

It has been suggested in other work that differences in forward and backward detected morphology are most likely to be manifested in the observation of smaller features. Specifically, several reports have shown the existence of segmented appearing fibrils in the backward channel, where these same features appear to be continuous in the forward geometry. We can now explain this phenomenon in terms of the difference in forward and backward coherence lengths associated with the respective relaxed phase matching considerations and intensity amplification due to QPM. As an example, we show the forward and backward collected images from Valonia cellulose in the top and bottom panels of Fig. 7. The NA and excitation wavelength are the same as used in Figure 5. These specimens are approximately 30 microns in thickness, and the MFP is ~130 microns (18). Thus the contrast in the backward channel (b) arises predominantly from direct quasi-coherent emission and will not contain a significant multiple scattered contribution. We note that the fibrils observed in the forward channel are long and continuous, whereas these frequently have a segmented appearance in the backward channel. We can now explain this observation by our assignment of F_SHG and B_SHG with relatively small and large Δk values, respectively, which assigns a shorter coherence length to the latter. This result predicts that if the fibril packing in the axial direction is on the order of the backward coherence length, destructive interference occurs in this channel. By contrast F_SHG is characterized by a relatively longer coherence length (with an upper bound limited by dispersion), and such destructive interference between fibrils does not contribute to the contrast in this channel. We stress that while small fibrils of diameter ~λ_SHG/10 (and domains) will be characterized by a F_SHG/B_SHG~1, and may appear better visualized in the backward channel, the small fibril size alone is not sufficient to produce the segmented morphology shown in several reports, as even small isolated fibrils would appear to be continuous although with a diminished intensity due to the absence of QPM, As a further example, Fig. 8 shows forward (a) and backward (b) images for oim skin, where the arrows denote local areas where segmented fibrils appear in the backward channel. These features are less prevalent than in cellulose as the matrix is less organized in the oim skin, whereas the cellulose is highly regular in its structure.(18) As a consequence of the randomness the QPM is less efficient and less spatially pervasive destructive interference will occur.

Fig. 7.

Forward (a) and Backward (b) SHG images of Valonia cellulose. Segmented features appear in the backward channel due to destructive interference. Scale bar=20 microns.

Fig. 8.

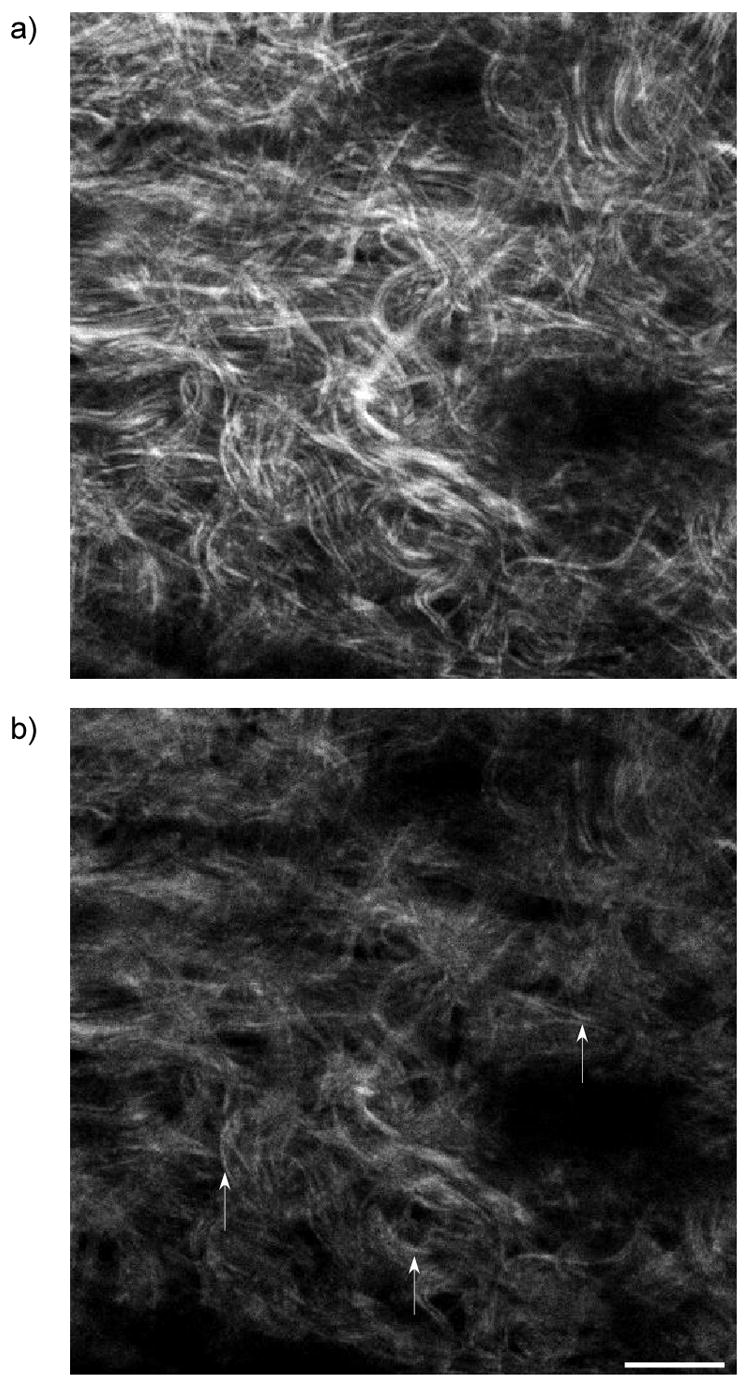
Forward (a) and backward images (b) for oim skin, where the arrows denote local areas where segmented fibrils exists in the backward channel. Scale bar=20 microns.

The findings of other researchers can also be viewed in this context. Han suggested that the amplitude of the second harmonic field E_2ω from an ensemble of collagen fibrils was related to a random distribution of dipoles, and that regularly packed lattices would support destructive interferences in all directions except for the transmission direction(11). By contrast, we suggest that the appropriate property is the distribution in Δk values and the observed morphological differences in terms of segmentation arise fundamentally from the difference in the forward and backward coherence lengths. This description can also be utilized to explain their observation of bright B_SHG from sclera. The hollow fibrils in this tissue are on the order of 300 nm and a priori would be expected to display produce predominantly F_SHG. However, they observed F_SHG/B_SHG~1. This result is predicted by our current theory if one associates the domain length with the shell sidewall (presumably much thinner than the diameter) rather than the fibril diameter. In related work, Williams et al(4) showed that the morphology in mature rat tail tendon fibrils displayed similar features in the forward and backwards collection geometries, whereas immature fibrils had a similar, segmented appearance to that shown here in Fig 7 (for cellulose). While based on structural considerations it was suggested this appearance was due to physical segmentation of secreted fibrils, we suggest it is also possible that this observed morphology could also have arisen from destructive interference in these effectively smaller domains and inter-fibril spacing. We also suggest the fibrils and inter fibril spacing of the mature tendons were sufficiently large to produce predominantly forward SHG and that the similar appearance in the backward channel may have been due to multiple scattering of the initial F_SHG.

5. Conclusions

The SHG measured in a tissue imaging experiment consists of both (quasi)-coherent as well as incoherent scattered components, where these arise from the initial emission and subsequent propagation, respectively. For full interpretation of the image data, these components need to be considered separately. In this paper we have presented a heuristic treatment of the initial SHG emission based on relaxed phasematching conditions, where we consider SHG producing domains to be fibrils or collection of small fibrils. Due to the polycrystalline nature of collagen we approximate the fibrillar structure as a quasi-periodic lattice of scatterers capable of providing axial momentum, allowing appreciable SHG buildup in the backward direction through QPM interactions. These relaxed conditions thus alter those associated with SHG from that of the purely coherent (and forward) case to that more appropriate for biological tissues where dispersion alone violates strict phase matching. Through this analysis, we can make predictions of the SHG conversion efficiency and emission directionality based on the domain sizes as well as the packing arrangement and density. A direct consequence of these relaxed phase matching conditions is that the backward SHG has a shorter coherence length than the forward emission. This difference can be used in a comparative analysis to explain emission directionality, conversion efficiency, as well as segmented topography seen only in the backward direction. Treatments based solely on fibril size cannot predict these behaviors and we must also consider the packing order. The presented treatment successfully explained our observations in the oim disease model. This method for predicting and interpreting the SHG creation should be broadly applicable to tissue analysis as it was derived from first principles. For example, by performing a comparative analysis between healthy and diseased tissues relative changes in quantification parameters (directionality, conversion efficiency) can be estimated without a priori knowledge of the molecular hyper-polarizability matrix. This current approach treating the initial generation, coupled with analysis of the multiple-scattered component, then provides a detailed picture of the measured SHG in fibrillar tissues and should find utility in future clinical applications.