Mechanotransduction, asthma, and airway smooth muscle

Abstract

Excessive force generation by airway smooth muscle is the main culprit in excessive airway narrowing during an asthma attack. The maximum force the airway smooth muscle can generate is exquisitely sensitive to muscle length fluctuations during breathing, and is governed by complex mechanotransduction events that can best be studied by a hybrid approach in which the airway wall is modeled in silico so as to set a dynamic muscle load comparable to that experienced in vivo.

Introduction

The degree of airway constriction during an asthma attack is set by the balance of contractile forces from the airway smooth muscle and the opposing forces from the airways. Such a force balance need not be static in the sense that the degree of airway constriction reaches a steady-state, and indeed, over the past decade numerous experimental and theoretical studies have shown that airway caliber is equilibrated dynamically rather than statically [1–15]. Indeed, the force-length curve of activated smooth muscle is constantly changing as the muscle adapts to its mechanical surroundings, such as the length to which it is stretched or the load against which it must contract.

The ability of a cell to respond to mechanical stimuli is termed mechanotransduction. It plays an important role in many physiologic and pathologic processes including stem cell differentiation, durotactic migration of cancer cells or leukocytes, tissue pattern formation during embryogenesis and growth, or endothelial alignment in response to fluid shear stress [16–18]. The smooth muscle cell shows a particularly pronounced and complex mechanical responsiveness that has recently been identified as a major player in the pathogenesis of asthma [15].

In this review we discuss mechanisms and pathways that lead to mechanical responsiveness of airway smooth muscle cells. Important details of smooth muscle mechanotransduction are still evolving, and comprehensive practical mathematical models of these processes are not yet available. To overcome this problem, we describe an unconventional hybrid approach to study the interaction between the airway smooth muscle and its surrounding mechanical milieu set by the airways, lung tissue, and respiratory muscle. In this approach, the mechanical milieu, or load, of the airway smooth muscle is modeled in silico and controls in real time the load against which real tracheal smooth muscle contracts. Such a muscle then behaves at any moment as if it were connected to the airway wall in vivo. The advantage of this hybrid strategy is that it retains complete knowledge and control of the many individual factors that set the muscle load but makes no assumptions about the muscle itself. Such a hybrid approach will remain invaluable as long as mathematical models of smooth muscle behavior fail to capture the dynamic remodeling and adaptation of smooth muscle in response to its mechanical environment.

Below we first outline a mathematical description of airway mechanics. Next, we review evidence showing that airway smooth muscle is a highly adaptable force generator that is exquisitely sensitive to external mechanical stimuli. Finally, we discuss the behavior of airway smooth muscle under realistic loading conditions, namely, those in which the smooth muscle loaded by the airway of an asthmatic lung and then exposed to tidal breathing.

Mathematical models of airway constriction

The diameter of an airway is set by a balance of the multiple forces that act to increase or to decrease the airway lumen. If these forces are known, then the airway diameter can be computed. The idealized geometry of an airway cross section and the forces acting upon it are shown in Fig. 1. To arrive at a mathematical expression that relates the airway diameter to these forces, we follow the approach suggested by Lambert et al. [19], Anafi and Wilson [20] and Latourelle et al. [21], and construct a so-called free-body diagram of the airway. To do so, the airway is imagined to be cut lengthwise (see Fig. 1), and the question is then asked what forces would be necessary to hold the two halves together. The answer is given by Laplace’s law for thin cylinders, which states that the tension (i.e., the force per unit airway length) carried by the airway wall equals the airway radius times the pressure difference across the airway wall (transmural pressure, P_tm). P_tm can be expressed as the sum of two components, namely the gas pressure difference (pressure in the airway lumen, P_lumen, minus alveolar pressure, P_alv), and the pressure arising from the mechanical stress of the lung parenchyma (P_p) that tethers the airways. The wall tension, too, can be decomposed into two components, namely the passive wall tension (τ_wall), and the active tension generated by the airway smooth muscle (τ_muscle). Below, we summarize how each component can be modeled. Details can be found in Refs. [20,21].

Fig. 1.

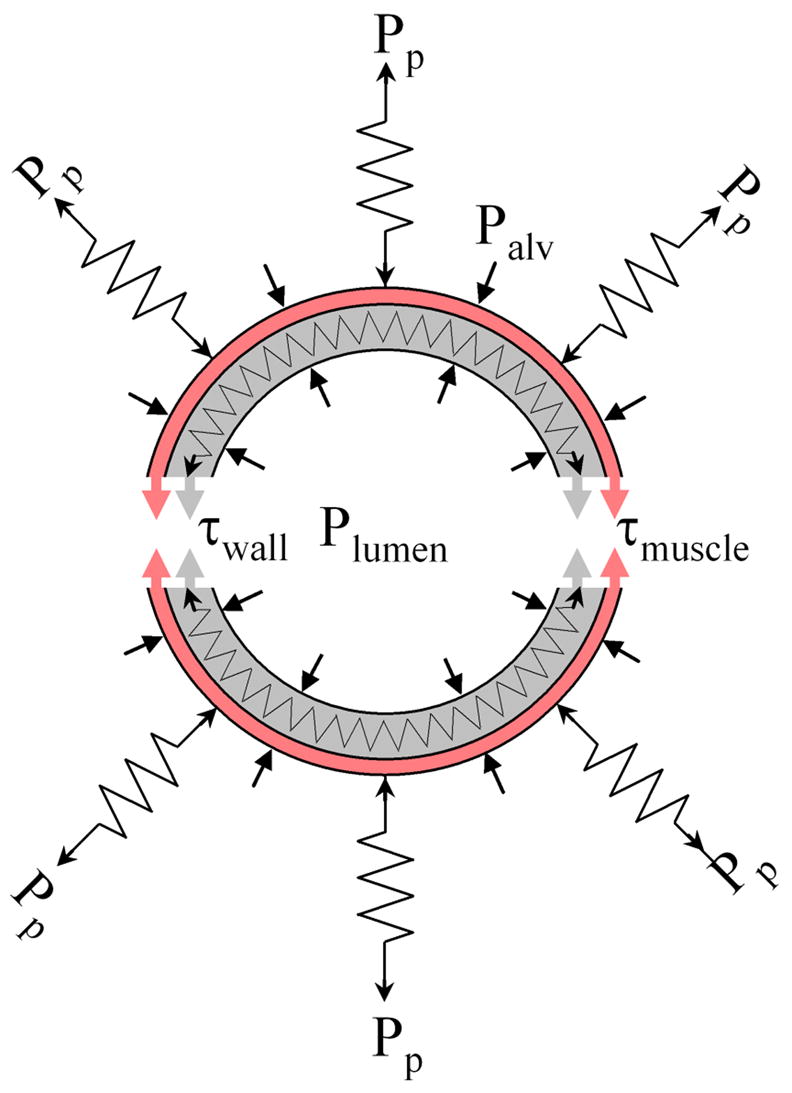
Schematic cross-section of an airway and surrounding lung parenchyma. The airway is held open by the tethering stress of the lung parenchyma (P_p) and is constricted by the airway smooth muscle tension (τ_muscle). Other forces that can either open or close the airway result from the differences between the alveolar pressure (P_alv) and airway lumen pressure (P_lumen), and the passive tension from stretching or compressing the airway wall tissue (τ_wall).

Transmural gas pressure difference (P_lumen − P_alv)

This pressure difference arises when the gas flow resistance of the airway causes a drop in the pressure between the airway entrance (P_aw) and exit into the alveolus (P_alv). During expiration, a positive feedback cycle leading to flow limitation and airway instability can arise in the following way: if the P_lumen − P_alv pressure difference becomes sufficiently negative, it can lead to a decrease in airway diameter, a subsequent increase in airway resistance and an even more negative P_lumen − P_alv pressure [20,22,23]. Anafi and Wilson modeled this interdependence between airway resistance, gas flow, and transmural gas pressure difference by a set of simple linear equations [20]. The most important finding of their work was to demonstrate that the transmural gas pressure difference and hence the mechanical load of an airway is not at all static but rather highly dynamic and history dependent. In particular, they showed that with sufficient smooth muscle constriction, the positive feedback cycle leading to airway collapse can already arise during quiet breathing.

Parenchymal tethering stress (P_p)

The parenchymal tethering stress provides the only significant force to keep small airways open. Lai-Fook [24] has shown that P_p is equal to the lung inflation pressure (P_L), i.e. the pressure difference between pleural pressure P_Pleura and P_alv, plus the parenchymal distortion stress that arises when the airway radius, r, differs from a reference value, r_ref, according to Pp = P_L + 2μ(r_ref−r)/r_ref. μ is the shear modulus of the lung parenchyma and also depends on P_L according to μ = 0.7 P_L [24].

Passive wall tension (τ_wall)

The relationship between the diameter and P_tm in dissected airways (i.e., τ_muscle, P_p, and P_alv are zero) has been measured by Hyatt et al. [22] and was later cast in an analytical relationship by Lambert et al. [23]. Especially in central airways, the passive wall tension can become negative at a small diameter and can therefore resist airway collapse. There have been numerous attempts to model the passive airway wall properties (reviewed in Ref. [21]), with conflicting results, for instance, on the importance of certain wall components (epithelium, submucosa) and their role in basement membrane folding. Insofar as measured data are available, they should be preferred over model estimates.

The system of equations above, taken together, define the tension that the airway smooth muscle must generate to attain a given radius, as the sum of the contributions from parenchymal tethering stress, gas pressure difference, and passive wall tension:

$${\tau }_{\mathit{muscle}}=r(P_{\mathit{pleura}}-P_{\mathit{alv}})\left(1+1.4\frac{r_{\mathit{ref}}-r}{r_{\mathit{ref}}}\right)+r(P_{\mathit{lumen}}-P_{\mathit{alv}})-{\tau }_{\mathit{wall}}$$ (1)

The right hand side of Eq. 1 describes the load against which the muscle contracts. This load changes greatly during tidal breathing with the pleural pressure fluctuations that drive the gas flow in and out of the lung. A typical load curve as predicted by Equ. 1 for the force-radius relationship of a normal 8^th generation airway for different pleura pressure is shown in Fig. 2.

Fig. 2.

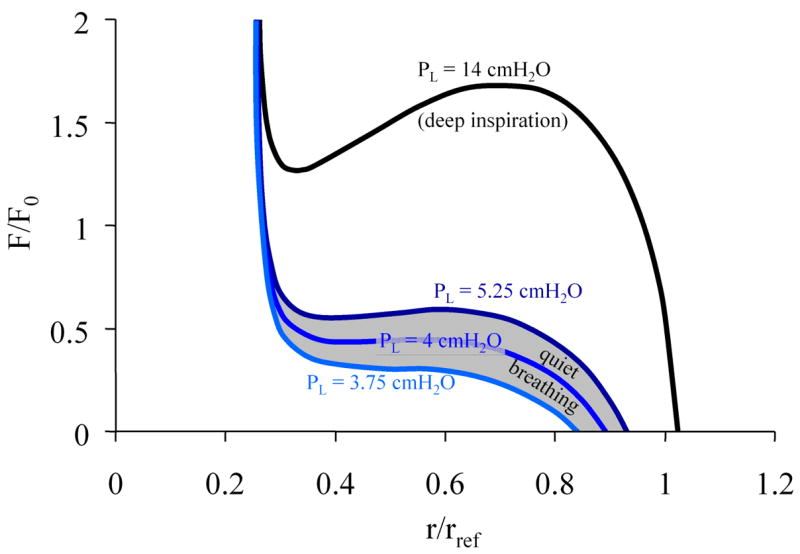
Steady-state load curve according to Eq. 1 for an 8^th generation human airway during quiet breathing and deep inspiration. Here, the lumen and alveolar pressure are assumed to be equilibrated (zero flow condition), hence transpulmonary pressure equals pleura pressure. The load curve is normalized to the maximal force F₀ that the smooth muscle of that airway can generate, and to a reference radius r_ref of the unconstricted airway at a transmural pressure of 10 cmH₂O.

The left-hand side of Equ. 1 is the force-length curve of the airway smooth muscle. The instantaneous radius of an airway is given by the intersection between the force-length relationship of the muscle and the load curve of the airway. Below we address the question of how the force-length relationship of airway smooth muscle can be modeled, or rather, we question whether this relationship can be adequately modeled at all.

Mathematical models of smooth muscle contraction

Acto-myosin bridge dynamics

In his landmark paper on muscle contraction, AF Huxley suggested a model of acto-myosin cross bridge interaction that that still provides, after 50 years, the mathematical basis and conceptual inspiration for today’s models of muscle contraction [25]. In this model, Huxley considered the simplest case of a fully activated muscle that at all times remained at optimal length (optimal filament overlap). The attachment and detachment events between myosin heads and their actin binding sites were modeled as first order kinetic rate processes that are sensitive to the position of the myosin head relative to the actin binding site. This position-dependence of the rate processes can be understood as arising from a non-symmetric free energy landscape of the actin-myosin interactions [26]. It should be noted, however, that experimental methods at that time were inadequate to obtain a detailed map of the free energy landscape [27] between single actin and myosin proteins. Lacking those details, Huxley simply assumed a plausible dependence of the rate processes upon muscle strain. Yet, despite its exceedingly simple structure, Huxley’s model exhibits an astonishing predictive power. For instance, it predicts how force or length changes of the muscle lead to a perturbation of the binding equilibrium (i.e., a reduction in the number) of the acto-myosin bridges. Accordingly, a brief, transient force increase leads to a long-lasting lengthening of the muscle, and a brief, transient length increase leads to a long-lasting force reduction and softening of the muscle. These model predictions have been qualitatively confirmed in numerous smooth muscle studies [2–5,8].

For quantitative predictions of smooth muscle behavior, the Huxley model has been extended by Hai and Murphy who introduced the idea that myosin can dephosphorylate while being attached to actin [28]. This so-called latch state of myosin, named so because the interactions with actin are greatly slowed down, can account for certain properties of smooth muscle after stimulation, such as a decrease in ATP-utilization and velocity of shortening over time [2,8]. But even without the latch state, the binding interaction between actin and myosin proteins, with no other regulatory processes involved, exhibit an extraordinarily complex mechanical sensitivity [8].

Cytoskeletal remodeling dynamics

Although the Huxley model with its latch state extension captures quite accurately the muscle’s response to small mechanical perturbations, it performs poorly when the muscle is subjected to larger length or force perturbations [1,5] (Fig. 3). To understand this behavior, other interactions than those between actin and myosin need to be considered. For instance, the binding interactions between the myosin proteins themselves within a thick filament can be overcome by excessive forces that lead to filament rupture, and the broken pieces can later be re-annealed [9]. It is conceivable to describe the myosin-myosin interaction too with a Huxley-type kinetic model, with rate constants that are dependent in force, filament length, and phosphorylation levels of certain regulatory proteins. Whether such an approach leads to a better understanding is questionable, however. Below, we give a cursory overview over the most important regulatory pathways and structural proteins involved in the mechanical signaling of smooth muscle cells.

Fig. 3.

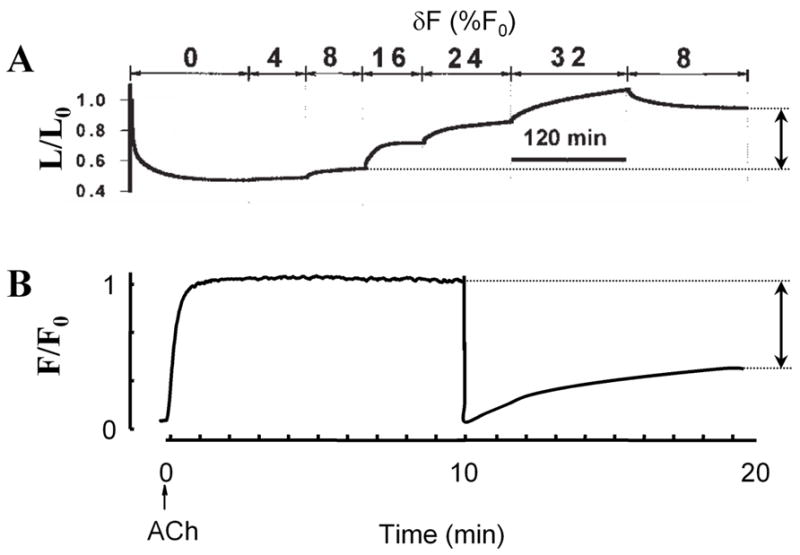
Smooth muscle response to large-scale force and length perturbations shows non-reversible behavior attributable to cytoskeletal remodeling. A: Muscle length vs. time during stimulation with acetylcholine. The first 120 min correspond to an isotonic shortening at F = 0.32 F₀. The muscle lengthens in response to sinusoidal force perturbations with amplitudes between 4% and 32% of maximum force (F₀) around a mean force of 0.32 F₀. After force perturbations are reduced to 8%, the muscle shortens incompletely (arrow). Adapted from Ref. [5]. B: Force vs. time during an isometric contraction at length L = L₀. After 10 min, the muscle length is reduced to 0.7 L₀. The subsequent force recovery is incomplete (arrow). Adapted from Ref. [12].

Unlike skeletal muscle with its regular, nearly crystalline and rather static ultrastructure, smooth muscle – as the name already suggests – is characterized by a more irregular and much less static contractile apparatus. In smooth muscle cells, the actin and myosin filaments still overlap, but they do not terminate at well-defined z-disks but instead are interconnected at multiple sites - the dense bodies or dense plaques - throughout the cell or the cell membrane, respectively [7,29]. Moreover, the actin and myosin filaments can lengthen, shorten, cross-link with each other, and – together with the dense plaques and dense bodies – they can completely disassemble or re-appear at a different location. The dominant physiological function of cytoskeletal remodeling is the continuous adaptation of the force-generating structures such that the smooth muscle is able to contract at maximum force over a very large length range. If given enough time to adapt, this length range can span several hundred percent, compared to usually less than 25% in skeletal muscle [10].

There is an abundance of structural and signaling molecules involved in orchestrating the cytoskeletal remodeling dynamics. Adhesion receptors such as integrins are transmembranen proteins that mechanically connect the extracellular matrix with intracellular focal adhesion proteins such as talin, vinculin, paxillin, zyxin, α-actinin [30]. Upon integrin activation, usually through binding to specific recognition sites at the extracellular matrix, the focal adhesion proteins cluster into what in smooth muscle cells is called a dense plaque [7,31]. Several members of the dense plaque can directly connect to actin filaments (talin, vinculin, α-actinin) while others, such as focal adhesion kinase, are involved in downstream signaling via mitogen-activated protein (MAP) kinases and members of the Ras superfamily of small GTPases such as Rho, Rac, and Cdc42, [31]. On the one hand, these signaling events lead to altered focal adhesion dynamics and actin remodeling; on the other hand, they can alter the phosphorylation level of myosin light chain kinase and Rho-kinase, which in turn phosphorylate the myosin light chains and hence influence the force generation and myosin filament assembly [9,32–34]. These processes are intertwined with second messenger signaling molecules including Ca2+/calmodulin, phosphatidylinositol, and cyclic adenosine monophosphate (cAMP) [12]. All this gives rise to complicated mechanical feedback pathways and adaptation processes that are currently not well understood. Two of them are described in more detail below.

Length adaptation

Length adaptation processes enable the muscle to quickly remodel its cytoskeleton and adapt it to its current length to achieve the most efficient force generation. The most pronounced length adaptation occurs upon muscle activation through membrane receptors that trigger intracellular Ca2+-responses and ultimately lead to an increase of acto-myosin cycling. In parallel with the resulting tension development, Ca2+ and other signaling molecules trigger multiple remodeling events including focal adhesion protein recruitment to the cell membrane, rapid actin polymerization, myosin filament formation, and cytoskeletal crosslinking [12]. Cytoskeletal remodeling dynamics is fastest during the early phase of contractile activation and then gradually slows down [1,12]. Once fully activated, the muscle cannot any longer efficiently adapt its tension generating apparatus to length changes: if the muscle length is decreased, the resulting non-ideal filament overlap cannot be ironed out (Fig. 3b), and if the length is increased, the resulting stress increase leads to breakage of bonds that the muscle cannot repair (Fig. 3a). As a consequence, the cytoskeletal structure remains frozen at the state in which it was during the onset of activation, and it carries this memory for a long time. It is only after the muscle has been relaxed that it can erase that memory and adapt its tension generating apparatus again to whatever length it is subjected to. In principle it would be possible to model those cytoskeletal adaptation processes with Huxley-type kinetic rate schemes. However, one would need rate constants that span the entire range from below one second to hours [14], and that would make such an approach highly impractical and susceptible to errors.

Force adaptation

A second group of force feedback and adaptation processes comprises mechano-sensing through cell adhesion receptors, focal adhesion proteins, and other tension-carrying structural proteins. It is currently unclear which proteins and receptors are able to sense mechanical forces, and by which mechanism they do so [17]. The physiological function of force sensing and the downstream adaptation processes is to guarantee that the chain of tension-carrying structures including extracellular matrix proteins integrins, focal adhesion proteins, and cytoskeletal filaments is sufficiently strong. For example, the application of mechanical forces to integrin receptors stimulates the growth of focal adhesion complexes and triggers actin polymerization [35]. Conversely, if contractile forces within the cell are relaxed, the size of the focal adhesions shrinks in proportion [36]. The signal transduction pathways involved in this type of force adaptation are largely identical to those described above, and as such, the resulting rate processes span a similarly large time range from below one second to hours. Force sensing, however, can also induce altered gene regulation [37], and the resulting adaptation processes can go on over the course of days and weeks. For instance, cyclic stretch applied to smooth muscle cells result over a time course of 10–12 days to an alignment of the cells perpendicular to the stretch direction and to an upregulation of contractile protein expression [13].

Behavior of airway smooth muscle under physiologic loading conditions

Returning once more to Eq. 1, we have seen that the right hand side that describes the load characteristics of the airway rests on well-established, fundamental, and in part century-old empirical observations, data, and theoretical models. In contrast, the left hand side of Eq. 1 that represents the active force-length relationship of the airway smooth muscle has only been incompletely characterized, and current mathematical models fail to include muscle length adaptation and a host of other phenomena associated with muscle stretch.

To solve this predicament, a hybrid approach was proposed by Laturelle et al. They used a real, isolated airway smooth muscle as an “analog computer” equivalent of the left hand side of Eq. 1. The muscle was attached to a servo-controller that was programmed to apply a physiological load according to the right hand side of Eq. 1. Unlike previous methods that used either time-varying length control, force control, or time-invariant auxotonic loads, Laturelle et al. used transpulmonary pressure as the controlled variable, while both muscle force and muscle length were left free to adjust as they would in vivo. With this method, the load could be altered to reflect specified changes of airway wall geometry, elasticity, parenchymal tethering, transpulmonary pressure, and temporal fluctuations associated with the tidal action of breathing. Hence, the isolated muscle was subjected to a dynamic microenvironment comparable to that experienced in vivo. The results obtained with this method confirmed that the airway caliber is equilibrated dynamically rather than statically, and for the first time provided quantitative estimates for the effect of tidal breathing and deep inspirations on airway caliber (Fig. 4).

Fig. 4.

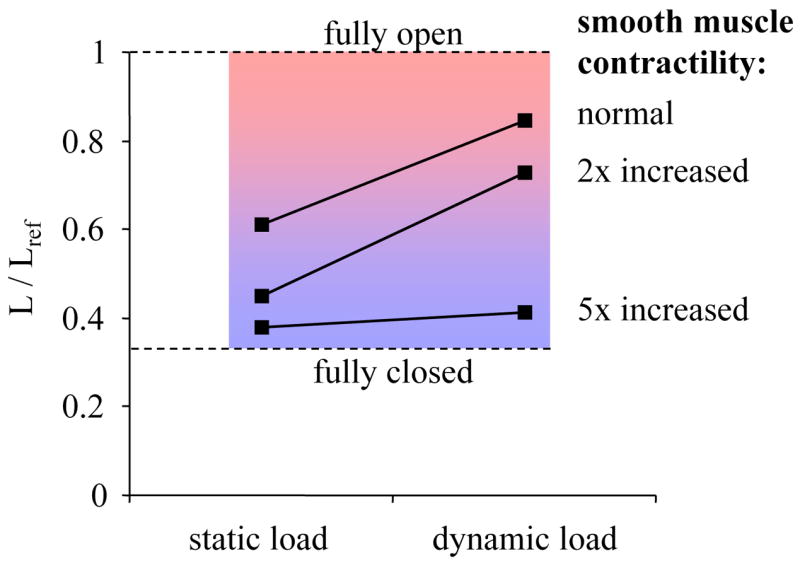
Length of fully activated smooth muscle in an 8^th generation human airway for a static load (constant pleural pressure of 4 cmH₂O) and a dynamic load. The dynamic load consisted of quiet breathing (pleural pressure amplitude 1.25 cmH₂O, 12 breaths/min), punctuated by deep inspirations (10 cmH₂O amplitude every 6 min). Muscle length was measured under the loading conditions for a normal airway, a mildly asthmatic airway with a 2-fold increase in smooth muscle mass, and a severely asthmatic airway with a 5-fold increase in smooth muscle mass. Dynamic loading lead to a substantial bronchodilation for both the normal and the mildly asthmatic airway, but failed to relax the severely asthmatic airway. Adapted from Ref. [38].

Recently, Oliver et al. used the same hybrid approach to study the sensitivity of muscle length to changes of tidal volume, muscle activation, and thickening of airway wall compartments [38]. They found that smooth muscle mass is the functionally dominant cause for excessive airway narrowing (Fig. 4), and they further showed that the mechanism accounting for this derangement is a positive feedback between muscle stiffness and airway stretch due to the action of tidal breathing and deep inspirations. This positive feedback cycle can be roughly outlined as follows. Muscle stretch due to tidal breathing and deep inspirations is a potent inhibitor of active muscle force [11], as a result of the mechanotransduction processes explained above. If muscle mass becomes too large, however, then the muscle and with it the airway stiffens and therefore stretches less, and because it stretches less it stiffens even more, and so on [38]. This positive feedback prevents the smooth muscle to become fully activated and hence prevents it to fully constrict the airways in the non-asthmatic, but in the asthmatic, it causes the smooth muscle to collapse to a fully activated state and to become so stiff that tidal breathing and deep inspirations can no longer inhibit active muscle force. The smooth muscle now finds itself in a mechanically static environment, and consequently, the bronchoprotective effect of mechanotransduction processes is abrogated.

Model translation to humans

Findings obtained thus far with a hybrid approach of a freshly dissected airway smooth muscle and a virtual human asthmatic airway have reinforced the long-held conclusion that the functionally dominant derangement accounting for airway hyperresponsiveness is increased smooth muscle mass [21,38]. The main mechanisms underlying airway hyperresponsiveness, however, are intrinsically dynamic, and are therefore unaccounted for in previous theoretical models, which are intrinsically static. Moreover, these findings are able to replicate the failure of deep inspirations to dilate the asthmatic airway, much as had been described by Salter [39] more than 150 years ago but had remained since that time unexplained. Indeed, these experiments imply that the failure of deep inspirations to relax the asthmatic airway is the proximal cause of airway hyperresponsiveness.

Conclusions

Smooth muscle that is being stretched by the mere action of tidal breathing remains relaxed, normally. In the asthmatic airway, however, constricted smooth muscle can become so stiff that it cannot be stretched, and hence cannot be relaxed, by deep breathing. The transition from normal to asthmatic smooth muscle behavior is governed by molecular processes that are exquisitely mechano-sensitive. Asthma drugs that target those molecular processes can be effectively studied in animal smooth muscle subjected to the dynamic load of a human asthmatic airway.