Controlling the rates of biochemical reactions and signaling networks by shape and volume changes

Abstract

In biological systems, chemical activity takes place in micrometer- and nanometer-sized compartments that constantly change in shape and volume. These ever-changing cellular compartments embed chemical reactions, and we demonstrate that the rates of such incorporated reactions are directly affected by the ongoing shape reconfigurations. First, we show that the rate of product formation in an enzymatic reaction can be regulated by simple volume contraction–dilation transitions. The results suggest that mitochondria may regulate the dynamics of interior reaction pathways (e.g., the Krebs cycle) by volume changes. We then show the effect of shape changes on reactions occurring in more complex and structured systems by using biomimetic networks composed of micrometer-sized compartments joined together by nanotubes. Chemical activity was measured by implementing an enzymatic reaction–diffusion system. During ongoing reactions, the network connectivity is changed suddenly (similar to the dynamic tube formations found inside Golgi stacks, for example), and the effect on the reaction is registered. We show that spatiotemporal properties of the reaction–diffusion system are extremely sensitive to sudden changes in network topology and that chemical reactions can be initiated, or boosted, in certain nodes as a function of connectivity.

Anyone who has seen a time-lapse movie of adherent cells is astonished by the high level of migratory movement and the violent changes in shape and size that occur during cell division, proliferation, and differentiation (1). Similarly, if we look inside the cell, we observe a plethora of migrational and structural rearrangements of interior compartments (2, 3). Some shape changes are fairly complex and involve transitions from compact to structured geometries, as well as changes in topology, dimensionality, and connectivity (Fig. 1A). Examples include the formation of tunneling nanotubules between cells (4, 5); budding-off and fusion of transport vesicles in the endoplasmic reticulum (ER)–Golgi complex; formation of tubular connections inside Golgi stacks as a function of, for example, traffic load (6); and fusion and retrieval of small vesicles during neurotransmitter release and recovery (7). A cell can regulate its volume in several ways (8), and tiny changes in size lead to dramatic changes in reactant concentration because of the r³ dependence on volume.

Fig. 1.

Shape changes of membrane-enclosed compartments and the effects of volume changes on an enzymatic reaction in a solitary lipid vesicle. (A) Schematic drawing showing examples of reversible biological shape transformations. (Top Left) A change in compartment volume. (Middle Left) A change in geometry during tubule formation and retraction. (Bottom Left) A change in geometry during vesicle release and retrieval. (Top Right) A bending transition similar to invaginations. (Middle Right) The formation and retraction of elaborate cell protrusions. (Bottom Right) Cellular compartments changing connectivity. (B) Extent of reaction in a solitary vesicle as a function of t, where the volume change is 100-fold. The red and the blue lines indicate fast and slow reactions, respectively. The upper solid lines indicate no volume change; the lower solid lines indicate very rapid volume change. Dashed lines represent an intermediate rate of volume change that significantly affects the reaction rate. (C) Solitary vesicle volume as a function of time. The dashed, dotted, and solid lines represent rapid, intermediate, and no volume change, respectively. The time at which the volume change is initiated (t = 0.01) is indicated by a vertical dashed line. (D–F) Dynamics of an enzymatic reaction taking place in a vesicle undergoing periodic volume contraction–dilation transitions. Shown are the transformation between V₁ and V₂ (D), the behavior of the concentration (E), and the extent of the reaction (moles) (F). The curves are numerical solutions to SI Appendix Eqs. S3–S5.

All cellular compartments contain chemical machinery, which means that biochemical reactions occur simultaneously with migration and shape changes (6, 9–12). It is well documented that changes in cell volume may affect intracellular signaling. For example, swelling can function as an anabolic signal triggering protein and glycogen synthesis, unlike cell shrinkage, which may lead to catabolic effects (13, 14). Also, optimal pH levels in hepatocytic lysosomes are maintained by cell volume regulation (15). Nalbant et al. (16) showed that the activation of Cdc42 (a member of the Rho family of small GTPases) was regulated by cell shape, an observation supported by numerical calculations of intracellular phosphorylation levels (17). Apparently, yeast cells go into hyperosmotic shock when exposed to high extracellular salt concentrations, which serves as a trigger for increased intracellular glycerol production. In work reported by Klipp et al. (18), a model integrating the high-osmolarity glycerol signaling system, gene expression, cellular metabolism, and, importantly, osmotic pressure and cell volume, was developed and compared with experimental studies of cell populations. It was concluded that control of cellular volume is crucial for the down-regulation of the signaling pathway. Furthermore, swelling and shrinkage of mitochondria (20–40% change in volume occurring within a few seconds) may affect ADP/ATP levels (19). It has also been shown (20) that Rac- and Rho-type GTPases can regulate cell shape (such as in the formation of protrusive lamellipodia) and cell retraction, as well as cortical tension, respectively. In addition, several local signaling networks have been identified that control cell shape and migration (21) in a hierarchical manner. In summary, numerous reports in the literature link the activity of the internal chemical machinery to dynamic changes in compartment volume and shape.

The fact that the interplay between chemistry and compartmental shape collectively governs the behavior of biochemical pathways in cells is of paramount importance but is often overlooked and poorly understood. This is primarily due to a lack of experimental techniques that permit dynamic rearrangement of biological or biomimetic compartments as a given biochemical reaction proceeds. However, as discussed above, the behavior of biochemical reactions can be investigated by performing experiments directly within cells after an appropriate stimulus (e.g., to change cell volume). It should also be possible to use a variety of drugs to produce alterations in volume and organelle shape, such as swelling of organelles (22) and reorganization of intracellular tubular networks (12), in combination with biochemical assays that track key chemical species. Another way to address the problem would be through theoretical investigations. For example, systematic studies have been conducted on how reaction times change as a result of shape transformations under conditions of a constant reaction volume (22, 23). These studies showed that alterations in reactor shape can lead to orders of magnitude changes in reaction times (23), as well as changes in noise characteristics (24). Here, by combining experimental and theoretical tools, we build on previous results in the following way. Beginning with a solitary-vesicle model, we demonstrate, for a given enzymatic reaction, how severe the rate and extent of volume change must be to influence the reaction rate in a desired way. Next, we use biomimetic nanotube–vesicle networks to investigate experimentally how changes in network connectivity can change enzymatic reaction–diffusion dynamics. We show that the rate of an enzymatic reaction within a network of connected containers can be increased or decreased in a given container as a function of network connectivity. Our results demonstrate that control of reactor volume and topology are direct ways of controlling the rates of embedded biochemical reactions, thereby regulating the activation/deactivation of entire signaling networks in biological compartments.

Results and Discussion

Controlling the Reaction Rate Inside a Solitary Vesicle.

The rate of a chemical reaction that takes place inside a solitary vesicle (representing an arbitrary biological structure such as an organelle or a cell) can be regulated by volume changes. It is intuitively clear that if the number of reactants (in moles) inside the vesicle remains constant, and if the vesicle volume is increased, the reactant concentration decreases, leading to a decreased reaction rate (defined as the number of moles converted per unit of time); likewise, if the volume is decreased, the reaction rate will increase. We are interested in understanding how an enzymatic reaction following Michaelis–Menten (MM) kinetics (Eq. 1) can be controlled dynamically by volume changes. Thus, in addition to kinetic (k_cat, k₁, and k₋₁) and thermodynamic or affinity parameters (K_M) pertaining to the reaction itself, knowledge of the rate and extent of a change in volume is necessary. In MM kinetics, the change in product concentration c_P(t) as a function of time t and volume V(t), can be written as

where K_M and k_cat are MM constants; c_S(t) and c_E(t) are the concentrations of substrate and enzyme, respectively; and k_V is the constant rate of volume change (details on modeling and numerics are provided in Materials and Methods). The first term on the right-hand side of Eq. 1 describes how the concentration of product changes as a function of enzyme activity, whereas the second term describes how the concentration varies as a result of a change in volume. However, concentration is an unsuitable measure of reaction activity in a situation where the volume is allowed to change. Therefore, we study the extent of the reaction in moles n_q(t) (q = E, S, P), which is a volume-independent measure obtained by multiplying concentration by volume at every time point, i.e., n_q(t) = c_q(t)V(t). To calculate the extent of the reaction as a function of time at different rates of volume change, we introduced the parameter k′_V = (k_cat/K_M) × n_E, which is a measure of enzymatic reaction efficiency (25) multiplied by the number of enzyme molecules n_E (assumed constant) that participate in the reaction. Thus, the ratio k_V/k′_V compares the rate of volume change with the efficiency of a MM reaction. Furthermore, introducing the dimensionless quantities c̄_q = c_q/K_M, t̄ = k_catt, and V̄ = V/(n_E/K_M) in Eq. 1 leads to

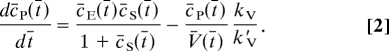Fig. 1B shows the extent of the reaction n_P(t)/n_S(0) as a function of t when the vesicle volume is increased 100-fold when going from V₁ to V₂ at three different volume expansion rates (k_V = 0, 10³, and 10⁵ dm³·s⁻¹) and for two different values of k_cat, representing a “fast” (k_cat = 100 s⁻¹, red) and a “slow” (k_cat = 10 s⁻¹, blue) reaction, respectively, under conditions c_S(0) = 100 μM, K_M = c_E (0) = 1 μM, and V₁ = 10⁻¹² dm³. The change in volume V(t)/V₁ is shown in Fig. 1C, and the time at which the vesicle volume expansion is initiated (t = 0.01) is indicated by vertical dashed lines in both graphs. The upper curves (solid) in Fig. 1B correspond to no volume change (k_V = 0 dm³·s⁻¹) for the two respective reaction rates and represent the situation where the reaction rate is at its maximum. The lower curves (solid) for the two k_cat values show the extent of the reaction when k_V = 10⁵ dm³·s⁻¹ for the situation where the inflation rate is so rapid that the reaction is stopped altogether. These two cases define the limiting behavior of achievable reaction rates, and between these two extremes resides a range of rates (shaded area) to which appropriate volume changes can be tuned. For example, when k_V = 10³ dm³·s⁻¹ (dotted lines), the extent of the reaction is reduced by 40% and 27% for k_cat = 100 s⁻¹ and k_cat = 10 s⁻¹, respectively, compared with k_V = 0 dm³·s⁻¹ for large times (t = 0.075). From Fig. 1B it is obvious that the faster the reaction rate, the faster the volume change required to inhibit the reaction.

In this example, we imposed a 100-fold increase in volume corresponding to an ≈4.7-fold increase in vesicle radius. For the parameters chosen, this approach brings the reaction to a halt at the highest volume expansion rate used. It should be noted that, for lesser volume changes, the effect will attenuate and that, as stated above, V₁ and V₂ give the respective extreme points for the rate of a reaction. Likewise, from the definition of k′_V = (k_cat/K_M) × n_E, reciprocal effects will be obtained for enzymes having different K_M values, where a higher apparent affinity (lower K_M values) will have the same effect on the extent of the reaction n_P(t)/n_S(0) as a function of t as will increased k_cat values. This result is logical because a higher-affinity interaction can be driven at lower c_S, with a longer lifetime of the E–S complex.

These results indicate that reactions can be turned on and off, and tuned, by volume changes, given that the rate of volume change out-competes the overall rate of product formation and that the actual size of the volume resulting from the expansion becomes so large that the substrate is diluted well below K_M. With this in mind, we now consider an example where a MM reaction takes place in a vesicle that undergoes a periodic volume dilation–constriction (Fig. 1D) from small (V₁) to large (V₂), where V₁/V₂ = 1/100, at a constant rate ±k_V for a given set of reaction constants (K_M, k_cat, and n_E). The concentration of product (green) and substrate (red) over time is shown in Fig. 1E, where the sudden periodic jumps to zero are caused by rapid dilation of the system when the vesicle is in its expanded state V(t) = V₂. Interestingly, Fig. 1F demonstrates further that when the vesicle is in its fully expanded state, the number of product and substrate molecules remains essentially constant dn_S/dt = −dn_P/dt ≈ 0, implying that the reaction has stopped. The reaction is then restarted as soon as the vesicle is shrunk back to V(t) = V₁.

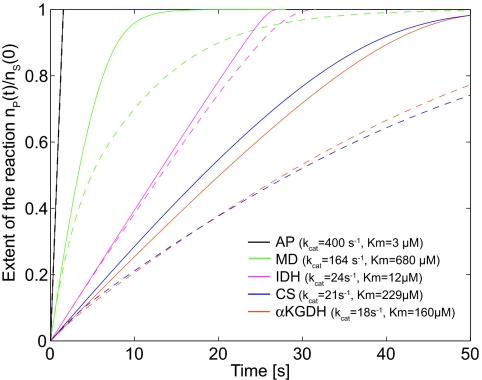
To determine whether volume changes could affect enzyme activity in the Krebs cycle, we applied the solitary-vesicle model to a mitochondrial-sized volume (diameter = 0.5 μm). For mitochondria, at least a 60% increase in diameter (≈4-fold increase in volume) has been observed (26), and the rate of volume change can be as high as k_V = 6 × 10⁻²⁰ m³/s (19). We studied four different enzymatic steps in the cycle: α-ketoglutarate dehydrogenase (α-KGDH) (27), isocitrate dehydrogenase (IDH) (28), citrate synthase (CS) (29), and malate dehydrogenase (MD) (30), where α-KGDH, IDH, and CS are considered rate-limiting. α-KGDH and CS have similar K_M (160 and 229 μM, respectively) and k_cat (21 and 18 s⁻¹, respectively) values compared with CS, which has a similar k_cat value (21 s⁻¹) but a much lower K_M value (12 μM) (see Fig. 2 legend for further kinetic data). Alkaline phosphatase (AP), used in the experiments described in the next section, is also included as a reference and is the reaction with the highest k_cat and lowest K_M values. The enzyme and substrate concentrations used were 2 μM and 1 mM, respectively (27–30). The extent of each enzymatic reaction (assumed to be independent of each other) is depicted in Fig. 2, where the solid lines correspond to the case of no volume change and the dashed lines correspond to the case when the mitochondria undergoes swelling with a rate k_V = 6 × 10⁻²⁰ m³/s, estimated from ref. 19. The expansion is continuous from t = 0 s, up to the point where a 4-fold volume increase is attained, after which the volume remains constant. The explicit behavior of V(t) is given in supporting information (SI) Fig. 5. Judging from Fig. 2, is seems that the volume expansion affects reaction rates especially for α-KGDH (magenta) and CS (blue) because they are slow (low k_cat). However, even though IDH (red) has a similar value of k_cat, it is more robust and less sensitive to the volume expansion because of the low value of K_M. The MD (green) reaction has a much higher k_cat value than KGDH and CS but is, nevertheless, sensitive to the volume change because K_M is high. AP (black) has both a high k_cat and a low K_M and is virtually unaffected by the volume expansion. Even though this is a very simplistic model, the calculations suggest that mitochondria—and small biological compartments in general—can employ volume swelling and shrinkage as a means of regulating the rates of biochemical reactions. To shut down the reactions of the cycle completely, the solitary-vesicle model predicts that the value of k_V must be increased by several orders of magnitude relative to the value used in this example, and the volume increase must be much greater than 4-fold. For example, to achieve a 50% reduction in the extent of the reaction at t = 20 s, volume must increase 50-fold at a rate k_V = 60 × 10⁻²⁰ m³/s (i.e., 10 times faster than shown in Fig. 2).

Fig. 2.

Enzymatic activity of mitochondrial enzymes when the mitochondria undergoes swelling. The inflation begins at t = 0 until the volume is increased 4-fold and then is kept constant. The solid lines show the rate of the reactions in a static mitochondrial volume, and the dashed lines correspond to the case in which the volume increases. The reactions are assumed to be independent of each other. The enzyme and substrate concentrations are 2 μM and 1 mM, respectively (27–30).

Controlling the Reaction Rate by Topology in a Biomimetic Network.

Several biological structures, such as the Golgi–ER system, are of a much more complex geometry and topology than solitary spheres. We therefore wished to examine whether a chemical reaction could be initiated or boosted in certain nodes (i.e., change of local rate of product formation) within a reactor network as a function of shape factors such as network connectivity. Specifically, we studied a topology change (linear-to-circular transformation by endpoint conjugation) in a four-container network under two different reaction conditions: (i) an enzyme-catalyzed reaction–diffusion model and (ii) an enzyme-catalyzed reaction–diffusion model with self-inhibition. Note that, in these experiments, the volume is kept constant and the observed changes in the spatiotemporal profiles of product formation are solely due to a change in container connectivity. A similar situation was considered in refs. 23 and 24; however, the structural changes considered here are not smooth.

First, we studied an enzymatic reaction evolving inside lipid bilayer networks composed of micrometer-sized vesicles (diameter ≈10–50 μm) connected by nanotubes (diameter ≈200 nm). The initial arrangement and connectivity of the vesicles, as well as any geometrical reconfiguration of the network during ongoing chemical processes, can be made arbitrary by microelectromanipulation of individual nanotubes and vesicles (31). The particular network transformations made here are shown schematically in Fig. 3 A–C, together with brightfield and fluorescence images of networks before and after endpoint conjugation (Fig. 3 D and E, respectively). For our experiments, we used Alexa-568-labeled alkaline phosphatase (≈4.5 μM, D_E = 6.1 × 10⁻¹¹ m²·s⁻¹) as the enzyme and fluorescein diphosphate (100 μM, D_S = 4.3 × 10⁻⁷ m²·s⁻¹) as the substrate, which react (k_cat = 4 × 10² s⁻¹ and K_M = 3 μM) to form fluorescein product (D_S ≈ D_P) detectable in a confocal fluorescence microscope. Also, a mathematical model describing chemical reactions in diffusion-driven reactor networks, developed in refs. 32 and 33, was implemented here with minor adjustments. Details are provided in Materials and Methods.

Fig. 3.

Transformation of a nanotube–vesicle network from linear to circular topology. (A) Initial network geometry, in which the enzymatic reaction was allowed to progress until network rearrangement. Network rearrangement is initiated by pulling a nanotube from the mother vesicle connected to the network. The dashed line indicates the trajectory the pipet will follow. (B) The nanotube is electrofused back to the mother vesicle, effectively creating a circular network topology. (C) The network self-organizes to its lowest energy state (minimal tube length), i.e., the nanotube travels back to γ₄ to reach the final state of the network. The final network topology can be predicted by correct initial positioning of the vesicles on the surface. (D and E) Transmitted light (D) and fluorescence (E) images of a circular-topology nanotube–vesicle network. The black, and white, dashed lines indicate the nanotubes connecting the containers; the red dashed line indicates the new link between γ₄ and γ₁. The images were obtained ≈10 min after network rewiring. (Scale bars, 10 μm.)

As a reference case, we considered a linear network consisting of four vesicles connected by three nanotubes (Fig. 4A Inset). Initially, vesicles γ₂–γ₄ contained substrate and no enzyme, and vesicle γ₁ contained enzyme only. As enzymes and substrate diffuse over the network, reactions occur, and the product concentration displays a cascade-like behavior in time and space. This behavior can be ascribed to the narrow tubes hindering the reactants from instantaneous mixing (32). This effect can be seen in Fig. 4A Upper, which shows the intensity of fluorescein (intensity ∝ concentration) in the vesicles as a function of time. The decay of the intensity curves for large times is mainly an effect of photobleaching. A numerical calculation (SI Appendix, Eqs. S9–S11) of the reference case is shown in Fig. 4A Lower and is in good agreement with experimental results.

Fig. 4.

Dynamics of an enzymatic reaction taking place in lipid nanotube networks undergoing a change in topology. (A) Behavior of the reaction in a static four-vesicle network. The production concentration displays a cascade-like behavior in time and space. This situation is referred to as the “reference case.” (B) Response of reaction behavior as the four-vesicle network undergoes a linear-to-circular topology change (Inset). The time at which the connection was made is represented by a vertical dashed line. The experimental results (Upper) are in good agreement with the numerical calculations (Lower). (C) A numerical study of the effect of product inhibition as the linear four-vesicle network (Upper) undergoes the same change in network structure as the reference network (Lower). The threshold product concentration at which inhibition takes place was set to η_P = 60 μM and is indicated by the horizontal dashed lines.

We then studied how a change in network topology (linear-to-circular transformation) affects the reaction rate in individual network nodes. Specifically, containers γ₁ and γ₄ were connected by a nanotube ≈50 min after the reaction was started, using microelectrofusion (Fig. 4B Inset). The temporal intensity profile in each vesicle is shown in Fig. 4B Upper. The new tubular connection results in an increased rate of product formation in γ₄, indicating that enzymes access this location more easily through the new link rather than by diffusing through the whole network. The experimental findings are well reproduced by the reaction–diffusion model (Fig. 4B Lower). A semiquantitative measure of the increase in product concentration in the experiments is given by the ratio of the (positive) slopes of the concentration curves (∝ rate of product formation): ⋅_P⁽⁴⁾/⋅_P⁽³⁾ ≈ 0.2 in Fig. 4A Upper (⋅_P⁽⁴⁾/⋅_P⁽³⁾ ≈ 0.3 in Fig. 4A Lower) and ⋅_P⁽⁴⁾/⋅_P⁽³⁾ ≈ 6 in Fig. 4B Upper (⋅_P⁽⁴⁾/⋅_P⁽³⁾ ≈ 4 in Fig. 4B Lower) (dot over symbol indicates time derivative). Please note that some variation in slopes and peak heights can occur as a result of, for example, variations in nanotube diameter, length, and extent of leakage (compare γ₄ in Fig. 4 A and B).

In addition, we wished to see how the reaction–diffusion system would be affected if also product inhibition was also present. This feature is inherent in many biochemical processes as a means of regulating production rate. Examples include end-product inhibition in metabolic chains (34) and in gene expression during protein synthesis (35). This case was studied numerically, and the inhibition E + P → E* was modeled as step-like (i.e., inhibition only takes place above a critical product concentration level η_P; below η_P, no inhibition occurs). However, as soon as inhibition commences, less substrate is consumed in the respective containers, effectively yielding a surplus of substrate compared with a noninhibited reaction. Thus, the difference in chemical potential between containers will be greater—a fact that is expected to change the spatiotemporal dynamics of the system because more substrate will be available for faster diffusion into neighboring containers. The topology change was induced at 8 min, instead of at 50 min, in an attempt to synchronize product formation in containers γ₃ and γ₄. Fig. 4C shows the distribution of product concentration in a static network (Fig. 4C Upper) and in a network undergoing a linear-to-circular topology change (Fig. 4C Lower). Fig. 4C Upper illustrates that the cascade behavior still applies under conditions of enzyme inhibition; however, the time separation between the product peaks is shorter, and product formation in γ₁ and γ₄ is pronounced compared with the reference case (Fig. 4A). This is likely caused by an increased diffusion of substrate into γ₁ and γ₄, respectively, as the reaction is halted in the other containers. Fig. 4C Lower shows the distribution of product concentration after a sudden topology change at 8 min. Here, the peak corresponding to vesicle γ₄ has a higher rate of product formation and is shifted to the left in the graph, coinciding in time with product formation in γ₃. Furthermore, product formation in γ₁ is attenuated as a result of the newly established conduit that additionally allow for diffusion of enzyme into γ₄. As in the reference system, the response to the topology change is fast and can be used to synchronize product formation in adjacent containers.

The cases discussed above indicate that nanotubes suddenly linking together distant parts of the network can either initiate or boost ongoing reactions by locally increasing the reactant concentration, an occurrence that may be exploited to control overall network dynamics. Note that the local amplification of reactant density in these three experiments is induced only by a change of connectivity, primarily facilitating enzyme passage, which is very different from on-site synthesis or external addition of catalysts (i.e., in our model, the number of enzyme molecules remains constant). Consequently, tubular connections found, for instance, inside Golgi stacks might dramatically change the reaction–diffusion dynamics of the system and may, therefore, serve as important instruments for controlling local synthesis of biochemical compounds.

Conclusions

Our results suggest that shape changes, such as the changes in volume or connectivity that are universal features of cellular processes, have a direct bearing on the rates of embedded reactions. The key to driving chemical reactions inside cells, whether receptor activation or enzyme activity, is affinity, which is defined by a constant in some unit of concentration. Although the numbers of receptors and enzyme molecules in a given system are constant on the time scales of the reactions, the numbers of ligands and substrates, respectively, can fluctuate dramatically. To drive a reaction, or an entire signaling pathway, de novo synthesis or transport of reactants can be used to create locally high concentrations (above a threshold concentration defined by the affinity constant). Here we show additionally that shape changes can also lead to locally high concentration levels. Both volume changes in solitary vesicles and connectivity changes in networks can lead to increased or decreased rates of product formation, either globally or locally, depending on how and when the change is made. Also, enzyme inhibition and long-distance connections may be used to alter (e.g., synchronize the dynamics of) spatially separated parts of the system. Consequently, a correct analysis and complete understanding of cellular processes can only be achieved if the biochemical reactions involved, and the fluctuating embedding environment, are considered simultaneously. Furthermore, cells can only use shape transformations “intelligently” to drive chemical reactions if the shape changes can be controlled. Apparently, such systems are ubiquitous, as is the case for the Rho- and Rac-GTPase pathways and a wide variety of metabolic pathways that control cell shape, volume, and migration (8, 16, 17).

Materials and Methods

Experiments.

A discussion of the chemicals used in this study, and of the formation of giant vesicles is presented in SI Materials and Methods.

Microscopy.

Rectangular coverslip glasses (no. 1 thickness), covered with a photoresist polymer SU-8 (31) containing lipid vesicle suspension, were placed on the microscope stage. A confocal laser scanning microscopy system (TCS SP2 RS; Leica) with a PL APO CS 63×/1.2 W CORR objective was used for acquisition of fluorescence images. The 488-nm line of the Ar laser was used for excitation of fluorescein, and emission was collected by a photomultiplier tube with sensitivity set in the 500- to 600-nm spectrum. During acquisition, images were line-averaged (two lines) every 30 s, and data were collected sequentially by two detectors to avoid bleedthrough. Simultaneously, images were collected from the reflected light of the scanning lasers. Data were evaluated with the Leica Lite program. Fluorescence intensities in each vesicle of the network were estimated by the program, in regions of interest (ROIs), including a background ROI. For each network, the ROIs had the same size, regardless of vesicle size, but could always fit into the smallest vesicle.

Micropipet-assisted formation of unilamellar networks.

Fabrication of unilamellar networks of nanotube-interconnected liposomes was performed as described in ref. 36. High-graduation micromanipulators (MWH-3; Narishige) allowed precise control of vesicle immobilization in the x–y–z position. Borosilicate micropipets were pulled on a CO₂ laser puller instrument (model P-2000; Sutter Instrument). A thin and flexible pipet with an orifice diameter of 200 nm was used for network formation. A microinjection system (CellTram vario; Eppendorf) and a pulse generator (Digitimer Stimulator DS9A; Welwyn) were used to control the electroinjections and the electroporation for insertion of micropipets.

Topology change of a linear network.

To perform the dynamical changes in the network, the technique (32, 36) was slightly modified. First, a linear network was created in which the vesicles were filled with substrate and enzyme accordingly. The reaction was monitored until a suitable time point where the change in topology could be performed. The topology change was done by taking an additional nanotube from the lipid source, transferring it along the network, and then electrofusing it back to the lipid source, thereby avoiding disturbance of the ongoing reaction. There is a good reason for constructing the link in this way, rather than simply pulling a tube from one vesicle and electrofusing it to the other. To obtain a pipet-attached tube from a vesicle, an electric pulse must be applied directly on the vesicle membrane, which would cause temporarily open pores, leading to leakage of molecules. Furthermore, the membrane material that is needed for the nanotube must flow from the lipid source over the whole network. The molecules in the network—specifically in the connecting nanotubes—would be dragged along by viscous coupling. Both of these effects would have a significant influence on the reaction dynamics because molecule concentrations would change in an uncontrolled manner throughout the network. These effects are avoided, or at least minimized, by the technique presented here. The network was initially constructed in such a way that it could self-organize (31) to the desired final state.

Theoretical Modeling and Numerical Calculations.

Enzymatic reactions in a solitary vesicle.

To calculate the effect of volume changes on the MM reaction

we consider a model in which the concentrations of substrate c_S(t), product c_P(t), and enzyme c_E(t) change over time t according to

and

where K_M = (k₋₁ + k_cat)/k₁ and k_cat are MM reaction constants, dV(t)/dt = k_V is the constant rate of volume change, and V(t) is the vesicle volume. The right-hand sides of Eqs. 4–6 reflect the fact that the concentrations may change as a result of (i) enzymatic conversion of substrate into product and (ii) a change in volume. Eqs. 4–6 were derived from the definition of concentration c_q(t) = n_q(t)/V(t) (q = E, S, P), where n_q is the number of moles (extent of the reaction) in combination with the chain rule. More details on the derivation are provided in SI Appendix.

Enzymatic reactions in networks undergoing changes in topology.

In refs. 32 and 33, a model for enzymatic reactions (MM) occurring inside nanofluidic networks was developed and is implemented here with minor adjustments. The rate equation describing the concentration of product, as function of time t in vesicle γ_j (i, j = 1, …, m), is

The first term on the right-hand side models the diffusion between the compartments. The sum is taken over all containers in the network, and the way in which the containers are connected is described by Λ_ij(t) = Λ_ji(t), where Λ_ij(t) = 1 (0) denotes that γ_i and γ_j are (are not) connected, and Λ_ii(t) = 0. Changes in connectivity at time τ between γ_i and γ_j are modeled as Λ_ij(t) = θ(t − τ), where θ(x) is the Heaviside step function. Geometrical parameters of the network are contained in the transport coefficient k_T,q^(ij) = πa²D_q/V_jL_ij, in which D_q is the diffusion constant of the molecules in the tubes, V_i is vesicle volume, and L_ij and a denote tube length and radius, respectively. The second term corresponds to the reaction between substrate and enzyme, and the third term accounts for photobleaching of fluorescent molecules (mainly product). The rate constants k_Δ,q^(j), as well as the tube radius a, serve as fitting parameters to the experiments. For completeness, in SI Appendix we provide the rate equations for the concentration of substrate, c_S(t), and enzyme, c_E(t), to which Eq. 7 is coupled. The equations were solved numerically by using the Euler backward (implicit) method (37).

Product inhibition.

We used a model in which, above a threshold level η_P, the product begins to inhibit the enzyme. To model this situation, the reaction term −k_inhibc_E^(j)c_P^(j) for c_P^(j)(t) ≥ η_P, and zero otherwise, was added to Eq. 7 and to the rate equation describing enzyme concentration (see SI Appendix, Eq. S3). The rate equations and the numerical values used also are provided in SI Appendix.