Metapopulation dynamics of Escherichia coli O157 in cattle: an exploratory model

Abstract

Livestock movement is thought to be a risk factor for the transmission of infectious diseases of farm animals. Simple mathematical models were constructed for the transmission of Escherichia coli serogroup O157 between Scottish cattle farms, and the models were used in a preliminary exploration of factors contributing to the levels of infection reported in the field. The results suggest that cattle movement can make a significant contribution to the observed prevalence of E. coli O157-positive farms, but is not by itself sufficient for the persistence of E. coli O157. The results also suggest that cattle movements involving infected farms with cattle shedding an exceptional amount of E. coli O157, ‘super-shedders’, also make a substantial contribution to the prevalence of infected farms. Simulations indicate that E. coli O157 could have reached the currently observed prevalence levels in less than a decade. Implications and findings from our models are discussed in relation to possible control of E. coli O157 in Scottish cattle.

1. Introduction

Escherichia coli O157 emerged in the 1980s and can now be found worldwide in a wide range of animals, including livestock, domestic pets, wild animals and humans (Beutin et al. 1993; Willshaw et al. 2001). In humans, the organism is typically pathogenic, causing conditions ranging from mild diarrhoea to haemorrhagic colitis and haemolytic uraemic syndrome (Karmali et al. 1985; Ackman et al. 1997; Chart 2000; Willshaw et al. 2001). Although less pathogenic in livestock, E. coli O157 can also cause diarrhoea in young calves (Sherwood et al. 1985). Escherichia coli O157 infection in humans can occur through contact with animals or via consumption of contaminated food products (Trevena et al. 1996; Milne et al. 1999; Willshaw et al. 2001). Cattle are regarded as a major reservoir for E. coli O157 (Beutin et al. 1993; Kobayashi et al. 2001), and studies to determine its prevalence have been conducted in recent years (Kobayashi et al. 2001; Kistemann et al. 2004; Matthews et al. 2006a; Gunn et al. in press). Recent studies have also demonstrated that there are associations between the distribution of human E. coli O157 infections and the density of cattle farms (Kistemann et al. 2004; Innocent et al. 2005).

Farms are not closed entities and, in general, a network of contacts exists between them. The general role of contact networks in the spread of infectious diseases is known to have important epidemiological implications (Lajmanovich & Yorke 1976; Woolhouse et al. 1997, 2005). Contacts can be made between farms if there are transfers of livestock. However, data on the movements of cattle have only recently become available (www.defra.gov.uk). This provides a unique opportunity to examine some of the processes that govern the distribution of E. coli O157 at a metapopulation scale. Of course, contacts between farms can also be made in various other ways, including movements of vehicles, livestock other than cattle and wildlife, which are not systematically recorded for all farms and therefore the level of between-farm contacts brought about in these ways is not known.

The aims of this paper are twofold. First, to construct a simple simulation model for the transmission of E. coli O157 within a Scottish farm-to-farm contact network that reproduces the level of E. coli O157-positive farms observed in field studies in Scotland. Second, to explore, using several variants of this model, the effect of cattle movements and other factors on the persistence of E. coli O157 within the Scottish farm network. The paper is organized as follows. We first describe the prevalence data from a field study involving a subset of Scottish cattle farms, where faecal pats were sampled and tested for the presence of E. coli O157. This is then followed by a description of the cattle movement data in Scotland. We then outline the construction of our simulation models and show the model results. The paper then finishes with a discussion that relates our findings to the observed data and the epidemiological implications of our models.

2. Data

2.1 Sampling procedure

Between March 2002 and February 2004, 481 farms were visited throughout Scotland as part of a survey to examine the prevalence of E. coli O157. Fresh faecal pats were sampled and tested for the presence of E. coli O157, and bacterial counts were determined by using the procedure described by Pearce et al. (2004). Briefly, 1 g of faeces from each sample was suspended in 9 ml of maximum recovery diluent (Oxoid Ltd, Basingstoke, UK) and 0.1 ml of suspension was spread onto each of two CT-SMAC plates, which were then incubated at 42°C for 24 h. Typical non-sorbitol fermenting colonies were counted and tested using anti-E. coli O157-coated latex reagent (Oxoid, Ltd). The limit of accurate enumeration using this method was 100 CFU g⁻¹ faeces (Pearce et al. 2004). Of the 481 farms sampled, 91 were positive for E. coli O157. However, count data were obtained only for 77 of the 91 positive farms. Fourteen farms were excluded from the analysis, as the level of E. coli O157 shedding was unknown. All analyses and model simulations performed in this study were therefore performed on a subset of 467 farms. It was found that some E. coli O157-positive animals shed exceptional amounts of E. coli O157 in comparison with other infected animals. Counts ranged from less than 100 (the limit of reliable enumeration) to more than 10⁶ CFU g⁻¹. Following Naylor et al. (2003), Omisakin et al. (2003) and Ogden et al. (2004) we define E. coli O157-positive animals shedding more than 10⁴ CFU g⁻¹ faeces as super shedders and the remaining E. coli O157-positive animals as normally infected animals. Furthermore, farms that contain super shedders are referred to as super shedding farms and farms that have no super shedders but only normally infected animals as normally infected farms. We define the term infected farms as a set of farms including normally infected and super shedding farms.

2.2 Farm prevalence

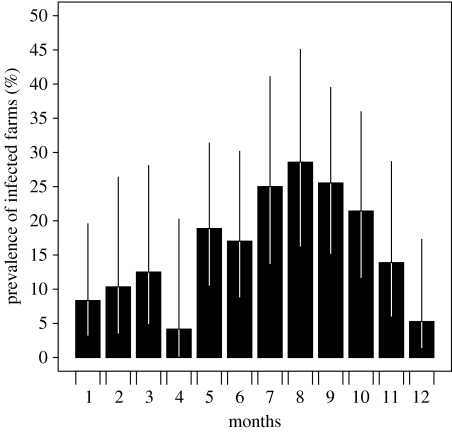
Out of the subset of 467 farms, 77 farms were tested positive for E. coli O157, giving an overall prevalence of 16.5%. Of these, 64 were normally infected farms and 13 were super shedding farms, giving a prevalence of super shedding farms of 2.8%. There is a seasonal pattern in the sample farm overall prevalence (figure 1): April has the lowest sample farm prevalence (4.17%) and August has the highest (28.57%).

Figure 1.

The prevalence of farms that tested positive for E. coli O157 for individual months of the year 2003. Seasonal pattern is evident and the prevalence of infected farms is highest in August and lowest in April.

2.3 On-farm prevalence

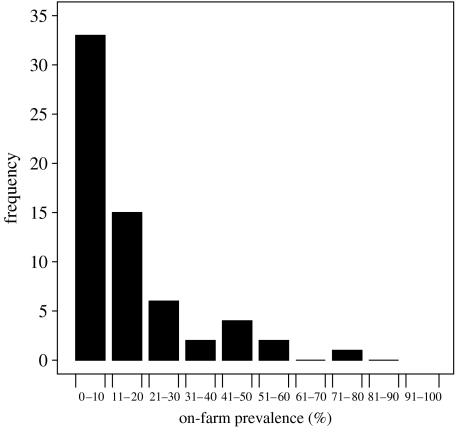
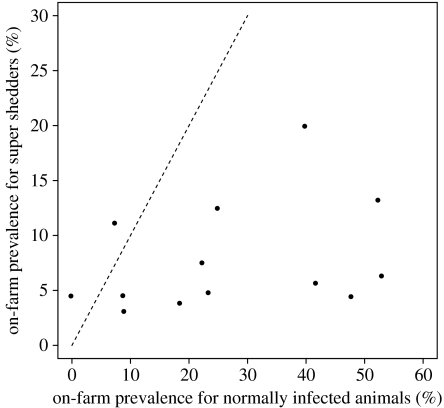
We define the on-farm prevalence of a given farm as the fraction or percentage of animals that tested positive for E. coli O157 on that farm. On-farm prevalence has two components: one is the on-farm prevalence of normally infected animals and the other is the on-farm prevalence of super shedding animals. For normally infected farms, the on-farm prevalence is the prevalence for normally infected animals. For super shedding farms, the on-farm prevalence has the super shedder component and might have a normally infected component. On the majority of normally infected farms, less than 10% of cattle are infected with E. coli O157 (figure 2). Of those 13 super shedding farms, only one farm had all infected cattle being super shedders, whereas the majority of infected cattle in the other 12 super shedding farms were normally infected (figure 3).

Figure 2.

A distribution of on-farm prevalence for 64 sampled E. coli O157-positive Scottish farms. Note that those farms contain only normally infected animals.

Figure 3.

A co-distribution of on-farm prevalence of super shedding and normally infected animals for 13 sampled E. coli O157-positive Scottish cattle farms. Note that those farms must contain at least one super shedding animal. The dashed diagonal line indicates where the prevalence of normally infected and super shedding animals is equal.

2.4 Movement data

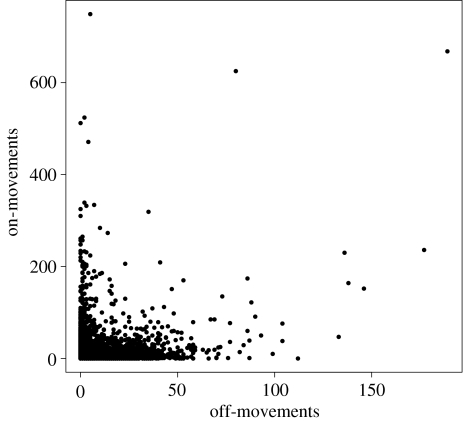
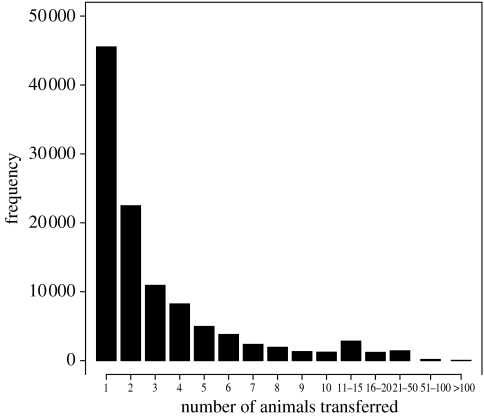
Cattle movement data were obtained from a subset of the Department of the Environment, Food and Rural Affair (DEFRA) Cattle Tracing System (CTS) for the year 2003. Only movements between Scottish cattle farms were considered (i.e. movements to or from other establishments, such as markets and abattoirs, and movements of cattle out of and into Scotland were ignored). From this dataset, we can extract information on individual movements between farms. Each movement is defined by the date of movement, the identities of the source and destination farms, and the number of animals transferred. There were 108 401 movements between Scottish cattle farms in the year 2003. Figure 4 summarizes how many times each of Scottish cattle farms exports (i.e. off-movements) and imports animals (i.e. on-movements). The data also show that the majority of movements involve only a few animals (figure 5). The movement data exhibit a seasonal pattern, with most movements occurring in April and October.

Figure 4.

A co-distribution of the numbers of off- and on-movements for all Scottish cattle farms in the year 2003. The number of off-movements of a given farm is defined as the number of times it sends away animals to other farms, while the number of on-movements of a given farm is defined as the number of times it receives animals from other farms.

Figure 5.

A distribution of the number of animals involved in each cattle movement between Scottish cattle farms in the year 2003.

3. Methods

3.1 Modelling framework

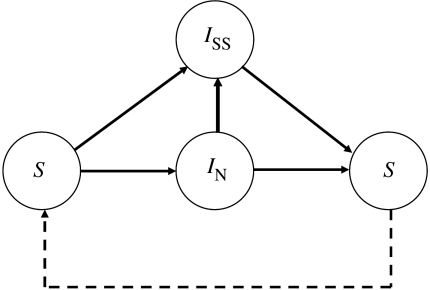
Our simulations track the infection status of all 17 198 cattle farms in Scotland, but we do not model the infection status of individual cattle. A farm can be susceptible (S), normally infected (I_N) or super shedding (I_SS). Farms are assumed to acquire infection either by importing infected cattle or from sources other than movements between Scottish cattle farms (we define this as other routes throughout the rest of the paper, taken to cover all possible mechanisms of short- and long-range spread between farms, including contamination of vehicles, movements of hosts other than cattle, contamination of feed, water supplies or shared pasture and imports of infected cattle from outside Scotland), and we define the following possible transitions between above-mentioned three states: a susceptible farm can become either a normally infected farm or a super shedding farm; a normally infected farm can become a super shedding farm; a normally infected farm or a super shedding farm can recover to become a susceptible farm; or a farm can remain unchanged in terms of its infectious status (figure 6). In our modelling framework, we assume that normally infected farms are short-lived compared with super shedding farms; therefore, for simplicity, we ignore the possibility that a super shedding farm becomes a normally infected farm.

Figure 6.

Possible routes of transitions between different states of a farm. A susceptible farm (S) can become either a normally infected (I_N) or a super shedding farm (I_SS). A normally infected farm can become a super shedding farm, but a super shedding farm cannot recover to become a normally infected farm. Both the normally infected and super shedding farms can recover to become susceptible again.

For a given farm, we define p_N and p_SS as the probabilities of an animal on that farm being a normally infected or a super shedding animal, respectively. For a susceptible farm, both probabilities are zero since there are no infected animals. When a susceptible farm acquires infection to become a normally infected farm, then p_SS remains zero and p_N takes a value sampled randomly from the observed distribution of on-farm prevalence of normally infected farms (figure 2). If a susceptible farm becomes a super shedding farm, then p_N and p_SS take values sampled randomly from the observed co-distribution of on-farm prevalences of super shedding farms (figure 3). When an infected farm recovers to become a susceptible farm, both p_N and p_SS are reset to zero. We next describe the details of the model simulations.

The time-interval for the model simulations is one month. At each time point, we perform the following operations. First, we construct the movement network according to the observed movement data for the relevant month of the year. For each movement, we identify from the data the identities of both source and destination farms, as well as the number of animals transferred. We then examine the infection status of the source farm and the transferred animals. There are three possible outcomes: (i) if the source farm is susceptible, then no transferred animals are infected, (ii) if the source farm is normally infected, then there is a probability p_N that a transferred animal is normally infected, or (iii) if the source farm is super shedding, then a transferred animal is either normally infected with probability p_N or a super shedding with probability p_SS. Since the majority of movements involve only a few animals, we therefore make the assumption that the on-farm prevalence of normally infected and/or super shedding animals is unaffected when animals are moved from a source farm.

Second, we examine the status of individual farms and decide on any changes to their infection status before the arrival of imported animals. There are four possibilities: (i) for a susceptible farm, there is a probability λ of acquiring infection from other sources and upon infection there is a probability θ of becoming a super shedding farm and a probability (1−θ) of being a normally infected farm, (ii) for a normally infected farm, there is a probability λθ of acquiring infection from other sources to become a super shedding farm, (iii) for a normally infected farm, there is a probability γ_N of recovering to become a susceptible farm, or (iv) for a super shedding farm, there is a probability γ_SS of recovering to become a susceptible farm.

Finally, imported animals reach their destination farms and further changes to the infection status of the destination farms can occur. There are four possibilities: (i) if all the animals imported are susceptible, then the status of the destination farm remains unchanged, (ii) if the destination farm is a susceptible farm and at least one of the imported animals is a super shedder, then the farm becomes a super shedding farm, (iii) if a destination farm is a susceptible farm and at least one of the animals received is a normally infected individual and none are super shedders, then the farm will become a normally infected farm, or (iv) if the destination farm is a normally infected farm, and at least one of the animals received is a super shedder, then the farm will become a super shedding farm.

For each model simulation, we assume an initial condition of one randomly chosen normally infected farm. Simulations are run from the month of January for 600 months (50 years). Since we have only the movement data for 1 year (the year 2003), we re-use the same movements each year. We note that reusing the same movement data each year might result in a less connected network than it may be in practice, and this, in turn, might affect the ability of E. coli infection take off in our model simulations. Models are programmed in Delphi v. 4 and simulated on a computer (CPU 1 GHz) with Microsoft Windows operating system.

3.2 Parameter values

The modelling framework requires the following four parameters: (i) the recovery rate for normally infected farms, γ_N, (ii) the recovery rate for super shedding farms, γ_SS, (iii) the rate at which a farm acquires infection from other sources, λ, and (iv) the fraction of susceptible farms acquiring infections from other sources that will become super shedding farms, θ. We assume that a super shedding farm remains infected longer than a normally infected farm, choosing recovery rates of 0.75 and 0.25 for γ_N and γ_SS, respectively. Our data suggest that 17% of infected farms are super shedding farms (13 out of 77). As super shedding farms remain positive for (on average) three times as long as normally infected farms [(1/0.25)/(1/0.75)], this generates a suitable value for θ of 0.057. We are thus left with one unknown parameter λ, which needs to be fitted such that the simulated prevalence of infected farms is comparable with the data. All parameter values are summarized in table 1.

Table 1.

Values of parameters used in our simulation models.

recovery probability for a normally infected farm, γN (month−1)	0.75
recovery probability for a super shedding farm, γSS (month−1)	0.25
fraction of farms infected from other sources that are super shedding farms, θ	0.057
rate of acquiring infection from other sources, λ, for model 1 (month−1)	0.09
rate of acquiring infection from other sources, λ, for model 2 (month−1)	0.10
rate of acquiring infection from other sources, λ, for model 3 (infected farm−1 month−1)	0.000034
rate of acquiring infection from other sources, λ, for model 4 (infected farm−1 month−1)	0.000037

3.3 Baseline models

An important assumption we make is the way in which a susceptible farm acquires infections from sources other than the movement of infected animals. In the above framework, we assume that a susceptible farm acquires infection from these other sources with a constant probability, λ. However, the risk of acquiring infection could be dependent on the density of infected farms (both the normally infected and super shedding farms). To incorporate this, we allow the probability of acquiring infections from other routes to be λI_tot, where I_tot is the total number of normally infected and super shedding farms. Such a modification also assumes that all infected farms contribute equally to the probability of a susceptible farm acquiring infection from other sources.

A further assumption we have made is that all farms have the same risk of acquiring infection from other sources, but in reality λ may vary between farms. To incorporate this possibility, we use a gamma distribution to characterize the heterogeneity in λ. We explore two cases: (i) there is no heterogeneity (i.e. the variance is zero) and (ii) there is a large variation in λ between farms and we simply assume that the variance is the square of the mean. In the latter case, we assign each farm a risk of acquiring infection sampled from a gamma distribution, with a mean λ and a variance λ².

These alternative assumptions present us with four baseline models. There are two density-independent models: one assumes a homogeneous λ (model 1), while the other assumes λ to vary between farms (model 2). There are also two density-dependent models: one assumes a homogeneous λ (model 3), while the other assumes λ to vary between farms (model 4).

3.4 Variants of the baseline models

We also construct several variants of the baseline models to explore the effect of certain components of the baseline models on the persistence of E. coli O157 within the Scottish farm network. Unless stated otherwise, all parameter values used in the model variants are the same as those for their respective baseline models. The model variants are as follows: baseline, this represents the baseline models as outlined above; variant 1, this assumes that no infections are introduced into a farm via routes other than importing infected cattle (i.e. λ=0); variant 2, this assumes that there are no cattle movements; variant 3, this assumes that no farm can gain super shedding status from routes other than cattle movements; variant 4, this assumes that there are no movements of super shedding animals; and variant 5, this assumes that there are no movements of any animals from super shedding farms.

4. Results

In order to generate a prevalence of infected farms comparable with that observed in the data, we adjust the values of λ for all the four baseline models. The estimated values of λ are summarized in table 1 and the resulting prevalences of infected farms are all within ±5% of the observed level. For the density-independent models, the probability of acquiring infection from routes other than cattle movement (λ) is 0.09 and 0.10 per month for model 1 (homogeneous λ) and model 2 (heterogeneous λ), respectively. This implies that a susceptible farm becomes infected from other sources once every 11 (1/0.09) or 10 (1/0.10) months. For density-dependent models, this probability is, on average, approximately 0.000034 and 0.000037 per infected farm per month for model 3 (homogeneous λ) and model 4 (heterogeneous λ), respectively. When density-dependent models are in a steady state, these two probabilities are multiplied by the number of infected farms to give a similar probability of acquiring infection from other sources as those in the density-independent models.

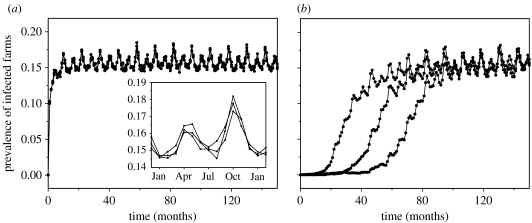
For the baseline models, the annual averaged prevalence of infected farms (i.e. averaging 12 monthly prevalence of infected farms throughout an year) ranges from 0.155 to 0.158 and the annual averaged prevalence of super shedding farms ranges from 0.039 to 0.041 (table 2). The large population of farms means that there was very little variation in outputs between simulations. For all density-independent baseline models, the simulated prevalence of E. coli O157 infections settles to a steady state within 2 years (figure 7a). For both the density-dependent baseline models, approximately 13% of the simulations show E. coli O157 infections taking place, and it usually takes 5–10 years to build up to the observed prevalence level (figure 7b). Simulations of all the baseline models show that once the steady-state level of infection is reached, then there exists a seasonal pattern in the prevalence level of infected farms every year, with a larger peak in October and a smaller peak in May (inset in figure 7a). However, this seasonal pattern does not correspond well with the observed seasonality in prevalence (figure 1).

Table 2.

Prevalence values of infected farms for baseline models and their respective variants (see text for their descriptions). There are two prevalence values per entry, with the left being the prevalence of all infected farms and the right being the prevalence of super shedding farms.

	baseline	variant 1	variant 2	variant 3	variant 4	variant 5
model 1	0.155, 0.039	0, 0	0.119, 0.020	0.121, 0	0.141, 0.020	0.138, 0.020
model 2	0.155, 0.041	0, 0	0.119, 0.022	0.120, 0	0.140, 0.022	0.137, 0.022
model 3	0.158, 0.040	0, 0	0, 0	0.016, 0	0.091, 0.012	0.068, 0.009
model 4	0.156, 0.041	0, 0	0, 0	0.036, 0	0.102, 0.015	0.086, 0.012

Figure 7.

Stochastic simulations of baseline models with heterogeneity in λ. In (a) the probability of acquiring infection from sources other than cattle movement is independent of the number of infected farms, whereas in (b) this probability is density dependent. Both (a) and (b) show three time-series, each of which is a stochastic realization of its respective baseline model. The inset in (a) is a zoom-in version of the time-series showing typical seasonal patterns in the prevalence of infected farms throughout a year. Similar time-series can be observed for models with no heterogeneity in λ.

The effects of different components of our models on the prevalence levels of infected and super shedding farms are summarized in table 2. The models suggest that E. coli O157 infection cannot take place and persist when farms do not acquire infection from routes other than cattle movements (model variant 1); in other words, once E. coli O157 is introduced into the Scottish cattle population, then it cannot persist through cattle movements alone. Despite this, our density-independent models suggest that cattle movements do make some contribution to the steady-state prevalence of infected farms; and furthermore, our density-dependent models suggest that cattle movements are essential for the persistence of infection (compare baseline models with model variant 2). Our results also show that super shedding infection cannot persist in the Scottish cattle population if the only route by which a farm can become a super shedding one is via importing super shedding cattle (model variant 3). The absence of movements of super shedding animals results in lower prevalence of infected farms with the prevalence of super shedding farms being reduced (model variant 4). The absence of movements of all animals from super shedding farms has a slightly greater impact (model variant 5).

Whether the rate of acquiring infection from other routes is density dependent or not also plays an important role in influencing the prevalence of infected farms. For all model variants except variant 1 (where there is no infection at all), the density-dependent models always generate a lower prevalence of infected farms than their density-independent counterparts (table 2). For model variant 2 (no cattle movements), density-independent models have reduced prevalence of infected farms while infections fail to take place at all for density-dependent models. For model variant 3 where farms cannot become super shedding farms via routes other than cattle movements, the results show that density-dependent models have their prevalence of infected farms greatly reduced to 0.016 or 0.036, whereas their density-independent counterparts have their prevalence of infected farms reduced slightly to 0.121 or 0.120. Similar effects can also be observed when there is no movement of either super shedding animals (model variant 4) or any animals from super shedding farms (model variant 5): when compared with the baseline model, density-dependent models always have a greater reduction in prevalence of infected farms than their density-independent counterparts.

For both the density-independent and density-dependent models, assuming λ to be heterogeneous between farms leads to a slightly higher parameter estimate than that for homogeneous λ. Alternative model variants indicate that there is an effect of variation in λ on the prevalence of infected farms. The effect is very slight for density-independent models, but very marked for the density-dependent counterparts (table 2). For density-dependent models, the model variants 3–5 show that having heterogeneous λ can lead to a higher prevalence of infected farms than that for homogenous λ.

5. Discussion and conclusion

The simple models of E. coli O157 dynamics developed here are intended to allow a preliminary exploration of the quantitative contribution of cattle movements to the levels of infection in a metapopulation of Scottish cattle farms. We note that our model is based on a relatively small number of Scottish cattle farms and the movement data of a single year, but our result is of a first step from which further and more detailed studies can be conducted. The model distinguishes two kinds of transmission: (i) mediated by the network of movements of cattle between Scottish farms and (ii) all other routes including the acquisition of infections from the wider environment in Scotland (e.g. via contaminated vehicles, movements of hosts other than cattle, contamination of feed or water supplies and imports of infected cattle from outside Scotland). Parameter values used to illustrate the behaviour of the model were chosen to be broadly consistent with (but were not formally fitted to) the data from a field study in Scotland.

As presented, the models suggest that cattle movements within Scotland alone are not sufficient to maintain E. coli O157 infection in the metapopulation (table 2; model variant 1), i.e. other routes of transmission are likely to be involved. However, it is possible that movements within Scotland still make a substantial contribution, but the extent of that contribution depends crucially on whether transmission via other routes is dependent or independent of the proportion of farms infected (cf. variant 2 of models 1 and 2 with the same variant of models 3 and 4). This is equivalent to saying that the contribution of movements to the level of infection depends on the degree to which cattle are the main reservoir of infection (density-dependent models) rather than the external environment (density-independent models). The density-dependent models suggest the plausible interval of 5–10 years from the first introduction of E. coli O157 into Scotland before currently observed levels of infection are reached. However, none of the models captures the observed seasonality in the levels of infection (cf. figure 1 with the inset in figure 7a), suggesting that seasonal variations in factors other than Scottish movement rates play a role.

The models used here are structured to reflect the observation that some infected cattle, so-called ‘super shedders’, excrete very high numbers of bacteria and are therefore presumed to be highly infectious (Matthews et al. 2006b). The contribution that movements of super shedders or other routes of acquisition of super shedder infections make to maintaining the observed levels of infection again depends on the degree to which cattle are the main reservoirs of infection (model variants 3 and 4). The models also explicitly incorporate heterogeneity between farms with regard to the network of cattle movements. Allowing heterogeneity in transmission via other routes has relatively small effects on the overall dynamics of infection (cf. models 1 and 2, models 3 and 4).

Some of the model variants considered here mimic possible effects of preventive measures: (i) restricting all movements or allowing movements only of uninfected cattle (variant 2), (ii) allowing movements only of non-super shedding cattle (variant 4), or (iii) allowing movements only from farms without super shedders (variant 5). For the models as presented, although all of these measures have some impact on the overall levels of infection, only measure (i) has the potential to lead to a major reduction when cattle are the main reservoir of infection (models 3 and 4, variant 2).

These preliminary results indicate a number of issues that merit more detailed study. Foremost among these is the suggestion that cattle movements may play a significant role in maintaining observed levels of E. coli O157 infection in the metapopulation of Scottish cattle farms. However, the importance of movements cannot be quantified without a better quantitative understanding of the role of reservoirs of infection outside the Scottish cattle population. Ultimately, more detailed and biologically realistic models, formally fitted to epidemiological data, may prove useful aids to the design of control or prevention programmes for this important zoonotic pathogen.