Parameter estimation and prediction for the course of a single epidemic outbreak of a plant disease

Abstract

Many epidemics of plant diseases are characterized by large variability among individual outbreaks. However, individual epidemics often follow a well-defined trajectory which is much more predictable in the short term than the ensemble (collection) of potential epidemics. In this paper, we introduce a modelling framework that allows us to deal with individual replicated outbreaks, based upon a Bayesian hierarchical analysis. Information about ‘similar’ replicate epidemics can be incorporated into a hierarchical model, allowing both ensemble and individual parameters to be estimated. The model is used to analyse the data from a replicated experiment involving spread of Rhizoctonia solani on radish in the presence or absence of a biocontrol agent, Trichoderma viride. The rate of primary (soil-to-plant) infection is found to be the most variable factor determining the final size of epidemics. Breakdown of biological control in some replicates results in high levels of primary infection and increased variability. The model can be used to predict new outbreaks of disease based upon knowledge from a ‘library’ of previous epidemics and partial information about the current outbreak. We show that forecasting improves significantly with knowledge about the history of a particular epidemic, whereas the precision of hindcasting to identify the past course of the epidemic is largely independent of detailed knowledge of the epidemic trajectory. The results have important consequences for parameter estimation, inference and prediction for emerging epidemic outbreaks.

1. Introduction

One of the main goals of epidemiological modelling is to provide guidelines for predicting and controlling disease outbreaks.This task can be achieved only if a reliable model is available and successfully parametrized. The model can subsequently be used to assess the impact of treatments on potential outbreaks and to predict future epidemics. Parameter estimation and subsequent testing of models against data form key steps in modelling ecological and epidemiological processes. However, these steps are not often given enough emphasis (Pascual & Kareiva 1996), owing to the lack of studies combining highly controllable experimental systems and involving biologically plausible yet tractable models.

Conventionally, epidemiologists consider single outbreaks for which some parameters are estimated from independent studies, while others are found based on the whole or part of the current outbreak (Anderson & May 1991; Britton 2001; Ferguson et al. 2001, 2003; Keeling et al. 2001; Bjornstad et al. 2002; Grenfell et al. 2002; Haydon et al. 2006). In practice, however, we might have additional information about other outbreaks of the disease, often occurring under similar conditions. Given that other epidemics provide additional information, we expect that if such information is incorporated into a modelling framework, parameter estimation and prediction of emerging epidemics could be significantly improved. There is a tendency, however, in conventional approaches to the analysis of replicated epidemics to average over replicates, whereby the results are represented by their mean with information about variability either completely missing or at best described in terms of a standard deviation (Grenfell et al. 1994; Kleczkowski et al. 1996). Thus, there is a need for a modelling protocol that enables us to study the properties of a single replicated outbreak and at the same time to describe properties of an ensemble of such outbreaks. Plant epidemiology, with its relative ease in generating replicate and highly controllable data, gives a unique opportunity to develop and test such a protocol (Kleczkowski et al. 1996; Gibson et al. 1999). The concept of an ensemble used here represents a set of actual or potential replicates of a biological system, created by repeating the experiment under the same macroscopic (or environmental) conditions without being able to control the microscopic detail.

Despite considerable insights in fitting models in ecology and epidemiology (Dennis et al. 1995; Pascual & Kareiva 1996; Finkenstadt & Grenfell 1998; Finkenstadt et al. 1998; Grenfell et al. 1998; Bjornstad et al. 2002; Ionides et al. 2006), parameter estimation in plant epidemiology is still often done under the (implicit or explicit) assumption that subsequent measurements are uncorrelated and that we only know the average behaviour of an ensemble of replicates. Very often this is not true and epidemic data are characterized by substantial levels of variability among the replicates and high correlation along each realization. Thus, there is an inherent conflict between the statistical methodology that ignores information contained in replicate data and the need to describe single replicates. For systems that possess a well-defined long-term behaviour, we can often exchange temporal and replicate averaging (Kleczkowski 2005). However, for epidemic outbreaks these two approaches are often not interchangeable. The number of infected individuals at any given time strongly depends upon the number at previous times, generating high degrees of temporal correlation along each disease progress curve. For such systems, predictability for a single replicate along its trajectory can be much higher than predictability for the ensemble of replicates (Kleczkowski 2005).

In this paper, we develop a modelling protocol that allows us to study the properties of an ensemble of epidemic outbreaks as a whole and at the same time describe individual outbreaks. We use a deterministic model to describe the main features of a single replicate behaviour, but augment this with probabilistic assumptions about parameter values (Kleczkowski et al. 1996; Kleczkowski 1998). The deterministic approach is chosen here over the fully stochastic one (Gibson et al. 1999, 2004) since differential equations are still the model form of choice for many studies describing plant, animal and human epidemics (Gilligan 2002). Information about replicate and population behaviour is combined within a hierarchical Bayesian approach. Such approaches have been widely used in social sciences (Goldstein 2003), ecology (Koop 2003; Clark & Gelfand 2006) and epidemiology (Zeger & Karim 1991; Taylor et al. 1994; Twisk et al. 1994), but have so far received little attention in the analysis of plant disease epidemics.

In addition to parameter estimation based upon single replicates, we study the predictability of the future of an epidemic outbreak based upon its history up to a certain point. This forecasting method is complemented by hindcasting, whereby we seek to reconstruct the past epidemic progress from later observations. This reconstruction allows us to estimate the initial levels of disease following introduction of a pathogen into the plant population. Such information about the early stages of epidemics or the levels and the potential of the initial inoculum is notoriously difficult to collect. Knowledge of the early epidemic stages is important, however, in estimating the risk of recurrent plant epidemics (Bailey & Gilligan 1999; Bailey et al. 2004).

We test the protocol using a series of well-controlled microcosm experiments involving replicated epidemics for the spread of a fungal pathogen, Rhizoctonia solani (Kühn) among radish (Raphanus sativus L.) plants in the presence or absence of a biocontrol agent, Trichoderma viride (Pers ex Grey). In previous papers (Kleczkowski et al. 1996; Gibson et al. 1999, 2004), we have presented experimental evidence for unexpectedly high levels of variability in the population dynamics of R. solani in the presence of the biological control agent. We have shown that small differences in the initiation of epidemics become magnified later in the season by the nonlinear character of the infection process. The variability in the progress of the disease is ‘quenched’ by changes in the host and pathogen behaviour—as plants become resistant, the rate of primary (soil-to-plant) and secondary (plant-to-plant) spread decreases. This results in substantial variability in the final size of the epidemic, affecting our ability to predict the severity of the outbreak and potential success of biological control. However, we show here that it is still possible to predict the level of disease in a single outbreak, provided we know its behaviour in the first few days.

Thus, the paper addresses five questions, all associated with the relationship between the between- and within-replicate variability. How can we fit a model to a single replicate and relate its parameters to other replicates? How can we combine information from an ensemble of replicated epidemics to study general features of this ensemble? How can we compare two sets of replicated data and assess the effects of treatments, exemplified here by the presence and absence of a biocontrol agent, T. viride? How can we use information about past outbreaks to predict an emerging epidemic? How long do we need to observe a new outbreak to be able to predict its future (or past) course with confidence? In addition, we also ask a more general question: can a deterministic model be augmented in such a way that it can be used to describe a replicated system characterized by a high degree of variability?

2. Material and methods

2.1 Experimental data

The experimental system was described by Kleczkowski et al. (1996) and Gibson et al. (1999, 2004). The data represent spread of a pathogen in a population of N=50 plant hosts. Seeds of radish were planted on a 5 by 10 regular (square) grid to a depth of 10 mm in clear plastic boxes (100 mm wide, 200 mm long and 100 mm deep), filled with 1.0 kg of white sand with a moisture content of 10% by weight. Ten inoculum units of mycelial discs, 1.0 mm in diameter, removed from the edge of a 5-day-old colony of R. solani growing in a Millipore filter over potato dextrose agar, and placed at a depth of 5 mm, were introduced at random locations into the population. Each treatment was replicated five times, with all conditions kept strictly identical in each treatment and replicate. The boxes were sealed and incubated in a growth chamber at 23°C and 16 hours light and 8 hours darkness cycle. The boxes were opened and scored daily for three weeks to record the number of infected (damped-off) plants in each replicate i=1, …, 5, Y_ij at each time t_j, j=1, …, 14.

2.2 Model

Two phases can be identified in the spread of R. solani in the plant population (Kleczkowski et al. 1996, 1997). There is an initial lag following the emergence of plants after which plants targeted by initial inoculum in the soil become infected (primary infections). Disease foci form and subsequently spread, with the dynamics becoming progressively slower as the plants become more resistant to infection (Kleczkowski et al. 1996). We summarize these processes by a deterministic model in the form of an ordinary differential equation describing the epidemics spread in a plant population subject to primary (soil-to-plant) and secondary (plant-to-plant) infections and decay in infectivity and susceptibility (adapted from Kleczkowski et al. (1996))

$$\frac{\text{d}Y}{\text{d}t}=(r_{\text{p}}(t)+r_{\text{s}}(t)Y)(N-Y),r_{\text{p}}(t)=r_{\text{p}}\text{exp}(-at),r_{\text{s}}(t)=r_{\text{s}}\text{exp}(-at),$$ (2.1)

where N is the total number of plants; Y is the number of infected plants; t is time; r_p represents the rates of primary infection and incorporates information about the density of initial inoculum; r_s describes the rate of secondary infections associated with focal expansion; and a corresponds to the quenching caused by the decay in susceptibility and is common to both primary and secondary infections. This equation belongs to a general class of S(E)IR models commonly used in plant, animal and human epidemiology (Anderson & May 1991; Gilligan & Kleczkowski 1997; Gilligan 2002). Here, we assume that all infected plants become diseased and there is no lag between infection and the expression of disease symptoms. The resulting disease progress curve has an initial rise towards a temporary plateau, followed by sigmoidal growth with the rate and asymptote varying among replicates,

$$Y(t)=\frac{r_{\text{p}}\left(1-\text{exp}\left(-\frac{r_{\text{p}}+r_{\text{s}}N}{a}(1-\text{exp}(-at))\right)\right)}{r_{\text{p}}+r_{\text{s}}N\text{exp}\left(-\frac{r_{\text{p}}+r_{\text{s}}N}{a}(1-\text{exp}(-at))\right)}\times N\equiv F(t;\mathit{\theta }),$$ (2.2)

where θ represents a vector of parameters.

2.3 Variability

In Kleczkowski et al. (1996), model (2.2) was used to describe the average behaviour of replicate epidemics. Thus, the ensemble average at each time point t_j, ${\langle Y\rangle }_j$, is computed from individual measurements $({\langle Y\rangle }_j=K^{-1}{\sum }_{i=1\dots K}{Y}_{ij})$ and assumed to follow model (2.2). Gibson et al. (1999) used a stochastic ‘version’ of equation (2.2) to describe the dynamics of each replicate epidemic and then combined the individual likelihoods in order to estimate the parameters common to the whole ensemble of epidemics. The infection levels in each replicate epidemic, Y_ij, represent the sum of individual processes involved in epidemic progress in a population of N=50 plants and up to 10 infection foci, each initiated by a unit of inoculum. There is a fundamental difference between the approach where model (2.2) is used to describe each individual outbreak (averaging over N individuals) and average behaviour of an ensemble of outbreaks (additional averaging over K replicates). Here, we use a similar approach to Gibson et al. (1999, 2004), but use the deterministic model (2.2) to describe the behaviour of each replicated epidemic Y_ij over time that distinguishes two sources of variability, within- and between-replicate variability.

We first consider the estimation of parameters for a collection of replicate epidemics. The link between the data and the model is provided by a likelihood function

$$l(\mathit{\Theta }|\mathit{y})=\text{Pr}({\mathit{y}}^{(1)}\wedge {\mathit{y}}^{(2)}\wedge \dots {\mathit{y}}^{(K)}|\mathit{\Theta })=\text{Pr}({\mathit{y}}^{(1)}|\mathit{\Theta })\times \text{Pr}({\mathit{y}}^{(2)}|\mathit{\Theta })\times \dots \text{Pr}({\mathit{y}}^{(K)}|\mathit{\Theta })$$ (2.3)

to describe the probability that in the ith replicate we obtain a particular (vector) result y⁽ⁱ⁾=(Y_ij)^T, conditioned on a particular value of the (vector) parameter Θ. In a general formulation, the vector parameter Θ encompasses all possible choices, including parameters common to all replicates, θ, and parameters specific for each replicate, θ⁽ⁱ⁾. We assume that individual realizations are statistically independent, resulting in further expansion in (2.3).

A traditional approach (‘fitting to the mean’) assumes that the vector of the parameters Θ is common to all replicates. Thus,

$$l(\mathit{\theta }|\mathit{y})=\text{Pr}({\mathit{y}}^{(1)}\wedge {\mathit{y}}^{(2)}\wedge \dots {\mathit{y}}^{(K)}|\mathit{\theta })=\text{Pr}({\mathit{y}}^{(1)}|\mathit{\theta })\times \text{Pr}({\mathit{y}}^{(2)}|\mathit{\theta })\times \dots \text{Pr}({\mathit{y}}^{(K)}|\mathit{\theta }),$$ (2.4)

where $\mathit{\theta }=(r_{\text{p}},r_{\text{s}},a)$. An alternative approach (‘fitting to the replicates’) is to consider a hierarchical model in which each replicate is described by a different (vector) parameter, ${\mathit{\theta }}^{(i)}=\left(r_{\text{p}}^{(i)},r_{\text{s}}^{(i)},a^{(i)}\right)$. The individual parameters are then assumed to be drawn from a certain distribution, characterized by another set of parameters (ω) called hyperparameters. Consider the following expression for the likelihood

$$l(\mathit{\omega }|\mathit{y})=\text{Pr}({\mathit{y}}^{(1)}|{\mathit{\theta }}^{(1)})\times \text{Pr}({\mathit{\theta }}^{(1)}|\mathit{\omega })\times \text{Pr}({\mathit{y}}^{(2)}|{\mathit{\theta }}^{(2)})\times \text{Pr}({\mathit{\theta }}^{(2)}|\mathit{\omega })\dots \text{Pr}({\mathit{y}}^{(R)}|{\mathit{\theta }}^{(R)})\times \text{Pr}({\mathit{\theta }}^{(K)}|\mathit{\omega })=\text{Pr}({\mathit{y}}^{(1)}\wedge {\mathit{y}}^{(2)}\wedge \dots {\mathit{y}}^{(K)}|\mathit{\omega }),$$ (2.5)

in which the (hyper)parameters, ω, describe the distribution of θ.

We use two models to describe the individual probability for a given (ith) replicate $\text{Pr}({\mathit{y}}^{(i)}|{\mathit{\theta }}^{(i)})$, representing the within-replicate variation. Since the data are given as low-integer values, it is natural to represent them by a binomial distribution, with an average given by $F(t;{\mathit{\theta }}^{(i)})$ and the population size of N. However, the binomial model fails to capture the essential features of the infection process and therefore significantly overestimates the within-replicate variability. We therefore also consider a normal distribution for $\text{Pr}({\mathit{y}}^{(i)}|{\mathit{\theta }}^{(i)})$, which has the added flexibility of a free parameter, a variance ${\sigma }_{\text{c}}^2$. The variance is assumed to be constant along each individual trajectory. The within-replicate variability represents the temporal uncertainty within the particular outbreak and can be associated with both demographic stochasticity and measurement error (Lande et al. 2003).

The distribution of individual parameters, $\text{Pr}({\mathit{\theta }}^{(i)}|\mathit{\omega })$, is assumed to be lognormal, so that $\text{ln}({\mathit{\theta }}^{(i)})$ is normally distributed and characterized by two hyperparameters each, mean μ and variance σ² (these are vectors corresponding to three parameters $(r_{\text{p}},r_{\text{s}},a)$), so that $\mathit{\omega }={(\mathit{\mu },{\mathit{\sigma }}^2)}^{\text{T}}$. In the simple approach adopted here we ignore correlation among parameters, but the model can be easily extended to incorporate it. The choice of the lognormal distribution allows us to keep the parameters positive while benefiting from the flexibility of the normal distribution. The between-replicate variability represents the uncertainty about which particular replicate is realized, and this is associated with demographic stochasticity as well as with environmental factors that affect replicates differentially.

Within a Bayesian interpretation, μ reflects our belief about the values of the parameters characterizing the ensemble as a whole, whereas σ² describes our uncertainty about these estimates. $\text{Pr}({\mathit{\theta }}^{(i)}|\mathit{\omega })$ may be interpreted as our belief in the values of parameters characterizing the particular ith outbreak conditioned on the hyperparameters ω, whereas $\text{Pr}({\mathit{y}}^{(i)}|{\mathit{\theta }}^{(i)})$ collectively reflect our belief in the size of the outbreak given the individual parameters θ⁽ⁱ⁾. Thus, we divide the total variability in the experiment into two components, the between-replicate variability ($\mathit{\omega }={(\mathit{\mu },{\mathit{\sigma }}^2)}^{\text{T}}$) and the within-replicate variability (fixed for the binomial model, fitted ${\sigma }_{\text{c}}^2$ for the normal model). Model predictions for the ith replicate at time t_j are denoted as y_i(t_j).

2.4 Priors

In specifying the priors, we assume that we possess minimal knowledge of past epidemic outbreaks. This leads to flat priors for the hyperparameters μ, represented in the simulations by a normal distribution with a large variance. We also consider a range of more informative priors by using past studies to guide us in the choice of the particular prior. Kleczkowski et al. (1996) and Gibson et al. (2004) have found that the primary and secondary infection rates are of an order of magnitude 0.01 d⁻¹, whereas the decay rate is of order 0.1 d⁻¹. We represent this knowledge as a normal prior for μ (centred at −4 for $r_{\text{p}}\text{and}{r}_{\text{s}}$ and −2 for a; note that μ is related to $\ln ({\mathit{\theta }}^{(i)})$ and not to θ⁽ⁱ⁾), with a large variance leading to a relatively broad prior distribution. For the replicate standard deviation (σ_c), we not only used a flat prior over the interval $(0,50]$, but also compared the results to an approximate 1/x prior for ${\sigma }_{\text{c}}^2$ (Barnett 1999). For the hyperparameter, σ², we assume that we have a strong prior belief that all replicate epidemics occur in similar environmental conditions and, therefore, we expect small between-replicate variability. A range of contrasting priors is considered for ${\mathit{\sigma }}_m^2$, represented by an exponential distribution $\text{exp}(-\lambda {\mathit{\sigma }}_m^2)$, m=1, …, 3, corresponding to $(r_{\text{p}},r_{\text{s}},a)$. Small values of λ represent a relatively shallow prior (e.g. λ=5, reflecting relatively weak prior belief in uniformity of the replicates) to a steep prior (λ=15, reflecting strong prior belief in uniformity of the replicates). We use λ=15 in the paper, but sensitivity to the prior form is addressed later.

Thus, the full model is given by

$$\{\begin{array}{c}{Y}_{ij}=F(t_j;{\mathit{\theta }}^{(i)})+{\sigma }_{\text{c}}{ϵ}_{ij}\\ \text{log}({\mathit{\theta }}^{(i)})\sim N(\mathit{\mu },{\mathit{\sigma }}^2)\\ {ϵ}_{ij}\sim N(0,1)\\ {\mu }_{r_{\text{p}}}\sim N(-4,1),{\mu }_{r_{\text{s}}}\sim N(-4,1),{\mu }_a\sim N(-2,1)\\ {\mathit{\sigma }}^2\sim \text{exp}(15),{\sigma }_{\text{c}}\sim U(0,50),\end{array}$$ (2.6)

where we listed the priors shown in the figures. The sensitivity of results to particular assumptions about the model structure and priors is discussed below.

2.5 Forecasting and hindcasting

Here, we focus on a single replicate epidemic for which we wish to estimate either the unknown future (forecasting) or unknown past (hindcasting) trajectories. Prediction is therefore performed on one replicate (i=K₁, where K₁ is selected from 1 to 5), assuming that we only possess limited information about the trajectory of the selected epidemic. The remaining K−1=4 replicates act as a ‘library’ of past outbreaks used to calibrate the model. Splitting the replicate set into the library and the emerging outbreak allows us to assess the ability of our model to predict out-of-sample. For forecasting, we assume that for the K₁-th replicate all data points up to a given point are known and the remaining course of the epidemic is to be estimated. To quantify the predictability, we assign the last point (j=14) to be of the particular interest for forecasting, since it represents the final size of the replicate epidemic.

For hindcasting, knowledge of the final points of the epidemic in replicate K₁ is assumed. Quantification of hindcasting is made at t=8 d. This time is known to be associated with a switch from primary to secondary infections for the R. solani–radish system (Kleczkowski et al. 1996, 1997) and is therefore of biological interest. Predictability (either forecasting or hindcasting) is quantified by computing a 95% highest predictive density region (HPDR) and its width (Barnett 1999). We use symmetric HPDRs and therefore compute values of Y corresponding to 2.5 and 97.5% quantiles of the marginal posterior distribution and then calculate the difference between the two points.

2.6 Parameter estimation

Parameter estimation and prediction were performed using Markov chain Monte Carlo methods with Gibbs sampling, implemented in WinBUGS (WinBUGS v. 1.4, MRC Biostatistics Unit, Institute of Public Health, Cambridge, UK). Typically, 50 000 iterations were performed to burn in and then the model was run for 50 000 iterations to collect the statistics. The Markov chains for lower tiers of the hierarchy (individual parameters) mixed well and the distributions were stable even after a very short burn-in period, with small correlations between subsequent Markov chain steps. In contrast, the chains for hyperparameters took longer to mix and hence we chose a long burn-in period. The results were also tested for consistency of estimates of posterior densities of parameters over replicate simulation runs. Convergence was assessed by running quantiles and the Gelman–Rubin convergence statistic, as modified by Brooks & Gelman (1998).

3. Results

3.1 Disease progress

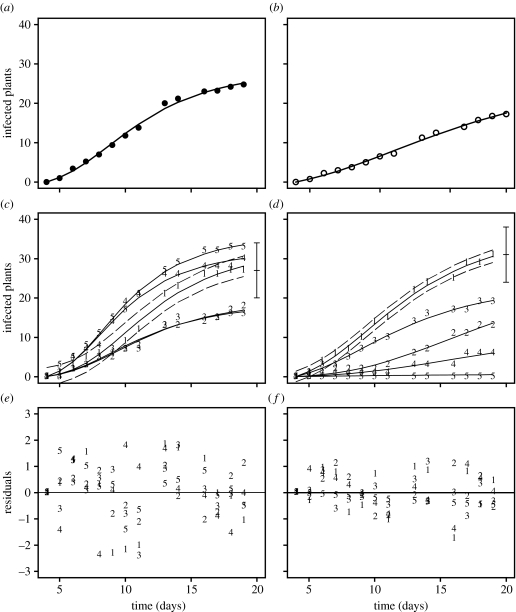
Average and replicate disease curves have a general sigmoidal shape, exhibiting strong correlation between successive observations (figure 1a–d) and large variability between replicate curves (figure 1c,d). The model (2.2) fits each replicate epidemic remarkably well (figure 1c,d), with small and uniform residuals (figure 1e,f), despite marked differences in shapes of individual curves and sizes of individual outbreaks. For some replicates, there is not enough information to estimate all three parameters successfully, for example if no or very little infection occurs or if it is present at low levels (replicates 2, 4 and 5 in the presence of T. viride). If we had no other information about replicate epidemics, it would not be possible to describe or predict such outbreaks. However, we can use estimated parameters for other replicates (replicates 1 and 3 in figure 1d) to enable the fit for the replicates that would have caused a problem if hierarchical Bayesian model had not been used (replicates 2, 4 and 5 in figure 1d). Despite large ensemble uncertainty, individual curves are smooth and their short-term behaviour can be predicted with considerable precision. This is reflected in a small value of the within-replicate uncertainty, represented by ${\sigma }_{\text{c}}^2$ (point estimates are ${\sigma }_{\text{c}}^2=1.13$ and ${\sigma }_{\text{c}}^2=0.66$ for the case without T. viride and for the case with the biocontrol, respectively; see the 95% credible intervals in figure 1c,d and the spread of residuals in figure 1e,f). The residual variance does not change through time (figure 1e,f). Neither of these two features is captured by the model (2.6) in which ϵ_ij are distributed according to the binomial distribution and we therefore show the results for the normal distribution only, in figure 1 and subsequent figures. Analysis of the autocorrelation (not shown here) suggests that there is no significant temporal correlation between residuals, except for replicate 5 where T. viride completely stops the spread of Rhizoctonia. This shows that most of the temporal autocorrelation seen in the disease progress data is removed by the deterministic model (2.2).

Figure 1.

Disease progress curves and residuals for damping-off of radish plants caused by R. solani in the absence (a,c,e) and in the presence (b,d,f) of the biocontrol agent, T. viride (Kleczkowski et al. 1996). (a,b) The average behaviour; circles represent observed data and lines the fit based upon the model of Kleczkowski et al. (1996), fitted to averaged replicate data. (c,d) The results of fitting model (2.2) to individual replicates, with solid lines representing the median of the simulated marginal posterior distribution of y_i(t_j). Broken lines show boundaries of the 95% high-density region based upon the normal approximation and for clarity are shown for replicate 1 only. Error bars show the maximum extent of the within-replicate variability assumed by the binomial model, for replicate 1 only. (e,f) Residuals for the fit in (c,d), respectively. In (c)–(f), data points are labelled 1–5 to indicate which replicate epidemic they represent. (This labelling is consistent across all subsequent figures.)

3.2 Parameter estimation

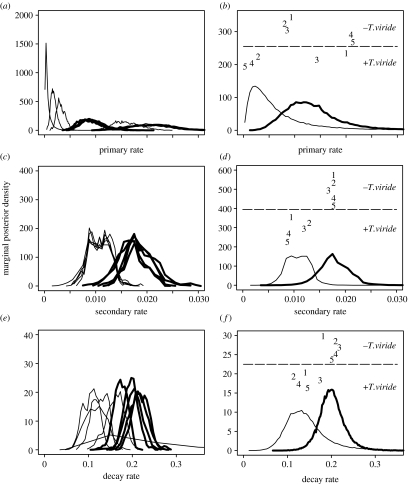
Hierarchical modelling allows us to estimate the parameters of individual epidemic outbreaks and at the same time to study features common to all replicated outbreaks. Information about individual outbreaks is given by a posterior distribution $\text{Pr}({\mathit{\theta }}^{(i)}|\mathit{\omega })$ of individual parameters, whereas common characteristics are characterized by posterior distributions of hyperparameters in the second tier of the hierarchy, Pr(μ) and $\text{Pr}({\mathit{\sigma }}^2)$. Figure 2 shows marginal posterior distributions of $\text{Pr}({\mathit{\theta }}^{(i)}|\mathit{\omega })$ and Pr(μ) for each of three parameters (lines). Figure 2b,d,f show how Pr(μ) compares with point estimates corresponding to individual replicates, $\text{Pr}({\mathit{\theta }}^{(i)}|\mathit{\omega })$ (points labelled as in figure 1). Point estimates (medians and 95% symmetrical credible intervals) are given in table 1 and compared with values obtained previously by a maximum-likelihood method (Gibson et al. 1999), which are similar to those obtained by Bayesian methods in Gibson et al. (2004). The parameter estimates are consistent with the earlier results, but our method allows simultaneous estimation of parameters for individual replicates.

Figure 2.

Marginal posterior densities for individual replicate parameters θ⁽ⁱ⁾ (a,c,e) and for population parameters μ (b,d,f), in the absence (thick line) and in the presence (thin line) of T. viride. In (b,d,f), labelled points represent modes of marginal posterior densities for individual replicate parameters θ⁽ⁱ⁾, while labels 1–5 indicate which replicate epidemic they represent. For ease of viewing, the labels are arbitrarily distributed vertically and separated by a dashed line. (a,b) Primary infection rate, r_p; (c,d) secondary infection rate, r_s; (e,f) decay rate, a.

Table 1.

Values of parameters obtained by fitting the model (2.2) to the replicate data. (Point estimates (medians) and symmetric 95% credible intervals are given here for the hyperparameters $\mathit{\mu }={({\mu }_{r_{\text{p}}},{\mu }_{r_{\text{s}}},{\mu }_a)}^{\text{T}}$ and for the within-replicate standard deviation σ_c. The binomial model assumes that within-replicate variability is described by a binomial distribution, whereas the normal model assumes a normal distribution. Two prior sets were used for the normal distribution to illustrate the relative insensitivity to the model assumptions. The flat prior corresponds to a large standard deviation in the normal distribution for μ(10³) and an approximately 1/x prior for ${\sigma }_{\text{c}}^2$, whereas the informative prior assumes standard deviation of 1 for the μ priors and uniform prior for ${\sigma }_{\text{c}}^2$. The values are compared with those of Gibson et al. (1999, 2004).)

model	rate of primary infection (rp)	rate of secondary infection (rs)	rate of decay (a)	s.d. (σc)
without biocontrol
binomial	0.018 (0.009–0.0420)	0.013 (0.004–0.025)	0.17 (0.07–0.25)
normal (flat prior)	0.014 (0.006–0.032)	0.016 (0.013–0.022)	0.19 (0.14–0.25)	1.13 (0.95–1.38)
normal (informative prior)	0.013 (0.005–0.029)	0.018 (0.012–0.024)	0.20 (0.15–0.27)	1.15 (0.96–1.40)
Gibson et al. (1999, 2004)	0.02265	0.0118	0.167
with biocontrol
binomial	0.006 (0.001–0.045)	0.006 (0.002–0.02)	0.09 (0.02–0.29)
normal (flat prior)	0.004 (0.000–0.024)	0.011 (0.008–0.015)	0.14 (0.08–0.25)	0.67 (0.56–0.81)
normal (informative prior)	0.005 (0.001–0.031)	0.011 (0.007–0.015)	0.14 (0.07–0.29)	0.67 (0.56–0.83)
Gibson et al. (1999, 2004)	0.0074	0.0102	0.127

The rates of primary infection are the most variable factor affecting disease progress (figure 2a,b). The biocontrol agent mainly affects the primary infections by reducing the overall level of infection, although there is some reduction in the rate of secondary infections (figure 2c,d) and the rate of decay (figure 2e,f). These results are consistent with Gibson et al. (1999, 2004), rather than with Kleczkowski et al. (1996), showing that a deterministic model with a ‘proper’ treatment of replicate behaviour exhibits behaviour similar to a fully stochastic model.

Marginal posterior distributions for individual replicate estimates $\text{Pr}({\mathit{\theta }}^{(i)}|\mathit{\omega })$ (figure 2a,c,e) are much narrower than Pr(μ) (figure 2b,d,f), reflecting the relative smoothness of each replicate disease progress curve. Modes of the distribution $\text{Pr}({\mathit{\theta }}^{(i)}|\mathit{\omega })$ are shown in figure 2 as point estimates. Two out of five replicates with T. viride are characterized by levels of primary infections very similar to the case without the control agent (figure 2a,b), whereas the remaining three replicates have much smaller values. Other parameters are much more consistent across the individual replicate estimates. Individual replicate estimates for the case without T. viride also show clustering in the values of the primary infection rate (replicates 1, 2, 3 versus 4, 5). The clustering is reflected in the differences among the individual disease progress curves (cf. figure 2a,b with figure 1c,d).

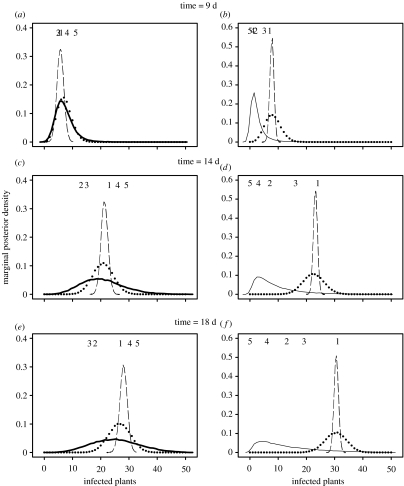
3.3 Predicting ensemble variability

If no information is available about which individual replicate we are likely to follow, prediction is linked to the between-replicate variability (figure 3). This figure shows marginal posterior density distribution $\text{Pr}(\mathit{y}|\mathit{\theta })$, representing our belief in the size of an epidemic based on the population of outbreaks rather than on an individual replicate. These predictions are necessarily very broad (as we do not know a priori which replicate will be realized) and strongly affected by the choice of the prior information about the hyperparameters σ² (see below for further discussion). There is a very clear distinction between the posterior distribution for the between-replicate variability with and without T. viride. Introduction of the biocontrol agent results in a highly skewed distribution. Thus, although most of the epidemics are controlled by the biocontrol agent, there is a substantial chance of an uncontrolled outbreak. This result reflects the difference between replicates 1–3 and 4 and 5 in the data (figures 1d and 2a; cf. data points in figure 3). The distributions are qualitatively similar to the posterior distributions reported by Gibson et al. (2004) for the fully stochastic model.

Figure 3.

Marginal posterior distributions for disease levels in the absence (a,c,e) and in the presence (b,d,f) of the biocontrol agent. Solid lines represent predictions for the population behaviour (between-replicate variability), whereas broken lines show predictions for one of the replicates (K₁=1; within-replicate variability) based upon the normal distribution model for $\text{Pr}({\mathit{y}}^{(i)}|{\mathit{\theta }}^{(i)})$. Points show the extent of the within-replicate variability for the binomial model. Labels 1–5 represent replicated data to indicate which replicate epidemic they represent.

The within-replicate variability is very small, as shown in figure 3 (broken line) by the posterior distribution of $\text{Pr}({\mathit{y}}^{(i)}|{\mathit{\theta }}^{(i)})\times \text{Pr}({\mathit{\theta }}^{(i)}|\mathit{\omega })$ under the assumption of the normal distribution for $\text{Pr}({\mathit{y}}^{(i)}|{\mathit{\theta }}^{(i)})$. This probability represents our belief in the size of the current ith outbreak and can be interpreted as model error, i.e. inability of the model to describe the existing replicate data. The narrow distribution in figure 3 is yet another manifestation of the smoothness of individual replicate data as contrasted with the uncertainty of the ensemble behaviour.

3.4 Forecasting

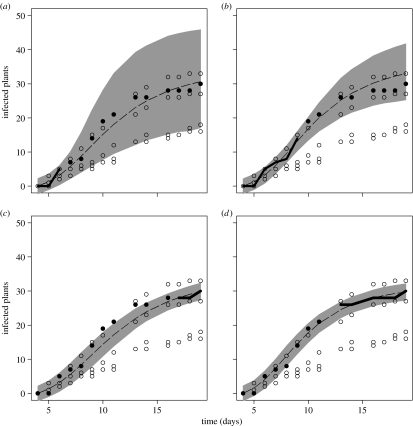
If only partial information about an individual replicate is given, forecasting may improve significantly with the amount of information we can supply (figure 4). As an example, we show the results for replicate K₁=4 without T. viride, but similar results are obtained for other replicates (cf. figure 5). When only the first three data points are known (including the trivial point Y_ij=0 for t=4 d), the HPDR is broad, reflecting relatively large uncertainty in forecasting. However, observing the outbreak for three more days (up to day 9) results in significant reduction of uncertainty associated with our predictions (quantified here by the 95% HPDR). It is worth noting that if we simply concentrate on point estimates of the disease progress instead of on the whole distribution (represented by the median of the predictive posterior distribution of y_K1(t_j) at each time point; broken line in figure 4), the prediction is remarkably good, even when based on the first 3 days only (figure 4a). In particular, the distinction between clusters of replicates (replicates 1, 2 and 3 versus 4 and 5) is clearly made, even if based on the first three points only (figures 4a and 1).

Figure 4.

Forecasting and hindcasting individual outbreaks. (a,b) show 95% highest predictive density regions (HPDRs) for forecasting one of the replicate epidemics from figure 1 (K₁=4). The thick line represents the ‘known’ part of the trajectory, whereas filled circles show the actual ‘future’ (or ‘past’) outbreak. Forecasting is based on (a) three (4–6 d) or (b) six (4–9 d) initial days of data. Hindcasting in (c,d) estimates the outbreak levels in the past based upon the last (c) three (17–19 d) or (d) six (13–19 d) data points. Open circles show replicates used as a library. The width of the HPDR at t=19 d (for forecasting) and 8 d (for hindcasting) is subsequently used to characterize predictability for individual replicates (figure 5). Broken lines show the median of the predictive posterior density.

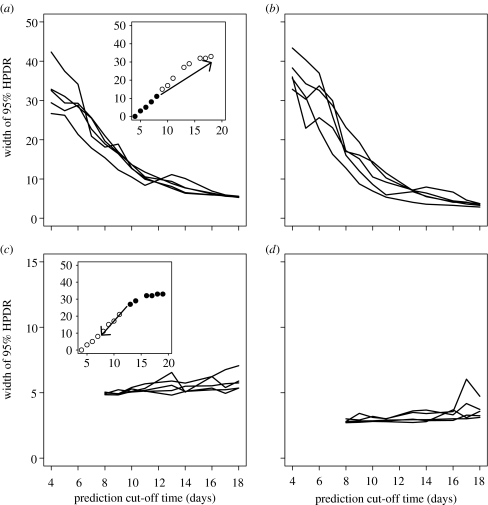
Figure 5.

Forecasting and hindcasting individual outbreaks. (a,b) The width of the 95% highest predictive density regions (HPDRs) for forecasting final levels (t=19 d) of replicate epidemics. (c,d) The width of the 95% high-density regions for hindcasting the disease levels at t=8 d. Cut-off time for forecasting is the date for the last measurement, whereas for hindcasting it is the earliest date for which data are assumed to exist. Plots (a,c) correspond to the case without and (b,d) with the biocontrol agent.

The results can be quantified by repeating the forecasting procedure for all lengths of periods of known data and for all replicates (figure 5a,b). Uncertainty associated with forecasting is very similar for all replicates, despite very different temporal progress and very different final sizes of the epidemics (compare figure 5 to figure 1c,d). When no information about the current outbreak is known (t=4 d in figure 5a,b), the uncertainty of our predictions for the final size of the epidemic is very high. However, once we observe the outbreak for several days, prediction uncertainty is significantly reduced. There appears to be a critical period (t=8–10 d) beyond which there is no significant improvement in the uncertainty of prediction. Predictability of epidemics with T. viride is initially lower than in the absence of biocontrol agent, but improves significantly with time. This is, paradoxically, due to the large separation of the disease progress curves seen in figure 1d and the large variability in the rate of primary infections (figure 2a,b). Thus, once the rate of primary infections can be estimated with sufficient precision, the future course of the epidemic can be predicted very well.

3.5 Hindcasting

In contrast to forecasting, hindcasting is characterized by low levels of variability (figures 4c,d and 5c,d). The uncertainty is also independent of the replicate and of the lengths of the period for which we know the data. This paradoxical behaviour (the knowledge of more data does not improve the predictability) is associated with a very strong link between the final level of the epidemic and the rate of primary infections. Thus, once we know the final level of the epidemic, we can estimate primary infections very well. Since in addition we also know the starting point (as all epidemics are initiated at t₁=0 at the level of Y_ij=0), the whole trajectory is then well defined. However, even though the uncertainty is relatively low, we still might be making a significant error in our estimation of infection levels in the middle of the epidemic, see figure 5c for t_i=9–14 d.

3.6 Sensitivity to model choice

The model is based upon three key assumptions: (i) normal distribution for the within-replicate variability, (ii) normal but very broad priors for the mean of the hyperparameters, and (iii) tight exponential priors for the variance of the hyperparameters. The sensitivity of the results to each of these assumptions is summarized below.

The within-replicate variability was modelled by two distributions: binomial and normal. There was no significant difference in the parameter estimates for either of the distributions, but the normal distribution modelled the residuals better (figure 1e,f), particularly the small variance of the residuals (figure 1c,d). The predictability (figure 5) was also qualitatively similar for models with normal and binomial distributions, although the uncertainty levels were higher in the binomial case.

We found that the prior assumption for σ² is the only model detail which affected the results in a substantial way. If we have a strong prior belief that all outbreaks come from the same population of epidemic outbreaks (i.e. we expect no significant between-replicate variability), we can choose λ to be large (steep prior; λ=15 as used here). This results in a relatively tight prediction for $\text{Pr}(\mathit{y}|\mathit{\theta })$ (as shown in figure 3), but creates problems for chain convergence. However, if we have no prior reason to believe that future outbreaks come from the same population (small λ; shallow prior), a new outbreak might be very different from the ones we have observed so far and the prediction is very uncertain. In contrast, the individual fits (figures 1–3) were not affected. For a shallow prior (small λ), the quality of the forecast (figure 5) was significantly lower when predicting early in the outbreak. However, once enough information about the particular replicate was collected, the predictability was independent of λ.

Unless prior knowledge was strongly concentrated around a specific value of μ, the posterior distribution for parameters was not affected (table 1). Similarly, the results were not significantly affected when the prior for ${\sigma }_{\text{c}}^2$ was changed. We conclude that the method presented here is not sensitive to a wide choice of priors or detailed model assumptions, although prior information can be used to narrow down the estimates in cases when data are variable.

The replication in this dataset is relatively low (five populations per treatment). However, parameter estimation worked very well in our case, despite large variability among the replicates, even if the priors were chosen to be uninformative.

4. Discussion

Analysis and prediction of disease outbreaks is central to our ability to prevent and control epidemics. Two strategies have been conventionally used to study disease spread. One approach is focused upon a single outbreak whereby information collected for other similar outbreaks is ignored. Alternatively, data are collected for replicated epidemics, but analysis is concentrated on average behaviour. This duality leads to a paradoxical situation whereby in some cases we do not even attempt to collect or search for replicate data (for large epidemic outbreaks) while the information about individual replicates is ignored when it is available (for controlled experiments, for example in plant epidemiology or livestock diseases). There are several problems associated with each of these approaches.

If we are dealing with a single realization, we need to make strong and often arbitrary assumptions about the underlying probabilistic model that has generated this realization. Without knowledge of other realizations it is impossible to estimate the parameters describing the error structure and magnitude and to validate the assumptions. Thus, while we can predict the future behaviour of the emerging epidemic based upon limited information available for the initial stages of the epidemic, we often cannot give realistic bounds on the risk associated with the particular outbreak. Incorporation of replicate information enables us to carry out the risk assessment.

However, when replicate data are available but the underlying stochastic model is oversimplified (like in the fitting-to-mean procedure), we encounter a problem of averaging nonlinear disease progress curves. In this case, averaging of individual disease curves produces an outcome that is not equivalent to the dynamics with average parameters (Kleczkowski 1998; Gibson et al. 1999). In many cases, the average behaviour might even belong to a completely different class of functions than the individual replicates (Kleczkowski 1998). As a result, parameter estimations based upon average disease progress curves cannot be used reliably for making inferences about the underlying biological processes.

Finally, data for replicate epidemics often contain much more information about the actual biological mechanisms than the average data or single realizations. When r_p is estimated for the case with T. viride, we see clustering of disease outbreaks into two subsets, with replicates 1 and 3 characterized by high levels of primary infection, whereas replicates 2, 4 and 5 exhibit suppressed levels of primary infection (cf. figure 2), with similar values for r_s and a. This result suggests that T. viride failed to protect against primary infections in outbreaks i=1 and 3 leading to particularly high levels of infection at the end of the respective epidemics (cf. figure 1d). The clustering of replicate estimates of r_p is also responsible for a long tail of the distribution Pr(μ) (cf. figure 2b) and for the increased variability in the presence of the biocontrol agent (cf. figure 3).

In this paper, we have also shown how to combine information about some past outbreaks with partial information about the current emerging epidemic. The hierarchical Bayesian framework can be extended to incorporate more informative prior knowledge about the epidemiological parameters than can subsequently be built into the model via priors for μ and σ². This will narrow down predictability for future outbreaks and lower the requirements for expensive collection of data.

The method we propose in this paper distinguishes between two types of variability. The within-replicate variability is associated with a single replicate and is characterized by the posterior distribution $\text{Pr}({\mathit{y}}^{(i)}|{\mathit{\theta }}^{(i)})$. The between-replicate variability describes uncertainty associated with repeated outbreaks and is characterized by the posterior distribution $\text{Pr}({\mathit{\theta }}^{(i)}|\mathit{\omega })$. We have used a deterministic model to describe the epidemiological dynamics, an approach still widely used in plant epidemiology. In this approach, variability is described phenomenologically, instead of emerging from the dynamics themselves. Thus, in the model formulation we do not provide any details about the mechanism generating the variability. It could be argued that three sources of variation can been identified in many ecological and epidemiological systems (Nisbet & Gurney 1982; Lande et al. 2003). Measurement error is linked to the sampling procedures, which is particularly imperfect in scoring plants for disease symptoms. We assume perfect scoring here and so ignore this element, but it can be incorporated either in the model (for example, as a cryptic phase; Gibson et al. 2004) or into the within-replicate variability. Demographic variability is conventionally associated with chance events leading to unpredictability even when run under identical conditions and can be potentially associated with the within-replicate variability in our model. Environmental variability is conventionally associated with aperiodic temporal fluctuations affecting all individuals in the population (Nisbet & Gurney 1982; Lande et al. 2003). The latter concept can be generalized to include spatial variability in which subpopulations are affected differentially by local variations in the environment. Gibson et al. (1999, 2004) have shown that between-replicate variability can be described by a stochastic model with no additional systematic variation among replicated epidemics. This result shows that a careful definition of environmental and demographic variability is needed for systems in which systematic variation may be present. We suggest that hierarchical Bayesian modelling provides a flexible framework in which to assign a part of the between-replicate variability to stochastic and another part to systematic (environmental) variation. To do this, however, we need to extend our approach to incorporate a stochastic version of model (2.2) (Gibson et al. 1999, 2004; Kleczkowski 2005).

In the Bayesian framework, posterior distributions can be interpreted in terms of probabilities of an outbreak reaching a certain size. Thus, the framework developed here can be extended to calculate risks associated with disease outbreaks (Keeling et al. 2001; Claessen et al. 2005a,b). It can also be built into expert systems that allow real-time monitoring and intervention based on partial information about disease outbreaks.

The modelling approach developed here for plant epidemics can also be applied for human and animal diseases. The model is based upon a standard SI model and extensions to more complicated systems can be considered, with primary infections corresponding to external imports of infective individuals (Keeling & Grenfell 2002). The concept of a replicate, however, needs careful consideration as it might be difficult to obtain data for outbreaks under carefully controlled and replicable conditions. Herds of animals, farms, wards, hospitals and regions can be approximately treated as replicated epidemics, even if small levels of coupling between them are present. It is also possible to study replicates over time in recurrent epidemics (e.g. Ionides et al. (2006)), provided the cohorts of individuals are sufficiently distinct so that the carry-over effects from one season to another can be neglected. Our method can be generalized to include the time when the epidemic starts. Hindcasting would then allow us to trace the origin and history of the current outbreak, for example AIDS and HIV infections (Lemey et al. 2003).

Central to our paper is the distinction between within- and between-replicate variability. In the Bayesian interpretation, the between-replicate variability corresponds to our degree of belief in the outbreak size without any reference to the particular replicate: what would the behaviour be, were the disease to invade again many times? The within-replicate variability reflects, in the Bayesian sense, our degree of belief in properties of each individual replicate: what is the future behaviour of a particular outbreak? Kleczkowski (2005) has shown that contrast between within- (or replicate) and between-replicate (or ensemble) variability has its origins in properties of a simple birth process. In the exponential phase of disease spread, small differences in the initial conditions are magnified by the subsequent dynamics. This generates large differences among realizations while keeping the individual growth curves relatively smooth. Since many biological processes are adequately approximated by the exponential function, we suggest that the method developed here can be applied to many epidemiological, ecological and even metabolic processes (Colman-Lerner et al. 2005).