Abstract
Monkeys made saccades to one of two peripheral targets based on the brightness of a central stimulus. Task difficulty was manipulated by varying the ratio of stimulus black-and-white pixels. Correct response probability for two monkeys varied directly with difficulty. Deep layer SC neurons exhibited robust presaccadic activity the magnitude of which was unaffected by task difficulty when the stimulus specified a saccade toward a target within the neuron’s response field. Activity after stimuli specifying saccades to targets outside the response field was affected by task difficulty, increasing as the task became more difficult. A quantitative model derived from studies of human decision-making was fit to the behavioral data. The model assumes that information from the stimulus drives two independent diffusion processes. Simulated paths from the model were compared with neuron activity, assuming that firing rate is linearly related to position in the accumulation process. The firing rate data show delayed availability of discriminative information for fast, intermediate, and slow decisions when activity is aligned on the stimulus and very small differences in discriminative information when aligned on the saccade. The model produces exactly these patterns of results. The accumulation process is highly variable, allowing the process both to make errors, as is the case for the behavioral performance, and also to account for the firing rate results. Thus the dual diffusion model provides a quantitative account for both the behavior in a simple decision-making task as well as the patterns of activity in competing populations of neurons.
INTRODUCTION
Research in neural decision making is at the point of identifying the mechanisms that implement simple decisions (Glimcher and Sparks 1992; Gold and Shadlen 2000; Hanes and Schall 1996; Horwitz and Newsome 1999, 2001; Kim and Shadlen 1999; Krauzlis and Dill 2002; McPeek and Keller 2002; Ratcliff et al. 2003a; Roitman and Shadlen 2002; Romo et al. 2002; Sparks 1999). In parallel to this work, psychology has produced a set of models that describe simple rapid two-choice decision making (Busemeyer and Townsend 1992, 1993; Diederich 1997; LaBerge 1994; Laming 1968; Link 1975; Link and Heath 1975; Pike 1966, 1973; Ratcliff 1978, 1981, 1988; Ratcliff and Rouder 1998, 2000; Ratcliff and Smith 2004; Ratcliff et al. 1999; Roe et al. 2001; Smith 1995; Smith and Ratcliff 2004; Smith and Van Zandt 2000; Stone 1960; Townsend and Ashby 1983). We present a diffusion model that explicitly relates these two domains in the context of a single experiment. The model is applied to simple two-choice decisions and accounts for both behavioral data, namely, accuracy and correct and error response time (RT) distributions, and single-cell firing rate data for two competing populations of neurons. The model assumes that information from the stimulus drives two accumulators that are independent diffusion processes. The accumulation rates driving the two processes sum to a constant so that the more evidence there is for one response, the greater the accumulation rate in that accumulator and the smaller the accumulation rate in the other accumulator. But once these accumulation rates are set for a particular trial, the two diffusion processes proceed independently. The accumulation process is highly variable, and this allows the process to make errors. The model is fit to the behavioral data and simulated paths are generated from the model. The assumption linking the paths to the single-cell firing data are that firing rate is linearly related to position in the accumulation process.
In previous work, Ratcliff, Cherian, and Segraves (2003a) (see also Ratcliff 2001b) collected neural recordings from the superior colliculus (SC) in a task that required the monkeys to decide whether the separation between two dots was large or small. The response was made by a saccade to one of two target lights to the left and right of the stimulus dots. One target light was located in the middle of the receptive field of a SC build-up cell and the other at a mirror image position. Behavioral difficulty was varied by providing variable feedback in which large and small separations were rewarded for large and small responses with probability 0.98, but separations in the middle were rewarded with intermediate probabilities. Ratcliff and colleagues (2003a) then fit a diffusion model (Ratcliff 1978, 1988, 2002; Ratcliff and Rouder 1998; Ratcliff et al. 1999) to the behavioral data, namely accuracy, and RT distributions for correct and error responses. They then showed that simulated sample paths of the diffusion model, derived from fits of the model to behavioral data, were able to predict the build-up of discriminative information in the neural firing rates. Unlike the dual diffusion model presented here, however, the model did not predict firing rates for the populations of neurons corresponding to the two choices.
More specifically, the diffusion model used by Ratcliff and colleagues (2003a) assumes a noisy accumulation process in which a single accumulator integrates information toward either of two decision criteria. The decision process was simulated using the parameters obtained from fits to the behavioral data and position in the process was used as an analog of firing rate. The model was able to predict the growth of information that discriminated between the two decisions, i.e., the difference in firing rates between the target and competing neurons. Specifically, the firing rate data were aligned either on the stimulus onset or on the saccade, and the firing rate data were divided into three groups depending on the behavioral RT, i.e., firing rates for the fastest third, intermediate third, and slowest third of the responses (cf., Hanes and Schall 1996; Sato et al. 2001). Discriminative information was obtained by subtracting the firing rate for neurons corresponding to the response and neurons corresponding to the competitor. The analysis showed delayed onset of discriminative information among the groups corresponding to fast, intermediate, and slow responses when firing rates were aligned on the stimulus, but there was little difference in the growth of discriminative information for the three groups when aligned on the saccade.
The diffusion model was able to fit these patterns of data reasonably well. The intuition behind this is that the model requires a great deal of variability in the accumulation process to produce both correct and error responses with a fixed drift rate driving the process, i.e., there has to be enough noise for the process to hit the correct boundary on some trials and the error boundary on other trials. Also when a process approaches a decision criterion, it is quite likely that it exits the process because variability is high. This means that processes that remain in the decision process for a long time have an average position near the starting point. Thus there is delayed availability of discriminative information when the process is aligned on stimulus onset because processes remain on average near the starting point. Also there is little difference in the growth of discriminative information when the process is aligned on the decision.
Despite the ability of the model to fit the growth of discriminative information, it is unable to fit the separate firing rate functions for the neurons corresponding to the two decisions. Although the diffusion model might be seen as a model of the difference between two processes separately accumulating evidence, no analysis that would connect the single diffusion process to two racing processes was presented.
Our aim in this article is to present a model closely related to the diffusion model, a dual diffusion model, in which evidence is accumulated in two separate accumulators. Other research has found that this model mimics the diffusion model over a number of sets of experimental data (Ratcliff and Smith 2004; and data from Ratcliff et al. 2004c), but comprehensive comparisons over a wider range of parameter values than those obtained in fits to existing data sets have not been carried out. The aim is to fit the behavioral data and then use the parameters to generate simulated paths of the processes in the two accumulators. The positions of the processes in the two diffusion processes are assumed to be the analog of firing rates. The nearer the position to a decision criterion, the higher the firing rate.
In a purely behavioral approach to the results we report, any shortcomings of the model would be supplemented with additional hypotheses to allow the model to better fit the data. But because we have both behavioral and neural data, so long as the model captures many of the phenomena in the data, misses between the model and data can focus attention on what might be key aspects of the data that require additional mechanisms to those already represented in the model. Such additions will provide a more accurate description of behavior and its neural substrates.
Preliminary reports of these findings have appeared in abstract form (Hasegawa et al. 2003, 2004).
METHODS
Animals and surgery
Two female adult rhesus monkeys (Macaca mulatta) were used for these experiments. Northwestern University’s Animal Care and Use Committee approved all procedures for training, surgery, and experiments performed. Each monkey received preoperative training followed by an aseptic surgery to implant a subconjunctival wire search coil, a plastic cilux recording cylinder aimed at the SC, and a titanium receptacle to allow the head to be held stationary during behavioral and neuronal recordings. All of these methods have been described in detail elsewhere (Dias and Segraves 1999; Helminski and Segraves 2003). Surgical anesthesia was induced with the short-acting barbituate thiopental (5–7 mg/kg iv) and maintained using isoflurane (1.0 –2.5%) inhaled through an endotracheal tube.
Behavioral task
The behavioral task was designed to satisfy a number of criteria. First, we wanted to use a different task than that used by Ratcliff and colleagues (2003a) to determine whether the empirical results obtained in that study replicated across stimuli and tasks and to allow us to argue that the decision process is not dependent of the specifics of the stimulus and task. Second, we wanted to use a task that had been successfully used in the human literature, both experimentally and as the basis for model fitting. Third, we wanted a task in which the stimulus did not vary on the same dimension as was used to make the response. The task we chose was a brightness-discrimination task. In the majority of earlier studies of decision-making in monkeys, the stimulus and response often have a strong spatial correspondence. For example, in a stimulus-detection task, a single light is presented with the required response an eye movement to it (Hanes and Schall 1996). The spatial location of the light is the same location as the target of the saccade. In a visual-search task, several dots are arranged in a circle, and when one of them changes color, the required response is a saccade to the location of the dot changing color (Bichot et al. 2001; Schall et al. 1995; Thompson et al. 1996). In other experiments, some aspect of the stimulus information physically indicates the response to be made. For example, in the random dot motion task, stimulus dots move in the direction of the saccade target (Horwitz and Newsome 2001; Newsome et al. 1989; Roitman and Shadlen 2002; Shadlen and Newsome 2001). In the task used by Ratcliff and colleagues (2003a), the separation of the dots was the stimulus dimension that determined which response was to be rewarded, but the vertical separation did not point in the direction of the response target. In the brightness-discrimination task, the brightness of the patch does not contain any spatial content.
The experiments in which the response is correlated with the stimulus suggests views of processing in which visual information flows through the system with little transformation. Thus if cells are driven by multiple factors, for example, if they are visually responsive while also increasing their firing rate during the guidance of motor activity, then based on the decision made about the stimulus, if the cell’s receptive field contains the target, it may be difficult to identify the factor responsible for increasing firing rates. This means that both sources are potentially telling the system the same thing, and it is hard to separate decision processes from stimulus information (but see Basso and Wurtz 1998). Although such cells do not usually fire unless the stimuli are relevant for planning saccades to a target inside the response field of the neuron, when the stimuli are relevant, it might be possible for some leakage to occur. With our paradigms, because visual information is uncorrelated with the response and visual stimulus information, no part of the differential increase in activity of a population of cells corresponding to one of the two decisions could be attributed to such leakage. This means that these paradigms are capable of providing information about decision processes that are decoupled from the stimulus information.
In this study, each monkey was trained to make a conditional saccade based on a brightness discrimination (Fig. 1A). After the monkey had fixated a small central spot (yellow spot; 0.25° diam) for 500 –1,000 ms, two peripheral targets appeared and remained on for the duration of the trial. The targets were located opposite to one another with one in the left hemifield, the other in the right hemifield. After an additional 800 ms of fixation, a brightness stimulus was presented at the central fixation point. The brightness stimulus consisted of a 2 × 2° square of white and black pixels. The monkey was free to make a saccade to one of the targets as soon as the stimulus appeared and was allowed ≤ 500 ms after stimulus appearance to complete the saccade. For the brightness-discrimination task, saccades to the target in the left hemifield were linked to discrimination of a bright stimulus and saccades to the target in the right hemifield linked to discrimination of a dark stimulus. A correct response was rewarded with a drop of water. Trials with saccades made to either response target light were scored as valid and included in the data used for this report, regardless of whether the saccade was rewarded or not. Trials in which the monkey failed to make a saccade, made a saccade that did not terminate at either response target, or made a saccade in < 120 ms after stimulus appearance were rejected.
FIG. 1.
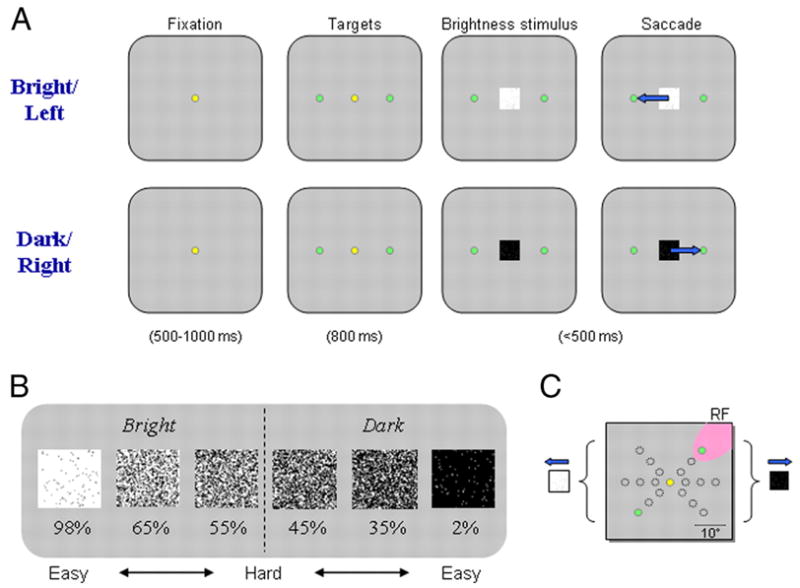
Oculomotor bridghtness-discrimination task. A: representative trials of the task for leftward/bright and rightward/dark responses. Each trial was initiated by fixation of a central spot (yellow dot) for 500 –1,000 ms. Next, 2 peripheral targets (green dots) appeared, 1 in each hemifield. After continued fixation of 800 ms, the brightness stimulus (square) was presented at the fixation point. Beginning with the appearance of the stimulus, the monkey was required to make a saccade, within 500 ms, to one of the peripheral targets, based on a discrimination of the brightness stimulus. For “bright” stimuli, saccades to the leftward target were rewarded, and for “dark” stimuli, saccades to the rightward target were reinforced. B: brightness stimuli. Task difficulty was manipulated by varying the percentage of white and black pixels. Numbers beneath the stimuli reflect the percentage of white pixels in the stimulus. C: pair of peripheral target locations were adjusted to place one target in a neuron’s response field (RF, shaded). The remaining target was positioned at a symmetric location in the opposite hemifield.
For the initial training on the brightness-discrimination task, we varied the ratio of pixels to create two stimuli with 95% black or white pixels. The monkeys required seven to nine training sessions to reach a performance level of ≥ 75% on this simplified version of the task. We then switched their training to the task with full range of difficulty levels, where the ratio of black and white pixels was adjusted to create three levels of difficulty for both bright and dark stimuli (easy, middle, and hard – e.g., 98, 65, 55% white or black pixels; Fig. 1B). The gray-colored background luminance was set to be the same as would be achieved with a 50% white pixels stimulus. These conditions were run in a pseudorandom fashion, using a shuffling algorithm to ensure that there would be a nearly equal number of trials for each condition. Unlike the variable reward probability introduced by Ratcliff and colleagues (2003a) to raise the level of difficulty, reward contingency remained constant across all brightness levels in the present experiments. As a result, brightness level was the only manipulation affecting task difficulty, and it was possible to achieve a success rate of 100% correct, rewarded trials for all stimulus conditions although the data show this did not happen.
During training, we presented nine pairs of target locations that were in three orientations (45° spacing) at three eccentricities (5, 10, and 15° away from the fixation point) in separate blocks (Fig. 1C). We used the REX system (Hays et al. 1982) running on a PC computer for behavioral control and eye-position monitoring. Visual stimuli were generated by a second PC controlled by the REX machine and rear-projected onto a tangent screen in front of the monkey by a CRT video projector (Sony VPH-D50, 75-Hz noninterlaced vertical scan rate, 1,024 × 768 resolution).
Recording
The location of the SC was confirmed by stereotaxic coordinates, the response properties of isolated neurons, and the characteristics of its topographically organized visual/motor map. We recorded from neurons in the deep layers of the SC. In this report, we define deep layers as all collicular layers located below the superficial layers (superficial gray and stratum opticum), including the intermediate and deep gray layers. Assurance that the neurons included in this study were confined to the deep layers of the SC is based on the fit of our electrode penetrations to the highly reproducible map of the SC, the ability to evoke saccades from our recording sites with current intensities of < 50 μA, and the match of recorded activity to established cell activity types in these layers (Cynader and Berman 1972; Mays and Sparks 1980; Munoz and Wurtz 1995; Robinson 1972). The recording of single- and multiunit activity was done with tungsten microelectrodes (A–M Systems) introduced through stainless steel guide tubes that pierced the dura, using a Crist grid system (Crist et al. 1988). A 16-channel Plexon system was dedicated to on-line spike discrimination and the generation of pulses marking action potentials, which were stored by the REX system. The Plexon system could isolate two neuron waveforms from each electrode. We normally used one or two electrodes for recording from a maximum of four neurons. A gap saccade task was used to aid in the classification of neurons based on established criteria (Munoz and Wurtz 1995). The gap task began with a variable period of fixation; after the disappearance of the fixation light, a gap period of 400 ms was inserted before the appearance of the peripheral target light. When the peripheral target appeared, the monkey was required to make a saccade to it within 500 ms and was rewarded after the completion of the correct movement. The gap task was also used to map the response field (RF), within which the maximal response was obtained. The neurons included in this study were all located in the saccade-related region of the SC and were chosen, in part, based on their exclusion of any responsiveness to a central visual stimulus. After the RF was defined by checking the on-line histograms in the REX system, we switched to the brightness-discrimination task, in which we presented one target in the RF (preferred location) and the other at a nonpreferred location set to the same amplitude and rotated 180° from the preferred location (Fig. 1C). Every difficulty condition for both bright and dark stimuli was tested > 30 times.
RESULTS
Behavioral results
For all 64 experimental sessions (37 in monkey 11 and 27 in monkey 12), the monkeys showed a smooth change in behavioral response as a function of stimulus brightness (Fig. 2, Table 1). The monkeys performed the task at a near perfect level when the stimulus was very bright (98% of white pixels) or very dark (2% of white pixels). On the other hand, their performance was in the range of 60 – 65% accuracy when the stimulus was only slightly bright (55%) or slightly dark (45%). The intermediate stimuli (65 or 35%) were associated with performance at a level of 80 –90% accuracy. These results convinced us that a monkey’s level of behavioral accuracy was dependent on the brightness of the central stimulus. The mean RT (saccadic latency referenced to appearance of the brightness stimulus), however, was fairly stable across the various difficulty conditions in both monkeys (206 ± 33 ms, n = 16,551 correct trials for monkey 11; 239 ± 61 ms, n = 8,209 correct trials for monkey 12), suggesting that the monkeys might have put more emphasis on a rapid response than on accuracy. Although one-way ANOVA for effect of brightness on saccadic latency was significant for both monkeys (P < 0.001), the range of this effect was small (monkey 11: 25 ms; monkey 12: 19 ms).
FIG. 2.
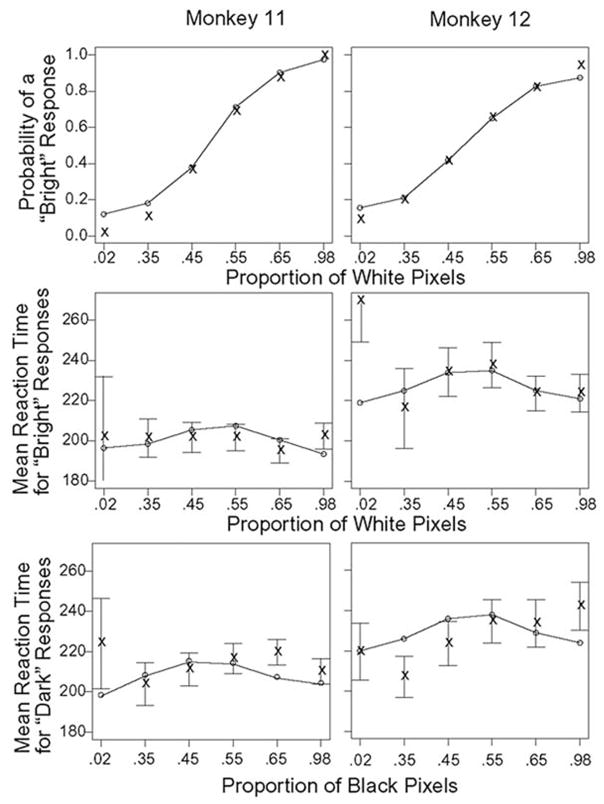
Mean accuracy and response time values for each monkey in the brightness judgment experiment. ×, data; ○-○ model’s best predictions. Bars represent ± 2 SE.
TABLE 1.
Effects of stimulus brightness on accuracy and saccade latency
| Trials
|
||||
|---|---|---|---|---|
| Brightness | Correct | Total | Percent Correct | Saccade Latency |
| Monkey 11 | ||||
| 2% | 2762 | 2817 | 98 | 208 ± 31 |
| 35% | 2751 | 3093 | 89 | 219 ± 34 |
| 45% | 2746 | 4308 | 64 | 215 ± 36 |
| 55% | 2755 | 4156 | 66 | 198 ± 34 |
| 65% | 2799 | 3263 | 86 | 194 ± 32 |
| 98% | 2738 | 2781 | 98 | 200 ± 35 |
| Average | 2759 | 3403 | 206 ± 33 | |
| Monkey 12 | ||||
| 2% | 1363 | 1472 | 93 | 249 ± 63 |
| 35% | 1361 | 1623 | 84 | 242 ± 64 |
| 45% | 1350 | 2260 | 60 | 242 ± 64 |
| 55% | 1364 | 2091 | 65 | 243 ± 62 |
| 65% | 1428 | 1734 | 82 | 230 ± 58 |
| 98% | 1343 | 1430 | 94 | 230 ± 56 |
| Average | 1368 | 1768 | 239 ± 61 | |
Values are means ± SD.
Effect of task difficulty
We recorded 137 neurons with presaccadic activity in the SC of the two monkeys (82 neurons from monkey 11; 55 neurons from monkey 12) while they performed the oculomotor brightness-discrimination task. The analyses included data from all cells identified as build-up cells by exhibiting build-up activity in the gap-saccade task. Build-up activity was monitored during the final 200 ms of the gap period, before the appearance of the target light, in a gap saccade task, and compared for significant increases (Wilcoxon sign-rank test, P < 0.05) above fixation period activity measured during the final 200 ms before the disappearance of the fixation light and beginning of the gap period. Figure 3 illustrates how the activity of a right SC neuron varied according to task difficulty. In the brightness-discrimination task, the cell exhibited strong activity after the appearance of “bright” stimuli instructing the monkey to make a saccade to the leftward target. The level of this activity for bright stimuli was similar for each of the three levels of difficulty (Fig. 3, A, C, and E). In contrast, the neuron’s activity generated after the appearance of “dark” stimuli instructing rightward saccades appeared to be modulated by task difficulty. The peak and mean frequencies of this activity increased as the task became more difficult (Fig. 3, B, D, and F). Thus a manipulation of task difficulty, induced by changing the brightness level of a central stimulus, altered the level of presaccadic activity for a collicular neuron with a peripheral activity field.
FIG. 3.
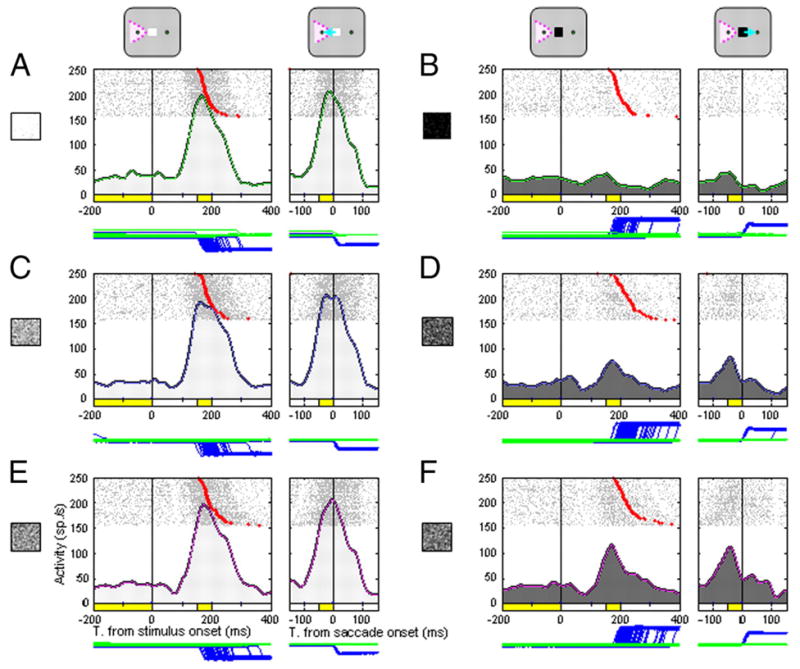
Activity of a superior colliculus (SC) neuron during the oculomotor brightness-discrimination task. Trials are synchronized to the appearance of the brightness stimulus (left, vertical line through each histogram) or the saccade onset (right). For rasters aligned to stimulus appearance, the red symbol in each trial indicates the beginning of the saccade. A, C, and E: trials where the monkey correctly identified a bright stimulus and made a leftward saccade into the neuron’s response field. B, D, and F: trials where the monkey identified a dark stimulus and made a rightward saccade away from the neuron’s response field. A and B: easy condition. C and D: middle condition. E and F: hard condition. The spike density histogram below each raster was generated by first convolving single trial neuronal activity using a Gaussian kernel with a sigma of 10 ms (Richmond et al. 1987), then averaging the spike density profile across trials. The eye position is shown as blue (horizontal) and green (vertical) traces under each histogram.
To quantify the magnitude of the activity for the neuron shown in Fig. 3, we measured activity during a stimulus-aligned and presaccadic epoch and plotted the average activity in relation to task difficulty (Fig. 4A). A two-way ANOVA with respect to decision content (bright/left and dark/right) and task difficulty (easy, middle, and hard) on activity during stimulus-aligned and presaccadic periods revealed that for both periods, there was a significant (P < 0.001) interaction between those factors; the effect of task difficulty was significant for dark/nonpreferred direction activity (P < 0.001) but not for bright/preferred direction activity (P > 0.05). Figure 4B plots data for another SC neuron that also exhibited a similar asymmetric modulation of activity. For this neuron, the preferred direction was rightward and linked to the “dark” stimulus.
FIG. 4.
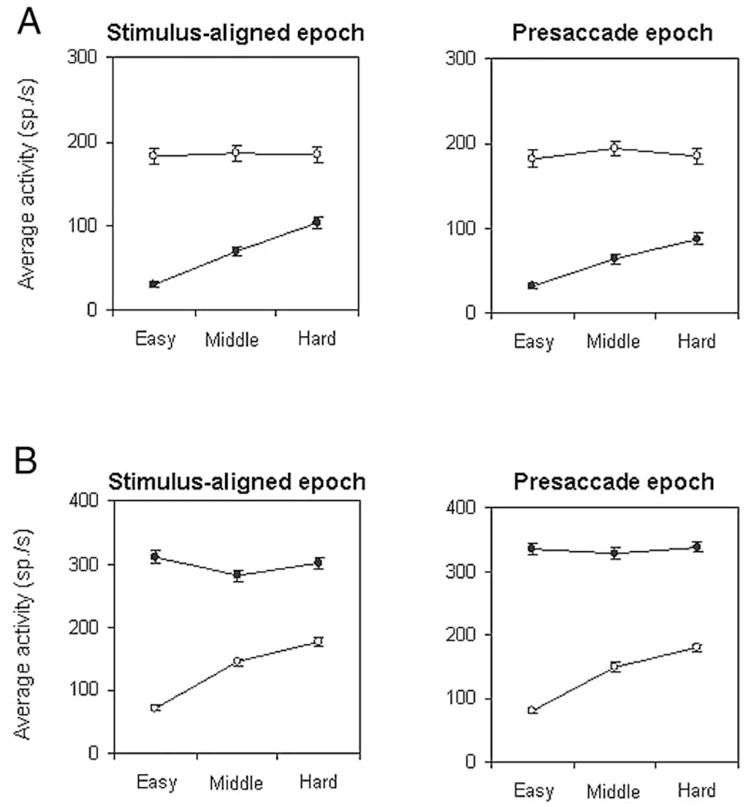
Two examples of the effect of task difficulty on neuronal activity. A: averages (± SE) of the activity of the neuron in Fig. 3 during the stimulus aligned epoch (left; 50 ms interval extending from 150 to 200 ms after the appearance of the brightness stimulus) and during the presaccadic epoch (right; 50 ms interval extending from 50 to 0 ms before the start of the saccade) are plotted against the different levels of task difficulty. ○ and ●, brighter and darker stimuli, respectively. B: another set of averages of activity for a neuron the response field of which was in the right hemifield. For this neuron, darker stimuli were linked to its preferred direction.
It is possible that this asymmetric modulation of activity could have been related to a selectivity for either the bright or dark range of brightness stimuli. We found, however, that the direction associated with modulation of activity was restricted to the nonpreferred location regardless of whether the trial included a bright or dark stimulus. We compared the magnitude of activity between easy and hard conditions at preferred and nonpreferred locations (Fig. 5). Our sample included 49 neurons whose preferred direction was to the left (bright stimulus), and 48 neurons whose preferred direction was to the right (dark stimulus). We restricted our sample to those neurons with average peak firing rates > 100 spike/s to determine whether firing rates for the nonpreferred direction approached zero for easy stimuli when the firing rate in the cells were high. Across the sample, activity during the presaccadic epoch was significantly greater for hard compared with easy conditions for the nonpreferred direction (Wilcoxon sign-rank test, P < 0.001). This bias was not seen for the preferred direction. We obtained similar results for activity measured during the stimulus-aligned epoch. The results of this analysis for the entire sample also held true in a cell-by-cell analysis. For each cell, we compared activities between easy and hard conditions. Although most neurons (94%, 91/97) did not show a significant (Mann-Whitney U test, P < 0.05) difference for the preferred direction, 60% (58/97) showed significantly greater activity for the difficult versus easy conditions in the nonpreferred directions. The activity for the nonpreferred direction peaked earlier than for the preferred direction (means of 33 vs. 9 ms prior to saccade onset). This can be seen for the cell illustrated in Fig. 3, where the saccade-aligned plots show that activity for the preferred direction sites continued to rise toward its peak after the activity for the nonpreferred direction had peaked and was beginning to fall. Across the sample of neurons such relatively earlier peaks for the nonpreferred direction sites were significant (Wilcoxon sign-rank test, P < 0.001).
FIG. 5.
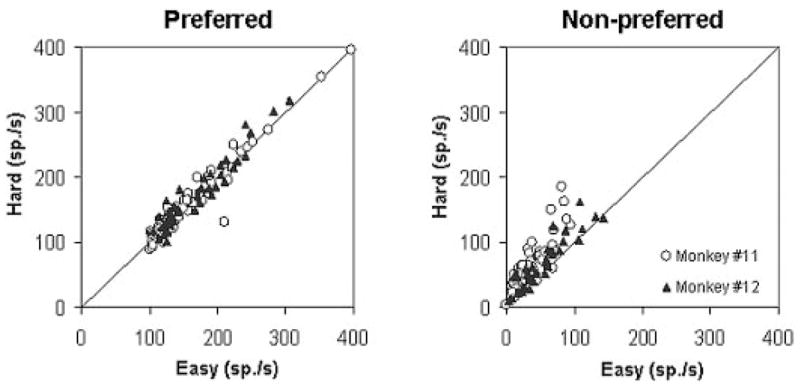
Effect of task difficulty on activity across the population of neurons. A pair-wise comparison (easy vs. hard) of average discharge rate in the 50-ms interval immediately before the saccade onset is shown. Each symbol represents activity for a single neuron. For the preferred direction (left), activity was similar for easy and hard conditions. For the nonpreferred direction (right) activity associated with the hard condition tended to be greater than it was for the easy condition.
To summarize the experimental results of this investigation: 1) the behavioral data show that accuracy declines as a function of difficulty and mean RT varies little as a function of difficulty. 2) Neural firing rates for neurons associated with the response build up rapidly prior to the saccade at about the same rate and to the same peak activity for all the conditions. 3) Neural firing rates for neurons associated with the competing response vary as a function of difficulty. The firing rate is low for the easy conditions and the firing rate increases with difficulty of the decision. This means that peak activity is correlated with accuracy. 4) The activity of neurons corresponding to the response peaks about 10 ms prior to the start of the saccade, while the peak activity of neurons corresponding to the competing response peaks ~ 35 ms prior to the saccade.
Dual diffusion model
Our model assumes that the decision process involves two racing diffusion processes as shown in Fig. 6. Figure 6 also shows the equation for the evolution of evidence as a function of time in the model along with a list of the parameters of the model. Evidence corresponding to the two decisions is accumulated in two separate accumulators each with a separate decision criterion (ca and cb). The accumulation process is very noisy, and noise is assumed to be normally distributed as in the Wiener diffusion process (e.g., Ratcliff 1978). Because we are using evidence in the accumulation process to mimic firing rates, it is assumed that evidence cannot go below zero. If an update to evidence in the process would have taken it below zero, it is reset to zero. The rate of accumulation of evidence varies as a function of difficulty in the task, but it is assumed that the sum of the rates for the two accumulators is constant across conditions (i.e., they are negatively correlated), this means, if one has a high drift rate, the other has a low drift rate. This assumption means that the total rate of information accumulation is the same across conditions. This assumption leads to one parameter for the sum of drift rates and one parameter for the drift rate for one accumulator for each condition; the other drift rate is the difference between the sum and the drift rate for the other accumulator.
FIG. 6.
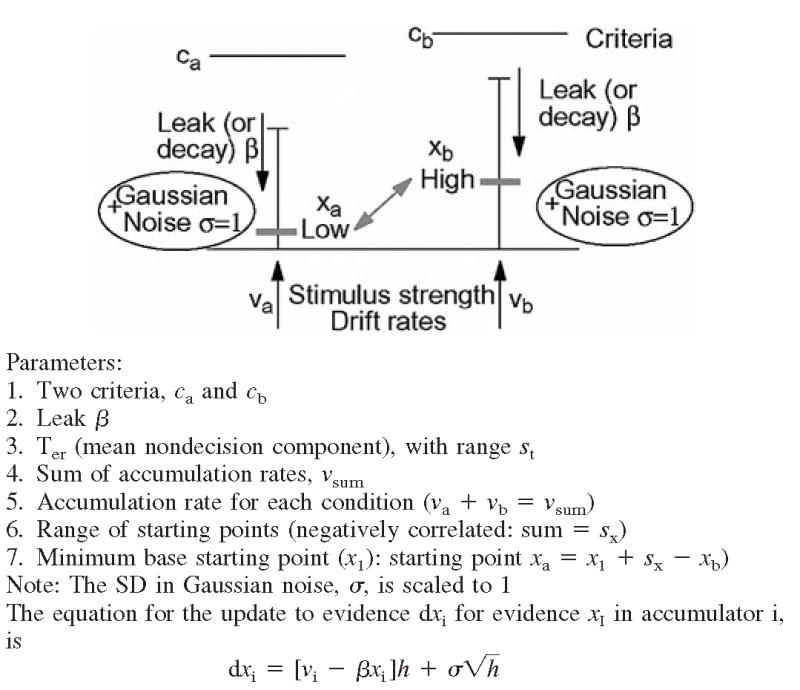
Illustration of the dual diffusion model and the parameters of the model. There are 2 accumulators with decision criteria ca and cb, accumulation rates va and vb (va + vb = vsum), starting points xa and xb (a random number x is selected from a uniform distribution with range sx and lower limit zero, and xa = x + xI and xb = sx − x + xI, where xI is a minimum baseline starting point), and decay rate (− βx). The equation for the update of evidence in accumulator i (dxi) at the bottom of the page has time steps of size h, set to 1 ms in the fits of the model to the behavioral data. Variability in processing within a trial (Gaussian noise) is normally distributed with SD σ= 1. Across trials, the nondecision components are uniformly distributed with mean Ter and range st.
An assumption in most of the recent modeling (see Ratcliff and Smith 2004) is that components of processing vary from trial to trial. This means that many of the parameters have a distribution of values associated with them. This trial-to-trial variability of parameters for some of the models is necessary to explain complex patterns of error versus correct RTs. Specifically, to produce fast errors, the diffusion model assumes variability in starting point from trial to trial (Laming 1968; Ratcliff et al. 1999). The dual diffusion model does not produce fast errors except in the most accurate conditions even with variability in starting points. If we assume that the starting points are negatively correlated, then fast errors that are obtained in some paradigms can be obtained. Negatively correlated starting points means that there is an initial bias toward one response alternative and a bias against the other. Specifically, we selected a random number, x, from a uniform distribution with range sx. The one starting point was xa = x + xI and the other was xb = sx − x + xI, with xI corresponding to a minimum baseline starting point. The way to interpret this negative correlation is that prior to the decision process there is a bias that could be produced by biases in outputs from upstream processes or biases left over from prior trials. This assumption allows this dual diffusion model to produce fast errors and so allows it to mimic Ratcliff’s diffusion model in application to human data.
To produce slow errors, the diffusion model (Ratcliff et al. 1999) assumes that drift rate is variable from trial to trial. Initial fits to the behavioral data from this study that included variability in drift rates produced estimates of variability that were small and so variability in drift was set to zero for subsequent fits.
As noted earlier, there is a great deal of variability within trials due to intrinsic noise in the accumulation process. This variability is necessary to produce error responses even when drift rates are high. Figure 7 illustrates variability in processing by presenting four simulated paths of the two diffusion processes. In two cases, the process represented by the black line wins, whereas in the other two cases, the process represented by the green line wins. The negative correlation in starting points can be seen in the initial starting levels: when one is high, the other is low. To model firing rates after a saccade is made, we assume when one process terminates, evidence decays back to the starting level.
FIG. 7.
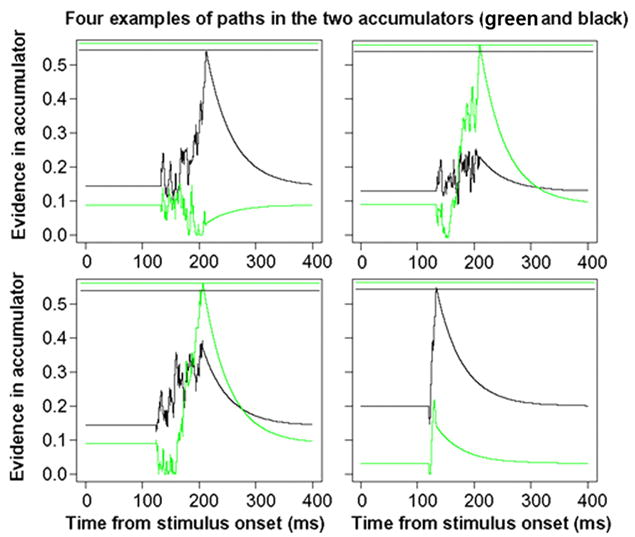
Examples paths of the accumulation of evidence for the same accumulation rate for each diffusion process. The 2 horizontal lines at the top of each panel represent the decision criteria (black for the black accumulator and green for the green accumulator).
For neural plausibility, it is often assumed that there is decay in evidence so that the amount of evidence is decremented by an amount in proportion to the evidence in the accumulator. We allowed decay in this model, but in fits to the data, we were able to produce the same quality of fits with decay set to zero. But as we see later, modulation of the size of this decay can account for some misses in model predictions and can potentially account for resting levels of evidence in the accumulators.
The nondecision components of processing are combined into a single parameter Ter which is assumed to be variable from trial to trial. Ratcliff and Tuerlinckx (2002) assumed a uniform distribution of variability with range st. A uniform distribution was assumed because it was simple and because convolution with a decision time distribution with larger SD produces a distribution with shape about the same as that of the decision time distribution. This means that the assumption about the shape of the distribution of nondecision components does not affect predictions of the model so long as the SD is three or more times smaller than that of the decision component.
One key feature of this model that is addressed later is that the stimulus information that drives the decision process is stationary. It assumes that prior to the decision process, there is no evidence accumulation. Then during the decision process, the mean and variance of the stimulus information driving the decision process both remain constant during the time taken to make a decision. For this experiment, it is natural to assume that the stimulus provides a constant perceptual representation that drives the decision process. However, in other work in which a stimulus is presented briefly and masked, we have conceptualized perceptual processing as producing a short-term memory representation of the relevant characteristics of the stimulus that then provides constant drift rate to the decision process (Ratcliff 2002; Ratcliff and Rouder 2000; Smith et al. 2004). Thus during the decision process, all the parameters of the process are constant over time. Then when one of the processes reaches a decision criterion, the decision is made (response output processes are initiated), and evidence decays back to the initial level. The view that perceptual processing produces a representation in memory that drives the decision process means that in our conceptualization, the stimulus is not simply directly tied to the decision process. This also suggests that issues of how stimuli are represented and how the representation drives the decision process need to be understood. Later, we will discuss relaxing some of these stationarity assumptions to better account for misses between predictions of the model and firing rate data.
A model very similar to this model is the leaky competing accumulator model of Usher and McClelland (2001) that has two accumulators with Gaussian distributed noise (i.e., 2 racing diffusion processes) and with decay in evidence. However, each accumulator is assumed to inhibit the other accumulator by an amount proportional to the evidence in the accumulator. We also fit this model, but decay and inhibition were modest in size, and the fits were qualitatively and quantitatively similar to those presented here. We take up this model in the general discussion. Also, versions of the dual diffusion model have been considered by Smith (2000) and by Ratcliff and Smith (2004).
Behavioral data fits
To generate predictions for fitting the model to data, the dual diffusion process is simulated with step size 1 ms (see Brown et al. 2006). To produce a set of accuracy and RT predictions for one condition and one set of parameter values, 20,000 simulations of the process are performed. This is repeated for each of the conditions in the experiment (for 6 different drift rates) to produce a set of predictions to be used to match the results for the six conditions in the experiment.
We fit the model to the behavioral data using the χ2 method presented in Ratcliff and Tuerlinckx (2002). In this method, a χ2 statistic is computed from both predictions and data to represent goodness of fit of the model to data. An iterative nonlinear minimization routine (SIMPLEX) (Nelder and Mead 1965) is used to minimize χ2 by adjusting parameter values. The fitting routine begins with an initial set of parameter values and a range for each of the parameter values (in our case, 10% of the parameter value). The algorithm produces n + 1 sets of parameter values based on the mean and ranges in the parameter values and then computes n + 1 χ2 values. The largest value of χ2 is selected, parameter values are adjusted, and the χ2 value is recomputed. The largest value of χ2 is again selected (which may or may not be a different one) and parameter values again adjusted until the process creeps toward a minimum χ2 value.
The parameter spaces of stochastic models of this kind have not been explored theoretically. For example, Usher and McClelland (2001) used a simulated annealing fitting method to produce fits to the data from a few experiments. This was done to address two main concerns, namely, that the model fitting process might fall into local minima or into regions where changes in parameter values do not change chi-square values. To allow our fitting program to deal with such problems, we ran the simplex minimization six times in succession using the parameters of the previous fit as the starting values with the original 10% ranges in the values. This was an attempt to functionally mimic Usher and McClelland’s method.
There was one parameter that was adjusted to attempt to produce better fits to the neural firing data, and that was the baseline level of activity in the accumulators. This was adjusted in a series of exploratory fits so that the baseline positions in the accumulators roughly match baseline activity in the firing rate functions so that the relative size of the baseline to peak positions matched those for the firing rate functions.
Figure 2 presents the fits of the model to accuracy and mean RT. Tables 2 and 3 present the parameter values of the model for the fits. The top two panels of Fig. 2 present the probability of the bright response as a function of the proportion of white pixels in the stimulus display. The model fits the accuracy values well except for the two dark stimuli for monkey 11 and the extreme stimuli (2 and 98% white pixels) for monkey 12 (maximum discrepancy of ~ 4 –5%). The bottom four panels of Fig. 2 show mean RT as a function of the proportion of white or black pixels in the display. The error bars represent ± 2 SE. There are significant misses to several of the conditions. Two of most note are correct responses when the proportion of black or white pixels is 0.98, i.e., the easiest conditions. The data from these conditions are quite unlike those we see for human subjects. Invariably, the conditions with the highest accuracy are also the fastest. Here we find the most accurate conditions are a little slower than less accurate conditions. We do not understand why this might have occurred except to point our that these two conditions were trained first, for several sessions, before the conditions with the lower proportions of black or white pixels were introduced later in training. There are also significant misses in the error RTs in the extreme conditions (0.02 white or black pixels). Because there are very few of these errors, a few responses might have been produced by guesses when attention had wandered, and these would have been counted as errors that would produce longer RTs.
TABLE 2.
Parameters of the dual diffusion model
| Monkey | ca | cb | sx | x1 | Ter | st | β | vsum |
|---|---|---|---|---|---|---|---|---|
| 11 | 0.442 | 0.563 | 0.195 | 0.052 | 156.3 | 50.2 | 4.459 | 10.10 |
| 12 | 0.535 | 0.557 | 0.231 | 0.028 | 143.7 | 50.6 | 2.097 | 5.11 |
TABLE 3.
Relative drift rates
| Monkey | v1 | v2 | v3 | v4 | v5 | v6 |
|---|---|---|---|---|---|---|
| 11 | 0.997 | 0.909 | 0.714 | 0.450 | 0.229 | 0.011 |
| 12 | 0.999 | 0.893 | 0.623 | 0.360 | 0.107 | 0.010 |
In the model, each drift rate is assumed to be greater or equal to zero, and the sum of the drift rates for the two accumulators is a constant. It may be possible to obtained better fits to accuracy for the extreme conditions by allowing one of the drift rates to be negative (with the same constant sum), and we explore this possibility in the DISCUSSION.
Figure 8 includes quantile probability functions (Ratcliff 2001a; Ratcliff and Smith 2004) that show quantiles of the RT distributions plotted against the probability that the response is made to the stimulus. In the quantile probability functions shown here, data from “bright” and “dark” responses are plotted separately. Data for each stimulus are used to produce RT quantiles, and these are plotted vertically on the y axis and their location on the x axis is the probability of the bright or dark response. This method of presenting data was developed by Ratcliff (2001a) to allow response probability and the shapes of the RT distributions for correct and error responses to be all displayed in one plot and allow visualization of how the different dependent variables co-vary. The gray ellipses around some of the points provide a representative sample of 95% confidence intervals around the data (see Ratcliff et al. 2003a).
FIG. 8.
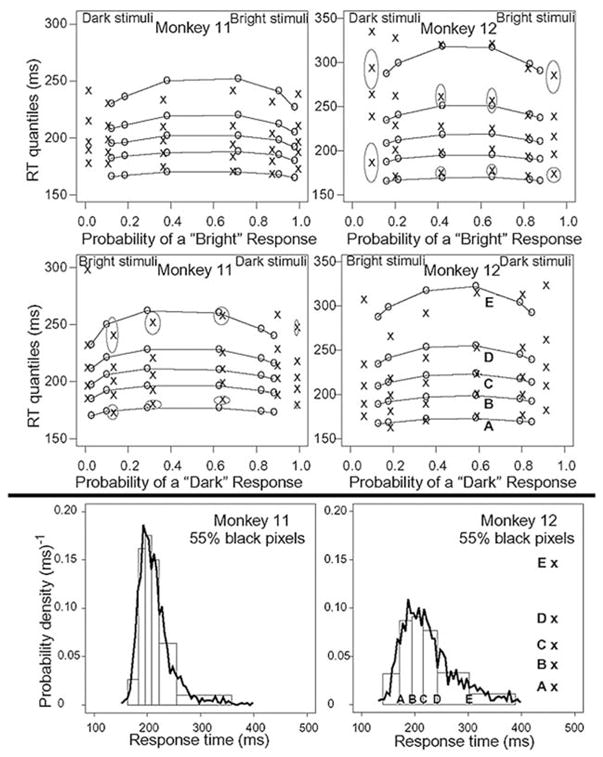
Quantile probability functions for each monkey (top 4 panels). The diffusion model (fitted values are ○, connected by —) were fit to the behavioral data (×). The 5 crosses in each column represent the 0.1, 0.3, 0.5 (median), 0.7, and 0.9 quantile response times for a particular condition. Their location on the x axis represents the probability that the response is made to the stimulus. The top 2 panels represent “bright” responses for stimuli with 2, 35, 45, 55, 65, and 98% white pixels moving from left to right across the figure. There are very few responses for the extreme error quantiles. To illustrate how the quantiles are related to RT distribution shape, the bottom 2 panels show RT distributions from 2 single conditions in the quantile probability functions above (see text for detailed description). The gray ellipses in the top four panels represent 95% confidence intervals on the quantile RTs and accuracy values. The SE is computed from the means across RTs and accuracy values across trials.
To illustrate how the quantiles are related to RT distribution shape, the bottom two panels show RT distributions from two single conditions in the quantile probability functions above, namely, correct dark responses for stimuli with 55% black pixels. The jagged lines are the histograms and the points labeled A–E in the middle right panel and on the x axis of the bottom right panel show the quantile RTs (the 2 extreme points to the left of A and to the right of E represent the 0.005 and 0.995 quantiles, respectively). Because there is a 0.2 probability mass difference between each of the 0.1, 0.3, 0.5, 0.7, and 0.9 quantiles, we can draw equal area rectangles between the points (the closer the quantiles, the higher the rectangles), and these are shown in the bottom two panels. They show that the histogram is well represented by the quantile density functions composed of the plotted rectangles. Because the pairs A–B and B–C are closer together than the points D–E and C–D, the distributions are right skewed as shown in the bottom panels.
Apart from the misses noted earlier, the general shapes of the RT distributions are captured by the model. In particular, both the empirical and theoretical RT distributions are skewed for all the conditions as can be seen by the wider separation of the 0.7 and 0.9 quantiles relative to the 0.1 and 0.3 quantiles.
In analyzing the data, we found that the monkeys had good days and bad days, i.e., mean RT could differ by 30 –50 ms between days. We produced two groups of data, one with faster days, the other with slower days. We fit the model to these two groups for the two monkeys and found that in each case, the only parameters that varied systematically were boundary setting, for the slower days it was 6% larger than for the faster days, and the sum of drift rates, which was 16% smaller for slow days than fast days. These two parameters do not trade off against each other because changes in boundary position produce changes in the leading edge of the distribution while changes in the sum of drift rates affects skew with only a very small effect on leading edge. Thus the model based interpretation is that on bad days, the monkeys get poorer information from the stimulus than on good days and adopt more conservative decision criteria than on good days.
It is possible to directly compare performance on human and monkey data on this brightness-discrimination task. In human data, accuracy is higher than for the monkey data. The human experiment (Ratcliff 2002; Ratcliff et al. 2003b) uses a presentation-time manipulation and a brightness manipulation as well as a speed-accuracy instruction manipulation. Presentation time does not have a large effect on performance, but as for the monkey data presented here, brightness has a large effect. The experiment here has the most difficult conditions with 0.45 and 0.55 white pixels, but in the human experiments, the conditions closest to these are 0.425, 0.475, 0.525, and 0.575 white pixels. Accuracy for the average of the 0.45 and 0.55 conditions for the monkey data are 0.65 and accuracy for the human data in the speed instruction condition is 0.75, and for the accuracy instruction condition, 0.80. We have fit the dual diffusion model to the human data, and the decision criteria are set to much larger values than for the fits to the monkey data (about double). If we increase the monkey decision criteria to the human speed instruction value, keeping all other parameters constant, the predicted accuracy value increased from 0.65 to 0.77, i.e., quite close to the human accuracy value.
Although the fits shown in Figs. 2 and 8 are not as good as those obtained for behavioral data for human subjects, they do capture most of the main features of the data. We now use them to produce predicted paths for the build up in evidence for the two accumulators.
Decision process paths and neural firing rates
To relate the dual diffusion model to the neural firing rate data, we make the simplest assumption: collicular build-up activity for the target and nontarget receptive fields correspond to the evidence in the two accumulators. The nearer the process is to the criterion, the higher the firing rate. The firing rate data presented are aggregates over trials for a single neuron and over sessions for different neurons. Thus the firing rate data are assumed to represent the behavior of the population of cells with build-up activity that are proposed to implement the decision.
To generate predicted average evidence in each accumulator (the analog of firing rates), we used the parameters of the model in Tables 2 and 3 to generate 2,000 simulated processes. These processes provide the amount of evidence in each accumulator as a function of time. The only parameter that was adjusted in fitting the behavioral data to accommodate the firing rate data is the initial level of evidence. This was adjusted manually in the process of fitting the behavioral data to produce initial levels of evidence that match the initial firing rates so that the relative differences between peak activity and baselines are similar to the firing rate data. Once one of the processes reaches a decision criterion, both processes are assumed to exponentially decay (with noise turned off) to the resting level with decay rates selected by eye to match the data (with exponential time constants 45 and 20 ms for monkeys 11 and 12, respectively). The other alignments that allow the model to predict the neural firing rate data involve aligning the functions on the time axis. Because the behavioral model combines encoding and response output (and other nondecision processes) into one parameter, this has to be divided up into a component prior to the decision process and a component after. This was done by eye, and for monkey 11, the estimate of the component of the nondecision component occurring after the presaccadic peak activity is 14 ms and for monkey 12, it is 10 ms. The other adjustment is vertical scaling from evidence to firing rate.
Firing rate data for RT tasks are typically plotted two ways (e.g., Hanes and Schall 1996; Roitman and Shadlen 2002), aligned on stimulus onset and aligned on the saccade (response initiation). There are small differences in mean RT across conditions and there are small differences in the initial onset of firing rates of neurons corresponding to the two decisions for both ways of plotting the firing rate data. In Ratcliff, Cherian, and Segraves (2003a), peak firing rates were about the same height across conditions in neurons corresponding to the decision made, but the peak firing rate in the neurons corresponding to the competing alternative becomes larger as the condition becomes more difficult [e.g., compare Fig. 8 of Ratcliff and colleagues (2003a) to Fig. 3 of this report].
Hanes and Schall (1996) grouped firing rate functions depending on the RT of the trial. This allowed the rate of growth of firing rates to be examined as a function of speed of the response. The patterns of results they obtained allowed more detailed qualitative tests of models of the growth of firing rate with time. Ratcliff, Cherian, and Segraves (2003a) found that when firing rates were aligned on the stimulus, firing rates for the fastest responses rose early in neurons corresponding to both the response made and the competing neurons. The initial rise was slower for slower responses. But the difference in the firing rates for neurons corresponding to the decision made and the competitor (the difference corresponding to discriminative information) was delayed for slower responses by as much as 80 ms (see also Sato and Schall 2001). For firing rates aligned on the saccade, there were differences in onset of firing rate functions prior to the saccade as large as 50 ms. But the growth of discriminative information (the difference in firing rates) was almost identical for firing rates corresponding to faster versus slower trials.
For data from this brightness-discrimination task, for firing rates aligned on stimulus onset, the functions for the fastest, middle, and slowest terciles rise at close to the same point in time but at different rates for both the target and competing neuron. Firing rates for the difference between the target and competitor represent the growth in discriminative information (both populations of neurons become active after stimulus onset, but information that discriminates between them can become available later), and this shows delays in onset for the slowest tercile relative to the middle tercile and the middle tercile relative to the fastest tercile. For data aligned on the saccade, the functions for the three terciles are similar. Only for the slowest tercile does the rise in activity begin a little earlier relative to the saccade and rise at a slower rate. The rise in discriminative information shows almost no difference between terciles.
This pattern of data suggests that on average, a successful model has to accumulate relatively little information prior to ~ 75–100 ms before the saccade initiation followed by a rapid build up, and this has to occur whether the stimulus to response duration is short or long. In the brightness-discrimination data presented in the following text, stimulus onset can be between 300 and 180 ms before the saccade for the first and third tercile, but the difference in the rise in discriminative information may only differ in onset by ≤20 ms.
We now show that the model fits the patterns of activity recorded in the brightness-discrimination experiment. After presenting the correspondence between the model predictions and neural firing rate data, we focus on the main misses between theory and data and how the model could be augmented to deal with these misses. As noted earlier, the model is stationary, that is, it assumes that the instant the decision process begins, the mean and variance of the stimulus information are both constant until the process hits a decision criterion at which point the decision process is over, that is, none of the parameters of the decision process change during the decision process. Augmentation focuses on how we might allow processes to be nonstationary which might better match what is known about the neurophysiology of this system.
Firing rates aligned on the stimulus
Figure 9 shows firing rate functions aligned on the stimulus for target and nontarget for correct responses (dark responses) for the 98% black pixel condition and 55% black pixel. The plots are for terciles of the data, that is, firing rate functions for the fastest third of the behavioral responses, the intermediate third, and the slowest third. For the activity for the target, the functions grow from ~ 100 ms after stimulus onset to peaks at ~ 180 and 200 ms for the first tercile to 220 and 270 ms for the longest tercile for monkeys 11 and 12, respectively. The predicted functions show about the correct relative heights and they decay at about the same rate as the data. But the functions miss in the initial rise, especially for monkey 12. For the activity for the nontarget, the peak activity levels for monkey 11 match, but for monkey 12, the peak is a little too high for the 55% black pixel condition and in all cases, the firing rates fall more quickly than the predictions. The results for the 65% black pixel condition fall between these shown here.
FIG. 9.
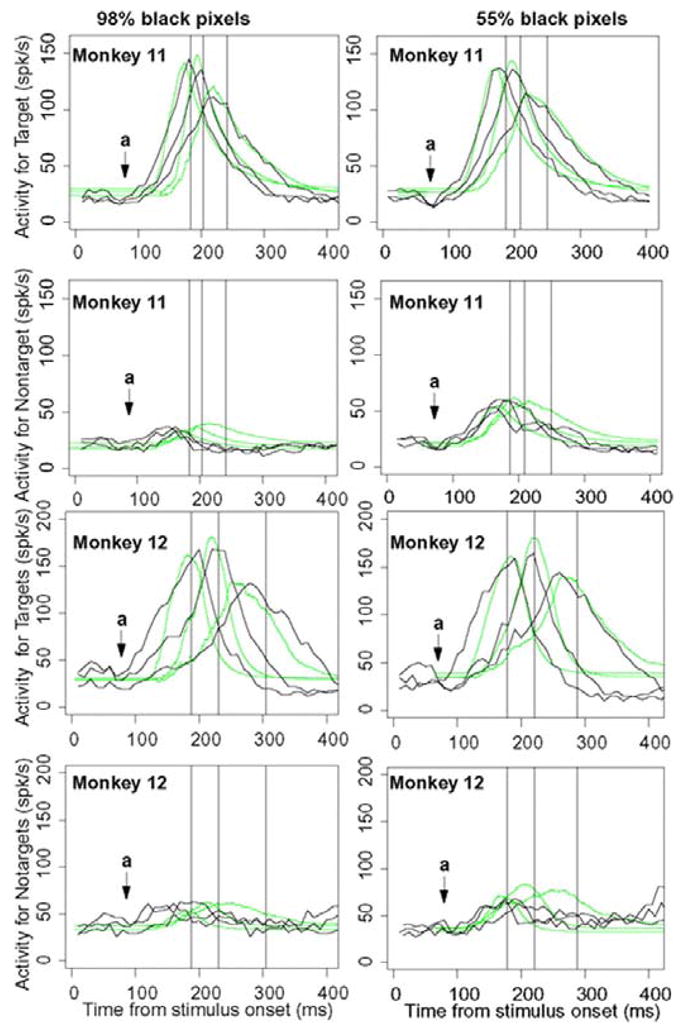
Neural firing rates averaged over cells and aligned on the stimulus. The firing rates are divided into thirds as a function the behavioral response (fastest third, middle third, and slowest third). Left: easy conditions, dark responses to 98% black pixels; right: difficult conditions, dark responses to 55% black pixels. First and 3rd rows: firing rates for cells the receptive field of which contained the target for the correct response when a correct response is made (target cell). Second and 4th rows: firing rates for cells the receptive field of which contained the target for the incorrect response when a correct response is made (nontarget cell). The solid lines are the data and the green lines are predictions from the dual diffusion model. The points marked “a” show what appears to be a suppression prior to the rise in activity leading to a decision. The vertical lines represent the median saccade initiation times for the 3 conditions.
There are other misses in the tail of the firing rate functions for monkey 12. A factor that is likely to contribute to this problem is that when the monkey moves its eyes to a target, there is no longer a target in the receptive field for the target neuron so activity will drop. Also, for the competing neuron, there is a large target (the stimulus) in its receptive field so activity can increase as is shown beginning at about 350 ms after stimulus onset (Fig. 9, bottom row).
Firing rates aligned on the saccade
Figure 10 shows the same firing rate data but aligned on the saccade. The predicted initial rises and peaks for correct responses to the targets match the data reasonably well, and the decay matches well. There are some misses in the initial rises on the order of tens of milliseconds, but overall the match between the empirical and theoretical shapes are reasonably good. The firing rate functions for the nontargets show a large and systematic miss. For the data, the competing functions produce bimodal functions (that appear in all the conditions) that rise to a peak and then dip ~ 20 ms prior to the saccade (dips marked by b in Fig. 10) and then rise again at the saccade to produce a second peak. The model can only produce a single peaked function. This dip also occurs in the data of Ratcliff, Cherian, and Segraves (2003a) (Fig. 10).
FIG. 10.
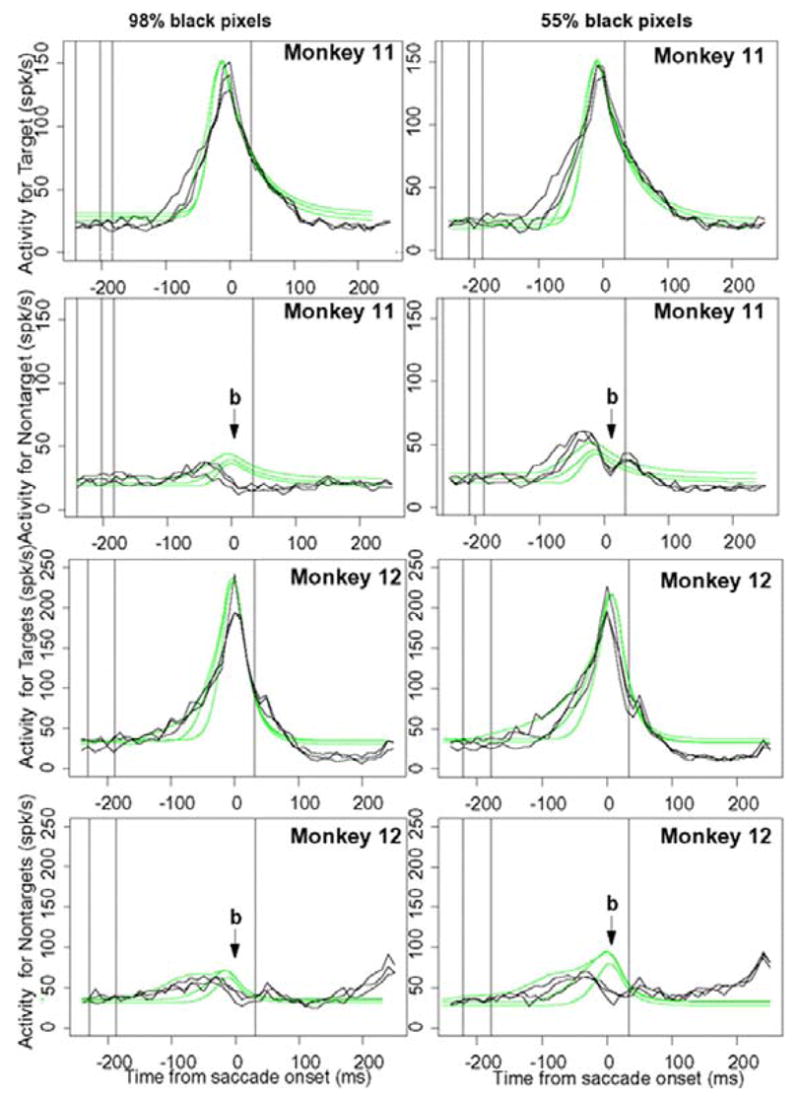
Neural firing rates averaged over cells and aligned on the saccade. Zero time is the median point at which the saccade begins and the vertical line to the right of 0 is the median point at which the saccade terminates on the choice target. Vertical lines to the left of 0 represent onset of the brightness stimulus. For monkey 12, stimulus onset for the slowest group of responses occurred before the earliest time represented by the x axis of these plots. The points “b” represent the points at which activity in the competing neurons dips just prior to the saccade initiation (see the text).
To illustrate the quality of the fit for firing rates aligned on stimulus and saccade, Fig. 11 provides 90% confidence intervals around the firing rate functions for the middle condition for the 55% black pixel conditions in Figs. 9 and 10. These confidence intervals were constructed using a bootstrap method. One hundred sets of firing rate functions were computed in the same way as in the preceding text except the data used to generate them were the same number of cells as the original sample; but these were randomly selected with replacement from the cells in the data. Thus in any set of bootstrap data, the data from a particular cell could occur zero, once, twice, or even more. This provides an estimate of variability that would occur if a new sample of cells were used to produce a new set of neural firing rate data.
FIG. 11.
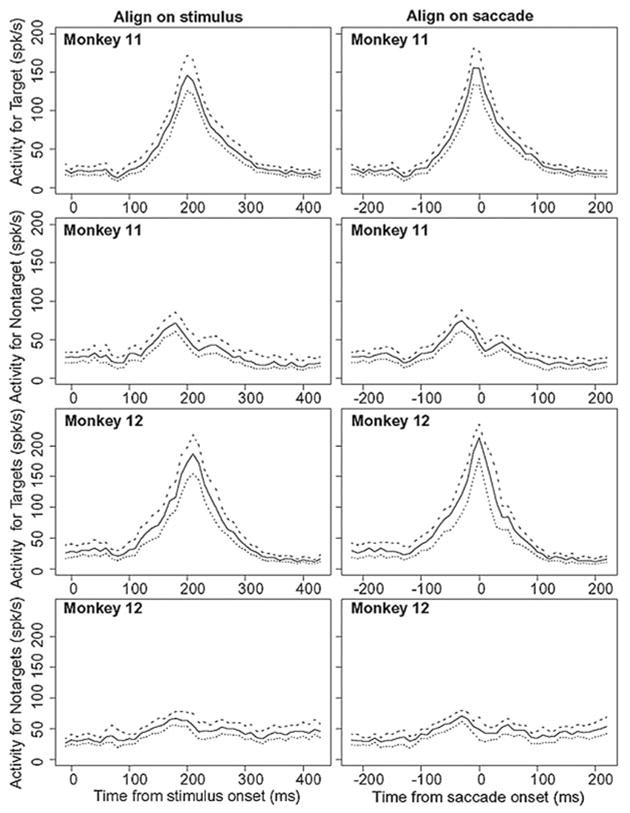
Quality of the fit for firing rates aligned on stimulus and saccade. A plot of the middle tercile of the firing rate functions shown in Figs. 9 and 10 for the 55% black pixel condition for alignment on the stimulus and saccade for the target and competitor cells. One hundred bootstrap samples were generate by randomly sampling with replacement from the data. Thus the data from a cell might be included 0 times, once, twice, or so on. The functions were sorted into order from highest to lowest based on the average firing rate for 50 ms around the peak. The 5th, middle, and 95th functions are plotted (•••, —, and ---, respectively). These represent 90% confidence intervals around the firing rates that would be obtained if different random samples of cells were selected.
Both the main two misses in Figs. 9 and 10, namely in the initial rise in many of the functions and the dip in the firing rates for competing neurons just prior to the saccade, seem to indicate nonstationarity in processing. The initial rise can be modeled by a ramp up of stimulus information or a release of inhibition (say from cells in the substantia nigra) and the dip prior to the saccade can be modeled by a sudden increase in global inhibition except in cells corresponding to the saccade. We discussed these possibilities shortly.
Difference in firing rates
Figure 12 shows the difference in firing rates and the differences in the amounts of evidence from the theoretical predictions for the functions shown in Figs. 9 and 10. These functions show the growth of discriminative information for fast, intermediate, and slow responses and as a function of two levels of stimulus intensity. The results show for functions aligned on the stimulus, discriminative information is delayed for slow versus fast responses both in the data and in the model predictions. The mismatch between the model and data was much less than in the individual functions (Fig. 9); this suggests that the misses in the initial growth were not the result of growth of information that discriminates between the two choices in the decision process. For functions aligned on the saccade, the growth of discriminative information began to rise 50 – 80 ms before the saccade and showed little difference for fast, intermediate, or slow responses. The predictions and the data match quite well (better than the individual functions in Fig. 10) except for a miss of 10 –20 ms in some initial rises. Some of the tails fall to asymptotes that are lower than the starting level for the reasons discussed in the preceding text.
FIG. 12.
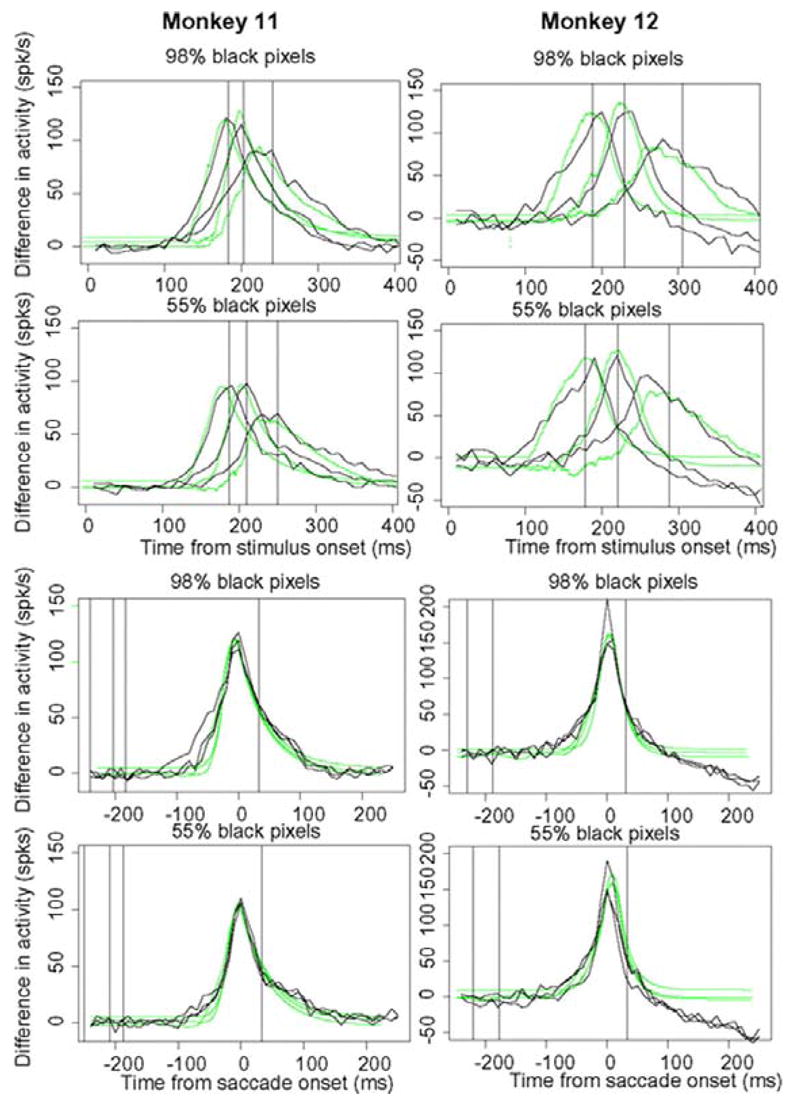
Firing rates for the growth of discriminative information. The functions are obtained by subtracting the target cell firing rates and competitor cell firing rates shown in Figs. 9 and 10.
We can also look to see if the relative heights of the firing rate functions for the data and model match each other. Figure 13 shows the peak activity for the stimulus-aligned data minus the baseline activity (the baselines used are the empirical firing rate functions at the highest activity prior to a dip, before the functions start to rise, i.e., prior to points marked “a” in Fig. 9) for the targets and nontargets averaged over monkeys and averaged over stimuli. We also average firing rate functions for bright responses to stimuli with 0.98 white pixels with firing rate functions for dark responses to stimuli with 0.98 black pixels (averaging 65% black pixel data with 65% white pixel data and well as 55% black pixel data with 55% white pixel data). The peak activities match quite well, but this is only to be expected given that the peak activities are about constant over conditions and the model predicts constant peaks. The peak activities for the competing response both show increasing functions, but the rise in the peak for the data is from a higher baseline and is slower than for the model. But the trend is in the right direction with a more difficult choice leading to a higher peak activity in the competing neurons. Note that the conditions with proportions of pixels 0.45 and 0.35 are error responses (where 0.55 and 0.65 provide the corresponding correct responses).
FIG. 13.
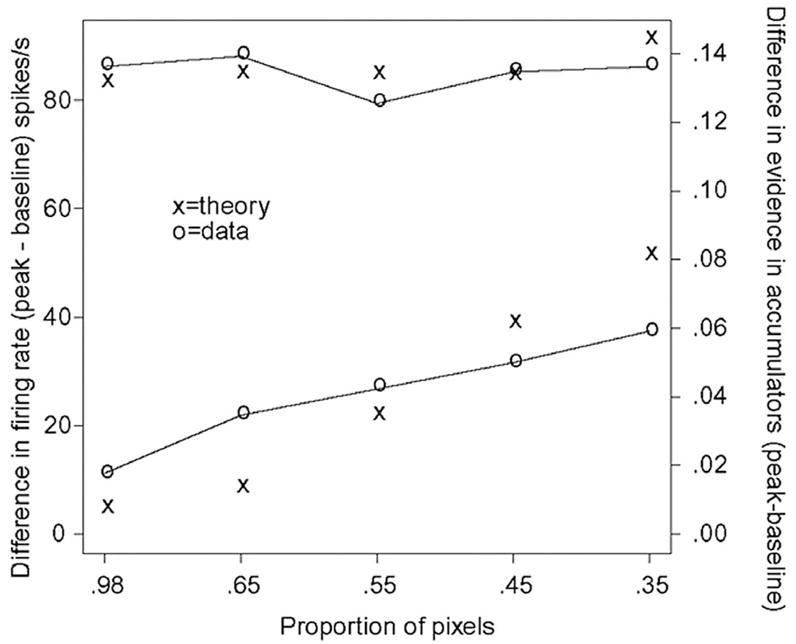
Empirical and predicted peak firing rates as a function of the proportion of black or white pixels. The nearly horizontal distribution of peak firing rates at the top of the plot are for activity when a cell’s response field contained the target for the correct response (target cell). The distribution with increasing slope at the bottom of the plot is for activity when a cell’s response field contained the target for the incorrect response (nontarget cell). Firing rates are for data aligned to stimulus onset.
We noted earlier that the competing activity shows a dip around the saccade (“b” in Fig. 10), and this reduces the height of the peak that would have been attained if there were no dip. With no dip, the empirical function would have been steeper and would have qualitatively matched the model better.
Variability in processing and delayed discriminative information
The ability of the model to predict delayed onset of discriminative information depends on the moment-by-moment variability in the sample paths of the diffusion process in an essential way. If the model was deterministic with stimulus information growing smoothly after stimulus onset, it would be unable to predict this finding.
The reason that the model is able to produce this pattern of delayed onset is that it has a high degree of variability in processing within a trial. The primary need for this high amount of variability is for the process to produce errors, especially in conditions where drift rate toward one alternative is high. The effect of high variability is to make processes that get near a decision criterion exit the process with relatively high probability. In contrast, if a process is not near the decision criterion, it is much less likely to exit quickly. It turns out that with the parameter values from the fit to the behavioral data, for a process that terminates relatively late in processing, the average position of a process early in processing is close to the starting position.
The predictions for this model for the availability of discriminative information are qualitatively the same as that for the two-boundary diffusion model (e.g., see predictions in Ratcliff 1988; Ratcliff et al. 2003a) (Fig. 11A). For the two boundary diffusion model, at some point in the process, either processes will have exited the process (terminated) or will still be in the process. Because of the relatively high amount of variability in processing, processes that have not terminated late in processing will have an average position earlier in processing that is relatively far away from the boundary (or else they would have exited).
The same factors were important in fitting data from a deadline task used by Meyer and colleagues (1988) using the diffusion model (Ratcliff 1988). In the experiment (using human subjects), a simple mixture model was used to extract the amount of partial information available at various points in time, and the results showed that partial information was available quickly and at a much lower accuracy level for processes that had terminated. The high degree of variability in processing required in the diffusion model to produce the correct patterns of accuracy and RT distributions also automatically produces predictions that match the data for average paths in the current study and partial information in the Meyer et al. paradigm.
DISCUSSION
Sequential sampling models have been proposed as a general decision mechanism for a range of different tasks (Busemeyer and Townsend 1993; Ratcliff 1978, 1981, 1988, 2002; Ratcliff and Rouder 1998, 2000; Ratcliff and Smith 2004; Ratcliff et al. 1999, 2001, 2003b, 2004a,b; Roe et al. 2001; Smith 1995; Thapar et al. 2003).
For the current experiment, the dual diffusion model fits the behavioral data moderately well, capturing the shape of the skewed RT distributions and accounting for the relationship between accuracy and RT. Under the assumption that paths in the dual diffusion process represent firing rates in the collicular build-up cells, the model predicted many of the major features of the neural firing rate data including the relative positions, onsets, and peak activity levels of the firing rate functions. But the model failed in important ways, and we argue that these misses can point to neurophysiological processes that are not captured by the model and that would need to be added to provide a more comprehensive account of the behavioral and neural data.
The results here and the results in Ratcliff, Cherian, and Segraves (2003a) show extraordinarily similar outcomes in both behavioral and neural processes for two quite different stimulus displays and different kinds of judgments. Furthermore, the dual diffusion model can fit both sets of data (data from Ratcliff et al. 2004c). This suggests a working hypothesis or view of processing that assumes that different sources of information from processing streams (e.g., different kinds of visual information such as brightness, color, motion, etc., and even auditory information) are combined just prior to the processes that implement the behavioral response.
Misses between theory and data
The details of the fits presented in Figs. 9 and 10 and the misses between theory and data (indicated by “a” and “b” in the figures) suggest that there are dynamical changes that are not captured in the stationary model. There are two aspects of the results that show systematic mismatches between the model and data. First, the initial rise in activity mismatches, and second, when firing rates are aligned on the saccade, there is a dip in activity in the competing neuron. Both of these effects can be at least qualitatively explained by changes in inhibition during the course of the decision process. First we examine the effect of ramping on the stimulus information to address the first miss, and then we turn to an inhibition interpretation.
As pointed out earlier, the dual diffusion model is a stationary one, i.e., one in which none of the processes or parameters change over time during the time course of the decision process. The issue of stationarity in the decision process has been addressed by Ratcliff and Rouder (2000), Ratcliff (2002), and Smith and colleagues (2004). They provided evidence that the stimulus representation of a briefly presented visual stimulus is the integrated representation of the stimulus in a visual short-term memory. This representation provides the drift rate that drives the accumulation process. The build-up of this representation has to be quite rapid because experimentally, a stimulus duration much > 80 ms increases the drift rate little. Ratcliff (2002) examined the effect of ramping up drift rate to mimic the growth of the visual short-term memory representation and found that the ramped process could not be discriminated from an unramped one based on behavioral data. Predictions from ramped process with four different values of drift rate were fit with the unramped model, and the unramped model produced slightly different parameter values to accommodate the differences. The effect of a ramped onset was to increase variability in starting point, to increase the variability in the nondecision components of processing, and to increase the mean nondecision time. The other parameters such as drift rates and boundary separation changed by < 3%. Thus at the behavioral level, the ramped and unramped models of these kinds will not be discriminable. But the growth of evidence in the process for the ramped process (the analog of firing rate) will have a more gradual rise than for the unramped process.
An alternative way to plausibly add a ramping up of the stimulus is to use inhibition. Experimentally, just before the firing rate functions begin to rise, there is a dip in activity (Li et al. 2006; Ratcliff et al. 2003a; Roitman and Shadlen 2002; Sato and Schall 2001; Segraves et al. 1999). This dip could be seen as a sharp increase in inhibition followed by a release. Even with a constant drift rate, a large release of inhibition over tens of milliseconds would mimic a ramping up of drift rate.
A dip in build-up cell activity after a cue and preceding a behavioral response has been examined closely by Li and colleagues (2006). The sources for inhibitory input that might cause this dip for a cell with an extra-foveal receptive field include collicular inputs from the foveal representation as well as from competing collicular sites representing other available targets (Basso and Wurtz 1998; Behan and Kime 1996; McPeek and Keller 2002; Mize et al. 1991; Munoz and Istvan 1998). This inhibition might also be attributed to inputs from other components of the oculomotor system, including the substantia nigra (Appell and Behan 1990; Arai and Keller 2005; Hikosaka and Wurtz 1983, 1985).
Simulating inhibition
To examine the effects of dynamic changes in inhibition, we chose to implement inhibition as modulating decay rate in the dual diffusion model. The initial rise in activity in both target and nontarget neurons begins between 20 and 40 ms prior to the predictions from the dual diffusion model. If we assume that initially the decay rate is very high (e.g., 50 compared with 2 and 4 for fits to the behavioral data for the 2 monkeys), then it is reduced linearly, we get a more gradual ramp up in activity in the target and competing accumulators. This produces a more gradual rise and accommodates about half the miss between the stationary model and data (in Figs. 9 and 10). If the ramp up was made nonlinear, then more of the difference might be accommodated. Or if the stimulus was ramped on along with the decrease in inhibition, then again more of the difference might be accommodated.
The suppression in activity in the competing neurons seen when the firing rates are aligned on the saccade (Fig. 10) can likewise be accommodated by an increase in decay in the process. If we assume that when activity in the accumulators corresponding to the decision reaches a certain level (e.g., 95% of the way toward threshold), decay in all competing accumulators is turned up to a high value (e.g., 25 times higher than that estimated in the fits to the data here, Table 2). Because the accumulators are independent, this change in inhibition hardly affects either the predictions for the behavioral data or the predictions for activity in the accumulator that reaches criterion because the process is highly likely to terminate once it is this close to the criterion. However, it does produce a lower peak and a dip in activity for the competing accumulator that matches the data.
Converging evidence for the involvement of general inhibition of this kind would come from a study in which recordings were made from sites away from the sites corresponding to both target and test alternatives. If this shows modulation corresponding to the initial drop and the inhibition just before saccade, then this will be evidence that the system is globally inhibiting, first everything, and second, neurons corresponding to every location except the target.
Altering assumptions about drift rates and noise
Variations on the early diffusion model have been proposed recently. These new models are couched in terms of neurophysiological plausibility, but as yet there is not enough neurophysiological data to discriminate them. They all have the advantage of fitting the behavioral data more or less well. And they have the potential to fit the neurophysiological data. The current state of this enterprise is that there have been relatively few comprehensive comparisons of models across data sets (e.g., see Ratcliff et al. 2004c), whereas at the same time there has been a lot of theoretical comparisons of the various variants of the models. One way to develop this research domain will involve comprehensive competitive testing of the models using real data, and the models will need to be evaluated using neurophysiological data (soon it will not be enough for a model to be vaguely “consistent with” neurophysiological data).
In an attempt to improve the fits of our model to the data, we first relaxed the assumption that neither drift rate for the accumulators can become negative, and second, we examined the effect of allowing the noise to be negatively correlated. Both of these assumptions are plausible. In the fits to data, noise is a major determinant of when the process crosses a decision criterion (e.g., Fig. 7), and there are neurophysiological data that suggest that neural firing rates are correlated.
When the drift rate in one accumulator is negative, the sample paths of the process will tend to remain in the vicinity of the lower bound at zero. Although such paths may cross the criterion because of the effects of noise alone, the probability of this occurring is less than if the drift is positive. The other accumulator will have a higher drift rate than the sum of the two, and this will make responses for the condition more accurate. This might allow the model to fit the data in Fig. 8 better by making the predicted accuracy values higher and so better match the data for the most accurate conditions.
We fit the dual diffusion model relaxing the assumption that both drift rates are positive and produced modestly better fits in χ2 terms (7.7% lower χ2 for monkey 11 and 5.2% lower χ2 for monkey 12). The reason the fits were better is that accuracy was increased a little for the extreme conditions that the model mispredicted. However, the improvement is only modestly better and the predicted and empirical accuracy values for the extreme conditions match only a little better. This is because the fit is a compromise between fitting the accuracy values (horizontal displacement between predictions and data) and quantile RTs (vertical displacement between predictions and data). For example, if the quantile functions in Fig. 8 are extended in the far right of the two middle panels so that the accuracy values line up with the data, the quantile RTs would have lower values than are displayed in the plot and the quality of the fit would be reduced. For monkey 12, Fig. 8, middle right, if the theoretical quantile functions were extended to the right for the extreme dark stimulus to align with the response proportions, then instead of the 0.9 quantile RT missing by ~ 30 ms (the vertical miss in the figure), it would miss by ~ 60 ms.
The assumption that noise in the neural processing system is correlated is an assumption that has been discussed and tested in the neurophysiological literature (e.g., Mazurek and Shadlen 2002; Zohary et al. 1994). The assumption that pools of neurons representing competing decisions have negatively correlated noise is an assumption that has been implemented in some recent modeling (Ditterich 2006). The idea is that in a particular time interval, if noise drives one process toward its criterion, it drives the other process away from its criterion. The correlation could vary from 0 to −1. If perfectly anti-correlated noise is implemented in a model with two accumulators, then this model has many of the features of the single diffusion process model (Ratcliff 1978; Ratcliff and Smith 2004). If, in addition, the decision rule is changed to a relative criterion (terminate the decision process when one accumulator gets more than a criterial amount greater than the other accumulator), then this two-accumulator model is equivalent to the traditional diffusion process (so long as evidence is allowed to go negative). However, if evidence is not allowed to go below zero, then the model will only approximate a diffusion process, and even when one accumulator gets little or no positive evidence, it will have a mean value above zero. Also a model with uncorrelated noise, no lower bound on evidence, and a relative criterion is formally identical to a diffusion process. This is because the difference between a pair of Gaussian processes is also a Gaussian process.
So there is a reasonably large set of possible models for a two-choice task. 1) The model can have two accumulators or one, 2) there can be decay in the accumulator or not, 3) accumulators can inhibit each other either pair wise, or from a pool of inhibition representing the sum of all activity, 4) the accumulation rates can be independent or negatively correlated, and 5) noise in the two accumulators can be negatively correlated to a greater or lesser degree. Some of these possibilities cannot be used together, e.g., the single diffusion process only has one sources of noise and so noise is implicitly anti-correlated. Various versions of these models have been examined in Bogacz et al. (2006), Ditterich (2006), and Ratcliff and Smith (2004). But there has been no comprehensive study of all the plausible combinations.
Here we examined the effect of assuming anti-correlated noise instead of uncorrelated noise in the dual diffusion model. We fit the model assuming that noise was negatively correlated −0.5 or −1. For a correlation of −1, a random number from a Gaussian distribution was generated on each time step, and this was added to one accumulator and subtracted from the other.
We fit the behavioral data with the dual diffusion model with anti-correlated noise (either −0.5 or −1). The effect of increasing the correlation in noise between the two accumulators is to increase error RTs relative to correct RTs. This is contrary to what is found in the data: errors are slightly faster than correct responses for monkey 11 and appreciably faster for monkey 12. Increasing the correlation in noise worsened the fits a little for monkey 11 and a lot for monkey 12. The result was that as the correlation increased in size from 0 to −0.5 to −1, the χ2 values worsened: for monkey 11, the increase in χ2 was modest, a 10% increase going from 0 to −0.5 correlation, and 24% from 0 to −1 correlation, and for monkey 12, the increase was much larger, 80% from 0 to −0.5 correlation, and 177% from 0 to −1 correlation. The reason for this is that error response times are modestly faster than correct responses for monkey 11, but are much faster for error responses than correct responses for monkey 12.
Anti-correlated noise also has an effect on the predicted firing rate functions for the competing accumulator; it makes the activity peak earlier than the time at which the target terminates. This occurs because a large proportion of terminations will involve a positive noise increment which correspond to a negative increment in the other accumulator. For monkey 11, the competitor activity peak is ~ 30 ms before the target peak. Even though this captures the position of the peak activity better than the dual diffusion model, other aspects of the predictions diverge from the experimental data. If we divide the responses into fast, intermediate, and slow, we find that the activity in the target and competitor rise at the same rate to half the peak activity beginning at ~ 150 ms before the decision. The activity in the competitor for the fastest third of responses does not rise above baseline and dips below baseline at the time of the decision (see Fig. 14). This suggests that the assumption of anti-correlated noise does not provide a better account of the earlier peak activity in the competing accumulator.
FIG. 14.
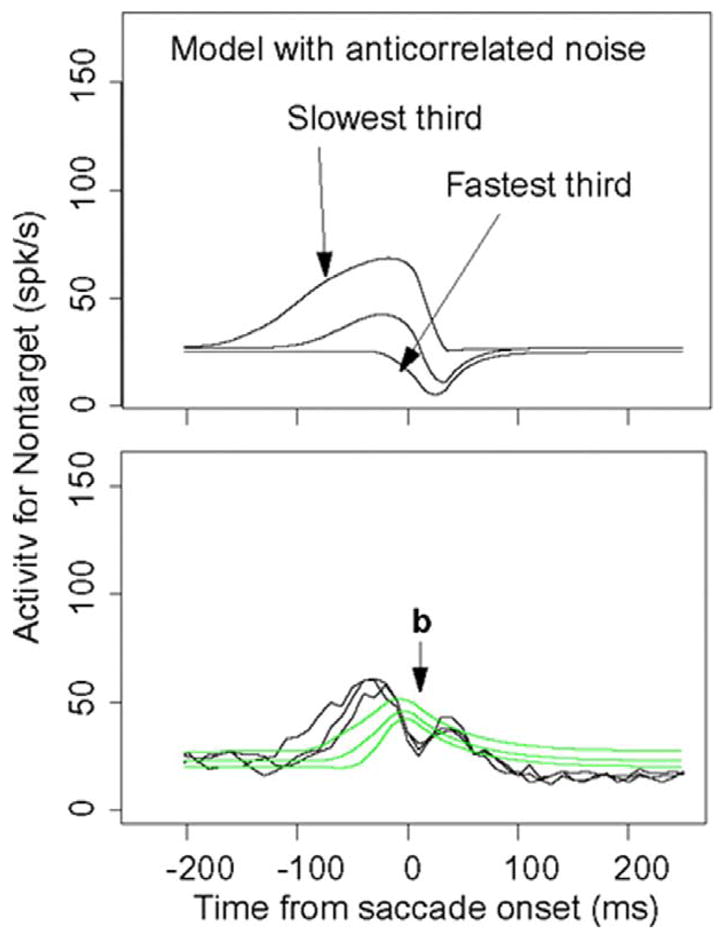
Effect of allowing noise to be negatively correlated. Predictions from the dual diffusion model with anti-correlated noise (top). The predictions are generated from the best fitting model to the behavioral data, and the predicted firing rate functions are plotted for the fastest, intermediate, and slowest third of responses. Bottom: neuron firing data used for this analysis along with the original dual diffusion model fits reproduced from Fig. 10, 2nd row, right panel.
A possible interpretation of the suppression and recovery of the firing rate at point “b” in Fig. 10 is that the SC neuron firing rates are being driven by earlier systems. The suppression reflects a local brief burst of inhibition acting on the SC, which, when removed, allows the firing rate in the competing neurons to recover. If activity in the whole processing stream was totally suppressed (and so was not being supported by other inputs), then there would be no recovery after point “b”.
Although we did not find that correlated noise between the accumulators helped produce better fits to our experimental data, as Ditterich (2006) shows, it is certainly worth examining further.
Other accumulator models
Another model of the class of dual diffusion models is the “leaky competing accumulator model” (Usher and McClelland 2001). Evidence is continuously distributed, accumulates in continuous time, just as in other diffusion process models, and is accumulated in separate accumulators for the different responses. The rate at which evidence accumulates in each accumulator, that is, drift rate of the diffusion process, is a combination of the quality of the information from the stimulus and two other components. The first component is decay in the amount of accumulated evidence (as in the dual diffusion model), and the other is inhibition from the other accumulator with the amount of inhibition growing as the amount of evidence in the other accumulator grows. If inhibition is large, the model exhibits features similar to the random walk and diffusion models because an increase in evidence for one alternative produces a decrease in evidence for the other alternative. In its assumption of cross-coupling between counters, the model also resembles an earlier, discrete-time model proposed by Heuer (1987).
We fit this model to the behavioral data in the same way as the dual diffusion model in the preceding text and found that it produced fits about as good as the dual diffusion model. This is not surprising because the dual diffusion model is almost nested in the leaky competing accumulator model (apart from negatively correlated starting points). In the fits of the leaky competing accumulator model, the amount of leakage and inhibition were modest: leakage or decay was 1.2 and 2.5 times larger for monkeys 11 and 12, respectively, relative to the values in Table 2 for the dual diffusion model, and decay had a value of about 1. As we noted earlier, removing both decay and inhibition produces fits of about the same quality. In particular, the inhibition was much too small (by 1–2 orders of magnitude) to produce the dip in processing in firing rates just prior to the saccade for the nontarget when firing rates are aligned on the saccade.
A more neurobiologically inspired model that is similar to the dual diffusion model is that of Mazurek and colleagues (2003) designed to account for performance in the random dot motion-discrimination task (e.g., Roitman and Shadlen 2002; Shadlen et al. 1996). The model is applied to data from a two-choice task, and it assumes that information about motion strength enters area MT and produces stimulation in direction sensitive neurons corresponding to the two choices. Activity from these populations is subtracted, and this value is used to drive two separate LIP processes corresponding to the two decisions, for example, right MT activity minus left MT activity drives right LIP activity and left MT activity minus right MT activity drives left LIP activity. The activity in the two LIP populations race to threshold to produce the decision.
In contrast to the dual diffusion model, the Mazurek and colleagues’ model is based on neurophysiology. It assumes delays between MT and LIP (as well as evidence entering MT from the stimulus), known correlations in firing rates among neurons in the populations, and noise (variability in processing) are produced by assumptions about spiking in the neural populations. However, this model does not go as far in accounting for data as does the dual diffusion model. It badly misses RTs for error responses and almost certainly would not predict the observed roughly symmetric RT distributions (Ditterich 2006). This is because models that assume accumulation to criterion will predict skewed distributions with increasing spread in the tail and mean RT increases (see Ratcliff and Smith 2004). Also, the behavior of the observed and predicted LIP physiology are only shown to be qualitatively similar rather than quantitatively matching (though the matches are reasonably good). In a recent report, Ditterich (2006) presents a diffusion model that includes the addition of a time-variant gain of the incoming visual motion signals with the result that it provides a closer fit between the model predictions and both the behavioral and firing rate data than was provided by the original model of Mazurek and colleagues.
The main problem with application of these models to the data from our experiment is that they are specific to MT and LIP and motion stimuli. However, despite these limitations, the model of Mazurek and colleagues (2003) and Ditterich (2006) articulate some of the features of modeling to which we should all aspire. They take the neurophysiological basis of processing seriously and attempt to model physiology and behavior in terms of known physiology of single cells and aggregates of single cells.
Neural plausibility of decay and inhibition in decision models
There have been justifications in terms of neural plausibility for various design characteristics in some stochastic accumulation models. In particular, Usher and McClelland (2001) have most strongly argued for a correspondence between the psychological and neural levels, a view that this paper endorses. But, whether a design feature actually implements the function as claimed is partially an empirical question. The specific issues concern Usher and McClelland’s discussion of decay in an accumulator and inhibition between accumulators. It has been argued that leakage or decay is required because neural firing rates are limited and have a maximum. Likewise, lateral inhibition is argued to be a mechanism used within a brain region to select the representation most consistent with the input, i.e., contrast enhancement.
For decay to be able to limit the predicted size of the firing rate to match the data, it would have to be of a size that was plausible. Likewise, for lateral inhibition to be plausible, it would have to be large enough to have a significant suppressive effect on firing rates, as is observed in the firing rate data just prior to the eye movement for cells corresponding to competing decision when aligned on the saccade.
For the dual diffusion model, we can compute the theoretical maximum average firing rate based on the transformation from position in the diffusion process to firing rates (shown in Figs. 9, 10, and 12) with decision criteria removed. The average asymptotic position with decision criteria removed is obtained if dx in the equation at the bottom of Fig. 6 is equal to 0. This occurs when (v – βx) = 0, so x = v/β. For the maximum value of drift, for monkeys 11 and 12, respectively, x = 2.5 and x = 2.4. For a middle value of drift (half the sum of drift rates), the values are 1.3 and 1.2. For the scaling in the experiments presented earlier, for monkey 11, evidence of 0.5 (average criterion setting) corresponds to a firing rate of 150 spike/s and for monkey 12, evidence of 0.54 correspond to a firing rate of 200 spike/s. Thus the theoretical asymptotic levels for the high drift conditions would be 750 and 880 spike/s for monkeys 11 and 12, respectively. These would be halved for drift rates of half these values. We feel that these theoretical asymptotic levels are too high for decay to be serving the purpose of limiting firing rates.
For the fits of the Usher and McClelland model to the behavioral data, the asymptotic levels are much higher because decay is lower, the asymptotic levels for high drift rates are 1,400 and 12,80 spike/s for monkeys 11 and 12, respectively. Inhibition is even lower than decay in the fits. For middle drift values, when one accumulator is near its maximum, inhibition on the other accumulator is ~ 10% of the drift term. With the variability in processing needed in the model, this amount of inhibition could not be discriminated empirically from a model without inhibition. Furthermore, this degree of inhibition is between 50 and 200 times too small to account for the dip in activity of competitor neurons prior to the saccade.
This discussion suggests that providing a mechanism in a model that is neurally plausible is not enough. It is necessary to make sure that the size of the effect produced by this mechanism is large enough to provide the function that is proposed. The preceding arguments about the size of the decay and leakage apply only to our fits to this data set. For other experiments, the calculation needs to be carried out to examine the size of the effects, which may in other cases provide exactly the effect sizes needed for the proposed processes.
Generality of the dual diffusion model
In other work to be submitted, we have found that the dual diffusion model fits human data almost as well as the original diffusion model, but this work is preliminary and firm conclusions have not yet been reached. It might be tempting to argue that the dual diffusion model should replace the original diffusion model, but it is not necessary that the same model should account for both human and monkey decision making. Probably the main conclusion that should be drawn is that models of the same sequential sampling class are capable of accounting quantitatively for much of the behavioral data and neural firing rate data in simple decision making.
The model as it is fit to the behavioral data is moderately complex and a simpler model might be able to provide about the same quality of fit. We prefer to present the full model so that components do not have to be added later to deal with different paradigms. As noted earlier, leakage could be eliminated from the model, and it would fit the data presented in this article. In some applications of the diffusion model (e.g., Ratcliff 2002; Ratcliff et al. 2003b), boundaries for the two choice could be set equal because response times and accuracy values are symmetric in the data. But in the data presented here, they are not symmetric. Similarly, in the same applications (Ratcliff 2002; Ratcliff et al. 2003b), drift rates for bright stimuli are the same numerical size as those for dark stimuli. However, again, this is not the case for these data. The starting points and variability in starting point could probably be set to zero and adequate fits to the behavioral data produced. However, this would produce the need for arbitrary assumptions about the base activity levels in the predicted neural firing rate functions.
Neurophysiological evidence for implementation of the decision process
A central question in any study like this is: where in the processing stream is the decision made? We believe that the decisions specified by different behavioral responses (e.g., manual, saccade, vocal) are implemented by different but similar neural systems. The decision process is likely distributed over several different sites with the particular combination for a task depending on the modalities of the stimulus and response. For eye-movement responses based on visual discriminations, cells in the lateral intraparietal cortex (LIP), frontal eye field (FEF), and SC all seem to exhibit activities that can be interpreted as being involved in decision making. These similarities might be expected given the anatomical connections of these three regions. The LIP and FEF are reciprocally interconnected, both cortical areas project to the SC, and the SC projects back to both the FEF and LIP (Andersen et al. 1990; Astruc 1971; Barbas and Mesulam 1981; Clower et al. 2001; Huerta et al. 1986, 1987; Komatsu and Suzuki 1985; Kunzle and Akert 1977; Kunzle et al. 1976; Lynch et al. 1994; Petrides and Pandya 1984; Sommer and Wurtz 2004; Stanton et al. 1988, 1995). Nevertheless, one might expect that there should be a progression in the decision-making processing stream from cortex to midbrain. Interactions between LIP and FEF appear to be more closely related to visual processing, whereas both LIP to SC and FEF to SC pathways are more directly involved in saccade generation (Ferraina et al. 2002; Segraves and Goldberg 1987; Sommer and Wurtz 2000). In comparing activity in LIP and SC in similar visuomotor tasks, Paré and Wurtz (2001) found neurons in LIP that projected to the SC to be more strongly dependent on visual stimulation, whereas SC neurons were more closely coupled to the oculomotor response. In addition, there is a convincing demonstration that the most significant contribution of the FEF to oculomotor processing is effected by means of its strong projection to the SC (Hanes and Wurtz 2001). We think that the SC is a good candidate for the location at which the decision is implemented in the saccadic system for two reasons. First, build-up cells in the SC seem to be the last place in the processing stream in which competition is observed. Second, the system seems to exhibit the right kinds of inhibitory processes that modulate processing prior to the decision process and in the competing build-up cells just prior to a saccade. However, this is little more than a guess and any part of the system including FEF, LIP, and SC could implement the decision or computations could be carried out that involve some or all of these regions.
Acknowledgments
We thank G. McKoon for extensive comments on this article and A. Nitzke and the staff of Northwestern’s Center for Comparative Medicine for animal care as well as Northwestern’s Instrument and Electronics Shops for machining and electronic hardware. We are grateful for the many constructive comments of the anonymous reviewers of this manuscript, including the suggestion that we explore the effects of correlated noise and negative drift rates on the model simulations.
GRANTS
Preparation of this article was supported by the National Institutes of Health Grants R01-MH-59893, R37-MH-44640, R01-EY-08212, K05-MH-01891, the Sumitomo Foundation, and Grant-in-Aid for Scientific Research on Priority Areas—Integrative Brain Research from the MEXT of Japan (18019048).
References
- Andersen RA, Asanuma C, Essick G, Siegel RM. Corticocortical connections of anatomically and physiologically defined subdivisions within the inferior parietal lobule. J Comp Neurol. 1990;296:65–113. doi: 10.1002/cne.902960106. [DOI] [PubMed] [Google Scholar]
- Appell PP, Behan M. Sources of subcortical GABAergic projections to the superior colliculus in the cat. J Comp Neurol. 1990;302:143–158. doi: 10.1002/cne.903020111. [DOI] [PubMed] [Google Scholar]
- Arai K, Keller EL. A model of the saccade-generating system that accounts for trajectory variations produced by competing visual stimuli. Biol Cybern. 2005;92:21–37. doi: 10.1007/s00422-004-0526-y. [DOI] [PubMed] [Google Scholar]
- Astruc J. Corticofugal connections of area 8 (frontal eye field) in Macaca mulatta. Brain Res. 1971;33:241–256. doi: 10.1016/0006-8993(71)90100-4. [DOI] [PubMed] [Google Scholar]
- Barbas H, Mesulam M-M. Organization of afferent input to subdivisions of area 8 in the rhesus monkey. J Comp Neurol. 1981;200:407–431. doi: 10.1002/cne.902000309. [DOI] [PubMed] [Google Scholar]
- Basso MA, Wurtz RH. Modulation of neuronal activity in superior colliculus by changes in target probability. J Neurosci. 1998;18:7519–7534. doi: 10.1523/JNEUROSCI.18-18-07519.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behan M, Kime NM. Intrinsic circuitry in the deep layers of the cat superior colliculus. Vis Neurosci. 1996;13:1031–1042. doi: 10.1017/s0952523800007689. [DOI] [PubMed] [Google Scholar]
- Bichot NP, Thompson KG, Rao SC, Schall JD. Reliability of macaque frontal eye field neurons signaling saccade targets during visual search. J Neurosci. 2001;21:713–725. doi: 10.1523/JNEUROSCI.21-02-00713.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychol Rev. 2006;113:700–765. doi: 10.1037/0033-295X.113.4.700. [DOI] [PubMed] [Google Scholar]
- Brown SD, Ratcliff R, Smith PL. Evaluating methods for approximating stochastic differential equations. J Math Psychol. 2006;50:402–410. doi: 10.1016/j.jmp.2006.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busemeyer JR, Townsend JT. Fundamental derivations from decision field theory. Math Social Sci. 1992;23:255–282. [Google Scholar]
- Busemeyer JR, Townsend JT. Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment. Psychol Rev. 1993;100:432–459. doi: 10.1037/0033-295x.100.3.432. [DOI] [PubMed] [Google Scholar]
- Clower DM, West RA, Lynch JC, Strick PL. The inferior parietal lobule is the target of output from the superior colliculus, hippocampus, and cerebellum. J Neurosci. 2001;21:6283–6291. doi: 10.1523/JNEUROSCI.21-16-06283.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crist CF, Yamasaki DSG, Komatsu H, Wurtz RH. A grid system and a microsyringe for single cell recording. J Neurosci Methods. 1988;26:117–122. doi: 10.1016/0165-0270(88)90160-4. [DOI] [PubMed] [Google Scholar]
- Cynader M, Berman N. Receptive-field organization of monkey superior colliculus. J Neurophysiol. 1972;35:187–201. doi: 10.1152/jn.1972.35.2.187. [DOI] [PubMed] [Google Scholar]
- Dias EC, Segraves MA. Muscimol-induced inactivation of monkey frontal eye field: effects on visually and memory-guided saccades. J Neurophysiol. 1999;81:2191–2214. doi: 10.1152/jn.1999.81.5.2191. [DOI] [PubMed] [Google Scholar]
- Diederich A. Dynamic stochastic models for decision making under time constraints. J Math Psychol. 1997;41:260–274. doi: 10.1006/jmps.1997.1167. [DOI] [PubMed] [Google Scholar]
- Ditterich J. Computational approaches to visual decision making. Novartis Found Symp. 2006;270:114–126. [PubMed] [Google Scholar]
- Ferraina S, Paré M, Wurtz RH. Comparison of cortico-cortical and cortico-collicular signals for the generation of saccadic eye movements. J Neurophysiol. 2002;87:845–858. doi: 10.1152/jn.00317.2001. [DOI] [PubMed] [Google Scholar]
- Glimcher PW, Sparks DL. Movement selection in advance of action in the superior colliculus. Nature. 1992;355:542–545. doi: 10.1038/355542a0. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Representation of a perceptual decision in developing oculomotor commands. Nature. 2000;404:390–394. doi: 10.1038/35006062. [DOI] [PubMed] [Google Scholar]
- Hanes DP, Schall JD. Neural control of voluntary movement initiation. Science. 1996;274:427–430. doi: 10.1126/science.274.5286.427. [DOI] [PubMed] [Google Scholar]
- Hanes DP, Wurtz RH. Interaction of the frontal eye field and superior colliculus for saccade generation. J Neurophysiol. 2001;85:804–815. doi: 10.1152/jn.2001.85.2.804. [DOI] [PubMed] [Google Scholar]
- Hasegawa YT, Hasegawa RP, Ratcliff R, Segraves MA. Activity in monkey superior colliculus during a brightness discrimination task. Soc Neurosci Abstr. 2003;29 [Google Scholar]
- Hasegawa YT, Hasegawa RP, Ratcliff R, Segraves MA. Asymmetric effect of task difficulty in monkey superior colliculus during an oculomotor brightness discrimination task. Soc Neurosci Abstr. 2004;30 [Google Scholar]
- Hays AV, Richmond BJ, Optican LM. A UNIX-based multiple process system for real-time data acquisition and control. WESCON Conf Proc. 1982;2:1–10. [Google Scholar]
- Helminski JO, Segraves MA. Macaque frontal eye field input to saccade-related neurons in the superior colliculus. J Neurophysiol. 2003;90:1046–1062. doi: 10.1152/jn.00072.2003. [DOI] [PubMed] [Google Scholar]
- Heuer H. Visual discrimination and response programming. Psychol Res. 1987;49:91–98. doi: 10.1007/BF00308673. [DOI] [PubMed] [Google Scholar]
- Hikosaka O, Wurtz RH. Visual and oculomotor functions of monkey substantia nigra pars reticulata. IV. Relation of substantia nigra to superior colliculus. J Neurophysiol. 1983;49:1285–1301. doi: 10.1152/jn.1983.49.5.1285. [DOI] [PubMed] [Google Scholar]
- Hikosaka O, Wurtz RH. Modification of saccadic eye movements by GABA-related substances. II. Effects of muscimol in monkey substantia nigra pars reticulata. J Neurophysiol. 1985;53:292–308. doi: 10.1152/jn.1985.53.1.292. [DOI] [PubMed] [Google Scholar]
- Horwitz GD, Newsome WT. Separate signals for target selection and movement specification in the superior colliculus. Science. 1999;284:1158–1161. doi: 10.1126/science.284.5417.1158. [DOI] [PubMed] [Google Scholar]
- Horwitz GD, Newsome WT. Target selection for saccadic eye movements: prelude activity in the superior colliculus during a direction-discrimination task. J Neurophysiol. 2001;86:2543–2558. doi: 10.1152/jn.2001.86.5.2543. [DOI] [PubMed] [Google Scholar]
- Huerta MF, Krubitzer LA, Kaas JH. Frontal eye field as defined by intracortical microstimulation in squirrel monkeys, owl monkeys, and macaque monkeys. I. Subcortical connections. J Comp Neurol. 1986;253:415–439. doi: 10.1002/cne.902530402. [DOI] [PubMed] [Google Scholar]
- Huerta MF, Krubitzer LA, Kaas JH. Frontal eye field as defined by intracortical microstimulation in squirrel monkeys, owl monkeys, and macaque monkeys. II. Cortical connections. J Comp Neurol. 1987;265:332–361. doi: 10.1002/cne.902650304. [DOI] [PubMed] [Google Scholar]
- Kim JN, Shadlen MN. Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat Neurosci. 1999;2:176–185. doi: 10.1038/5739. [DOI] [PubMed] [Google Scholar]
- Komatsu H, Suzuki H. Projections from the functional subdivisions of the frontal eye field to the superior colliculus in the monkey. Brain Res. 1985;327:324–327. doi: 10.1016/0006-8993(85)91528-8. [DOI] [PubMed] [Google Scholar]
- Krauzlis R, Dill N. Neural correlates of target choice for pursuit and saccades in the primate superior colliculus. Neuron. 2002;35:355–363. doi: 10.1016/s0896-6273(02)00756-0. [DOI] [PubMed] [Google Scholar]
- Kunzle H, Akert K. Efferent connections of cortical area 8 (frontal eye field) in Macaca fascicularis. A reinvestigation using the autoradiographic technique. J Comp Neurol. 1977;173:147–164. doi: 10.1002/cne.901730108. [DOI] [PubMed] [Google Scholar]
- Kunzle H, Akert K, Wurtz RH. Projection of area 8 (frontal eye field) to superior colliculus in the monkey. An autoradiographic study. Brain Res. 1976;117:487–492. doi: 10.1016/0006-8993(76)90754-x. [DOI] [PubMed] [Google Scholar]
- LaBerge DA. Quantitative models of attention and response processes in shape identification tasks. J Math Psychol. 1994;38:198–243. [Google Scholar]
- Laming DRJ. Information Theory of Choice Reaction Time. New York: Wiley; 1968. [Google Scholar]
- Li X, Kim B, Basso MA. Transient pauses in delay-period activity of superior colliculus neurons. J Neurophysiol. 2006;95:2252–2264. doi: 10.1152/jn.01000.2005. [DOI] [PubMed] [Google Scholar]
- Link SW. The relative judgement theory of two choice response time. J Math Psychol. 1975;12:114–135. [Google Scholar]
- Link SW, Heath RA. A sequential theory of psychological discrimination. Psychometrika. 1975;40:77–105. [Google Scholar]
- Lynch JC, Hoover JE, Strick PL. Input to the primate frontal eye field from the substantia nigra, superior colliculus, and dentate nucleus demonstrated by transneuronal transport. Exp Brain Res. 1994;100:181–186. doi: 10.1007/BF00227293. [DOI] [PubMed] [Google Scholar]
- Mays LE, Sparks DL. Dissociation of visual and saccade-related responses in superior colliculus neurons. J Neurophysiol. 1980;43:207–232. doi: 10.1152/jn.1980.43.1.207. [DOI] [PubMed] [Google Scholar]
- Mazurek ME, Roitman JD, Ditterich J, Shadlen MN. A role for neural integrators in perceptual decision making. Cereb Cortex. 2003;13:1257–1269. doi: 10.1093/cercor/bhg097. [DOI] [PubMed] [Google Scholar]
- Mazurek ME, Shadlen MN. Limits to the temporal fidelity of cortical spike rate signals. Nat Neurosci. 2002;5:463–471. doi: 10.1038/nn836. [DOI] [PubMed] [Google Scholar]
- McPeek RM, Keller EL. Saccade target selection in the superior colliculus during a visual search task. J Neurophysiol. 2002;88:2019–2034. doi: 10.1152/jn.2002.88.4.2019. [DOI] [PubMed] [Google Scholar]
- Meyer DE, Irwin DE, Osman AM, Kounios J. The dynamics of cognition and action: mental processes inferred from speed-accuracy decomposition. Psychol Rev. 1988;95:183–237. doi: 10.1037/0033-295x.95.2.183. [DOI] [PubMed] [Google Scholar]
- Mize RR, Jeon CJ, Hamada OL, Spencer RF. Organization of neurons labeled by antibodies to gamma-aminobutyric acid (GABA) in the superior colliculus of the Rhesus monkey. Vis Neurosci. 1991;6:75–92. doi: 10.1017/s0952523800000924. [DOI] [PubMed] [Google Scholar]
- Munoz DP, Istvan PJ. Lateral inhibitory interactions in the intermediate layers of the monkey superior colliculus. J Neurophysiol. 1998;79:1193–1209. doi: 10.1152/jn.1998.79.3.1193. [DOI] [PubMed] [Google Scholar]
- Munoz DP, Wurtz RH. Saccade-related activity in monkey superior colliculus. I. Characteristics of burst and buildup cells. J Neurophysiol. 1995;73:2313–2333. doi: 10.1152/jn.1995.73.6.2313. [DOI] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A simplex method for function minimization. Comput J. 1965;7:308–313. [Google Scholar]
- Newsome WT, Britten KH, Movshon JA. Neuronal correlates of a perceptual decision. Nature. 1989;341:52–54. doi: 10.1038/341052a0. [DOI] [PubMed] [Google Scholar]
- Paré M, Wurtz RH. Progression in neuronal processing for saccadic eye movements from parietal cortex area lip to superior colliculus. J Neurophysiol. 2001;85:2545–2562. doi: 10.1152/jn.2001.85.6.2545. [DOI] [PubMed] [Google Scholar]
- Petrides M, Pandya DN. Projections to the frontal cortex from the posterior parietal region in the rhesus monkey. J Comp Neurol. 1984;228:105–116. doi: 10.1002/cne.902280110. [DOI] [PubMed] [Google Scholar]
- Pike AR. Stochastic models of choice behavior: response probabilities and latencies of finite Markov chain systems. Br J Math Stat Psychol. 1966;21:161–182. doi: 10.1111/j.2044-8317.1966.tb00351.x. [DOI] [PubMed] [Google Scholar]
- Pike R. Response latency models for signal detection. Psych Rev. 1973;80:53–68. doi: 10.1037/h0033871. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychol Rev. 1978;85:59–108. [Google Scholar]
- Ratcliff R. A theory of order relations in perceptual matching. Psychol Rev. 1981;88:552–572. [Google Scholar]
- Ratcliff R. Continuous versus discrete information processing: modeling the accumulation of partial information. Psychol Rev. 1988;95:238–255. doi: 10.1037/0033-295x.95.2.238. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. International Encyclopedia of the Social and Behavioral Sciences. Oxford, UK: Elsevier; 2001a. Diffusion and random walk processes; pp. 3668–3673. [Google Scholar]
- Ratcliff R. Putting noise into neurophysiological models of simple decision making. Nat Neurosci. 2001b;4:336–337. doi: 10.1038/85956. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. A diffusion model account of response time and accuracy in a brightness discrimination task: fitting real data and failing to fit fake but plausible data. Psychonom Bull Rev. 2002;9:278–291. doi: 10.3758/bf03196283. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Cherian A, Segraves M. A comparison of macaque behavior and superior colliculus neuronal activity to predictions from models of two-choice decisions. J Neurophysiol. 2003a;90:1392–1407. doi: 10.1152/jn.01049.2002. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Gomez P, McKoon G. A diffusion model account of the lexical decision task. Psychol Rev. 2004a;111:159–182. doi: 10.1037/0033-295X.111.1.159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling response times for two-choice decisions. Psychol Sci. 1998;9:347–356. [Google Scholar]
- Ratcliff R, Rouder JN. A diffusion model account of masking in letter identification. J Exp Psychol: Hum Percept Perform. 2000;26:127–140. doi: 10.1037//0096-1523.26.1.127. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychol Rev. 2004;111:333–367. doi: 10.1037/0033-295X.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. The effects of aging on reaction time in a signal detection task. Psychol Aging. 2001;16:323–341. [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. A diffusion model analysis of the effects of aging on brightness discrimination. Percept Psychophys. 2003b;65:523–535. doi: 10.3758/bf03194580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. A diffusion model analysis of the effects of aging on recognition memory. J Mem Language. 2004b;50:408–424. [Google Scholar]
- Ratcliff R, Thapar A, Smith PL, McKoon G. Aging and response times: a comparison of sequential sampling models. In: Duncan J, McLeod P, Phillips L, editors. Measuring the MInd: Speed, Control, and Age. Oxford, UK: Oxford; 2004c. pp. 3–32. [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating parameters of the diffusion model: approaches to dealing with contaminant reaction times and parameter variability. Psychonom Bull Rev. 2002;9:438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, McKoon G. Connectionist and diffusion models of reaction time. Psychol Rev. 1999;106:261–300. doi: 10.1037/0033-295x.106.2.261. [DOI] [PubMed] [Google Scholar]
- Richmond BJ, Optican LM, Podell M, Spitzer H. Temporal encoding of two-dimensional patterns by single units in primate inferior temporal cortex. I. Response characteristics. J Neurophysiol. 1987;57:132–146. doi: 10.1152/jn.1987.57.1.132. [DOI] [PubMed] [Google Scholar]
- Robinson DA. Eye movements evoked by collicular stimulation in the alert monkey. Vis Res. 1972;12:1795–1808. doi: 10.1016/0042-6989(72)90070-3. [DOI] [PubMed] [Google Scholar]
- Roe RM, Busemeyer JR, Townsend JT. Multialternative decision field theory: a dynamic connectionist model of decision making. Psychol Rev. 2001;108:370–392. doi: 10.1037/0033-295x.108.2.370. [DOI] [PubMed] [Google Scholar]
- Roitman JD, Shadlen MN. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J Neurosci. 2002;22:9475–9489. doi: 10.1523/JNEUROSCI.22-21-09475.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romo R, Hernâandez A, Zainos A, Brody C, Salinas E. Exploring the cortical evidence of a sensory-discrimination process. Philos Trans R Soc Lond B Biol Sci. 2002;357:1039–1051. doi: 10.1098/rstb.2002.1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato T, Murthy A, Thompson KG, Schall JD. Search efficiency but not response interference affects visual selection in frontal eye field. Neuron. 2001;30:583–591. doi: 10.1016/s0896-6273(01)00304-x. [DOI] [PubMed] [Google Scholar]
- Sato T, Schall JD. Pre-excitatory pause in frontal eye field responses. Exp Brain Res. 2001;139:53–58. doi: 10.1007/s002210100750. [DOI] [PubMed] [Google Scholar]
- Schall JD, Hanes DP, Thompson KG, King DJ. Saccade target selection in frontal eye field of macaque. I. Visual and premovement activation. J Neurosci. 1995;15:6905–6918. doi: 10.1523/JNEUROSCI.15-10-06905.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segraves MA, Cherian A, Ratcliff R. Rhesus monkey performance and superior colliculus activity during a reaction time task. Soc Neurosci Abstr. 1999;25:1920. [Google Scholar]
- Segraves MA, Goldberg ME. Functional properties of corticotectal neurons in the monkey’s frontal eye field. J Neurophysiol. 1987;58:1387–1419. doi: 10.1152/jn.1987.58.6.1387. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Britten KH, Newsome WT, Movshon JA. A computational analysis of the relationship between neuronal and behavioral responses to visual motion. J Neurosci. 1996;16:1486–1510. doi: 10.1523/JNEUROSCI.16-04-01486.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J Neurophysiol. 2001;86:1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
- Smith PL. Psychophysically principled models of visual simple reaction time. Psychol Rev. 1995;102:567–591. [Google Scholar]
- Smith PL. Stochastic dynamic models of response time and accuracy: a foundational primer. J Math Psychology. 2000;44:408–463. doi: 10.1006/jmps.1999.1260. [DOI] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R. Psychology and neurobiology of simple decisions. Trends Neurosci. 2004;27:161–168. doi: 10.1016/j.tins.2004.01.006. [DOI] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R, Wolfgang BJ. Attention orienting and the time course of perceptual decisions: response time distributions with masked and unmasked displays. Vision Res. 2004;44:1297–1320. doi: 10.1016/j.visres.2004.01.002. [DOI] [PubMed] [Google Scholar]
- Smith PL, Van Zandt T. Time-dependent Poisson counter models of response latency in simple judgment. Br J Math Stat Psychol. 2000;53:293–315. doi: 10.1348/000711000159349. [DOI] [PubMed] [Google Scholar]
- Sommer MA, Wurtz RH. Composition and topographic organization of signals sent from the frontal eye field to the superior colliculus. J Neurophysiol. 2000;83:1979–2001. doi: 10.1152/jn.2000.83.4.1979. [DOI] [PubMed] [Google Scholar]
- Sommer MA, Wurtz RH. What the brain stem tells the frontal cortex. I. Oculomotor signals sent from superior colliculus to frontal eye field via mediodorsal thalamus. J Neurophysiol. 2004;91:1381–1402. doi: 10.1152/jn.00738.2003. [DOI] [PubMed] [Google Scholar]
- Sparks DL. Conceptual issues related to the role of the superior colliculus in the control of gaze. Curr Opin Neurobiol. 1999;9:698–707. doi: 10.1016/s0959-4388(99)00039-2. [DOI] [PubMed] [Google Scholar]
- Stanton GB, Bruce CJ, Goldberg ME. Frontal eye field efferents in the macaque monkey. I. Subcortical pathways and topography of striatal and thalamic terminal fields. J Comp Neurol. 1988;271:473–492. doi: 10.1002/cne.902710402. [DOI] [PubMed] [Google Scholar]
- Stanton GB, Bruce CJ, Goldberg ME. Topography of projections to posterior cortical areas from the macaque frontal eye fields. J Comp Neurol. 1995;353:291–305. doi: 10.1002/cne.903530210. [DOI] [PubMed] [Google Scholar]
- Stone M. Models for choice reaction time. Psychometrika. 1960;25:251–260. [Google Scholar]
- Thapar A, Ratcliff R, McKoon G. A diffusion model analysis of the effects of aging on letter discrimination. Psychol Aging. 2003;18:415–429. doi: 10.1037/0882-7974.18.3.415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson KG, Hanes DP, Bichot NP, Schall JD. Perceptual and motor processing stages identified in the activity of macaque frontal eye field neurons during visual search. J Neurophysiol. 1996;76:4040–4055. doi: 10.1152/jn.1996.76.6.4040. [DOI] [PubMed] [Google Scholar]
- Townsend JT, Ashby FG. The Stochastic Modelling of Elementary Psychological Processes. Cambridge, UK: Cambridge Univ. Press; 1983. [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: the leaky, competing accumulator model. Psychol Rev. 2001;108:550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, Newsome WT. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature. 1994;370:140–143. doi: 10.1038/370140a0. [DOI] [PubMed] [Google Scholar]


