Skip to main content
NCBI home page
Acta Crystallographica Section D: Biological Crystallography logoLink to Acta Crystallographica Section D: Biological Crystallography
. 2007 Dec 4;64(Pt 1):40–48. doi: 10.1107/S0907444907053516

Dealing with structural variability in molecular replacement and crystallographic refinement through normal-mode analysis

Marc Delarue a,*
PMCID: PMC2394787  PMID: 18094466

The possibility of taking into account large-amplitude collective movements of a given model by using a subset of low-frequency normal modes is evaluated for molecular replacement and refinement using X-ray data or cryo-EM maps.

Keywords: normal-mode analysis, molecular replacement, refinement

Abstract

Normal-mode analysis (NMA) can be used to generate multiple structural variants of a given template model, thereby increasing the chance of finding the molecular-replacement solution. Here, it is shown that it is also possible to directly refine the amplitudes of the normal modes against experimental data (X-ray or cryo-EM), generalizing rigid-body refinement methods by adding just a few additional degrees of freedom that sample collective and large-amplitude movements. It is also argued that the situation where several (conformations of) models are present simultaneously in the crystal can be studied with adjustable occupancies using techniques derived from statistical thermodynamics and already used in molecular modelling.

1. Introduction

It is well known that the success of molecular replacement (MR) depends strongly on the accuracy and completeness of the structural model(s) at hand. Recently, several new techniques and websites have been set up and made available to the crystallographic community to address this issue by linking together existing pieces of software in a very effective way (see, for example, Claude et al., 2004 ▶; Keegan & Winn, 2007 ▶). Because several decisions must be made concerning (i) truncation of the model in uncertain parts; (ii) the actual protocol for sequence alignment and homology modelling; and (iii) the choice of the MR software, the consensus approach is to derive a variety of models and try MR for all of them one by one (see, for example, Delarue, 2007 ▶, and references therein).

In this review, we will try to address a different but related problem, namely the problem of conformational sampling to optimize the success rate of MR. In addition, we will be concerned with the refinement of a model against X-ray or cryo-EM experimental data in the presence of large-amplitude structural changes arising either from ligand (or cofactor) binding, crystallization in a different space group or simply because the available models are from different species caught in different conformations.

We argue that normal-mode analysis (NMA) is a powerful tool to generate structural diversity (decoys) starting from just one structure so that in some cases it can improve the signal-to-noise ratio of the MR score in a dramatic way. Furthermore, we show that it is possible to directly refine the amplitudes of the normal modes against experimental data (X-ray or cryo-EM), allowing a radius of convergence that is unattainable with more standard and traditional refinement methods.

Finally, we briefly address the situation in which several models are present simultaneously in the crystal asymmetric unit (multi-copy refinement) and show that techniques derived from molecular modelling and mean field theory (MFT) can handle this case in a natural way through the refinement of adjustable occupancies (Koehl & Delarue, 1996 ▶). This also suggests that structural diversity can be approached in MR not by scanning each possible model one by one, but rather by treating all (fixed) models in an all-in-one-go fashion and just refining their weights.

2. What are normal modes and what are they good for?

2.1. Definition

By definition, normal modes are the eigenvectors of the matrix of the second derivatives (or Hessian matrix) of the energy: H ij = ∂2 V/∂x i∂x j. The frequencies ωk are the square roots of the associated eigenvalues λk. For a molecule containing N atoms described in a Cartesian coordinate system, the dimension of H is 3N × 3N. The 3N components of each eigenvector (mode) describe the evolution of each atomic coordinate along that mode. The modes can be sorted by ascending associated frequency, starting with the first six modes with zero frequencies that describe the overall translation and rotation motions of the molecule. At a given temperature, the lowest frequency modes are the ones that are the most likely to reproduce large-amplitude movements (see below).

If the potential energy is purely harmonic and can be written as x T Hx (where x T denotes the transpose of x), which is always the case locally if the first-order derivatives of the potential energy are zero, i.e. if the mechanical system is at equilibrium, then the equations of motion around this equilibrium position can be written down analytically. The motion r i(t) of each atom i is just the superposition (linear combination) of normal modes, modulated by sine functions of known frequency ωk with amplitudes c k and some phase shift ϕk, along eigenvectors u k i,

2.1.

2.2. Simplified harmonic potentials: ENM and variants thereof

Normal modes have been used since the mid-1980s for macromolecules, following the work of Brooks & Karplus (1983 ▶), Go et al. (1983 ▶) and Levitt et al. (1985 ▶). However, it was not until recently that this method became truly widespread. This change of affairs was permitted by two factors: (i) the use of simpler energy potential functions, which renders unnecessary the energy-minimization step before diagonal­izing H, and (ii) the realisation that only the calculation of the top 5–10% lowest frequency modes is really necessary, instead of the full spectrum. These two factors allowed much faster normal-mode calculations, while at the same time the simple elastic potential first derived by Tirion (1996 ▶) was shown to be able to capture most of the interesting and biologically relevant movements of proteins (Tama & Sanejouand, 2001 ▶) and molecular motors such as polymerases (Delarue & Sanejouand, 2002 ▶), the GroEL chaperonin (Zheng, Liao et al., 2007 ▶), helicases (Zheng, Brooks et al., 2007 ▶) and even the ribosome (Tama et al., 2003 ▶).

The Tirion potential energy (elastic network model or ENM) is of the type

2.2.

where the sum is restricted to those pairs of atoms (i, j) whose distance d ij is less than a certain cutoff, usually 10 Å, and d ij 0 is the equilibrium value of d ij (see also Bahar et al., 1997 ▶).

This potential energy was further simplified by Hinsen (1998 ▶), who showed that a coarse-grained potential based on the same idea but restricted to CA-only coordinates performed almost equally well. Finally, Sanejouand and coworkers developed a method to calculate ENM normal modes for all atoms in almost the same CPU time as the CA-only model, using the so-called rotation–translation–block (RTB) method that projects all degrees of freedom of a given group of atoms (one residue or more) onto the six rotation–translation degrees of freedom of that block (Tama & Sanejouand, 2001 ▶).

2.3. Collective and large-amplitude movements are well described by low-frequency modes

Because of the graph-like and highly connected nature of the model (see Fig. 1 ▶), it is clear from the outset that the ENM should be good for predicting collective movements: if one pulls one residue, its neighbours will be moved through the spring network, then the neighbours of the neighbours and so on. Also, the models produced by deformation along normal modes should retain protein-like geometry because the interatomic distances are restrained to near-native values; in particular, secondary structures are preserved. Moreover, because of the equipartition of energy, each normal mode carries the same energy, which implies that at a given temperature the amplitudes of movement along low-frequency normal modes are always larger than the amplitude of movement along high-frequency modes (see Fig. 2 ▶). Finally, because of the speed of the calculation, it became possible to check the relevance of the ENM low-frequency modes to the description of known structural transitions on a database scale. This was first accomplished by Krebs et al. (2002 ▶), who used the so-called ‘overlap coefficient’ Ok (Hinsen, 1998 ▶; Tama & Sanejouand, 2001 ▶) to quantify the agreement between the movement predicted for a particular normal mode and an ‘observed’ movement, namely through the dot product of the difference vector Δr between two known structures of the same macromolecule and each normal mode u k (see Fig. 3 ▶),

2.3.

These authors showed that the mean value of the maximum overlap coefficient was around 0.56 and that on average known structural transitions can be described with two modes that happen to tend to be among the very lowest frequency ones (Krebs et al., 2002 ▶).

Figure 1.

Figure 1

Open in a new tab

Elastic network representation of the glutamine-binding protein 1ggg, as output by NOMAD-Ref (Lindahl et al., 2006 ▶). This figure was drawn with PyMOL (DeLano, 2002 ▶).

Figure 2.

Figure 2

Open in a new tab

Influence of a steeper and steeper harmonic potential for the closed form compared with a constant harmonic curve for the open form on the crossing point between the two curves. The closed form is represented by a family of harmonic curves on the right and the open form is on the left with just one harmonic curve. It can be seen that the steeper the potential of the closed form, the closer the crossing point to the closed form. At a constant temperature (horizontal line), the amplitude of the movement away from the equilibrium position is smaller for steeper potentials.

Figure 3.

Figure 3

Open in a new tab

Overlap coefficient Ok (see equation 3) for low-frequency modes (k = 1–106) for the open and closed forms of the glutamine-binding protein (PDB codes 1ggg and 1wdn). The cumulated score is also represented (dashed line).

Further tests of the validity of the ENM model and the deduced NMA were conducted by systematically comparing predicted and measured crystallographic B factors (Kundu et al., 2002 ▶; Kondrashov et al., 2006 ▶). This led to a mean overall correlation coefficient of 0.64 for more than 100 high-resolution X-ray structures when packing interactions are included.

For a given open/closed structural transition (e.g. adenylate kinase or hexokinase), normal modes derived from the open form are usually better at describing the structural change than those derived from the closed form: a possible explanation is that the open form, which has less links and contacts than the closed form, has a less steep harmonic well, thereby shifting the crossing point between the two harmonic curves towards the final state in a naïve one-dimensional representation (see Fig. 2 ▶). This means that one can travel further towards the final state along normal modes derived from the open state, compared with the reverse situation where normal modes are derived from the closed state and the target is the open state.

2.4. How many modes are needed to represent the full transition?

At this stage, it should be made clear that even though normal modes generally represent a much better basis set to describe a structural transition than a randomly generated basis set, the full transition can only be described by the complete set of normal modes. We refer the reader to Van Wynsberghe & Cui (2006 ▶) for the point that more than just a handful of modes are needed to reproduce the atomic displacement correlation matrix. Normal modes are nevertheless convenient because a partial set of them (usually the 10–20 lowest frequency ones) can often describe most of the transition, routinely 90–95% (see, for example, Delarue & Sanejouand, 2002 ▶). Here, the range 90–95% refers to the cumulated square t n = Inline graphic of the overlap co­efficient Ok, which is the correct way to measure how the different orthogonal normal modes (1…n) cooperate to describe a given transition. Interestingly, the quantity tn allows the a priori calculation of how much the root-mean-square deviation (r.m.s.d.) between the two forms can be reduced by applying the best amplitudes c 1…c n (in the sense of minimum r.m.s.d. with the target) along this subset of normal modes (1…n),

2.4.

where r.m.s.d.(n) is the r.m.s.d. of a model deformed along n normal modes after applying the best amplitudes to obtain the minimum r.m.s.d. with the target model and r.m.s.d.(0) is the initial r.m.s.d. of the unperturbed model (Lindahl & Delarue, 2005 ▶).

This formula gives a posteriori the maximum possible reduction of the r.m.s.d. when deforming a model along a given subset of normal modes (up to mode number n) and explains most of the data of Petrone & Pande (2006 ▶). The take-home lesson (and warning message) is that even with a cumulated overlap of 90% (or 95%), there is still 32% (or 22%) of the r.m.s.d. decrease to be explained. Still, for a structural transition with a 7 Å r.m.s.d., such as in adenylate kinase, this means a reduction of the r.m.s.d. to 2.2 Å (or 1.5 Å), which is enough to bring the model into the radius of convergence of conventional refinement programs. The problem of course is that one does not know a priori how many modes are necessary and which are the most relevant.

2.5. How to select the biologically relevant modes

A recurrent question in the field is how to select a priori the best subset of normal modes. Two recent studies have addressed this problem. One of them argues that the bio­logically relevant modes are the most robust ones when using slightly different versions of the ENM (Nicolay & Sanejouand, 2006 ▶). The other one relies on more biological (evolutionary) information, namely a multialignment of closely related sequences, to strengthen or weaken the links between the pairs of atoms in the ENM (Zheng et al., 2006 ▶) depending on the degree of sequence conservation of the different positions involved.

This problem is particularly acute when studying structural transitions that are not a priori well described by low-frequency normal modes, namely loop movements. However, in certain cases, such as the TIM-barrel active site (Kurkcuoglu et al., 2006 ▶), it could be shown that normal modes can actually be used in a meaningful way. This is also the case for some Ser-Thr kinases, which undergo large loop movements upon activation. By carefully filtering for normal modes that do have an influence on the particular loop they are interested in, Abagyian and coworkers showed they could identify a restricted subset of normal modes explaining most of the transition (Casavotto et al., 2005 ▶).

2.6. Generating decoys

We terminate this section by concluding that normal modes, when used with caution, form an excellent basis set for deforming a model around an equilibrium position and sampling its conformations using as few degrees of freedom as possible. This actually has recently been used by Summa & Levitt (2007 ▶) to generate decoys and test various energy functions with a powerful minimizer for their ability to refine back the decoys to the true energy minimum. Equivalently, it is clear that normal modes can be used to improve the chance of successful refinement in the presence of experimental data, i.e. to increase the radius of convergence of such methods.

2.7. Websites

A number of websites have recently been implemented to make these methods available in a user-friendly manner; these include NOMAD-Ref from our group (http://lorentz.dynstr.pasteur.fr/index1.php; Lindahl et al., 2006 ▶) and also elNémo (http://www.elnemo.org; Suhre & Sanejouand, 2004a ▶), ANM from I. Bahar’s group (http://www.ccbb.pitt.edu/anm; Eyal et al., 2006 ▶) and AD-ENM from W. Zheng (http://enm.lobos.nih.gov), as well as webnm@ (http://www.bioinfo.no/tools/normalmodes; Hollup et al., 2005 ▶) derived from K. Hinsen’s MMTK Toolkit.

3. NMA and crystallography

3.1. Crystallographic B factors: early use of NMA to refine them and validation of the ENM

Historically, the refinement of B factors was the first application of normal-mode analysis to X-ray macromolecular crystallography. This was accomplished by several groups at the beginning of the 1990s (Diamond, 1990 ▶; Kidera & Go, 1992 ▶; Kidera et al., 1992 ▶) using standard force fields for NMA. However, this type of refinement was superseded by TLS (Painter & Merritt, 2006 ▶ and references therein).

Conversely, the fit between calculated B factors [B = (8π2/3)〈u 2〉] and experimental B factors was first used to evaluate the relevance of the ENM to the reproduction of biologically significant movements by Bahar et al. (1997 ▶) using a scalar version of the elastic model (the Gaussian Network Model) and then by Phillips and coworkers to test several variants of the ENM (Kundu et al., 2002 ▶; Kondrashov et al., 2006 ▶) on a larger scale of over 100 high-resolution X-ray structures. In particular, these authors were able to show that by using two different elastic constants for linked pairs of atoms within less than R c = 10 Å, depending on whether these atoms were chemically bonded or not, they could improve the correlation coefficient between the calculated and measured B factors from 0.64 to 0.75. More recently, Song & Jernigan (2007 ▶) showed that by including rigid-body movements the correlation coefficient increases to 0.81.

Finally, but quite recently, the full vectorial prediction power of the ENM was put to the test by the same group (Kondrashov et al., 2007 ▶) using a set of high-resolution X-ray structures with refined anisotropic B factors or ADPs. In this case, several implementations of the ENM were again tested as well as normal modes derived from the CHARMM potential. Given the very encouraging results, it is likely that the use of ENM and NMA will gain wider use for B-factor refinement. Indeed, the group of J. Ma recently published two papers showing the benefit of a variant of the CA-based ENM (including harmonic constraints on bond angles and pseudo-dihedral angles) to refine large macromolecular systems at medium resolution (Poon et al., 2007 ▶; Chen et al., 2007 ▶) with about an order of magnitude fewer parameters than the TLS method.

In most applications of the ENM (see, for example, Lindahl & Delarue, 2005 ▶), the B factors are used to calibrate the elastic constant C of the model (see equation 2). The use of molecular dynamics to calibrate C in the presence of explicit solvent can be found in Hinsen et al. (2000 ▶).

3.2. NMA and structural diversity in MR: one-dimensional scans and template generation

However, as stated earlier, there is an even more obvious application of NMA to X-ray crystallography and that is the generation of model variants produced by systematically varying the amplitude of a given mode in a given range. Systematic one-dimensional scans of a given mode can be easily implemented, as well as two-dimensional scans: for each point of the grid search, the model is deformed and its crystallographic score, i.e. R factor, is then calculated (Suhre & Sanejouand, 2004a ▶,b ▶). Generating random linear combinations of a limited set of modes is also possible, deforming the initial model r i 0 into

3.2.

with randomly generated amplitudes ck; it is then possible to sample conformational flexibility within a given r.m.s.d. range (NOMAD-Ref; Lindahl et al., 2006 ▶). Scanning more than two modes is computationally prohibitive. One then has to resort to direct minimization of an R factor or, equivalently, the maximization of a correlation factor.

3.3. Direct refinement of NM amplitudes against X-ray data: radius of convergence

The nonlinear problem of fitting the amplitudes of a restricted set of (low-frequency) normal modes to a given diffraction data set is easily stated. Each structure factor F calc(H) of a model deformed with amplitudes ck along a subset of normal modes (1…Nmod) takes the form

3.3.

Its modulus |F calc(H)| is then used to calculate the global score that needs to be maximized.

3.3.

where CC represents the usual correlation coefficient. This can be achieved by standard conjugate-gradient minimization routines that only need first derivatives of the score. These derivatives can be obtained analytically. This is actually very similar to what was originally performed by M. Tirion using X-­ray fibre-diffraction data (Tirion et al., 1995 ▶).

For single-crystal diffraction data a number of tests have been performed with both calculated and experimental data (Delarue & Dumas, 2004 ▶). Firstly, these tests showed that the program can function as a rigid-body minimizer by using only the first six degrees of freedom. Secondly, if more degrees of freedom are allowed than those used to generate the calculated diffraction data, the program correctly refines their amplitude to 0. Thirdly, by generating many deformed models of a given mean r.m.s.d. and recording what proportion of these models is correctly refined back to the true solution, it could be established that the radius of convergence of the model was about 8 Å using 8 Å resolution calculated diffraction data. Finally, the program was tested with real experimental data obtained from the PDB for the two forms of citrate synthase (PDB codes 5csc and 6csc) and maltodextrin-binding protein (PDB codes 1anf and 1omp) and the results were excellent using either five or ten modes (Delarue & Dumas, 2004 ▶). A direct application to MR was presented in the case of polymerase β (PDB codes 1bpx and 1bpy), which showed that when replacing the rigid-body fitting program after the translation function by the normal-mode amplitude refinement (NOMAD-Ref; Lindahl et al., 2006 ▶), the score of the list of potential solutions was modified in such a way that false positives were down-weighted and the true solution now emerged as that with the highest score (Delarue & Dumas, 2004 ▶).

3.4. Available software and websites

NOMAD-Ref (Lindahl et al., 2006 ▶; http://lorentz.dynstr.pasteur.fr/index1.php) and elNémo (Suhre & Sanejouand, 2004a ▶; http://www.elnemo.org) are available online. Both offer the generation of systematically perturbed models along a given set of normal modes, either separately or as a random mixture of modes matching a user-preset r.m.s.d. The generated trajectories are concatenated PDB files that can be visualized either with PyMOL (DeLano, 2002 ▶) or VMD (Humphrey et al., 1996 ▶).

Nomad-Ref (Lindahl et al., 2006 ▶) can also accept normal-mode amplitude refinement jobs in any space group; the user is asked to give the input PDB file for the model to be refined and the formatted data set of the X-ray data, along with the space group, unit-cell parameters and number of modes.

Successful subsequent examples of the use of this software are described by Kondo et al. (2006 ▶) for NOMAD-Ref and by Akif et al. (2005 ▶) for CaspR and elNémo.

We terminate this section by stressing that the conjugate-gradient refinement of amplitudes described above (Delarue & Dumas, 2004 ▶) and implemented in NOMAD-Ref (Lindahl et al., 2006 ▶) is meant to be used after rotation and translation functions in MR, in place of the rigid-body refinement program (Navaza, 2001 ▶). It requires the rough positioning of the model but can tolerate large errors in the positioning.

4. NMA and cryo-EM (flexible fitting)

When a map, even at low resolution, is available, refinement can be performed either in real space or reciprocal space. The same principles at work in NMA refinement using X-ray data can also be applied with low-resolution cryo-EM data. This is easily seen in real space and was indeed described as ‘normal-mode flexible fitting’, with test cases by Tama and coworkers (Tama et al., 2004a ▶,b ▶), and was subsequently applied to various experimental situations (Mitra et al., 2005 ▶). A slightly more elaborate version of this method was implemented by Hinsen et al. (2005 ▶), also in a real-space formulation, and applied to Ca2+ sarkoplasmic ATPase cryo-EM data. We also described the same type of idea but in a reciprocal-space formulation (Delarue & Dumas, 2004 ▶). The only modification concerns the score in (3), which should now deal with phased structure factors, and this is performed by replacing every product A·B of two real numbers A and B by the complex analogue Re(A·B*).

4.

where it is understood that the mean value 〈F(H)〉 has been subtracted from each phased structure factor. It works extremely well for all the test cases that we have tried, with either synthetic data (citrate synthase, r.m.s.d. = 3.0 Å; adenylate kinase, r.m.s.d. = 7.1 Å) or real experimental data (Ca2+ sarkoplastic ATPase, data courtesy of K. Hinsen & J. J. Lacapère). As is already well known, the radius of convergence is even larger in the presence of phase information than when using only structure-factor moduli.

The case of adenylate kinase is described in more detail in Fig. 4 ▶, with the envelope in cyan and the CA-trace model in magenta. The starting model is the open form (Fig. 4 ▶ a) and the target is the calculated envelope at 10 Å resolution of the closed form (Fig. 4 ▶ b). The amplitudes of ten modes were refined and found to match the expected values closely.

Figure 4.

Figure 4

Open in a new tab

Refinement in an envelope: the case of adenylate kinase (PDB codes 1ake and 4ake). Left, the open form (CA trace) and its envelope at 10 Å resolution (cyan). Right, the refined open form (CA trace) in the envelope of the closed form at 10 Å resolution (cyan).

Other simpler approaches consist of generating systematically perturbed models along one particular mode using, for example, the elNémo web server and then proceeding with the standard MR procedure into the cryo-EM map (Trapani et al., 2006 ▶) for each perturbed model.

The advantage of working in reciprocal space is that it can in principle deal with any kind of regular periodic system. We also implemented a version of the algorithm that works with noncrystallographic symmetry (NCS). As usual, it is best to use an R free criterion (in this case, a ‘CCfree’ criterion) to prevent overfitting (Brünger, 1993 ▶).

The program was used with success by Schaffitzel et al. (2006 ▶) for a large macromolecular assembly through the web interface NOMAD-Ref (Lindahl et al., 2006 ▶).

The same type of algorithm was also implemented in a new program and website called NORMA (Suhre et al., 2006 ▶) based on the earlier rigid-body refinement and molecular-replacement pro­gram URO designed for cryo-EM data by Navaza et al. (2002 ▶), as well as the normal-modes calculation package of Y.-H. Sanejouand. The main differences from NOMAD-Ref are (i) the search for the best amplitudes of the normal modes is stochastic, using the simplex method in a simulated-annealing scheme (Press et al., 2002 ▶), and (ii) there is a much more elaborate algorithm involving macrocyles which periodically recalculates normal modes in alternation with regularization cycles for the geometry of the chain using REFMAC (Murshudov et al., 1997 ▶). Examples and test cases are described both online (http://www.elnemo.org/NORMA) and in the original article (Suhre et al., 2006 ▶).

5. Dealing with structural diversity and refinement: plugging in all possible models and refining their weights

In the preceding section, we have shown that knowledge and generation of conformational diversity through a well parameterized model can help MR. Because trying all models one by one is a very tedious process, this naturally leads to the following question: can one try to refine all the available possible models in a single cycle by weighting each of them with an adjustable weight and refining these weights? The expectation is of course that irrelevant models will be refined to zero occupancy if they make no contribution to the experimental data F obs(H).

This is actually related to another issue that has recently been repeatedly raised in the crystallographic community (de Bakker et al., 2006 ▶), namely how to most faithfully represent the conformational diversity of a model in the crystal environment, especially at low resolution (Furnham, Blundell et al., 2006 ▶; Furnham, Dore et al., 2006 ▶). This goes back to the concept of ‘multicopy refinement’ as defined by Burling & Brünger (1994 ▶). The idea is to simultaneously refine a number of models (typically 8–10) that ‘do not see each other’ but contribute equally to the agreement with the experimental F obs(H). The problem of course is that in doing so one introduces 8–10 times more parameters (coordinates) to be refined, thereby often leading to overfitting. One possible cure to the problem is to resort to dihedral (internal) angle refinement, with about 7–8 times less variables than in the Cartesian coordinates system (Pellegrini et al., 1997 ▶), leaving the ratio (No. of observations/No. of fitted parameters) virtually unchanged. We think that the weights of the different models should also be refined, because there is no reason to believe that each state is equally populated. This actually adds a very small number of variables and our feeling is that it ought to be supported by any refinement program for physical reasons.

In the following test case, we address the simpler case in which the models are fixed and their weight is adjustable and refined against the experimental data (R factor). In MR, this could also be implemented in the usual translation function with little modification of the original code. In the same vein, it should be possible to derive a multicopy version of the rotation function with a score that uses calculated structure factors as the weighted means of structure factors of the possible individual models; the idea is then to refine the weights for each orientation in an effort to increase the signal-to-noise ratio (work in progress).

To test the feasibility of this approach, we performed the following experiment: a total of 25 different models corresponding to 25 increasing amplitudes along one particular normal mode was generated for citrate synthase. Calculated structure factors were generated for one particular model corresponding to amplitude m = 20 and set as F obs. As a starting point all models are equally probable and receive an equal initial probability p m = 1/25. The calculated structure factor for this particular ensemble of models is just the weighted average of all structure factors of the different models F m(H),

5.

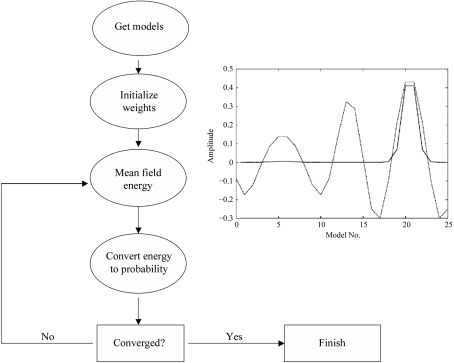
Next we performed mean-field optimization of the weights using the correlation between F calc and F obs as a score. The mean field main cycle performs in the usual way, deriving first the ‘energy’ of each model in the framework of mean field theory; this energy is then converted into a probability using a Boltzmann-like formula (Koehl & Delarue, 1994 ▶, 1996 ▶). When this has been performed for all models, a new energy can be computed and the next cycle can begin until the weights no longer vary (self-consistency condition; see flowchart in Fig. 5 ▶).

Figure 5.

Figure 5

Open in a new tab

Mean field refinement of the weights of 25 different models against diffraction data calculated solely from model 20. The flowchart of the algorithm (see Koehl & Delarue, 1994 ▶, 1996 ▶) is shown, with an inset representing the result of the mean field refinement of amplitudes (continuous line) and comparison with a normal conjugate-gradient refinement (dashed line).

More precisely, if one defines a free energy of the form

5.

where S is the entropy Inline graphic, T is the temperature and R is the usual crystallographic factor, then minimizing the free energy with respect to pm gives (Kubo, 1965 ▶)

5.

where β = 1/T and Em = ∂R/∂pm.

The refinement starts with uniform values of the weights, which are updated at each cycle of the refinement until a self-consistent solution is obtained; at each cycle the derivatives are evaluated at the current solution, i.e. the current set of (pm) values (see Delarue & Orland, 2000 ▶). The proportionality factor Z is determined by using the normalization condition 1 = Inline graphic. The temperature governs the contrast between the different populations. We implemented this method and tested it for the above-mentioned example. For the sake of simplicity the derivatives were calculated numerically, but they could of course be calculated analytically. Convergence was achieved in about 20–30 cycles, leading to a dominant weight for the true expected solution. A control experiment in which the weights were simply refined by conjugate-gradient techniques failed to give the expected result (see inset in Fig. 5 ▶).

In a more general way, it is clear that techniques derived from molecular modelling can be used in the context of crystallographic model refinement by adding one more term to the energy criterion, as derived by imposing the conformity of the F calc(H) to the F obs(H) moduli. Specifically, the issue of dealing with different conformers could benefit from standard statistical thermodynamics techniques, attributing a adjustable weight to each possible copy, which has been used by many authors for side-chain positioning (Koehl & Delarue, 1994 ▶). If a map is available, this could be performed in real space (see MUMBO; Stiebritz & Muller, 2006 ▶) with a score that is just the opposite of the electron density at the tentative position of the atoms. If no phases are available, one would have to resort to a reciprocal-space score based on structure-factor moduli. The derivatives in the ‘mean field energy’ in (11) then give rise to pseudo-two-body interactions that can effectively be dealt with by mean field techniques (Koehl & Delarue, 1996 ▶).

6. Conclusion

Because the normal-mode representation of conformational flexibility has been validated both through the analysis of a database of protein movements and correlation with experimental B factors, its use as a refinement tool has recently emerged. This is true not only for B-factor refinement but also for model refinement. One simple idea that has proved useful is to refine the amplitudes of the normal modes against diffraction data so as to reproduce model deformations through a much reduced set of degrees of freedom.

Furthermore, the inherent flexibility of macromolecules is now well documented and widely recognized as an essential feature that is necessary to explain their biological activity. It seems best to guide the generation of meaningful structural variants with experimental data, e.g. NMR (Best et al., 2006 ▶) or crystallography (Levin et al., 2007 ▶). Performing an en­semble average in crystallography where each copy receives an equal weight is not really possible, as statistical sampling would require many thousands of copies to be refined with a single data set (hopefully, the stable conformations would appear many times in the refined ensemble). Instead, the number of copies that can be refined simultaneously is limited to about 10–12. However, refining the weights of this limited number of copies is possible and does not appreciably change the ratio No. of observed data/No. of fitted parameters. Recent studies using an equal weight for each copy convincingly show that it helps to reduce both R work and R free (Levin et al., 2007 ▶), but that the number of copies needed to explain the data, as assessed by the decrease in R free, can vary from one system to another. We argue here that refining the weights of the different copies, while adding a negligable number of degrees of freedom, should precisely take care of this problem: unneeded copies will have their weight refined to a very small value (pm < 0.01). Additionally, assigning a weight to each possible (fixed) structural model in MR may accelerate structure solution in a straightforward manner. Preliminary tests show that such a weight refinement against experimental data for a series of structural variants of a given model is indeed possible and robust.

Acknowledgments

I thank Ph. Dumas for helpful comments on the manuscript, P. Koehl for useful advice and generating the scripts leading to Fig. 1 ▶, and Y.-H. Sanejouand for his freely available NMA and ENM code and numerous enjoyable discussions. This work was funded in part by an ACI grant from CNRS (IMPBIO 045).

References

  1. Akif, M., Suhre, K., Verma, C. & Mande, S. C. (2005). Acta Cryst. D61, 1603–1611. [DOI] [PubMed]
  2. Bahar, I., Atligan, A. R. & Erman, B. (1997). Fold. Des.2, 173–181. [DOI] [PubMed]
  3. Bakker, P. de, Furnham, N., Blundell, T. L. & DePristo, M. A. (2006). Curr. Opin. Struct. Biol.16, 160–165. [DOI] [PubMed]
  4. Best, R. B., Lindorff-Larsen, K., DePristo, M. A. & Vendruscolo, M. (2006). Proc. Natl Acad. Sci. USA, 103, 10901–10906. [DOI] [PMC free article] [PubMed]
  5. Brooks, B. & Karplus, M. (1983). Proc. Natl Acad. Sci. USA, 80, 6571–6575. [DOI] [PMC free article] [PubMed]
  6. Brünger, A. T. (1993). Acta Cryst. D49, 24–36. [DOI] [PubMed]
  7. Burling, F. T. & Brünger, A. T. (1994). Isr. J. Chem.34, 165–175.
  8. Casavotto, C. N., Kovacs, J. A. & Abagyan, R. (2005). J. Am. Chem. Soc.127, 9632–9640. [DOI] [PubMed]
  9. Chen, X., Poon, B. K., Dousis, A., Wang, Q. & Ma, J. (2007). Structure, 15, 955–962. [DOI] [PMC free article] [PubMed]
  10. Claude, J. B., Suhre, K., Notredame, C., Claverie, J. M. & Abergel, C. (2004). Nucleic Acids Res.32, W606–W609. [DOI] [PMC free article] [PubMed]
  11. DeLano, W. L. (2002). The PyMOL Molecular Graphics System. DeLano Scientific, Palo Alto, CA, USA.
  12. Delarue, M. (2007). Macromolecular Crystallography, edited by M. R. Sanderson & J. V. Skelly, pp. 97–114. Oxford University Press.
  13. Delarue, M. & Dumas, P. (2004). Proc. Natl Acad. Sci. USA, 101, 6957–6962. [DOI] [PMC free article] [PubMed]
  14. Delarue, M. & Orland, H. (2000). Acta Cryst. A56, 562–574. [DOI] [PubMed]
  15. Delarue, M. & Sanejouand, Y.-H. (2002). J. Mol. Biol.320, 1001–1024. [DOI] [PubMed]
  16. Diamond, R. (1990). Acta Cryst. A46, 425–435. [DOI] [PubMed]
  17. Eyal, E., Yang, L. N. & Bahar, I. (2006). Bioinformatics, 22, 2619–2627. [DOI] [PubMed]
  18. Furnham, N., Blundell, T. L., DePristo, M. A. & Terwilliger, T. C. (2006). Nature Struct. Mol. Biol.13, 184–185. [DOI] [PubMed]
  19. Furnham, N., Dore, A. S., Chirgadze, D. Y., de Bakker, P., DePristo, M. A. & Blundell, T. L. (2006). Structure, 14, 1313–1320. [DOI] [PubMed]
  20. Go, N., Noguti, T. & Nishikawa, T. (1983). Proc. Natl Acad. Sci. USA, 80, 3696–3700. [DOI] [PMC free article] [PubMed]
  21. Hinsen, K. (1998). Proteins, 33, 417–429. [DOI] [PubMed]
  22. Hinsen, K., Petrescu, A. J., Dellerue, S., Bellissent-Funel, M. C. & Kneller, G. (2000). Chem. Phys.261, 25–37.
  23. Hinsen, K., Reuter, N., Navaza, J., Stokes, D. L. & Lacapère, J. J. (2005). Biophys. J.88, 818–827. [DOI] [PMC free article] [PubMed]
  24. Hollup, S. M., Salensminde, G. & Reuter, N. (2005). BMC Bioinformatics, 6, 52–60. [DOI] [PMC free article] [PubMed]
  25. Humphrey, W., Dalke, A. & Schulten, K. (1996). J. Mol. Graph.14, 33–38. [DOI] [PubMed]
  26. Keegan, R. M. & Winn, M. D. (2007). Acta Cryst. D63, 447–457. [DOI] [PubMed]
  27. Kidera, A. & Go, N. (1992). J. Mol. Biol.225, 457–475. [DOI] [PubMed]
  28. Kidera, A., Inaka, K., Matsuhima, M. & Go, N. (1992). J. Mol. Biol.225, 477–486. [DOI] [PubMed]
  29. Koehl, P. & Delarue, M. (1994). J. Mol. Biol.239, 249–275. [DOI] [PubMed]
  30. Koehl, P. & Delarue, M. (1996). Curr. Opin. Struct. Biol.2, 222–226. [DOI] [PubMed]
  31. Kondo, J., Urzhoumtsev, A. & Westhof, E. (2006). Nucleic Acids Res.34, 676–685. [DOI] [PMC free article] [PubMed]
  32. Kondrashov, D. A., Cui, Q. & Phillips, G. N. Jr (2006). Biophys. J.91, 2760–2767. [DOI] [PMC free article] [PubMed]
  33. Kondrashov, D. A., van Wynsberghe, A. W., Bannen, R. M., Cui, Q. & Phillips, G. N. Jr (2007). Structure, 15, 169–177. [DOI] [PMC free article] [PubMed]
  34. Krebs, W. G., Alexandrov, V., Wilson, C. A., Echols, N., Yu, H. & Gerstein, M. (2002). Proteins, 48, 682–695. [DOI] [PubMed]
  35. Kubo, R. (1965). Statistical Physics. Amsterdam: North Holland.
  36. Kundu, S., Melton, J. S., Sorensen, D. C. & Phillips G. N. Jr (2002). Biophys J.83, 723–732. [DOI] [PMC free article] [PubMed]
  37. Kurkcuoglu, O., Jernigan, R. L. & Doruker, P. (2006). Biochemistry, 45, 1173–1182. [DOI] [PMC free article] [PubMed]
  38. Levin, E. J., Kondrashov, D. A., Wesenberg, G. E. & Phillips G. N. Jr (2007). Structure, 15, 1040–1052. [DOI] [PMC free article] [PubMed]
  39. Levitt, M., Sander, C. & Stern, P. S. (1985). J. Mol. Biol.181, 423–447. [DOI] [PubMed]
  40. Lindahl, E., Azuara, C., Koehl, P. & Delarue, M. (2006). Nucleic Acids Res.34, W52–W56. [DOI] [PMC free article] [PubMed]
  41. Lindahl, E. & Delarue, M. (2005). Nucleic Acids Res.33, 4496–4506. [DOI] [PMC free article] [PubMed]
  42. Mitra, K., Schaffitzel, C., Shaikh, T., Tama F., Jenni, S., Brooks, C. L. III, Ban, N. & Frank, J. (2005). Nature (London), 438, 318–324. [DOI] [PMC free article] [PubMed]
  43. Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240–255. [DOI] [PubMed]
  44. Navaza, J. (2001). Acta Cryst. D57, 1367–1372. [DOI] [PubMed]
  45. Navaza, J., Lepault, J., Rey, F. A., Álvarez-Rúa, C. & Borge, J. (2002). Acta Cryst. D58, 1820–1825. [DOI] [PubMed]
  46. Nicolay, S. & Sanejouand, Y.-H. (2006). Phys. Rev. Lett.96, 078104–078112. [DOI] [PubMed]
  47. Painter, J. & Merritt, E. A. (2006). Acta Cryst. D62, 439–450. [DOI] [PubMed]
  48. Pellegrini, M., Gronberg-Jensen, N., Kelly, J. A., Pfluegl, G. M. & Yeates, T. O. (1997). Proteins, 29, 426–432. [DOI] [PubMed]
  49. Petrone, P. & Pande, V. S. (2006). Biophys. J.90, 1583–1593. [DOI] [PMC free article] [PubMed]
  50. Poon, B. K., Chen, X., Lu, M., Vyas, N. K., Quiocho, F. A., Wang, Q. & Ma, J. (2007). Proc. Natl Acad. Sci. USA, 104, 7869–7874. [DOI] [PMC free article] [PubMed]
  51. Press, W. H., Flannery, B. P., Teukolsky, S. A. & Vetterling, W. T. (2002). Numerical Recipes, 2nd ed. Cambridge University Press.
  52. Schaffitzel, C., Oswald, M., Berger, I., Abrahams, J. P., Koerten, H. K., Koning, R. I. & Ban, N. (2006). Nature (London), 444, 503–506. [DOI] [PubMed]
  53. Song, G. & Jernigan, R. L. (2007). J. Mol. Biol.369, 880–893. [DOI] [PMC free article] [PubMed]
  54. Stiebritz, M. T. & Muller, Y. A. (2006). Acta Cryst. D62, 648–658. [DOI] [PubMed]
  55. Suhre, K., Navaza, J. & Sanejouand, Y.-H. (2006). Acta Cryst. D62, 1098–1100. [DOI] [PubMed]
  56. Suhre, K. & Sanejouand, Y.-H. (2004a). Nucleic Acids Res.32, W610–W614. [DOI] [PMC free article] [PubMed]
  57. Suhre, K. & Sanejouand, Y.-H. (2004b). Acta Cryst. D60, 796–799. [DOI] [PubMed]
  58. Summa, C. M. & Levitt, M. (2007). Proc. Natl Acad. Sci. USA, 104, 3177–3182. [DOI] [PMC free article] [PubMed]
  59. Tama, F., Miyashita, O. & Brooks, C. L. III (2004a). J. Mol. Biol.337, 985–999. [DOI] [PubMed]
  60. Tama, F., Miyashita, O. & Brooks, C. L. III (2004b). J. Struct. Biol.147, 315–326. [DOI] [PubMed]
  61. Tama, F. & Sanejouand, Y.-H. (2001). Protein Eng.14, 1–6. [DOI] [PubMed]
  62. Tama, F., Valle, M., Frank, J. & Brooks, C. L. III (2003). Proc. Natl Acad. Sci. USA, 100, 9319–9323. [DOI] [PMC free article] [PubMed]
  63. Tirion, M. (1996). Phys. Rev. Lett.77, 1905–1908. [DOI] [PubMed]
  64. Tirion, M., ben-Avraham, D., Lorenz, M. & Holmes, K. C. (1995). Biophys. J.68, 5–12. [DOI] [PMC free article] [PubMed]
  65. Trapani, S., Abergel, C., Gutsche, I., Horcajada, C., Fita, I. & Navaza, J. (2006). Acta Cryst. D62, 467–475. [DOI] [PubMed]
  66. Van Wynsberghe, A. W. & Cui, Q. (2006). Structure, 14, 1647–1653. [DOI] [PubMed]
  67. Zheng, W., Brooks, B. R. & Thirumalai, D. (2006). Proc. Natl Acad. Sci. USA, 103, 7664–7669. [DOI] [PMC free article] [PubMed]
  68. Zheng, W., Brooks, B. R. & Thirmulai, D. (2007). Biophys. J.93, 2289–2299. [DOI] [PMC free article] [PubMed]
  69. Zheng, W., Liao, J. C., Brooks, B. R. & Doniach, S. (2007). Proteins, 67, 886–896. [DOI] [PubMed]

Articles from Acta Crystallographica Section D: Biological Crystallography are provided here courtesy of International Union of Crystallography

RESOURCES