An introduction to molecular replacement

An outline is given of the basic features of the molecular-replacement method for solving crystal structures.

Abstract

Molecular replacement is fundamentally a simple trial-and-error method of solving crystal structures when a suitable related model is available. The underlying simplicity of the method is often obscured by the mathematical trickery required to make the searches computationally tractable. This introduction sketches the essential issues in molecular replacement without going into technical details. General search strategies are discussed and the alternative Patterson and likelihood approaches are outlined.

1. Introduction

The term ‘molecular replacement’ (MR) is generally used to describe the use of a known molecular model to solve the unknown crystal structure of a related molecule. MR enables the solution of the crystallographic phase problem by providing initial estimates of the phases of the new structure from a previously known structure, as opposed to the other two main methods for solving the phase problem, i.e. experimental methods (which measure the phase from isomorphous or anomalous differences) or direct methods (which use mathematical relationships between reflection triplets and quartets to bootstrap a phase set for all reflections from phases for a small or random ‘seed’ set of reflections). The use of MR has naturally become more common as the database of known structures expands. MR is currently used to solve up to 70% of deposited macromolecular structures and at its best has the advantages of being fast, cheap and highly automated.

In principle, MR is very simple. We have a model that we assume approximates the unknown structure and a set of measured diffraction intensities. We then try all possible orientations and positions of the model in the unknown crystal and find where the predicted diffraction best matches the observed diffraction. The model at this point is the best fit to the target structure. The phases for the reflections of the unknown crystal are then ‘borrowed’ from the phases calculated from the model as if it were the model that had crystallized in the unknown crystal and an initial map is calculated with these borrowed phases and the experimentally observed amplitudes. The crystallographer therefore relies on the measured amplitudes to supply the information for rebuilding of the model so that it more closely resembles the target structure. At this point, the MR problem becomes a crystallo­graphic refinement problem.

The MR method raises a number of issues and this paper discusses these issues without attempting to explain the detail of the calculations. These are the following:

• (i) how to choose a suitable model and how to improve models;

• (ii) how to score each orientation and position so as to find when the model best fits the target structure: different target functions will have different degrees of discrimination between the solution and noise;

• (iii) how to search for solutions: strategies for exploring rotations and translations;

• (iv) computational tricks to speed up calculations.

These four aspects of MR are essentially independent. Failure of MR can arise from suboptimal choices in any of the categories. It is fairly obvious that a poor model, low-quality target function or coarse sampling of search space could fail to give a solution, but slow calculations can also prevent structure solution because they limit the number of MR trials that can be performed. Without the computational tricks that speed up MR searches, the searches can take a very long time indeed, even with current computer technology. The computational tricks for speeding up the calculations require some relatively sophisticated mathematics and descriptions of these tricks dominate much of the literature, which can obscure the underlying simplicity of the concepts.

This paper does not attempt to be a comprehensive review of the literature. Early papers were collected by Michael Rossmann, one of the pioneers of the method (Rossmann, 1972 ▶), and there are more recent reviews of rotation functions (Navaza, 2001 ▶) and translation functions (Tong, 2001 ▶). There is also a volume of previous CCP4 proceedings on MR, which contains many useful papers (published as the October 2001 issue of Acta Crystallographica Section D), as well as the other papers in this issue.

1.1. General search strategy

Each molecule needs six parameters to define its orientation and position: three rotation angles and three translations (e.g. α, β, γ; t_x, t_y, t_z). If there are N molecules in the asymmetric unit, then a total of 6N parameters are needed to define the solution. An exhaustive search can take a very long time. As a very rough example: for three angles over the range 0–­360°, 0–180° and 0–360° at intervals of 2.5°, N _rotation = 1.5 × 10⁶ grid points (this can be reduced to perhaps ∼0.9 × 10⁶ points using Lattman angles; Lattman, 1972 ▶), and for three translations in a unit cell of 100 × 100 × 100 Å at 1 Å intervals N _translation = 10⁶ grid points (or fewer in the Cheshire cell; see §6.2). A six-dimensional search then covers N _rotation = 1.5 × 10¹² points. This number is enormously reduced if the two searches can be separated and the translation search only carried out for the best point (or few best points) found in the rotation search: the number of test points in this example is then N _rotation + N _translation = 2.5 × 10⁶ points per rotation solution. For this reason, most programs split the search in this way and pick a relatively small number of good solutions from the rotation search to test in translation searches. Searches in six dimensions are possible, but they may take a very long time: programs using these methods generally avoid an exhaustive six-dimensional search in favour of genetic or evolutionary, random or limited sampling of solutions [e.g. EPMR (Kissinger et al., 1999 ▶), SOMoRe (Jamrog et al., 2003 ▶), Queen Of Spades (Glykos & Kokkinidis, 2001 ▶) and COMO (Tong, 1996 ▶); see also Fujinaga & Read, 1987 ▶; Chang & Lewis, 1997 ▶].

Splitting the search does have a major consequence. In a six-dimensional search or the second three-dimensional search, all parameters (α, β, γ; t _x, t _y, t _z) are defined at each search point, so the correct structure factor F _c(α, β, γ; t _x, t _y, t _z) can be calculated and then compared with the observed F _obs in a scoring function. However, in the first three-dimensional search on rotation, the correct F _c(α, β, γ) cannot be calculated with an unknown translation and so cannot be compared directly with F _obs. There are two ways around this problem, using different approaches and different scoring functions.

• (i) ‘Traditional’ rotation searches are based on the Patterson function, scoring the overlap between observed and model Pattersons in a region around the origin where the function is dominated by self-vectors from within the molecule which are independent of translation (§3.2).

• (ii) ‘Maximum-likelihood’ methods use a statistical approach in reciprocal space to average over all possible values of the unknown translation (§4).

2. Selecting a model

Choosing and preparing a suitable model is arguably the most critical step in MR. Good models have low r.m.s. deviation from the target structure and high completeness; that is, they model a high proportion of the scattering from the target structure with high accuracy. When MR fails, it is nearly always because the model does not match the unknown structure well enough. However, it is impossible to describe ‘well enough’ by giving general limits on r.m.s. deviations and completeness. Moreover, a model that has previously failed to give a solution for a target structure in one crystal form may be able to solve the same target structure for the target in a different space group or with better experimental data for the same crystal form. Almost by definition, better models increase the signal to noise of the MR search, but for different sets of experimental variables the noise in the search will vary enormously although the ‘signal’ from the search model may be the same.

Generally, low r.m.s. deviation between two structures is indicated by high sequence identity. Potential model structure templates are therefore identified by sequence-comparison searches. It is best to then improve upon the model structure templates by omitting regions of large sequence diversity, which are likely to be different and therefore merely add noise to the search, and possibly truncating different side chains to common atoms (Vagin & Teplyakov, 1997 ▶), C^γ atoms (Schwarzenbacher et al., 2004 ▶) or alanine. Since the B factors of the atoms also determine the scattering, modifications to the B factors, for example lowering the B factors for the hydrophobic core of the protein and increasing them in the surface-exposed residues, can also make for a better model (Lebedev et al., 2008 ▶; see MOLREP documentation, http://www.ccp4.ac.uk/dist/html/molrep.html). Where there are several possible models, none of which is expected to be significantly better than another a priori, the search should be repeated with each model or alternatively all the models grouped together as an ensemble (as in Phaser). It is worth considering that if an MR search is difficult primarily because the model is extremely poor then the time spent attempting to obtain a solution with that model is usually inversely proportional to the usefulness of a solution once it has been obtained (see §9).

Unfortunately, proteins with similar sequences do not always have similar tertiary structures. It is not necessarily true even for identical sequences, as the binding of ligands or even different crystal packing environments can lead to rigid-body motions of groups of secondary-structure elements (i.e. hinge motions between structure domains). Some proteins can even undergo a conformational change that rearranges secondary-structure elements (for example, the serpin family of proteins). Although the latter case would be extremely difficult to predict even if such a change was expected, potential conformational changes involving rigid-body motions of domains can usually be spotted by the presence of obvious hinge regions in a structure. For use as a model, these template structures should either be split into the separate domains and the domains used separately as MR models (allowing the change in orientation and position between domains to be picked up by the MR search) or the conformational change should be modelled in advance, for instance along calculated normal modes (Suhre & Sanejouand, 2004 ▶; Delarue, 2008 ▶). The former case has the advantage that fewer searches need to be run, but may fail because the completeness of the structure is low in the search for the first domain. The latter case has the advantage of high completeness of the model but, unless potential hinge motions are sampled extremely finely, even the best model amongst the set is likely to have a relatively high r.m.s. deviation from the target structure.

3. Patterson methods

3.1. Properties of the Patterson function

The Patterson function is the Fourier transform of the squared structure amplitude |F|² with phases set to zero. It is equivalent to FT(FF*) = FT(F) ⊗ FT(F*), where FT() denotes Fourier transform, F* is the complex conjugate of F and ⊗ denotes convolution, i.e. the convolution of the structure [FT(F)] with the structure inverted through the origin [FT(F*)]. This corresponds to a map of interatomic vectors (or strictly interpoint vectors) with the weights of the vectors proportional to the scattering from the atoms.

Pattersons are extremely useful because they can be calculated directly from the observed data, as phase information is not required. They can also be calculated from the model by ignoring the phase component of the calculated structure factor. The Patterson derived from the observed data is the vector map of the contents of the crystal and thus contains not only intramolecular self-vectors but also other vectors (see below) generated by the presence of crystallo­graphic and noncrystallographic symmetry. The Patterson of the model structure would be equally complicated if generated in the same crystal form. However, the model Patterson can be calculated in any crystal form. For the purposes of MR it is much better (in fact essential) to put the model structure in a P1 crystal with a large unit cell such that there is a large space between molecules (the resulting ‘crystal’ is not physically reasonable). The unit cell needs to be large enough that the corresponding Patterson consists of a set of vectors clustered around the origin, separated by a gap from the vector cluster around the neighbouring origins in the Patterson lattice. The model’s intramolecular self-vectors, and only the self-vectors, then lie within a sphere around the origin.

The crystal Patterson is more complicated than the model Patterson from a model in a large P1 unit cell. Depending on the space group, it contains the following:

• (i) multiple sets of self-vectors rotated by the crystal symmetry rotations;

• (ii) overlap between self-vector sets from neighbouring origins;

• (iii) cross-vectors between different molecules which depend on unknown translations.

Unlike the model Patterson, cutting out a sphere around the origin does not give a simple Patterson of one molecule, but nonetheless if the sphere is small enough then most of the enclosed vectors will be intramolecular self-vectors, since vectors between molecules are generally longer. We can use this property to select mostly self-vectors in a rotation search when the translation is unknown.

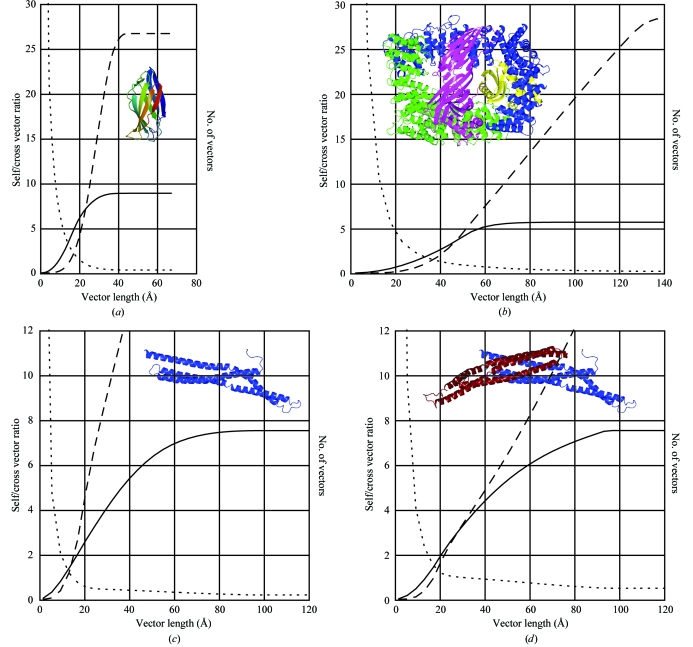
How well are the self-vectors separated from the cross-vectors? Clearly, this depends on the structure and the packing in the crystal. Fig. 1 ▶ shows how the ratio of self-vectors to cross-vectors varies as a function of vector length for a few examples. A larger cutoff radius is appropriate for a larger structure. Fig. 1 ▶(a) shows a small protein (119 residues) where the cross-over point with 50% of cross-vectors is 22 Å: a suitable integration radius might be ∼10–15 Å. For the large complex in Fig. 1 ▶(b) (1730 residues) the cross-over point is 47 Å and an integration radius of 25–30 Å could be used. Large molecules have more ‘inside’ than smaller ones, which is why a large molecule may be easier to solve by MR than a small one.

Figure 1.

The separation between self-vectors and cross-vectors as a function of vector length (radius from the Patterson origin) for some example structures. In each case, the solid line is the number of self-vectors, the dashed line is the number of cross-vectors and the dotted line is the self/cross vector ratio. (a) A small protein, 119 residues, size ∼23 × 23 × 50 Å, space group P2₁2₁2₁, PDB code 1gyu. (b) A larger heterotetramer, 1730 residues, ∼80 × 80 × 100 Å, space group P3₁21, PDB code 1gw5. (c) An elongated monomer, 217 residues, ∼25 × 25 × 110 Å, space group P3₁21, PDB code 1uru. (d) The equivalent dimer, 434 residues, ∼25 × 25 × 145 Å, calculated in space group P3₁.

Elongated molecules and oligomers present particular problems. For an elongated model, a spherical integration mask is obviously not ideal. If the model is a monomer that is part of a tight oligomer, then there are many short cross-vectors between monomers. Fig. 1 ▶(c) shows the vector separation for an elongated monomer which is part of the dimer shown in Fig. 1 ▶(d): in such a case, a dimer model may be a better search object as the many short cross-vectors for the monomer become self-vectors in the dimer. Another way of looking at this is that you already know the relationship between the monomers, so you might as well use this information.

3.2. Patterson rotation function

The Patterson has the property that rotating the model rotates the intermolecular vectors by the same angle. For the Patterson rotation function (see, for example, Navaza, 2001 ▶), we rotate the radius-limited Patterson of the model and score how well it matches the unrotated radius-limited Patterson from the observed data. Restricting the radius evades the problem of not knowing the translation. It is important that the model is placed in a box which is large enough that all intermolecular vectors are outside the search volume; the box size must be at least the largest molecular radius plus the search sphere radius.

Crystal symmetry makes the observed Patterson more complicated: if there are N _sym rotational (primitive) symmetry operators then there are N _sym sets of intramolecular vectors around the origin which smear out the signal, so the signal-to-noise ratio is worse for high-symmetry space groups (also because there are more cross-vector sets which contribute to the noise). In the full rotation search, the model Patterson will overlay correctly with the true structure N _sym times, so there will be N _sym related solutions. Alternatively, at least in some cases, the known crystallographic symmetry can be used to reduce the required range of the search.

The match can be measured as various functions in Patterson space, such as a product function or a correlation coefficient, or as the equivalent to the Patterson product function in reciprocal space. The Patterson product function RF is

that is, the product of the observed crystal Patterson P _observed(u) and the rotated model Patterson P _model(R, u) integrated over all points u in Patterson space within a sphere of radius r _max centred on the origin and excluding the origin peak out to a radius r _min. At any rotation R, the contribution of a point u is only large if peaks coincide in both the crystal Patterson and the rotated model Patterson. This function can be evaluated either in Patterson space (Huber, 1965 ▶; Brünger, 1990 ▶), as implemented in the programs X-PLOR and CNS), over any volume, not necessarily a sphere (Vellieux, 1995 ▶), or by a Fourier transform in reciprocal space. The reciprocal-space version can be made fast by a clever factorization, the ‘fast rotation function’ (Crowther, 1972 ▶; Navaza, 1994 ▶), but only for a sphere.

3.3. Patterson translation function

If the crystal has any rotational symmetry operators (i.e. does not belong to space group P1), then the Patterson also contains ‘cross-vectors’ between atoms belonging to different molecules related by symmetry. If we translate the molecule relative to the symmetry operator (in the plane perpendicular to the axis), then the symmetry-related molecule moves in a different direction and the cross-vectors change. The cross-vectors are thus sensitive to the translation (relative to a symmetry axis) while the self-vectors are not. If one of the axes does not have a symmetry axis perpendicular to it (e.g. the monoclinic axis in P2₁), then translation along this axis does not change the Patterson: however, since the origin is defined with respect to symmetry axes, in such a case the translation is arbitrary: there is no translation to define!

If we know (or wish to test) the orientation of the model from the rotation search, we can calculate model structure factors for every possible shift vector t. The best match with the observed data can then be found by a Patterson product (correlation) search (Fujinaga & Read, 1987 ▶). The translation search is relative to the crystallographic symmetry operators: with no symmetry (space group P1) if the model is translated the Patterson stays the same, so we can place the model anywhere we like in the cell and there is no need for a search. As the model is translated in the plane perpendicular to a rotation axis, the cross-vectors change. Self-vectors within the molecule remain the same and can be subtracted from both the observed and calculated Pattersons to improve the signal-to-noise ratio. The Patterson translation function for a translation t is defined as the product of the observed and model Pattersons, integrated over the whole cell,

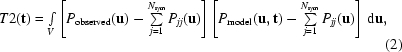where P _observed(u) is the crystal Patterson at point u, P _model(u, t) is the model Patterson shifted by the search vector t and the P _jj terms are the calculated self-vectors. As for the rotation function, this function can be evaluated as a three-dimensional search combining all symmetry operators, either in Patterson space or efficiently in reciprocal space by a fast Fourier transform (Harada et al., 1981 ▶; Navaza & Vernoslova, 1995 ▶; Tong, 2001 ▶).

4. A probability approach

The ‘maximum-likelihood’ method asks the question: for any postulated orientation and position of the model (R, t), what is the probability of obtaining the structure amplitudes that we observe? We can then choose the most likely solution (Bricogne, 1992 ▶; Read, 2001 ▶), an intuitively obvious approach (McCoy, 2004 ▶).

Patterson functions are relatively easily to visualize, since they have a physical meaning (a vector map); it is much more difficult to visualize what is going on in reciprocal space. The functions used for the maximum-likelihood rotation and translation functions are best understood by visualizing probability functions in reciprocal space. We can approximate the probability functions for the reciprocal-space structure factors as Gaussian functions (‘bell-shaped’ curves). The Gaussian probabilities arise from the basic ‘central limit’ theorem (that the distribution of an average tends to a Gaussian, even when the distribution from which the average is calculated is non-Gaussian: this was historically known as the ‘law of errors’) and ‘random walks’ in reciprocal space.

Although we think of the solution for the rotation and translation of the model with respect to the target structure in terms of only one asymmetric unit, to obtain this solution all copies in the unit cell have to be considered. In the Patterson functions, this means the consideration of cross-vectors. In the likelihood function, it means considering the structure factors from all the copies in the unit cell and how they sum to form the total structure factor for each reflection h,

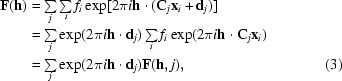where C _j and d _j are the rotation and translation parts of the jth crystal symmetry operator, x _j are fractional coordinates and F(h, j) is the (complex) molecular transform of the molecule corresponding to the jth symmetry operator. The orientation of a model gives rise to the amplitude of the structure-factor contributions; the position gives rise to the phase of the model contributions.

4.1. Likelihood translation function

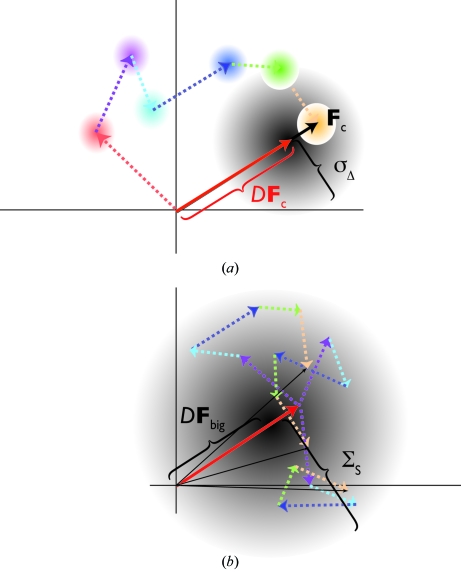
For a given (possibly correct, possibly not) orientation of the model, the model is placed sequentially at grid points throughout the translationally unique volume of the unit cell. At each search position the amplitude and the phase of all the structure factors making up the total structure factor sum is known and therefore the total structure factor can be calculated. This is a key point: although the correct position of the model is not known, for each hypothesis of the position of the model the translation (and hence phase) is known. For each reflection, each partial structure factor in the sum will have a small error arising from errors in the model, which can be modelled as a two-dimensional Gaussian (by the central limit theorem). The total error is also a two-dimensional Gaussian (again by the central limit theorem) of variance σ_Δ ² (Fig. 2 ▶ a) centred on D F _c, where D (0 ≤ D ≤ 1) is given by the correlated component of the atomic errors (see Read, 1990 ▶ and McCoy, 2004 ▶ for a more complete explanation of D and σ_Δ). This then is the probability of observing a particular F _o, i.e. P(F _o|F _c).

Figure 2.

Error distributions for a structure factor in the complex plane. (a) The full structure factor for a translation search arises from the summation of contributions from each asymmetric unit (in this case six), leading to a two-dimensional Gaussian probability distribution. (b) In a rotation search five of the contributions (coloured arrows) can be considered as a random walk from the sixth (F _big), leading to a larger two-dimensional Gaussian (three example random walks are shown).

If the observed structure factors were phased, we would not need any further manipulations to calculate the probability that we want (although we also would not have a phase problem!). The phased observed structure factor F _o would lie in the complex plane, as does the probability distribution for F _o given the calculated structure factor P(F _o|F _c). However, we do not know the phase of the observed structure factor and so the probability function for the phased calculated structure factor must be converted to that for an unphased calculated structure factor. The loss of an unknown variable (called a nuisance variable) from a probability distribution can be achieved by ‘integrating out’ the variable. The removal of the nuisance phase variable leads to the so-called Rice distribution for P(|F _o|||F _c|) (Sim, 1959 ▶; Read, 1990 ▶). This Rice function gives the probability for each putative translation, from which the most likely is selected as the solution to the translation problem.

4.2. Likelihood rotation function

The maximum-likelihood rotation function is conceptually similar to the maximum-likelihood translation function (or, at least, more similar than the Patterson-based rotation and translation functions). For a maximum-likelihood rotation function, the model is rotated sequentially on an angular grid through the unique angular space and the orientation that predicts the data with highest probability is selected. Again, although the correct orientation of the model is unknown, for each hypothesis the orientation is known. At each search orientation only the amplitude of the structure factors for each symmetry-related component making up the total structure-factor sum is known. The relative phase of each component is not known, so the total structure factor cannot be calculated. However, there is still something that we can say statistically about the calculated structure factor. Although we cannot sum up the structure-factor components, we know whether they are large or small. A lot of small structure factors could only lead to a small structure factor, while large structure factors could lead to a much larger total structure factor. This is expressed statistically as a random walk of the components, which again leads to a two-dimensional Gaussian. This two-dimensional Gaussian is much broader (has a much higher variance) than the two-dimensional Gaussian probability distribution for the translation function, which only arises from the errors in the positions of the atoms (in fact, this small error contribution is also added to the random-walk error for the rotation function). Again, this probability function describes the probability of P(F _o|F _c) and the nuisance phase must be integrated out, giving another Rice distribution for P(|F _o|||F _c|). A slightly better probability function can be derived by arbitrarily fixing the phase of the largest component structure factor, leading to a two-dimensional Gaussian offset from the origin (Fig. 2 ▶ b; for a full explanation, see Read, 2001 ▶; McCoy, 2004 ▶).

Note that the larger the number of symmetry operators, the larger the uncertainty introduced by the random walk, which is why the rotation search is less clear in higher symmetry space groups. On the other hand, with more symmetry operators, the random walk is approximated better as a Gaussian (Read, 2001 ▶).

4.3. Combining probabilities

The Rice functions describing the probabilities for each reflection are combined to give the overall probability function: the best solution will not score the highest likelihood for each reflection, but will give the highest likelihood over the whole data set. If the reflections are assumed to be independent, then the total likelihood is the product of the reflection likelihoods. This is an approximation, as the presence of solvent and noncrystallographic symmetry means that the reflections are not independent. The correlations between reflections are very important to solvent flattening, noncrystallographic symmetry averaging and direct methods, but they impossibly complicate the problem for maximum-likelihood MR (and refinement, since the maximum-likelihood translation-function likelihood is the same as the ML refinement target) and the correlations are ignored by necessity. Fortunately, in the context of MR the errors introduced by the approximation are minor compared with other larger errors. The probabilities for each reflection can be combined into a total score as a function of rotation or translation, total probability P(R, t) = Π_h P[|F _o(h)|||F _c(h, R, t)|] or, more usefully, the log probability log[P(R, t)] = 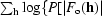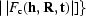, which avoids numerical extremes, which are inconvenient in a computer. The program Phaser (McCoy et al., 2007 ▶) uses a log-likelihood gain relative to an expected ‘random’ score and a ‘Z score’, a multiple of the r.m.s. value taken from a random sample of rotations or translations.

5. Comparison of Patterson and likelihood methods

The maximum-likelihood method explicitly models errors, both experimental (σ_F) and of the model (r.m.s. coordinate error), whereas Patterson methods assume there are no errors, which is clearly not true. This is one of the reasons that likelihood methods are more robust and generally give clearer solutions in difficult cases (Read, 2001 ▶).

The two approaches use different methods to deal with the unknown translation problem in the rotation search. Patterson methods restrict the scoring to a volume (sphere) around the origin, which largely selects intramolecular vectors, while the likelihood method integrates out the unknown translation by a random walk. It can be shown that the Patterson rotation function is a mathematical approximation to the full rotation likelihood function, being essentially the first term in the Taylor series expansion of the likelihood rotation function (Storoni et al., 2004 ▶). The likelihood rotation-function method has the significant advantage that fragments of the structure already placed can be easily used to enhance the signal for the subsequent placement of other components in the asymmetric unit.

Both methods have some control parameters set by the user, in addition to the choice of model. The resolution of the data used is one variable: higher resolution gives better discrimination between correct and incorrect solutions for a correct model, but less tolerance of an inappropriate model. Likelihood methods should be less sensitive to resolution cutoffs, as high-resolution data are automatically down-weighted, depending on the error estimates. Typically, 2.5–4 Å is a good range to try. Other user variables are the radius of integration in Patterson rotation searches and the error estimate on the model in likelihood methods. Although a successful MR solution does not demand high-resolution data, nor unusually accurate data, losing all the strong low-resolution reflections, e.g. by overloading the detector, is bad at least for Patterson methods, since these reflections dominate the Patterson function.

6. Search strategies and descriptions

For the purposes of MR, the coordinates of a molecule are described as a series of vectors in an orthogonal coordinate frame in angstroms and we need to describe rotations and translations which move the coordinates into a new frame; for each atom i, x _i′ = Rx _i + t, where R is a rotation matrix and t is a translation vector. Translations are generally straightforward, but it is usually more convenient to describe a rotation as three angles rather than as a rotation matrix. Unfortunately, there are many different ways of doing this: these are discussed for instance in Evans (2001 ▶) (see also Navaza, 2001 ▶), but briefly rotation in three dimensions may be expressed (i) as polar angles, e.g. as a rotation by an angle κ around an axis whose direction is defined by two other angles (e.g. ω from the pole and ϕ around the equator, somewhat like latitude and longitude), (ii) as Eulerian angles, as three successive rotations around principal axes, e.g. a rotation by γ around z, by β around y and then by α around z [the convention used by Phaser (McCoy et al., 2007 ▶), AMoRe (Navaza, 1994 ▶) and MOLREP (Vagin & Teplyakov, 1997 ▶)], i.e. R = R _z(α)R _y(β)R _z(γ) or (iii) as Lattman angles, defined in terms of Euler angles as θ⁺ (= α + γ), β and θ⁻ (= α − γ) (Lattman, 1972 ▶). Note that in any angular representation there are points of ambiguity, so that there may be multiple ways of decomposing a rotation matrix into angles. For instance, in polar angles if κ = 0, i.e. no rotation, it does not matter which axis you do not rotate about. With the typical definition of Eulerian angles, if β = 0 or 180° the outer rotations by α and γ become coincident, so only α + γ or α − γ are defined.

The main difference between the use of the different angle conventions is the ease with which the rotation can be visualized and whether a uniform sampling of space can be achieved. The three Euler angles are simpler to store and print than nine-element rotation matrices. Rotations in terms of polar angles are the easiest transformations to visualize, particularly when the results are plotted on κ sections. Lattman angles are locally orthogonal, so provide a better search space than the original Euler angles for generating, for example, a pseudo-hexagonal close-packed grid of angles. Confusions in rotations can also arise as some authors prefer to consider rotating the axis system, rather than rotating the object in the opposite direction. It is also common to move the model prior to use in the search, so that the centre of mass is at the origin and the moments of inertia lie along the axes. The transformation may then apply to this reoriented model rather that to the original model coordinates. Programs such as Phaser hide these internal machinations from the user, but AMoRe, for instance, does not.

6.1. Rotation searches and symmetry

There will be a solution to the rotation problem for each orientation of the target structure in the unit cell. However, most search programs only search a unique volume of rotational space. The expression of crystallographic symmetry in Eulerian angles is quite complex, although the resulting restrictions on the search volumes in terms of Eulerian angles are relatively straightforward. If there is more than one component of the asymmetric unit to be searched for (with the same or different search models), this pre-defined unique rotational search volume will not necessarily result in solutions that give close-packed molecules. Note that crystallographic symmetry operators work on fractional rather than orthogonal coordinates.

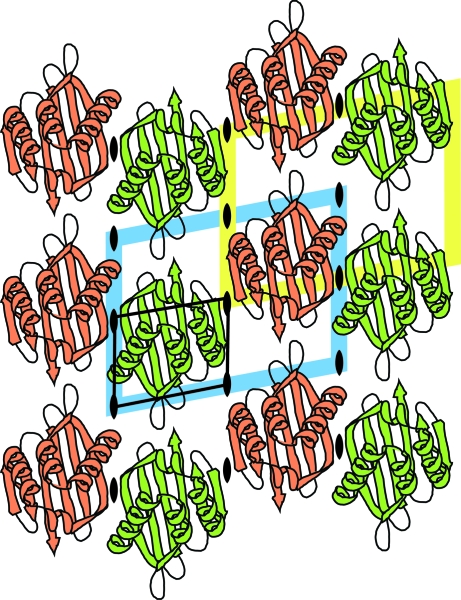
6.2. Translational search volume

In any crystal containing symmetry elements there are multiple ways of defining the cell origin. For example, in the two-dimensional example in Fig. 3 ▶ the cell origin may be placed on any of the dyads and there are four distinct options differing by a translation of half a unit cell in either direction. Shifting the origin by half a cell changes the unknown phases but does not change the amplitudes, so the alternatives are not distinguishable in a translation search. A translation search is relative to a symmetry element, so will give solutions which repeat each half a cell, i.e. we only need to search a quarter of this two-dimensional cell: this is the so-called ‘Cheshire cell’ (see, for example, Tong, 2001 ▶). Defining the Cheshire cell used to be an intellectual challenge left to the user, but modern programs have the volumes tabulated.

Figure 3.

Alternative origins in plane group p2. The cell origin may be placed on any of the dyad axes, giving four possibilities: two are shown in blue and yellow. A translation search need only search a quarter of the cell, the ‘Cheshire’ cell, shown as a thin black line.

If there is more than one molecule per asymmetric unit, placing the first molecule defines the origin, so searches for additional molecules need to cover the whole (primitive) unit cell.

6.3. Space groups

Unlike structures phased by isomorphous replacement methods, it is not possible to obtain a structure in the wrong enantiomorph by MR, since the correct hand is implicit in the search model. However, systematic absences are not always a reliable indicator of translational symmetry operators and they cannot distinguish between enantiomorphic space groups. The rotation search depends only on the crystal point group, but it is often necessary to test multiple space groups in the translation search in order to distinguish different enantiomorphic groups (e.g. P4₁ and P4₃) or groups with different translations (e.g. all eight possible space groups of the form P2_x2_x2_x in the orthorhombic system). This need only be performed for the first molecule in the asymmetric unit.

7. Computational tricks

A simple-minded brute-force search is very slow even on modern computers, so various tricks have been used to speed up calculations. Much of the difficulty in reading the literature on molecular replacement arises from these tricks and their mathematical details.

7.1. Splitting into three-dimensional searches

Splitting the search into two three-dimensional searches was discussed above and appears not to miss solutions that would be found in a full six-dimensional search, provided that sufficient rotation solutions are used in the translation searches: this is equivalent to a limited six-dimensional search.

7.2. Factorization

Many score functions (e.g. the Patterson product function) can be factorized into a part dependent on the molecule alone (the molecular transform) and a part dependent on the search variable (rotation or translation) in such a way that a fast Fourier transform can be used to calculate the score. If the optimum score function cannot be factorized, it may be possible to calculate an approximation which can be factorized and thus be calculated rapidly in order to find candidate solutions and then to rescore these with the full slow function: this is performed, for example, for the rotation search in Phaser, where the likelihood target cannot be factorized (Storoni et al., 2004 ▶).

A simple case of factorization can be seen in factorizing the structure factor needed for a translational search; factorizing the expressions for a rotation search is more complicated. If we shift the molecule by a search vector t, the structure-factor expression becomes

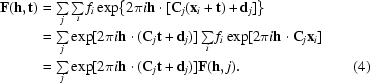The molecular-transform terms F(h, j) for each symmetry operator j can thus be calculated once for all translations and summed over all reflections and over all symmetry operators.

7.3. Grid size

The grid size for the search needs to be fine enough that solutions are not missed, but the potential solutions can be optimized by rigid-body refinement, avoiding the need for a very fine grid.

8. Search-tree strategies

If there are multiple molecules in the asymmetric unit, then the molecules have to be found one at a time, which leads to a complicated tree search of all possibilities. As an example, the following is a rough outline of the search strategy in Phaser (other automated programs follow a similar scheme).

• (i) Rotation search for the first molecule: this should pick up the orientations of all the molecules, as well as possibly false solutions. Select candidate solutions (e.g. by default, Phaser selects scores >75% of the difference between the search mean and the maximum score).

• (ii) For each selected solution, search translations, perhaps in multiple space groups (often the crystal point group is known, but the space group is ambiguous). Choose the best space group and select solutions to keep.

• (iii) For each translation solution, check crystal packing and reject solutions that overlap.

• (iv) Rigid-body refinement of all solutions, cluster solutions which are close together and prune out duplicates.

• (v) For each solution from step (iv), consider this as a fixed solution for molecule 1 (this defines the origin for space groups with ambiguity in the position of the origin) and begin the search for the next (second) molecule. Repeat from step (i) until all molecules are found.

• (vi) Rank the overall solutions.

In such a search, there is a difficult balance between efficiency from early pruning of ‘wrong’ solutions and incorrectly rejecting true solutions. Other search strategies may be more appropriate for difficult MR problems (McCoy, 2007 ▶).

This search strategy takes advantage of the property of the rotational likelihood target function that molecules already placed in the asymmetric unit can be used to enhance the signal in the search for subsequent molecules. Patterson search methods do not easily lend themselves to the use of this information and so the rotational search must be performed for each search model in isolation.

9. How do you know that the solution is right?

The R factor for the initial solution can be very high (55%) even though the models are correctly placed. If the MR process gives one solution that clearly stands out in scores from the next best solution, it is likely to be correct. The principal test for a correct and useful solution is that the maps phased from the solution model should show new and plausible information that was not present in the model. This might be side chains or loops that were different in the model and the unknown structure. If in doubt, you can deliberately leave out parts of the model to see if these parts reappear in the resulting maps. Composite omit maps are a systematic and exhaustive check using this principle. Blocks of the model are successively omitted from the map calculation and the resulting densities for the volumes of the omitted blocks spliced together so that none of the density has ‘seen’ the portion of the model it covers (Bhat, 1988 ▶; Vellieux & Dijkstra, 1997 ▶; Hodel et al., 1992 ▶). The prime-and-switch method uses more sophisticated density-modification methods to remove model bias (Terwilliger, 2004 ▶). At high resolution, automatic model-building procedures such as ARP/wARP are good ways of confirming the solution and reducing model bias. At low resolution (say worse than 3 Å) you should be very cautious and suspicious of the results. Very poor models may not enable anything new to be interpreted in the maps and although the solution may be correct, refinement is unsuccessful in removing the severe model bias. One of the most important tricks of MR is to know when to give up and use experimental phasing!