Skip to main content
PMC home page
Acta Crystallographica Section D: Biological Crystallography logoLink to Acta Crystallographica Section D: Biological Crystallography
. 2007 Dec 4;64(Pt 1):61–69. doi: 10.1107/S090744490705024X

Iterative model building, structure refinement and density modification with the PHENIX AutoBuild wizard

Thomas C Terwilliger a,*, Ralf W Grosse-Kunstleve b, Pavel V Afonine b, Nigel W Moriarty b, Peter H Zwart b, Li-Wei Hung a, Randy J Read c, Paul D Adams b,*
PMCID: PMC2394820  PMID: 18094468

The highly automated PHENIX AutoBuild wizard is described. The procedure can be applied equally well to phases derived from isomorphous/anomalous and molecular-replacement methods.

Keywords: model building, model completion, macromolecular models, Protein Data Bank, structure refinement, PHENIX

Abstract

The PHENIX AutoBuild wizard is a highly automated tool for iterative model building, structure refinement and density modification using RESOLVE model building, RESOLVE statistical density modification and phenix.refine structure refinement. Recent advances in the AutoBuild wizard and phenix.refine include automated detection and application of NCS from models as they are built, extensive model-completion algorithms and automated solvent-molecule picking. Model-completion algorithms in the AutoBuild wizard include loop building, crossovers between chains in different models of a structure and side-chain optimization. The AutoBuild wizard has been applied to a set of 48 structures at resolutions ranging from 1.1 to 3.2 Å, resulting in a mean R factor of 0.24 and a mean free R factor of 0.29. The R factor of the final model is dependent on the quality of the starting electron density and is relatively independent of resolution.

1. Introduction

Iterative model building and refinement is a powerful approach to obtaining a complete and accurate macromolecular model. The approach consists of cycles of building an atomic model based on an electron-density map for a macromolecular structure, refining the structure using the refined structure as a basis for improving the map and building a new model. This type of approach has been carried out in a semi-automated fashion for many years, with manual model-building iterating with automated refinement (Jensen, 1997 ▶). More recently, with the development first of ARP/wARP (Perrakis et al., 1999 ▶) and subsequently of other procedures including RESOLVE iterative model building and refinement (Terwilliger, 2003b ▶), RAPPER (DePristo et al., 2005 ▶) and hip-hop refinement (Ondráček, 2005 ▶), the entire process has become highly automated.

Despite the high degree of sophistication and automation of these procedures, many improvements remain to be made, particularly in the automation of the process at low resolutions, in the completion of models and in model editing and validation. The AutoBuild wizard has been developed as part of the PHENIX project (Adams et al., 2002 ▶) as a second-generation tool for iterative model building, density modification and refinement with these needs in mind. Here, we describe the current features of the AutoBuild wizard and the application of the wizard to a set of structures from a library of experimentally phased structures.

2. Methods

2.1. Iterative model rebuilding, density modification and refinement

The purpose of the AutoBuild wizard is to provide a highly automated system for model rebuilding and completion. The wizard design allows the user to specify data files and parameters through an interactive GUI or alternatively through keyworded scripts. The AutoBuild wizard begins with data files with structure-factor amplitudes and uncertainties, along with either experimental phase information or a starting model, typically from molecular replacement. It then carries out cycles of model building and structure refinement alternating with model-based density modification and produces a relatively complete atomic model.

The AutoBuild wizard has been designed for ease of use combined with maximal user control, with as many parameters set automatically by the wizard as possible, but maintaining parameters accessible to the user through a GUI and through keyword-based scripts. The wizard uses the input/output routines of the cctbx library (Grosse-Kunstleve et al., 2004 ▶) allowing data files of many different formats, so that user data need not be converted to any particular format before using the wizard. Use of the phenix.refine refinement package (Afonine et al., 2005b ▶) in the AutoBuild wizard allows a high degree of automation of refinement so that neither the user nor the wizard is required to specify parameters for refinement. The phenix.refine package automatically includes a robust bulk-solvent model and automatically places solvent molecules (Afonine et al., 2005a ▶).

The five core modules in the AutoBuild wizard are (i) building a new model into an electron-density map, (ii) rebuilding an existing model, (iii) refinement, (iv) iterative model building beginning from experimental phase information and (v) iterative model building beginning from a model. These five procedures are described in the next sections.

The standard procedures available in the AutoBuild wizard that are based on these modules include (1) model building and completion starting from experimental phases, (2) rebuilding a model from scratch, with or without experimental phase information, and (3) rebuilding a model in place, maintaining connectivity and sequence register. In cases where the starting point is a set of experimental phases and structure-factor amplitudes, procedure (1) is normally carried out and the resulting model is then rebuilt with procedure (2). In cases where the starting point is a model (e.g. from molecular replacement) and experimental structure-factor amplitudes, procedure (3) is normally carried out if the starting model differs by less than about 5% in sequence from the desired model; otherwise, procedure (2) is used.

2.2. Building a model into an electron-density map

The AutoBuild wizard has a multi-step procedure for building an initial model into an electron-density map. In this procedure, several models are built, refined and recombined with each other to create new models. If a model is available from a previous step or is provided by the user, this model can also be recombined with the other models. After each stage of building there is a single ‘best’ model and any number of additional models that have been constructed up to that point.

Initial models are scored based on the number of residues built (N built), the number of residues assigned to the sequence (N placed) and the number of chains in the model (N chains). A large number of chains typically indicates that there are many places where chain connectivity is broken. The score (Q) is calculated as Q = N built + N placed − 2 × N chains. Once a model is obtained with an R factor below a pre-set threshold (typically 0.40), then low R factors are used instead of high Q score to identify the best model.

The model-building process begins with (i) building several models into the electron-density map with RESOLVE (Terwilliger, 2003a ▶). The RESOLVE model-building procedure uses a convolution-based search for helices and strand fragments in the map and this search gives results that depend on the precise orientations of the helix and strand templates that are used in the search. Consequently, a relatively diverse set of models can be created by simply varying the parameters of this convolution search. Typically, three models are built in the first step of the AutoBuild model-building procedure. The best model is refined with phenix.refine as described below, including automatic placement of waters and the use of NCS if present, and all models (refined and unrefined) are used in the next step.

The models created in step (i) above are then combined (ii) into a single model using the RESOLVE ‘extend-only’ model-building procedure. In this procedure, a model or models are cut into overlapping segments (typically ten residues long) and are extended as far as possible into the electron density by RESOLVE model building. The resulting set of overlapping segments is then combined into one or more chains by scoring the segments based on length and fit to density and iteratively extending the highest scoring segment by joining another segment to it, crossing over in a place where two or more sequential Cα atoms in the two segments superimpose within a small distance (typically 1 Å).

Once a ‘best’ single model has been obtained from step (ii) above, attempts are made to improve this model (1) by rebuilding in the region outside the current model and (2) by using two methods to try to fit loops. The rationale for rebuilding in the region outside the current model is that the thresholds for the fit of a segment of a model being built are set based on the overall r.m.s.d. of the map in the region containing the macromolecule. If there are some parts of the molecule that are more poorly defined, then these parts might never be built as the density is not high enough in that region. By masking off the region of the molecule that has been built already, the thresholds can be more reasonably determined for the remaining region containing the macromolecule. Additionally, by focusing on a small region of the map where no model has been built, an extensive search for helices and strands can be carried out in a reasonable amount of computing time. A partial model containing segments of the model that can be built outside the region containing the current model is then added to the current set of working models and is recombined with the other working models as in step (ii) above.

Two methods are used to attempt to build loops. One method is to identify all pairs of C-termini and N-termini of existing chains that are near each other (typically within 15 Å) and to try to extend the C-terminus of the first chain and the N-terminus of the second chain in a way that leads to at least one amino acid overlapping with a low r.m.s.d. for main-chain atoms (typically 1 Å). All such connecting segments that are found are then added as if they were another partial model to the current set of working models as in step (ii) above. The second method for building loops is to use the sequence alignment of the current best model to identify short segments that are missing from the chain and to use the above method to try to fill in the loop. This method differs from the case where the sequence alignment is unknown in that the precise number of amino acids in the loop is known. Once a set of loops has been built, a new model is created by grafting these loops onto the current best model, creating a new model with the loops built. This model is then recombined with the other working models as in step (ii) above.

2.3. Rebuilding an existing model

The AutoBuild wizard has two procedures for rebuilding a model. One is to build a model from scratch exactly as described above, except recombining the best parts of the model to be rebuilt with the new model during that building process. The second procedure for rebuilding a model is quite different; this is the ‘rebuild-in-place’ procedure in which an existing model is rebuilt in segments without adding or deleting residues.

The rebuild-in-place procedure has the advantage that no parts of the model are ‘lost’ in rebuilding, but has the dis­advantage that no new model is built. It is best suited to situations where the model is essentially complete and close to correct yet significant local main-chain corrections need to be made to improve the model. The rebuild-in-place procedure is based on the loop-fitting algorithms described above, combined with a procedure for the recombination of two chains that have different conformations but are aligned and have the same residues. The rebuild-in-place option is well suited to the rebuilding of high-sequence similarity models derived from molecular replacement.

In the first step of the rebuild-in-place procedure, the rebuild-in-place method in RESOLVE is used to sequentially rebuild overlapping segments of the model. A segment, typically six residues long, is removed from the model. The loop-fitting algorithm described above is then used to rebuild this segment, maintaining the identities of the residues in the loop and the length of the loop. During the loop-fitting process, the orientations of the residues at the two ends of the resulting gap are varied slightly by randomizing the coordinates of the main-chain atoms of these residues by a small distance (typically an r.m.s.d. of 0.5 Å). As the loop-residue positions are generated by extending from the last amino acid in the chain, this randomization has the effect of introducing diversity into the loops that are created. If a new loop conformation can be found, it is used to replace the existing loop. If no acceptable conformation is found, the existing loop is maintained. The process is repeated, offsetting the loop building by five residues at a time, until the entire model (except the very ends of each chain) has been rebuilt. In the second step of the rebuild-in-place procedure, the model created by rebuilding overlapping segments is recombined with the original model, taking the best-fitting segments of each model. This crossover process is carried out by aligning the two models, identifying all the places where crossover can occur as corresponding Cα atoms that are within a small distance of each other (typically 0.5 Å) and choosing whichever model has the higher local map correlation for each segment of the model from one crossover point to the next. Once a recombined model has been obtained, side chains are rebuilt using a highly curated rotamer library (Lovell et al., 2000 ▶) instead of the rotamer libraries originally created for RESOLVE model building (Terwilliger, 2003a ▶).

2.4. Refinement with phenix.refine

A complete description of the phenix.refine program will be published elsewhere; here, we outline the features used by the AutoBuild wizard in automated model-building procedures. Depending on the quality of the initial electron-density map, the models undergoing refinement may be quite incomplete and contain significant coordinate and/or displacement parameter errors. Therefore, the methods described here have been designed to be fault-tolerant, a necessary requirement for an automated procedure. Firstly, a robust automatic bulk-solvent correction and anisotropic scaling procedure is used to account for the scattering from disordered solvent in the crystal and to correct for any anisotropic diffraction (Afonine et al., 2005a ▶). Coordinate refinement is performed by LBFGS minimization (Liu & Nocedal, 1989 ▶) of the target function E xyz with respect to atomic coordinates, while keeping all other parameters fixed. Exyz can be a least-squares target (LS; Afonine et al., 2005a ▶), an amplitude-based maximum-likelihood target (ML; Afonine et al., 2005a ▶) or a phased maximum-likelihood target (MLHL; Pannu et al., 1998 ▶). In the refinement of atomic displacement parameters (ADPs), the target E ADP is minimized with respect to isotropic ADPs while all other model parameters are fixed. E ADP is defined as

2.4.

Here, N atoms is the total number of atoms in the model, the inner sum is extended over all M atoms in the sphere of radius R around atom i, r ij is the distance between two atoms i and j, B i and B j are the corresponding isotropic ADPs and k is a user-defined constant. By default, R and k are fixed at 5.0 Å and 1.0, respectively, but they can also be refined. The restraint term is scaled to the crystallographic X-ray target by comparison of the X-ray and ADP restraint gradients (Afonine et al., 2005b ▶). This ADP restraint function makes use of the following ideas.

  • (i) A bond is almost rigid; therefore, the ADPs of bonded atoms are similar (Hirshfeld, 1976 ▶).

  • (ii) The ADPs of spatially close (nonbonded) atoms are similar (Schneider, 1996 ▶).

  • (iii) The bond rigidity and therefore the difference between the ADPs of bonded atoms is related to the absolute values of the ADPs. Atoms with higher ADPs can have larger differences (Ian Tickle, CCP4 Bulletin Board).

We have implemented a completely automated protocol for updating the ordered solvent model during the refinement process. If requested by the user (and by default in the AutoBuild wizard), waters are updated (added and removed) in each macro cycle. In the same macro cycle, the complete structure including the updated water structure is subjected to coordinate and ADP refinement. Updating the ordered solvent model involves the following steps.

  • (i) Elimination of waters present in the initial model based on user-defined cutoff criteria by ADP, occupancy and inter-atomic distances (water–water, macromolecule–water).

  • (ii) Location of peaks in a cross-validated likelihood-weighted difference map (Read, 1986 ▶; Urzhumtsev et al., 1996 ▶).

  • (iii) Confirmation of peaks found in the previous step using a 2mF obs − DF calc map.

  • (iv) Elimination of peaks in regions occupied by the macromolecule as determined by the current bulk-solvent mask.

  • (v) Elimination of peaks that are too close to each other (the default minimum distance is 2.0 Å; the strongest peak of two close peaks is retained).

  • (vi) Elimination of peaks that are too close to macromolecular atoms (the default minimum distance is 1.8 Å).

  • (vii) Elimination of peaks that are too far away from macromolecular atoms (the default maximum distance is 6.0 Å).

  • (viii) Elimination of peaks based on the evaluation of tabulated empirical distance distributions derived from the analysis of high-resolution models in the PDB (Afonine et al., 2005a ▶). Distance distributions between water O atoms and macromolecular C, N and O atoms are tabulated. Only peaks with a good fit to at least one distance distribution are retained.

It is not uncommon for macromolecular crystal structures to have more than one copy of a molecule in the asymmetric unit, generating some form of noncrystallographic symmetry (NCS). This symmetry is exploited in the model-building procedure and can also be used in the refinement of the structures in phenix.refine. Briefly, the sequence of the input model is subject to pairwise sequence alignment (Needleman & Wunsch, 1970 ▶; Smith & Waterman, 1981 ▶) to identify similar molecules in the model. If any relationships are found, least-squares superposition of the structures is performed (Kearsley, 1989 ▶) and the coordinate deviation is calculated. If the root-mean-square deviation between the coordinates is below a user-specified tolerance (default 3.0 Å), NCS restraints are applied to the related coordinates during structure refinement. The default NCS restraints are very tight (0.1 Å r.m.s.d. for both main-chain and side-chain NCS-related pairs).

2.5. Iterative model building beginning from an experimental map

The AutoBuild wizard has one procedure for initial iterative model building beginning from an experimental electron-density map and a second procedure for iterative rebuilding and completion of an initial model. These procedures are based in part on the ‘build’ and ‘rebuild’ procedures in the RESOLVE model-building script (Terwilliger, 2003b ▶), although they contain additional steps, as described above.

The procedure for model building from an experimental electron-density map consists of cycles of two basic steps. These steps are (i) using experimental phase information and any additional phase information available in statistical density modification (Terwilliger, 2000 ▶) to create a new working electron-density map and (ii) building and refining a model based on this new map as described in §2.2 above.

For density modification, several sources of additional phase information are used when available. One is any noncrystallographic symmetry information (NCS) as implemented in RESOLVE (Terwilliger, 2002 ▶). NCS is deduced from the coordinates of heavy-atom sites if available and also directly from the current atomic model of the macromolecule as described above if the sequence has been aligned. A second source of information is the presence of recognizable local patterns of density in the electron-density map (Terwilliger, 2003c ▶) and a third is the presence of density matching a helical or strand template in the map (Terwilliger, 2001 ▶). A fourth source of information consists of any partial models of the macromolecule that have been built. For the purpose of identifying patterns in the electron-density map, a composite omit map is produced each cycle in which model information is excluded from the omitted region (Terwilliger, 2003b ▶).

The approach used to carry out density modification in this ‘build’ procedure has several steps. Firstly, electron-density information from local patterns of density and helical and strand locations are combined. Both the identification of local patterns of density and identification of helical and strand fragment procedures result in a pseudo-electron-density map with density that has some information about the true electron-density map. Relative weights for these maps are chosen such that the weighted average pseudo-electron-density map has the highest possible correlation with the current working map. The resulting pseudo-electron-density map is then used as a target for statistical density modification in the same way that NCS and model-based information is incorporated, except that the uncertainty associated with this target map is arbitrarily set to a very high value (typically the r.m.s.d. of the current electron-density map) so as not to overly emphasize this information (Terwilliger, 2003b ▶,c ▶).

The phase probability distributions obtained are then used as prior phase information in a second density-modification step that includes model information as well as any NCS and solvent-flattening information (Terwilliger, 2003b ▶). The models obtained in any previous cycles are used to calculate a composite target model map (Terwilliger, 2003b ▶) and the target model map is scaled to match the working map as closely as possible, including only grid points near the positions of atoms in the model (typically within 2.5 Å). The r.m.s.d. between the working map and this target map at these grid points is used as the uncertainty for the values in the target map in statistical density modification (Terwilliger, 2003b ▶). The map obtained from this statistical density-modification procedure is then used for model building.

2.6. Iterative density modification, model building and refinement beginning from a model

The AutoBuild wizard procedure for iterative model building beginning from a partial model is similar to the procedure starting from experimental phase information, but there are differences resulting from the fact that the phases available are from a partial model. Owing to model bias, the methods for identifying local patterns of density and for finding helices and strands used when starting from experimental phase information are not effective and are therefore skipped. Additionally, the starting map used in the final density-modification step comes from the model and not from experimental phases.

The procedure for density modification beginning from a model uses model-based phase probabilities as the starting point for density modification. A composite target map is calculated from any models available from previous cycles, just as in the procedure described in §2.4. This map is then used as a target for statistical density modification, using the same procedure for calculating uncertainties in the target density that was used for the incorporation of pattern-based density information in §2.4 (i.e. simply using the r.m.s.d. of the map as the uncertainty). The resulting phases and map are then used in statistical density modification including NCS and solvent flattening, yielding a density-modified model-based electron-density map. This map is then used as a starting point for density modification that includes model information as well as any NCS and solvent-flattening information as described in §2.4. The prior phase probabilities for this density-modification step consist only of any experimental phase information that is available (so there is no prior phase information in cases where the rebuilding is performed with no experimental phase information).

3. Results and discussion

3.1. Outline of AutoBuild wizard operation

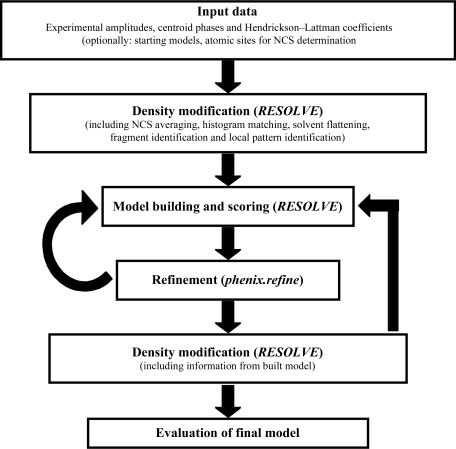
A schematic of the operation of the AutoBuild wizard in a case where experimental phase information is available is shown in Fig. 1 ▶. The wizard begins with experimental structure-factor amplitudes and estimates of crystallographic phases, optionally encoded as Hendrickson–Lattman coefficients (Hendrickson & Lattman, 1970 ▶). The phase information is improved by using statistical density modification to improve the correlation of NCS-related density in the map (if present) and to improve the match of the distribution of electron densities in the map with those expected from a model map (Terwilliger, 2000 ▶). This improved map is then used to build and refine an atomic model. In subsequent cycles, the models from previous cycles are used as a source of phase information in statistical density modification, iteratively improving the quality of the map used for model building. Additionally, during the first few cycles additional phase information is obtained by detecting and enhancing (i) the presence of commonly found local patterns of density in the map and (ii) the presence of density in the shape of helices and strands. The final model obtained is analyzed for residue-based map correlation (Branden & Jones, 1990 ▶) and density at the coordinates of individual atoms, and an analysis including a summary of atoms and residues that are in strong, moderate or weak density and out of density is provided.

Figure 1.

Figure 1

Open in a new tab

Outline of AutoBuild wizard operation beginning from experimental phase information.

3.2. Application of the AutoBuild wizard to model building beginning from structure-factor amplitudes and experimental estimates of phases

We have developed and tested the AutoBuild wizard by using it to build atomic models for structures in the PHENIX structure library where experimental phase information (MIR, MAD or SAD) was available. In each case the structure had been solved previously and an atomic model was available. The PHENIX AutoSol wizard was used to (re)-solve the structure and the AutoBuild wizard was then used with default settings to iteratively build and refine a model.

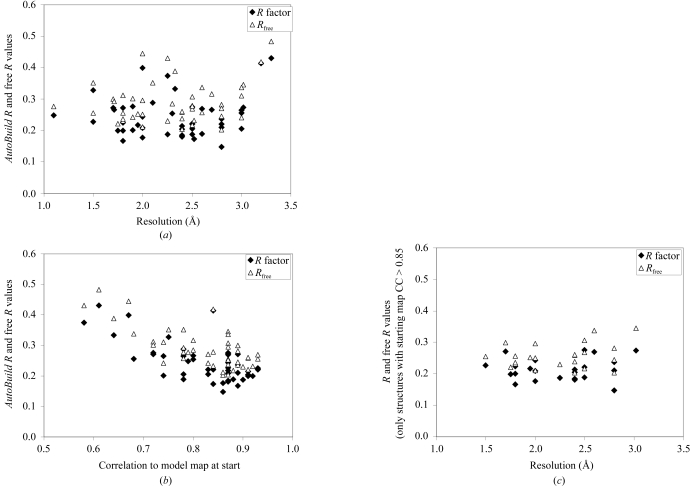
Fig. 2 ▶(a) illustrates the R factors and free R factors obtained in this test on 48 MAD, SAD and MIR structures at resolutions ranging from 1.1 to 3.2 Å. The median R factor for these 48 structures is 0.22 and the median free R factor is 0.28; the corresponding means are 0.24 and 0.29, respectively. Somewhat surprisingly, the R factors and free R factors do not have a strong dependence on resolution. They do, however, have a strong dependence on the quality of the starting density-modified electron-density map. This is illustrated in Fig. 2 ▶(b), which shows the R and free R factors from Fig. 2 ▶(a) plotted as a function of the correlation coefficient of this map with a model map calculated from the known structure. Fig. 2 ▶(c) shows the same data as Fig. 2 ▶(a), except that only the structures built beginning with the highest quality starting maps (with a map correlation to that of the known structure at least 0.85) are shown. Fig. 2 ▶(c) also shows little relationship between R factor and resolution. Taken together, the data in Fig. 2 ▶ indicate that a key determinant of the overall correctness of the models produced by the AutoBuild wizard, as assessed by R and free R factors, is the quality of the starting density-modified experimental map and that the resolution of the structure has a much smaller effect.

Figure 2.

Figure 2

Open in a new tab

R factors (closed diamonds) and free R factors (open triangles) of final models obtained with the AutoBuild wizard for 48 structures from the PHENIX structure library beginning with experimental phases obtained with the AutoSol wizard. (a) R and free R factors as a function of resolution of the data used in modelling. (b) R and free R factors as a function of the correlation coefficient of the starting density-modified experimental map. (c) R factors as in (a), except that only structures with a correlation coefficient of the starting density-modified experimental map of greater than 0.85 are included.

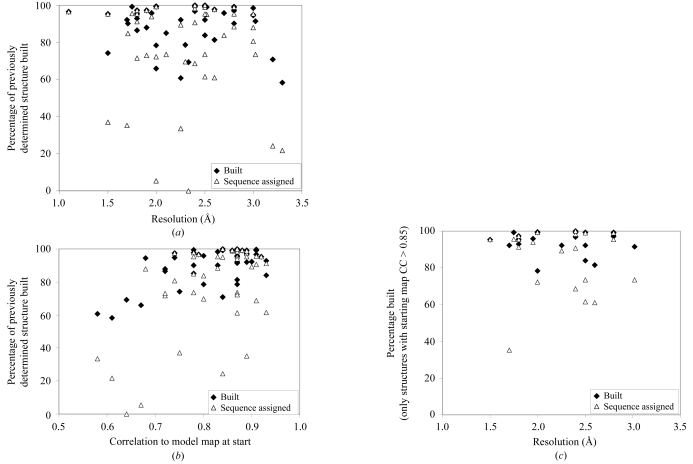
Figs. 3 ▶(a) and 3 ▶(b) illustrate the completeness of the models obtained as a function of the resolution of the data and of the quality of the starting density-modified electron-density map. The median percentage of residues built is 95% and the median percentage of residues assigned to the sequence is 90% (means of 90% and 78%, respectively). The percentage of residues built depends more on the quality of the starting map than on the resolution of the data, although neither of these variables correlates very closely with the completeness of the models. Fig. 3 ▶(c) illustrates that the completeness of the models is somewhat related to the resolution of the data for the subset of cases where a high-quality (map CC > 0.85) starting density-modified map was available, but only weakly so.

Figure 3.

Figure 3

Open in a new tab

Completeness of main-chain model (closed diamonds) and assignment of residues to sequence (open triangles) of final models in Fig. 2 ▶. (a) Completeness as a function of resolution of the data used in modelling. (b) Completeness as a function of the correlation coefficient of the starting density-modified experimental map to the model map. (c) Completeness as a function of resolution as in (a), except that only structures with a correlation coefficient of the starting density-modified experimental map of greater than 0.85 are included.

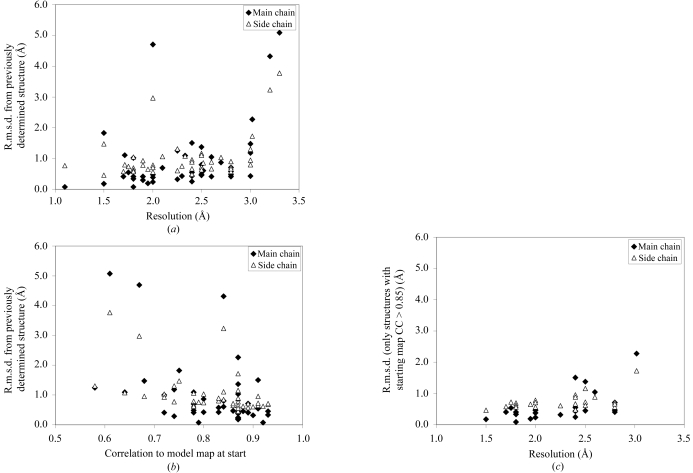
It seemed likely that the resolution of the data would have a significant influence on the details of the atomic model, even if the overall correctness of the model as measured by R factors and completeness was not strongly resolution-dependent. Figs. 4 ▶(a) and 4 ▶(b) show the r.m.s. differences between the coordinates of atoms in the AutoBuild models and those of the models previously obtained for the same structures. In Fig. 4 ▶(a) these are plotted as a function of the resolution of the data and in Fig. 4 ▶(b) they are plotted as a function of the quality of the starting electron-density maps. Surprisingly, there is not a strong relationship between the resolution of the data and the r.m.s.d. between the models obtained and those obtained previously for these structures. The median value of the r.m.s.d. of main-chain atoms for structures based on data from 1.1 to 1.9 Å resolution is 0.57 Å, while the corresponding value for structures based on data from 2.0 to 3.2 Å resolution is 0.47 Å. There is a weak correlation (Fig. 4 ▶ b) between the ability of the AutoBuild wizard to reproduce the previously obtained structural models and the quality of the starting map. When only structures beginning with a high-quality map (map CC > 0.85) are considered (Fig. 4 ▶ c), there is a weak relationship between resolution of the data and the r.m.s.d. between the models built by the AutoBuild wizard and the previously built models.

Figure 4.

Figure 4

Open in a new tab

Main-chain (closed diamonds) and side-chain (open triangles) r.m.s.d. of final models in Fig. 2 ▶ compared with refined models previously obtained for the same structures. (a) R.m.s.d. as a function of resolution of the data used in modelling. (b) R.m.s.d. as a function of the correlation coefficient of the starting density-modified experimental map. (c) R.m.s.d. as in (a), except that only structures with a correlation coefficient of the starting density-modified experimental map of greater than 0.85 are included.

3.3. Application of the AutoBuild wizard to model rebuilding starting from molecular-replacement solutions

The AutoBuild wizard was applied to structure rebuilding of a model derived from molecular replacement. A number of different criteria can be applied to estimate the success of molecular replacement; correlation coefficients for the MR solution and free R values after an initial round of refinement are two commonly used approaches. A more stringent test is the application of model rebuilding using automated methods, for example ARP/wARP (Perrakis et al., 1999 ▶) or the PHENIX AutoBuild wizard described here. If a molecular-replacement solution can be rebuilt without manual intervention, yielding a new model that has reasonable chemical structure while also showing differences from the starting model, it can be reasonably concluded that the MR solution is correct. To test this hypothesis, we performed molecular replacement and subjected the resulting structure to automated model rebuilding. Experimental data to 2.4 Å resolution for α2u-globulin (PDB code 2a2u; Chaudhuri et al., 1999 ▶) were obtained from the Protein Data Bank. A single monomer of the mouse urinary protein structure (PDB code 1jv4; Kuser et al., 2001 ▶) was used as a search model. Molecular replacement, searching for the four molecules in the asymmetric unit, was performed using Phaser (Storoni et al., 2004 ▶; McCoy et al., 2005 ▶) within the PHENIX AutoMR wizard. A clear solution for all four molecules was found. From this solution four other models were created: one monomer was removed to generate a 75% complete model, two monomers were removed to generate a 50% complete model, two monomers were randomly rotated and translated to generate a complete model with 50% of the structure incorrectly placed and the whole tetramer was randomly rotated and translated to generate an incorrectly placed but complete model. Each model was input to the AutoBuild wizard and success was monitored by the final free R value and the number of residues built (Table 1 ▶). When the MR solution is correct and complete or correct and 75% complete it is possible to arrive at a close to complete model with the correct amino-acid sequence after automated building with the PHENIX AutoMR wizard. When the MR solution is incorrect it is not possible to rebuild the model, as indicated by the R factors and the number of residues built. When the model is correct but incomplete (50%) or complete and partially (50%) incorrect automated building is unable to recover the missing or incorrectly placed parts owing to the large initial phase error from the input coordinates.

Table 1. Results of the AutoBuild wizard applied to molecular-replacement models derived for α2u-globulin using data to 2.4 Å.

R factors were calculated using phenix.refine. The deposited α2u-globulin structure contains 688 amino-acid residues arranged in four chains of 172 residues each. Calculation of R factors for the deposited model (PDB code 2a2u), using all available data and the deposited cross-validation set, after one cycle of refinement with phenix.refine produced R and free R factors of 0.196 and 0.235, respectively.

Starting model Final R factors (Rfree/R) Residues built R.m.s.d. (Å) (No. of matching residues)
Correct, 100% complete 0.232/0.196 628 0.3 (628)
Correct, 75% complete 0.252/0.205 567 0.2 (528)
Correct, 50% complete 0.472/0.410 265 0.45 (58)
50% correct, 50% incorrect 0.496/0.432 378 0.63 (32)
Incorrect, 100% complete 0.524/0.456 20 N/A (0)
Open in a new tab

4. Conclusions

The AutoBuild wizard has been developed as a highly automated tool for building and refining macromolecular structures. This procedure can be equally well applied to phases derived from isomorphous/anomalous and molecular-replacement methods. In the case of molecular replacement, the success of automated model building is a strong indicator of the correctness and completeness of the molecular-replacement solution.

We have found that the AutoBuild wizard can yield highly complete and well refined models, with half of the structures in our sample built to at least 95% completeness and the worst built to 58% completeness. Somewhat surprisingly, the final R factors and free R factors depended little on the resolution of the data and much more strongly on the quality of the starting density-modified electron-density map. These results are encouraging for the prospect of generating even more complete models at moderate resolution.

There remain many aspects of model completion that are not yet fully implemented in the AutoBuild wizard. These include building models for regions that are poorly ordered and those that are well ordered but contain multiple conformations. Other aspects that are not implemented are the validation of models, the editing of models to remove segments that are unlikely to be correct and automated placement of ligands. The extension of automated model building and refinement to resolutions lower than about 3.2 Å also presents challenges in model building, although recent developments suggest that this difficulty may be surmountable (DiMaio et al., 2006 ▶).

Acknowledgments

The authors would like to thank the NIH for financial support of the PHENIX project (1P01 GM063210) and the PHENIX Industrial Consortium for financial support. This work was partially supported by the US Department of Energy under Contract No. DE-AC02-05CH11231. RJR is supported by a Principal Research Fellowship from the Wellcome Trust (UK). The algorithms described here are available in the PHENIX software suite (http://www.phenix-online.org).

References

  1. Adams, P. D., Grosse-Kunstleve, R. W., Hung, L.-W., Ioerger, T. R., McCoy, A. J., Moriarty, N. W., Read, R. J., Sacchettini, J. C., Sauter, N. K. & Terwilliger, T. C. (2002). Acta Cryst. D58, 1948–1954. [DOI] [PubMed]
  2. Afonine, P. V., Grosse-Kunstleve, R. W. & Adams, P. D. (2005a). Acta Cryst. D61, 850–855. [DOI] [PMC free article] [PubMed]
  3. Afonine, P. V., Grosse-Kunstleve, R. W. & Adams, P. D. (2005b). CCP4 Newsl.42, contribution 8.
  4. Branden, C. I. & Jones, T. A. (1990). Nature (London), 343, 687–689.
  5. Chaudhuri, B. N., Kleywegt, G. J., Björkman, J., Lehman-McKeeman, L. D., Oliver, J. D. & Jones, T. A. (1999). Acta Cryst. D55, 753–762. [DOI] [PubMed]
  6. DePristo, M. A., de Bakker, P. I. W., Johnson, R. J. K. & Blundell, T. L. (2005). Structure, 13, 1311–1319. [DOI] [PubMed]
  7. DiMaio, F., Shavlik, J. & Phillips, G. N. (2006). Bioinformatics, 22, e81–e89. [DOI] [PubMed]
  8. Grosse-Kunstleve, R. W., Sauter, N. K. & Adams, P. D. (2004). IUCr Comput. Commission Newsl.3, 22–31.
  9. Hendrickson, W. A. & Lattman, E. E. (1970). Acta Cryst. B26, 136–143.
  10. Hirshfeld, F. L. (1976). Acta Cryst. A32, 239–244.
  11. Jensen, L. H. (1997). Methods Enzymol.277, 353–366. [DOI] [PubMed]
  12. Kearsley, S. K. (1989). Acta Cryst. A45, 208–210.
  13. Kuser, P. R., Franzoni, L., Ferrari, E., Spisni, A. & Polikarpov, I. (2001). Acta Cryst. D57, 1863–1869. [DOI] [PubMed]
  14. Liu, D. C. & Nocedal, J. (1989). Math. Program.45, 503–528.
  15. Lovell, S. C., Word, J. M., Richardson, J. S. & Richardson, D. C. (2000). Proteins, 40, 389–408. [PubMed]
  16. McCoy, A. J., Grosse-Kunstleve, R. W., Storoni, L. C. & Read, R. J. (2005). Acta Cryst. D61, 458–464. [DOI] [PubMed]
  17. Needleman, S. & Wunsch, C. (1970). J. Mol. Biol.48, 443–453. [DOI] [PubMed]
  18. Ondráček, J. (2005). Acta Cryst. A61, C163.
  19. Pannu, N. S., Murshudov, G. N., Dodson, E. J. & Read, R. J. (1998). Acta Cryst. D54, 1285–1294. [DOI] [PubMed]
  20. Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol.6, 458–463. [DOI] [PubMed]
  21. Read, R. J. (1986). Acta Cryst. A42, 140–149.
  22. Schneider, T. (1996). Proceedings of the CCP4 Study Weekend. Macromolecular Refinement, edited by E. Dodson, M. Moore, A. Ralph & S. Bailey, pp. 133–144. Warrington: Daresbury Laboratory.
  23. Smith, T. F. & Waterman, M. S. (1981). J. Mol. Biol.147, 195–197. [DOI] [PubMed]
  24. Storoni, L. C., McCoy, A. J. & Read, R. J. (2004). Acta Cryst. D60, 432–438. [DOI] [PubMed]
  25. Terwilliger, T. C. (2000). Acta Cryst. D56, 965–972. [DOI] [PMC free article] [PubMed]
  26. Terwilliger, T. C. (2001). Acta Cryst. D57, 1755–1762. [DOI] [PMC free article] [PubMed]
  27. Terwilliger, T. C. (2002). Acta Cryst. D58, 2082–2086. [DOI] [PMC free article] [PubMed]
  28. Terwilliger, T. C. (2003a). Acta Cryst. D59, 38–44. [DOI] [PMC free article] [PubMed]
  29. Terwilliger, T. C. (2003b). Acta Cryst. D59, 1174–1182. [DOI] [PMC free article] [PubMed]
  30. Terwilliger, T. C. (2003c). Acta Cryst. D59, 1688–1701. [DOI] [PMC free article] [PubMed]
  31. Urzhumtsev, A. G., Skovoroda, T. P. & Lunin, V. Y. (1996). J. Appl. Cryst.29, 741–744.

Articles from Acta Crystallographica Section D: Biological Crystallography are provided here courtesy of International Union of Crystallography

RESOURCES