Three difficult MR cases are reported in which the orientation of a search oligomer or its internal parameters were determined and the oligomer was positioned according to the maximal value of the correlation coefficient in a series of translation searches. Such an exhaustive search was feasible because of constraints on the model parameters derived from the self-rotation function.
Keywords: molecular replacement, exhaustive search
Abstract
The efficiency of the cross-rotation function step of molecular replacement (MR) is intrinsically limited as it uses only a fraction of the Patterson vectors. Along with general techniques extending the boundaries of the method, there are approaches that utilize specific features of a given structure. In special cases, where the directions of noncrystallographic symmetry axes can be unambiguously derived from the self-rotation function and the structure of the homologue protein is available in a related oligomeric state, the cross-rotation function step of MR can be omitted. In such cases, a small number of yet unknown parameters defining the orientation of the oligomer and/or its internal organization can be optimized using an exhaustive search. Three difficult MR cases are reported in which these parameters were determined and the oligomer was positioned according to the maximal value of the correlation coefficient in a series of translation searches.
1. Introduction
Molecular replacement (MR) is a common phasing technique in macromolecular crystallography and its use is increasing with the rise in the number of structures in the Protein Data Bank (PDB; Berman et al., 2002 ▶). Typically, a user will supply a homologous model and the experimental X-ray data to one of the popular MR programs, such as AMoRe (Navaza, 1994 ▶), CNS (Brünger et al., 1998 ▶), MOLREP (Vagin & Teplyakov, 1997 ▶) or Phaser (Read, 2001 ▶). Alternatively, X-ray data and target sequence will be fed into one of the MR pipelines, such as BALBES (Long et al., 2008 ▶) or MrBUMP (Keegan & Winn, 2007 ▶). If the correct solution is produced, in most cases it will be successfully rebuilt and refined to acceptable R factors.
A failure to refine an MR solution usually means that the solution is incorrect. However, twinning or partial crystal disorder may hinder the refinement of correct MR solutions (Wittmann & Rudolph, 2007 ▶; Trame & McKay, 2001 ▶). In addition to this, some correct MR solutions cannot be refined because the difference between the target structure and MR solution is beyond the convergence limits of the refinement programs (see, for example, Fleming et al., 1998 ▶).
There are cases in which a correct MR solution, even one that fails to refine, is a valuable and possibly the only source of initial phases. Generally, difficult MR phasing is required in cases where crystals are poorly reproducible or non-isomorphous and for proteins expressed in eukaryotic cells, where SeMet incorporation is difficult to achieve. Difficult MR is often preferable to experimental phasing for radiation-sensitive crystals. While such crystals may withstand radiation exposure during native data collection, they are likely to be damaged during the longer exposures required for multiple anomalous dispersion (MAD) data collection (Bourenkov & Popov, 2006 ▶).
There are three issues to be addressed when difficult MR appears to be the only approach to phasing: which methods can facilitate the MR search, how to validate the MR solution and how to improve phases. MAD or multiple isomorphous replacement (MIR) data are frequently used for validation and phase improvement. Anomalous/isomorphous substructures with multiple and/or partially occupied sites are difficult to solve, but they can easily be found in difference Fourier synthesis using MR phases, thus confirming the correctness of the MR solution. Experimental phases can be further used to improve poor estimates of phases provided by MR (Czjzek et al., 2001 ▶). Schuermann & Tanner (2003 ▶) proposed that anomalous differences from S atoms should routinely be collected and used in MR structure determination. An interesting method is described by Grininger et al. (2004 ▶), in which the correctness of the molecular-replacement solution was verified by identifying radiation-damage-induced structural changes.
The presence of noncrystallographic symmetry (NCS) can be advantageous for structure determination by MR. In many cases the orders and directions of NCS axes can be determined on the basis of experimental data using the self-rotation function (SRF; Rossmann & Blow, 1962 ▶). Translational NCS can be detected using the native Patterson synthesis. A comparison of experimental functions and functions generated from MR solutions is a good validation tool. Two of many examples are given by Makino et al. (2005 ▶) and Keillor et al. (2003 ▶).
The presence of NCS (excluding that generated by pure translation) allows phase improvement by averaging (Bricogne, 1974 ▶). Often, a conserved oligomer is a better search model for MR than a monomer. In many cases, the oligomer models are readily available in the PDB and these are routinely used for MR trials in MR pipelines (Keegan & Winn, 2007 ▶; Long et al., 2008 ▶). The locked rotation function (LRF) and locked translation function (LTF) were developed to build an oligomer from monomers and to orient it in accordance with the SRF (Tong, 2001 ▶). The resulting oligomer is used in a conventional translation-function (TF) search. NCS analysis has to be performed with special care when NCS is used directly for structure determination (as in the LRF/LTF method). An interesting example of misleading the SRF was reported by Asojo et al. (2003 ▶).
The point-group symmetry of an oligomer is an approximate symmetry and its deviation from the exact symmetry may be too large for methods based on averaging of the Patterson function (LRF/LRF) to be successful. The selection of cross-rotation function (cross RF) peaks obeying NCS (CRANS; Lilien et al., 2004 ▶) is free of this disadvantage. An interesting example in which the selection criterion was based on both the SRF and the electron-microscopy reconstruction of a trimer was presented by Trapani et al. (2006 ▶). A technique in which no restrictions are imposed on the organization of the oligomer is the multi-copy search (Vagin & Teplyakov, 2000 ▶) implemented in MOLREP.
Conventional three-dimensional implementations of Patterson superposition methods suffer from a low signal-to-noise ratio at the rotation-search step. The exhaustive six-dimensional search at low resolution enhanced by multi-start local optimization against all data (SOMoRe; Jamrog et al., 2003 ▶) or six-dimensional stochastic optimization employing, for example, evolutionary programming (EPMR; Kissinger et al., 1999 ▶) allow this problem to be avoided. Moreover, a stochastic approach proved to be successful in solving a 23-dimensional MR problem (Queen of Spades; Glykos & Kokkinidis, 2003 ▶). These methods are especially relevant in cases of low solvent content (Nakai et al., 2003 ▶).
As a variation of a six-dimensional search, the TF search can be conducted for a comprehensive sample of orientations of the search model (Sheriff et al., 1999 ▶). In general, an exhaustive search over some parameters of the model can be combined with conventional MR. For example, a one-parameter family of hexamers generated from a homologous trimer were tested by conventional MR (Leonard et al., 2006 ▶); all possible orientations of the idealized transmembrane helices forming symmetric helical bundles were generated and used in an MR search (Strop et al., 2007 ▶).
In the presence of NCS in the target crystal, the availability of a related oligomeric search model makes it possible to reduce the number of dimensions of the search space. As a result, the orientations (and in some cases the internal parameters) of the oligomer can be scanned by a systematic exhaustive search using a TF and the cross RF step can therefore be omitted. This paper presents three examples of successful structure solution using an NCS-constrained exhaustive search.
2. Methods
The NCS-constrained exhaustive search is applicable when protein quaternary structure is proven to be conserved by analysis of several homologues, when there is strong evidence for the target protein being a similar oligomer and when the problems with the conventional MR are shown to occur at the cross RF step.
2.1. Technical details
The implementations described in this paper require some data and model manipulations, but automation of these operations seems to be straightforward. In the simplest cases (the first two examples) the procedure is as follows. The orientations of the NCS axes are defined from an SRF, the axes of the reference oligomer are aligned with the NCS axes and a table of allowed oligomer orientations relative to the reference orientation is created using a text editor. This table is used for TF trials and substitutes for the table containing the angular coordinates of cross RF peaks. Depending on the crystallographic and NCS symmetries, several non-equivalent reference orientations may be required. In the cases where the internal organization of the (larger) oligomer is varied, a new model is generated for each TF trial (as in the third example).
The problems of analysis and the validation of a huge amount of potential solutions intrinsic to the exhaustive search are less relevant for the constrained exhaustive search. When the number of scanned parameters is reduced to one or two, visual analysis of the resulting one- or two-parameter function is possible. Several such functions can be generated for differently modified search models and different weighting of the data to find the point in the parameter space that persistently reproduces a high value of the target function, the highest correlation coefficient (CC) in the TF search.
The NCS-constrained exhaustive search is also applicable when a biological oligomer is located on the crystallographic axis (or axes). One possibility is to use a correct part of the oligomer (say a half of a tetramer) in the TF search. Another possibility is to expand the data into a lower symmetry space group, such that the relevant crystallographic axes are treated as NCS axes and, for the correct TF solution, the oligomer molecular axis will appear in the position of the ‘switched-off’ crystallographic axis (a validation criterion). Although different sections of the overall parameter space are scanned in these two approaches, the number of unknown parameters is the same. Thus, these approaches would be equally reliable unless packing considerations are used in the TF search. In the second approach, the correct TF solution is less likely to be rejected based on the packing constraints, as the contacts between oligomers are looser than those between parts of the same oligomer.
2.2. Oligomeric model
To find out whether the NCS-constrained search is applicable to a particular case and to find a suitable search model, it is necessary to investigate the conservation of the quaternary structure of the protein in a series of homologues. As an alternative to visual inspection of the structures using molecular graphics with generation of crystal symmetry equivalents, the quaternary structure database PISA (Krissinel & Henrick, 2004 ▶) can be used. It may happen that while within a family of related proteins all representatives have a higher oligomeric state, e.g. tetramers, only lower symmetry oligomers, e.g. dimers, are conserved and these will be better models for MR and for a constrained exhaustive search.
Another prerequisite of the method is the presence of a similar oligomer in the target crystal structure. While this question cannot be answered with certainty before the structure is determined, an agreement between several indicators can support the proposed hypothesis. The oligomeric state of the protein in the crystal can be assessed directly in two ways. Firstly, it is checked whether the number of subunits per AU can be chosen to satisfy the hypothesized oligomeric state and at the same time to give a reasonable solvent content of the crystal (Matthews, 1968 ▶). Secondly, the point-group symmetry of the hypothesized oligomer has to be consistent with the SRF (Rossmann & Blow, 1962 ▶). The complete protein oligomer can be partially generated by crystallographic symmetry. Therefore, analysis of the oligomeric state of the protein in a crystal requires the knowledge of the crystal symmetry, particularly the presence of proper rotation elements in the space group. In the case of a conserved oligomer, the quaternary structure of the protein in the crystal is usually the same as in solution and the number of protein subunits in the oligomer can be estimated from size-exclusion chromatography and/or analytical ultracentrifugation studies (Lebowitz et al., 2002 ▶).
In general, none of the above indicators gives an unambiguous result. Thus, for several monomers per AU, analysis based on the expected solvent content of the crystal gives a range rather than the exact number of monomers in the AU. This is because the solvent content varies between crystals. Similarly, measurements in solution are often inconclusive owing to the experimental errors. In theory, the SRF reveals peaks corresponding to the point-group symmetry of an oligomer. However, there could be various complications. In the case of high crystallographic symmetry and/or high point-group symmetry of the oligomer, these peaks can be weak or even undetectable. In another limiting case, the interaction of NCS operators with crystallographic symmetry can create the impression of higher symmetry of the oligomer. Crystal twinning can contribute to both effects. The case reported by Asojo et al. (2003 ▶) illustrates the latter complication. In this example, the inference that led to a correct conclusion also involved analysis of the native Patterson map, in which the high non-origin peaks indicative of the translational NCS were not present.
2.3. Analysis of cross RF from a conventional MR trial
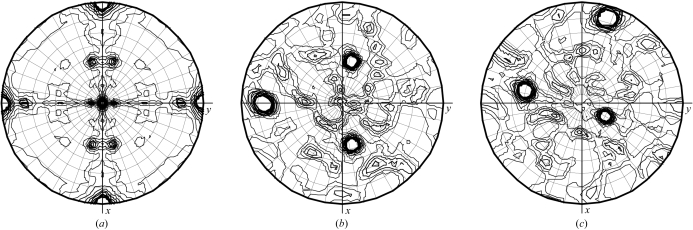
We assume that a conserved homologous oligomer has already been used as a search model in conventional MR trials and that none of the putative MR solutions can be refined. In the case of an oligomeric search model, the cross RF step of MR can be specifically validated, as only orientations consistent with NCS could be correct. Visual analysis can be performed as follows. For each of several highest peaks of cross RF used during the previous MR attempt, the search model is brought into a corresponding orientation and structure amplitudes from this model are computed in P1 with target cell dimensions. Calculations in P1 allow interactions between NCS and crystallographic symmetry to be avoided and thus simplify the analysis. If the SRF for one of the orientations is consistent with the native SRF (Fig. 1 ▶) this is probably a correct cross RF solution and a more thorough TF search may be required in this case. Otherwise, it is worth omitting the cross RF step and trying an NCS-constrained exhaustive search.
Figure 1.
Validation of cross RF peaks using the SRF in the case of an oligomer search model. (a) The χ = 180° section of a native SRF indicates 222 molecular symmetry. (b, c) χ = 180° sections of an SRF in P1 generated using F calc from a tetrameric search model in orientations corresponding to the fourth (correct) and eighth (incorrect) highest peaks of the cross RF. The consistency of the peaks in (a) and (b) suggest that the fourth cross RF peak is likely to be a correct cross RF solution. This figure was generated using MOLREP (Vagin & Teplyakov, 1997 ▶), Proteus vulgaris tryptophanase data (PDB code 1ax4; Isupov et al., 1998 ▶) and the Citrobacter intermedius tetrameric tyrosine phenol-lyase model (PDB code 1tpl; Antson et al., 1993 ▶).
3. Examples
In this paper, the NCS-constrained exhaustive search is illustrated by three examples. The first example is discussed in more detail.
3.1. Structure solution of the oxygenating component of 3,6-diketocamphane monooxygenase from Pseudomonas putida
3.1.1. Background
The 3,6-diketocamphane monooxygenase from P. putida is a Baeyer–Villiger monooxygenase enzyme involved in the oxidative-degradation pathway of (−)-camphor. It is reported to be a loose trimeric complex containing an NADH dehydrogenase subunit and a homodimeric FMN-binding oxygenating component (DKMO; Jones et al., 1993 ▶). A subunit of DKMO has a molecular weight of 42 kDa (McGhie et al., 1998 ▶). The DKMO gene is located on the large CAM plasmid (Shaham et al., 1973 ▶) of P. putida and the protein has not been cloned to date. DKMO was purified from wild-type P. putida cells after induction by excess (±)-camphor. The protein was crystallized in space group P212121 (McGhie et al., 1998 ▶). The a and b unit-cell parameters were the same for all crystals (55 and 93 Å, respectively), but c varied between different crystals in the range 140–165 Å. Attempts to solve the DKMO structure by MIR were hampered by crystal non-isomorphism. The SeMet MAD approach was not possible owing to the absence of a cloned gene. An attempt was made to solve the DKMO structure by MAD using a halogen substructure (Dauter & Dauter, 1999 ▶) with data collected to 2.5 Å at the bromine peak, inflection and high-energy remote wavelengths from a crystal soaked for 30 s in 1 M NaBr. This crystal had unit-cell parameters a = 54.9, b = 93.3, c = 140.8 Å. Although the data appeared to contain a strong anomalous signal, no solution could be found for the positions of the anomalous scatterers. Therefore, MR seemed to be the most promising way of obtaining initial estimates of the phases. MR trials were performed using the bromide-derivative data and 2.0 Å synchrotron data collected from a native crystal with unit-cell parameters a = 55.0, b = 93.4, c = 162.0 Å.
3.1.2. Model preparation and preliminary MR trials
PSI-BLAST (Altschul et al., 1997 ▶) found several flavin-binding proteins with known structure that were remote homologues of DKMO, the closest one being the bacterial luciferase from Vibrio harveyi (Fisher et al., 1995 ▶). Both the α- and the β-subunits of the αβ heterodimeric luciferase had 16% sequence identity with DKMO; however, the α-subunit appeared to be a better search model as it was aligned over a longer range of amino acids (346 compared with 283).
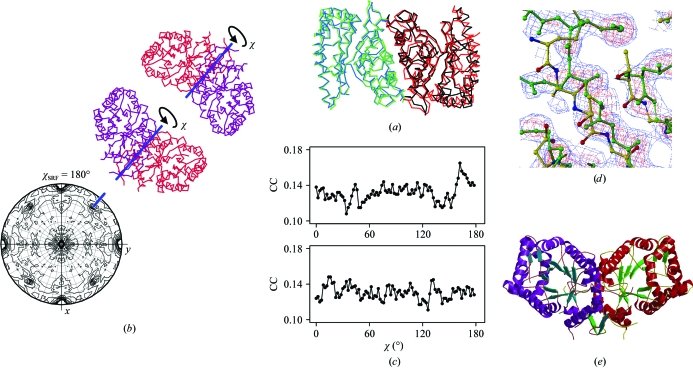
The specific volume for two subunits per AU was 2.46 Å3 Da−1 (50% solvent) for the native crystal. An absence of proper crystallographic dyads in P212121 suggested one dimeric DKMO molecule per AU. The SRF calculated using native DKMO data had a noncrystallographic peak at ϕ = 78.4°, ψ = 40.8°, χ = 180.0° and its symmetry equivalents (Fig. 2 ▶ b), indicating orientation of a molecular dyad of a DKMO dimer.
Figure 2.
Structure solution of DKMO (a) The superposition of β2 and αβ dimers of bacterial luciferase from V. harveyi indicates conservation of a dimer. (b) Bottom, χ = 180° section of the SRF defining the orientation of the NCS dyad in the DKMO structure; top, reference orientations of the search model (synthetic α2 dimer) in which the molecular dyads are aligned with the NCS twofold axis (blue lines). (c) TF searches were performed for both reference dimers rotated around the twofold axis by the variable angle χ. The highest correlation coefficient (CC) in the TF search was plotted as a function of χ. The highest peak at 165° in the top plot corresponds to the correct orientation. (d) 2F o − F c (blue) and F o − F c (red) electron-density maps after REFMAC refinement of the MR model (colored by atom type) with DMMULTI external phases superposed on the final refined structure of DKMO (green). (e) Ribbon representation of the DKMO dimer. This figure was prepared using BOBSCRIPT (Esnouf, 1997 ▶), MOLREP and R (R Development Core Team, 2005 ▶).
The MR search was performed using MOLREP. Not surprisingly, considering the rather low level of sequence identity, an MR solution was not found for either the α- nor β-luciferase subunits. The structures of an αβ-heterodimer (PDB code 1luc; Fisher et al., 1995 ▶) and a β2 homodimer (PDB code 1xkj; Tanner et al., 1997 ▶) are known for bacterial luciferase and both form an identical interface (Fig. 2 ▶ a), which is also conserved in other known homologues. A synthetic α2 luciferase homodimer was generated for the MR search by superimposing an α-subunit onto a β-subunit of the αβ-heterodimer.
No solution could be found by conventional MR with the synthetic α2 model. An SRF validation of the top ten peaks of the cross RF indicated that they are not solutions. Therefore, it was concluded that the cross RF is a ‘weak link’ in the structure determination of the DKMO and accordingly a table of orientations of the dimeric search model consistent with the SRF was used for the TF search instead of a table of cross RF peaks.
3.1.3. Structure determination
Firstly, two dimeric models were generated; in each case, the molecular dyad was aligned with one of the symmetry-equivalent NCS dyads (Fig. 2 ▶ b). The model in which the N-termini of the subunits are pointing towards the origin is further referred to as a minus model and the other model is referred to as a plus model. In this setup, any orientation of the dimeric model which is consistent with the SRF can be generated by a rotation of one of the two models around the selected NCS dyad.
Secondly, the table of rotations around the NCS axis was prepared in polar angles, which are used in MOLREP to define orientation. The first two polar angles (ϕ, ψ) were the same for all these rotations, as they defined the direction of the rotation axis along which the axes of the dimers were aligned. These two angles were taken from the table of SRF peaks. The angle χ was varied from 0° to 180° (owing to the twofold symmetry of the dimer) with a step of 2°. The generation of two dimeric search models in the first step was necessary to make the table of rotations and consequently the presentation of the results as simple as possible.
The cross RF step of the MR was thus omitted and several TF searches were carried out for 90 orientations for each of the two dimeric models (Fig. 2 ▶ b) using MOLREP. High-resolution cutoffs of 4, 5 and 6 Å were tried. For each of them, the TF search was carried out for the full atomic model, for the model modified according to the target sequence and for the polyalanine model. The resolution cutoffs and model modifications were applied implicitly using the corresponding keyword in MOLREP. In this setup, a single run of MOLREP was performing the TF search for all 90 orientations of one of the dimeric models for a given resolution cutoff and model modification. From each such run, a plot of the highest CC in the TF search versus the angle χ was generated (Fig. 2 ▶ c). With a sequence identity as low as 16% one cannot rely on a single high peak on a single plot. This was one reason why a collection of plots for several high-resolution cutoffs and model modifications was analyzed. No consistent peaks were observed for the minus model. For the plus model one of the orientations had a persistently higher CC in the TF search for all tested resolution ranges and for both the polyalanine model and the sequence-corrected model. Although the TF solutions for this orientation were not consistent in different runs, the found orientation seemed to be correct. Therefore, in the next step the polyalanine α2 dimeric model in this orientation was refined using REFMAC (Murshudov et al., 1997 ▶) with two monomers defined as separate rigid bodies. This refinement was conducted in P1, thus excluding rotational symmetry equivalents and corresponding intermolecular interatomic vectors, which are not reliable until a clear TF solution has been found (Grosse-Kunstleve & Adams, 2001 ▶). The TF search with the refined dimeric model gave a convincing solution in P212121. The new model was still imperfect and the electron density after iterative averaging (DM; Cowtan, 1994 ▶) and restrained refinement with external DM phases (REFMAC) was difficult to interpret.
Nevertheless, the refinements improved the model and it was positioned by conventional MR in the bromide-derivative crystal using the remote-wavelength data. The phases from this model might already be sufficient for the identification of some of the bromine sites in the difference Fourier synthesis. However, in order to facilitate the determination of the anomalous substructure, the phases for the bromide-derivative crystal were improved using multi-crystal averaging (DMMULTI; Cowtan, 1994 ▶) involving both the native data and the remote-wavelength data from the derivative. This phase improvement by multi-crystal averaging was possible because of a significant difference between the unit-cell parameters of the native and the derivative crystals. The anomalous difference Fourier synthesis was then calculated using the peak-wavelength data and the averaged phases at 10–3 Å resolution. 18 peaks with heights of 6–14σ were interpreted as bromine sites. These bromine coordinates were used in three-wavelength MAD phasing with MLPHARE (Otwinowski, 1991 ▶) to give a FOM of 0.26 to 2.5 Å (0.63 to 6 Å).
The MAD phases for the bromide-derivative data and the model phases for the native data were the starting phases for the final round of multi-crystal averaging. The MR model of the native crystal was refined using these averaged phases to give combined maps of good quality (Fig. 2 ▶ d) that were sufficient to build a complete atomic model of DKMO (Fig. 2 ▶ e), which was further refined to an R cryst of 16.3% and an R free of 23.3% (Isupov et al., 2008 ▶). The subunit of DKMO and the α-subunit of luciferase can be superimposed with an r.m.s.d. of 1.83 Å for 253 matching Cα atoms (out of 378 in the DKMO sequence).
3.2. Stucture solution of anti-TRAP from Bacillus licheniformis
3.2.1. Background
Anti-TRAP is a small protein of 53 amino acids which regulates the activity of tryptophan attenuation protein (TRAP; Antson et al., 1999 ▶) in Bacillus. Anti-TRAP from B. licheniformis was crystallized in space group P21, with unit-cell parameters a = 118.5, b = 99.8, c = 123.2 Å, β = 117.6° (Shevtsov et al., 2008 ▶). The only homologue of known structure is B. subtilis anti-TRAP (PDB code 2bx9; Shevtsov et al., 2005 ▶), which is a dodecameric particle with cubic 23 point-group symmetry (Fig. 3 ▶ a). The sequence identity between B. subtilis and B. licheniformis anti-TRAP is 64%.
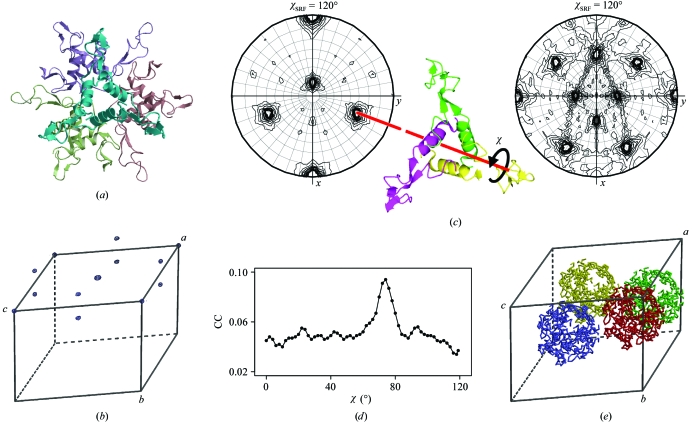
Figure 3.
Solution of the structure of anti-TRAP from B. licheniformis. (a) Ribbon diagram of the dodecamer of anti-TRAP from B. subtilis. (b) Native Patterson synthesis, in which three strong non-equivalent non-origin peaks are present. (c) 120° and 180° sections of an SRF, indicating the orientations of twofold and threefold NCS axes. The trimeric search model (centre) was oriented so that its threefold molecular axis was aligned with the NCS threefold axis (red lines). TF searches were performed for a series of orientations related to that shown by a rotation around the molecular threefold axis by the variable angle χ. (d) The highest CC in the TF search is plotted as a function of χ. (e) The MR solution with four dodecamers in the asymmetric unit, which are related by the translational NCS. This figure was prepared using BOBSCRIPT, MOLREP, CCP4mg (Potterton et al., 2004 ▶) and R.
The native Patterson synthesis of B. licheniformis anti-TRAP contained three strong non-origin peaks at (0.5, 0.13, 0.0), (0.5, 0.0, 0.5) and (0.0, 0.13, 0.5), with heights of 0.4, 0.4 and 0.16 relative to the origin peak, respectively (Fig. 3 ▶ b). This suggested that the AU contains four anti-TRAP particles related by translational NCS. The SRF had strong features at χ values of 180°, 120° (Fig. 3 ▶ c) and 90°, which correspond to the 432 symmetry. This means that the NCS axes are in special orientations with respect to the crystallographic twofold axis (two of the four NCS triads are orthogonal to the crystallographic axis). These data may suggest that the asymmetric unit of the crystal contains either four dodecamers with 23 point-group symmetry (the high apparent symmetry of SRF in this case is the consequence of special orientations of the NCS axes) or four 24-mers with 432 symmetry. However, in the second case one of the six diagonal dyads of a 24-mer would be parallel to a crystallographic twofold screw axis and such an arrangement would generate strong peaks in the native Patterson synthesis at y = 1/2 which were not observed. Moreover, four 24-mers would result in an impossible specific volume and solvent content and therefore this possibility can be excluded. The specific volume in the case of four dodecamers is 2.35 Å3 Da−1 and the solvent content is 47%.
3.2.2. Models and preliminary MR trials
Owing to the high sequence similarity between the two proteins, MR searches were conducted with full atomic models of B. subtilis anti-TRAP oligomers. Despite the identical molecular symmetry of the B. subtilis and B. licheniformis anti-TRAP particles, no solution was found for the dodecameric search model. The cross RF did not contain strong features and its top peaks failed SRF validation, suggesting a different organization of the dodecamers in the anti-TRAP proteins from B. subtilis and B. licheniformis. Also, no MR solution was found for the monomeric model, probably because it is only a small part of the AU content.
The trimeric search model (Fig. 3 ▶ c) appeared attractive because of the presence of a trimeric B. licheniformis anti-TRAP species in solution (Shevtsov et al., 2008 ▶). However, the top 20 cross RF peaks for this model failed the SRF validation. Therefore, a constrained exhaustive search with a trimeric model was used for structure determination.
3.2.3. Structure determination and analysis
The trimeric model of B. subtilis anti-TRAP was positioned so that its molecular threefold axis was parallel to one of the NCS threefolds, with the N-termini of the subunits pointing away from the origin. Owing to the special orientation of the NCS axes in relation to the crystallographic 21 axis, one of the symmetry equivalents of the search trimer had the N-termini pointing towards the origin; the ‘flipped-over’ second model was therefore not required. A table of peaks in polar coordinates was prepared for the TF search as described in §3.1.3. The angle χ was varied with a 2° step over the range 0–120°, which was sufficient owing to the threefold symmetry of the model. The translation search was carried out for each of these 60 orientations using the data in the resolution range 15–4.2 Å.
Fig. 3 ▶(d) shows the dependence of the highest CC in the TF search on χ, with a clear solution at χ = 74°. The CC at this global maximum is 9.4%, while for the other maxima on the plot it is below 6%. The found solution was fixed and the search was repeated for other NCS threefold axes until a full dodecamer was built. The resulting dodecamer was used as a search model for the next step of structure solution, in which four dodecamers related by translational NCS were located using a conventional MR. Although these dodecamers had the same point-group symmetry as the original B. subtilis model, they were built differently from structurally conserved trimers (see Shevtsov et al., 2008 ▶ for details). This example underlines the importance of using a conserved protein multimer for MR.
When the model containing four B. licheniformis anti-TRAP dodecamers was refined using REFMAC, the refinement stalled at a free R factor of 43% (R factor = 33%). Main-chain breaks were observed in 2F o − F c synthesis and the water structure was poorly defined. Therefore, one dodecamer which had fewer main-chain breaks in the density was resubmitted to MR. The resulting structure was easily refined to an R factor of 19.7% and a free R factor of 25.4% (Fig. 3 ▶ e). Subsequent analysis revealed an overall shift of the crystal structure by (a + c)/4 of the initial MR solution relative to the final model1.
3.3. Structure solution of thioredoxin peroxidase B from human erythrocytes
3.3.1. Background
Peroxiredoxins are ubiquitous antioxidant enzymes. Thioredoxin peroxidase B (TPx-B) is a 2-Cys peroxiredoxin with a monomer molecular weight of 22 kDa. The protein was purified from dated blood packs and crystallized in space group P21, with unit-cell parameters a = 88.9, b = 107.0, c = 119.5 Å, β = 110.9°. Native synchrotron data were collected to 1.7 Å.
Attempted MIR did not work owing to poor native crystal isomorphism. The SeMet MAD approach was not possible, as the protein was purified from the native source. Analytical ultracentrifugation, gel-filtration chromatography and specific volume calculations were inconclusive regarding the oligomeric state of the protein, suggesting eight to 12 subunits in the oligomer. The SRF calculated with MOLREP revealed that TPx-B is a decamer with 52 molecular symmetry (Figs. 4 ▶ a and 4 ▶ b).
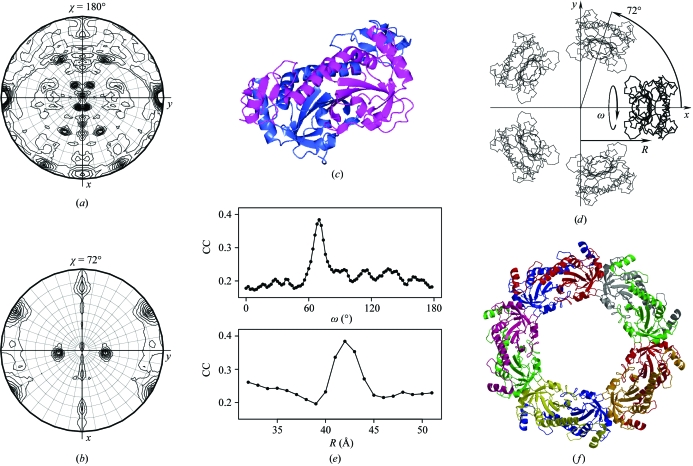
Figure 4.
Solution of the structure of thioredoxin peroxidase B (TPx-B) from human erythrocytes. Sections of the SRF corresponding to rotations by (a) 180° and (b) 72° indicate the 52 point-group symmetry of the TPx-B molecule and define the orientations of NCS fivefold and twofold axes. (c) The hORF06 dimer, a building block of the search model. (d) The search model with two variable parameters, the angle ω and the distance R. (e) Two sections of a two-dimensional search space crossing the point corresponding to the correct decamer: the highest CC in the TF search versus ω and versus R. (f) The final decameric TPx-B structure. This figure was prepared using MOLREP, CCP4mg, BOBSCRIPT and R.
3.3.2. Model preparation and structure solution
The closest available homologue, dimeric hORF06 (PDB code 1prx; Choi et al., 1998 ▶; Fig. 4 ▶ c), shared 30% sequence identity with TPx-B. No MR solution was found for monomeric or dimeric hORF06 models.
A polyalanine model of hORF06, which contained amino acids 1–189 out of 224 in order to cut off a poorly conserved domain, was used for the generation of all possible decamers with 52 point-group symmetry. A dimeric model was positioned with its centre of mass at the origin of the coordinate system, its molecular dyad coincident with the coordinate axis x and the N-terminal face of the dimer pointing in the negative direction. A two-parameter family of decamers satisfying the SRF was generated by applying the following sequence of transformations to this dimer. Firstly, the dimer was translated by a distance R along the x axis and rotated by an angle ω about its molecular dyad. The values of R and ω were the two variable parameters of the model. The new dimer was rotated by ±72° and ±144° around z and the resulting dimers were joined to form a decamer with point-group symmetry 52 (Fig. 4 ▶ d). Finally, the decamer was rotated to align its molecular dyads with the NCS dyads known from the SRF (Fig. 4 ▶ a). An inspection of the possible packing of the dimers in the decamer suggested R to be within the ranges 32–51 Å or −51 to −32 Å. Positive and negative values of R corresponded to two types of packing, with the N-terminal face of the dimer pointing towards or outwards the centre of the decamer, respectively. Owing to the twofold symmetry of the dimers, the ω search range was 0–180°. A total of 3600 decamers were generated, with two types of packing, 1 Å steps in R and 2° steps in ω. The TF search was conducted with these models using AMoRe in the resolution range 10–5 Å. This was performed using a csh script in which one cycle included generation of a decamer and a TF with this decamer as the search model. For each decamer the highest value of CC was stored to generate a two-dimensional plot of CC against R and ω (Fig. 4 ▶ e). The only strong peak in this plot (R = 42 Å, ω = 70°) corresponded to the correct structure.
Subsequent phase improvement involved rigid-body refinement, restrained refinement (REFMAC), tenfold NCS averaging (DM) and restrained refinement with external DM-averaged phases (REFMAC). The TPx-B model was rebuilt and refined to an R factor of 0.192 and an R free of 0.256 (PDB code 1qmv; Schröder et al., 2000 ▶; Fig. 4 ▶ f).
Acknowledgments
This work would not have been possible without the data provided by Fred Antson, Mikhail Shevtsov, Ewald Schröder and Jennifer Littlechild. This work was supported by NIH (AAL; grant No. 1 RO1 GM069758-03).
Footnotes
This shift corresponds to an alternative choice of the origin in the smaller cell defined by the pseudotranslation vector (a + c)/2. Such a false MR solution is indistinguishable from the correct solution at the MR stage of structure determination and moreover it cannot be corrected by subsequential refinement, although it produces interpretable difference electron-density maps. Currently, such cases are automatically handled by the program ZANUDA at http://www.ysbl.york.ac.uk/YSBLPrograms/index.jsp.
References
- Altschul, S. F., Madden, T. L., Schaffer, A. A., Zhang, J., Zhang, Z., Miller, W. & Lipman, D. J. (1997). Nucleic Acids Res.25, 3389–3402. [DOI] [PMC free article] [PubMed]
- Antson, A. A., Demidkina, T. V., Gollnick, P., Dauter, Z., von Tersch, R. L., Long, J., Berezhnoy, S. N., Phillips, R. S., Harutyunyan, E. H. & Wilson, K. S. (1993). Biochemistry, 32, 4195–4206. [DOI] [PubMed]
- Antson, A. A., Dodson, E. J., Dodson, G., Greaves, R. B., Chen, X. & Gollnick, P. (1999). Nature (London), 401, 235–242. [DOI] [PubMed]
- Asojo, O. A., Boulègue, C., Hoover, D. M., Lu, W. & Lubkowski, J. (2003). Acta Cryst. D59, 1165–1173. [DOI] [PubMed]
- Berman, H. M. et al. (2002). Acta Cryst. D58, 899–907. [DOI] [PubMed]
- Bourenkov, G. P. & Popov, A. N. (2006). Acta Cryst. D62, 58–64. [DOI] [PubMed]
- Bricogne, G. (1974). Acta Cryst. A30, 395–405.
- Brünger, A. T., Adams, P. D., Clore, G. M., DeLano, W. L., Gros, P., Grosse-Kunstleve, R. W., Jiang, J.-S., Kuszewski, J., Nilges, M., Pannu, N. S., Read, R. J., Rice, L. M., Simonson, T. & Warren, G. L. (1998). Acta Cryst. D54, 905–921. [DOI] [PubMed]
- Choi, H. J., Kang, S. W., Yang, C. H., Rhee, S. G. & Ryu, S. E. (1998). Nature Struct. Biol.5, 400–406. [DOI] [PubMed]
- Cowtan, K. D. (1994). Jnt CCP4/ESF–EACBM Newsl. Protein Crystallogr.31, 34–38.
- Czjzek, M., Arnoux, P., Haser, R. & Shepard, W. (2001). Acta Cryst. D57, 670–678. [DOI] [PubMed]
- Dauter, Z. & Dauter, M. (1999). J. Mol. Biol.289, 93–101. [DOI] [PubMed]
- Esnouf, R. (1997). J. Mol. Graph.15, 132–134. [DOI] [PubMed]
- Fisher, A. J., Raushel, F. M., Baldwin, T. O. & Rayment, I. (1995). Biochemistry, 34, 6581–6586. [DOI] [PubMed]
- Fleming, T. M., Jones, C. E., Piper, P. W., Cowan, D. A., Isupov, M. N. & Littlechild, J. A. (1998). Acta Cryst. D54, 671–674. [DOI] [PubMed]
- Glykos, N. M. & Kokkinidis, M. (2003). Acta Cryst. D59, 709–718. [DOI] [PubMed]
- Grininger, M., Ravelli, R. B. G., Heider, U. & Zeth, K. (2004). Acta Cryst. D60, 1429–1431. [DOI] [PubMed]
- Grosse-Kunstleve, R. W. & Adams, P. D. (2001). Acta Cryst. D57, 1390–1396. [DOI] [PubMed]
- Isupov, M. N., Antson, A. A., Dodson, E. J., Dodson, G. G., Dementieva, I. S., Zakomirdina, L. N., Wilson, K. S., Dauter, Z., Lebedev, A. A. & Harutyunyan, E. (1998). J. Mol. Biol.276, 603–623. [DOI] [PubMed]
- Isupov, M. N., Beecher, J., McGhie, E. J., Schröder, E., Bourenkov, G., Lau, P. & Littlechild, J. A. (2008). In preparation.
- Jamrog, D. C., Zhang, Y. & Phillips, G. N. (2003). Acta Cryst. D59, 304–314. [DOI] [PubMed]
- Jones, K. H., Smith, R. T. & Trudgill, P. W. (1993). J. Gen. Microbiol.139, 797–805. [DOI] [PubMed]
- Keegan, R. M. & Winn, M. D. (2007). Acta Cryst. D63, 447–457. [DOI] [PubMed]
- Keillor, J. W., Lherbet, C., Castonguay, R., Lapierre, D., Martinez-Oyanedel, J., Fothergill-Gilmore, L. A. & Walkinshaw, M. D. (2003). Acta Cryst. D59, 532–534. [DOI] [PubMed]
- Kissinger, C. R., Gehlhaar, D. K. & Fogel, D. B. (1999). Acta Cryst. D55, 484–491. [DOI] [PubMed]
- Krissinel, E. & Henrick, K. (2004). Acta Cryst. D60, 2256–2268. [DOI] [PubMed]
- Lebowitz, J., Lewis, M. S. & Schuck, P. (2002). Protein Sci.11, 2067–2079. [DOI] [PMC free article] [PubMed]
- Leonard, P. M., Brzozowski, A. M., Lebedev, A., Marshall, C. M., Smith, D. J., Verma, C. S., Walton, N. J. & Grogan, G. (2006). Acta Cryst. D62, 1494–1501. [DOI] [PubMed]
- Lilien, R. H., Bailey-Kellogg, C., Anderson, A. C. & Donald, B. R. (2004). Acta Cryst. D60, 1057–1067. [DOI] [PubMed]
- Long, F., Young, P., Vagin, A. & Murshudov, G. (2008). Acta Cryst. D64, 125–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGhie, E. J., Isupov, M. N., Schröder, E. & Littlechild, J. A. (1998). Acta Cryst. D54, 1035–1038. [DOI] [PubMed]
- Makino, D. L., Larson, S. B. & McPherson, A. (2005). Acta Cryst. D61, 173–179. [DOI] [PubMed]
- Matthews, B. W. (1968). J. Mol. Biol.33, 491–497. [DOI] [PubMed]
- Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240–255. [DOI] [PubMed]
- Nakai, T., Ishijima, J., Masui, R., Kuramitsu, S. & Kamiya, N. (2003). Acta Cryst. D59, 1610–1618. [DOI] [PubMed]
- Navaza, J. (1994). Acta Cryst. A50, 157–163.
- Otwinowski, Z. (1991). Proceedings of the CCP4 Study Weekend. Isomorphous Replacement and Anomalous Scattering, edited by W. Wolf, P. R. Evans & A. G. W. Leslie, pp. 80–86. Warrington: Daresbury Laboratory.
- Potterton, L., McNicholas, S., Krissinel, E., Gruber, J., Cowtan, K., Emsley, P., Murshudov, G. N., Cohen, S., Perrakis, A. & Noble, M. (2004). Acta Cryst. D60, 2288–2294. [DOI] [PubMed]
- R Development Core Team (2005). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org.
- Read, R. J. (2001). Acta Cryst. D57, 1373–1382. [DOI] [PubMed]
- Rossmann, M. G. & Blow, D. M. (1962). Acta Cryst.15, 24–31.
- Schröder, E., Littlechild, J. A., Lebedev, A. A., Errington, N., Vagin, A. A. & Isupov, M. N. (2000). Structure Fold. Des.8, 605–615. [DOI] [PubMed]
- Schuermann, J. P. & Tanner, J. J. (2003). Acta Cryst. D59, 1731–1736. [DOI] [PubMed]
- Shaham, M., Chakrabalty, A. M. & Gunsalus, I. C. (1973). J. Bacteriol.116, 944–949. [DOI] [PMC free article] [PubMed]
- Sheriff, S., Klei, H. E. & Davis, M. E. (1999). J. Appl. Cryst.32, 98–101.
- Shevtsov, M. B., Chen, Y., Gollnick, P. & Antson, A. A. (2005). Proc. Natl Acad. Sci. USA, 102, 17600–17605. [DOI] [PMC free article] [PubMed]
- Shevtsov, M. B., Isupov, M. N., Chen, Y., Gollnick, P. & Antson, A. A. (2008). In preparation.
- Strop, P., Brzustowicz, M. R. & Brunger, A. T. (2007). Acta Cryst. D63, 188–196. [DOI] [PMC free article] [PubMed]
- Tanner, J. J., Miller, M. D., Wilson, K. S., Tu, C. S. & Krause, K. L. (1997). Biochemistry, 36, 665–672. [DOI] [PubMed]
- Tong, L. (2001). Acta Cryst. D57, 1383–1389. [DOI] [PubMed]
- Trame, C. B. & McKay, D. B. (2001). Acta Cryst. D57, 1079–1090. [DOI] [PubMed]
- Trapani, S., Abergel, C., Gutsche, I., Horcajada, C., Fita, I. & Navaza, J. (2006). Acta Cryst. D62, 467–475. [DOI] [PubMed]
- Vagin, A. & Teplyakov, A. (1997). J. Appl. Cryst.30, 1022–1025.
- Vagin, A. & Teplyakov, A. (2000). Acta Cryst. D56, 1622–1624. [DOI] [PubMed]
- Wittmann, J. G. & Rudolph, M. G. (2007). Acta Cryst. D63, 744–749. [DOI] [PubMed]