Optimizing Screening for Acute Human Immunodeficiency Virus Infection with Pooled Nucleic Acid Amplification Tests

Abstract

Recent studies have shown the public health importance of identifying individuals with acute human immunodeficiency virus infection (AHI); however, the cost of nucleic acid amplification testing (NAAT) makes individual testing of at-risk individuals prohibitively expensive in many settings. Pooled NAAT (or group testing) can improve efficiency and test performance of testing for AHI, but optimizing the pooling algorithm can be difficult. We developed simple, flexible biostatistical models of specimen pooling with NAAT for the identification of AHI cases; these models incorporate group testing theory, operating characteristics of biological assays, and a model of viral dynamics during AHI. Pooling algorithm sensitivity, efficiency (test kits used per individual specimen evaluated), and positive predictive value (PPV) were modeled and compared for three simple pooling algorithms: two-stage minipools (D2), three-stage hierarchical pools (D3), and square arrays with master pools (A2m). We confirmed the results by stochastic simulation and produced reference tables and a Web calculator to facilitate pooling by investigators without specific biostatistical expertise. All three pooling strategies demonstrated improved efficiency and PPV for AHI case detection compared to individual NAAT. D3 and A2m algorithms generally provided better efficiency and PPV than D2; additionally, A2m generally exhibited better PPV than D3. Used selectively and carefully, the simple models developed here can guide the selection of a pooling algorithm for the detection of AHI cases in a wide variety of settings.

Nucleic acid amplification testing (NAAT) has revolutionized testing for infectious diseases (17), but the technique remains expensive (6, 9, 27) and exhibits poor predictive value in many settings. In the last decade, laboratories have turned to specimen pooling or group testing strategies to increase both the efficiency and the predictive value of NAAT for use in screening for rare diseases (23, 24, 27, 31). In group testing, biological specimens are pooled together, and these pools (rather than the individual specimens) are initially tested. If a pool tests positive, further testing is required to identify individual positive specimens; however, if the pool tests negative, all specimens in that pool are declared negative. Thus, group testing can lead to a decrease in the average number of tests required per specimen evaluated compared to individual testing. Group testing can also lead to higher specificity and thus to higher positive predictive values in a screening setting.

The idea of group testing to increase the efficiency of case detection was popularized by Dorfman (5), whose work was motivated by syphilis screening in military inductees. Subsequently, group testing techniques have been applied to other infectious viruses, including human immunodeficiency virus (HIV) (1, 23, 24, 31), hepatitis B and C viruses (23), and West Nile virus (3). Group testing has also found broader application in blood banks (23, 25), entomology (34), genetics (11), pharmaceuticals (14), analytical chemistry (37), and information theory (36). More recently, a number of public health laboratories in the United States (18, 27, 28, 30, 32) and elsewhere (4, 10, 29, 33) have adopted new clinical HIV testing algorithms that incorporate specimen pooling with NAAT to identify acute HIV infection (AHI) in the period before HIV antibodies develop.

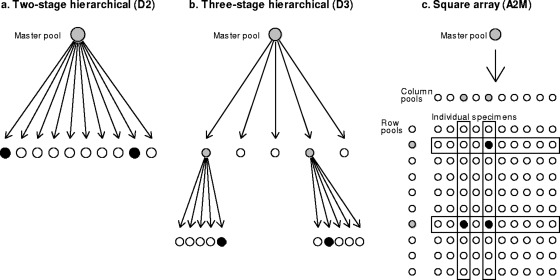
As group testing has been applied in a wide variety of fields, extensions of Dorfman's original “minipool” algorithm (5) (Fig. 1a) have been proposed. For example, Finucan (8) extended Dorfman's minipools to a three-stage, hierarchical configuration (Fig. 1b). More recently, Phatarfod and Sudbury (26) and others (2, 15, 16, 37) have proposed array-based pooling strategies (Fig. 1c).

FIG. 1.

Schematic diagrams of three pooled testing strategies considered: D2, D3, and A2m. Positive pools are in gray; positive specimens are in black. In D2 (a), a positive master pool is broken down into individual specimens. One or more of these specimens may be positive. In D3 (b), a positive master pool is broken down into multiple subpools, all of which are tested. Positive subpools are broken into individual specimens, and one or more of these specimens may be positive. In A2m (c), if a master pool is positive, row and column pools are tested, some of which may be positive. Specimens at the intersection of positive row and column pools are tested individually; some or all of these may be positive.

Properties of these different group testing algorithms have been reported extensively in the biostatistics literature. For example, if the prevalence of disease p is known and there is no test error (i.e., 100% sensitivity and specificity), then the optimally efficient size of the master pool (i.e., the first and largest pool tested in a pooling algorithm) is known to be approximately p^−1/2 for Dorfman minipools, and p^−2/3 for three-stage hierarchical pools (8). Closed-form solutions of the operating characteristics for many pooling strategies have been derived. These results enable the examination of various levels of prevalence, sensitivity, and specificity on the efficiency and positive predictive value (PPV) of group testing algorithms (11, 15, 16, 22). However, much of this work has been highly technical and too theoretical to be directly useful to the laboratory directors and technicians most likely to implement pooled testing for AHI in clinical or public health settings. Likewise, no formal investigation of which strategies might be best for case detection of AHI has been undertaken.

Our goals in this paper were therefore to (i) develop simple, flexible models of group testing for NAAT-based AHI case detection, incorporating explicit assumptions about viral dynamics during AHI and known operating characteristics of enzyme-linked immunosorbent assays (ELISAs) for antibodies and NAATs; (ii) employ these models to compare levels of pooling algorithm sensitivity (PAS), efficiency, and PPVs of different pooling strategies for detection of AHI; and (iii) demonstrate how these models can guide pooling algorithm selection in real-world applications (4, 10, 27-29, 33).

MATERIALS AND METHODS

Decision-making framework.

Models were developed to determine the best pooling strategy for a given testing situation. Four questions were identified as key to this process. (i) What practical considerations restrict the pooling strategies available to the laboratory? (ii) How do pool size and the choice of assay for NAAT affect the ability of a pooling algorithm to detect patients with AHI in a testing population? (ii) Given the assay and maximum pool size, what efficiencies can be expected for different pooling strategies in testing populations with different prevalences of AHI? (iv) How can pooling strategies be expected to impact the accuracy of NAAT results, in terms of the PPV?

The first question, addressed in the Discussion, considers throughput (number of samples to be processed per unit time), desired turnaround time, and available resources (budget, technology, personnel, assays) and frames the range of strategies a laboratory can consider for a real-world application. The three remaining questions were addressed using appropriate statistical models as described below.

Group testing strategies examined.

We examined the three testing strategies shown in Fig. 1. The first was the two-stage Dorfman minipool strategy (or “D2”) (5). In the first stage of D2, the master pool comprising all specimens is tested; if the master pool tests positive, all component individual specimens are tested (the second of the two stages). The second strategy was an extension of D2 into a three-stage hierarchical form (“D3”) (8, 13), in which a master pool is first tested; if the master pool tests positive, then the component subpools are tested. Last, the individual specimens which comprise each positive subpool are tested. Only “square” D3 pools were examined (e.g., a master pool of 25 comprising 5 subpools of 5 specimens each), as this configuration of D3 is approximately optimal in the absence of test error (8). The third pooling strategy was a two-dimensional array (“A2m”) with master pool testing (15, 16). As in D2 and D3, the master pool is tested in the first stage of A2m; if the master pool tests positive, then pools comprising all specimens of each row and each column of the array are tested simultaneously. All specimens at points of intersection between positive rows and positive columns are then retested. In the event of a positive row but no positive columns (or vice versa), all specimens in the positive row are tested. Since testing row and column pools occurs in a single step of the testing process, A2m (like D3) is a three-stage pooling algorithm. Only A2m algorithms with an equal number of rows and columns were considered.

Defining AHI prevalence.

In most published examples of specimen pooling to identify AHI (10, 27-29, 32), individual specimens were first screened for chronic HIV infection using an ELISA for antibodies; ELISA-negative specimens were then pooled and tested using HIV NAAT for the presence of virus. We therefore defined AHI prevalence as the proportion of antibody-negative individuals in the population of interest who would individually test positive by NAAT. By definition, prevalent AHI cases fall within a time window bounded by the date at which an individual would first test positive by NAAT and the date at which that individual would first test positive by ELISA. The expected length of this sensitivity window (w) (i.e., the expected number of days between NAAT positivity and seroconversion) depends on the particular ELISA and NAAT being employed (19, 35). Given a NAAT with a lower limit of detection (LLD) of 100 copies/ml, Fiebig et al. (7) estimated that w would be 84 days (95% confidence interval [CI], 42 to 125) for a second-generation ELISA, 9 days (95% CI, 5 to 12) for a third-generation ELISA, and 5 (95% CI, 2 to 9) for a fourth-generation ELISA (which includes antigen as well as antibody testing).

Modeling PAS.

While the maximum acceptable pool size (MAPS) for a pooling application is driven in part by logistical considerations (see Discussion), pooling almost always results in the loss of sensitivity compared to individual testing. Thus, bounding pool size may also be necessary to limit loss of sensitivity. We defined pooling algorithm sensitivity (PAS) as the probability that a truly positive specimen will be declared positive by a particular pooling algorithm, and assay sensitivity as the probability that a truly positive specimen will be declared positive by an individual NAAT. PAS was modeled as a function of assay sensitivity under the following assumptions. (i) AHI cases present uniformly throughout the sensitivity window period. (ii) During the first weeks of AHI, an individual's viral load rapidly increases from being undetectable to very high levels (>10⁷ copies/ml) at a constant exponential rate R (7); thereafter, HIV remains detectable by any available NAAT. (iii) The probability a pool is declared positive is a deterministic function of the amount of virus in the pool. (iv) PAS is affected by dilution only in the first stage of a pooling algorithm. Assumption iv is based on the intuition that viral load will increase in subpools compared to positive master pools due to decreased dilution. Thus, if a master pool correctly tests positive, one would expect at least one subpool to also test positive. This expectation is in line with laboratory experience in North Carolina (27, 28), Seattle (32), and South Africa (33), where positive master pools have rarely failed to give rise to at least one positive subpool.

Modeling pooling efficiency and PPV.

Efficiency of a pooling algorithm was defined as the expected number of NAATs required per individual specimen evaluated, ignoring confirmatory retesting of individual positive specimens. Thus, the efficiency of individual testing is 1, and an efficiency of less than 1 indicates that the pooling algorithm will require fewer tests on average than individual testing. The PPV of a pooling algorithm (henceforth, simply PPV) was defined as the probability that a specimen identified as positive at the end of a pooling algorithm was in fact truly positive (again, ignoring confirmatory retesting). Pooling efficiency and PPV for D2, D3, and A2m were modeled using formulae adapted from the group testing literature. These calculations require specification of PAS, of AHI prevalence, and of assay specificity, which is the probability that a truly negative specimen will be declared negative by an individual NAAT. These models assume that assay specificity is not affected by pool size and that specimens are independent and identically distributed with the probability of being positive equal to a known AHI prevalence p in the population. Predictions of these deterministic formulae were confirmed with stochastic simulations.

RESULTS

Relationship between pool size, assay sensitivity, and PAS.

Based on the model assumptions above, PAS is equivalent to the proportion of days of the sensitivity window during which positive specimens would be detectable in a master pool (accounting for dilution). Given w, R (measured in log₁₀ copies/ml/day increase), and the size of the master pool N, it follows that

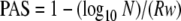(1)

When we solve equation 1 for N, we get:

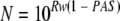(2)

Therefore, MAPS must be less than or equal to N given in equation 2 in order to achieve a sensitivity of at least PAS.

For a particular ELISA, there exists a one-to-one correspondence between w and the LLD of NAAT. For instance, suppose a particular NAAT has a known LLD and w (e.g., Fiebig et al. [32] report an LLD of 100 copies/ml and a w of 9 when used with a third-generation ELISA [32]). Then a different NAAT with a different LLD (LLD′) has a w′ as follows:

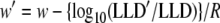(3)

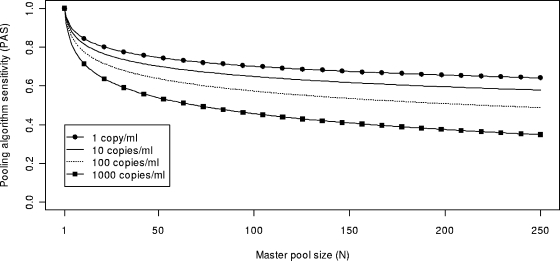
Figure 2 was produced by combining equations 1 and 3, and it shows PAS as a function of N with an R value of 0.52 log₁₀ copies/ml/day (i.e., a doubling time of ∼14 h) (7, 21) for NAATs with various LLDs, assuming the samples were first screened (and found negative) with a third-generation ELISA (7). In Fig. 2, increases in pool size from 16 to 100 reduced the likelihood of AHI detection by 15 to 30 percent. In practice, effects of relatively large increases in pool size on PAS might be offset by choosing a NAAT with a lower LLD.

FIG. 2.

Model of PAS as a function of master pool size (N) for hypothetical NAATs with different lower limits of detection. The model assumes use of a third-generation ELISA and a rate of exponential increase of HIV viral load during early AHI of 0.52 log₁₀ copies/ml/day.

Pooling efficiency and PPV.

Formulae for pooling efficiency and PPV for D2, D3, and A2m are given in the supplemental material. For purposes of comparing the predicted performance of pooling algorithms across a range of plausible AHI prevalences (4, 10, 18, 27-30, 32, 33), assay specificities, and PAS values, estimated values for efficiency and PPV for optimally efficient algorithms are shown in Table 1 and Tables S1, S2, and S3 in the supplemental material. Separate tables were generated for different MAPS values; each table displays the optimally efficient master pool size for the given MAPS, with the corresponding efficiency and PPV. In addition, a Web calculator which can produce the results presented in the tables is available at the website of M.G.H. (http://www.bios.unc.edu/∼mhudgens/optimal.pooling.htm).

TABLE 1.

Optimal master pool size and corresponding efficiency and PPV for D2, D3, and A2m in the presence of errors, for MAPS of 100^a

NAAT assay specificity	Prevalence	PAS
		0.95									0.85									0.75
		D2			D3			A2m			D2			D3			A2m			D2			D3			A2m
		Pool	Effic.	PPV	Pool	Effic.	PPV	Pool	Effic.	PPV	Pool	Effic.	PPV	Pool	Effic.	PPV	Pool	Effic.	PPV	Pool	Effic.	PPV	Pool	Effic.	PPV	Pool	Effic.	PPV
1.0	10−6	100	0.010	1.000	100	0.010	1.000	100	0.010	1.000	100	0.010	1.000	100	0.010	1.000	100	0.010	1.000	100	0.010	1.000	100	0.010	1.000	100	0.010	1.000
	10−5	100	0.011	1.000	100	0.010	1.000	100	0.010	1.000	100	0.011	1.000	100	0.010	1.000	100	0.010	1.000	100	0.011	1.000	100	0.010	1.000	100	0.010	1.000
	10−4	100	0.019	1.000	100	0.012	1.000	100	0.012	1.000	100	0.018	1.000	100	0.012	1.000	100	0.012	1.000	100	0.017	1.000	100	0.011	1.000	100	0.012	1.000
	10−3	33	0.061	1.000	100	0.029	1.000	100	0.029	1.000	35	0.058	1.000	100	0.027	1.000	100	0.027	1.000	37	0.054	1.000	100	0.025	1.000	100	0.025	1.000
	10−2	11	0.190	1.000	25	0.129	1.000	25	0.135	1.000	11	0.180	1.000	25	0.119	1.000	36	0.124	1.000	12	0.169	1.000	36	0.110	1.000	36	0.113	1.000
	10−1	4	0.577	1.000	9	0.563	1.000	49	0.573	1.000	4	0.542	1.000	9	0.515	1.000	49	0.515	1.000	5	0.507	1.000	9	0.468	1.000	49	0.457	1.000
0.99	10−6	100	0.020	0.009	100	0.011	0.465	100	0.012	0.343	100	0.020	0.008	100	0.011	0.439	100	0.012	0.318	100	0.020	0.007	100	0.011	0.411	100	0.012	0.292
	10−5	100	0.021	0.080	100	0.011	0.830	100	0.012	0.838	100	0.021	0.073	100	0.011	0.822	100	0.012	0.823	100	0.021	0.065	100	0.011	0.812	100	0.012	0.804
	10−4	100	0.029	0.330	100	0.013	0.901	100	0.014	0.980	100	0.028	0.317	100	0.013	0.900	100	0.014	0.977	100	0.027	0.303	100	0.013	0.899	100	0.014	0.975
	10−3	33	0.071	0.706	100	0.030	0.910	100	0.031	0.996	35	0.067	0.691	100	0.028	0.910	100	0.029	0.995	37	0.064	0.675	100	0.026	0.910	100	0.027	0.995
	10−2	11	0.199	0.906	25	0.132	0.961	36	0.139	0.997	12	0.189	0.898	25	0.123	0.961	36	0.128	0.997	12	0.177	0.897	36	0.113	0.951	36	0.116	0.997
	10−1	4	0.583	0.976	9	0.567	0.983	49	0.577	0.980	4	0.549	0.975	9	0.519	0.983	49	0.519	0.980	5	0.513	0.969	9	0.471	0.983	49	0.460	0.980
0.95	10−6	100	0.060	0.000	100	0.018	0.008	100	0.023	0.006	100	0.060	0.000	100	0.018	0.007	100	0.023	0.005	100	0.060	0.000	100	0.018	0.006	100	0.023	0.005
	10−5	100	0.061	0.004	100	0.018	0.067	100	0.023	0.057	100	0.061	0.003	100	0.018	0.061	100	0.023	0.052	100	0.061	0.003	100	0.018	0.055	100	0.023	0.046
	10−4	100	0.069	0.031	100	0.020	0.336	100	0.025	0.373	100	0.068	0.029	100	0.020	0.320	100	0.025	0.348	100	0.067	0.026	100	0.019	0.301	100	0.025	0.321
	10−3	34	0.110	0.194	100	0.039	0.562	100	0.042	0.829	36	0.106	0.180	100	0.037	0.557	100	0.040	0.816	39	0.102	0.165	100	0.035	0.552	100	0.038	0.800
	10−2	11	0.235	0.585	25	0.147	0.801	36	0.155	0.951	12	0.224	0.562	25	0.137	0.800	49	0.142	0.942	13	0.213	0.539	25	0.126	0.799	64	0.129	0.933
	10−1	4	0.610	0.878	9	0.586	0.914	49	0.595	0.901	4	0.575	0.876	9	0.537	0.914	49	0.535	0.901	5	0.537	0.851	9	0.488	0.914	49	0.474	0.901

^aPool, pool size; Effic., efficiency. Efficiency is measured as tests per specimen; efficiency of individual testing is therefore 1.

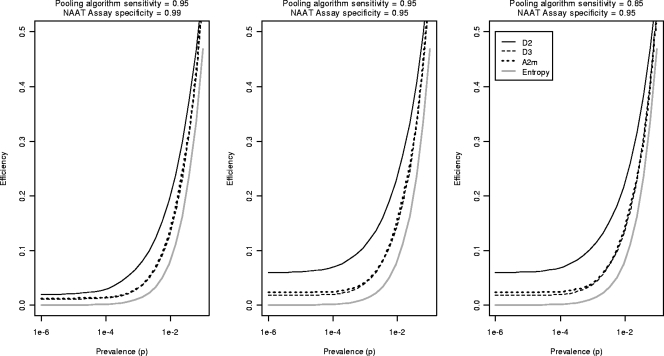
Figure 3 shows graphs of the optimal efficiency for D2, D3, and A2m over a range of AHI prevalences, specificities, and PAS values. Figure 3 also shows the “entropy value” (2), the theoretical best possible efficiency that can be achieved using any group testing algorithm for a given prevalence. All three pooling strategies greatly increase testing efficiency, often resulting in 10-fold or greater reductions in test usage compared to individual testing. Gains in efficiency due to pooling are substantially better at lower prevalences. For the entire range of prevalences considered, D3 and A2m have comparable efficiencies and are each more efficient than D2, though this gap narrows considerably at higher AHI prevalences. Reductions in assay specificity (center and left panels of Fig. 3) reduce the testing efficiency of D2 algorithms; the efficiencies of D3 and A2m are more robust with changes in assay specificity.

FIG. 3.

Optimal pooling efficiency for a range of prevalences assuming a MAPS of 100, by pooling strategy. Efficiency is measured as tests per screened specimen. The figure shows the “entropy value” for efficiency, the theoretical best efficiency possible with any pooling algorithm.

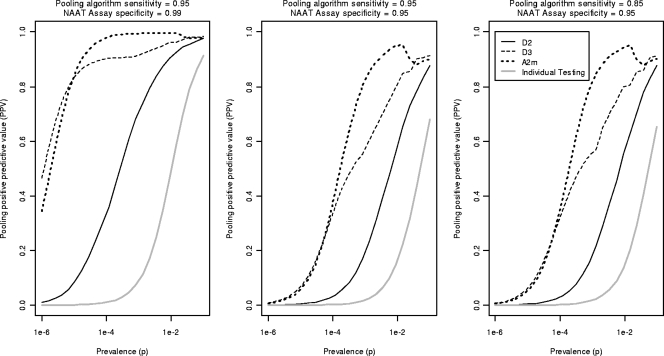
Figure 4 shows the PPV for the optimally efficient algorithms considered in Fig. 3, along with the PPV of individual testing. The results indicate that D3 and A2m algorithms will in general confer meaningfully greater PPVs than will D2. In addition, the figure shows many situations in which the PPV of A2m is superior to that of D3. For instance, at AHI prevalences similar to those observed in North Carolina (p ≅ 2 × 10⁻⁴) (27, 28), A2m algorithms should result in clinically significant gains in PPV compared to D3 algorithms. The advantage of the A2m algorithm is most striking where the assay specificity is reduced. All three pooling strategies result in substantial increases in PPV compared to individual NAAT results.

FIG. 4.

Pooling PPV for pooling configuration that achieves best possible efficiency, with a maximum acceptable pooling size (MAPS) of 100, for a range of prevalences by pooling strategy. These PPVs correspond exactly to the efficiency graphs in Fig. 3. Also shown is the PPV for individual testing.

DISCUSSION

Group testing for AHI case detection clearly offers substantial advantages in both efficiency and PPV compared to individual NAAT. The specific choice of pooling strategy can meaningfully affect these factors and can also affect PAS. By characterizing the relationships between pooling algorithm performance, AHI prevalence in the testing population, and NAAT performance characteristics, we have derived models to guide laboratories interested in pooling for detection of AHI.

The efficiency and accuracy of all group testing strategies depend on the prevalence of AHI as well as on the specificity and sensitivity of the NAAT. In general, optimal master pool sizes decrease as AHI prevalence increases. D3 appeared to best optimize pooling efficiency over the widest range of prevalences among algorithms considered here. However, A2m pools often showed comparable efficiency and better PPV than D3 with imperfect assay specificity (Fig. 3 and 4). Where efficiencies are comparable, then, A2m may provide a more robust approach for case identification applications of pooling.

In contrast, the D2 algorithm is the simplest to execute and (as a two-stage algorithm) has the benefit of reducing turnaround time for reporting positive results compared to D3 or A2m; perhaps for these reasons, D2 has been used widely by blood banks (23, 25). However, D2 testing is generally less efficient than D3 or A2m, except where the prevalence of AHI is high. Moreover, the performance of D2 is markedly susceptible to reduced specificity: even with small master pool sizes (for example, 25 specimens), the presence of an occasional false-positive NAAT affects the efficiency and PPV of D2 to a much greater extent than comparable D3 or A2m pools at most AHI prevalences (Table S3 in the supplemental material). This effect is due to increased serial retesting of specimens in D3 and A2m compared to D2. D2 should therefore be considered only where there is high confidence in both assay specificity and laboratory quality assurance.

A crucial concern in pooling is the loss of NAAT sensitivity due to dilution of positive specimens in pools of increasing size. For instance, Fig. 2 shows that, for a fixed w and R, increases in the master pool size can lead to a substantial loss in sensitivity to detect AHI cases; however, these results also show that a very sensitive NAAT can partially offset this dilution effect. Even where pooling large numbers of specimens is possible (i.e., in high-throughput laboratories or retrospective research studies), the best AHI detection strategy ultimately requires both a sensitive NAAT and limited master pool size.

The results of this study may prove useful in planning real-world pooling programs. Preliminary considerations in this planning process, summarized in Table 2, should include assessment of (i) the laboratory setting, (ii) end-user requirements, and (iii) characteristics of the testing population.

TABLE 2.

Recommended approach to pooling algorithm selection^a

Factor(s)	Area(s) affected
Laboratory setting
Training, quality assurance, quality control	Feasibility of pooling for NAAT
Availability of robotics	MAPS; acceptable algorithm complexity
No. of personnel	Possible frequency of NAAT runs (turnaround time)
Economic resources (assay budget, per assay cost)	Minimal acceptable efficiency (maximum allowable test usage)
Available assay sensitivity	MAPS; algorithm performance (efficiency, PPV)
Available assay specificity	Algorithm performance
End-user requirements
Required turnaround time	MAPS; maximum no. of pooling stages
Required accuracy for NAAT screen	Minimum acceptable PAS; minimum acceptable positive predictive value
Testing population
Anticipated throughput (rate of specimen arrival)	MAPS
No. of AHI anticipated; AHI prevalence	Algorithm performance

^aSummary of important factors to be discussed in the planning process. Most of the factors listed serve to limit the available range of strategies a program can consider. Information on the characteristics of the NAAT assay to be utilized and anticipated AHI prevalence can then be used to find relevant estimates of performance for remaining candidate algorithms from Table 1 and Tables S1, S2, and S3 in the supplemental material. The ultimate algorithm choice will reflect a balance of program needs and capacity.

Laboratory setting.

Planners should consider the available technology and quality assurance when implementing pooling. While manual pooling of specimens is technologically simple and feasible in low-resource settings (10, 29), the process is labor intensive and requires extreme care with specimen handling, rigorous quality control, and ongoing quality assurance. However, our experiences in North Carolina and China have been that whenever we find a positive pool, we are always able to identify the sample or samples that made the pool positive. While the serial retesting of specimen pooling algorithms reduces the impact of “pure” (noncontamination) false positives on the overall PPV, a contaminated primary specimen may be indistinguishable from a truly positive specimen. Moreover, D2, D3, and A2m strategies potentially require increasing numbers of samples to be drawn from each primary sample tube (2, 3, and 4 samples, respectively), thus increasing the risk of contamination. The availability of robotics may therefore be a prerequisite for using A2m, as well as for using larger pool sizes (in our experience, those greater than 50), where the risk of contamination is also increased. Before settling on a final choice, planners must also determine the level of testing efficiency necessary given available resources; how many runs may be performed per week given available personnel; what is known about the cost, sensitivity, and specificity for the assays available to the lab; and how many freeze-thaw cycles will be necessary for a pooling algorithm, as the sensitivity of NAAT may be reduced when stored samples undergo more than three or four freeze-thaw cycles (20).

End-user requirements.

Different end-user applications may have different needs with regard to turnaround time (e.g., consider a retrospective study using stored samples compared to a blood bank). For the three algorithms considered, negative results can be returned after a single stage of testing, while positive results require two (D2) or three (D3, A2m) stages. End users will also have different requirements in terms of accuracy. Researchers with time and resources to perform confirmatory tests might be less concerned with the PPV of an algorithm than public health authorities who plan to intervene immediately upon identifying an AHI case.

Testing population.

The expected throughput can limit possible pool size and should therefore be known in advance. Labs must accumulate enough specimens to complete master pools before testing these pools; if specimens are slow in coming, the lab may face the choice of delaying scheduled runs or wasting resources by running assays with suboptimal numbers of specimens. Some knowledge of the expected AHI prevalence in the testing population is likewise required to estimate pooling algorithm efficiency and accuracy and, in turn, to select an approximately optimal pooling configuration.

Once the foregoing assessment has been completed, many planners will decide to limit the MAPS for their pooling application. For this reason, Table 1 and Tables S1, S2, and S3 in the supplemental material have been organized into four parts by MAPS (values of 100, 225, 49, and 25, respectively). Optimal pooling algorithms for any value of MAPS may also be determined through use of the Web calculator.

This research has several important limitations. First, model predictions may be deceptively precise, obscuring inherent uncertainty and variation in the distribution and prevalence of positive samples in the testing population; for instance, AHI prevalence will rarely fall usefully on a power of ten, as in Table 1. For these reasons, model predictions should be considered approximate. An iterative or “sensitivity analysis” approach to finding the best pooling algorithm may be warranted in many situations. For instance, the investigator can assess the robustness of the model predictions by investigating the extent to which deliberate variations in input parameters affect optimal master pool size, efficiency, and PPV. Second, as noted above, contamination of individual specimens (prior to pooling) can undermine pooling-related gains in accuracy and efficiency, and it is not comprehensively addressed in this paper. Interference or inhibition of NAAT by biological material or additives (e.g., heparin) from multiple specimens is an important consideration as well (12, 20, 26, 38). Third, we did not consider higher-order algorithms (four-stage hierarchical pools, cubic arrays) that might be possible using robotics. Preliminary investigations indicate that the efficiency gained with such algorithms tends to be relatively small compared to the complexity and reduced turnaround time such strategies typically require (results not shown). Likewise, we did not consider rectangular pooling algorithms (e.g., A2m with 8 rows and 12 columns). Last, while pooling may be applicable to a wide variety of problems in medicine and public health beyond case detection of AHI, many of the assumptions and parameters included in this report will vary widely between diseases and populations. Thus, these results should be generalized to other settings cautiously.

While pooled testing will work accurately and efficiently in combination with second-, third-, or fourth-generation ELISAs, the choice of ELISA used for prescreening samples can nonetheless alter the performance of pooling algorithms. Newer “third-generation” (IgM-sensitive) and “fourth-generation” (combined antigen-antibody) ELISAs detect infections earlier in seroconversion than older assays. When used to prescreen samples for RNA pooling, these sensitive ELISAs themselves may detect some cases of AHI. For this reason, the apparent prevalence of AHI will be reduced when RNA pooling is used in conjunction with a higher-generation ELISA. The effects of using higher-generation ELISAs on the accuracy and efficiency of pooling algorithms are the subject of current investigation (for example, see reference 4).

Despite these limitations, the values of efficiency obtained from these models can accurately predict real-world experiences. For example, Pilcher et al. (28) observed an efficiency of 0.018 using a near-optimal D3 testing strategy of 90:10:1 with a prevalence of 0.0002 and an assay specificity of 0.99. Given w of 84 days and R of 0.52 log₁₀ copies/ml/day, equation 1 indicates that PAS is approximately 0.95. We can use Table 1 to bound the efficiency of pooled testing at 0.013 on the lower end (for a prevalence of 10⁻⁴) and 0.030 on the high end (for a prevalence of 10⁻³), while the Web calculator estimates the efficiency in the range of 0.015 to 0.017 (for square D3 pools of 100 and 81, respectively); all these estimates are consistent with the experiences reported by Pilcher et al. (28). An efficiency of approximately 0.02 means that approximately 2,200 NAAT kits were required to test 109,000 samples (27). At $50 per NAAT, optimized pooled testing saved over $5,000,000 compared to the costs of individual NAATs for the same population.

For AHI testing using specimen pooling, the tables and algorithms presented here provide a resource for research and public health laboratories interested in finding cases of AHI in a wide variety of settings. Correct application of these algorithms will in general substantially improve the efficiency and PPV of case finding relative to individual testing.