Ancestrally high elastic modulus of gecko setal β-keratin

Abstract

Typical bulk adhesives are characterized by soft, tacky materials with elastic moduli well below 1 MPa. Geckos possess subdigital adhesives composed mostly of β-keratin, a relatively stiff material. Biological adhesives like those of geckos have inspired empirical and modelling research which predicts that even stiff materials can be effective adhesives if they take on a fibrillar form. The molecular structure of β-keratin is highly conserved across birds and reptiles, suggesting that material properties of gecko setae should be similar to that of β-keratin previously measured in birds, but this has yet to be established. We used a resonance technique to measure elastic bending modulus in two species of gecko from disparate habitats. We found no significant difference in elastic modulus between Gekko gecko (1.6 GPa±0.15 s.e.; n=24 setae) and Ptyodactylus hasselquistii (1.4 GPa±0.15 s.e.; n=24 setae). If the elastic modulus of setal keratin is conserved across species, it would suggest a design constraint that must be compensated for structurally, and possibly explain the remarkable variation in gecko adhesive morphology.

1. Introduction

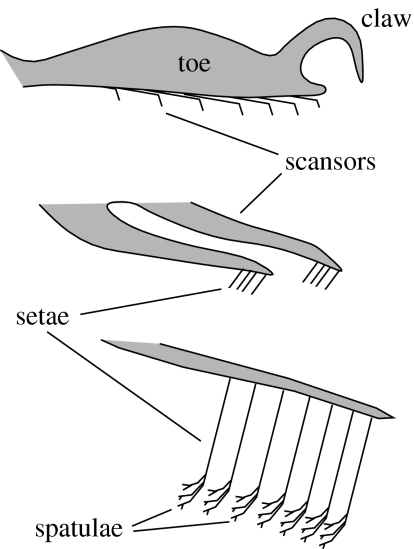
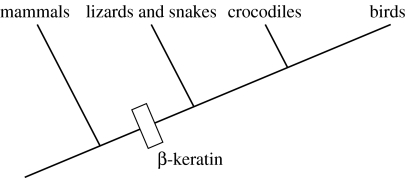
Geckos rapidly scale both vertical and inverted surfaces using fibrillar adhesive pads with some unique and impressive qualities. The adhesive is self-cleaning (Hansen & Autumn 2005) and strong, yet orientation-dependent, allowing them to detach with minimal force (Autumn et al. 2000). Conventional pressure-sensitive adhesives (e.g. tape) are characterized by a relatively low Young's modulus (less than 1 MPa; Dahlquist 1966), relying on the compliance of the material to create the intimate contact between surfaces necessary for intermolecular adhesion. Fibrillar adhesives are thought to rely instead on an array of high aspect ratio beams to form a structure that is effectively compliant while materially stiff (Autumn et al. 2006). The basic units of the gecko adhesive, called ‘setae’ (figure 1) are composed predominantly of β-keratin (Maderson 1964; Alibardi 2003). The molecular structure and composition of β-keratin has been well characterized in bird feathers and scales (Gregg & Rogers 1984; Gregg et al. 1984), and mechanical testing has revealed feather keratin to be a relatively stiff material (approx. 2.50 GPa; Bonser & Purslow 1995), three orders of magnitude higher in Young's modulus than the Dahlquist criterion for tack (figure 2). Surprisingly, few attempts have been made at characterizing the mechanical properties of β-keratin beyond research on bird feathers, despite the fact that it is found in all members of non-mammalian amniotes (figure 3). Among them, the material properties of gekkonid setal keratin have yet to be established.

Figure 1.

Generalized structure of an adhesive gecko foot.

Figure 2.

Representative materials along a continuum of Young's moduli. Materials with Young's modulus over 1 MPa are not considered sticky according to the Dahlquist criterion for tack.

Figure 3.

Origin of β-keratin among amniotes.

If synthetic fibrillar adhesives existed, we could directly manipulate their structure and material to determine how these parameters affect their performance. Such synthetic versions are in the works (Sitti & Fearing 2002; Geim et al. 2003; Northen & Turner 2005; Yurdumakan et al. 2005; Majidi et al. 2006), but in the meantime investigators have created mathematical models to predict the advantages of fibrillar adhesive design. This ongoing effort demands some estimate of the material properties of the modelled fibres. Since the basic molecular structure and composition of β-keratin is thought to be widely conserved across birds and reptiles (Fraser & Parry 1996; Sawyer et al. 2000), it is appropriate that most authors choose an estimate of Young's modulus for gecko setal keratin between 1 and 4 GPa (Jagota & Bennison 2002; Campolo et al. 2003; Persson 2003; Gao & Yao 2004; Glassmaker et al. 2004; Majidi et al. 2005; Spolenak et al. 2005; Tang et al. 2005; Autumn et al. 2006), on the order of values found for feathers. Other estimates range up to 15 GPa (based on unpublished data; Sitti & Fearing 2003).

This outstanding unknown parameter demands direct measurement owing to its importance in models of adhesion as well as understanding the material's evolution. Has natural selection optimized β-keratin for fibrillar adhesion, or do geckos possess the same β-keratin as their ancestors? Although the helical β-sheet structure of β-keratin is thought to be conserved, the underlying amino acids are not. Recent work by Alibardi (Alibardi & Toni 2005) suggests that geckos and birds converged independently on their keratinous fibrils (setae and feathers, respectively) by evolving low molecular weight β-keratins that are then polymerized into long filaments. Keratin filaments are in turn cross-linked together longitudinally by disulfide bonds (Rizzo et al. 2006). Increased cross-linkage could increase the material stiffness (Parbhu et al. 1999). Stiffness has also been found to depend on orientation of the keratin fibrils along the feather rachis (Cameron et al. 2003). Without direct measurements, there remains the possibility of variation in both the tensile and the bending moduli depending on what types of β-keratin molecules are manufactured and how they are assembled in the animal.

Geckos have diverged ecologically such that they inhabit humid tropical as well as arid desert environments, and encompass both diurnally and nocturnally active species. If the material properties of setal β-keratin are variable, some species could conceivably benefit from evolutionary pressure driving changes in stiffness or viscoelasticity (e.g. through increased or decreased degrees of cross-linkage) to compensate for the effects of extreme environments. Alternatively, if material properties are constrained across gekkonids, that pressure could drive structural changes instead. Another important consideration is how setae age; depending on the species, a gecko must use the same setae for weeks or months between moults. Setae are not adhesive in their resting state, but must deform by bending to generate adhesive force (Autumn et al. 2000; Autumn & Hansen 2006). If material properties change significantly over time, this bending (and therefore adhesive function) may be compromised towards the end of the moulting cycle.

The objective of our experiment is to quantify the material properties of gekkonid setal keratin from two species: Gekko gecko, a well-studied tropical species, and Ptyodactylus hasselquistii, a desert dweller. Our principle aim is to determine how β-keratin varies in stiffness between birds and lizards. However, we have chosen these species with the reasoning that, if any geckos exhibit differences in elastic modulus due to their ancestral environment, we should see a difference between two species from greatly disparate habitats.

2. Methods

2.1 Animals

We harvested setae from four individuals of G. gecko and four individuals of P. hasselquistii. Animals were cared for by the Office of Laboratory Animal Care at the University of California, Berkeley, and seta removal was performed in accordance with Animal Use Protocol no. R137.

2.2 Data collection

Individual setae were isolated and mounted at the base to the tip of a pin with Gapper gap-filling adhesive (Partsmaster, Dallas, TX). A 250 μm diameter glass sphere (Jaygo, Inc., Union, NJ) was then mounted to the tip (branched end) of the seta. When the glue hardened, only the stalk was exposed and deformable, while base and branched tips were rigidly fixed (figure 4). We collected data for 4–10 setae from each individual gecko.

Figure 4.

(a) Schematic of seta preparation for elastic modulus measurements. (b) Still from high-speed video of seta immediately prior to perturbation.

The mounted seta was placed in front of a Photron FastCam-X 1024 PCI high-speed camera (Photron USA, Inc., San Diego, CA) with a custom microscope attachment and illuminated with Fiberlite Series 180 fibre optic lights (Dolan-Jenner Industries, Inc., Lawrence, MA). The seta was then perturbed (by ‘flicking’) several times from the left and the right. We recorded the resultant motion at 500 or 1000 fps. We then determined the natural frequency by counting the number of frames between the initial release and the instant closest to the return to initial position and dividing 2π by this time period. We recorded relative humidity (RH) and temperature continuously throughout the experiment using the Omegaette HH310 temperature humidity probe (Omega Engineering Inc., Stamford, CT), which was mounted near the seta.

Although no seta was tested more than once, we did continue to mount setae from the same sample at progressively longer times following the date of harvest to determine whether material properties change over time once the seta has been separated from the animal.

2.3 Scanning electron microscopy

Each seta was subsequently sputter-coated with iridium to a 5 nm thickness using a MED 020 Modular High Vacuum Coating System (BAL-TEC AG, Balzers, Lichtenstein) and imaged at high magnification with a scanning electron microscope (Philips/FEI XL-30 ESEM, Hillsboro, OR). From these images, we determined the width of each seta as well as its effective length (the portion of the stalk free of glue). In cases where glue appeared to cover a significant proportion of the stalk, we noted this so that we could test for a statistical effect and exclude them if necessary.

2.4 Beam vibration model

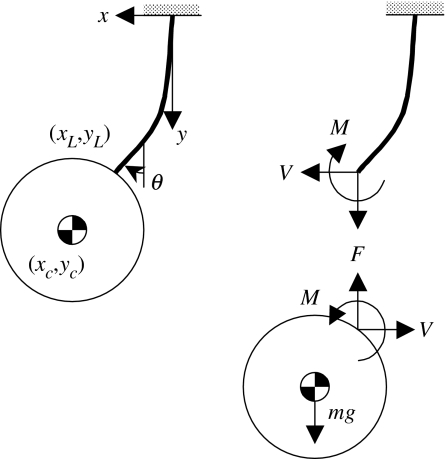
We inferred the elastic modulus from kinematic and morphological data using an Euler–Bernoulli beam vibration model that describes the motion of a resonating cylindrical beam with a given radius, length and natural frequency, loaded at the tip with a sphere of a given radius and density.

As illustrated in figure 5, a setal stalk is oriented vertically with a spherical bead suspended at its bottom end and a rigid support at the top. Let L denote the seta length and define the arc length s such that s=0 at the top support. At each end, the seta is assumed to be ‘built-in’ to the contacting substrate and is thus subject to both a point force and moment at s=0 and L. For a lateral displacement x=x(s) and slope θ=θ(s) along the length of the fibre, it follows from linear beam theory that

$$\theta (s)=3\left({\theta }_L-2\frac{x_L}{L}\right){\left(\frac{s}{L}\right)}^2-2\left({\theta }_L-3\frac{x_L}{L}\right)\left(\frac{s}{L}\right),$$ (2.1)

where x_L≔x(L) and θ_L≔θ(L). The tip configuration {x_L, θ_L} is determined by the shear force V and moment M imparted by the glass bead at s=L. Referring to the free-body diagram in figure 2b, it follows from the constitutive laws that

$${\theta }_L=\frac{V{L}^2}{2EI}+\frac{ML}{EI}\text{and}{x}_L=\frac{V{L}^3}{3EI}+\frac{M{L}^2}{2EI},$$ (2.2)

where E is the elastic modulus; I=πR⁴/4 is the area moment of inertia; and R is the stalk radius. The bead centre of mass has coordinates {x_c, y_c}, and so it follows from linear and angular momentum balance that

$$V=-m{\ddot{x}}_c\text{and}M\approx mc\left\{-{\ddot{x}}_c-(g-{\ddot{y}}_c){\theta }_L\right\}-J{\ddot{\theta }}_L,$$ (2.3)

where m is the mass of the bead; g is gravitational acceleration; and J=(2/5)mc² is the bead mass moment of inertia,

$${\ddot{x}}_c\approx {\ddot{x}}_L+c{\ddot{\theta }}_L-c{\theta }_L{\dot{\theta }}_L^2\text{and}{\ddot{y}}_c\approx -{\int }_0^L\{\theta \ddot{\theta }+{\dot{\theta }}^2\}-c{\theta }_L{\ddot{\theta }}_L-c{\dot{\theta }}_L^2.$$ (2.4)

Figure 5.

Kinematic and free-body diagrams for a setal stalk of length L and radius R loaded with a spherical bead of radius c and mass m.

Substituting equation (2.1) into (2.4) yields ${\ddot{y}}_c$ only in terms of x_L, θ_L and their time derivatives. Next, substituting (2.4) into the balance equations (2.3) and then substituting the solutions for V and M into (2.2) results in a system of two equations that are only in terms of x_L, θ_L, ${\dot{x}}_L$, ${\dot{\theta }}_L$, ${\ddot{x}}_L$ and ${\ddot{\theta }}_L$. Solving for ${\ddot{x}}_L$ and ${\ddot{\theta }}_L$ allows the system to be represented in the form $\dot{\mathbf{z}}=\mathbf{f}(\mathbf{z})$, where $\mathbf{z}={({\theta }_L,{\dot{\theta }}_L,x_L,{\dot{x}}_L)}^{\text{T}}$. The resonant frequency ω of the seta–bead system is equal to the smaller of the two natural frequencies obtained from solving $\dot{\mathbf{z}}=\mathbf{f}(\mathbf{z})$. These natural frequencies correspond to the eigenvalues of the Jacobian to f(z) at the equilibrium point z=(0 0 0 0)^T. From the eigenvalue corresponding to ω, it follows that

$$E=\frac{1}{6I}{\omega }^2\{3L\left(J+m{c}^2\right)+m{L}^3+3mcL\left(L-\frac{g}{{\omega }^2}\right)+\cdots L\sqrt{3m{L}^2\left(\frac{mgc}{{\omega }^2}-J\right)+{\left[3\left(J+m{c}^2\right)+m{L}^2+3mc\left(L-\frac{g}{{\omega }^2}\right)\right]}^2}\}.$$ (2.5)

2.5 Statistics

We tested for effects of species, individual, temperature, RH, age and glue coverage using ANOVA (for single effect tests) or multiple regression on average elastic modulus values calculated for each seta. All analyses were conducted with JMP v. 6.0 statistics software (SAS Institute, Cary, NC).

3. Results

We found no significant difference (p=0.38; table 1) in elastic modulus between Gekko gecko (1.6 GPa±0.15 s.e.; n=24 setae) and P. hasselquistii (1.4 GPa±0.15 s.e.; n=24 setae). Ptyodactylus setae were significantly longer than Gekko setae (p=0.0002), but were associated with significantly lower natural frequencies (p<0.0001). Data from both species were pooled for the remaining analyses. Setae that appeared to have minor amounts of glue along the length of the stalk were included in all analyses as they were not found to be significantly different in stiffness from the rest of the setae (p=0.76). There were no individual effects among animals (p=0.32). Multiple regression revealed no effect of temperature, RH or age on elastic modulus (table 2).

Table 1.

Elastic bending modulus of Gekko gecko and P. hasselquistii setae, with morphological and kinematic parameters used to calculate the modulus.

	Gekko gecko	Ptyodactylus hasselquistii
elastic modulus (GPa)	1.6 GPa±0.15 s.e.	1.4 GPa±0.15 s.e.
sample size
individuals	4	4
setae	24	24
trials	165	194
setal morphology
length (μm)	94.9 μm±3.1 s.e.	112.4 μm±3.1 s.e.
width (μm)	4.5 μm±0.11 s.e.	4.7 μ±0.11 s.e.
natural frequency (Hz)	820 Hz±15 s.e.	630 Hz ±14 s.e.

Table 2.

Multiple regression revealed no environmental or age effects on stiffness of gecko setae.

	estimate	std. error	t-ratio	p>|t|
temperature	0.0856	0.128	0.67	0.509
relative humidity	−0.0121	0.0106	−1.14	0.263
RH*temperature	−0.000965	0.00829	−0.12	0.908
days since harvest	0.00762	0.0251	0.30	0.763

Setal diameter did not change noticeably along the portion of the shaft we examined in this experiment, indicating that our assumption of a cylindrical shape was valid. Many setae do have a slightly tapered base, which we took care to cover with glue. We performed a sensitivity analysis to determine the possible effect of this tapering on the stiffness were it to go unaccounted for, and found that we would underestimate the stiffness by no more than 15% for the differences in diameter we observed in setae.

Preliminary data demonstrated that unaltered setae are overdamped and require a load to induce resonating behaviour. We observed one seta from Ptyodactylus that repeatedly recovered halfway to its resting position in approximately 1–2 ms. The remainder of the recovery period varied from 4 to 20 ms. Of the loaded setae, some were effectively straight and resonated within the plane of the seta. Others had obvious curvature, which caused out of plane resonance. We believe this accounted for most of the variation we observed across setae.

4. Discussion

Previous research has shown that mechanical properties of keratin can vary with temperature (Bonser & Purslow 1995), RH (Taylor et al. 2004), the orientation of the constituent keratin fibrils (Cameron et al. 2003) and the degree of cross-linkage among fibrils (Parbhu et al. 1999). Our experiments indicate that elastic modulus of gekkonid setal keratin (grand mean: 1.5 GPa±0.11 s.e.; n=48 setae) is similar in magnitude to that of β-keratin found in feather rachis (Bonser & Purslow 1995; Bonser 2000), supporting the hypothesis that β-keratin material properties, in addition to structure (Fraser & Parry 1996), are conserved across birds and reptiles. Furthermore, we found no effect of age on elastic modulus, suggesting that, if adhesive function is compromised over the course of a moulting cycle, it is probably not due to a change in material properties. While physical degradation is theoretically possible, there is currently no real evidence that adhesive function degrades over the time span of a typical moulting cycle. Autumn et al. (2006) found that the frictional coefficient of even very old scansors (2+ years) remained similar to fresh ones.

We recorded RH and temperature to detect potential variation in stiffness with these factors. The resulting experimental range in temperature was very small (5–7°C), so it is not surprising that we found no effect of temperature on elastic modulus (table 2). Bonser & Purslow (1995) measured a 50% increase in the storage modulus of feather β-keratin over a 100°C decrease in temperature, suggesting that whatever effect we may have found over a more extensive temperature range is probably not biologically relevant. They also found little effect of strain rate on the storage modulus over 0.1–10 Hz, suggesting that viscoelastic effects are minimal for β-keratin structures. We found no effect of RH, which was measured over a more relevant range in both species (16–64% RH), although the data were not evenly distributed over this range. Taylor et al. (2004) found a 2.5-fold increase in elastic modulus (from 1.47 to 3.66 GPa) between 100 and 0% RH during tensile testing of a feather rachis, suggesting that further experimentation may reveal an effect in gecko setae as well. Future studies investigating the acute effect of atmospheric variables on the stiffness of gecko setal keratin must include controlled manipulation of temperature and RH over an extended, biologically relevant range. Based on our results alone, it does not appear that these two species have evolved materially different types of setal keratin to deal with their ancestrally disparate habitats.

We recognize that material properties might yet be found to vary from species to species, but we have not discussed the potential consequences. To what extent does elastic modulus influence the function of a fibrillar adhesive? Fibrillar adhesives are thought to operate as arrays of compliant beams that, by individually bending, can conform well to even rough substrates, creating the real contact area necessary for intermolecular adhesion. If we consider the seta a flexible cylinder of radius r and length l, with elastic modulus E, the flexural stiffness, k_f, of the structure can be estimated as

$$k_f=\frac{3\pi r^{4}E}{4l^3}.$$ (4.1)

In fact, the bending stiffness of the seta is much less sensitive to elastic modulus than either radius or length. Doubling the stiffness of the beam would require a 100% increase in the elastic modulus, but only a 19% increase in radius (or 26% decrease in length). While we have not undertaken an exhaustive study of material properties of setal keratin across all gecko species, it is unlikely that undiscovered variation in elastic modulus will be relevant to the adhesive function. Setal morphology, which varies over an order of magnitude in width and two orders of magnitude in length across fibrillar adhesive organisms (Schleich & Kästle 1986), appears to compensate for the fixed properties of β-keratin.

This reliance on structure over material has important implications for engineers who wish to fabricate fibrillar adhesives. For a given material, one could theoretically synthesize a wide diversity of sticky structures, assuming that the aspect ratio of the beams falls within an acceptable range. Researchers have fabricated fibrillar adhesives from less stiff materials (3 MPa), with a resulting adhesive force only four times that of the smooth material (Kim & Sitti 2006), compared with the orders of magnitude improvement observed in gecko setae (Autumn et al. 2000). It is not clear how stiff the material must be to achieve the self-cleaning, wear-resistant and orientation-dependent properties seen in geckos. Since geckos inherited the setal material of their ancestors, we cannot conclude that theirs is the ‘ideal’ elastic modulus for all fibrillar adhesives because it predates the origin of those structures; 1 GPa is clearly effective, but 100 MPa might be sufficient and 10 GPa might be even better. Available data from feathers have indicated that elastic modulus increases and decreases along the rachis in flying birds (Bonser & Purslow 1995), and this change in material properties appears to be related to increased alignment among β-keratin microfibrils when compared with feathers of flightless birds, which lack oriented fibrils (Cameron et al. 2003; Bonser et al. 2004). We know from previous microscopy work that β-keratin fibrils in the setae of at least two species are aligned in a parallel fashion (Hemidactylus, Alibardi 2003; Gekko, Rizzo et al. 2006), suggesting that natural selection has driven gecko setae to be as stiff as possible within their developmental framework. It is worth noting that arthropod adhesive setae are derived from a composite material (cuticle) known to vary from 1 kPa to tens of gega Pascal in stiffness (Vincent 2002). While it is probable that most arthropod adhesive setae are also quite stiff (Orso et al. 2006), there remains the possibility of beneficial variation in elastic modulus across insects and spiders since the composition of their exoskeleton can vary (and consequently be acted upon by natural selection). Further investigation into the relationship between material properties and morphology of arthropod adhesive setae will reveal much towards optimizing the material properties of synthetic fibrillar adhesives.

This research provides a first step towards understanding the material properties of reptilian fibrillar adhesives, but many future directions remain to be explored. We present data describing the elastic behaviour of gecko setae, but we also observe an obvious damping effect, which could have very important consequences for attachment during perturbations. Furthermore, our results deal only with the bending stiffness of setae. Once attached, setae are loaded in a tensile manner to support the body weight of the animal, and we expect the tensile elastic modulus to be equally important in understanding fibrillar adhesive function. The tensile elastic modulus from eight species of birds ranged from 1.78 to 2.71 GPa (Bonser & Purslow 1995), suggesting that gecko setae might be stiffer when loaded in tension, unless there is a significant difference in microfibril density. These are important questions awaiting further research.

5. Conclusions

Engineers have long recognized the advantages of stiff materials in fabrication, and it appears that fibrillar adhesive organisms also benefit from these advantages. High elastic modulus correlates with a lower coefficient of expansion (Barker 1963), higher melting temperature (Ashby 1998) and greater resistance to adhesive wear (Bhushan 2002). Temperature and wear resistance could benefit geckos during rapid wall climbing, which involves high-velocity interfacial rubbing, and allow geckos to maintain functional adhesive pads for months at a time between moults. Soft, tacky adhesives leave transfer layers and have a tendency to clog with particles and debris, preventing repeated use, while gecko adhesives self-clean. Stiffer fibres can be more densely packed without clumping, creating more contact area for intermolecular adhesion (Sitti & Fearing 2003).

We can now conclude with greater confidence that the elastic modulus of β-keratin has been well conserved across birds and reptiles. As such, it is not surprising that evolution has produced a wide range of morphological variation in gecko setae to compensate for this material constraint (Schleich & Kästle 1986). Geckos inherited a relatively stiff integumentary material from their ancestors, and the result has been the evolution of a unique adhesive with many desirable traits.