Tensile and dynamic mechanical analysis of the distal portion of mussel (Mytilus edulis) byssal threads

Abstract

Dynamic mechanical analysis was used to record the behaviour of hydrated and dehydrated byssal threads under tensile stress and during dynamic thermal cycling. Fresh byssi, and byssi aged two weeks prior to testing, were used to further study the effects of age on the mechanical properties of this material. It was found that while older threads demonstrated increased stiffness, age did not necessarily affect their ultimate tensile strength. Dehydration had a more pronounced effect on thread stiffness and also increased the ultimate strength of the material. In their dry state, byssal threads displayed multiple yield points under tension and these, it is suggested, could equate to different phases within the bulk of the material. Dynamic analysis revealed glass transition (T_g) and ecologically relevant operational temperatures for byssi, where their modulus (E′) remained constant. These discoveries are related to the ecological function of byssal threads and to the emerging field of biomimetics.

1. Introduction

‘Self-healing’ polymers with the potential to recover from yield and creep are considered a high-value commodity in the field of materials development. Post-yield deformation of a material is considered by engineers to be an irreversible phenomenon, following on from the elastic or ‘Hookean’ phase of the material's behaviour under stress. Yielding of a material marks the onset of plastic character, leading to non-recoverable extension and imminent failure. Some natural block-copolymers, including mussel byssus and spider drag line silk, have surmounted this issue, however, and are capable of near total post-yield recovery as well as toughness comparable to that of Kevlar (Gosline et al. 2002). Unusually, given the potential rewards of such research, there are currently only a handful of published reports specifically studying the mechanical properties of byssal threads and three of these are now more than 20 years old.

Mussels (Mytilus edulis) are common marine bivalve molluscs, of importance to commercial fisheries and the anti-biofouling sector (Kingsbury 1981; Forteath et al. 1984; Edyvean et al. 1985; Southgate & Myers 1985; Relini & Monranari 1999; Nishida et al. 2003) as well as to materials scientists who are interested in their attachment apparatus, the byssal thread. The byssus is, nowadays, regarded as an inspirational material for the development of advanced biomimetic fabrics, as well as for adhesives that cure effectively underwater, but their exploitation began as far back as ancient Greece where byssal threads were woven into fine clothing.

Byssal threads are composed primarily of five proteins (termed mefp (M. edulis foot protein) 1–5) and byssal collagen. They are divided broadly into three areas: (i) the root that is embedded in the base of the muscular foot; (ii) the threads (proximal and distal regions) that are produced along a ventral groove that runs the length of the foot; and (iii) the attachment disc, or plaque, which mediates adhesion to the substratum (Waite et al. 1998; figure 1). Based on X-ray diffraction, it is estimated that the distal portion of the byssal thread consists of at least approximately 50% collagen triple helices and approximately 50% unidentified β-pleated sheets that could be a separate phase of the byssal collagen (Ruddall 1955). Qin & Waite (1995) partially sequenced this material (named (pre)Col-D) and isolated a homotrimer with α-chain mass approximately 60 kDa, although this monomer is now thought to have a mass in the range of 95–97 kDa (personal communication, anonymous referee).

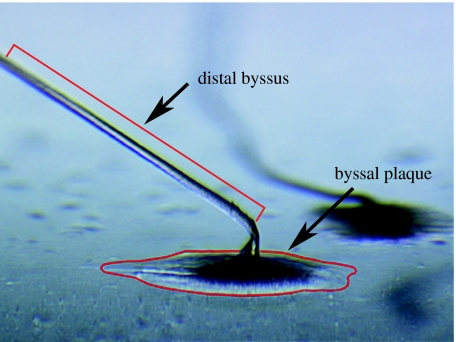
Figure 1.

A light micrograph of the adhesive plaque secreted by M. edulis to facilitate its attachment to surfaces. The distal region of the byssal thread, the material used in the present study, can be seen extending towards the body of the mussel.

Using Mytilus californianus, Mytilus trossulus and Mytilus galloprovincialis, Bell & Gosline (1995) showed that the tough distal region of a byssal thread is of high strength and somewhat ‘overdesigned’. This excessive strength, it was proposed, may be a by-product of its yielding character. This conclusion was drawn since threads invariably give way at the weaker proximal end or in the plaque before the distal portion approaches its ultimate strain. On average, the recorded yield force ranged from 52 to 81% of the force required for structural failure and this, theoretically, outperforms an equivalent byssus of steel threads. Byssi achieve this by exploiting more than twice as much of their potential maximum strength as elasticity, when compared with steel. The resulting compliance of byssi allows transfer of load between threads; something the stiffer steel threads could not achieve. The yield of the distal byssus is manifested in a sharp loss of stiffness at approximately 35 MNm⁻² where 0.5 cm of extension can be achieved with essentially no increase in force. Price (1981) showed ultimate stress of 83±15 MNm⁻² for M. edulis distal byssus and Smeathers & Vincent (1979) an ultimate strain of 0.66±0.01 before breaking.

Waite et al. (1998) provided further data for the ultimate tensile stress and strain of the distal portion of the byssus, suggesting a behaviour that is consistent with a multi-component material, in which one component deforms semi-permanently but later recovers when the load is transferred to another, more elastic, component (although no direct evidence for this was presented). That is for this material, ‘yield’, contrary to the accepted definition of the term, is not necessarily permanent. This phenomenon could be the result of a reversible cross-linking mechanism, involving metal complexion binding or covalent bonding. Peptidyl-dopa provides excellent metal-binding sites and the histidine-rich sequences in the terminal regions of preCols are strongly reminiscent of other metal-binding peptides.

Gosline et al. (2002) provide a comprehensive study on this topic, clarifying several important points. In a reappraisal of previous data, they drew the conclusion that more work is clearly needed before a useful understanding of these structures can be claimed. Further, they make the point that no studies have yet investigated the changes in yield properties that occur when the byssi dry out; an obvious requirement for an intertidal organism (all previous studies have used hydrated byssi). This, it is proposed, may cause them to ‘achieve greater strength with little compromise in extensibility’. Indeed, Qin & Waite (1995) suggested that the mussel is in a paradoxical position of needing to produce a thread that is both strong under tension and able to effectively absorb shock. Vaccaro & Waite (2001) described specific yield points on their stress/strain curves as ‘elusive’, implying that identification of any points of yield except the final, catastrophic, one was difficult, a restriction probably imposed by the apparatus used (an MTS Bionix tensile tester). The present study will use dynamic mechanical analysis (DMA), a more sensitive technique, the resolution of which allows a somewhat more detailed analysis of the mechanical behaviour of byssi. DMA involves tensile analysis of materials over a temperature range and, when used in combination with its tensile mode, allows conclusions to be drawn regarding the strength, modulus, glass transition point and polymerization/crosslinking of materials. Previously, workers have been restricted to simple descriptions of byssal behaviour, being linear at low strain followed by a yield, post-yield plateau and stiffness before breaking (Vaccaro & Waite 2001). In this study, multiple yields prior to failure in byssal threads will be demonstrated and the effects of age and hydration on behaviour will be investigated.

2. Materials and methods

2.1 Mussel culture and acquisition of threads

Mussels of 5.0±0.5 cm (longest length) were collected from the harbour at Blyth (01.31 W 55.08 N) and maintained in filtered natural seawater (approx. 32 ppt) at 10°C for one month prior to experimentation. The seawater was changed weekly after the mussels had been fed Tetraselmis chui (500 ml, culture concentration approximately 10⁵ cells per ml).

For byssal deposition, mussels were removed from the culture and placed in 500 ml polypropylene containers with artificial seawater (ASW; Tropic Marine). ‘Fresh’ byssi, less than 24 h post deposition, were collected by severing the threads at the proximal end and scraping the plaque from the container using a razor blade. Threads were carefully handled with fine tweezers and stored in 5°C ASW until use. Aged byssi were obtained by storing threads in ASW from the mussel culture for two weeks after deposition, followed by collection in the same manner.

Dehydrated byssi were prepared by aerial exposure for 10 min at 25°C.

2.2 Measurements in tensile mode

For all measurements, a Perkin–Elmer Pyris Diamond DMA was used and this machine allowed data acquisition in either ‘dynamic’ or ‘tensile’ mode. The latter allows measurements to be made either under a controlled rate of increase of strain or controlled rate of increased applied stress. For tensile measurements in the hydrated state, the liquid chamber of the DMA was filled with approximately 500 ml tap water. Threads were loaded into the DMA so that there was no ‘slack’ and the distal portion of the threads would immediately be under tension as the motor was engaged. Tensile measurements were run for 10 min at 500 μm min⁻¹ extension rate.

Most measurements were taken using a 5 mm sample length, where each end of the thread was clamped firmly across the testing section of the DMA to prevent slippage. The maximum total extension for the machine, however, was 10 mm and hydrated byssi were found to be highly elastic. In order to obtain a value for ultimate tensile strength in these threads (i.e. in order to ‘snap’ the threads), the sample length was decreased to 2.5 mm to allow a possible 7.5 mm extension. For measurements using a 2.5 mm sample length, the extension rate was dropped to 250 μm min⁻¹ to compensate for the increased strain. In turn, these tests were run over 20 min to compensate for the 50% decrease in extension rate. Although many threads were tested, only 7–10 threads of each kind gave clear and reliable output. These were used for analysis.

2.3 Measurements in dynamic mode

Dynamic analysis was carried out at a frequency of 1 Hz and in the range of −10 to 110°C, with a temperature increase of 0.5°C min⁻¹. Minimum tension/compression force was set to 5 mN and 1.2× gain.

Owing to differences in the mechanical properties of hydrated and dehydrated byssi, best results for dry byssi were acquired by using an initial force amplitude of 10 mN. This was increased to 20 mN for hydrated measurements. However, due to the method by which DMA controls force on the sample, this difference in initial force did not persist throughout the cycling and after the initial few cycles had completed, the threads experience similar loading irrespective of the initial force used. The initial tensile force, Ft, is given by the equation

$$F\text{t}=F\text{base}+F0\text{gain}\times F0,$$

where Fbase is the value entered as the minimum initial force, F0gain is the tension/compression force gain and F0 is the initial force amplitude default value. The instrument takes an initial measurement with the sample in this force condition, using the specified alternating strain amplitude; in this case, 20 μm. The instrument then recalculates the static force to be applied by calculating a new value of F0 based upon the measured modulus of the sample and the strain amplitude. This process repeats throughout the test and is designed to keep the sample under tension—even during the downward phase of the sinusoidal cycle.

2.4 Calculation of geometrical expressions

All geometrical expressions were calculated in their standard manner. Engineering stress, for instance in calculations of ultimate tensile stress for the threads, was calculated as applied force (F) over cross-sectional area (A)

$$\sigma =\frac{F}{A}.$$

Byssal threads were observed under an Olympus BH-2 optical microscope and diameter measurements were taken to ensure that variability between threads did not mask results. The cross-sectional area of the distal portion of byssal threads was found to reduce slightly where it met the proximal thread and the byssal plaque; however, thickness in the middle of the distal portion (where all measurements were taken) was considered constant along the 5 mm/2.5 mm working length. Measurements of byssal threads from mussels of this size revealed little variability in thickness between threads so, for all calculations, a mean byssal thread diameter of 70 μm and a circular cross-section were assumed; recording measurements for each individual thread prior to testing would have been incredibly time consuming due to the large number tested.

Strain, or the proportionate extension of the material in response to the applied stress, was calculated as

$$ϵ=\frac{\delta \ell }{{\ell }_{\text{o}}},$$

where ${\ell }_{\text{o}}$ is the original length of the material and $\delta \ell$ is the extension. The units of length are, therefore, cancelled and strain can be considered a proportion.

Stiffness, or the resistance of an elastic body to deflection by an applied force, has units of Nm⁻¹ and was calculated using

$$k=\frac{P}{\delta },$$

where P is applied force and δ is displacement. This describes the resilience of the threads to an applied force and Young's (or elastic) modulus (E) is derived from stress over strain for a material under tension. This is used in the dynamic measurements. All data (with the exception of dynamic data) were transformed from force/time/extension data to stress versus strain curves. Dynamic data are presented as changes in modulus (E) and damping/energy dissipation (tan δ) over a temperature range.

3. Results

3.1 Tensile analysis

3.1.1 Hydrated byssi

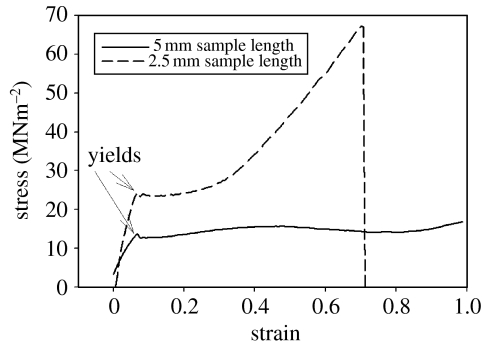
The results from tensile testing with fresh, hydrated byssi (figure 2) showed similar trends to those presented in previous studies. The initial linearly elastic phase generally ended abruptly in a distinct yield at a mean stress of 22.9 MNm⁻² for a 70 μm diameter thread. Multiple yields were never observed in hydrated byssi and this agrees closely with the observations of Bell & Gosline (1995). For a 5 mm sample length, this initial yield was followed by an approximately 4 mm extension with no proportional increase in load. Bell & Gosline's (1995) yield estimate of 52–81% of the failure load would suggest a force in the range of 45–71 MNm⁻² to test the thread to destruction using the present figures. It was, in fact, found (using a shorter 2.5 mm sample length) that a mean force of 62.1 MNm⁻² (table 1) was required to snap fresh, hydrated threads (figure 2; table 1). Although there is some variability between the data presented by the two studies, this variability is to be expected considering the geographically disparate populations of mussels and methodologies used for testing. It is considered, therefore, that the results of the present method can be compared directly to those produced by different methodologies in the published literature, although provide more detailed traces of the behaviour of threads during stress and strain.

Figure 2.

The tensile behaviour of fresh, hydrated mussel byssus demonstrating ‘Hookean’ stress/strain characteristics (5 and 2.5 mm sample lengths).

Table 1.

A summary of the data acquired from mussel byssus tensile measurements. (All data are means. Strain is calculated from final recorded values and E is calculated from force at 1 mm extension. Errors are standard deviations.)

	ultimate tensile stress (MNm−2)	extension to failure (mm)	failure strain	E (MNm−2)	Ki (Nm−1)	K2 (Nm−1)	K3 (Nm−1)	Kf (Nm−1)
fresh hydrated	62.1±8.85	>5.00	>1.0	48.6	57.87±41.6	—	—	74.5
aged hydrated	68.4±20.10	>5.00	>1.0	—	20.74±13.96	—	—	—
fresh dehydrated	80.7±14.95	1.95	0.39±0.11	239.5	395.83±11.0	210.71	171.36	182.17
aged dehydrated	83.3±31.52	2.00	0.4±0.18	339.5	806.00±435.1	327.6	259.07	201.48

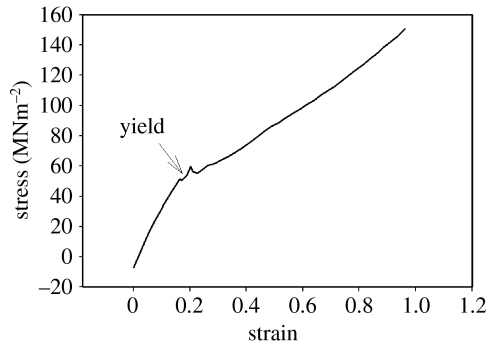
Older byssi (figure 3) had apparently different characteristics to fresh byssi in the same hydrated state. There was no obvious post-yield plateau and extension continued after the yield point in a more or less linear fashion. When averaged across all threads, however, no significant difference in initial stiffness (k_i) was found between byssi aged in the laboratory for two weeks (with k_i mean 20.74 Nm⁻¹) and fresh threads (k_i mean 57.87 Nm⁻¹, table 1), suggesting that, until the yield point at least, age did not significantly affect the tensile properties of these threads.

Figure 3.

Tensile stress/strain characteristics of aged, hydrated byssi (5 mm sample length).

It was noted that for all hydrated byssi (fresh and aged), the initial yield occurred at around 0.5–1 mm extension (0.1–0.2 strain), but that this extension required a consistently higher force for aged threads. Initial yields in older hydrated byssi were followed, not by a plateau of plastic behaviour, but by an immediate recovery of stiffness (figure 3) with force increasing in direct proportion with extension until failure.

3.2 Dehydrated byssi

Age did not seem to affect the graphical trend displayed by extending dehydrated byssi to the same degree as it did in the hydrated samples, with fresh and old threads behaving in a strikingly similar manner (figures 4 and 5 in comparison to 2 and 3). Age had a significant effect (table 1) on the initial stiffness (K_i) of dehydrated (Mann–Whitney W=17; P=0.014) byssi, but not on hydrated byssi. Aged, dehydrated byssi were stiffer than fresh dehydrated byssi—perhaps evidence of progressive crossliking over time, whereas this age-related difference was not evident in the hydrated state. Ultimate tensile strength was not affected by age in either the hydrated or dehydrated state, but was significantly affected by hydration state (Mann–Whitney W=20; P=0.024). Dry threads were consistently stronger than hydrated threads (table 1).

Figure 4.

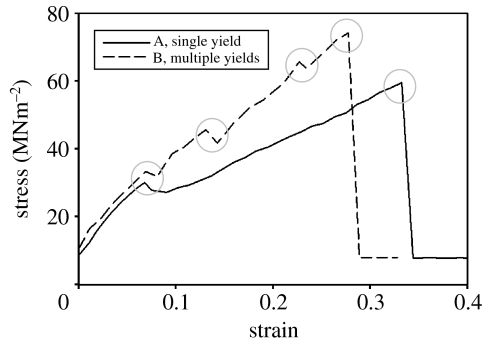
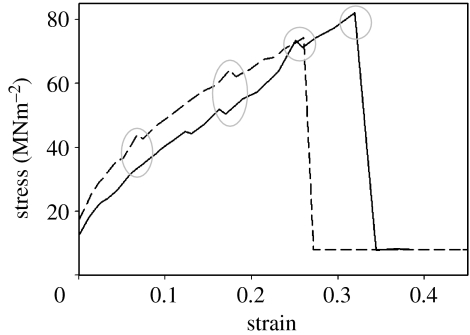
Typical plots showing the multiple yields evident during the stretching and subsequent failure of dehydrated fresh byssi (5 mm sample length). Yield points are highlighted.

Figure 5.

Two plots demonstrating the typical yielding behaviour of dehydrated, aged byssal threads (5 mm sample length). Yields tended to occur in similar locations for all threads, although not all yields were always evident in every thread. These yield points are highlighted.

Dry byssi showed two distinctly different characteristics in equal measure (figure 4). These two behaviours were manifested as either multiple (up to four) yields in predictable locations, or one initial yield followed by a recovery of stiffness as in the hydrated state (figure 2). It is suggested that byssi demonstrating this response were, perhaps, not completely dehydrated (figure 4, curve ‘A’). Figure 4 curve ‘B’ is a tensile plot for fresh byssi demonstrating four distinct yield points, the first of which occurs at around 0.1 N and 0.3 mm (0.06 strain) extension in both fresh byssi (figure 4‘A+B’) and aged byssi (figure 5).

Consistency in the location of yields on the tensile plots, and their spacing, suggested design rather than random cohesive failure of byssal threads. Further, ‘sample slippage’ was discounted as the cause since, on occasion, slippage was observed and manifested differently on the traces. Traces from slipping samples were different enough from those used in the analysis to allow confidence in the result. The mean stiffness of the byssi at each of these yield points (K_i–K₃ and the final, K_f, yield) was calculated and is presented in table 1 with the average ultimate tensile stress and extension to failure of these threads. The considerable difference in initial stiffness between fresh and aged dehydrated byssi was reduced progressively throughout subsequent yields and the final stiffness (K_f) of the dehydrated and hydrated byssi was not significantly different.

The moduli of fresh hydrated byssi were significantly different (Mann–Whitney W=15; P=0.012) from fresh dehydrated byssi, confirming that dehydration stiffens the threads and increases their strength, while compromising elasticity. Fresh hydrated byssi demonstrated stiffness at K_f that was considerably higher than their initial stiffness, suggesting a form of strain hardening, a phenomenon that occurs when loading is carried beyond the yielding region of a material. This seems not to operate with byssi in the dry state where stiffness was reduced with progressive yields. Unfortunately, the absence of intermediate yields in hydrated byssi precluded the comparison of trends here.

3.3 Dynamic analysis

3.3.1 Dehydrated byssi

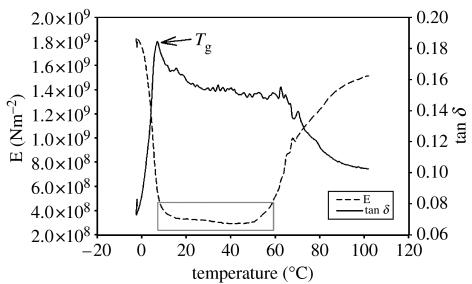
Used in dynamic mode, the DMA provided useful information about the behaviour of byssi when exposed to stress/strain and thermal cycling. Initially, tests were run dry, using a frequency of 1 Hz and a heating rate of 0.5°C min⁻¹. The initial force amplitude was set to 10 mN. From an initial temperature of −5°C, tan δ (a measure of energy dissipated as heat) increased rapidly to a peak at around 6°C (figure 6), suggesting increasing movement of the constituent proteins and resultant heat production through friction. This transition (T_g) from the byssus as a rigid, glassy substance to an elastic material was observed at this temperature several times. Following the glass transition, tan δ levelled out, before dropping off around 60–80°C. This is confirmed by a corresponding increase in modulus (E′), i.e. stiffening of the thread at the same temperature. (NB The modulus recorded from dynamic testing is the storage modulus (E′) rather than the true Young's modulus (E), as was calculated from the tensile plots.)

Figure 6.

The changes in storage modulus (E′) and heat dissipation (tan δ) that occurred during dynamic analysis of byssi under a force of 10 mN in dry conditions. The operational temperature range of the byssus is highlighted.

At an initial force amplitude of 10 mN in the dry, the ‘operational’ temperature of byssal threads was shown to be between approximately 10 and 50°C where E′ is constant (figure 6). Within this range, the threads had a stable modulus (E′) of approximately 300–400 MNm⁻². Outside this temperature, the mechanical properties of the threads changed significantly.

3.4 Hydrated byssi

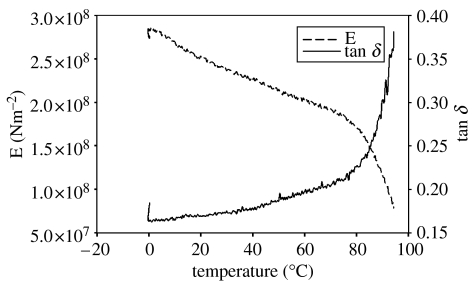
Unlike dry byssi, hydrated byssi were not damaged during the initial cycles of the DMA, so an initial force amplitude of 20 mN was used. The results suggested significant interaction of the threads with water, softening them and making them more elastic. Unlike in figure 6, where there is significant loss of energy through heat dissipation over the course of the testing, it can be seen from figure 7 that, in its hydrated state, byssus is far more elastomeric. The increase in tan δ at approximately 80°C suggests the onset of protein denaturation; were mussel byssi truly elastomeric, all energy would be directed towards the stretching of the material and none would be dissipated as heat. This increase in heat loss was coincident with thread stiffening over the range approximately 80°C, indicating that hydration does not protect the byssal thread from the effects of increased temperature. Importantly, in water, there were no clear limits for the operating temperature range of byssi. Instead, there was a gradual increase in energy dissipation (tan δ) and decrease in modulus (E′) over a broad temperature range. Modulus (E′), over the temperature range normally experienced by byssi in their natural environment (approx. 4–20°C), was approximately 270 MNm⁻². Accounting for variation introduced by thread thickness and sample loading, this value is comparable to the results of tensile testing in table 1.

Figure 7.

The changes in modulus (E′) and heat dissipation (tan δ) that occurred during dynamic analysis of byssi under a force of 20 mN in the hydrated state.

4. Discussion

Bell & Gosline (1995), in their discussion of the tenacity of adhesion of M. californianus, suggested that any chain is only as strong as its weakest link. They were referring to the byssal thread in its entirety and, particularly, the excessive strength of the distal byssus in relation to the proximal portion of the thread and the plaque. However, this adage could be applied equally well to the constituent proteins within the distal byssus. In the present study, tensile measurements of dry byssi suggest the possibility that the three or four distinct and predictable yield points in the byssal material may relate to three or four different constituents to the byssal thread, or, alternatively, three or four phases within a single collagenous protein complex. If direct evidence for this were identified in the future, it would support the predicted ‘multi-component’ nature of the threads.

The progressive reduction in stiffness at each yield point for dehydrated byssi implied that less force was required at each stage to cause cohesive failure within the thread. Only after the first, strongest, phase is broken, do the others take the strain of the mechanical test. If this were an adaptation, then one might expect that progressively stronger forces would be needed to initiate subsequent yielding behaviour, suggesting that the observed trend probably does not operate in nature and simply provides insight into the composition of the byssi. In reality, byssi will always be hydrated when they experience the stress of wave battering, so these 3–4 putative phases probably combine to facilitate the high yield stress and elastic behaviour shown in figure 2. Bell & Gosline (1995) also argued that the function of the distal byssus was not to maximize attachment strength but, instead, to absorb much of the energy that is directed towards dislodging the mussel. These results reinforce that hypothesis since, although dehydration increases the ultimate tensile strength of distal byssi, this strength will never be realized in nature as the thread will always fail proximally or in the plaque first. Further, strength is only achieved by sacrificing elasticity and, therefore, force dampening potential in the thread. Without its elasticity, the byssal thread would not function as an effective shock absorber and in its capacity for redistributing stress to neighbouring threads, thus reducing the stress experienced by any one thread.

The byssal threads, in fact, display a gradient of elasticity, ranging from very low E (approx. 50 MNm⁻²) in the proximal portion of the thread to high E (approx. 500 Nm⁻²) at the distal end, depending on the gradient of two main structural collagens, Col-D and Col-P (Waite et al. 2004). Not only is the proximal portion of the thread discrete in terms of composition and behaviour when compared to the distal thread, but the grading of material properties also continues down the length of the distal byssus, presumably to prevent the concentration of any applied stress into a singularity at the weakest point on the thread, increasing the risk of failure. In Waite et al. (2004) the authors presented two models in an attempt to predict the gradients of these proteins along the length of a byssal thread. One model suggested a random arrangement of preCol-D, preCol-P and non-graded preCol-NG (the pre-collagen monomers), whereas the second model proposed a more linear arrangement of the collagen proteins, with a gradual shift from predominantly preCol-P to predominantly preCol-D. This second model also predicted the observed 10-fold increase in E towards the distal end of the thread, suggesting to the authors that this model may be the most probable representation of the natural system. Here, the results would also favour the second model, as this arrangement would be far more probable to present yields in predictable locations on a stress/strain curve.

It makes good sense that the combination of several phases into one material reaps the benefits of each component, while mitigating the negative aspects associated with any individual constituent (Harris 1980), although this multi-component approach is not without its drawbacks. It is entirely possible that any one of these multiple yields could represent, for example, the delamination of the varnish coating surrounding the thread during strain. Connections between materials of different E are fraught with problems and are the primary reason for the graded structure of the byssal thread. This may be especially problematic when the connections between the varnish and the underlying collagens are dehydrated, since they almost certainly have very different E and, therefore, will deform at different rates. These connections probably also rely on water to some degree for their molecular cohesion. There is, however, no suggestion that this arrangement is redundant. On the contrary, hydration of the thread (as would naturally be the case in the intertidal) demonstrated that multiple yields were no longer displayed and, instead, a single yield was evident. This strongly suggests that the byssal proteins interact with water to manifest the important mechanical properties of the distal byssus, i.e. its ability to yield and deform with little applied force long before its point of cohesive failure and, subsequently, to recover from that yield and ‘heal’. Some byssi (figure 4) did not display multiple yields and it is suggested that this is due to water retention perpetuating their hydrated character. The stiffness of aged dehydrated byssi was reduced dramatically after each yield, suggesting that more cohesive damage was being done than in fresh byssi.

That byssal threads are collagenous in nature has been known since the work of Mercer (1952), Jackson et al. (1953) and Rudall (1955). Benedict & Waite (1986), could not extract the collagen they knew to be present in the distal byssus for sequencing, although they presented data for three polypeptides (putative collagen subunits) extracted from the proximal region with M_rs of 53, 55 and 65 kDa, respectively. If subunits such as these were present in the distal byssus, then this too could go some way to explaining the multiple yielding behaviour of dehydrated byssi. In fact, Col-D was shown by Qin & Waite (1995) to contain three identical α-like chains with a molecular mass 60 kDa.

Qin & Waite (1995) demonstrated that the distal region of the byssal thread is, in fact, predominated by Col-D. The silk fibroin-like flanking domains of Col-D provide stiffness to the extensible collagen fibres and, since silk fibroin lacks the side chains necessary for crosslinking, it is suggested that DOPA-rich domains may instead be important in this role. The silk-like flanking domains may also confer heat stability to the material, given that low stability is predicted for generalized collagen (e.g. Lazarev et al. 1999 and enclosed references). Rudall (1955) predicted a major β-pleated sheet motif in the distal byssus and suggested that this could constitute a separate phase of the collagen structure. In this way, the arrangement of β-sheets, α-chains, collagen and fibroin domains is reminiscent of a synthetic block-copolymer, whose multi-component nature would probably produce multiple yields similar to those presented here.

Bell & Gosline (1995) found that the initial stiffness (k_i) (measured to first yield) of their field-collected byssi (also presumed older than lab deposited byssi) was significantly greater than those deposited in the laboratory when tested hydrated. This was not the case here (table 1), although the data for fresh byssi were considerably more variable than for older byssi, possibly masking any trend. Presumably, this increased variability can be attributed to fresh byssi being at different stages of crosslinking and that, after two weeks, this crosslinking was complete. Older, fully crosslinked, byssi on the other hand were shown (table 1) to be stiffer than fresh byssi when dehydrated. This difference disappears in the hydrated state, suggesting that old byssi are probably just as effective as fresh ones under natural conditions.

From the present calculations (table 1), it is clear that the distal byssal material is relatively strong for such an elastic substance, with an ultimate tensile strength similar to that of nylon (75 MNm⁻²). These results compare well with those from previous studies by Price (1981) with M. edulis and Bell & Gosline (1995) with M. californianus. Distal byssus is certainly much stronger than the proximal byssus, reaffirming the theory that its design must be optimized for factors other than strength. There seems no reason (i) for the distal portion of the thread to develop this strength when other regions are considerably weaker and (ii) to require this increased strength when dehydrated, for which significant adaptation would be necessary. Instead, it is more probable that the multi-component nature of byssus is designed for elasticity and recovery from yield—as seen hydrated—rather than ultimate strength. In summary, elasticity of the threads is shown to be seriously compromised by dehydration. Dehydration had clear effects on the yielding characteristics and stiffness of the byssi, as well as on their ultimate tensile strength, with dehydrated byssi typically showing multiple yields and greater stiffness. Age, over a two-week period, seemed not to seriously affect the function of the byssus. These observations have clear ecological relevance for an organism that needs to optimize adhesion with a limited energy budget and that is exposed to a greater degree of predation while immersed.

As well as its improved resolution and sensitivity over a tensile tester, the principal advantage of using DMA in this study was the ability to investigate the behaviour of threads under tension and through a thermal cycle, both hydrated and dehydrated. Even with this sensitivity, however, dry measurements of byssal threads were taken using an initial force amplitude of 10 mN, a very low force, to cycle the thread without damaging it and producing misleading traces. When dynamic testing was attempted at the more commonly used 20 mN setting, threads would often snap during the initial phase of dynamic analysis, or while going through the 0–10°C temperature glass transition range. Those that survived the initial cycle were generally damaged and produced unreliable plots. This low initial force did not affect the force experienced by the thread during dynamic cycling, as explained in the methodology, and so the results in figure 6 at 10 mN and those in figure 6 at 20 mN are comparable.

The only previous study to employ dynamic testing towards mussel byssi was Carrington & Gosline (2004). In actual fact, their measurements were repeated tensile tests to investigate the effects of strain rate on byssal threads, not DMA as it is presented here; however, their observation that previously unstressed byssal threads dissipate considerable energy during a strain cycle beyond their yield point was interesting. Carrington & Gosline's quasi-dynamic testing used increasing frequency and, presumably, constant temperature to acquire general trends of E′ and tan δ for the threads, whereas the present study used a complementary technique of constant frequency and increasing temperature to produce far more detailed plots of material behaviour. The glass transition point (T_g) of a polymer is generally considered to be the most important material characteristic as far as material properties are concerned, primarily owing to its effects on mechanical behaviour, but also owing to the concurrent changes that also occur within the bulk of the material at this temperature. These include coefficients of thermal expansion, heat capacity, refractive index, mechanical damping, nuclear magnetic resonance behaviour and electrical properties (Nielsen 1974). T_g was identified for byssal threads in dry conditions and this is important since, below the critical 6°C temperature, the thread would no longer function for its intended use. The identification of this T_g also allows speculation on the degree of crosslinking within the material. Glass transitions vary from −123°C for common polydimethyl siloxane (PDMS) rubber to 100°C for polystyrene and in excess of 300°C for highly cross-linked phenol formaldehyde resins (Nielsen 1974). In synthetic polymers, long-chain aliphatic groups, and ether and silicon–oxygen linkages build flexibility into polymers and reduce T_g, although little is known about the behaviour of protein polymers in this regard. What is known is that bulky molecular flanking groups, such as silk fibroin, elastin or glycine to state the present example, should decrease molecular flexibility and raise T_g, providing that proteins behave in a similar way to synthetic polymers. Further, increasing the polarity of a polymer increases T_g, a possible repercussion of the polar Mefp proteins.

The resistance of the distal byssus to high temperatures was equally impressive, only beginning to loose structure at approximately 50–60°C (both hydrated and dehydrated) supporting the observation by Chomczynski & Sacci (1987) that this material has a melting point in excess of 90°C. This loss of structure was suggested by a stiffening (increasing E′) of the byssus after 50–60°C; a temperature unlikely to be approached in nature. Dehydration was also shown to affect the moduli and tan δ of the threads, with dehydrated threads being considerably less elastic (E≃400 MNm⁻²) than hydrated threads (E≃270 MNm⁻²). These values are comparable to small-strain rubber (10–100 MNm⁻²) or low-density polyethylene (200 MNm⁻²) and lower than plastic materials such as nylon (3000 MNm⁻²).

From the tensile measurements, it became clear that byssal threads interact with water to manifest the material properties so important to the function of the byssus. Thus, it was important that dynamic measurements too were conducted in the hydrated state. The methodology was repeated for hydrated byssi although, for obvious reasons, the threads could not be tested below 0°C in water. The dynamic profile of hydrated byssi (figure 7) was less dramatic with no obvious glass transition. Instead, there was a gradual decrease in modulus with increasing temperature. This was in stark contrast to the stiffening that occurred when dry, again suggesting that interaction with water made the material more elastomeric and that, due to the plasticizing effects of water, T_g occurs at a lower, unrecorded, temperature. This profile suggests that the behaviour of the byssal thread would be predictable and reliable over a wide range of temperatures and strain rates when hydrated: just what a mussel attached to an exposed and wave-swept shore would require from an attachment mechanism.

It seems then, that techniques such as DMA can be used by biologists to look past the simple mechanical properties of materials and, in addition, to make assumptions about the composition of biological samples as if they were synthetic polymers. Although the multiple yielding behaviour of the distal byssus in its dehydrated state does not accurately replicate its natural behaviour, it does allow us to speculate on the composition of the thread. Hopefully, future research using modern proteomics and molecular techniques will continue to elucidate the composition of byssal collagen which, surely, has huge potential as a synthetic biopolymer for applications as wide and varied as shock resistant cabling to biomedical applications (Demming 1999).