Rest period duration of the coronary arteries: Implications for magnetic resonance coronary angiography

Abstract

Magnetic resonance (MR) and computed tomography coronary imaging is susceptible to artifacts caused by motion of the heart. The presence of rest periods during the cardiac and respiratory cycles suggests that images free of motion artifacts could be acquired. In this paper, we studied the rest period (RP) duration of the coronary arteries during a cardiac contraction and a tidal respiratory cycle. We also studied whether three MR motion correction methods could be used to increase the respiratory RP duration. Free breathing x-ray coronary angiograms were acquired in ten patients. The three-dimensional (3D) structure of the coronary arteries was reconstructed from a biplane acquisition using stereo reconstruction methods. The 3D motion of the arterial model was then recovered using an automatic motion tracking algorithm. The motion field was then decomposed into separate cardiac and respiratory components using a cardiac respiratory parametric model. For the proximal-to-middle segments of the right coronary artery (RCA), a cardiac RP (<1 mm 3D displacement) of 76±34 ms was measured at end systole (ES), and 65±42 ms in mid-diastole (MD). The cardiac RP was 80±25 ms at ES and 112±42 ms at MD for the proximal 5 cm of the left coronary tree. At end expiration, the respiratory RP (in percent of the respiratory period) was 26±8% for the RCA and 27±17% for the left coronary tree. Left coronary respiratory RP (<0.5 mm 3D displacement) increased with translation (32% of the respiratory period), rigid body (51%), and affine (79%) motion correction. The RCA respiratory RP using translational (27%) and rigid body (33%) motion correction were not statistically different from each other. Measurements of the cardiac and respiratory rest periods will improve our understanding of the temporal and spatial resolution constraints for coronary imaging.

I. INTRODUCTION

Magnetic resonance (MR) imaging may be used for noninvasive detection and staging of coronary artery disease. However, physiologic motion during an MR acquisition causes blurring and ghosting artifacts in the images.^1,2 Two-dimensional (2D) MR images can be acquired during a breath hold, with electrocardiogram (ECG) gating and short readouts used to freeze the motion of the heart during the cardiac contraction.^3,4 The technique requires the use of thick imaging slices (3–5 mm) that can cause partial volume effects and signal averaging when visualizing submillimeter pathologies.

Three-dimensional (3D) magnetic resonance coronary angiography (MRCA) provides volumetric images with higher isotropic resolution and signal-to-noise ratio (SNR). Volumetric data simplifies the visualization of tortuous and non-planar vessels that are difficult to capture in a planar 2D slice.⁵ However, 3D MRCA requires longer imaging times during which respiratory motion can cause blurring that leads to overestimation of vessel lumen size and undetected stenoses.⁶

Gating the MR acquisition to both the cardiac and respiratory cycles is one method for freezing the motion of the coronary arteries. Data are acquired for a short period of time whenever the two gating triggers coincide. Increasing the duration of the data acquisition window reduces the overall duration of the scan, but could introduce motion artifacts. Motion correction could be used to increase the length of the data acquisition window, thereby reducing total scan durations without compromising image quality.^7-10

In this paper, we studied the quiescent periods of minimum coronary motion during a cardiac cycle and during a tidal respiratory breath. These rest periods were quantified from free breathing x-ray coronary angiograms using a mathematical modeling technique for separating the cardiac and respiratory motion fields. The results provide important insight into calculating the spatial and temporal resolution limits of MR coronary acquisitions. The results are also applicable to cardiac computed tomography (CT) acquisitions which suffer from motion related artifacts secondary to a data acquisition window of approximately 100 ms.

Finally, we investigated the ability of three different MR motion correction methods to model the motion of the coronary arteries during breathing. The relatively longer period of the respiratory cycle, as compared to the cardiac cycle, suggests that respiratory motion is more responsible for the low duty cycle of a cardiac and respiratory gated MRCA acquisition. The results of our respiratory motion analysis is important for understanding the utility of MR respiratory motion correction techniques for increasing imaging duty cycle, and therefore reducing scan durations for MRCA.

II. MATERIALS AND METHODS

A. Patients

Patients referred for diagnostic left heart catheterization were recruited to participate in an institutional review board (IRB) approved protocol. Unstable patients and emergency cases were excluded from participation in this study. Conventional cine biplane coronary angiograms were obtained in eight male and two female patients that gave written informed consent. Their mean age was 65±11 years (age range, 51–85 years). Four patients had mild dilated cardiomyopathy, and two had mild to moderate hypertrophic disease. The mean ejection fraction measured by ventriculography was 58±8% (range, 40%–65%).

B. Imaging

Imaging was performed with a Siemens biplane HICOR Angiography system (Siemens, Erlangen, Germany). Images were acquired at 30 frames per second, digitized, and archived onto compact disk in digital imaging and communications in medicine (DICOM) format. The raw 512×512 images were extracted using custom software on a personal computer running Linux, and postprocessing was performed using MATLAB (The MathWorks Inc., Natick, MA). A separate computer with digital acquisition system recorded the patients' ECG and a timing signal from the Siemens imaging system, which allowed the cardiac phase of each image to be computed retrospectively.

Coronary arteriography was performed using conventional techniques. A hand injected bolus of iodinated contrast agent was administered at the coronary ostia. Opacified arteries were visible for 3–6 s, spanning several cardiac cycles and approximately one breath. Patients were given no breathing commands in order to avoid making them conscious of their breathing; therefore we studied spontaneous tidal respiration.

C. Recovering the motion of the coronary arteries

A 3D+t (three dimensional plus time) model of the coronary arteries was reconstructed from biplane cine angiograms. For each patient, a static 3D model of the coronary arteries, Y₀, was reconstructed from one image pair at diastasis using a semiautomatic algorithm for stereo reconstruction of 3D curves from 2D projections.¹¹ Dynamic programming was used to optimize the reconstruction using an epipolar constraining function.

The 3D motion of the arteries was then recovered using an automatic motion tracking algorithm.¹² The algorithm computes the 3D deformation of Y₀ which is consistent with the temporally varying angiograms, subject to a constraint on the 3D length change of the arteries, and to a constraint on the spatial regularity of the 3D deformation field. The motion field

$$\mathcal{M}(\mathbf{q},t)=\mathbf{q}+\mathbf{d}(\mathbf{q},t)$$ (1)

is defined as a 3D displacement field, d, for points q ∈ Y₀ ∈ ℝ³. d:ℝ³ → ℝ³ is a 3D displacement vector generated by a 3D tensor product B-spline (B-solid)

$$\mathbf{d}(\mathbf{q},t)=\sum _{i=0}^{n_i-1}\sum _{j=0}^{n_j-1}\sum _{k=0}^{n_k-1}{b}_{i,p}\left(q_x\right)b_{j,p}\left(q_y\right)b_{k,p}\left(q_z\right){\mathbf{u}}_{\mathit{ijk}}\left[t\right],$$ (2)

where the {u_ijk[t] ∈ ℝ³} are the n_i×n_j×n_k control point vectors for image t, and the {b._,p :ℝ → ℝ} are the pth degree B-spline basis functions defined over a uniform knot vector.¹³ C² continuity of the deformation field is maintained over the B-solid volume by using cubic B-spline basis functions (p=3).

While M operates on 3D points q in the coronary tree, we adopt the shorthand notation

$${\mathrm{Y}}_t=\mathcal{M}[{\mathrm{Y}}_0,t]$$ (3)

to represent the transformation of the entire coronary tree from time zero, Y₀, to its state Y_t at time t.

A 3D rms errors of 0.69 mm was found for the reconstruction and motion tracking procedure using a coronary phantom. A more complete description of this energy minimization algorithm and results of validation experiments can be found in Ref. 12.

D. Separating cardiac and respiratory motion

The recovered deformation field, M, represents the motion of the coronary arteries while the heart is beating and the patient is breathing. A cardiac respiratory parametric model is used to decompose the motion field into independent cardiac and respiratory motion fields.¹⁴ The (i , j ,k)th control point's variation over a set of images, u_ijk[t] ∈ M, can also be written as a function of cardiac (χ_t) and respiratory phase (ρ_t)

$${\mathbf{u}}_{\mathit{ijk}}\left[t\right]\equiv {\mathbf{u}}_{\mathit{ijk}}[{\chi }_t,{\rho }_t].$$ (4)

The cardiac phase (χ) represents the percentage of the cardiac cycle with the QRS peak at χ =0. Intra-patient and inter-patient heart rate variability is normalized using the following method. In a study of 121 male subjects,¹⁵ it was determined that total electromechanical systole QS₂ (seconds) was related to heart rate HR (beats/min) by

$${\mathit{QS}}_2=-0.0021\times \mathit{HR}+0.546.$$ (5)

In order to work with a total cardiac phase (χ) interval of [0, 1), we chose to normalize to an idealized 60 beat/min heart rate. Using Eq. (5), a heart rate of 60 beats/min yields a systolic interval duration of 0.42 s. The diastolic interval is (1–0.42)=0.58 s.

For each patient R-R interval, we computed a systolic and diastolic subinterval using the instantaneous heart rate measured from the ECG. The systolic interval was then linearly re-mapped to the cardiac phase interval [0, 0.42). Similarly, the diastolic interval was linearly mapped to the cardiac phase interval [0.42, 1). For example, with a heart rate of 80 beats/min, the cardiac period is 0.75 s and QS₂=0.378. Thus, data during the systolic interval of [0,0.378) s following the QRS peak, was linearly scaled and mapped to the ρ interval [0, 0.42). Data from the diastolic interval [0.378,0.75) s following the QRS peak, was linearly scaled and mapped to the ρ interval [0.42, 1).

The respiratory phase (ρ) was measured directly from the images by taking a profile through the diaphragm. The displacement of the diaphragm-lung interface relative to end expiration is used as a measure of respiratory phase; ρ=0 at end expiration, and ρ = ±1 at end inspiration. The sign of ρ depends on whether the image is acquired during inspiration (+) or expiration (−).

We hypothesize that there exists a function û_ijk(χ,ρ) defined for any combination of cardiac and respiratory phases, and that u_ijk[χ_t,ρ_t] is a sampling of that function. We model û_ijk(χ,ρ) as the sum of two periodic B-spline parametric functions

$${\widehat{\mathbf{u}}}_{\mathit{ijk}}(\chi ,\rho )=\sum _{\ell =0}^{n_{\chi }-1}{b}_{\ell ,p_{\chi }}\left(\chi \right){\mathbf{v}}_{\ell }+\sum _{m=0}^{n_{\rho }-1}{b}_{m,p_{\rho }}\left(\rho \right){\mathbf{v}}_{m+n_{\chi }},$$ (6)

where {v ∈ ℝ³} are the n_χ+n_ρ control point vectors, and the {b._,p :ℝ → ℝ} are the pth degree B-spline basis functions defined over a uniform and periodic knot vector.

The first sum of Eq. (6) represents the cardiac motion, and the second represents the respiratory motion. This formulation captures the temporal smoothness characteristic of physiologic motion, and the periodicity of the cardiac and respiratory cycles. The function supports interpolation of the deformation field at cardiac-respiratory phase combinations other than those captured in the angiogram. Most importantly, the function facilitates the separation of the cardiac and respiratory motion.

The set of modeled control points û_ijk(χ,ρ) combine to form the coronary transformation function M̂, which is an approximation of M [see Eqs. (1) and (2)].In Ref. 14, 3D rms errors were computed between coronary trees evaluated using M and M̂ [Eq. (3)]. The mean plus one standard deviation of these rms values was submillimeter in 15 of 16 patient validation experiments.

E. Measuring the rest period duration

Standardized coronary segments were defined to facilitate inter-patient comparisons.¹⁶ The proximal two thirds of the right coronary artery (RCA), spanning the distance from the coronary ostium to the acute margin of the heart, was studied in four patients. In seven patients, we studied the proximal 5 cm of the left coronary tree, which included the left main, and the proximal segments of the left anterior descending and circumflex arteries.

The cardiac respiratory parametric model was fit to each motion tracked dataset. A set of respiration-only B-solid deformation fields, M̂_R, was created by evaluating Eq. (6) at different respiratory phases, for a constant cardiac phase in diastasis. These new deformation fields represent the motion of the coronary tree due only to respiration. Evaluating Eq. (6) at different cardiac phases, with respiratory phase held at end expiration, yielded a cardiac-only deformation field, M̂_C.

1. Cardiac rest period

The cardiac deformation field M̂_C was sampled at 100 points during a cardiac contraction, and a set of 3D coronary models was generated at each of these cardiac phases (0≤χ_i<1). For each cardiac phase χ_i, we calculated the longest symmetric time window centered at χ_i such that the motion of all of the points along the arteries during that time interval was less than some 3D threshold ε

$$\underset{t}{\arg \max }(\parallel {\widehat{\mathcal{M}}}_C({\mathbf{q}}_i,{\chi }_j)-{\widehat{\mathcal{M}}}_C({\mathbf{q}}_i,{\chi }_k)\parallel <∊)$$ (7)

subject to the following constraints:

$$\forall {\mathbf{q}}_i\in {\mathrm{Y}}_0,$$ (8)

$$\forall {\chi }_j:\mid {\chi }_j-{\chi }_i\mid \le \frac{t}{2},$$ (9)

$$\forall {\chi }_k:\mid {\chi }_k-{\chi }_i\mid \le \frac{t}{2}.$$ (10)

This rest period duration is reported in milliseconds and measures a quiescent period with respect to a specific maximum allowed 3D motion.

2. Respiratory rest period

The respiratory deformation field M̂_R was similarly sampled at 100 points over a respiratory cycle (−1≤ρ<1). The respiratory rest period is reported in milliseconds and as a percentage of the patient's respiratory cycle in an attempt to normalize for the variability in breathing rate among patients.

F. Motion corrected respiratory rest period

To assess the applicability of different MR motion correction methods, we computed a motion corrected respiratory rest period (MCRRP) for the respiratory motion. The three motion models we studied were: (1) 3D translation, T; (2) 3D rigid body transformation, R; and (3) 3D affine deformation, A. The rigid body transformation represents translation and rotation in three dimensions. The affine transformation models translation, rotation, scaling, and shearing.

The coronary tree model, Y_EE, at end expiration (ρ=0) was used as a reference, and the coronary models at the other respiratory phases, Y_j, were registered to the reference using one of the three linear transformations (T, R, or A). The transformations can be recovered with a closed form linear least squares method since the pairwise matching of points between Y_j and Y_EE is known [remember: both trees are related to Y₀ by M̂_R, see Eq. (3)].

The rest period duration was then recomputed for the registered coronary trees using the method described in the previous section. This new metric, the MCRRP, quantifies how well the given transformations account for the motion of the coronary tree by studying the residual motion field.

G. Statistics

Measurements are reported as a mean ± one standard deviation. Comparisons were made using a two-tailed student's t-test with significance level of 0.05. Multiple pairwise comparisons for a set of results were made with a Bonferroni corrected t-test.¹⁷

III. RESULTS

In the four right coronary datasets, the patients had a mean heart rate of 64±9 beats/min (range, 55–75 beats/min) and a mean respiratory rate of 14.6±2.2 breaths/min (range, 12.5–17.6 breaths/min). The mean 3D length of the reconstructed proximal third of the RCA was 39±10 mm (range, 29–43 mm). The mean 3D length of the middle third of the RCA was 36±5 mm (range, 32–43 mm).

In the seven left coronary datasets, the patients had a mean heart rate of 64±7 beats/min (range, 56–74 beats/min), and a mean respiratory rate of 15.7±4.2 breaths/min (range, 9.4–21.4 breaths/min).

Figure 1 shows the 3D displacement of the left main ostium over a cardiac cycle, and the RCA ostium over a tidal breath. The cardiac motion plot suggests that periods of minimal motion may occur at end systole (χ≈0.4) and at mid diastole (χ≈0.7). The respiratory motion plot suggests that periods of minimal motion may be found at end expiration (ρ=0) and at end inspiration |ρ|=1).

Fig. 1.

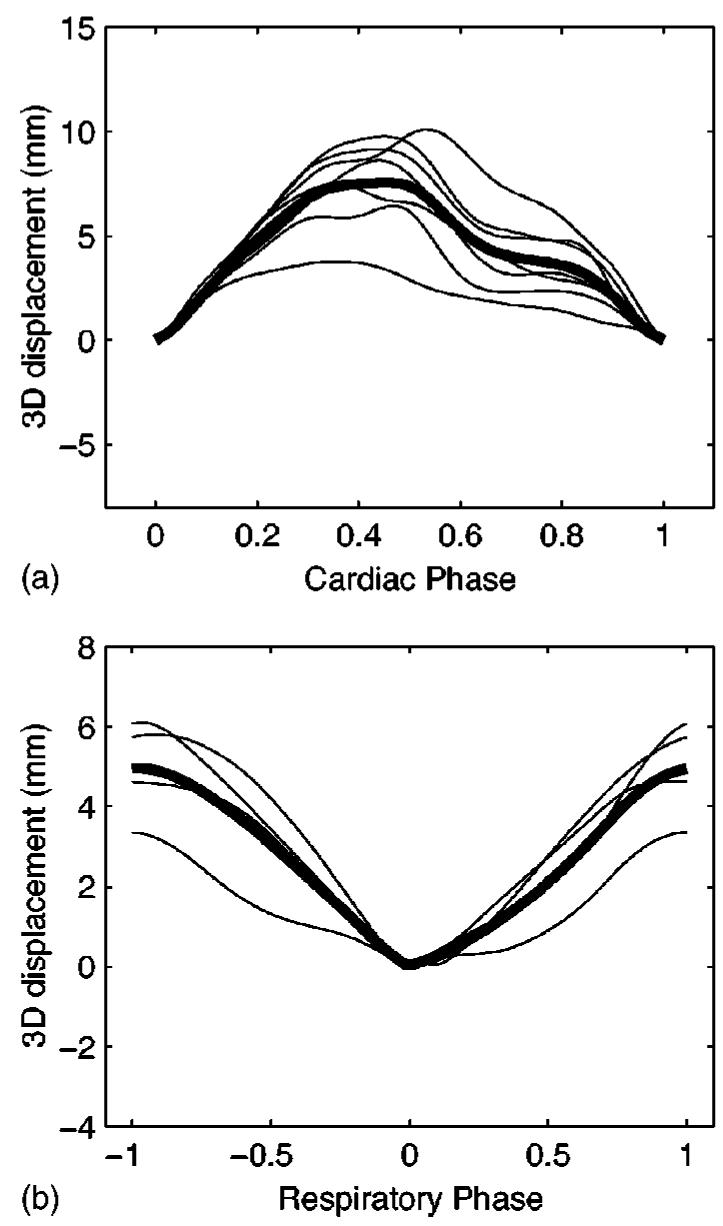
(a) Magnitude 3D displacement of the left main origin during the cardiac contraction. Breathing has been arrested at end expiration. The plot shows individual results for seven patients (thin lines) and the mean displacement (thick line). (b) Magnitude 3D displacement of the right coronary artery ostium during a tidal breath. The cardiac contraction has been arrested at mid diastole (diastasis). The plot shows individual results for four patients (thin lines) and the mean displacement (thick line).

A. Cardiac rest period

Figure 2 shows the rest period duration as a function of the cardiac cycle for the right coronary artery in four patients and for the left coronary tree in seven patients. In these examples, the rest period was defined as the amount of time during which the 3D motion of the artery was less than 1 mm. The plots show that the motion of the heart during the cardiac contraction is smallest at end systole (χ≈0.4), and at mid diastole (χ≈0.7).

Fig. 2.

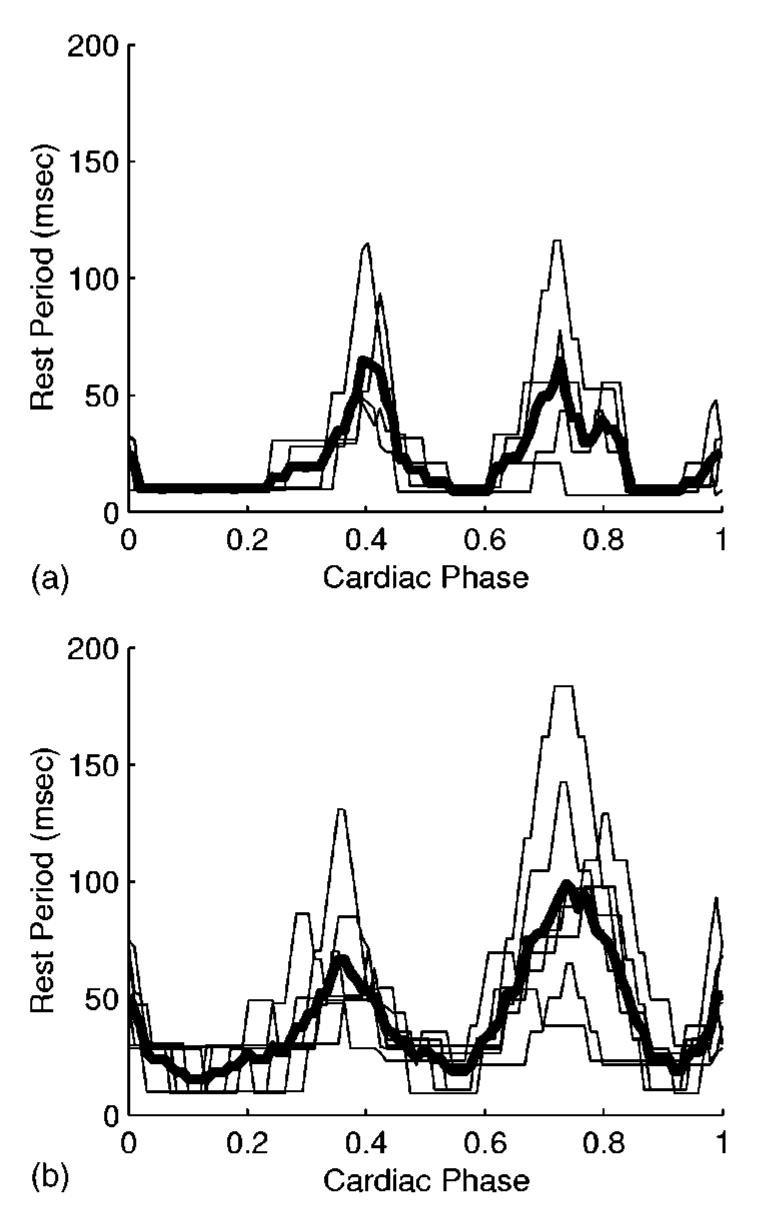
Rest period duration during a cardiac contraction for the (a) right and (b) left coronary arteries. The maximum allowed 3D motion of the artery is 1 mm. The graphs show individual results (thin lines) for four patients in (a) and seven patients in (b). The mean rest period durations are plotted as thick lines. Cardiac phase (χ) represents the percentage of the cardiac cycle, with χ =0 set to correspond to the QRS peak. End systole corresponds to χ≈0.4.

For an allowed 3D motion of 1 mm of the right coronary artery, the end-systolic rest period duration was 76±34 ms (range, 47–115 ms). The rest period was centered at χ =0.41±0.02 (range, 0.39–0.43). The mid-diastolic rest period duration was 65±42 ms (range, 21–116 ms) and was centered at χ =0.72±0.04 (range, 0.68–0.77).

For the left coronary tree, the end-systolic rest period duration was 80±25 ms (range, 52–131 ms) for an allowed 3D motion of 1 mm. The rest period was centered at χ =0.38±0.04 (range, 0.30–0.43). The mid-diastolic rest period duration was 112±42 ms (range, 65–183 ms) and it was centered at χ =0.74±0.06 (range, 0.63–0.81).

Rest period is defined with respect to a given amount of coronary motion. Therefore, as the amount of tolerated motion increases, so does the rest period duration. This relationship is demonstrated in Table I which shows the rest period duration for a range of 3D motion tolerances.

Table I.

Cardiac rest period for the right and left coronary arteries. The systolic and mid-diastolic rest period duration are measured in milliseconds (ms).

Allowed 3D motion (mm)	Rest period duration (ms)
	Right coronary		Left coronary
	Systolic	Diastolic	Systolic	Diastolic
0.5	41±21	30±19	41±15	55±22
1.0	76±34	65±42	80±25	112±42
1.5	105±40	109±71	114±29	168±65
2.0	131±43	135±86	148±33	197±60
2.5	164±40	171±108	184±37	224±61

B. Respiratory rest period

Figure 3 shows the rest period duration during a spontaneous tidal respiratory cycle for the right coronary artery in four patients and for the left coronary tree in seven patients. In these examples, the rest period was defined as the amount of time during which the 3D motion of the artery was less than 1 mm. The plots indicate that there are periods of minimal motion at end expiration (ρ=0) and at end inspiration (ρ= ±1).

Fig. 3.

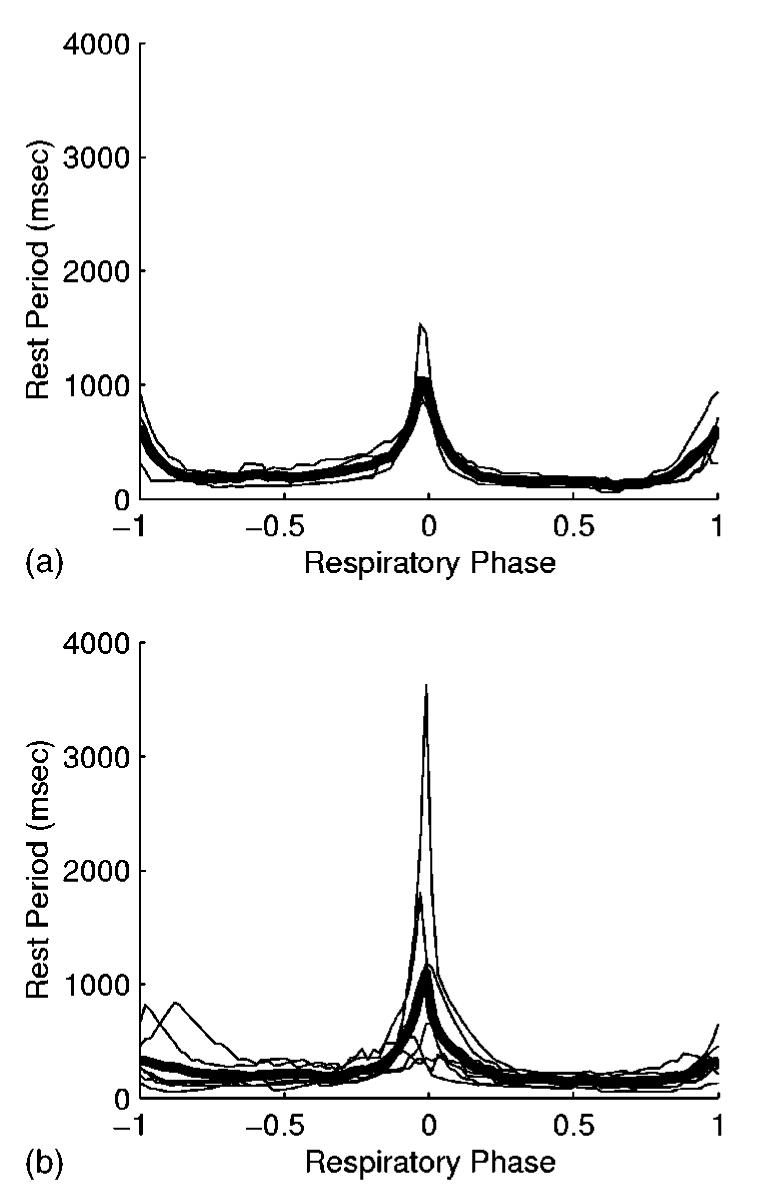
Rest period duration during a tidal breath for the (a) right and (b) left coronary arteries. The maximum allowed 3D motion of the artery is 1 mm. The graphs show individual results (thin lines) for four patients in (a) and seven patients in (b). The mean rest period durations are plotted as thick lines. Respiratory phase (ρ) is 0 at end expiration, and ρ = ±1 at end inspiration. The sign of ρ indicates inspiration (+) or expiration (−).

For the right coronary artery, the end-expiration rest period was 1065±320 ms (range, 844–1536 ms) for an allowed 3D motion of 1 mm. This was equal to 26±8% (range, 18%–37%) of the patients' respiratory period. The end-inspiration rest period was 655±227 ms (range, 415–939 ms), or 16±8% (range, 9%–28%) of the respiratory cycle.

For 1 mm of allowed motion of the left coronary tree, the end-expiration rest period was 1232±1172 ms (range, 391–3629 ms). As a percentage of the patients' respiratory period, the end-expiration rest period was 27±17% (range, 9%–57%). The end-inspiration rest period was 444±273 ms (range, 156–839 ms), or 11±6% (range, 5%–21%).

Table II provides the respiratory rest period duration as a percentage of the respiratory cycle duration for a range of motion tolerances.

Table II.

Respiratory rest period for the right and left coronary arteries. The end-expiration (EE) and end-inspiration (EI) rest period duration are reported as a fraction of the respiratory cycle duration (%).

Allowed 3D motion (mm)	Rest period duration (% of cycle)
	Right coronary		Left coronary
	EE	EI	EE	EI
0.5	17±8	10±6	18±14	6±3
1.0	26±8	16±8	27±17	11±6
1.5	33±8	20±9	33±16	14±7
2.0	39±9	25±11	39±16	18±9
2.5	45±9	28±12	45±15	23±10

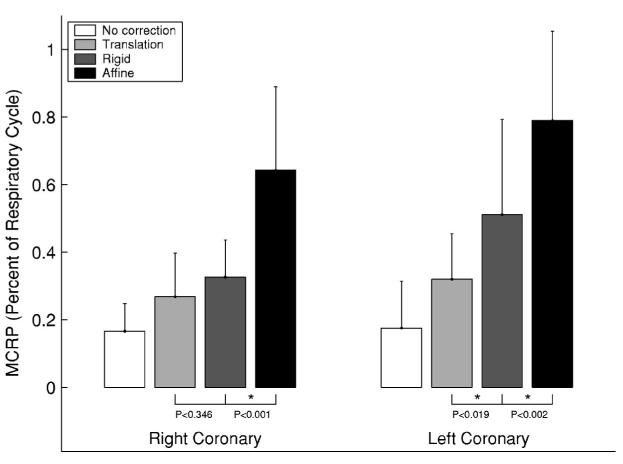
C. Motion corrected respiratory rest period

Figure 4 shows the effect of motion correction on the rest period at end expiration. The graph shows that as the degrees of freedom of the motion model are increased (translation <rigid<affine), the MCRRP duration also increases.

Fig. 4.

Motion corrected respiratory rest period (MCRRP) duration at end expiration: A comparison of three different motion models. The physiologic motion is shown as a base line reference. Two Bonferroni corrected t-tests were performed for each artery to test for incremental differences in the MCRRP. A group-wise statistical significance of α<0.05 is indicated by an asterisk (*). P values are provided for all t-tests.

For a tolerated 3D motion of 0.5 mm, the physiologic rest period of the left coronary tree was measured previously to be 18±14% of the tidal respiratory cycle. Translation was able to model the motion of the left coronary arteries for 32±13% of the tidal respiratory cycle with the same motion tolerance. The MCRRP increased to 51±28% of the cycle with the rotational degrees of freedom provided by the rigid body motion model. The affine motion model extended the MCRRP to 79±26% of the respiratory cycle.

Rigid body motion modeled the respiratory motion for a significantly longer portion of the respiratory cycle than translation motion alone (P<0.019, Bonferroni t-test for paired samples and two comparisons). The affine deformation model modeled the respiratory motion for a significantly longer fraction of the respiratory cycle than the rigid body transformation (P<0.002, Bonferroni t-test for paired samples and two comparisons).

For the right coronary artery, there was no statistical improvement with the rigid body model (MCRRP mean, 33±11%) over the translation motion model (MCRRP mean, 27±13%). The affine motion model was able to model the motion for 64±25% of the respiratory cycle. This was a statistically significant improvement over the rigid body motion model (P<0.001, Bonferroni t-test for paired samples and two comparisons).

IV. DISCUSSION

The prescribed volumetric spatial resolution of a MR or computed tomography (CT) protocol is only one determinant of the true resolution of the acquisition. Temporal resolution plays an important role in defining the true resolving power of a given imaging technique. In this paper, we present an analysis of the cardiac and respiratory motions of the heart, with a specific focus on the quiescent periods of these cycles.

The analysis presented in this paper is based on a single breath for each patient. Variability in the respiratory rate, amplitude, and breathing mechanics could influence the observed rest period. However, the nature of the angiographic procedure, in which contrast agent is injected into the coronary arteries displacing normal blood flow, does not allow for longer injections to study these effects.

To the best of our knowledge, there are no reports of the coronary respiratory rest period duration. The technical limitation has been the difficulty in separating the cardiac and respiratory motion of the arteries. Our work on the cardiac respiratory parameter model has made this possible.¹⁴ This mathematical modeling technique allows us to study the dynamics of the respiratory cycle in patients by providing a mechanism for freezing the motion coming from the cardiac contraction.

A. Comparison to previous studies of the cardiac rest period

Confidence in our results is obtained by comparing them with a previous report of the coronary artery rest period. The cardiac respiratory parametric model allowed us to mathematically freeze the breathing motion of our free-breathing, beating, coronary data. Thus, we were able to analyze only the cardiac motion of the arteries.

Wang et al. studied the rest period during the cardiac contraction with x-ray angiograms acquired during a breath hold.¹⁸ The mid-diastolic rest period was defined as motion less than 1 mm in any of the in-plane directions visualized with an orthogonal biplane acquisition. Thus, the upper bound on the 3D motion was approximately $\sqrt{3}=1.73\mathrm{mm}$. The mean rest period durations were reported as 120 ms (range, 66–200 ms) for the right coronary artery and 161 ms (range, 66–333 ms) for the left coronary tree. For a 3D motion limit of 1.75 mm, we measured similar mean rest periods of 124 ms (range, 35–222 ms) for the right coronary artery and 178 ms (range, 94–257 ms) for the left coronary tree.

B. Respiratory motion correction for MRCA

Respiratory motion correction during MR imaging of the heart typically uses navigator echoes¹⁹ to measure the position of the diaphragm. This one-dimensional displacement is then used to estimate the state (position, orientation, etc.) of the heart so that the proper amount of correction can be applied.²⁰ Whereas cardiac gating windows are described in the temporal domain, respiratory gating windows are described in the spatial domain. For example, data might be acquired whenever the diaphragm is within 5 mm of a reference position.

Unfortunately, we were not able to make 3D spatial measurements of diaphragmatic displacement during respiration. There were no landmarks on the diaphragm that could be identified in the projection images and used to generate a 3D reconstruction. This was further complicated by the fact that the contours of the diaphragmatic silhouette, viewed from different projection angles, did not necessarily correspond to the same material tissue.

Nonetheless, our measure of respiratory phase (ρ) was a 2D approximation of diaphragmatic displacement measured from one of the projection images.¹⁴ Based on empirical measurements of the range of diaphragmatic displacement during free breathing,^21,22 we mapped the normalized phase measurement (0≤|ρ|<1) to represent a displacement of 0 to 15 mm. This relationship allowed rest period durations to be converted from a temporal to a spatial measurement.

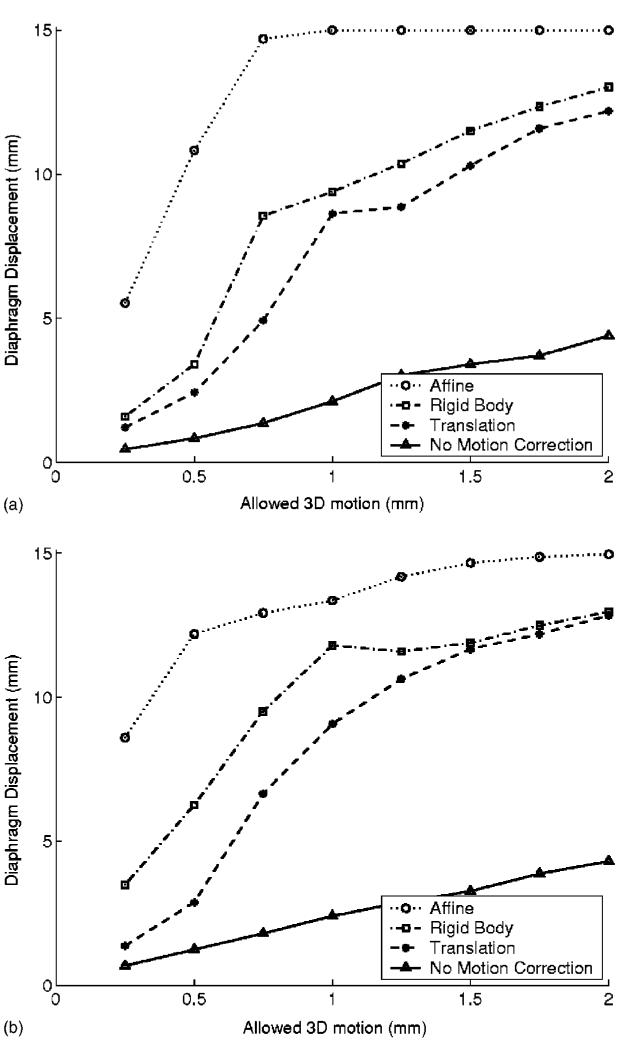
Figure 5 shows the relationship between the width of a diaphragmatic gating window at end expiration to the amount of motion that would be observed at the coronary arteries. The solid lines show that a 5 mm respiratory gating window without motion correction would introduce up to 2 mm of motion at the coronary artery segments we studied. The coronary arteries have diameters ranging from 2.0 to 3.9 mm for the proximal-to-distal right coronary artery, and 1.8–3.7 mm for the left main, and proximal-to-middle segments of the left anterior descending and circumflex arteries.²³ Detection of a 25% stenosis of a 2-mm-diam vessel requires an image resolution of approximately 0.5 mm, which could not be achieved with this respiratory gating condition. The use of translational motion correction with the same 5 mm diaphragmatic gating window reduced the residual motion of the arteries to between 0.5 and 1 mm. For small diaphragmatic gating windows, rigid body motion correction offers a larger marginal improvement in resolution for the left coronary tree, than for the right coronary.

Fig. 5.

Respiratory rest period duration for different imaging requirements: A comparison of three different motion models. (a) Right coronary artery and (b) left coronary tree. Diaphragmatic displacement was not directly measured, but estimated for each patient using the respiratory phase and an average respiratory displacement of 15 mm.

Figure 5 can be used to prescribe the correct diaphragmatic gating window size and appropriate motion correction technique for a given image resolution and scan duration requirements. If 0.5 mm of respiratory motion could be tolerated during an acquisition, than Fig. 5(a) shows that for the right coronary artery, there would be almost no advantage to using a rigid body motion correction technique compared to a simpler translational motion correction method. Affine motion correction could theoretically provide a significant improvement in scan efficiency, but the need to estimate 12 parameters makes it a more complex technique to implement in a patient specific approach.¹⁰

V. SUMMARY

In conclusion, we quantified the rest periods of the coronary arteries during the cardiac and respiratory cycles using patient data obtained during spontaneous free breathing. MR motion correction techniques were shown to significantly increase the respiratory rest periods, with varying degrees of efficacy depending on the complexity of the motion correction method. Using affine motion correction, the right coronary artery can be frozen, to within 0.5 mm of residual motion, for 64% of the tidal respiratory period. The affine corrected rest period is 79% of the tidal respiratory period for the left coronary tree. Ultimately, the success of motion correction depends on the existence of accurate models of the motion, and/or the ability to estimate the state of the heart at any given time. The variability of respiratory motion suggests that a patient-specific motion correction paradigm is warranted.