Abstract
Signal transduction is an important process that transmits signals from the outside of a cell to the inside to mediate sophisticated biological responses. Effective computational models to unravel such a process by taking advantage of high-throughput genomic and proteomic data are needed to understand the essential mechanisms underlying the signaling pathways. In this article, we propose a novel method for uncovering signal transduction networks (STNs) by integrating protein interaction with gene expression data. Specifically, we formulate STN identification problem as an integer linear programming (ILP) model, which can be actually solved by a relaxed linear programming algorithm and is flexible for handling various prior information without any restriction on the network structures. The numerical results on yeast MAPK signaling pathways demonstrate that the proposed ILP model is able to uncover STNs or pathways in an efficient and accurate manner. In particular, the prediction results are found to be in high agreement with current biological knowledge and available information in literature. In addition, the proposed model is simple to be interpreted and easy to be implemented even for a large-scale system.
INTRODUCTION
Signal transduction is the primary means that cells respond to the external stimuli of the environment such as growth factors and nutrients. Furthermore, signal transduction plays an essential role in coordinating metabolism, cell proliferation and differentiation. Generally, external signal or stimulus is transduced into a cell through an ordered sequence of biochemical reactions inside the cell. In many signal transduction processes, the number of proteins and other molecules participating in these events increases as the process proceeds from the initial stimulus, which results in a “signal cascade”. However, experimentally identifying every reaction and component even in a relatively simple signaling pathway may require a concerted and decade-long effort due to the complexity of biochemical reactions in a living cell (1,2). Recently, with the rapid advances in high-throughput biotechnologies, a tremendous amount of experiment data are increasingly accumulated, which provides insights into the components and reactions involved in signal transduction. Therefore, it is necessary to develop new computational methods to capture the details of signaling networks by exploiting high-throughput genomic and proteomic data.
Since signal transduction is a process of biochemical reactions achieved by a cascade of protein interactions, protein–protein interaction (PPI) data are a direct information source related to pathways, and thereby have been extensively explored to elucidate the mechanisms underlying signal transduction (3). For example, Scott et al. (4) proposed a variant of the color coding algorithm to reconstruct signaling pathways from yeast PPI network. In the color coding method, a number of candidate pathways are firstly found with a score assigned to each candidate and the top scoring pathways are then assembled into a signaling network. By integrating both PPI and microarray data, Steffen et al. (5) developed an algorithm, namely Netsearch, to reconstruct signaling networks. In the Netsearch method, they also rank the candidate pathways and then aggregate top scoring pathways into a signaling network. In addition, Liu and Zhao (6) proposed a new score function for predicting the order of signaling pathway components by employing both protein interaction and microarray data. Recently, several computational methods have been proposed for recovering signaling networks by reconstructing PPI networks with functional information (7,8). Note that the method to detect signaling pathways described in (7) is actually the one proposed in (6), which is denoted as pairwise correlation here. Despite various technical differences, existing methods mainly aim at finding a subnetwork from PPI dataset whose members have either strong expression correlation or reliable interactions depending on the weights of edges defined for the PPI network. However, most of them generally cannot directly find a signaling network as a whole, i.e. they first identify separate linear pathways and then heuristically assemble them into a signaling network. Therefore, the solutions may be inconsistent and usually result in missing important components due to the limited prediction power.
In this work, we present a novel computational method based on an integer linear programming (ILP) model for detecting signal transduction networks (STNs) in an accurate manner by integrating PPI data with gene expression profiles, which is simple in algorithm and efficient in computation. In our method, we formulate signaling network detection as an optimization problem that aims at finding an optimal subnetwork starting from membrane proteins and ending at transcription factors (TFs). Different from the existing methods, the proposed ILP model treats a signaling network as a whole entity rather than heuristically ranking and assembling individual linear pathways. In particular, our method is flexible for various constraints and has no restriction on the network structures. Therefore, we are able to exploit all available information from experiment results or literature, and directly uncover a general signaling network in an integrated and accurate manner rather than a particular pathway. Since a relaxed linear programming (LP) algorithm is adopted to solve the optimization problem, it is efficient and able to handle large-scale problems without numerical difficulty. The numerical experiments on yeast MAPK signaling pathways demonstrate the effectiveness and efficiency of the proposed method compared with the existing methods, e.g. more components in main chains of pheromone response pathway and filamentation pathway are correctly identified by our proposed method. In particular, the prediction results are found to be in high agreement with current biological knowledge and available information from literature.
MATERIALS AND METHODS
PPI and gene expression datasets
In this work, three PPI datasets are employed, including DIP (9), DIP Core (10) and SPA (7). The DIP dataset is obtained from the DIP database (9), which includes 4839 proteins and 14 319 interactions. The confidence scores for PPIs in the DIP dataset are calculated as described in (11). The DIP Core dataset contains interactions determined by at least one small scale experiment or at least two independent experiments. The DIP Core dataset is downloaded from the DIP database in 2007 (20070107), and contains 2558 proteins and 5967 interactions. The SPA dataset consists of proteins that are possibly involved in cellular communication and signal transduction mechanism, and has been successfully applied to signaling pathway recovery (7). The SPA dataset contains 1363 proteins and 3721 interactions. Table 1 shows the details of the PPI data used in this work.
Table 1.
PPI and gene expression data used in detecting STNs
| Dataset | #proteins | #interactions | |
|---|---|---|---|
| Protein | DIP (9) | 4839 | 14319 |
| –protein | DIP Core (10) | 2558 | 5967 |
| interactions | SPA (7) | 1363 | 3721 |
| Dataset | #genes | #samples | |
| Carbon sources (12) | 6383 | 4 | |
| Gene | Stress response (13) | 6446 | 5 |
| expression | Rosetta compendium (14) | 6316 | 300 |
| profiles | Diauxic shift(15) | 6065 | 7 |
| Phosphate metabolism (16) | 6283 | 8 |
Furthermore, five gene expression datasets are used in this work, including Carbon sources (12), Stress response (13), Rosetta compendium (14), Diauxic shift (15) and Phosphate metabolism (16). The details of the gene expression data are summarized in Table 1. Since different signaling pathways are activated under different conditions, we used different gene expression datasets and their combinations to discover signaling pathways. All the gene expression data except Diauxic shift [from GEO (17), Accession number: GSE28] are obtained from the authors' web sites, and normalized. In particular, the expression data measured under 37°C to 25°C shock in Stress response dataset (13) are used in this work. For the combination of Carbon sources (12) and Diauxic shift (15), only genes with 2-fold expression change are selected. For other expression datasets or combinations, no gene selection is performed due to the relatively smaller expression changes in these datasets. Based on gene expression levels, irrelevant protein interactions corresponding to low expression changes of genes are eliminated, thereby significantly reducing false positives and improving the accuracy. The details about how to use the PPI and gene expression data will be described in Experimental results section.
ILP model for detecting STNs
Given the possible starting and ending points (e.g. membrane proteins and TFs), we propose a new method for detecting STNs. In this article, one PPI network is represented as a weighted undirected graph G(V,E,W), where the vertex vi∈V represents a protein and the edge E(i, j) denotes the experimentally observed interaction between proteins i and j. The weight wij∈W accompanying the edge E(i, j) represents either confidence score of the interaction or expression correlation coefficient based on gene expression data. In this work, we do not discriminate genes and their protein products.
In the weighted network, a linear path of specific length m from a starting node to a ending node is assigned a score, which equals to the sum of the weights on the edges in the path, where the length of the path is the number of proteins involved in the path. Similarly, the score of a subnetwork is the sum of the weights accompanying the edges of the network, and the network size is the number of proteins in the subnetwork. Generally, the specific starting proteins of STNs are membrane proteins because a signal transduction process usually starts from a receptor protein in a cell, whereas the ending proteins are TFs. Given an undirected weighted network G(V,E,W) and the possible starting and ending components of signaling pathways, we aim at finding a compact connected subnetwork with maximum weight from the network G, which is seen as the putative STN.
To accomplish the above mission, we propose a novel ILP model to extract STNs, given membrane proteins, TFs and a weighted PPI network. The ILP model for uncovering a STN is described as follows:
 |
1 |
 |
2 |
 |
3 |
 |
4 |
 |
5 |
 |
6 |
 |
7 |
 |
8 |
where wij is the weight of edge E(i, j) in the undirected weighted network G, xi is a binary variable for protein i to denote whether protein i is selected as a component of the STN, and yij is also a binary variable to denote whether the biochemical reaction represented by E(i, j) is a part of the STN. λ is a positive penalty parameter to control the trade-off between the STN weight and STN size, and |V| is the total number of proteins in the PPI network. The constraint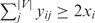 
is to ensure that xi has at least two linking edges once it is selected as a component of the STN, whereas the constraint 
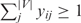means that each starting protein or ending protein has at least one link to or from other proteins. These two constraints ensure that the components in the subnetwork are as connected as possible. The constraints yij ≤ xi and yij ≤ xj mean that if and only if proteins i and j are selected as the components of STN, the biochemical reaction denoted by the edge E(i, j) should be considered. Equation (6) is the condition for any protein known involved in the STN, e.g. from the experiment results or literature.
The first term in the above cost function of Equation (1) implies that we aim at finding a STN with maximum weight, while the second term is used to control the STN size or the number of biochemical reactions in the STN to force a compact structure, because each PPI represented by E(i, j) actually corresponds to a biochemical reaction. Intuitively, if λ is small, e.g. zero, all of possible links are selected, i.e. the derived subnetwork is large and connected; on the other hand, if λ is large, it is a small subnetwork. Therefore, the idea behind the model is that we intend to extract a compact and connected subnetwork that accomplishes the signal transduction process. Such setting on the problem is reasonable because cells should play their roles with as less energy as possible from the evolutionary viewpoint, whereas more energy consumption may lead to crosstalks among different pathways and reduce the specificity of distinct signaling pathways (18,19). This criterion is also consistent with the parsimony principle that is widely adopted in other areas of computational biology such as phylogeny tree construction (20) and gene network reconstruction (21). Note that the signaling network in this article means the one between the given membrane protein and TF, which means that we focus on extracting one signaling network at each time. The aim of our model is to find a compact signaling network while preserving the specificity of the signaling network. The crosstalk between distinct signaling networks is not taken into account here. Although the model works in a parsimonious way, the redundancy of the extracted signaling networks is not necessarily reduced since the parameter λ balances the parsimonious effect and the redundancy. In other words, depending on λ that balances the parsimonious effect and redundancy, more related pathways may be included in the result.
The model described earlier is a standard ILP problem. To make the model suit for large-scale PPI networks, we relax the constraints from binary variables xi∈{0,1} and yij∈{0,1} to continuous variables xi∈[ < xrefref − type="bibr"rid="B0" > 0</xref>,<xrefref − type="bibr"rid="B1" > 1</xref > ] and yij∈[ < xrefref − type="bibr"rid="B0" > 0</xref>,<xrefref − type="bibr"rid="B1" > 1</xref > ]. With such relaxations, we can adopt any LP algorithm to solve the problem in an efficient manner (theoretically in polynomial time). The experimental results show that such relaxation is both efficient and effective, i.e. we almost always obtain integral solutions although there is no theoretical proof. The ILP model used in this work is actually the relaxed LP model.
The model has one scalar parameter λ to control the size of the derived STN, which has clear geometric meaning and thereby can be tuned in a relatively easy manner. Furthermore, the parameter λ enables the biologists to view the STN in a hierarchical way, where a small λ generates a large STN and vice versa. Therefore, it is possible for one to flexibly choose an interesting STN in this way by adjusting λ. Here, we give a rule to determine the value of parameter λ. Firstly, we define the density of an extracted signaling network as follows:
 |
9 |
where wij is the weight of edge E(i, j) and n is the total number of components in the signaling network. Generally, λ corresponding to the largest D is chosen in this article, and the resulted subnetwork is regarded as the putative STN accordingly. Specifically, we test λ by changing from 0 to 1 with the interval of 0.05 and choose λ corresponding to the largest D. In this article, the optimization toolbox of MATLAB is employed for the above optimization problem, and the uncovered STNs are drawn using Pajek (22).
Evaluation
To evaluate the significance of the STN found by the proposed method, two quality measures are employed: P-value and functional enrichment. In the original PPI network, a STN is found with the cost S (the minimum value of the objective function in Equation (1)), where the STN starts from a membrane protein M and ends at a TF T. To check the significance of the STN detected from the PPI network, a number of random networks are generated by shuffling the edges of the original network, while preserving the degree of each node. The procedure of generating random networks is repeated for 1000 times in this work. For each random network, the same model is employed to find a subnetwork starting from M and ending at T. The P-value of the STN detected from the original PPI network is defined as the probability that a subnetwork with a cost less than or equal to S is found in one random network.
To calculate the functional enrichment of the components in the extracted signaling networks, the biological process annotations in Gene Ontology (23) are assigned to the proteins in STN. The probability that the components of the signaling network have the same function can be calculated through a hypergeometric distribution with Gene Ontology Term Finder (http://db.yeastgenome.org/cgi-bin/GO/goTermFinder.pl). The P-value for a specific term can be calculated by the following formula:
 |
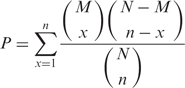10 |
where N denotes the total number of proteins in the SGD database (24), n denotes the number of proteins in SGD annotated by the specific term, M denotes the total number of proteins in the STN and x denotes the number of components in the STN annotated by the term. Furthermore, the P-value is corrected for multiple testing by Bonferroni correction.
EXPERIMENTAL RESULTS
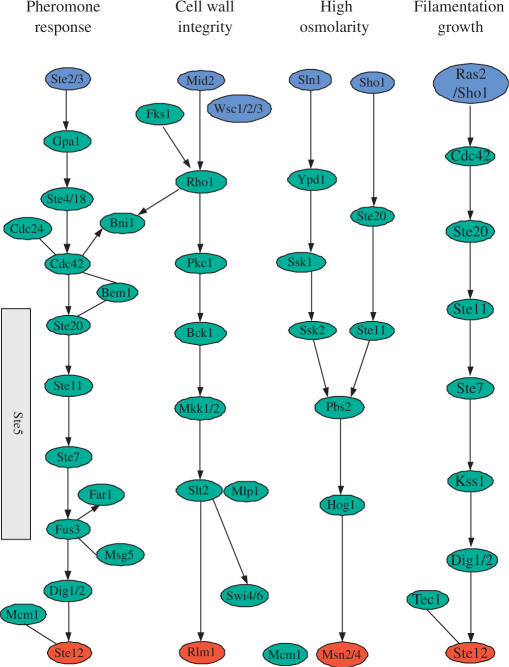
We conducted two experiments to test the proposed method, i.e. identify STN based only on PPI data (with a pre-processing scheme) in Detecting signaling network based on PPI data section, and identify STN based on both PPI and gene expression data (without any pre-processing scheme) in Detecting signaling networks based on integrated data section. In this work, the yeast MAPK signaling pathways were used to validate the proposed methods. Figure 1 shows the four yeast MAPK signaling pathways deposited in KEGG (25), and these signaling pathways were used as gold standards in this article.
Figure 1.
The yeast MAPK signaling pathways from KEGG (25), where the blue circles are starting nodes and the red ones are ending nodes.
Detecting signaling networks based on PPI data
To evaluate the performance of our model, we applied it to extract signaling networks from yeast PPI network. The PPI data were obtained from the DIP database (9) and also used by Scott et al. (4). In this case, the weight in Equation (1) was defined as the confidence score of PPI. The ILP model was applied to find two known yeast MAPK signaling pathways: pheromone response and filamentous growth. Generally, the PPI networks generated by high-throughput techniques are very large. For example, there are about 4839 proteins and 14 319 interactions in the PPI network used here. In such a network, there are many components that are far from the starting or ending nodes of the signaling network, which do not likely belong to the signaling network. Therefore, the Depth First Search (DFS) algorithm was employed to reduce the network size, remove the obviously irrelevant nodes and restrict the search space into a realistic and meaningful one. The smaller PPI network generated by DFS consists of all possible paths of length 6–9 with overlapping, and the interactions among proteins in this network are all from the original PPI network. Consequently, two smaller PPI networks were generated by DFS for extracting the two MAPK signaling pathways, respectively. Note that this kind of pre-processing has been widely used in the literature (4–7).
As mentioned in the preceding section, λ controls the size of the detected network. By varying λ from a small value to a large one in Equation (1), we can obtain signaling networks with different sizes, i.e. from a complicated network to a linear pathway. Numerical results confirm that a detected larger network always covers a smaller one. Therefore, we can have a series of nested networks by changing λ, where a smaller one is viewed to be more likely involved in the STN since it is covered by all larger networks, but a larger one includes more components.
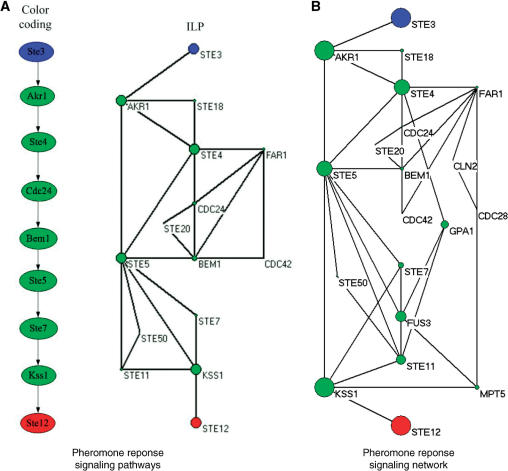
For the pheromone response pathway, our model was applied to find a signaling network starting from membrane protein STE3 and ending at TF STE12, and the curve for determining λ can be found in Figure 1 of the Supplementary Data. Figure 2A shows the pheromone response pathways detected by color coding (4) and ILP model (with a large λ, λ = 0.85), respectively. Comparing the results by our method and color coding based on the same dataset (4), we can see that the signaling pathway detected by our method covers the one by color coding. Furthermore, other proteins, i.e. STE18, FAR1, STE20, CDC42, STE50 and STE11, were also detected by our method.
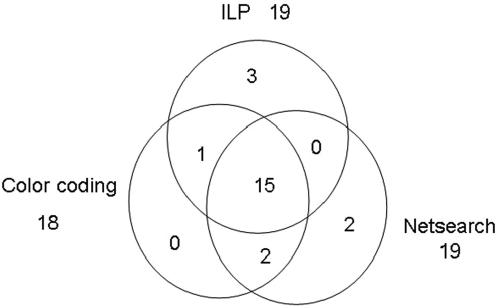
Figure 2B shows the signaling network by ILP with a smaller λ (λ = 0.8). Clearly, it covers the one shown in Figure 2A. This signaling network consists of 19 proteins. By comparing the detected signaling network with those found by Netsearch (5) and color coding (4), we can easily verify that most of the components of the three signaling networks are common. Compared with the signaling network of the same size detected by Netsearch (5), although our model did not find proteins SST2, DIG1, DIG2 and SPH1 (not in the main chain, see Figure 1), we detected STE50 that has been identified by the color coding method (4), and detected STE20 and CDC42, which are involved in the main chain of the pheromone pathway (see Figure 1). Compared against the color coding method, our method did not find DIG1 and DIG2, but detected MPT5, which has been identified by the Netsearch method (4). In particular, the ILP model successfully detected STE20 in the main chain (see Figure 1). Furthermore, the proposed method identified two new proteins, i.e. CLN2 and CDC28, where CLN2/CDC28p complexes repress the pheromone signaling (26,27). Therefore, the signaling network found by the proposed method is biologically plausible. In addition, Figure 3 shows the number of components shared among the STNs by ILP, Netsearch and color coding. It can be easily seen that most of the detected components are shared among the three methods.
Figure 2.
The pheromone response pathways, where the blue circles are starting points and the red ones are ending points of the pathways, and the size of each circle is proportional to the sum of scores of the paths that it is involved in. (A) The pathways by color coding and ILP model (λ = 0.85); (B) Pheromone response signaling network discovered by ILP model with a smaller λ (λ = 0.8).
Figure 3.
Venn diagram for the number of proteins shared among the STNs by ILP, Netsearch and color coding.
Table 2 shows the P-values of functional enrichment on 5 GO terms for members in the signaling network found by our proposed method. It can be easily seen that most of the members in the extracted signaling network have similar functions. In addition, the P-value of the uncovered STN obtained with the random networks as background is smaller than 10− 15, which demonstrates the significance of the extracted STN. From the above results, clearly our method is a good complement to the existing algorithms, whereas the ILP model is easy to be implemented and simple to be interpreted.
Table 2.
The P-values of functional enrichment for pheromone response signaling network found by ILP
| GO term | P-value | #proteins in the signaling network annotated | #proteins in SGD annotated |
|---|---|---|---|
| Response to pheromone | 5.25e-34 | 19 | 94 |
| Pheromone-dependent signal transduction | 1.27e-32 | 15 | 28 |
| Regulation of conjugation with cell fusion | 5.27e-32 | 15 | 30 |
| Sexual reproduction | 5.99e-32 | 19 | 118 |
| Signal transduction | 1.75e-21 | 17 | 225 |
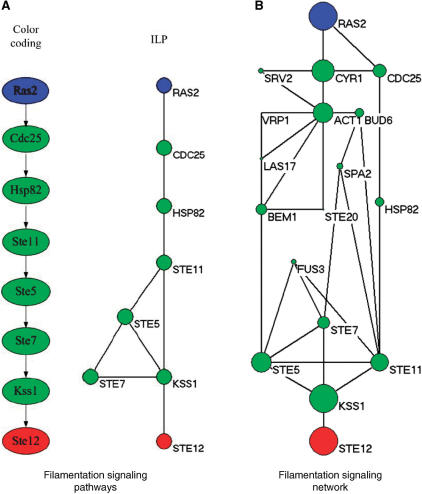
For the filamentous growth invasion pathway, our model was applied to detect the signaling network starting from membrane protein RAS2 and ending at TF STE12, and the curve for determining λ can be found in Figure 2 of the Supplementary Data. Figure 4A, respectively, shows the signaling pathways detected by color coding (4) and our method (λ = 0.90). It can be seen from Figure 4A that the signaling pathway uncovered by our method matches the known signaling pathway (see Figure 1) to a large extent. The CDC25 and HSP82, which do not appear in the pathway of KEGG, were detected due to the missing link between RAS2 and CDC42 in the PPI network. With the same dataset, the ILP model can find the identical signaling pathway of the same size as that by color coding. In addition, the ILP model found several additional links compared against the color coding method. The additional links may imply alternative signaling pathways, since such redundant mechanisms can compensate single protein disruptions and keep signal transduction unblocked (1,2).
Figure 4.
The signaling pathways for filamentous growth, where the blue circles are starting points and the red ones are ending points, and the size of each circle is proportional to the sum of scores of the paths that it is involved in. (A) The pathways by color coding and ILP model (λ=0.90). (B) The filamentation signaling network by the ILP model (λ=0.90).
Figure 4B shows the filamentation signaling network of a larger size detected by the ILP model (λ = 0.90). The signaling network consists of 18 proteins, where the proteins CDC25, SPA2, CYR1, FUS3, HSP82 and BEM1 are assumed to be known and involved in the signaling pathway to test the effectiveness of the additional information. Although it is difficult to know exactly all the proteins involved in a signaling pathway, some components and casual relationships in the signaling pathway can be obtained from literature (1,2). Actually, it is easy to include those conditions into the formulation of ILP by simply adding linear constraint [i.e. Equation (6)] for such a case, which is one of the major advantages of the proposed method. It can be seen from Figure 4B that the detected signaling network matches the one found by Netsearch (5) to a large extent. The HSC82 detected by Netsearch is not in our network because there is a direct interaction between STE11 and HSP82. The result by ILP does not include proteins ABP1, DIG1, DIG2 and BNI1, but instead two other proteins VRP1 and LAS17 were found because VRP11, LAS17, BEM1, BUD6 and SRV2 occur in the same complex (28) and may have similar functions. Furthermore, LAS17 forms complex with ABP1 (28), implying that LAS17 has similar functions as ABP1. In particular, our method found STE20 that is in the main chain of filamentation pathway (see Figure 1) while Netsearch failed to detect it.
Table 3 shows the P-values of functional enrichment on 5 GO terms for members in the signaling network by our method. From Table 3, it can be seen that most of the members in the signaling network have similar functions. In addition, the P-value of the extracted STN calculated with random networks as background is smaller than 10− 15, which indicates the significance of the uncovered STN.
Table 3.
The P-values of functional enrichment for filamentation singling network found by ILP
| GO term | P-value | #proteins in the signaling network nnotated | #proteins in SGD annotated |
|---|---|---|---|
| Reproduction | 4.13e–14 | 14 | 328 |
| Growth | 4.76e–13 | 11 | 143 |
| Filamentous growth | 4.05e–11 | 10 | 97 |
| Signal transduction | 1.31e–12 | 12 | 225 |
| Cell communication | 5.20e–12 | 12 | 252 |
From the results described earlier, we can see that the proposed ILP model is effective for uncovering signaling networks from only PPI data. Furthermore, the ILP model is simple and flexible for various conditions, and is able to detect the signaling networks directly instead of heuristical multistage procedure like Netsearch and color coding.
Detecting signaling networks based on integrated data
In the previous section, our method works well even by using only PPI data, partly because the confidence scores of yeast PPIs were estimated with high precision. However, PPIs for many organisms have no confidence scores or have not been estimated properly. On the other hand, a tremendous amount of gene expression data are nowadays available, and provide insights into signaling pathways. In this part, we investigated whether the integration of gene expression profiles (microarray data) with PPI data can improve the performance of the proposed method. Different from Detecting signaling networks based on PPI data Section, we directly apply the ILP model to the data without any pre-processing (e.g. DFS) here. In addition to the two signaling pathways described earlier, the proposed method was also applied to detect the cell wall integrity and high osmolarity (HOG) pathways. Table 4 shows the details of integration of PPI and gene expression datasets used here. For the three pathways including pheromone response, filamentation and cell wall integrity, the DIP Core (10) dataset was employed. For the HOG pathway, the SPA interaction data constructed by Arga et al. (7) were used here because there are many missing interactions in DIP Core data for the HOG pathway. In the integrated data, the weight wij in Equation (1) is the absolute value of correlation coefficients based on the gene expression data, where the network structure is determined by PPI. Furthermore, to see the performance of different methods, precision and recall were employed in this work, where precision is defined as the percentage of components detected by the computational methods that are also in the KEGG pathway, and recall is the percentage of components in the KEGG pathway that are detected by the computational methods. Note that these statistical measures can only be seen as a rough reference, since there is no gold standard for those cases, i.e. the true signaling networks are not available.
Table 4.
Integration of PPIs with gene expression datasets for detecting yeast MAPK pathways
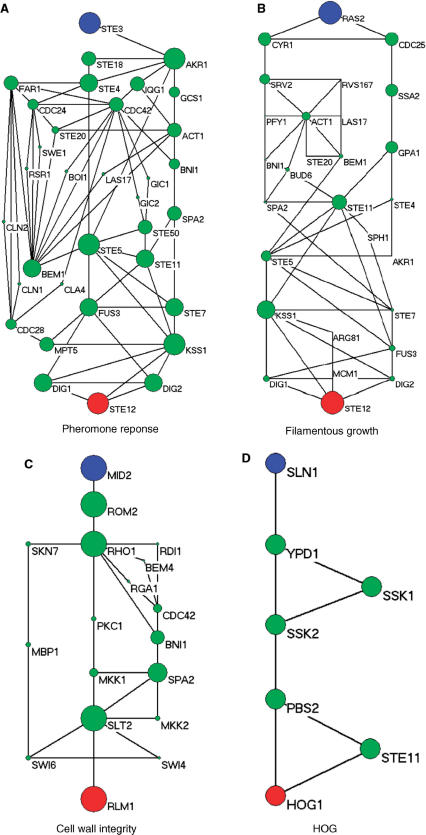
Figure 5 shows the signaling networks uncovered by the ILP model, where only pathways linking membrane proteins and TFs are illustrated, and the size of each circle in the signaling network is proportional to the sum of scores of the paths that it is involved in. The curves for determining optimal λ can be found in Figures 3–5 of the Supplementary Data. Figure 5A shows the pheromone response pathway (λ = 0.50), which contains 34 proteins. It can be seen that all the components in the main chain have been successfully uncovered by our model, especially including CDC42 and STE20, where both CDC42 and STE20 are not found by Netsearch (5) while STE20 is not found by the color coding (4). Compared with the signaling networks detected by Netsearch (5) and color coding (4), we can see that the ILP model can uncover almost all the components found by the two existing methods except GPA1, SST2 and SPH1, which are not in the main chain (see Figure 1) and have low expression correlations (< 0.5) with other members in the signaling network. However, our method successfully identified STE20 and BNI1, where the former is in the main chain and the latter has been confirmed in KEGG (25). Furthermore, the detected signaling network contains several additional proteins. Among these proteins, it has been confirmed that they are relevant to the pheromone response, i.e. CDC28-CLN1 and CDC28-CLN2 complexes repress the start of pheromone signaling (26), IQG1 mediates the regulatory effects of CDC42 on ACT1 (29), RSR1 is the upstream regulator of CDC42p (30), GIC1p and GIC2p are downstream effectors of the CDC42p small GTPase (30), GCS1 is GTPase-activating protein (31), LAS17 is actin assembly factor (24), BOI1 is implicated in polar growth (24), and SPA2 forms a complex with BUD6 and BNI1 (32).
Figure 5.
Yeast MAPK signaling networks detected by ILP model based on integrated data, where the blue circles are starting points and the red ones are ending points.
Table 5 shows the comparison of ILP model with other existing methods including color coding (4), Netsearch (5) and Pathfinder (8) with respect to precision and recall. In Table 5, we can learn that our proposed method can find the maximum number of components deposited in the KEGG signaling pathway, whereas Pathfinder got the highest precision. However, Pathfinder adopted the reconstructed PPI network in the computation. It can be seen from the results that, despite the simplicity, our method performs comparably well with existing methods. It should be noted that such comparison is not so reliable, since the true signaling networks are not known and KEGG mainly contains linear pathways instead of signaling networks. Table 6 shows the functional enrichment of the pheromone signaling network, where we can see that most of the members in the signaling network have similar functions. Furthermore, the P-value of extracted STN calculated with the background random networks is smaller than 10− 15, which verified the effectiveness of the proposed method and significance of the extracted STN. In addition, STNs of different sizes for pheromone pathway by adjusting λ can be found in Figure 6 of the Supplementary Data.
Table 5.
Comparison of various methods in detecting pheromone signaling network
| Method | Precision (%) | Recall (%) |
|---|---|---|
| ILP (λ = 0.50) | 47 | 80 |
| Color coding | 83 | 75 |
| Pathfinder | 88 | 75 |
| Netsearch | 74 | 70 |
Table 6.
The P-values of functional enrichment for pheromone response signaling network found by ILP based on integrated data
| GO term | P-value | #proteins in the signaling network annotated | #proteins in SGD annotated | ||
|---|---|---|---|---|---|
| Response to pheromone | 4.71e–30 | 21 | 94 | ||
| Signal transduction during conjugation | 3.08e–27 | 15 | 28 | ||
| Pheromone-dependent signal transduction | 3.08e–27 | 15 | 28 | ||
| Signal transduction | 6.40e–26 | 23 | 209 | ||
| Cell communication | 3.36e–25 | 23 | 224 |
Figure 5B shows the filamentation signaling network detected by the ILP model starting from RAS2 and ending at STE12 (λ = 0.50), which contains 28 proteins. It can be seen that our method can detect all the components in the main chain except CDC42 due to the incompleteness of the PPI data used in this article. Compared with Netsearch, our method successfully found STE20, but missed ABP1, HSC82, FUS1 and HSP82 that are not in the main chain. Specifically, HSP82 was not detected by our model because it is not included in the PPI network due to its low expression change, HSC82 was not included due to the missing link between CDC25 and HSC82, while FUS1 has not been confirmed to be related to the filamentation signaling pathway. Despite the failure to detect HSP82 and HSC82, our method detects SSA2 that is also stress gene similar to HSP82 and HSC82 (33). Furthermore, instead of ABP1, we identified three other members including actin assembly factor LAS17, actin-associated protein RVS167 and PFY1. These three proteins are in the same complex with SRV2, BUD6 and ABP1 (28), which implies that they have similar functions. SPH1 is included due to its strong correlation with STE7 and STE11, where SPH1 activates STE7 (34). The rest of the proteins are included because these proteins are shared among different pathways and have strong correlations.
Table 7 shows the comparison among various methods in terms of precision and recall. In this case, the Pathfinder detects the maximum number of components involved in the KEGG filamentation pathway but has the lowest precision, whereas the ILP model performs comparably well with the other methods. This example demonstrates that no method can always perform best and different methods are complementary to each other. Table 8 shows the functional enrichment of the filamentation signaling network, where we can see that most of the members in the signaling network have similar functions. Furthermore, the P-value of extracted STN calculated with the background random networks is smaller than 10− 15, which also demonstrates the effectiveness of the proposed method and the significance of the identified network. In addition, STNs of different sizes by the ILP is given in Figure 7 of the Supplementary Data.
Table 7.
Comparison of various methods in detecting filamentation signaling network
| Method | Precision (%) | Recall (%) |
|---|---|---|
| ILP (λ = 0.50) | 29 | 73 |
| Pathfinder | 28 | 82 |
| Netsearch | 33 | 64 |
Table 8.
The P-values of functional enrichment for filamentation response signaling network found by ILP based on integrated data
| GO term | P-value | #proteins in the signaling network | #proteins in SGD annotated |
|---|---|---|---|
| Filamentous growth | 1.47e-19 | 15 | 97 |
| Signal transduction | 3.51e-17 | 17 | 225 |
| Reproduction | 2.82e-19 | 20 | 328 |
| Cell surface receptor linked signal transduction | 3.96e-17 | 12 | 54 |
| Growth | 9.81e-19 | 16 | 143 |
Figure 5C shows the cell wall integrity signaling network by our method starting from MID2 and ending at RLM1 (λ = 0.15). From the figure, we can see that all the members in the main chain were successfully detected except BCK1. Compared with the one found by Netsearch, the ILP model did not find FKS1, GIC2, ACT1, BUD6, BCK1, SPH1 and SMD3 due to the missing interactions in the PPI network used in this article, but successfully detected two TFs SWI4 and SWI6 that are in the main chain of cell wall pathway (Figure 1). In addition, our method found several other members including MBP1 that forms a complex with SWI6p (28), RHO1 effectors SKN7 (35), and BEM4p involved in the RHO1-mediated signaling pathway (36). Table 9 summarizes the performance of our method and Netsearch in detecting cell wall signaling network. Although the true signaling network is not available, the comparison results demonstrate the effectiveness of the proposed method. Table 10 shows the functional enrichment of the cell wall signaling network found by ILP, where we can see that most of the members in the signaling network have similar functions. Furthermore, the P-value of extracted STN calculated with the background random networks is 0.002, which implies the significance of the network derived by the proposed method. In addition, STNs of different sizes by the ILP can be found in Figure 8 of the Supplementary Data.
Table 9.
Comparison of ILP with Netsearch in detecting cell wall signaling network
| Method | Precision (%) | Recall (%) |
|---|---|---|
| ILP (λ =0.15) | 56 | 63 |
| Netsearch | 50 | 56 |
Table 10.
The P-values of functional enrichment for cell wall integrity signaling network found by ILP based on integrated data
| GO term | P-value | #proteins in the signaling network annotated | #proteins in SGD annotated |
|---|---|---|---|
| Signal transduction | 1.59e–14 | 13 | 225 |
| Cell communication | 7.12e–14 | 13 | 252 |
| Intracellular signaling cascade | 6.98e–11 | 10 | 155 |
| Small GTPase mediated signal transduction | 8.01e–11 | 8 | 61 |
| Cell structure morphogenesis | 1.21e–07 | 8 | 149 |
Figure 5D shows the HOG signaling pathway found by the ILP model starting from SLN1 and ending at HOG1 (λ = 0.90). It can be seen from the figure that the main chain was successfully recovered by our method. Furthermore, the member STE11 involved in the signaling network was also detected. Aside from this, several new links among the members were also discovered, which may correspond to alternative signaling pathways. To further test the performance of the proposed method, we also searched the possible paths of length 6–7 from the same integrated network that has been used by the ILP model. The paths starting from SLN1 and ending at HOG1 were found with DFS algorithm. All the detected paths were ranked by employing pairwise correlation according to the sum of the weights for the edges in the paths as described in (6,7). From the ranking list (found in text1 of the Supplementary Data), we can see that the signaling pathway found by the ILP model was ranked at 75. In other words, the HOG pathway cannot be found by simply ranking the possible linear paths in this case although such a strategy is adopted by existing methods (6,7). The existing methods utilizing the pairwise correlation between proteins failed to detect the HOG pathway in this case because the HOG pathway is not a linear path and there are additional links among members in the main chain of pathway. In contrast, our method handles the HOG pathway as a global entity and thereby performs better. This example clearly confirms the efficiency and effectiveness of the proposed method.
From the results described earlier, we can see that with the integration of PPI and gene expression profiles, our method is indeed effective for uncovering signaling networks. In particular, many putative components of signaling networks not detected by the existing methods have been identified, e.g. we found STE20 for pheromone and filamentation pathways, and SWI4 and SWI6 for cell wall integrity. Although Pathfinder can also detect STE20, it works by reconstructing the PPI network whereas our method works on the original PPI network. In addition, the overlap between the published results and the ones uncovered by the ILP model confirms the effectiveness and prediction power of the proposed method.
DISCUSSIONS AND CONCLUSIONS
Signal transduction is one of the most important biological processes that cells respond to the external stimuli, and plays an important role in coordinating metabolism, cell proliferation and differentiation. In this article, we presented a novel model for unraveling signaling networks based on PPI and gene expression data. In particular, we formulated signaling network identification as an optimization problem. The proposed method utilizes LP algorithm to efficiently find the optimal subnetworks with maximum weights and compact network structure, which are seen as putative STNs. Compared with existing methods, our method is simple in both algorithm and computation, since it can detect the signaling networks from protein interaction data directly instead of heuristically ranking and assembling the candidate signaling pathways. In addition, our method can handle a large-scale system without numerical difficulty due to the LP algorithm.
The model has one scalar parameter λ to control the size of the derived STN, which has clear geometric meaning and thereby can be tuned in a relatively easy manner. A simple rule was provided in this article to determine the parameter λ. According to the numerical computations, this rule works well except for detecting the filamentation pathway based on PPI data, where the PPI network is very dense and the weights are distributed uniformly. In fact, the existing methods (4,5,7) also face the similar problem in controlling the STN size, which is usually determined heuristically with prior information. On the other hand, depending on different values of λ, we are able to find out subnetworks with different sizes, and reveal the hierarchical structure of the signaling networks. The signaling network is seen as an undirected graph in this article because PPIs are usually undirected or can also be considered as bidirected. However, our model can be easily extended to uncover directed STNs by slightly modifying the constraints in the model, provided that the directed high-throughput data are available. In addition, although there is no theoretical proof, we always obtain unique optimal solutions numerically for all cases in this article at a fixed λ mainly due to different weights on edges.
The results on known yeast MAPK signaling pathways demonstrate that our model can uncover the known signaling pathways to a large extent, and the uncovered STNs match most parts of those published results, which confirm the effectiveness and prediction power of the proposed method. On the other hand, the results also make it clear that there is no a single method that can perform the best in all cases. Despite its simplicity, the ILP model performs comparably well with existing methods in detecting the yeast MAPK signaling networks. Therefore, our proposed model can be a good complement to the existing methods. Furthermore, the results also show that the integration of protein interaction with gene expression can considerably improve the performance of the proposed model compared against only PPI data analysis. Note that in addition to integrating PPI with gene expression data, other information such as function and location information can also be easily incorporated into the proposed model. Understanding the mechanisms of signal transduction in a cell is essential to uncover the pathway from a drug to its target gene, and thereby accelerating the development of new drugs. In the future, we will further apply our method to discover the drug-target networks, i.e. pathways from drugs to target genes.
SUPPLEMENTARY DATA
Supplementary Data is available at NAR Online.
ACKNOWLEDGEMENTS
The authors thank Prof. Nielsen for providing the SPA PPI data. The authors would like to thank the anonymous reviewers for their valuable suggestions to improve the article. Funding to pay the Open Access publication charges for this article was provided by ERATO Aihara Complexity Modelling Project, JST. This work was partly supported by National Natural Science Foundation of China (No.10701080) and National High Technology Research and Development Program of China (2006AA02Z309).
Conflict of interest statement. None declared.
REFERENCES
- 1.Albert R, DasGupta B, Dondi R, Kachalo S, Sontag E, Zelikovsky A, Westbrooks K. A novel method for signal transduction network inference from indirect experimental evidence. J. Comput. Biol. 2007;14:927–949. doi: 10.1089/cmb.2007.0015. [DOI] [PubMed] [Google Scholar]
- 2.Li S, Assmann S, Albert R. Predicting essential components of signal transduction networks: a dynamic model of guard cell abscisic acid signaling. PLoS Biol. 2006;4:e312. doi: 10.1371/journal.pbio.0040312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhao X, Chen L, Aihara K. Automatic modeling of signal pathways from protein–protein interaction networks. In: Brazma A, Miyano S, Akutsu T, editors. Vol. 6 of Serias on advances in bioinformatics and computational biology; Proceedings of The 6th Asia Pacific Bioinformatics Conference; Singapore: Imperial College Press; 2008. pp. 287–296. [Google Scholar]
- 4.Scott J, Ideker T, Karp R, Sharan R. Efficient algorithms for detecting signaling pathways in protein interaction networks. J. Comput. Biol. 2006;13:133–144. doi: 10.1089/cmb.2006.13.133. [DOI] [PubMed] [Google Scholar]
- 5.Steffen M, Petti A, Aach J, D'haeseleer P, Church G. Automated modelling of signal transduction networks. BMC Bioinformatics. 2002;3:34. doi: 10.1186/1471-2105-3-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Liu Y, Zhao H. A computational approach for ordering signal transduction pathway components from genomics and proteomics data. BMC Bioinformatics. 2004;5:158. doi: 10.1186/1471-2105-5-158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Arga KY, Önsan Z, Kiidar B, Ölgen K, Nielsen J. Understanding signaling in yeast: Insights from network analysis. Biotechnol. Bioeng. 2007;97:1246–1258. doi: 10.1002/bit.21317. [DOI] [PubMed] [Google Scholar]
- 8.Bebek G, Yang J. Pathfinder: Mining signal transduction pathway segments from protein–protein interaction networks. BMC Bioinformatics. 2007;8:335. doi: 10.1186/1471-2105-8-335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Xenarios I, Salwnski L, Duan XJ, Higney P, Kim SM, Eisenberg D. Dip, the database of interacting proteins: A research tool for studying cellular networks of protein interactions. Nucleic Acids Res. 2002;30:303–305. doi: 10.1093/nar/30.1.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Deane CM, Salwinski L, Xenarios I, Eisenberg D. Protein interactions: Two methods for assessment of the reliability of high throughput observations. Mol. Cell. Proteomicss. 2002;1:349–356. doi: 10.1074/mcp.m100037-mcp200. [DOI] [PubMed] [Google Scholar]
- 11.Sharan R, Suthram S, Kelley RM, Kuhn T, McCuine S, Uetz P, Sittler T, Karp RM, Ideker T. From the cover: Conserved patterns of protein interaction in multiple species. Proc. Natl Acad. Sci. USA. 2005;102:1974–1979. doi: 10.1073/pnas.0409522102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Daran-Lapujade P, Jansen MLA, Daran J, van Gulik W, de Winde JH, Pronk JT. Role of transcriptional regulation in controlling fluxes in central carbon metabolism of saccharomyces cerevisiae: a chemostat culture study. J. Biol. Chem. 2004;279:9125–9138. doi: 10.1074/jbc.M309578200. [DOI] [PubMed] [Google Scholar]
- 13.Gasch AP, Spellman PT, Kao CM, Carmel-Harel O, Eisen MB, Storz G, Botstein D, Brown PO. Genomic expression programs in the response of yeast cells to environmental changes. Mol. Biol. Cell. 2000;11:4241–4257. doi: 10.1091/mbc.11.12.4241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armour CD, Bennett HA, Coey E, He YD, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- 15.DeRisi JL, Iyer VR, Brown PO. Exploring the metabolic and genetic control of gene expression on a genomic scale. Science. 1997;278:680–686. doi: 10.1126/science.278.5338.680. [DOI] [PubMed] [Google Scholar]
- 16.Ogawa N, DeRisi J, Brown PO. New components of a system for phosphate accumulation and polyphosphate metabolism in saccharomyces cerevisiae revealed by genomic expression analysis. Mol. Biol. Cell. 2000;11:4309–4321. doi: 10.1091/mbc.11.12.4309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Edgar R, Domrachev M, Lash AE. Gene Expression Omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 2002;30:207–210. doi: 10.1093/nar/30.1.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bardwell L, Zou X, Nie Q, Komarova NL. Mathematical models of specificity in cell signaling. Biophys. J. 2007;92:3425–3441. doi: 10.1529/biophysj.106.090084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zou X, Chen Y, Pan Z. Modeling and optimization of the specifficity in cell signaling pathways based on a high performance multi-objective evolutionary algorithm. Lect. Notes Comput. Sci. 2006;4247:774–781. [Google Scholar]
- 20.Hill T, Lundgren A, Fredriksson R, Schioth HB. Genetic algorithm for large-scale maximum parsimony phylogenetic analysis of proteins. Biochim. Biophys. Acta, 2005;1725:19–29. doi: 10.1016/j.bbagen.2005.04.027. [DOI] [PubMed] [Google Scholar]
- 21.Wang L, Xu Y. Haplotype inference by maximum parsimony. Bioinformatics. 2003;19:1773–1780. doi: 10.1093/bioinformatics/btg239. [DOI] [PubMed] [Google Scholar]
- 22.Batagelj V, Pajek 2007. http://vlado.fmf.uni-lj.si/pub/networks/pajek/, access date: October, 2007.
- 23.Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight S, Eppig JT, et al. Gene ontology: Tool for the unification of biology. The gene ontology consortium. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cherry JM, Adler C, Ball C, Chervitz SA, Dwight SS, Hester ET, Jia Y, Juvik G, Schroeder M, et al. Sgd: Saccharomyces genome database. Nucleic Acids Res. 1998;26:73–79. doi: 10.1093/nar/26.1.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kanehisa M, Goto S, Hattori M, Aoki-Kinoshita KF, Itoh M, Kawashima S, Katayama T, Araki M, Hirakawa M. From genomics to chemical genomics: New developments in kegg. Nucleic Acids Res. 2006;34 doi: 10.1093/nar/gkj102. (Database issue), D354–D357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Oehlen LJ, Cross FR. G1 cyclins CLN1 and CLN2 repress the mating factor response pathway at Start in the yeast cell cycle. Genes Dev. 1994;8:1058–1070. doi: 10.1101/gad.8.9.1058. [DOI] [PubMed] [Google Scholar]
- 27.Oehlen LJ, Cross FR. Potential regulation of ste20 function by the cln1-cdc28 and cln2-cdc28 cyclin-dependent protein kinases. J. Biol. Chem. 1998;273:25089–25097. doi: 10.1074/jbc.273.39.25089. [DOI] [PubMed] [Google Scholar]
- 28.Mewes HW, Amid C, Arnold R, Frishman D, Gldener U, Mannhaupt G, Mnsterkötter M, Pagel P, Stmpflen V, et al. Mips: Analysis and annotation of proteins from whole genomes. Nucleic Acids Res. 2004;32 doi: 10.1093/nar/gkh092. (Database issue): D41–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Osman MA, Cerione RA. Iqg1p, a yeast homologue of the mammalian iqgaps, mediates cdc42p effects on the actin cytoskeleton. J. Cell. Biol. 1998;142:443–455. doi: 10.1083/jcb.142.2.443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kawasaki R, Fujimura-Kamada K, Toi H, Kato H, Tanaka K. The upstream regulator, Rsr1p and downstream effectors, Gic1p and Gic2p, of the Cdc42p small GTPase coordinately regulate initiation of budding in Saccharomyces cerevisiae. Genes Cells. 2003;8:235–250. doi: 10.1046/j.1365-2443.2003.00629.x. [DOI] [PubMed] [Google Scholar]
- 31.Poon P, Wang X, Rotman M, Huber I, Cukierman E, Cassel D, Singer RA, Johnston GC. Saccharomyces cerevisiae Gcs1 is an ADP-ribosylation factor GTPase-activating protein. Proc. Natl Acad. Sci. USA. 1996;93:10074–10077. doi: 10.1073/pnas.93.19.10074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Virag A, Harris SD. Functional characterization of aspergillus nidulans homologues of saccharomyces cerevisiae spa2 and bud6. Eukaryot. Cell. 2006;5:881–895. doi: 10.1128/EC.00036-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Serikawa KA, Xu XL, MacKay VL, Law GL, Zong Q, Zhao LP, Bumgarner R, Morris DR. The transcriptome and its translation during recovery from cell cycle arrest in saccharomyces cerevisiae. Mol. Cell. Proteomics. 2003;2:191–204. doi: 10.1074/mcp.D200002-MCP200. [DOI] [PubMed] [Google Scholar]
- 34.Roemer T, Vallier L, Sheu YJ, Snyder M. The Spa2-related protein, Sph1p, is important for polarized growth in yeast. J. Cell Sci. 1998;111:479–494. doi: 10.1242/jcs.111.4.479. [DOI] [PubMed] [Google Scholar]
- 35.Helliwell SB, Schmidt A, Ohya Y, Hall MN. The Rho1 effector Pkc1, but not Bni1, mediates signaling from Tor2 to the actin cytoskeleton. Curr. Biol. 1998;8:1211–1214. doi: 10.1016/s0960-9822(07)00511-8. [DOI] [PubMed] [Google Scholar]
- 36.Hirano H, Tanaka K, Ozaki K, Imamura H, Kohno H, Hihara T, Kameyama T, Hotta K, Watanabe T, et al. ROM7/BEM4 encodes a novel protein that interacts with the Rho1p small GTP-binding protein in Saccharomyces cerevisiae. Mol. Cell. Biol. 1996;16:4396–4403. doi: 10.1128/mcb.16.8.4396. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.