Abstract
How does natural selection lead to cooperation between competing individuals? The Prisoner's Dilemma captures the essence of this problem. Two players can either cooperate or defect. The payoff for mutual cooperation, R, is greater than the payoff for mutual defection, P. But a defector versus a cooperator receives the highest payoff, T, while the cooperator obtains the lowest payoff, S. Hence, the Prisoner's Dilemma is defined by the payoff ranking T > R > P > S. In a well-mixed population, defectors always have a higher expected payoff than cooperators, and therefore natural selection favors defectors. The evolution of cooperation requires specific mechanisms. Here we discuss five mechanisms for the evolution of cooperation: direct reciprocity, indirect reciprocity, kin selection, group selection and network reciprocity (or graph selection). Each mechanism leads to a transformation of the Prisoner's Dilemma payoff matrix. From the transformed matrices, we derive the fundamental conditions for the evolution of cooperation. The transformed matrices can be used in standard frameworks of evolutionary dynamics such as the replicator equation or stochastic processes of game dynamics in finite populations.
Keywords: Prisoner's Dilemma, evolution of cooperation, direct and indirect reciprocity, kin selection, group selection, network (graph) selection
1. Introduction
Evolutionary biologists are fascinated by cooperation. We think this fascination is entirely justified, because cooperation is essential for construction. Whenever evolution ‘constructs’ a new level of organization, cooperation is involved. The very origin of life, the emergence of the first cell, the rise of multi-cellular organisms, and the advent of human language are all based on cooperation. A higher level of organization emerges, whenever the competing units on the lower level begin to cooperate. Therefore, we propose that cooperation is a third fundamental principle of evolutionary dynamics besides mutation and selection. Evolution occurs in populations of reproducing individuals. Inaccurate reproduction can lead to mutation. Mutation can lead to selection. Selection can lead to cooperation.
Cooperation is always vulnerable to exploitation by defectors. Hence, the evolution of cooperation requires specific mechanisms, which allow natural selection to favor cooperation over defection. In this paper, we discuss five such mechanisms, and for each mechanism we derive the fundamental condition for the evolution of cooperation.
The meaning of the word ‘cooperation’ in evolutionary biology is more specific than just ‘working together’. In the narrow sense, ‘cooperation’ and ‘defection’ are the two possible actions that are defined by the Prisoner's Dilemma. The payoff matrix of the Prisoner's Dilemma (Rapoport and Chammah 1965; Axelrod 1984) is given by
| (1.1) |
The entries of the payoff matrix refer to the row player. If a cooperator, C, interacts with another cooperator, both get payoff R, which is the ‘reward for mutual cooperation. If a cooperator, C, meets a defector, D, the cooperators gets the ‘sucker's payoff’, S, while the defector gets the highest payoff of the game, T, which denotes the ‘temptation of defect’. Two defectors obtain the payoff P, which stands for the ‘punishment’ of mutual defection. The game is a Prisoner's Dilemma if
| (1.2) |
The payoff matrix (1.1) together with the ranking (1.2) can be seen as mathematical definitions of ‘cooperation’ and ‘defection’.
In a broader sense, ‘cooperation’ can be used as referring to an action where one individuals pays a cost for another individual to receive a benefit. But this definition alone need not lead to a Prisoner's Dilemma. It is, for example, also compatible with a snow-drift game (Hauert and Doebeli 2004; Hauert et al. 2006; Nowak 2006a), where cooperators and defectors can coexist without the need for a mechanism for the evolution of cooperation. In this article, we use ‘cooperation’ and ‘defection’ in the narrow sense as defined by the context of an underlying Prisoner's Dilemma game.
In the Prisoner's Dilemma, defectors dominate cooperators unless a mechanism for the evolution of cooperation is at work. We will discuss five mechanisms for the evolution of cooperation: direct reciprocity, indirect reciprocity, kin selection, group selection and network reciprocity (or graph selection). Direct reciprocity is the idea that there are repeated encounters between the same two individuals: my action depends on what you have done to me in previous encounters. For indirect reciprocity there are repeated encounters in a population of individuals: my action depends on what you have done to me and to others. Kin selection occurs whenever games are played between genetically relatives. Group selection refers to the mechanism where competition not only occurs between individuals, but also between groups. Network reciprocity operates in structured populations, where cooperators can prevail over defectors by forming clusters.
All five approaches have led to different mathematical investigations, but here we show that the essential properties of each mechanism can be described by a transformation of the Prisoner's Dilemma payoff matrix. From these transformed matrices we can immediately derive the fundamental conditions for the evolution of cooperation. Our analysis reveals how each mechanism operates at a fundamental level. But we do not claim that every aspect of each mechanism can be studied in the same way. For example, very different calculations are needed to find good strategies for direct or indirect reciprocity (Nowak and Sigmund 1992, 1993; Ohtsuki and Iwasa 2004, 2006). Furthermore, the population structure of group selection is entirely different to that of network reciprocity. In our opinion it is also incorrect to argue that kin selection refers to the same process as group selection. Inclusive fitness theory leads to fairly general methods for analyzing evolutionary dynamics, but does not imply that the driving force for all evolution of cooperation is kin selection. We will revisit this point in the discussion.
This paper is an extension of earlier work (Nowak 2006b), which investigates a simplified Prisoner's Dilemma given by two parameters, b and c, denoting respectively the benefit and cost of cooperation. In this case, we have R = b − c, S = −c, T = b and P = 0, which implies the restriction R + P = T + S. In contrast, the general Prisoner's Dilemma, which is studied here, has four parameters, displays a richer dynamical behavior and leads to generalizations of the fundamental rules presented in (Nowak 2006b). Moreover, for kin selection, group selection and network reciprocity, the full Prisoner's Dilemma allows coexistence between cooperators and defectors if R + P < T + S and bi-stability if R + P > T + S. Neither of these outcomes are possible for the simplified Prisoner's Dilemma with R + P = T + S.
We begin with some simple remarks on evolutionary game dynamics. Then we discuss each of the five mechanisms. Finally, we summarize the key findings and discuss their limitations.
2. Evolutionary Game Dynamics
Evolutionary game dynamics describe frequency dependent selection. The fitness of an individual is not constant, but depends on the relative abundance (= frequency) of various strategies (= phenotypes) in the population. The outcome of the game is related to reproductive success. Payoff determines fitness. Reproduction can be genetic or cultural. Genetic reproduction means that individuals leave genetic offspring which inherit their strategy. Cultural reproduction means that individuals are imitated by others; thereby strategies reproduce by imitation or learning. The first ideas of evolutionary game theory appeared in papers by Hamilton (1964), Trivers (1971) and Maynard Smith and Price (1973). Books on evolutionary game theory include (Maynard Smith 1982; Weibull 1995; Samuelson 1997; Hofbauer and Sigmund 1998; Gintis 2000; Cressman 2003; Nowak 2006a). For recent reviews see (Hofbauer and Sigmund 2003; Nowak and Sigmund 2004). Evolutionary game theory is a general approach to evolutionary dynamics with constant selection being a special case.
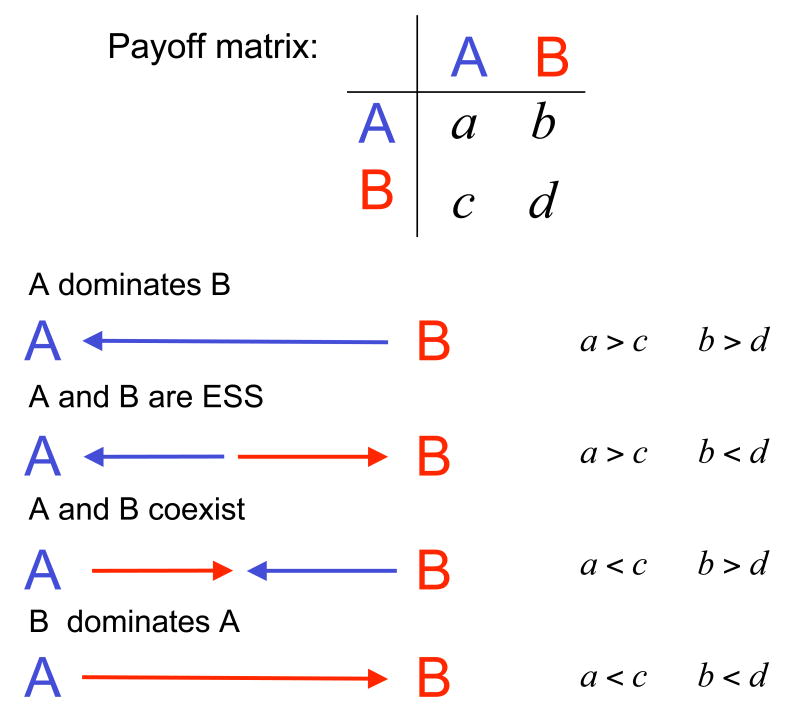
Consider a game between two strategies, A and B, given by the payoff matrix
| (2.1) |
The entries denote the payoffs for the row player. Thus, strategy A obtains payoff a when playing another A player, but payoff b when playing a B player. Likewise, strategy B obtains payoff c when playing an A player and payoff d when playing a B player.
If a > c and b > d, then A dominates B. In this case, it is always better to use strategy A. The expected payoff of A players is greater than that of B players for any composition of a well-mixed population. A is an unbeatable strategy in the sense of (Hamilton 1967). If instead a < c and b < d, then B dominates A and we have exactly the reverse situation (Fig 1).
Figure 1. Evolutionary dynamics of a two-player, two-strategy game.
The entries of the matrix specify the payoff for the row player. There are four possibilities: (i) if a > c and b > d, then strategy A dominates strategy B; (ii) if a > c and b < d, then both A and B are evolutionarily stable strategies (ESS); the game is bi-stable and is called a ‘coordination game’; (iii) if a < c and b > d, then both strategies are best replies to each other, and we have a Hawk-Dove game, where both strategies coexist; (iv) if a < c and b < d, then B dominates A.
If a > c and b < d, then both strategies are best replies to themselves, which leads to a ‘coordination game’. In a population where most players use A, it is best to use A. In a population where most players use B, it is best to use B. A coordination game leads to bi-stability: both strategies are stable against invasion by the other strategy.
If a < c and b > d, then both strategies are best replies to each other, which leads to a ‘Hawk-Dove game’ (Maynard Smith 1982). In a population where most players use A, it is best to use B. In a population where most players use B, it is best to use A. A Hawk-Dove game leads to co-existence between the two strategies.
If a > c then A is a strict Nash equilibrium. Likewise, if b < d then B is a strict Nash equilibrium. A strategy which is a strict Nash equilibrium is always an evolutionarily stable strategy (ESS). An ESS is stable against invasion by a small fraction of mutants using the other strategy in an infinitely large, well-mixed population (Maynard Smith 1982). In the terminology of evolutionary graph theory (Lieberman et al. 2005), a well-mixed population is given by a complete graph with identical weights: any two individuals are equally likely to interact with each other. Note that the ESS condition does not imply protection by selection in a finite population (Nowak et al. 2004).
3. Direct Reciprocity
In a non-repeated Prisoner's Dilemma, it is best to defect no matter which strategy is adopted by the other player (because R < T and S < P). But if there are repeated encounters between the same two individuals, then direct reciprocity can emerge and lead to the evolution of cooperation (Trivers 1971, 1985). Direct reciprocity is based on the idea ‘I help you and you help me.’ In each round the two players must choose between cooperation and defection. With probability w there is another round. With probability 1 − w the game is over. Hence, the average number of interactions between two individuals is 1/(1 − w).
There are many conceivable deterministic and stochastic strategies for the repeated Prisoner's Dilemma (Axelrod and Hamilton 1981; Axelrod 1984; Milinski 1984; Molander 1985; May 1987; Kraines and Kraines 1989; Fudenberg and Maskin 1990; Nowak and Sigmund 1990, 1992, 1993; Imhof et al. 2005), and the game can be played with simultaneous or alternating moves (Nowak and Sigmund 1994). But for the purpose of this paper we only need to consider two very simple strategies. Our defectors, D, defect in every move. Our cooperators, C, play tit-for-tat: they start with a cooperation and then do whatever the other player has done in the previous move.
If two cooperators meet, they cooperate all the time. If two defectors meet, they defect all the time. If a cooperator meets a defector, the cooperator cooperates in the first round and defects afterwards, while the defector defects in every round. The payoff matrix is given by
| (3.1) |
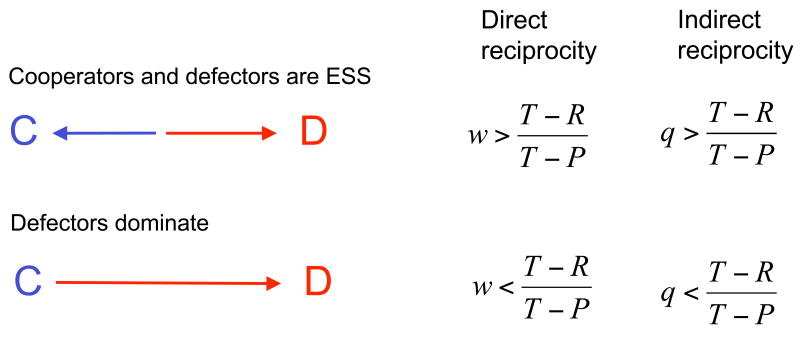
Note that defectors, D, are always ESS (because P > S). Cooperators are ESS if
| (3.2) |
Hence there are two possibilities: (i) if inequality (3.2) holds then both cooperation and defection are ESS, and the game is a coordination game; (ii) if inequality (3.2) does not hold then defection dominates cooperation (Fig 2). Therefore, inequality (3.2) represents a minimum requirement for the evolution of cooperation. If there are sufficiently many rounds, then direct reciprocity can lead to the evolution of cooperation. This argument is related to the Folk theorem (Fudenberg and Maskin 1986; Binmore 1991; Fudenberg and Tirole 1991).
Figure 2. Direct and indirect reciprocity can lead to the evolution of cooperation.
While direct reciprocity is based on repeated encounters between the same two individuals, indirect reciprocity uses the experience of others. Defectors are always ESS. Cooperators are ESS if w or q exceed (T − R)/(T − P), where w is the probability of another round in direct reciprocity, and q is the coefficient of social acquaintanceship under indirect reciprocity.
4. Indirect Reciprocity
As Richard Alexander (1987) has noted, ‘indirect reciprocity arises out of direct reciprocity in the presence of interested audiences’. For direct reciprocity, my decision is based on what you have done to me in previous encounters. For indirect reciprocity my decision is also based on what you have done to others. Indirect reciprocity represents the concept ‘I help you and somebody will help me.’ Indirect reciprocity is based on reputation (Nowak and Sigmund 1998a). Each event can be seen as an interaction between two people, according to a single Prisoner's Dilemma game given by payoff matrix (1.1). Each game is observed by others. Cooperation is costly, but leads to the reputation of being a helpful individual. Defection is more profitable in the short run, but leads to a bad reputation. Natural selection favors strategies that base their decision to cooperate or to defect on the reputation of oneself and of others (Nowak and Sigmund 1998a,b, 2005; Lotem et al. 1999; Fishman et al. 2001; Leimar and Hammerstein 2001; Fishman 2003; Panchanathan and Boyd 2003, 2004; Takahashi and Mashima 2003; Brandt and Sigmund 2004, 2005; Ohtsuki and Iwasa 2004, 2006, 2007). Experimental studies confirm that helpful individuals are more likely to receive help in the future (Wedekind and Milinski 2000; Dufwenberg et al. 2001; Milinski et al. 2002, 2006; Engelmann and Fischbacher 2002; Wedekind and Braithwaite 2002; Bolton et al. 2005; Rockenbach and Milinski 2006).
In order to derive a necessary condition for the evolution of cooperation by indirect reciprocity, let us study the interaction between two basic strategies: (i) defectors who always defect and (ii) cooperators who cooperate unless they know the reputation of the other person to indicate a defector. The parameter q denotes the probability to know the reputation of another individual. A cooperator always cooperates with another cooperator, but cooperates with a defector only with probability 1−q. Defectors never cooperate. We obtain the payoff matrix
| (4.1) |
This payoff matrix leads to exactly the same analysis as we have performed for direct reciprocity in the previous section. We obtain the same results, with q instead of w (Fig 2). The probability to know the reputation of another player must exceed a certain threshold value,
| (4.2) |
If this condition holds, then indirect reciprocity can lead to the evolution of cooperation.
5. Kin Selection
The concept of kin selection arose from the idea that evolutionary games are often played between individuals who are genetic relatives (Hamilton 1964, 1996; Maynard Smith 1964; Cavalli-Sforza and Feldman 1978; Grafen 1979, 1985; Queller 1985, 1992; Frank 1998; Taylor 1996; Taylor and Frank 1996; Rousset and Billiard 2000; West et al. 2002; Griffin and West 2003; Foster et al. 2006; Taylor et al. 2007). A gene which encodes altruistic behavior toward another individual promotes its own survival, if it is also present in the recipient of the altruistic act. The ‘state of the art’ approach is to calculate relatedness using population dynamics (Griffin and West 2002; Taylor et al. 2007; Wild and Taylor 2004; Wild and Traulsen 2007) and the Price equation (Price 1970; Taylor 1989). Another approach is called ‘direct fitness’ (Taylor and Frank 1996; Taylor et al. 2007).
But for the purpose of this paper, we use a method that was originally proposed by Maynard Smith (1982) for the Hawk-Dove game. Consider a population where the average relatedness between interacting individuals is given by r, which is a number between 0 and 1. The payoff received by the other player is added to your own payoff multiplied by r. The sum is divided by 1 + r in order to keep the total payoff between two players constant. Therefore, we obtain the modified payoff matrix
| (5.1) |
Cooperators are ESS if
| (5.2) |
Defectors are ESS if
| (5.3) |
The evolutionary outcome depends on the relative ranking of r, rC and rD. We must distinguish two parameter regions (Fig 3).
Figure 3. Kin selection, group selection and network reciprocity can lead to the evolution of cooperation.
For kin selection, the parameter r is the coefficient of genetic relatedness between individuals. For group selection, the parameters m and n denote respectively the number of groups and the number of individuals per group (group size). For network reciprocity, we have FC = (T − R)k2 − (T − P)k + (R + P − T − S) and FD = (P − S)k2 − (R − S)k − (R + P − T − S), where k is the degree of the graph (that is the number of neighbors of each individual). For all three models we find: if R + P > T + S, then cooperators and defectors cannot co-exist; if R + P < T + S, then cooperators and defectors cannot simultaneously be ESS.
I. If R + P > T + S then rD > rC. There are three possibilities: (i) if rD > rC > r then defectors dominate; (ii) if rD > r > rC then both cooperators and defectors are ESS; (iii) if r > rD > rC then cooperators dominate.
II. If R + P < T + S then rC > rD. Again there are three possibilities: (i) if rC > rD > r then defectors dominate; (ii) if rC > r > rD then neither cooperators nor defectors are ESS; (iii) if r > rC > rD then cooperators dominate.
In the degenerate case, R + P = T + S, we have rC = rD. Then either C dominates (when r > rC) or D dominates (when r < rD). Neither coexistence, nor bi-stability between C and D are possible. The case R + P = T + S is called ‘equal gains from switching’ (Nowak and Sigmund 1990): when switching from C to D while playing against C the gain is T − R and while playing against D the gain is P − S. The condition T − R = P − S implies that the two gains are equal. The two-parameter Prisoner's Dilemma, where cooperators pay a cost, c, for the other person to receive a benefit, b, leads to equal gains from switching, because T + b, R = b − c, P = 0 and S = −c (Nowak 2006b). In this special case, inequalities (4.2) and (4.3) lead to r > c/b, which is Hamilton's rule.
6. Group Selection
Group selection is based on the idea that competition occurs not only between individuals but also between groups. Many models of group selection have been proposed over the years (Wynne-Edwards 1962; Williams 1966; Wilson 1975; Maynard Smith 1976; Slatkin and Wade 1978; Uyenoyama and Feldman 1980; Crow and Aoki 1982; Leigh 1983; Wilson 1983; Harvey et al. 1985; Nunney 1985; Harpending and Rogers 1987; Szathmáry and Demeter 1987; Michod 1999; Boyd and Richerson 2002; Kerr and Godfrey-Smith 2002; Paulsson 2002; Fletcher and Zwick 2004; Traulsen et al. 2005; Wilson and Hölldobler 2005; Bowles 2006; Killingback et al. 2006). Here we use an approach described by (Traulsen and Nowak 2006). A population is subdivided into m groups. The maximum size of a group is n. Individuals interact with others in the same group according to a Prisoner's Dilemma. The fitness of an individual is 1 − ω + ωF, where F is the payoff and ω the intensity of selection. At each time step, an individual from the entire population is chosen for reproduction proportional to fitness. The offspring is added to the same group. If the group reaches the maximum size, it can split into two groups with a certain probability, p. In this case, a randomly selected group dies to prevent the population from exploding. The maximum population size is mn. With probability 1 − p the group does not divide. In this case, a random individual of that group is chosen to die. For small p, the fixation probability of a single cooperator in the entire population is given by the fixation probability of a single cooperator in a group times the fixation probability of that group. The model can be extended to include migration (Traulsen and Nowak 2006), but this is not needed here.
The payoff matrix that describes the interactions between individuals of the same group is given by
| (6.1) |
Between groups there is no game dynamical interaction in our model, but groups divide at rates that are proportional to the average fitness of individuals in that group. The multi-level selection is an emerging property of the population structure. Therefore one can say that cooperator groups have a constant payoff R, while defector groups have a constant payoff P. Hence, in a sense the following ‘game’ of constant selection describes the competition between groups
| (6.2) |
Again the ‘fitness’ of a group is 1 − ω + ωF where F is its ‘payoff’. Surprisingly, for weak selection (w ≪ 1) and large n and m, the essence of the overall selection dynamics on two levels can be described by a single payoff matrix, which is the sum of matrix (6.1) multiplied by the group size, n, and matrix (6.2) multiplied by the number of groups, m (Nowak 2006b). The result is
| (6.3) |
The intuition for adding the two matrices multiplied with the respective population size is as follows. For fixation of a new strategy in a homogeneous population using the other strategy, first the game dynamics within one group of size n have to be won and then the game dynamics between m groups have to be won. For weak selection and large m and n, the overall fixation probability is the same as the fixation probability in the single game using the combined matrix 6.3 and population size, mn. We derive the addition formula of matrix 6.3 in Appendix A. Therefore, some aspects of the stochastic selection process on two levels can be studied by a standard replicator equation using the combined matrix.
From matrix (6.3) we see that cooperators are ESS if
| (6.4) |
Defectors are ESS if
| (6.5) |
Again there are two parameter regions defined by R + P > T + S and R + P < T + S. The same six cases apply as for kin selection, but the thresholds have different values (Fig 3).
7. Network Reciprocity
Spatial games can lead to cooperation in the absence of any strategic complexity : cooperators can coexist with defectors and sometimes even outcompete them (Nowak and May 1992). This effect is called ‘spatial reciprocity’. Spatial games are usually played on regular lattices such as square, triangular or hexagonal lattices (Nowak and May 1992; Herz 1994; Rand and Wilson 1995). Evolutionary graph theory (Lieberman et al. 2005) is a general approach to study the effect of population structure or social networks on evolutionary or ecological dynamics (Durrett and Levin 1994; Hassell et al. 1994; Nakamaru et al. 1997, 1998; Skyrms and Pemantle 2000; Abramson and Kuperman 2001; Ebel and Bornholdt 2002; Hauert and Doebeli 2004; Rousset 2004; Santos and Pacheco 2005; Szabó et al. 2005; Vukov and Szabó 2005; May 2006; Santos et al. 2006; Vukov et al. 2006; Wu et al. 2006). The individuals of a population occupy the vertices of a graph. The edges denote who interacts with whom. In principle, there can be two different graphs (Ohtsuki et al. 2007): the ‘interaction graph’ determines who plays with whom; the ‘replacement graph’ determines who competes with whom for reproduction. Here we assume that the interaction and replacement graphs are identical. Network reciprocity is a generalization of spatial reciprocity to graphs (Ohtsuki et al. 2006): on graphs cooperators form clusters which can enable them to outcompete defectors.
We consider a ‘two coloring’ of the graph: each vertex is either a cooperator or a defector. Each individual interacts with all of its neighbors according to the standard payoff matrix (1.1). The payoffs are added up. The fitness of an individual is given by 1 − ω + ωF where ω ∈ [0, 1] denotes the intensity of selection and F denotes the payoff for this individual. Here we consider evolutionary dynamics according to death-birth updating (Ohtsuki et al. 2006): in each time step a random individual is chosen to die; then the neighbors compete for the empty site proportional to their fitness. There are many different updating mechanisms for games on graphs and some of them lead to very different results (Nakamaru et al. 1997, 1998; Ohtsuki et al. 2006). As yet there is no classification of all possible updating rules on graphs.
A calculation using pair approximation on regular graphs (where each vertex has k edges) leads to a deterministic differential equation which describes how the expected frequency of cooperators (and defectors) changes over time (Ohtsuki and Nowak 2006a). This differential equation turns out to be a standard replicator equation (Taylor and Jonker 1978; Hofbauer et al. 1979; Zeeman 1980) with a modified payoff matrix. For the interaction between cooperators and defectors on a graph with degree k > 2, the modified payoff matrix is of the form
| (7.1) |
where
| (7.2) |
For a derivation of this transformation see (Ohtsuki and Nowak 2006a). Cooperators are ESS if R > T − H or
| (7.3) |
Defectors are ESS if S + H < P or
| (7.4) |
Note that
We have two parameter regions when k > 2 (Fig 3):
I. If R + P > T + S then FD > FC. There are three possibilities: (i) if FD > FC > 0 then defectors dominate; (ii) if FD > 0 > FC then both cooperators and defectors are ESS; (iii) if 0 > FD > FC then cooperators dominate.
II. If R + P < T + S then FC > FD. Again there are three possibilities: (i) if 0 > FC > FD then cooperators dominate; (ii) if FC > 0 > FD then neither cooperators nor defectors are ESS; (iii) if FC > FD > 0 then defectors dominate.
In the degenerate case, R + P = T + S, we have FC = FD and therefore either cooperators or defectors dominate; neither bi-stability nor coexistence are possible. The same is true for graphs with k = 2 (Ohtsuki and Nowak 2006b).
8. Conclusion
We have studied five mechanisms for the evolution of cooperation. Each mechanism leads to a transformation of the Prisoner's Dilemma payoff matrix. From the transformed matrices, we have derived the fundamental condition for each mechanism to facilitate the evolution of cooperation. The transformed matrices can also be used to study evolutionary success in finite populations (Nowak 2006a,b).
Direct reciprocity can lead to evolution of cooperation if
| (8.1) |
The parameter w denotes the probability of playing another round in the repeated Prisoner's Dilemma game.
Indirect reciprocity can lead to evolution of cooperation if
| (8.2) |
The parameter q denotes the probability of knowing the reputation of the other person. It is a measure for the degree of social acquaintanceship in the population.
Kin selection can lead to evolution of cooperation if
| (8.3) |
The parameter r denotes the fraction of the payoff of the other person that is added to my payoff. It can be seen as a measure for genetic relatedness in the population. The notation ‘min{x, y}’ means to take the smaller value of either x or y. In our case, this notation is a simple way to cover the two cases R + P > T + S and R + P < T + S.
Group selection can lead to evolution of cooperation if
| (8.4) |
The parameters m and n denote respectively the number of groups and the group size.
Network reciprocity can lead to evolution of cooperation if
| (8.5) |
where
| (8.6) |
| (8.7) |
The parameter k is the degree of the regular graph.
For kin, group and graph selection, the original Prisoner's Dilemma matrix is tranformed into a new matrix
| (8.8) |
given by 5.1, 6.3, and 7.1, respectively. We note that for each of the transformed matrices, the sign of R′ + P′ − S′ − T′ is the same as the sign of R + P − S − T. Therefore, the sign of R + P − S − T determines which evolutionary outcomes are possible for the transformed payoff matrix. If R + P − T − S > 0, then cooperators and defectors cannot simultaneously be ESS in the transformed game. If R + P − T − S < 0, then cooperators and defectors cannot coexist in the transformed game. If R + P − T − S = 0, then either cooperators or defectors must dominate.
For direct and indirect reciprocity, conditional strategies are needed. In contrast, kin selection, group selection and network reciprocity can support the evolution of unconditional cooperators.
Our approach has certain limitations which should be discussed. We have studied particular models of kin selection, group selection and network reciprocity. For each mechanism, other models should be investigated and might lead to (slightly) different results. We wish to think, however, that we have chosen the simplest possible approaches and that our findings reflect the essence of each mechanism. Adding further complexity is always possible and sometimes useful.
We might not have discussed all possible mechanisms for the evolution of cooperation. For example, it is unclear at present if ‘green beards’ constitute an independent mechanism for the evolution of cooperation (Keller and Ross 1998; Riolo et al. 2001; Traulsen and Schuster 2003; Traulsen and Nowak 2007) or require a spatial setting ( = network reciprocity) (Jansen and van Baalen 2006). Active linking on graphs (Pacheco et al. 2006) is a powerful method to get cooperation, but can be viewed as a special form of direct reciprocity: cooperators have longer lasting interactions than defectors. Volunteering is the idea that individuals can choose to participate in a Prisoner's Dilemma or remain loners (Hauert et al. 2002). Volunteering leads to a relaxed social dilemma where some frequency of cooperation is (neutrally) stable even in well-mixed populations. Volunteering can also stabilize punishment (Fowler 2005; Brandt al. 2005; Hauert et al. 2007).
Punishment (Yamagishi 1986; Clutton-Brock and Parker 1995; Fehr and Gächter 2002; Sigmund et al. 2001; Camerer and Fehr 2006; Rockenbach and Milinski 2006), sometimes also called ‘strong reciprocity’ (Boyd et al. 2003; Bowles and Gintis 2004), is not a mechanism for the evolution of cooperation, but an extension of the basic game from two possible actions (cooperation and defection) to three (cooperation, defection and punishment). All models of punishment are either based on direct or indirect reciprocity: if I punish someone who has defected with me, I use direct reciprocity; if I punish someone who has defected with others, I use indirect reciprocity.
Indirect reciprocity is the key mechanism for understanding the evolution of any pro-social behavior in humans. Humans obviously take a keen interest in following social interactions between other people and make decisions based on what has happened between others. Indirect reciprocity provides the right selection pressure for both social intelligence and human language.
It is sometimes proposed that kin selection and group selection refer to the same mechanism for the evolution of cooperation (Dugatkin and Reeve 1994; Lehmann and Keller 2006; Ratnieks 2006; West et al. 2007; Lehmann et al. 2007). Although there could be overlap between the two mechanisms in some cases, we do not consider this to be a useful perspective, in general. For example, kin selection could lead to cooperation in well-mixed populations, if there is some form of kin recognition. Such a process has nothing in common with group selection. Vice versa, there can be group selection in the setting of cultural evolutionary dynamics, where the members of each group are not genetic relatives. It would be strange to call such a process ‘kin selection’. In our opinion, the term kin selection should refer exclusively to situations where an evolutionary game occurs between genetic relatives (as originally proposed by Maynard Smith, 1964).
Inclusive fitness theory has given rise to fairly general methods for calculating evolutionary dynamics (Grafen 1985, 2006; Taylor 1989; Frank 1998; Michod 1999; Rousset and Billiard 2000; Rousset 2004; Lehmann et al. 2007; Wild and Traulsen 2007). These methods can be used to derive certain aspects of direct reciprocity (Fletcher and Zwick 2006), group selection (Lehmann et al. 2007; Wild and Traulsen 2007) and network reciprocity (Taylor et al. 2007). But inclusive fitness itself is not a mechanism for the evolution of cooperation. Instead it is a method for calculating evolutionary dynamics. For example, inclusive fitness calculations can also be used to study the evolution of spiteful behavior (Hamilton 1970; Gardner and West 2004a,b). Wilson (2007) points out that inclusive fitness is only a ‘measure’ but gives no account of the selective forces that drive eusocial evolution. Similarly, the methods of evolutionary game theory can be used to analyze all aspects of the evolution of cooperation, but nobody would claim that evolutionary game theory itself is a mechanism for the evolution of cooperation.
In a recent paper, Lehmann et al (2007) have used inclusive fitness theory to rederive some results of the group selection model proposed by Traulsen and Nowak (2006). While it is always interesting to have different derivations for the same result, the conclusion of Lehman et al (2007) that group selection and kin selection are the same process does not follow from their work. Furthermore, Lehmann et al (2007) claim incorrectly that they have derived all results of Traulsen and Nowak (2006), which is not the case, because Lehmann et al (2007) only investigate the simplified Prisoner's Dilemma, while Traulsen and Nowak (2006) derive results for a general payoff matrix. This is an important difference, because Lehmann et al (2007) base their work on the approach of (Rousset and Billiard 2000), which is only valid for the degenerate case R + P = T + S, see (Wild and Traulsen 2007).
If one wishes to search for a unifying principle that applies to all five mechanisms for the evolution of cooperation, which are discussed here, then one can point to assortment. Each mechanism must achieve that cooperators are more likely to cooperate with each other than with defectors. Assortment can be reached by repeated interactions between two individuals (direct reciprocity), monitoring social interactions (indirect reciprocity), kin recognition (kin selection), competition between groups (group selection) or cluster formation (network reciprocity, graph selection). Assortment, however, is not a mechanism for evolution of cooperation, but the consequence of a mechanism. The crucial question is always how assortment is achieved.
In summary, we have presented five mechanisms for the evolution of cooperation. For each mechanism we derive a transformation of the Prisoner's Dilemma payoff matrix. The transformed matrices lead to five fundamental rules for the evolution of cooperation.
Figure 4. Each mechanism can be described by a transformation of the Prisoner's Dilemma payoff matrix.
The transformed matrices lead directly to the crucial conditions for the evolution of cooperation. Cooperation can evolve, if either cooperators are ESS or defectors are not ESS (that is whenever defectors do not dominate cooperators). For network reciprocity we have used the abbreviation H = [(k + 1)(R − P) − T + S]/[(k + 1)(k − 2)] where k > 2 is the degree of the graph (number of neighbors per individual).
Acknowledgments
We thank Arne Traulsen and the referees for their insightful comments and suggestions. Support from the John Templeton foundation and the NSF/NIH joint program in mathematical biology (NIH grant R01GM078986) is gratefully acknowledged. The Program for Evolutionary Dynamics at Harvard University is sponsored by Jeffrey Epstein.
Appendix A. The addition formula for group selection
In the limit of slow group division, most groups have size n and are homogeneous when they divide. Hence, the fixation probability ρC of a single cooperator is the product of the fixation probability within the group φC, and the fixation probability of the cooperator group ΦC (Traulsen and Nowak 2006).
Under the assumptions of weak selection (w ≪ 1), large group size n (n ≫ 1) and large number of groups m (m ≫ 1), we find that
| (A.1) |
Within a group, interacting individuals play the game given by matrix 6.1, and between groups, the game is described by matrix 6.2.
Therefore,
| (A.2) |
Equation A.2 is simply the fixation probability for weak selection of a single A player in a population of size mn engaged in the game
| (A.3) |
The constant factor 1/mn in the matrix A.3 only weakens the selection and has no effect on the sign of ρC − 1/(mn).
References
- Abramson G, Kuperman M. Social games in a social network. Phys Rev E. 2001;63:030901. doi: 10.1103/PhysRevE.63.030901. [DOI] [PubMed] [Google Scholar]
- Alexander R. The biology of moral systems. New York: Aldine De Gruyter; 1987. [Google Scholar]
- Axelrod R. The evolution of cooperation. Basic Books; New York: 1984. [Google Scholar]
- Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
- Binmore K. Fun and Games. Heath; Lexington, MA: 1991. [Google Scholar]
- Bolton GE, Katok E, Ockenfels A. Cooperation among strangers with limited information about reputation. J Public Econ. 2005;89:1457–1468. [Google Scholar]
- Boyd R, Richerson PJ. Group beneficial norms spread rapidly in a structured population. J Theor Biol. 2002;215:287–296. doi: 10.1006/jtbi.2001.2515. [DOI] [PubMed] [Google Scholar]
- Boyd R, Gintis H, Bowles S, Richerson PJ. The evolution of altruistic punishment. PNAS. 2003;100:3531–3535. doi: 10.1073/pnas.0630443100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowles S, Gintis H. The evolution of strong reciprocity: cooperation in heterogeneous populations. Theor Pop Biolo. 2004;65:17–28. doi: 10.1016/j.tpb.2003.07.001. [DOI] [PubMed] [Google Scholar]
- Bowles S. Group competition, reproductive leveling, and the evolution of human altruism. Science. 2006;314:1569–1572. doi: 10.1126/science.1134829. [DOI] [PubMed] [Google Scholar]
- Brandt H, Sigmund K. The logic of reprobation: assessment and action rules for indirect reciprocity. J Theor Biol. 2004;231:475–486. doi: 10.1016/j.jtbi.2004.06.032. [DOI] [PubMed] [Google Scholar]
- Brandt H, Sigmund K. Indirect reciprocity, image scoring, and moral hazard. PNAS. 2005;102:2666–2670. doi: 10.1073/pnas.0407370102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandt H, Hauert C, Sigmund K. PNAS. 2005;103:495–497. doi: 10.1073/pnas.0507229103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camerer CF, Fehr E. When does “Economic Man” dominate social behavior? Science. 2006;311:47–52. doi: 10.1126/science.1110600. [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza LL, Feldman MW. Darwinian selection and “altruism”. Theor Popul Biol. 1978;14(2):268–280. doi: 10.1016/0040-5809(78)90028-x. [DOI] [PubMed] [Google Scholar]
- Clutton-Brock TH, Parker G. Sexual coercion in animal societies. Anim Behav. 1995;49:1345–1365. [Google Scholar]
- Cressman R. Evolutionary Dynamics and Extensive Form Games. MIT Press; Cambridge. MA: 2003. [Google Scholar]
- Crow JF, Aoki K. Group selection for a polygenic behavioral trait: a different proliferation model. Proc Natl Acad Sci USA. 1982;79:2628–2631. doi: 10.1073/pnas.79.8.2628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dufwenberg M, Gneezy U, Güth W, van Damme E. Direct vs indirect reciprocity: an experiment. Homo Oecon. 2001;18:19–30. [Google Scholar]
- Dugatkin LA, Reeve HK. Behavioral ecology and levels of selection: dissolving the group selection controversy. In: Peter J, Slatter G, et al., editors. Advances in the Study of Behavior. Vol. 23. 1994. pp. 101–133. [Google Scholar]
- Durrett R, Levin S. The importance of being discrete (and spatial) Theor Pop Biol. 1994;46:363–394. [Google Scholar]
- Ebel H, Bornholdt S. Coevolutionary games on networks. Phys Rev E. 2002;66:056118. doi: 10.1103/PhysRevE.66.056118. [DOI] [PubMed] [Google Scholar]
- Engelmann D, Fischbacher U. Indirect reciprocity and strategic reputation building in an experimental helping game. Univ Zürich working paper no 132 2002 [Google Scholar]
- Fehr E, Gächter S. Cooperation and punishment in public goods experiments. Am Econ Rev. 2000;90:980–994. [Google Scholar]
- Fehr E, Gächter S. Altruistic punishment in humans. Nature. 2002;415:137–140. doi: 10.1038/415137a. [DOI] [PubMed] [Google Scholar]
- Fehr E, Fischbacher U, Gächter S. Strong reciprocity, human cooperation and the enforcement of social norms. Human Nature. 2002;13:1–25. doi: 10.1007/s12110-002-1012-7. [DOI] [PubMed] [Google Scholar]
- Fischbacher U, Gächter S, Fehr E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ Lett. 2001;71:397–404. [Google Scholar]
- Fishman MA, Lotem A, Stone L. Heterogeneity stabilises reciprocal altruism interaction. J Theor Biol. 2001;209:87–95. doi: 10.1006/jtbi.2000.2248. [DOI] [PubMed] [Google Scholar]
- Fishman MA. Indirect reciprocity among imperfect individuals. J Theor Biol. 2003;225:285–292. doi: 10.1016/s0022-5193(03)00246-7. [DOI] [PubMed] [Google Scholar]
- Fletcher JA, Zwick M. Strong altruism can evolve in randomly formed groups. J Theor Biol. 2004;228:303–313. doi: 10.1016/j.jtbi.2004.01.004. [DOI] [PubMed] [Google Scholar]
- Fletcher JA, Zwick M. Unifying the theories of inclusive fitness and reciprocal altruism. Am Nat. 2006;168:252–262. doi: 10.1086/506529. [DOI] [PubMed] [Google Scholar]
- Foster KR, Wenseleers T, Ratnieks FLW. Kin selection is the key to altruism. Trends in Ecology and Evolution. 2006;21:57–60. doi: 10.1016/j.tree.2005.11.020. [DOI] [PubMed] [Google Scholar]
- Fowler JH. Altruistic punishment and the origin of cooperation. PNAS. 2005;102:7047–7049. doi: 10.1073/pnas.0500938102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank SA. Foundations of Social Evolution. Princeton University Press; Princeton. NJ: 1998. [Google Scholar]
- Fudenberg D, Maskin E. Folk Theorem for repeated games with discounting or with incomplete information. Econometrica. 1986;54:533–554. [Google Scholar]
- Fudenberg D, Maskin E. Evolution and Cooperation in Noisy Repeated Games. Am Econ Rev. 1990;80:274–279. [Google Scholar]
- Fudenberg D, Tirole J. Game Theory. MIT Press; Cambridge. MA: 1991. [Google Scholar]
- Gardner A, West SA. Spite and the scale of competition. J of Evol Biol. 2004a;17:1195–1203. doi: 10.1111/j.1420-9101.2004.00775.x. [DOI] [PubMed] [Google Scholar]
- Gardner A, West SA. Spite among siblings. Science. 2004b;305:1413–1414. doi: 10.1126/science.1103635. [DOI] [PubMed] [Google Scholar]
- Gintis H. Game Theory Evolving. Princeton Univ Press; Princeton. NJ: 2000. [Google Scholar]
- Grafen A. The hawk-dove game played between relatives. Anim Behav. 1979;27:905–907. [Google Scholar]
- Grafen A. A geometric view of relatedness. Oxford Surveys Evol Biol. 1985;2:28–89. [Google Scholar]
- Grafen A. Various remarks on Lehmann and Keller's article. J Evol Biol. 2006;19(5):1397–1399. doi: 10.1111/j.1420-9101.2006.01161.x. [DOI] [PubMed] [Google Scholar]
- Griffin AS, West SA. Kin selection: fact and fiction. Trends in Ecology and Evolution. 2002;17:15–21. [Google Scholar]
- Griffin AS, West SA. Kin discrimination and the benefit of helping in cooperatively breeding vertebrates. Science. 2003;302:634–636. doi: 10.1126/science.1089402. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. The genetical evolution of social behaviour. J Theor Biol. 1964;7:1–16. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. Extraordinary sex ratios. Science. 1967;156:477–488. doi: 10.1126/science.156.3774.477. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. Selfish and spiteful behavior in an evolutionary model. Nature. 1970;228:1218–1220. doi: 10.1038/2281218a0. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. Narrow Roads of Gene Land: I Evolution of Social Behaviour. W.H. Freeman; Oxford: 1996. [Google Scholar]
- Harpending H, Rogers A. On Wright's mechanism for intergroup selection. J Theor Biol. 1987;127:51–61. doi: 10.1016/s0022-5193(87)80160-1. [DOI] [PubMed] [Google Scholar]
- Harvey PH, Partridge L, Nunney L. Group selection and the sex ratio. Nature. 1985;313:10–11. [Google Scholar]
- Hassell MP, Comins HN, May RM. Species coexistence and self-organizing spatial dynamics. Nature. 1994;370:290–292. [Google Scholar]
- Hauert C, De Monte S, Hofbauer J, Sigmund K. Volunteering as Red Queen mechanism for cooperation in Public Goods Game. Science. 2002;296:1129–1132. doi: 10.1126/science.1070582. [DOI] [PubMed] [Google Scholar]
- Hauert C, Doebeli M. Spatial structure often inhibits the evolution of cooperation in the Snowdrift game. Nature. 2004;428:643–646. doi: 10.1038/nature02360. [DOI] [PubMed] [Google Scholar]
- Hauert C, Michor F, Nowak MA, Doebeli M. Synergy and discounting of cooperation in social dilemmas. J Theor Biol. 2006;239:195–202. doi: 10.1016/j.jtbi.2005.08.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauert C, Traulsen A, Brandt H, Nowak MA, Sigmund K. Via freedom to coercion: the emergence of costly punishment. Science. 2007 doi: 10.1126/science.1141588. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herz AVM. Collective phenomena in spatially extended evolutionary games. J Theor Biol. 1994;169:65–87. doi: 10.1006/jtbi.1994.1130. [DOI] [PubMed] [Google Scholar]
- Hofbauer J, Schuster P, Sigmund K. A note on evolutionary stable strategies and game dynamics. J Theor Biol. 1979;81:609–612. doi: 10.1016/0022-5193(79)90058-4. [DOI] [PubMed] [Google Scholar]
- Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge University Press; Cambridge. UK: 1998. [Google Scholar]
- Hofbauer J, Sigmund K. Evolutionary Game Dynamics. Bull Am Math Soc. 2003;40:479–519. [Google Scholar]
- Imhof LA, Fudenberg D, Nowak MA. Evolutionary cycles of cooperation and defection. P Natl Acad Sci USA. 2005;102:10797–10800. doi: 10.1073/pnas.0502589102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen VAA, van Baalen M. Altruism through beard chromodynamics. Nature. 2006;440:663–666. doi: 10.1038/nature04387. [DOI] [PubMed] [Google Scholar]
- Keller L, Ross KG. Selfish genes: a green beard in the red fire ant. Nature. 1998;394:573–575. [Google Scholar]
- Kerr B, Godfrey-Smith P. Individualist and multi-level perspectives on selection in structured populations. Biol Philos. 2002;17:477–517. [Google Scholar]
- Killingback T, Bieri J, Flatt T. Evolution in group-structured populations can resolve the tragedy of the commons. Proc R Soc B. 2006;273:1477–1481. doi: 10.1098/rspb.2006.3476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraines D, Kraines V. Pavlov and the prisoner's dilemma. Theory and Decision. 1989;26:47–49. [Google Scholar]
- Lehmann L, Keller L. The evolution of cooperation and altruism. A general framework and classification of models. J Evol Biol. 2006;19:1365–1725. doi: 10.1111/j.1420-9101.2006.01119.x. [DOI] [PubMed] [Google Scholar]
- Lehmann L, Keller L, West S, Roze D. Group selection and kin selection: two concepts but one process. PNAS. 2007;104:6736–6739. doi: 10.1073/pnas.0700662104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leigh EG. When does the good of the group override the advantage of the individual? Proc Natl Acad Sci USA. 1983;80:2985–2989. doi: 10.1073/pnas.80.10.2985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leimar O, Hammerstein P. Evolution of cooperation through indirect reciprocity. Proc R Soc Lond B. 2001;268:745–753. doi: 10.1098/rspb.2000.1573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman E, Hauertand C, Nowak MA. Evolutionary dynamics on graphs. Nature. 2005;433:312–316. doi: 10.1038/nature03204. [DOI] [PubMed] [Google Scholar]
- Lotem A, Fishman MA, Stone L. Evolution of cooperation between individuals. Nature. 1999;400:226–227. doi: 10.1038/22247. [DOI] [PubMed] [Google Scholar]
- May RM. More evolution of cooperation. Nature. 1987;327:15–17. [Google Scholar]
- May RM. Network structure and the biology of populations. Trends in Ecol & Evol. 2006;21:394–399. doi: 10.1016/j.tree.2006.03.013. [DOI] [PubMed] [Google Scholar]
- Maynard Smith J. Group selection and kin selection. Nature. 1964;200:1145–1147. [Google Scholar]
- Marynard Smith J, Price GR. The logic of animal conflict. Nature. 1973;264:15–18. [Google Scholar]
- Maynard Smith J. Group selection. Quart Rev Biol. 1976;51:277–283. [Google Scholar]
- Maynard Smith J. Evolution and the Theory of Games. Cambridge University Press; Cambridge. UK: 1982. [Google Scholar]
- Michod RE. Darwinian Dynamics. Princeton Univ. Press; Princeton. NJ: 1999. [Google Scholar]
- Milinski M. A predator's costs of overcoming the confusion-effect of swarming prey. Animal Behav. 1984;32:1157–1162. [Google Scholar]
- Milinski M, Semmann D, Krambeck HJ. Reputation helps solve the ‘tragedy of the commons’. Nature. 2002;415:424–426. doi: 10.1038/415424a. [DOI] [PubMed] [Google Scholar]
- Milinski M, Semmann D, Krambeck HJ, Marotzke J. Stabilizing the Earth's climate is not a losing game: Supporting evidence from public goods experiments. PNAS. 2006;103:3994–3998. doi: 10.1073/pnas.0504902103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molander P. The optimal level of generosity in a selfish, uncertain environment. Journal of Conflict Resolution. 1985;29:611–618. [Google Scholar]
- Nakamaru M, Matsuda H, Iwasa Y. The evolution of cooperation in a lattice-structure population. J Theor Biol. 1997;184:65–81. doi: 10.1006/jtbi.1996.0243. [DOI] [PubMed] [Google Scholar]
- Nakamaru M, Nogami H, Iwasa Y. Score-dependent fertility model for the evolution of cooperation in a lattice. J Theor Biol. 1998;194:101–124. doi: 10.1006/jtbi.1998.0750. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Sigmund K. The evolution of stochastic strategies in the prisoner's dilemma. Acta Appl Math. 1990;20:247–265. [Google Scholar]
- Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. [Google Scholar]
- Nowak MA, Sigmund K. Tit for Tat in heterogenous populations. Nature. 1992;355:250–253. [Google Scholar]
- Nowak MA, Sigmund K. A strategy of win-stay, lose-shift that outperforms tit for tat in Prisoner's Dilemma. Nature. 1993;364:56–58. doi: 10.1038/364056a0. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Sigmund K. The alternating Prisoner's Dilemma. J Theor Biol. 1994;168:219–226. [Google Scholar]
- Nowak MA, Sigmund K. Evolution of indirect reciprocity by image scoring. Nature. 1998a;393:573–577. doi: 10.1038/31225. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Sigmund K. The dynamics of indirect reciprocity. J Theor Biol. 1998b;194:561–574. doi: 10.1006/jtbi.1998.0775. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Sigmund K. Evolutionary dynamics of biological games. Science. 2004;303:793–799. doi: 10.1126/science.1093411. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Sigmund K. Evolution of indirect reciprocity. Nature. 2005;437:1291–1298. doi: 10.1038/nature04131. [DOI] [PubMed] [Google Scholar]
- Nowak MA. Evolutionary Dynamics. Harvard Univ. Press; Cambridge. MA: 2006a. [Google Scholar]
- Nowak MA. Five rules for the evolution of cooperation. Science. 2006b;314:1560–1563. doi: 10.1126/science.1133755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunney L. Group selection, altruism, and structure-deme models. Am Nat. 1985;126:212–230. [Google Scholar]
- Ohtsuki H, Iwasa Y. How should we define goodness? Reputation dynamics in indirect reciprocity. J Theor Biol. 2004;231:107–120. doi: 10.1016/j.jtbi.2004.06.005. [DOI] [PubMed] [Google Scholar]
- Ohtsuki H, Iwasa Y. The leading eight: social norms that can maintain cooperation by indirect reciprocity. J Theor Biol. 2006;239:435–444. doi: 10.1016/j.jtbi.2005.08.008. [DOI] [PubMed] [Google Scholar]
- Ohtsuki H, Hauert C, Lieberman E, Nowak MA. A simple rule for the evolution of cooperation on graphs and social networks. Nature. 2006;441:502–505. doi: 10.1038/nature04605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsuki H, Nowak MA. The replicator equation on graphs. J Theor Biol. 2006a;243:86–97. doi: 10.1016/j.jtbi.2006.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsuki H, Nowak MA. Evolutionary games on cycles. Proc R Soc B. 2006b;273:2249–2256. doi: 10.1098/rspb.2006.3576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsuki H, Iwasa Y. Global analyses of evolutionary dynamics and exhaustive search for social norms that maintain cooperation by reputation. J theor Biol. 2007;244:518–531. doi: 10.1016/j.jtbi.2006.08.018. [DOI] [PubMed] [Google Scholar]
- Ohtsuki H, Pacheco J, Nowak MA. Evolutionary graph theory: breaking the symmetry between interaction and replacement. J Theor Biol. 2007 doi: 10.1016/j.jtbi.2007.01.024. Submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pacheco JM, Traulsen A, Nowak MA. Active linking in evolutionary games. J Theor Biol. 2006;243:437–443. doi: 10.1016/j.jtbi.2006.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panchanathan K, Boyd R. A tale of two defectors: the importance of standing for evolution of indirect reciprocity. J Theor Biol. 2003;224:115–126. doi: 10.1016/s0022-5193(03)00154-1. [DOI] [PubMed] [Google Scholar]
- Panchanathan K, Boyd R. Indirect reciprocity can stabilize cooperation without the second-order free rider problem. Nature. 2004;432:499–502. doi: 10.1038/nature02978. [DOI] [PubMed] [Google Scholar]
- Paulsson J. Multileveled selection on plasmid replication. Genetics. 2002;161:1373–1384. doi: 10.1093/genetics/161.4.1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price GR. Selection and covariance. Nature. 1970;227:520–521. doi: 10.1038/227520a0. [DOI] [PubMed] [Google Scholar]
- Queller DC. Kinship, reciprocity and synergism in the evolution of social behaviour. Nature. 1985;318:366–367. [Google Scholar]
- Queller DC. A General Model for Kin Selection. Evolution. 1992;46:376–380. doi: 10.1111/j.1558-5646.1992.tb02045.x. [DOI] [PubMed] [Google Scholar]
- Rand DA, Wilson HB. Using spatio-temporal chaos and intermediate-scale determinism to quantify spatially extended ecosystems. Proceedings: Biol Sciences. 1995;259:111–117. [Google Scholar]
- Rapoport A, Chammah AM. Prisoner's dilemma: a study in conflict and cooperation. Univ. of Mich. Press; Ann Arbor. MI: 1965. [Google Scholar]
- Ratnieks FLW. The evolution of cooperation and altruism: the basic conditions are simple and well known. J Evol Biol. 2006;19:1413–1414. doi: 10.1111/j.1420-9101.2006.01172.x. [DOI] [PubMed] [Google Scholar]
- Riolo R, Cohen MD, Axelrod R. Evolution of cooperation with reciprocity. Nature. 2001;414:441–443. doi: 10.1038/35106555. [DOI] [PubMed] [Google Scholar]
- Rockenbach B, Milinski M. The efficient interaction of indirect reciprocity and costly punishment. Nature. 2006;444:718–723. doi: 10.1038/nature05229. [DOI] [PubMed] [Google Scholar]
- Rousset F. Genetic Structure and Selection in Subdivided Populations. Princeton Univ. Press; Princeton. NJ: 2004. [Google Scholar]
- Rousset F, Billiard S. A theoretical basis for measures of kin selection in subdivided populations: finite populations and localized dispersal. J Evol Biol. 2000;13:814–825. [Google Scholar]
- Samuelson L. Evolutionary Games and Equilibrium Selection. MIT Press; Cambridge. MA: 1997. [Google Scholar]
- Santos FC, Pacheco JM. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys Rev Lett. 2005;95:098104. doi: 10.1103/PhysRevLett.95.098104. [DOI] [PubMed] [Google Scholar]
- Santos FC, Pacheco JM, Lenaerts T. Cooperation prevails when indviduals adjust their social ties. PLoS Comput Biol. 2006;2:1284–1291. doi: 10.1371/journal.pcbi.0020140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigmund K, Hauert C, Nowak MA. Reward and punishment. PNAS. 2001;98:10757–10762. doi: 10.1073/pnas.161155698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skyrms B, Pemantle R. A dynamic model of social network formation. Proc Natl Acad Sci USA. 2000;97:9340–9346. doi: 10.1073/pnas.97.16.9340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M, Wade MJ. Group selection on a quantitative character. PRoc Natl Acad Sci USA. 1978;75:3531–3534. doi: 10.1073/pnas.75.7.3531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szabó G, Vukov J, Szolnoki A. Phase diagrams for an evolutionary prisoner's dilemma game on two-dimensional lattices. Phys Rev E. 2005;72:047107. doi: 10.1103/PhysRevE.72.047107. [DOI] [PubMed] [Google Scholar]
- Szathmáry E, Demeter L. Group selection of early replictors and the origin of life. J Theor Biol. 1987;128:463–486. doi: 10.1016/s0022-5193(87)80191-1. [DOI] [PubMed] [Google Scholar]
- Takahashi N, Mashima R. Working paper series No 29. Center for the study of cultural and ecological foundations of the mind, Hokkaido University; Japan: 2003. The emergence of indirect reciprocity: is the standing strategy the answer? [Google Scholar]
- Taylor PD, Jonker LB. Evolutionarily stable strategies and game dynamics. Math Bio Sci. 1978;40:145–156. [Google Scholar]
- Taylor PD. Evolutionary stability in one-parameter models under weak selection. Theoretical Population Biology. 1989;36:125–43. [Google Scholar]
- Taylor PD. Inclusive fitness arguments in genetic models of behaviour. J Math Biol. 1996;34:654–674. doi: 10.1007/BF02409753. [DOI] [PubMed] [Google Scholar]
- Taylor PD, Frank S. How to make a kin selection model. J Theor Biol. 1996;180:27–37. doi: 10.1006/jtbi.1996.0075. [DOI] [PubMed] [Google Scholar]
- Taylor PD, Wild G, Gardner A. Direct fitness or inclusive fitness: how should we model kin selection. J Evol Biol. 2007;20:296–304. doi: 10.1111/j.1420-9101.2006.01196.x. [DOI] [PubMed] [Google Scholar]
- Traulsen A, Schuster HG. Minimal model for tag-based cooperation. Phys Rev E. 2003;68:046129. doi: 10.1103/PhysRevE.68.046129. [DOI] [PubMed] [Google Scholar]
- Traulsen A, Sengupta AM, Nowak MA. Stochastic evolutionary dynamics on two levels. J Theor Biol. 2005;235:393–401. doi: 10.1016/j.jtbi.2005.01.019. [DOI] [PubMed] [Google Scholar]
- Traulsen A, Nowak MA. Evolution of cooperation by multilevel selection. PNAS. 2006;103:10952–10955. doi: 10.1073/pnas.0602530103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traulsen A, Nowak MA. Chromodynamics of cooperation in finite populations. PLoS One. 2007;2:e270. doi: 10.1371/journal.pone.0000270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trivers R. The evolution of reciprocal altruism. Q Rev Biol. 1971;46:35–37. [Google Scholar]
- Trivers R. Social Evolution. Benjamin/Cummings; Menlo Park. CA: 1985. [Google Scholar]
- Uyenoyama MK, Feldman MW. Theories of kin and group selection: a population genetic perspective. Theor Pop Biol. 1980;17:380–414. doi: 10.1016/0040-5809(80)90033-7. [DOI] [PubMed] [Google Scholar]
- Vukov J, Szabó G. Evolutionary prisoner's dilemma game on hierarchical lattices. Phys Rev E. 2005;71:036133. doi: 10.1103/PhysRevE.71.036133. [DOI] [PubMed] [Google Scholar]
- Vukov J, Szabó G, Szolnoki A. Evolutionary prisoner's dilemma game on hierarchical lattices. Cooperation in the noisy case: Prisoner's dilemma game on two types of regular random graphs. Phys Rev E. 2006;74:067103. doi: 10.1103/PhysRevE.73.067103. [DOI] [PubMed] [Google Scholar]
- Wedekind C, Milinski M. Cooperation through image scoring in humans. Science. 2000;288:850–852. doi: 10.1126/science.288.5467.850. [DOI] [PubMed] [Google Scholar]
- Wedekind C, Braithwaite VA. The long-term benefits of human generosity in indirect reciprocity. Curr Biol. 2002;12:1012–1015. doi: 10.1016/s0960-9822(02)00890-4. [DOI] [PubMed] [Google Scholar]
- Weibull J. Evolutionary Game Theory. MIT Press; Cambridge. MA: 1995. [Google Scholar]
- West SA, Pen I, Griffin A. Cooperation and competition between relatives. Science. 2006;296:72–75. doi: 10.1126/science.1065507. [DOI] [PubMed] [Google Scholar]
- West SA, Griffin AS, Gardner A. Social semantics: altruism, cooperation, mutualism, strong reciprocity and group selection. J Evol Biol. 2007 doi: 10.1111/j.1420-9101.2006.01258.x. In press. [DOI] [PubMed] [Google Scholar]
- Wild G, Taylor P. A kin-selection approach to the resolution of sex-ratio conflict between mates. J theor Biol. 2004;236:126–136. doi: 10.1016/j.jtbi.2005.03.003. [DOI] [PubMed] [Google Scholar]
- Wild G, Traulsen A. The different limits of weak selection and the evolutionary dynamics of finite populations. J Theor Biol. 2007 doi: 10.1016/j.jtbi.2007.03.015. To appear in. [DOI] [PubMed] [Google Scholar]
- Williams GC. Adaption and Natural Selection: a Critique of Some Current Evolutionary Thought. Princeton Univ. Press; Princeton. NJ: 1966. [Google Scholar]
- Wilson DS. A theory of group selection. Proc Nat Acad Sci USA. 1975;72:143–146. doi: 10.1073/pnas.72.1.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson DS. The group selection controversy and current status. Annu Rev Ecol Syst. 1983;14:159–187. [Google Scholar]
- Wilson EO. Sociobiology: The new synthesis. Harvard Univ. Press; Cambridge. MA: 1975. [Google Scholar]
- Wilson EO. What drives eusocial evolution? 2007. In press. [Google Scholar]
- Wilson EO, Hölldobler B. The Ants. Harvard Univ. Press; Cambridge. MA: 1990. [Google Scholar]
- Wilson EO, Hölldobler B. Eusociality: origin and consequences. Proc Natl Acad Sci USA. 2005;102:13367–13371. doi: 10.1073/pnas.0505858102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z, Xu X, Huang Z, Wang S, Wang Y. Evolutionary prisoner's dilemma game with dynamic preferential selection. Phys Rev E. 2006;74:021107. doi: 10.1103/PhysRevE.74.021107. [DOI] [PubMed] [Google Scholar]
- Wynne-Edwards VC. Animal Dispersion in Relation to Social Behavior. Oliver and Boyd; Edinburgh: 1962. [Google Scholar]
- Yamagish T. The provision of a sanctioning system as a Public Good. J of Personality and Social Psychology. 1986;51:110–116. [Google Scholar]
- Zeeman EC. Population dynamics from game theory. In: Nitecki A, Robinson C, editors. Proceedings of an International Conference on Global Theory of Dynamics Systems. Lect Notes in Math 819; Berlin: Springer; 1980. [Google Scholar]